 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Логарифмические уравнения 13 задание.
В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.
Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант2018)
а) Решите уравнение cos2x = 1-cos(п/2-x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-5п/2;-п].
Алгоритм решения:
- t
- Делаем обратную замену и решаем простейшие тригонометрические уравнения.
- Строим числовую ось.
- Наносим на нее корни.
- Отмечаем концы отрезка.
- Выбираем те значения, которые лежат внутри промежутка.
- Записываем ответ.
Решение:
1.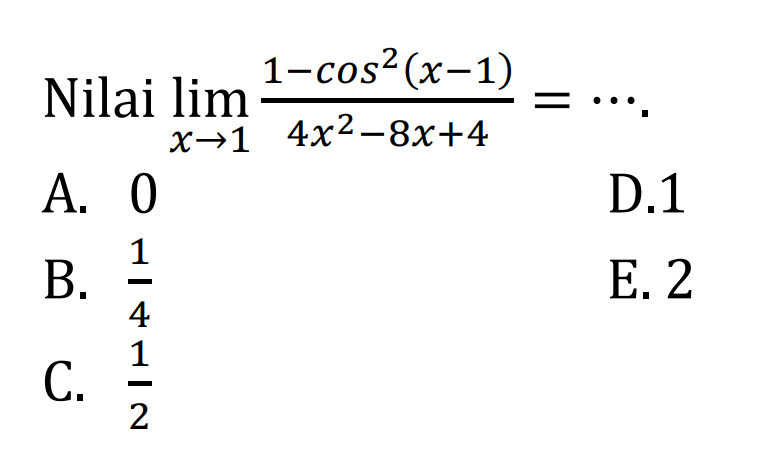 Преобразуем правую часть равенства, используя формулу приведения cos(π/ 2−x )=sinx . Имеем:
Преобразуем правую часть равенства, используя формулу приведения cos(π/ 2−x )=sinx . Имеем:
сos2x = 1 – sin x .
Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:
cos(2х)=1−2sin 2 х
Получаем такое уравнение: 1−sin 2 x =1− sinx
Теперь в уравнении присутствует только одна тригонометрическая функция sinx .
2. Вводим замену: t = sinx . Решаем получившееся квадратное уравнение:
1−2t 2 =1−t,
−2t 2 +t =0,
t (−2t +1)=0,
t = 0 или -2t + 1 = 0 ,
t 1 = 0 t 2 = 1/2.
3. Делаем обратную замену:
sin x = 0 или sin x = ½
Решаем эти уравнения:
sin x =0↔x =πn, nЄZ
sin(x )=1/2↔x = (-1) n ∙(π/6) + πn, nЄZ .
Следовательно, получаем два семейства решений.
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).
3. Красным цветом помечаем концы промежутка.
4. В указанном промежутке расположены три корня что три корня: −2π ;−11π/ 6 и −7π/ 6.
а) πn, nЄZ; (-1) n ∙(π/6) + πn, nЄZ
б) −2π ;−11π 6;−7π 6
Второй вариант задания (из Ященко, №1)
Алгоритм решения:
- Заменяем эту функцию переменной
- Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.
- Строим координатную плоскость и окружность единичного радиуса на ней.
- Отмечаем точки, являющиеся концами отрезка.
- Выбираем те значения, которые лежат внутри отрезка.
- Записываем ответ.
Решение:
1. Вводим замену t = 4 cos х. тогда уравнение примет вид:
Вводим замену t = 4 cos х. тогда уравнение примет вид:
Решаем квадратное уравнение с помощью формул дискриминанта и корней:
D=b 2 – c = 81 – 4∙4∙2 =49,
t 1 = (9 – 7)/8= ¼, t 2 = (9+7)/8=2.
3. Возвращаемся к переменной х:
1. Строим координатную плоскость и окружность единичного радиуса на ней.
2. Отмечаем точки, являющиеся концами отрезка.
3. Выбираем те значения, которые лежат внутри отрезка..
Это корни . Их два.
а)
б)
Третий вариант задания (из Ященко, № 6)
Алгоритм решения:
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.
- Решаем неравенства для каждого случая.
- Записываем ответ.
Решение:
1. По формулам приведения .
По формулам приведения .
2. Тогда данное уравнение примет вид:
3. Вводим замену . Получаем:
Решаем обычное квадратное уравнение с помощью формул дискриминанта и корней:
Главная
Уметь решать показательные и логарифмические уравнения очень важно для успешной сдачи единого государственного экзамена по математике профильного уровня. Важно
Во-первых , задание № 13 варианта КИМ ЕГЭ пусть нечасто, но все же иногда представляет собой именно такое уравнение, которое нужно не просто решить, но и (аналогично заданию по тригонометрии) выбрать корни уравнения, удовлетворяющие какому-либо условию.
Так, один из вариантов 2017 года включал следующее задание:
а) Решите уравнение 8 x – 7 . 4 x – 2 x +4 + 112 = 0.
б) Укажите корни этого уравнения, принадлежащие отрезку .
Ответ: а) 2; log 2 7 и б) log 2 7.В другом варианте было такое задание:
а) Решите уравнение 6log 8 2 x – 5log 8 x + 1 = 0
б) Найдите все корни этого уравнения, принадлежащие отрезку .
Ответ: а) 2 и 2√2 ; б) 2.Встречалось и такое:
а) Решите уравнение 2log 3 2 (2cos x ) – 5log 3 (2cos x ) + 2 = 0.
б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 5π/2].
Ответ: а) {π/6 + 2πk; -π/6 + 2πk, k∊Z} и б) 11π/6; 13π/6.Во-вторых , изучение методов решения показательных и логарифмических уравнений является хорошей , так как в основных методах решения и уравнений, и неравенств фактически используются одни и те же математические идеи.
Основные методы решения показательных и логарифмических уравнений несложно запомнить, их всего пять: сведение к простейшему уравнению, использование равносильных переходов, введение новых неизвестных, логарифмирование и разложение на множители.
Отдельно стоит метод использования свойств показательной, логарифмической и других функций при решении задач: иногда ключом к решению уравнения является область определения, область значений, неотрицательность, ограниченность, четность входящих в него функций.
Как правило, в задаче № 13 встречаются уравнения, требующие применения перечисленных выше пяти основных методов. Каждый из этих методов имеет свои особенности, которые необходимо знать, так как именно их незнание приводит к ошибкам при решении задач.
Какие типичные ошибки совершают экзаменуемые?
Нередко при решении уравнений, содержащих показательно-степенную функцию, школьники забывают рассмотреть один из случаев выполнения равенства. Как известно, уравнения такого вида равносильны совокупности двух систем условий (см. ниже), речь идет о случае, когда a(x ) = 1
Данная ошибка связана с тем, что решая уравнение экзаменуемый формально использует определение показательной функции (y = ax , a>0, a ≠ 1): при а ≤ 0 показательная функция действительно не определена,
А вот при а = 1 определена, но не является показательной, так как единица в любой действительной степени тождественно равна самой себе.
А значит если в рассматриваемом уравнении при а (x ) = 1 возникает верное числовое равенство, то соответствующие значения переменной будут корнями уравнения.Еще одна ошибка – применение свойств логарифмов без учета области допустимых значений. Например, хорошо знакомое многим свойство «логарифм произведения равен сумме логарифмов», оказывается, имеет обобщение:
log a (f (x )g (x )) = log a │f (x )│ + log a │g(x )│, при f (x )g (x ) > 0, a > 0, a ≠ 1Действительно, для того, чтобы было определено выражение в левой части этого равенства, достаточно, чтобы произведение функций f и g было положительным, но сами функции при этом могут быть как одновременно больше, так и одновременно меньше нуля, поэтому при применении данного свойства необходимо использовать понятие модуля.
И таких примеров можно привести немало.
Поэтому для эффективного освоения методов решения показательных и логарифмических уравнений лучше всего воспользоваться услугами , который сумеет рассказать о подобных «подводных камнях» на примерах решения соответствующих экзаменационных задач.
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно .
Вы можете:Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 13 в экзамене ЕГЭ, задачи на логарифмы, ким ЕГЭ 2017, подготовка к ЕГЭ профиль математика, Математика профиль, решение уравнений и логарифмов, решение задач на показательные уравнения ЕГЭ, вычисление свойств логарифмов, показательно-степенная функция, задачи по математике профильного уровня, применение свойств логарифмов, решение задач на корни, задачи ЕГЭ 2017 по показательным уравнениям, подготовка к егэ выпускникам 11 класса в 2018 году, поступающим в технический вуз.
Задание №13 ЕГЭ по математике профильного уровня ⋆ СПАДИЛО
В 13 задании профильного уровня ЕГЭ по математике необходимо решить уравнение, но уже повышенного уровня сложности, так как с 13 задания начинаются задания бывшего уровня С, и данное задание можно назвать С1. Перейдем к рассмотрению примеров типовых заданий.
Разбор типовых вариантов заданий №13 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант2018)
[su_note note_color=”#defae6″] а) Решите уравнение cos2x = 1-cos(п/2-x) б) Найдите все корни этого уравнения, принадлежащие промежутку [-5п/2;-п]. [/su_note]
Алгоритм решения:
Пункт а)
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие тригонометрические уравнения.

Пункт б)
- Строим числовую ось.
- Наносим на нее корни.
- Отмечаем концы отрезка.
- Выбираем те значения, которые лежат внутри промежутка.
- Записываем ответ.
Решение:
Пункт а) 1. Преобразуем правую часть равенства, используя формулу приведения cos(π/2−x)=sinx. Имеем:
сos2x = 1 – sin x.
Преобразуем левую часть уравнения, используя формулу косинуса двойного аргумента, с использованием синуса:
cos(2х)=1−2sin2 х
Получаем такое уравнение: 1−sin 2x=1− sinx Теперь в уравнении присутствует только одна тригонометрическая функция sinx. 2. Вводим замену: t = sinx. Решаем получившееся квадратное уравнение:
1−2t2=1−t,
−2t2+t=0,
t (−2t+1)=0,
t = 0 или -2t + 1 = 0,
t1 = 0 t2 = 1/2.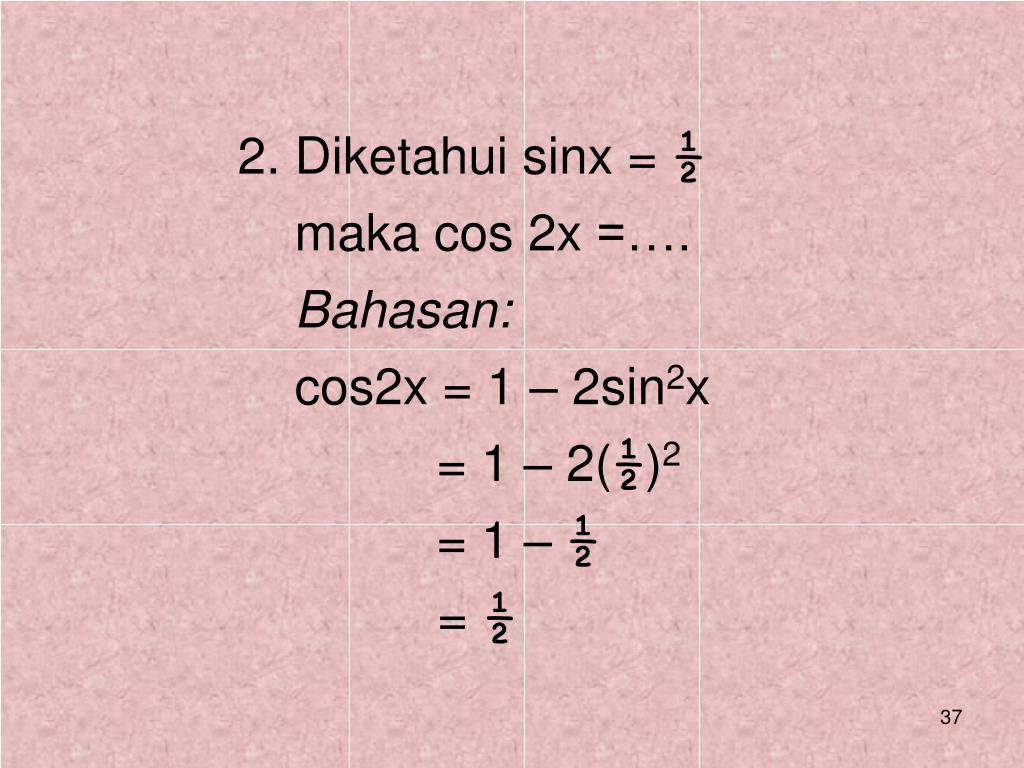
3. Делаем обратную замену:
sin x = 0 или sin x = ½
Решаем эти уравнения:
sin x =0↔x=πn, nЄZ
sin(x)=1/2↔x= (-1)n∙(π/6)+ πn, nЄZ.
Следовательно, получаем два семейства решений. Пункт б):
1. В предыдущем пункте получено два семейства, в каждом из которых бесконечно много решений. Необходимо выяснить, какие из них, находятся в заданном промежутке. Для этого строим числовую прямую.
2. Наносим на нее корни обоих семейств, пометив их зеленым цветом (первого) и синим (второго).
3. Красным цветом помечаем концы промежутка. 4. В указанном промежутке расположены три корня что три корня: −2π;−11π/6 и −7π/6. Ответ: а) πn, nЄZ; (-1)n∙(π/6)+ πn, nЄZ б) −2π;−11π6;−7π6
Второй вариант задания (из Ященко, №1)
[su_note note_color=”#defae6″]
а) Решите уравнение .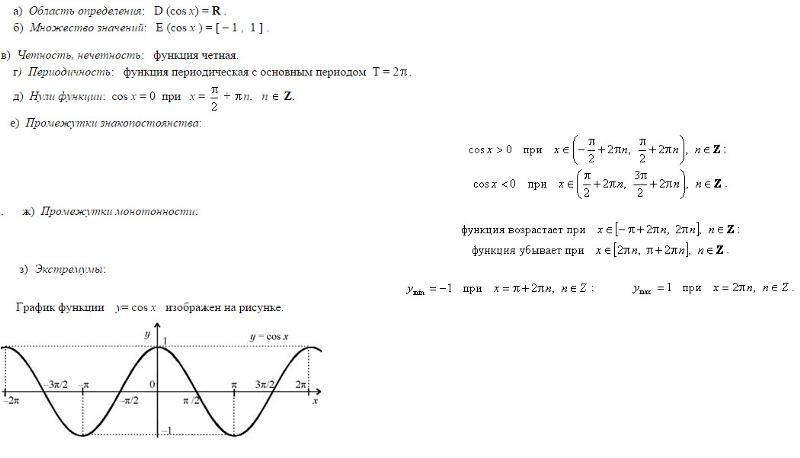 б) Найдите все корни этого уравнения, принадлежащие отрезку .
[/su_note]
б) Найдите все корни этого уравнения, принадлежащие отрезку .
[/su_note]
Алгоритм решения:
Пункт а)
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, потом тригонометрические уравнения.
Пункт б)
- Строим координатную плоскость и окружность единичного радиуса на ней.
- Отмечаем точки, являющиеся концами отрезка.
- Выбираем те значения, которые лежат внутри отрезка.
- Записываем ответ.
Решение:
Пункт а) 1. Вводим замену t = 4cos х. тогда уравнение примет вид: Решаем квадратное уравнение с помощью формул дискриминанта и корней:
D=b2 – c = 81 – 4∙4∙2 =49,
t1= (9 – 7)/8= ¼, t2 = (9+7)/8=2.
3. Возвращаемся к переменной х: Пункт б)
1. Строим координатную плоскость и окружность единичного радиуса на ней.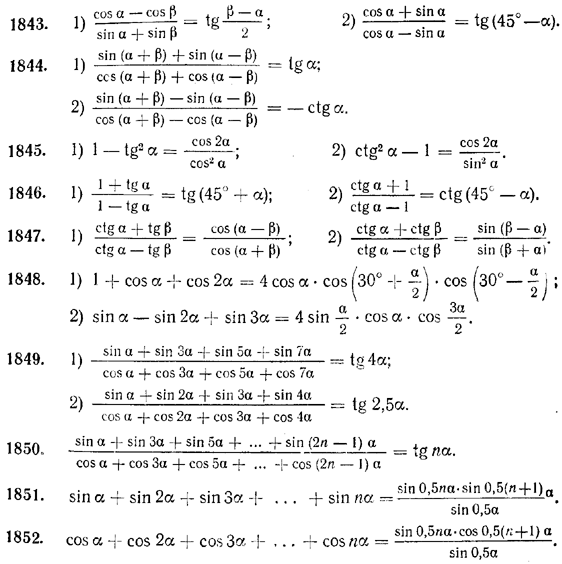 2. Отмечаем точки, являющиеся концами отрезка.
3. Выбираем те значения, которые лежат внутри отрезка.. Это корни . Их два.
Ответ:
а)
б)
2. Отмечаем точки, являющиеся концами отрезка.
3. Выбираем те значения, которые лежат внутри отрезка.. Это корни . Их два.
Ответ:
а)
б)
Третий вариант задания (из Ященко, № 6)
[su_note note_color=”#defae6″] а) Решите уравнение . б) Найдите все корни этого уравнения, принадлежащие отрезку . [/su_note]
Алгоритм решения:
Пункт а)
- При помощи тригонометрических формул приводим уравнение к виду, содержащему только одну тригонометрическую функцию.
- Заменяем эту функцию переменной t и решаем получившееся квадратное уравнение.
- Делаем обратную замену и решаем простейшие показательные, а затем тригонометрические уравнения.
Пункт б)
- Решаем неравенства для каждого случая.
- Записываем ответ.
Решение:
а)
1. По формулам приведения .
2. Тогда данное уравнение примет вид: 3. Вводим замену . Получаем: Решаем обычное квадратное уравнение с помощью формул дискриминанта и корней: Оба корня положительны.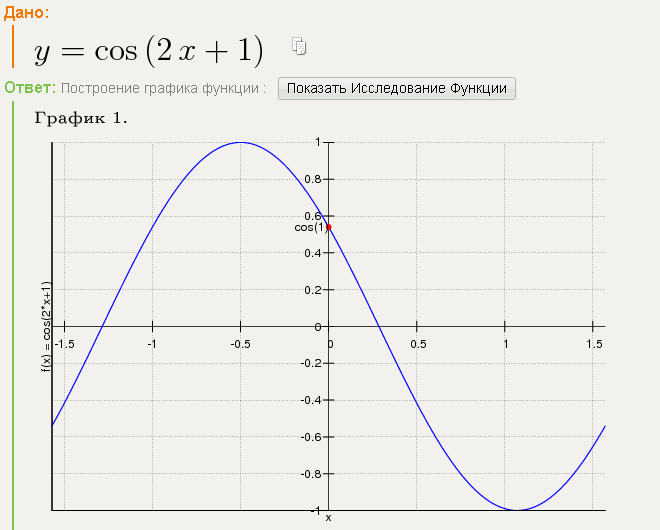 2=1
2=1
567 8 9 > >>
Тригонометрические уравнения — формулы, решения, примеры. Методы решения тригонометрических уравнений Разложение на множители тригонометрических уравнений примеры
Методы решения тригонометрических уравнений.
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида (см. выше ) и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.
1. Алгебраический метод.
(метод замены переменной и подстановки).
2. Разложение на множители.
П р и м е р 1. Решить уравнение: sin x + cos x = 1 .
Р е ш е н и е. Перенесём все члены уравнения влево:
Sin x + cos x – 1 = 0 ,
Преобразуем и разложим на множители выражение в
Левой части уравнения:
П р и м е р 2. Решить уравнение:
cos
2 x +
sin x ·
cos x = 1.
Решить уравнение:
cos
2 x +
sin x ·
cos x = 1.
Р е ш е н и е. cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,
Sin x · cos x – sin 2 x = 0 ,
Sin x · (cos x – sin x ) = 0 ,
П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.
Р е ш е н и е. cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4x cos 2x = 2 cos ² 4x ,
Cos 4x · (cos 2x – cos 4x ) = 0 ,
Cos 4x · 2 sin 3x · sin x = 0 ,
1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,
3. Приведение к однородному уравнению.Уравнение
называется однородным от носительно sin и cos , если все его члены
одной
и
той
же степени
относительно sin и cos одного
и
того
же
угла . а ) перенести все его члены в левую часть; б ) вынести все общие множители за скобки; в ) приравнять все множители и скобки нулю; г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на cos (или sin ) в старшей степени; д ) решить полученное алгебраическое уравнение относительно tan . sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2. Р е ш е н и е. 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x , Sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 , Tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 , Корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда 1) tan x = –1, 2) tan x = –3, |
4.
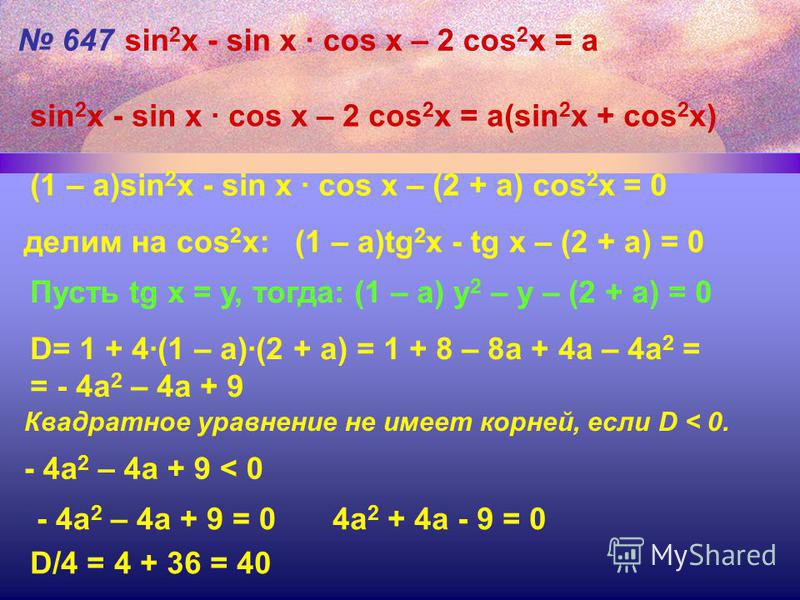 Переход к половинному углу.
Переход к половинному углу.Рассмотрим этот метод на примере:
П р и м е р. Решить уравнение: 3 sin x – 5 cos x = 7.
Р е ш е н и е. 6 sin (x / 2) · cos (x / 2) – 5 cos ² (x / 2) + 5 sin ² (x / 2) =
7 sin ² (x / 2) + 7 cos ² (x / 2) ,
2 sin ² (x / 2) – 6 sin (x / 2) · cos (x / 2) + 12 cos ² (x / 2) = 0 ,
tan ² (x / 2) – 3 tan (x / 2) + 6 = 0 ,
. . . . . . . . . .
5. Введение вспомогательного угла.
Рассмотрим уравнение вида :
a sin x + b cos x = c ,
Где a , b , c – коэффициенты; x – неизвестное.
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin (здесь — так называемый вспомогательный угол ), и наше уравнение прини
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители.
 Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
 Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Значит cosx ≠ 0 и можно поделить уравнение на cosx. ПолучимОтвет:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x. Получимtg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.

Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ: 0.
Тема: «Методы решения тригонометрических уравнений».
Цели урока:
образовательные:
Сформировать навыки различать виды тригонометрических уравнений;
Углубление понимания методов решения тригонометрических уравнений;
воспитательные:
Воспитание познавательного интереса к учебному процессу;
Формирование умения анализировать поставленную задачу;
развивающие:
Формировать навык проводить анализ ситуации с последующим выбором наиболее рационального выхода из нее.
Оборудование: плакат с основными тригонометрическими формулами, компьютер, проектор, экран.
Начнем урок с повторения основного приема решения любого уравнения: сведение его к стандартному виду. Путем преобразований линейные уравнения сводят к виду ах = в, квадратные – к виду ax 2 + bx + c =0.
 В случае тригонометрических уравнений необходимо свести их к простейшим, вида: sinx = a , cosx = a , tgx = a , которые легко можно решить.
В случае тригонометрических уравнений необходимо свести их к простейшим, вида: sinx = a , cosx = a , tgx = a , которые легко можно решить.В первую очередь, конечно, для этого необходимо использовать основные тригонометрические формулы, которые представлены на плакате: формулы сложения, формулы двойного угла, понижения кратности уравнения. Мы уже умеем решать такие уравнения. Повторим некоторые из них:
Вместе с тем существуют уравнения, решение которых требует знаний некоторых специальных приемов.
Темой нашего урока является рассмотрение этих приемов и систематизация методов решения тригонометрических уравнений.
Методы решения тригонометрических уравнений.
1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции с последующей заменой переменной.
Рассмотрим каждый из перечисленных методов на примерах, но более подробно остановимся на двух последних, так как два первых мы уже использовали при решении уравнений.

1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции.
2. Решение уравнений методом разложения на множители.
3. Решение однородных уравнений.
Однородными уравнениями первой и второй степени называются уравнения вида:
соответственно (а ≠ 0, b ≠ 0, с ≠ 0).
При решении однородных уравнений почленно делят обе части уравнения на cosx для (1) уравнения и на cos 2 x для (2). Такое деление возможно, так как sinx и cosx не равны нулю одновременно – они обращаются в нуль в разных точках. Рассмотрим примеры решения однородных уравнений первой и второй степени.
Запомним это уравнение: при рассмотрении следующего метода – введение вспомогательного аргумента, решим его другим способом.
4. Введение вспомогательного аргумента.
Рассмотрим уже решенное предыдущим методом уравнение:
Как видим, получается тот же результат.
Рассмотрим еще один пример:
В рассмотренных примерах было, в общем, понятно, на что требуется разделить исходное уравнение, чтобы ввести вспомогательный аргумент.
 Но может случиться, что не очевидно, какой делитель выбрать. Для этого существует специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть дано уравнение.
Но может случиться, что не очевидно, какой делитель выбрать. Для этого существует специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть дано уравнение.Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений- Кочкина Зинаида Васильевна
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (158 кБ)
“Кто смолоду делает и думает сам,
тот становится потом
надежнее, крепче и умнее”
В. ШукшинЦели урока:
- закрепить и проверить навыки решения простейших тригонометрических уравнений;
- уметь упрощать тригонометрические выражения и применять при решении уравнений;
I.
 Повторение ЗУН:
Повторение ЗУН: 1. Найди соотношение в данной таблице:
sin t = а t = arc…. a + πn, n – Z cos t = а t = arc… a + πn, n – Z tg t = a t = ± arc… a + 2πn, n – Z ctg t = а t = (-1)ⁿarc… a + πn, n – Z 2. Вспомни формулы:
- sin²t
- cos²t = a
- tg²t = a
- ctg²t = a
t =
t =
t =
t =
3. Заполни таблицу:
cos²α + sin²α = cos²α – sin²α = 2sinα cosα = sinα cosβ + cosα sin β = sinα cosβ – cosα sin β = cos α cosβ + sinα sin β = cos α cosβ – sinα sinβ = II.
 Работа по группам:
Работа по группам:Задание 1-й группе:
Решите уравнение: sin4x•cos4x = 1/4(2sin4x·cos 4x = 1/2
sin 8x = 1/2
8x = (-1)ⁿ п/6 + пn \·1/8
x = (-1)ⁿ п/48+ пn/8, п – Z)Задание 2 группе:
Решите уравнение: 2cos²2x – cos2x = 0(cos2x (2 cos2x – 1) = 0
1. cos2x = 0
2x = п/2 + пn
x = п/4 + пn/2, n – Z2. 2 cos2x – 1 = 0
cos2x = 1/2
2x = ± п/3 + 2пn
x = ± п/6 + пn, n – Z)Защита групп.
III. Самостоятельная работа с взаимопроверкой:
Задания 1 варианта:
Решите уравнение:
Задания 2 варианта:
Решите уравнение:
Взаимопроверка.
IV. Самостоятельная работа с выбором ответа.
Решите уравнения:
V. Итог работы.
Каждому ученику дается лист знаний, он сам себе ставит оценки.

Лист знаний Ф. И.————————————————
№ Этап
Оценки: № заданий, в которых допущены ошибки или не успели решить 1 Найди соотношение 2 Вспомни формулы 3 Заполни таблицу 4 Работа по группам 5 С/р с взаимопроверкой 6 Тест с выбором ответа Средний балл оценок: __________________
Приложение
Мэтуэй | Популярные задачи
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найти точное значение загар (30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найти точное значение арктан(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение cos(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар (45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек(45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 9235 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктан(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт.  )/3
)/342 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение тан(пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение соз(30) 47 Найти точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение соз(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение сек(60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найти точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение загар((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 пи)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение угловой синус(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найти точное значение КСК(45) 83 Упростить арктан(квадратный корень из 3) 84 Найти точное значение грех(135) 85 Найти точное значение грех(105) 86 Найти точное значение грех(150 градусов) 87 Найти точное значение sin((2pi)/3) 88 Найти точное значение загар((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найти точное значение грех(пи/2) 91 Найти точное значение сек(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение угловой синус(0) 95 Найти точное значение грех(120 градусов) 96 Найти точное значение желтовато-коричневый ((7pi)/6) 97 Найти точное значение соз(270) 98 Найти точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразование градусов в радианы 88 градусов Cos2x — Формула, Идентичность, Примеры, Доказательство
Cos2x — одно из важных тригонометрических тождеств, используемых в тригонометрии для нахождения значения тригонометрической функции косинуса для двойных углов.
 2x (cos квадрат x) и ее формулу.
2x (cos квадрат x) и ее формулу.1. Что такое Cos2x? 2. Что такое формула Cos2x в тригонометрии? 3. Вывод Cos2x с использованием формулы сложения углов 4. Cos2x В терминах sin x 5. Cos2x В пересчете на cos x 6. 92x Формула9. Как применить идентификацию Cos2x? 10. Часто задаваемые вопросы по Cos2x Что такое Cos2x?
Cos2x — важная тригонометрическая функция, которая используется для нахождения значения функции косинуса для составного угла 2x. Мы можем выразить cos2x через различные тригонометрические функции, и каждая из его формул используется для упрощения сложных тригонометрических выражений и решения задач интегрирования.
 Cos2x — это тригонометрическая функция двойного угла, которая определяет значение cos при удвоении угла x.
Cos2x — это тригонометрическая функция двойного угла, которая определяет значение cos при удвоении угла x.Что такое формула Cos2x в тригонометрии?
Cos2x — важное тождество в тригонометрии, которое можно выразить по-разному. Его можно выразить с помощью различных тригонометрических функций, таких как синус, косинус и тангенс. Cos2x является одним из тригонометрических тождеств двойного угла, поскольку рассматриваемый угол кратен 2, то есть удвоен по отношению к x. Запишем тождество cos2x в разных формах:
- cos2x = cos 2 х — sin 2 х
- cos2x = 2cos 2 х — 1
- cos2x = 1 — 2sin 2 x
- cos2x = (1 — тангенс 2 х)/(1 + тангенс 2 х)
Вывод формулы Cos2x с использованием формулы сложения углов
Мы знаем, что формула cos2x может быть выражена в четырех различных формах. Мы будем использовать формулу сложения углов для функции косинуса, чтобы получить тождество cos2x.
 Обратите внимание, что угол 2x можно записать как 2x = x + x. Также мы знаем, что cos (a + b) = cos a cos b — sin a sin b. Мы будем использовать это, чтобы доказать идентичность для cos2x. Используя формулу сложения углов для функции косинуса, подставьте a = b = x в формулу для cos (a + b).
Обратите внимание, что угол 2x можно записать как 2x = x + x. Также мы знаем, что cos (a + b) = cos a cos b — sin a sin b. Мы будем использовать это, чтобы доказать идентичность для cos2x. Используя формулу сложения углов для функции косинуса, подставьте a = b = x в формулу для cos (a + b).cos2x = cos (x + x)
= cos x cos x — sin x sin x
= cos 2 x — sin 2 x
Отсюда имеем cos2x = cos
- 2 — 9 грех 2 x
Cos2x В терминах sin x
Теперь, когда мы получили cos2x = cos 2 x — sin 2 x, мы выведем формулу для cos2x только с точки зрения функции синуса. Мы будем использовать тождество тригонометрии cos 2 x + sin 2 x = 1, чтобы доказать, что cos2x = 1 — 2sin 2 x. Имеем
cos2x = cos 2 x — sin 2 x
= (1 — sin 2 x) — sin 2 x [Потому что cos 2 9 x9 sin 1 x09 + 1 ⇒ cos 2 x = 1 — sin 2 x]
= 1 — sin 2 x — sin 2 x
= 1 — 2Sin 2 x
906 = 1 — 2Sin 2 x906 = 1 — 2Sin 2 9091 x906 = 1 — 2Sin 2 9091 x= 1 — 2sin 2 x в пересчете на sin x.

Cos2x В пересчете на cos x
Точно так же, как мы получили cos2x = 1 — 2sin 2 x, мы выведем cos2x через cos x, то есть cos2x = 2cos 2 x — 1. Мы будем использовать тригонометрические тождества cos2x = cos 2 x — sin 2 x и cos 2 x + sin 2 x = 1, чтобы доказать, что cos2x = 2cos 2 x — 1. Имеем 2
x= cos 2 x — (1 — cos 2 x) [Потому что cos 2 x + sin 2 x = 1 ⇒ sin 2 x = 1 — cos 2 x]
= cos 2 cos x
= 2cos 2 x — 1
Следовательно, мы имеем cos2x = 2cos 2 x — 1 через cosx
Cos2x С точки зрения загара x
Теперь, когда мы получили cos2x = cos 2 x — sin 2 x, мы получим cos2x через tan x. Мы будем использовать несколько тригонометрических тождеств и тригонометрических формул, таких как cos2x = cos 2 x — sin 2 x, cos 2 x + sin 2 x = 1, и tan x = sin x/cos x.
 We have,
We have,cos2x = cos 2 x — sin 2 x
= (cos 2 x — sin 2 x)/1
= (cos 2 x — sin 2 x)/( cos 2 x + sin 2 x) [Потому что cos 2 x + sin 2 x = 1]
х)/( cos 2 х + sin 2 х) на cos 2 х.(cos 2 x — sin 2 x)/(cos 2 x + sin 2 x) = (cos 2 x/cos 2 x — sin 2 90 2 x)/( cos 2 x/cos 2 x + sin 2 x/cos 2 x)
= (1 — tan 2 x)/(19 tan 2)/(19 tan 2)/(19 tan 2)/(19
x)/(19 x) x) [Поскольку тангенс x = sin x / cos x]Следовательно, мы имеем cos2x = (1 — тангенс 2 x)/(1 + тангенс 92x = (cos2x + 1)/2 ⇒ cos 2 x = (cos2x + 1)/2
Как применить идентификацию Cos2x?
Формулу Cos2x можно использовать для решения различных математических задач. 2x = (cos2x + 1)/2.
2x = (cos2x + 1)/2.
☛ Статьи по теме:
- Тригонометрические соотношения
- Тригонометрическая таблица
- Формула Sin2x
- Обратные тригонометрические соотношения
Часто задаваемые вопросы по Cos2x
Что такое идентичность Cos2x в тригонометрии?
Cos2x является одним из тригонометрических тождеств двойного угла, поскольку рассматриваемый угол кратен 2, то есть удвоен по отношению к x. Его можно выразить с помощью различных тригонометрических функций, таких как синус, косинус и тангенс.
Что такое формула Cos2x?
Cos2x может быть выражен через различные тригонометрические функции, такие как синус, косинус и тангенс. Его можно выразить следующим образом:
- cos2x = cos 2 x — sin 2 x
- cos2x = 2cos 2 х — 1
- cos2x = 1 — 2sin 2 x
Что такое производная от cos2x?
Производная cos2x равна -2 sin 2x. Производную от cos2x можно легко рассчитать по формуле d[cos(ax + b)]/dx = -asin(ax + b)
Производную от cos2x можно легко рассчитать по формуле d[cos(ax + b)]/dx = -asin(ax + b)
Какой интеграл от cos2x?
Интеграл от cos2x можно легко получить по формуле ∫cos(ax + b) dx = (1/a) sin(ax + b) + C. Таким образом, интеграл от cos2x определяется как ∫cos 2x dx = (1/2) sin 2x + C.
Что такое Cos2x с точки зрения sin x?
Формулу cos2x можно выразить через sinx. Формула имеет вид cos2x = 1 — 2sin 2 x через sin x.
Что такое Cos2x с точки зрения tan x?
Формулу cos2x можно выразить через tanx. Формула имеет вид cos2x = (1 — tan 92x — 1, то есть cos2x = 2cos 2 x — 1.
Решения NCERT по математике для 11-го класса (обновлено на 2022-2023 гг.)
Решения NCERT по математике для 11-го класса (обновлено на 2022-2023 гг.) Получите обновления NCERT Solutions для класса 11 по математике на хинди и английском языке Medium для сессии CBSE 2022–2023.
Глава 1: Множества
Глава 2: Отношения и функции
Глава 3: Тригонометрические функции
Глава 4: Принцип математической индукции
Глава 5: Комплексные числа и квадратные уравнения
Глава 6. Линейные неравенства
Линейные неравенства
Глава 7. Перестановки и комбинации
Глава 8. Биномиальная теорема
Глава 9. Последовательности и ряды
Глава 10. Прямые линии
Глава 11. Конические сечения
Глава 12. Введение в трехмерную геометрию
Глава 13 : Пределы и производные
Глава 14: Математическое обоснование
Глава 15: Статистика
Глава 16: Вероятность
Решения NCERT для 11 класса по математике были разработаны, чтобы помочь учащимся понять концепции, изучаемые в учебнике, предписанном в программе CBSE 2022-23 и подготовить их к экзаменам.
Решения объясняются шаг за шагом и включают примеры, помогающие учащимся применять концепции в Академии Тивари. Решения также включают практические упражнения с ответами, чтобы учащиеся могли проверить свое понимание.
Решения NCERT для 11-го класса по математике на английском языке и языке хинди для первого и второго семестра 2022–2023 годов представлены в качестве последних учебников CBSE. Эти решения CBSE предписаны NCERT (Национальный совет по исследованиям и обучению в области образования). В 11-м классе NCERT по математике в учебную программу включено 16 глав по математике для 11-го класса.
В 11-м классе NCERT по математике в учебную программу включено 16 глав по математике для 11-го класса.
Все главы с упражнениями Математика класса 11 Решения NCERT хорошо проверены опытным учителем математики. Это лучшие учебные материалы для учащихся, которые ищут решение по математике для 11 класса на 2022-2023 учебный год. Учащиеся UP Board также могут скачать решение UP Board для 11 класса по математике здесь. Вы также можете БЕСПЛАТНО скачать книгу NCERT по математике для 11 класса в формате PDF.
Найдите приведенные ниже ссылки для всех глав, мудрых упражнениями NCERT Solutions для математики класса 11, которые развеют все ваши сомнения по каждой сумме. Это поможет вам получить хорошие оценки на выпускном экзамене. Просто загрузите PDF-файл NCERT Solutions for Class 11 Maths для всех упражнений БЕСПЛАТНО.
Решения NCERT для математики для класса 11, все главы
Вы можете скачать бесплатное приложение NCERT Solutions для математики для класса 11, все главы с упражнениями, просто щелкнув указанные ниже ссылки с упражнениями здесь. Вы можете изучать и практиковать все решения в онлайн-узле, а для автономного обучения вы также можете БЕСПЛАТНО скачать математические решения NCERT Class 11 для всех глав, PDF-файлы с упражнениями бесплатно ниже. Эти решения Chapter Wise NCERT для математики класса 11 доступны на хинди и английском языках здесь. И вы также можете поделиться этими решениями по главам по математике для 11 класса в PDF-файлах со своими одноклассниками. Здесь вы также получаете решения UP Board и решения NCERT Exemplar Class 11 Maths Solutions, которые дают вам представление о шаблоне экзаменационных вопросов. Вы можете получить оптимальные оценки с помощью этих четко определенных решений по математике для 11-го класса.
Вы можете изучать и практиковать все решения в онлайн-узле, а для автономного обучения вы также можете БЕСПЛАТНО скачать математические решения NCERT Class 11 для всех глав, PDF-файлы с упражнениями бесплатно ниже. Эти решения Chapter Wise NCERT для математики класса 11 доступны на хинди и английском языках здесь. И вы также можете поделиться этими решениями по главам по математике для 11 класса в PDF-файлах со своими одноклассниками. Здесь вы также получаете решения UP Board и решения NCERT Exemplar Class 11 Maths Solutions, которые дают вам представление о шаблоне экзаменационных вопросов. Вы можете получить оптимальные оценки с помощью этих четко определенных решений по математике для 11-го класса.
NCERT Class 11 Math Chapters
В NCERT Class 11 Math Chapters 16 глав, основанных на последней программе правления CBSE. Некоторого ученика 11-го класса беспокоит обширная учебная программа 11-го класса по математике по сравнению с их ранним 10-м классом. Поскольку в 11-м классе представлено много новых тем. Множества, тригонометрические функции, принцип математической индукции, принцип математической индукции, линейные неравенства, перестановки и комбинации, введение в трехмерную геометрию, статистику и вероятность и т. д.
Множества, тригонометрические функции, принцип математической индукции, принцип математической индукции, линейные неравенства, перестановки и комбинации, введение в трехмерную геометрию, статистику и вероятность и т. д.
Решения NCERT для 11-го класса по математике, глава 1 — Множества
В этом решении NCERT для 11-го класса по математике, глава 1, Множества, вы узнали подробные сведения о множествах и их представлении. Здесь вы получаете «набор» с его различными свойствами.
Класс 11 Математика Глава 1 на английском языке Medium
Упражнение 1.1 на английском языке
Упражнение 1.2 на английском языке
Упражнение 1.3 на английском языке
Упражнение 1.4 на английском языке
Упражнение 1.5 на английском языке
Упражнение 1.6 на англ. Хинди
Разное 1 на хинди
Решения UP Board и NCERT для класса 11. Математика, глава 1. Наборы включают пустое множество, равные множества, конечные и бесконечные множества, подмножества, степенное множество, универсальное множество и т. д. Учащиеся знакомятся с понятиями объединения и Пересечение множеств, которое помогает учащимся также научиться рисовать диаграммы Венна. Общее количество обложек глав в Книге по математике для 11-го класса – 6. Здесь вы можете скачать бесплатные решения NCERT для 11-го класса по математике в формате PDF, чтобы учиться в любом месте и в любое время. Вы можете найти наборы глав для 11-го класса математических решений на языке хинди и английском языке здесь.
д. Учащиеся знакомятся с понятиями объединения и Пересечение множеств, которое помогает учащимся также научиться рисовать диаграммы Венна. Общее количество обложек глав в Книге по математике для 11-го класса – 6. Здесь вы можете скачать бесплатные решения NCERT для 11-го класса по математике в формате PDF, чтобы учиться в любом месте и в любое время. Вы можете найти наборы глав для 11-го класса математических решений на языке хинди и английском языке здесь.
Решения NCERT для класса 11 по математике, глава 2 — Отношения и функции
Эти решения NCERT по математике для класса 11, глава 2 — Отношения и функции предоставляют вам решение с учетом упражнений, охватывающее все суммы задач, как предписано в последнем учебнике CBSE.
Класс 11 Математика Глава 2 на английском языке Средний
Упражнение 2.1 на английском языке
Упражнение 2.2 на английском языке
Упражнение 2.3 на английском языке
Разное 2 на английском языке
Класс 11 Математика Глава 2 на хинди Средний
Упражнение 2. 1 на хинди
1 на хинди
Упражнение 2.2 на хинди
Упражнение 2.3 на хинди
Разное 2 на хинди
Пошаговые решения для всех задач с суммами легко понимаются учащимися 11 класса. В этой Главе 2 Математических решений NCERT для класса 11 вы можете узнать об определении отношения, концепциях упорядоченных пар, количестве элементов в декартовом произведении двух конечных множеств, декартовом произведении множеств, графических диаграммах, домене, ко-области и диапазон отношения. А также вы узнаете здесь о полиномиальных, рациональных, модульных, логарифмических знаковых, экспоненциальных и функциях наибольшего целого числа с графическим представлением и т. Д. Все решения NCERT для класса 11 по математике, глава 2, отношения и функции, основаны на 12th Class Maths Book Solution. Вы также можете скачать бесплатно Решения NCERT для математики для 11 класса в формате PDF без какой-либо регистрации. Найдите наборы глав для 12-го класса по математике на языке хинди и английском языке здесь и узнайте, какой из них соответствует вашим потребностям.
Решения NCERT по математике для класса 11 Глава 2. Отношения и функции содержит три упражнения, и вы можете скачать БЕСПЛАТНЫЕ PDF-файлы здесь, чтобы учиться в автономном режиме.
Математика для 11 класса Глава 2 Упражнение 2.1 Решение
Математика для 11 класса Глава 2 Упражнение 2.2 Решение обсуждение отрицательных углов, метод измерения углов в радианах.
Класс 11 Математика Глава 3 на английском языке Medium
Упражнение 3.1 на английском языке
Упражнение 3. 2 на английском языке
2 на английском языке
Упражнение 3.3 на английском языке
Упражнение 3.4 на английском языке
Упражнение 3.5 на английском языке
Разное 3 на английском языке Класс 37 Глава 109 Hindi Medium
Упражнение 3.1 на хинди
Упражнение 3.2 на хинди
Упражнение 3.3 на хинди
Упражнение 3.4 на хинди
Упражнение 3.5 на хинди
Разное 3 на хинди
Тригонометрические решения для класса 11 и математические преобразования от одной меры к другой, а также. Учащиеся UP Board среднего уровня могут загрузить решения UP Board для 11 класса по математике на хинди Medium. Вы можете узнать все об изучении тригонометрического отношения к тригонометрическим функциям, общем решении тригонометрических уравнений, знаках, домене и диапазоне тригонометрических функций в графическом представлении. В этом классе 11 Math NCERT Chapter 3 — Trigonometric Functions есть четыре упражнения, в которых учащиеся знают о sin 2x, cos 2x, tan 2x, sin 3x, cos 3x, tan 3x и т. д. Вы также можете загрузить неограниченное количество решений NCERT для математики класса 11. ПДФ здесь. Решение для 11-го класса по математике очень полезно для вашего выпускного экзамена. Найдите оба решения по математике в главе «Тригонометрические функции» класса 12 на языке хинди и на английском языке.
д. Вы также можете загрузить неограниченное количество решений NCERT для математики класса 11. ПДФ здесь. Решение для 11-го класса по математике очень полезно для вашего выпускного экзамена. Найдите оба решения по математике в главе «Тригонометрические функции» класса 12 на языке хинди и на английском языке.
Математика для 11 класса, глава 3. Упражнение 3.1. Решение
Математика для 11 класса, глава 3. Упражнение 3.2. Решение 12 Математика, глава 4, с упражнениями, основанными на решении учебника по математике для 11-го класса.
Математика для 11 класса, глава 4 на английском языке Medium
Упражнение 4.1 на английском языке
Математика для 11 класса, глава 4 на хинди Medium
Упражнение 4.1 на хинди
В этой главе вы узнаете о индукции и мотивации приложения с помощью натуральных чисел. И индуктивное подмножество действительных чисел. В этой главе есть задачи, связанные с принципом математической индукции, а также с его приложениями. Евклид, известный своими работами по геометрии, доказал, что число простых чисел бесконечно. Эта глава 4 NCERT по математике для 11 класса очень важна и для учащихся. Просто нажмите здесь и получите математические решения для упражнений. Решения NCERT для математики класса 11 в формате PDF доступны бесплатно. Решения NCERT для класса 11 Математика Глава 4 Принцип математической индукции также является важной темой, которая должна стать хорошей практикой. Найдите здесь Глава Принцип математической индукции, класс 11 Математические решения на языке хинди и английском языке.
Решения NCERT для 11-го класса по математике, глава 5. Комплексные числа и квадратные уравнения
NCERT Решения для 11-го класса по математике, глава 5. Комплексные числа и квадратные уравнения со всеми упражнениями хорошо решены опытным учителем математики.
Класс 11 Математика Глава 5 на английском языке Средний
Упражнение 5.1 на английском языке
Упражнение 5.2 на английском языке
Упражнение 5.3 на английском языке
Разное 5 на английском языке
Класс 11 Математика Глава 5 на хинди Средний
Упражнение 5.1 на хинди
Упражнение 5.2 на хинди
Упражнение 5.3 на хинди
Разное 5 на хинди
Все задачи составлены таким простым способом, чтобы учащиеся могли избавиться от всех сомнений и концепций. Как только вы правильно поймете концепцию, вы сможете легко приступить ко всем упражнениям. В этой главе 5 представлены подробные сведения об алгебраических свойствах комплексных чисел, утверждении основной теоремы алгебры, представлении комплексных чисел в плоскости Аргана и полярных координатах, а также о решениях квадратных уравнений и т. д. В этом решении NCERT всего три упражнения для Глава 5 по математике для 11 класса, основанная на решении для 12-го класса по математике. Загрузите неограниченное количество бесплатных решений NCERT для упражнений по математике в формате PDF. Учащийся может изучать и практиковать математические решения для глав 11 «Комплексные числа» и «Квадратные уравнения» на языке хинди и английском языках.
Как только вы правильно поймете концепцию, вы сможете легко приступить ко всем упражнениям. В этой главе 5 представлены подробные сведения об алгебраических свойствах комплексных чисел, утверждении основной теоремы алгебры, представлении комплексных чисел в плоскости Аргана и полярных координатах, а также о решениях квадратных уравнений и т. д. В этом решении NCERT всего три упражнения для Глава 5 по математике для 11 класса, основанная на решении для 12-го класса по математике. Загрузите неограниченное количество бесплатных решений NCERT для упражнений по математике в формате PDF. Учащийся может изучать и практиковать математические решения для глав 11 «Комплексные числа» и «Квадратные уравнения» на языке хинди и английском языках.
Класс 11 Математический со всеми упражнениями. Здесь вы узнали о концепции линейных неравенств, как следует из названия.
Здесь вы узнали о концепции линейных неравенств, как следует из названия.
Класс 11 Математика Глава 6 на английском языке Medium
Упражнение 6.1 на английском языке
Упражнение 6.2 на английском языке
Упражнения 6.3 на английском языке
Разное 6 на английском языке
класс 11 Математика 6 Глава 6 в среде хинди
Упражнение 6.1 в хинди
Упражнение 6.2 в хинди
Упражнение 6.3 на хинди
Неизвестно 6 in in hindi 9090
 Здесь вы можете загрузить и поделиться решениями NCERT для математики класса 11 в формате PDF. Найдите обе главы «Линейные неравенства, класс 11, математические решения» на языке хинди и на английском языке.
Здесь вы можете загрузить и поделиться решениями NCERT для математики класса 11 в формате PDF. Найдите обе главы «Линейные неравенства, класс 11, математические решения» на языке хинди и на английском языке. Математика для 11 класса Глава 6. Упражнение 6.1. Решение
Математика для 11 класса. Глава 6. Упражнение 6.2. Решение
Решения NCERT для 11 класса. Глава 7 Перестановки и комбинации со всеми упражнениями здесь. Если у вас есть какие-либо сомнения в NCERT Solutions for Class 11 Maths Chapter 7, тогда эти решения с мудрыми суммами упражнений — лучший инструмент, чтобы развеять все ваши сомнения и концепции.

Класс 11 Математика Глава 7 на английском языке Medium
Упражнение 7.1 на английском языке
Упражнение 7.2 на английском языке
Упражнение 7.3 на английском языке
Упражнение 7.4 на английском языке Упражнение 7.1 на хинди
Упражнение 7.2 на хинди
Упражнение 7.3 на хинди
Упражнение 7.4 на хинди
Разное 7 на хинди
Есть четыре упражнения, основанные на решении 12th Class Maths Book Solution, которое включает в себя все вопросы, охватывающие все темы, присутствующие в Главе 7 Решения NCERT по математике для 11 класса. Просто нажмите на ссылку и получите бесплатные решения NCERT для математики Class11 в формате PDF. Получите и учитесь как для перестановок, так и для комбинаций, математические решения класса 11 на хинди и английском языках.
Математика для 11 класса Глава 7 Упражнение 7. 1 Решение
1 Решение
Математика для 11 класса Глава 7 Упражнение 7.2 Решение все задачи объясняются и решаются учителем математики, имеющим многолетний опыт работы по этому предмету.
Класс 11 Математика Глава 8 на английском языке Medium
Упражнение 8.1 на английском языке
Упражнение 8.2 на английском языке
Разное 8 на английском языке
Математика для класса 11 Глава 8 на хинди Средний
Упражнение 8.1 на хинди
Упражнение 8.2 на хинди
Разное 8 на хинди
Все решения проверяются и тщательно проверяются специалистами по математике. Это решение NCERT для 11-го класса по математике, глава 8, которое основано на решении из книги по математике 11-го класса, охватывает историю, формулировку и доказательство биномиальной теоремы для положительных интегральных индексов. В этой главе вы познакомились с треугольником Паскаля, биномиальным разложением и его простыми приложениями. В этой главе два упражнения. Просто щелкните по ссылкам ниже и изучите БЕСПЛАТНЫЕ математические решения класса 11 по биномиальной теореме в главе на языке хинди и английском языке.
В этой главе вы познакомились с треугольником Паскаля, биномиальным разложением и его простыми приложениями. В этой главе два упражнения. Просто щелкните по ссылкам ниже и изучите БЕСПЛАТНЫЕ математические решения класса 11 по биномиальной теореме в главе на языке хинди и английском языке.
Решения NCERT для 11-го класса по математике, глава 9. Последовательности и серии
Эти бесплатные решения NCERT для 11-го класса по математике, глава 9, последовательности и серии для всех упражнений очень полезны для учащихся 11-го класса.
Математика для 11-го класса, глава 9 Английский Средний
Упражнение 9.1 на английском языке
Упражнение 9.2 на английском языке
Упражнение 9.3 на английском языке
Упражнение 9.4 на английском языке
Разное 9 на английском языке
Класс 11 Математика Глава 9 на хинди Средний
Упражнение 9.1 на хинди
Упражнение 9.2 на хинди
Упражнение 9.3 на хинди
Упражнение 9. 4 на хинди
4 на хинди
Разное 9 на хинди отношения между А.М. и GM, а также формулы для сумм специальных рядов и многое другое. Всего в главе 9 представлено четыре упражнения, основанных на решении учебника по математике для 11-го класса. Это помогает учащимся понять все концепции и логику, данные в главе, решая все суммы в ней. Загрузите БЕСПЛАТНЫЕ решения NCERT для 11-го класса по математике, глава 9просто нажав на эти ссылки ниже. Загрузите PDF-файл NCERT Solutions for Class 11 Maths и поделитесь им со своим другом. Получите здесь Последовательности глав и серий Решения по математике для класса 11 на языке хинди и английском языке.
NCERT Solutions for Class 11 Math Chapter 10 — Straight Lines
NCERT Solutions for Class 11 Math Chapter 10 Straight Lines помогает учащимся напомнить главу о двухмерной геометрии предыдущего класса.
Класс 11 Математика Глава 10 на английском Средний
Упражнение 10.1 на английском языке
Упражнение 10.2 на английском языке
Упражнение 10. 3 на английском языке
3 на английском языке
Разное 10 на английском языке
класс 11 Математика 10 в среде хинди
Упражнение 10.1. на хинди
Смещение начала координат, многочисленные формы уравнений линии, параллельной оси, угол между двумя линиями, наклон линии и форма точки-наклона, форма пересечения наклона, форма пересечения двух точек, точка пересечения и т. д. Вы можете также узнайте здесь о точке пересечения двух линий, расстоянии точки от формы линии и многом другом. В Решениях NCERT для 11-го класса по математике, глава 10, есть три упражнения. Только практикуйтесь и тщательно повторяйте, чтобы получить хорошие оценки по математике для 11-го класса. Загрузите PDF-файл «Решения NCERT для математики класса 11» и узнайте, когда вы также будете в автономном режиме. Все решения основаны на учебнике по математике 11-го класса. Глава Прямые линии Класс 11 Решения по математике на языке хинди.
Решения NCERT для математики класса 11, глава 11 — конические сечения
Это бесплатное решение NCERT для математики класса 11, глава 11, конические сечения, подробно описывает концепцию конических сечений. Коническое сечение – это кривая, полученная пересечением поверхности конуса с плоскостью.
Коническое сечение – это кривая, полученная пересечением поверхности конуса с плоскостью.
Класс 11 Математика Глава 11 на английском языке Средний
Упражнение 11.1 на английском языке
Упражнение 11.2 на английском языке
Упражнение 11.3 на английском языке
Упражнение 11.4 на английском языке
Разное 11 на английском языке
Класс 11 Математика Глава 11 В Хинди Среда
УПРАЖНЕНИЕ 11.1 В Хинди
Упражнение 11,2 на хинди
Упражнение 11,3 в хинди
Упражнения 11,4 На хинди
. эллипс, гипербола, парабола, точка, прямая и пара пересекающихся прямых как вырожденные с коническим сечением. Все стандартные уравнения и простые свойства окружности, параболы, эллипса и гиперболы также представлены в главе 11. Всего в этой главе представлены четыре упражнения, основанные на решении учебника по математике для 11-го класса. Просто нажмите и найдите NCERT Solutions for Class 11 Maths Chapter 11. Получите бесплатные решения NCERT для Class X Maths в формате PDF без какой-либо регистрации. Здесь вы найдете математические решения для глав 11 класса «Конические сечения» на языке хинди и на английском языке.
Здесь вы найдете математические решения для глав 11 класса «Конические сечения» на языке хинди и на английском языке.
Решения NCERT для математики 11-го класса Глава 12. Введение в трехмерную геометрию
Решения NCERT для математики 11-го класса Глава 12 Введение в трехмерную геометрию — важная глава. Здесь вы можете получить бесплатные решения для упражнений, представленные в NCERT Solutions for Class 11 Math Chapter 12.
Class 11 Math Chapter 12 in English Medium
Упражнение 12.1 на английском языке
Упражнение 12.2 на английском языке
Упражнение 12.3 на английском языке
Разное 12 на английском языке
Класс 11 Математика Глава 12 на хинди Средний
Упражнение 12.1 на хинди
Упражнение 12.2 на хинди
Упражнение 12.3 на хинди координатных осей и координатных плоскостей в трех измерениях, расстояние между двумя точками и формула сечения, координаты точки, подробно. Здесь вы можете лучше понять все суммы задач. Вы можете получить больше баллов на выпускном экзамене по математике для 11 класса, хорошо попрактиковавшись с этими решениями.
Вы можете получить больше баллов на выпускном экзамене по математике для 11 класса, хорошо попрактиковавшись с этими решениями.
Решения NCERT по математике для класса 11, глава 13. Пределы и производные
Здесь, в этой математике для класса 11, решения NCERT, глава 13. Пределы и производные, вы узнаете об исчислении, которое представляет собой математику, посвященную изучению изменения значения. функции и точек в области изменения.
Класс 11 Математика Глава 13 на английском языке Средний
Упражнение 13.1 на английском языке
Упражнение 13.2 на английском языке
Разное 13 на английском языке
Класс 11 Математика Глава 13 на хинди Средний
Упражнение 13.1 на хинди
Упражнение 13.2 на хинди
Разное 13 на хинди
Здесь вы можете получить представление о производной, а также простое определение предела и некоторую алгебру пределов. А в конце главы вы узнаете описание производной и некоторую алгебру производных. Всего есть два упражнения и разное упражнение, которое охватывает все темы в Главе 13 Решения NCERT по математике для 11 классов. Просто нажмите на указанные ниже ссылки и получите БЕСПЛАТНЫЕ решения NCERT для решений NCERT по математике для класса 11 в формате PDF. Здесь вы можете получить все решения для 11-го класса по математике от профессионального учителя математики. А также найдите математические решения класса 11 «Пределы и производные» на хинди и английском языках.
Всего есть два упражнения и разное упражнение, которое охватывает все темы в Главе 13 Решения NCERT по математике для 11 классов. Просто нажмите на указанные ниже ссылки и получите БЕСПЛАТНЫЕ решения NCERT для решений NCERT по математике для класса 11 в формате PDF. Здесь вы можете получить все решения для 11-го класса по математике от профессионального учителя математики. А также найдите математические решения класса 11 «Пределы и производные» на хинди и английском языках.
NCERT Solutions for Class 11 Math Chapter 15-Statistics
Статистика имеет дело с данными, собранными для определенных целей. В этом NCERT Solutions for Class 11 Maths Chapter 15 Statistics представлены некоторые важные показатели дисперсии.
Класс 11 Математика Глава 15 на английском языке Средний
Упражнение 15.1 на английском языке
Упражнение 15.2 на английском языке
Упражнение 15.3 на английском языке
Разное 15 на английском языке
Класс 11 Математика Глава 15 на хинди Средний
Упражнение 15. 1 на хинди
1 на хинди
Упражнение 15.2 на хинди
Упражнение 15.3 на хинди
Разное 15 на хинди
Это также дает знания об их методах расчета для разгруппированных и сгруппированных данных. Учащиеся могут изучить диапазон, среднее отклонение, анализ дисперсии распределения частот и стандартное отклонение разгруппированных или сгруппированных данных и т. д. В Решениях NCERT для 11-го класса по математике, глава 15, есть три упражнения. Нажмите на ссылки ниже и получите БЕСПЛАТНЫЕ решения NCERT для 11-го класса. Математика PDF без ограничений здесь. Вы также можете выучить и скачать главу Статистика Класс 11 Решения по математике на языке хинди и английском языке.
Решения NCERT для математики для 11-го класса, глава 16 — Вероятность
Решения NCERT для математики для 11-го класса, глава 16 Вероятность четко определена с пошаговыми решениями, чтобы учащиеся могли легко понять концепцию.
Класс 11 Математика Глава 16 на английском языке Средний
Упражнение 16. 1 на английском языке
1 на английском языке
Упражнение 16.2 на английском языке
Упражнение 16.3 на английском языке
Разное 16 на английском языке
Класс 11 Математика Глава 16 на хинди Средний9 Упражнение 16.1 на хинди
Упражнение 16.2 на хинди
Упражнение 16.3 на хинди
Разное 16 на хинди
Здесь вы можете правильно понять понятие вероятности. Вы можете решить все три упражнения в этой главе, которые основаны на решении учебника по математике для 11-го класса. Это решение NCERT для класса 11 по математике, глава 16, охватывает случайные эксперименты, возникновение результатов событий, выборочные пространства, представление множества, события и т. Д. Просто нажмите здесь и получите все решения NCERT для класса 11 по математике в формате PDF, чтобы практиковать мудро, ничего не платя. Учащиеся могут получить решения по математике для вероятностного класса 11 главы на языке хинди и английском языке здесь.
Мы в Tiwari Academy помогаем всем учащимся найти лучшие способы решения математических задач, используя свои логические навыки. С помощью этих решений NCERT для всех глав по математике для 11 класса упражнения могут стать хорошим шагом в мир математики и добиться большего успеха не только на выпускном экзамене, но и помогут вам в старших классах. Кроме того, учащиеся смогут получить представление о вопросе Performa из этих образцов документов NCERT по математике для 11 класса. Поэтому вам предлагается изучить и тщательно практиковать все упражнения из приведенных выше ссылок.
С помощью этих решений NCERT для всех глав по математике для 11 класса упражнения могут стать хорошим шагом в мир математики и добиться большего успеха не только на выпускном экзамене, но и помогут вам в старших классах. Кроме того, учащиеся смогут получить представление о вопросе Performa из этих образцов документов NCERT по математике для 11 класса. Поэтому вам предлагается изучить и тщательно практиковать все упражнения из приведенных выше ссылок.
Как подготовиться к математике для 11 класса Все главы
Глава 1: Наборы
Набор является основой сегодняшних решений NCERT для математики для 11 класса Глава 1, Наборы, мы изучим наборы и их представление. Он включает в себя определение, а также свойства различных типов множеств. Набор, который не содержит ни одного элемента, называется пустым набором, нулевым набором или пустым набором. Точно так же множество, которое пусто или состоит из определенного числа элементов, называется конечным. В противном случае множество называется бесконечным. Мы должны знать об операциях множества, таких как объединение, пересечение, сопряженные и непересекающиеся множества, равное и эквивалентное множество. Понятия подмножеств, универсальных множеств и диаграммы Венна широко используются в математике 11 класса. Разное упражнение Главы 1 Класс 11 Математика описывает приложения набора и его теорем.
Мы должны знать об операциях множества, таких как объединение, пересечение, сопряженные и непересекающиеся множества, равное и эквивалентное множество. Понятия подмножеств, универсальных множеств и диаграммы Венна широко используются в математике 11 класса. Разное упражнение Главы 1 Класс 11 Математика описывает приложения набора и его теорем.
Глава 2: Отношения и функции
Отношения и функции по математике 11 класса подготовьте твердое тело на основе 12 класса по математике Глава 1 Отношения и функции. В классе 11 мы узнаем о перекрестном произведении двух или трех наборов, чтобы получить заказанную пару. Этот факт помогает нам понять концепции отношений и функций в упражнении 2.2 и в разделе «Разное» по математике для 11 класса. Знаете ли вы, почему учащиеся сталкиваются с трудностями при выполнении NCERT Solutions for Class 11 Math Chapter 2, Relations and Functions? Единственная причина в том, что они не выполнили должным образом концепции главы 2 11-го класса по математике. Глава 2 по математике 11 класса является основой главы 1 12 класса «Отношения и функции».
Глава 2 по математике 11 класса является основой главы 1 12 класса «Отношения и функции».
Глава 3: Тригонометрические функции
Первое упражнение NCERT Solutions for Class 11 Math В главе 3 «Тригонометрические функции» объясняется, как преобразовать радианы в градусы или градусы в радианы. Студентам пока удобнее пользоваться градусной мерой. В старших классах чаще всего мы используем только радианы. Вот почему теперь начните практиковаться в радианах, а не в градусах. Упражнение 3.2 объясняет, как знаки тригонометрических функций меняются от одного квадранта к другому. Все формулы в упражнении 3.3 будут часто использоваться в большинстве глав 12-го класса по математике. Если кто-то не в состоянии понять эти формулы, он столкнется с проблемой в 12 классе по математике и физике.
Глава 4: Принцип математической индукции
Принцип математической индукции говорит нам, что если выражение истинно для двух последовательных натуральных чисел, то оно будет истинным для всех. Чтобы проверить это, мы возьмем, что оно верно для некоторого натурального числа k, и попробуем доказать, что оно верно и для k + 1. Таким образом, мы попытаемся доказать это для двух последовательных натуральных чисел. PMI полезен не только в NCERT Solutions for Class 11 Maths Chapter 4, Principle of Mathematical Induction, но и в высших учебных заведениях. Есть два блока вопросов с 1 по 18 и с 19до 24. На экзаменах контрольные работы состоят как минимум из одного вопроса из каждого раздела.
Чтобы проверить это, мы возьмем, что оно верно для некоторого натурального числа k, и попробуем доказать, что оно верно и для k + 1. Таким образом, мы попытаемся доказать это для двух последовательных натуральных чисел. PMI полезен не только в NCERT Solutions for Class 11 Maths Chapter 4, Principle of Mathematical Induction, но и в высших учебных заведениях. Есть два блока вопросов с 1 по 18 и с 19до 24. На экзаменах контрольные работы состоят как минимум из одного вопроса из каждого раздела.
Глава 5: Комплексные числа и квадратные уравнения
В классе 10 Математика Глава 4 Квадратные уравнения, если дискриминант отрицательный, мы не смогли найти решения. Мы рассмотрим здесь ту же ситуацию, но получим решения. Теперь мы можем найти корни уравнений, даже если D отрицательно. Это стало возможным именно благодаря комплексным числам. В NCERT Solutions for Class 11 Maths Глава 5, Комплексные числа и квадратные уравнения, мы можем найти действительные, а также мнимые корни любого квадратного уравнения. Квадратные корни комплексного числа также можно получить в дополнительном разделе. Класс 11 Математика Глава 5 Разное Упражнение очень важно для полного знания комплексных чисел.
Квадратные корни комплексного числа также можно получить в дополнительном разделе. Класс 11 Математика Глава 5 Разное Упражнение очень важно для полного знания комплексных чисел.
Глава 6: Линейные неравенства
В Решениях NCERT для класса 11 Математика Глава 6, Линейные неравенства, мы будем изучать линейные неравенства только с одной и двумя переменными. Представление на числовой прямой, поиск наборов решений в виде действительных чисел, целых чисел и задач, основанных на задачах со словами, являются общими темами этой главы. Упражнение 6.3 является основным упражнением с точки зрения экзамена. Его вес максимален по отношению к другим упражнениям. Это упражнение также полезно в классе 12 по математике, глава 12, LPP. Эту главу легче набрать достаточно хорошо на экзаменах CBSE.
Глава 7: Перестановки и комбинации
В Решениях NCERT для класса 11 Математика Глава 7, Перестановки и комбинации, мы изучим некоторые основные методы подсчета. Это позволит нам ответить на множество вопросов, фактически не перечисляя и не упорядочивая элементы. Перестановки будут полезны, чтобы быстро узнать количество различных способов. В качестве первого шага мы познакомимся с приемами перестановок. Класс 11 Математика Глава 7 Разное Вопросы Упражнения требуют применения как перестановки, так и комбинации для ответов. Эти темы полезны для расчета вероятности в 11 классе по математике, глава 16.
Перестановки будут полезны, чтобы быстро узнать количество различных способов. В качестве первого шага мы познакомимся с приемами перестановок. Класс 11 Математика Глава 7 Разное Вопросы Упражнения требуют применения как перестановки, так и комбинации для ответов. Эти темы полезны для расчета вероятности в 11 классе по математике, глава 16.
Глава 8: Биномиальная теорема
NCERT Решения для 11-го класса по математике Глава 8, Биномиальная теорема содержит два упражнения. В упражнении 8.1 представлены простые суммы биномиальных разложений с двумя членами. Применение общих терминов описано в упражнении 8.2. Как и в других главах, разное в этой главе также оценивает экзамены или тесты. В 11th Math мы знаем формулу разложения в 3 или 4 степени, но с помощью биномиальной теоремы мы можем расширить выражение с любым количеством степеней. В математике 11 класса в качестве индексов используются только натуральные числа. Биномиал также допускает отрицательные степени, но не в программе CBSE для класса 11 на 2022–2023 годы.
Глава 9: Последовательности и серии
Решения NCERT для 11 класса по математике Глава 9, Последовательности и ряды содержит следующий шаг 10 класса по математике Глава 5 A P. Мы сделали A P в 10 классе, поэтому об A.P. суммы есть в 11 классе по математике. Теперь мы изучим среднее арифметическое, среднее геометрическое, связь между А.М. и Г.М. и основанные вопросы. Мы также узнаем о специальных рядах в формах суммы n членов последовательных натуральных чисел, суммы n членов квадратов натуральных чисел и суммы n членов кубов натуральных чисел. 11 класс математика глава 9нужно больше практики, чтобы хорошо знать концепции.
Глава 10: Прямые линии
Решения NCERT для математики для класса 11 Глава 10, Прямые линии содержит краткое напоминание о 2-D из предыдущих классов. В дополнительной части мы узнаем о смещении начала координат, наклоне линии и угле между двумя линиями. Упражнение 10.1 включает простые вопросы, в основном основанные на понятиях математики для 10 класса. В следующих упражнениях мы узнаем о линиях, параллельных оси, форме точки-наклона, форме наклона-пересечения, двухточечной форме, форме пересечения и нормальной форме. Получение расстояния точки от линии является зачетом на экзаменах. Эта глава немного сложнее по сравнению с другими. Поэтому нужно больше внимания уделять практике, чтобы получить хорошие оценки на тестах или экзаменах.
В следующих упражнениях мы узнаем о линиях, параллельных оси, форме точки-наклона, форме наклона-пересечения, двухточечной форме, форме пересечения и нормальной форме. Получение расстояния точки от линии является зачетом на экзаменах. Эта глава немного сложнее по сравнению с другими. Поэтому нужно больше внимания уделять практике, чтобы получить хорошие оценки на тестах или экзаменах.
Глава 11: Конические сечения
В NCERT Solutions for Class 11 Math Chapter 11, Conic Sections мы будем изучать такие кривые, как окружности, эллипсы, параболы и гиперболы. Просто попробуйте узнать, кто назвал эти кривые? Почему изучение этих кривых выделено в рубрику «Коники»? В упражнении 11 по математике 11.1 объясняются термины и уравнения, относящиеся только к кругу, тогда как в упражнении 11.2 для параболы. Упражнения 11.3 и 11.4 по математике для 11 класса объясняют эллипс и гиперболу соответственно. Мы должны знать о фокусах, вершинах, длине большой и малой оси, эксцентриситете и длине прямой кишки эллипса, а также гиперболы. В наше время эти кривые используются в таких областях, как движение планет, проектирование телескопов и во многих других областях.
В наше время эти кривые используются в таких областях, как движение планет, проектирование телескопов и во многих других областях.
Глава 12: Введение в трехмерную геометрию
В 10 классе по математике мы узнали о расстоянии между двумя точками на двумерной плоскости. Здесь, в 12-й главе математики 11-го класса, мы можем найти такое же расстояние в трехмерной плоскости. В начале главы описаны основы квадрантного октанта. Что бы мы ни делали в 10-м классе по математике в упражнении 7.2, то же самое нужно повторить с концепцией трехмерной геометрии. Только одно отличается, это Формула Раздела. В классе 10 по математике мы разделяем линию или сегмент линии на определенное соотношение внутри, но в классе NCERT Solutions for Class 11 Math Chapter 12, Introduction to Three Dimension Geometry внутренне и внешне применимы оба.
Глава 13: Пределы и производные
Концепция NCERT Solutions for Class 11 Math Chapter 13, Introduction to Limits and Derivatives является новой для учащихся. Здесь они узнают, как найти значение функции, используя ограничения. Производные с использованием первого принципа — одна из хороших тем для экзаменов. Мы должны попытаться сделать почти все производные, используя первый принцип. Концепции LHL и RHL полезны для проверки функции независимо от того, существуют ли ее пределы или нет. После выполнения главы 13 по математике для 11 класса каждый должен выполнить математические упражнения 5.2, 5.3 и 5.4 для 12 класса, чтобы лучше понять концепцию производных.
Здесь они узнают, как найти значение функции, используя ограничения. Производные с использованием первого принципа — одна из хороших тем для экзаменов. Мы должны попытаться сделать почти все производные, используя первый принцип. Концепции LHL и RHL полезны для проверки функции независимо от того, существуют ли ее пределы или нет. После выполнения главы 13 по математике для 11 класса каждый должен выполнить математические упражнения 5.2, 5.3 и 5.4 для 12 класса, чтобы лучше понять концепцию производных.
Глава 14: Математическое мышление
В математическом языке есть два вида рассуждений — индуктивный и дедуктивный. NCERT Solutions for Class 11 Maths Chapter 14, Mathematical Reasoning следует дедуктивному рассуждению. Здесь мы узнаем о ПРЕДЛОЖЕНИИ, которое называется математически приемлемым утверждением, если оно либо истинно, либо ложно, но не то и другое одновременно. Имея дело с высказываниями, мы обычно обозначаем их строчными буквами p, q, r подобно буквам. В этой главе также рассматривается отрицание высказывания; Составные утверждения со связующим словом и окончательные утверждения о принятии решения.
Глава 15: Статистика
Упражнение 15.1 класса 11 по математике содержит вопросы об отклонениях среднего значения, моды и медианы. Здесь мы будем иметь дело со всеми показателями центральных тенденций, такими как среднее отклонение и диапазон. Расчет будет включать как сгруппированные, так и разгруппированные ряды данных. Решения NCERT для класса 11 по математике В главе 15 «Статистика» будут обсуждаться вопросы осквернения и непрерывного распределения частот. Коэффициент вариации с использованием вопросов, основанных на дисперсии и стандартном отклонении, часто встречается на экзаменах. Ускоренный метод поиска дисперсии и стандартного отклонения одинаково полезен для экзаменов.
Глава 16: Вероятность
Вероятность всегда упоминается как тема для подсчета очков во всех классах. Он также получает баллы на экзаменах Совета CBSE. Решения NCERT для математики класса 11, глава 16, вероятность является основой для математики класса 12, глава 13, вероятность. Если вы хотите получить хорошие оценки по вероятности в 12-м классе, вы должны изучить все понятия в 11-м классе. Упражнение 16.1 основано на примере пространства и простых идеях вероятности. Следующие упражнения включают в себя события, которые являются исключительными, исчерпывающими или концепциями наборов. Разное Упражнение, содержащее хорошие вопросы для практики, жизненно важно для классного теста или выпускных экзаменов.
Если вы хотите получить хорошие оценки по вероятности в 12-м классе, вы должны изучить все понятия в 11-м классе. Упражнение 16.1 основано на примере пространства и простых идеях вероятности. Следующие упражнения включают в себя события, которые являются исключительными, исчерпывающими или концепциями наборов. Разное Упражнение, содержащее хорошие вопросы для практики, жизненно важно для классного теста или выпускных экзаменов.
Важность решений NCERT для изучения математики в классе 11 от Tiwari Academy
Решения NCERT для изучения математики в классе 11 от Tiwari Academy имеют множество преимуществ. Вы можете получить глубокое понимание общей концепции всех приведенных глав в книгах NCERT (Национальный совет по исследованиям и обучению в области образования). Основные преимущества решений Learn Class 11 Maths NCERT от Tiwari Academy:
- Лучшее понимание концепций
- Более быстрый процесс обучения
- Простой способ понять
- Решения в PDF-файле
- Полностью бесплатно
- На основе последней версии учебного плана CBSE
1.
 Лучшее понимание концепций
Лучшее понимание концепцийРешения NCERT для 11-го класса по математике Все главы Академии Тивари содержат простые, но исчерпывающие объяснения. Все решения решаются опытным учителем математики, имейте в виду лучшее понимание концепций.
2. Ускоренный процесс обучения
Мы в Tiwari Academy предоставляем все решения в обоих режимах на хинди и английском языке, чтобы вы могли легко понять основные понятия лучше и быстрее. Вы усваиваете концепции намного быстрее, а также быстро учитесь.
3. Простой метод для понимания
Все решения по математике хорошо разработаны в виде простого пошагового метода, так что учащийся может легко понять все суммы упражнений. Студенты могут очистить все концепции и логику каждой суммы.
4. Решения в файле PDF
Все решения NCERT по математике для 11 класса. Все главы, упражнения в Tiwari Academy доступны в удобном формате PDF, так что вы можете скачать их и изучать, когда хотите учиться или в автономном режиме. А также вы можете поделиться этими PDF-файлами с друзьями. Здесь вы можете скачивать неограниченное количество PDF-файлов.
А также вы можете поделиться этими PDF-файлами с друзьями. Здесь вы можете скачивать неограниченное количество PDF-файлов.
5. Совершенно бесплатно
Все решения NCERT по главам доступны здесь БЕСПЛАТНО. Вам не нужно ничего платить здесь, а также нет необходимости в каком-либо входе и регистрации.
6. На основе последней версии программы CBSE
Все решения основаны на обновленной программе CBSE и охватывают все вопросы, как в учебниках NCERT. Все решения по главам соответствуют последним книгам NCERT и описываются шаблоном в соответствии с рекомендациями, выпущенными NCERT.
Чем математические решения CBSE 11 от NCERT полезны для выпускных экзаменов?
CBSE Class 11 Математика является важным предметом для учащихся. Поскольку учебная программа CBSE 11 по математике является эталоном для любого учащегося, это будет отражаться в будущих отчетах об успеваемости. CBSE строго следует книгам NCERT по подготовке к экзаменам. CBSE Class 11 Math Solutions of NCERT — лучший инструмент для студентов при подготовке к выпускным и конкурсным вступительным экзаменам. Понятия, представленные в этих решениях простым способом, предназначены для лучшего понимания. Пошаговые решения опытного учителя математики с помощью простого метода могут легко понять сложные проблемы наиболее эффективным способом. Так что вы можете получить высокие оценки на выпускном экзамене.
Понятия, представленные в этих решениях простым способом, предназначены для лучшего понимания. Пошаговые решения опытного учителя математики с помощью простого метода могут легко понять сложные проблемы наиболее эффективным способом. Так что вы можете получить высокие оценки на выпускном экзамене.
Часто задаваемые вопросы о решениях NCERT для 11-го класса по математике
Как решения NCERT для 11-го класса по математике от Tiwari Academy могут помочь нам в достижении высоких результатов тестов?
Преподаватели-эксперты Академии Тивари организовали решения NCERT в соответствии с учебной программой совета CBSE. Они предоставляют решения CBSE NCERT для математики класса 11 с широким спектром решаемых задач, которые могут быть очень полезны для достижения высоких результатов тестов. Вопросы решают опытные учителя математики, имеющие большой опыт преподавания предмета. Кроме того, решения NCERT доступны для бесплатной загрузки на веб-сайте Академии Тивари.
Сколько глав в экзамене за первый семестр 11 класса по математике?
Всего в 11 классе математики 16 глав, но на экзаменах первого семестра будут заданы вопросы только из семи глав, упомянутых ниже. Первая глава — Множества , глава -2 — Отношения и функции , Глава 5: Комплексные числа и квадратные уравнения, Глава 9: Последовательность, Глава 16: Вероятность, Глава 10: Прямые линии, Глава 13: Пределы и производные и Глава 15: Статистика.
Математика в 11 классе сложная?
Некоторым учащимся математика в 11-м классе дается сложно, так как в 11-м классе им вводятся новые темы. Кроме того, учебная программа 11-го класса по математике чрезвычайно обширна по сравнению с предыдущим 10-м классом. Но решения NCERT для математики класса 11 для всех глав помогут вам очистить все понятия, и вы сможете получить хорошие оценки на экзамене.
Достаточно ли NCERT для математики в 11 классе?
NCERT — это лучшие ресурсы для подготовки к экзаменам CBSE Board для 11-го класса.


 Отдельно стоит метод использования свойств показательной, логарифмической и других функций при решении задач: иногда ключом к решению уравнения является область определения, область значений, неотрицательность, ограниченность, четность входящих в него функций.
Отдельно стоит метод использования свойств показательной, логарифмической и других функций при решении задач: иногда ключом к решению уравнения является область определения, область значений, неотрицательность, ограниченность, четность входящих в него функций.
 Поэтому для эффективного освоения методов решения показательных и логарифмических уравнений лучше всего воспользоваться услугами , который сумеет рассказать о подобных «подводных камнях» на примерах решения соответствующих экзаменационных задач.
Поэтому для эффективного освоения методов решения показательных и логарифмических уравнений лучше всего воспользоваться услугами , который сумеет рассказать о подобных «подводных камнях» на примерах решения соответствующих экзаменационных задач.

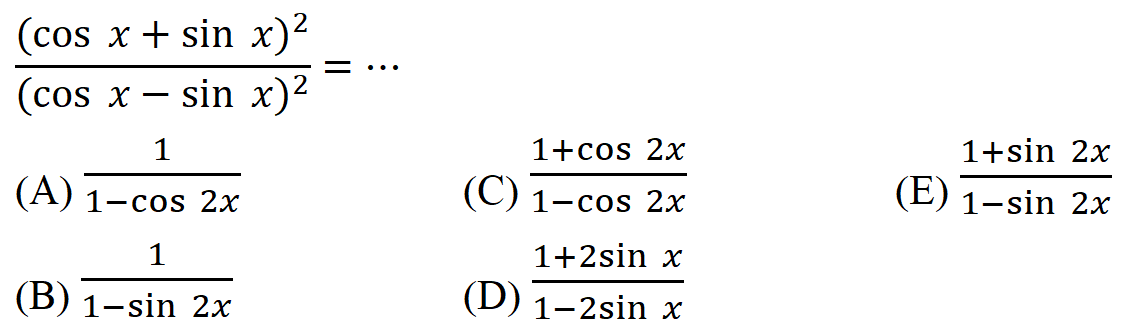 Чтобы
решить
однородное
уравнение,
надо:
Чтобы
решить
однородное
уравнение,
надо: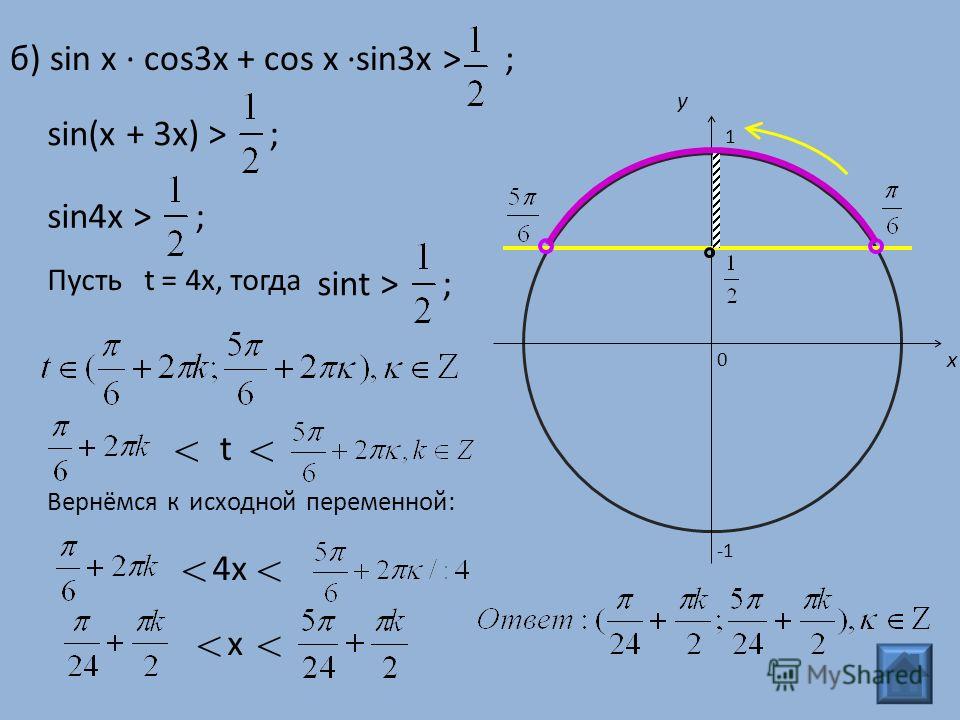 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.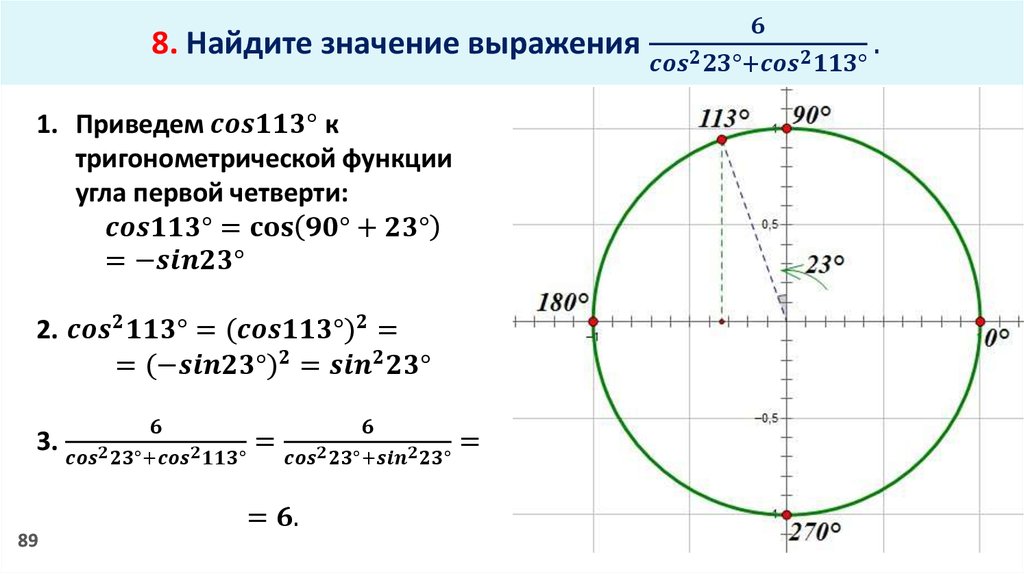 Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.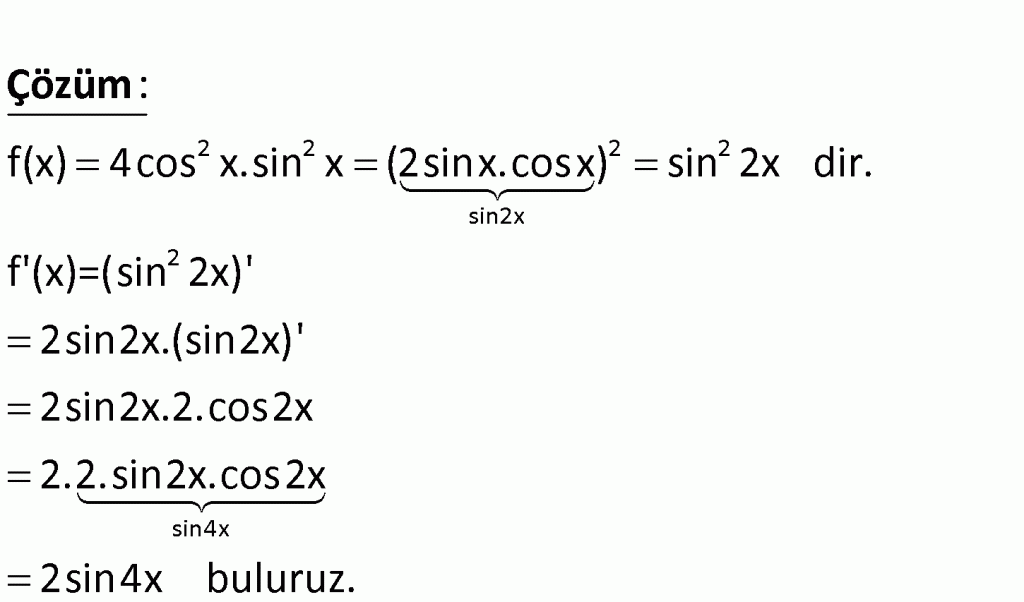 Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
 В случае тригонометрических уравнений необходимо свести их к простейшим, вида: sinx = a , cosx = a , tgx = a , которые легко можно решить.
В случае тригонометрических уравнений необходимо свести их к простейшим, вида: sinx = a , cosx = a , tgx = a , которые легко можно решить.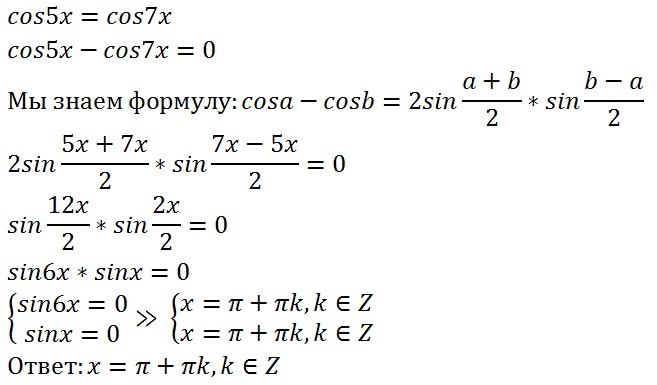
 Но может случиться, что не очевидно, какой делитель выбрать. Для этого существует специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть дано уравнение.
Но может случиться, что не очевидно, какой делитель выбрать. Для этого существует специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть дано уравнение. Повторение ЗУН:
Повторение ЗУН: 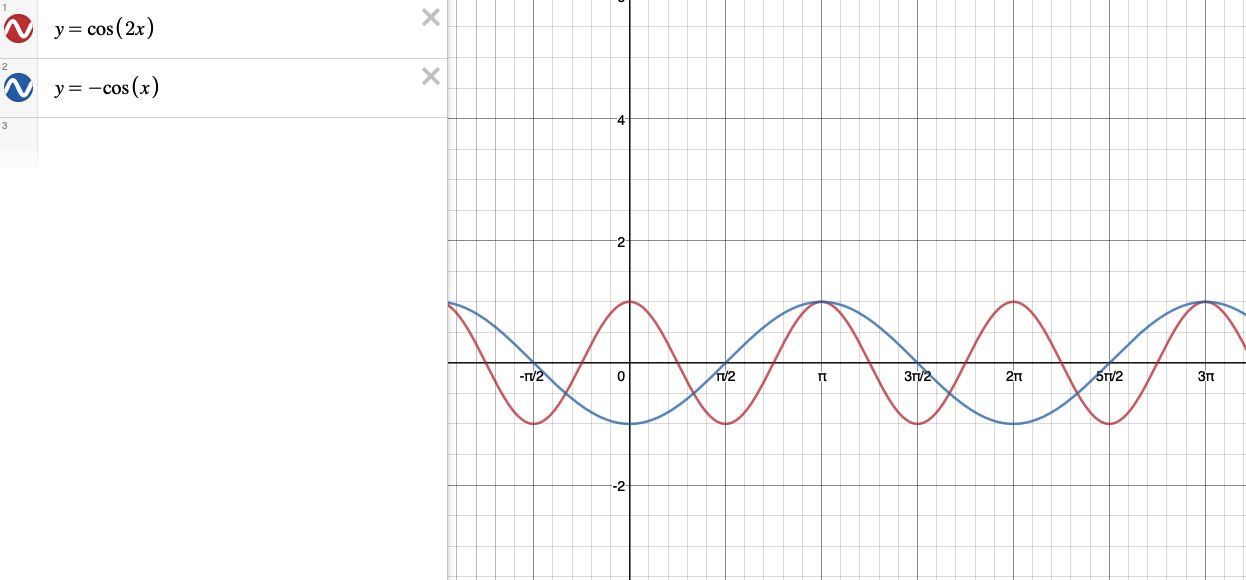 Работа по группам:
Работа по группам:
 )/3
)/3 2x (cos квадрат x) и ее формулу.
2x (cos квадрат x) и ее формулу. Cos2x — это тригонометрическая функция двойного угла, которая определяет значение cos при удвоении угла x.
Cos2x — это тригонометрическая функция двойного угла, которая определяет значение cos при удвоении угла x. Обратите внимание, что угол 2x можно записать как 2x = x + x. Также мы знаем, что cos (a + b) = cos a cos b — sin a sin b. Мы будем использовать это, чтобы доказать идентичность для cos2x. Используя формулу сложения углов для функции косинуса, подставьте a = b = x в формулу для cos (a + b).
Обратите внимание, что угол 2x можно записать как 2x = x + x. Также мы знаем, что cos (a + b) = cos a cos b — sin a sin b. Мы будем использовать это, чтобы доказать идентичность для cos2x. Используя формулу сложения углов для функции косинуса, подставьте a = b = x в формулу для cos (a + b).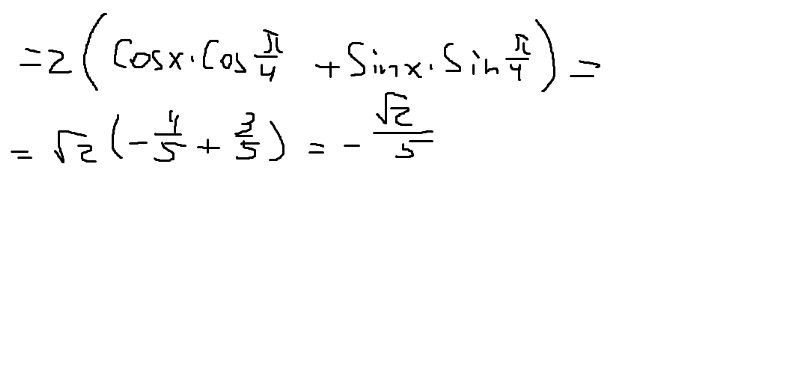
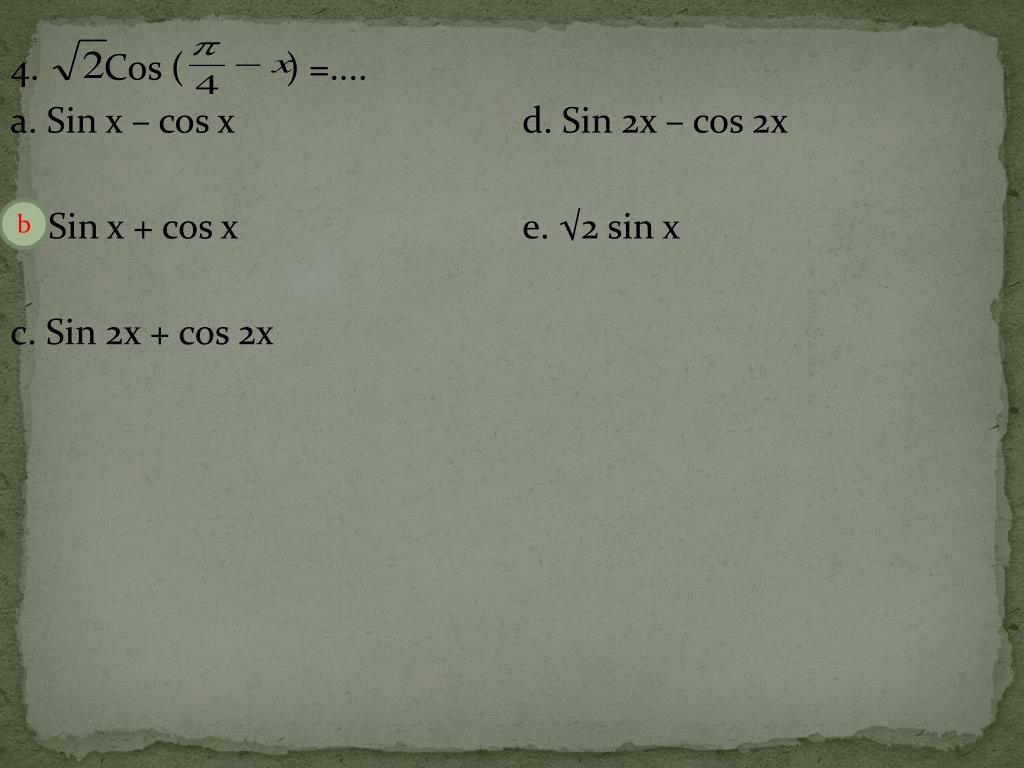 We have,
We have,