2.1.2. Дискретные случайные величины
Определение. Случайную величину x называют Дискретной, если множество ее возможных значений образует конечную или бесконечную последовательность чисел, т. е. конечно или счетно.
Пусть возможные значения дискретной случайной величины x упорядочены по возрастанию
X 1 ≤ X2 ≤¼≤ X N ≤¼. .
Рассмотрим события Ai, Содержащие все элементарные события w, приводящие к значению Xi:
A I={w: X = X I }, I=1, 2, ¼
Пусть Pi обозначает вероятность события Ai :
Pi = R (Ai)=R(w: x = xi ), i=1, 2, ¼ .
События Ai — несовместные События, которые составляют разбиение пространства элементарных событий Ω, т. е. Ω = Ai .
Тогда для вероятностей Pi выполняются свойства
P i ³ 0, i=1, 2, ¼ =
 (2.2)
(2.2)Закон распределения Дискретной случайной величины задается Рядом распределения.
Ряд распределения дискретной случайной величины x может быть представлен таблицей, в первой строке которой помещают возможные значения Xi , а во второй — вероятности Pi , соответствующие этим значениям.
X | X1 | X2 | …Xn… |
PI | P1 | P2 | …Pn… |
Кроме ряда распределения, дискретная случайная величина может быть задана с помощью Функции распределения.
Определение. Функция распределения F(X) случайной величины X это такая функция переменной X, которая равна вероятности того, что случайная величина примет значение, меньшее, чем заданное X,
F (X)=P(w:¦ (w) £ x) (2. 3)
3)
Для всех действительных чисел X.
Для дискретной случайной величины функция распределения определяется как сумма вероятностей для тех значений случайной величины, которые меньше заданного X. Обозначим через В(X) множество возможных значений случайной величины x, предшествующих числу X:
B(X) = {Xi: Xi £ X}. (2.4)
Тогда формулу (2.3) можно записать в виде
F (X) = . (2.5)
Приведем несколько примеров функций распределения дискретных случайных величин.
Пример 2.3. Правильный кубик подбрасывают один раз, и величина x обозначает число очков, выпавшее на его верхней грани. Построим функцию распределения этой случайной величины.
Решение. Обозначим через X возможные значения случайной величины x. В данном примере X={1,2,3,4,5,6}, и вероятность появления грани с любым количеством очков равна РI =.
Напишем ряд распределения этой дискретной случайной величины.
Х | 1 | 2 | 3 | 4 | 5 | 6 |
Р |
Построим функцию распределения по формуле (2.5). Для этого на числовой оси отметим точки из множества X. Они разбивают числовую ось OX
На интервалы (-∞,1), [1,2) [2,3) [3,4) [4,5) [5,6) [6,+ ∞) .Последовательно будем вычислять функцию распределения на каждом из указанных выше интервалов. При любом множество B(X)={Xi : Xi £X} не содержит возможных значений случайной величины, т. е. является пустым множеством. Тогда по формуле (2.5)
F(X)=0.
При любом множество будет состоять из одного значения — 1:
В(X)={Xi : Xi £ X}={1}. Тогда по формуле (2.5)
F(X)=P1 =.
При любом Множество B(X)={Xi : Xi £ X}={1,2}. Тогда по формуле
F(X)=P1+ P2=.
При любом множество
F(X)=P1+ p2+ p3=.
При любом Множество B(X)={Xi : Xi £ X}={1,2,3,4}. Тогда
F(X)=P1+ p2+ p3+ p4=.
При любом множество B(X)={Xi : Xi £ X}={1,2,3,4,5} .Тогда
F(X)=P1+ p2+ p3+ p4+ p5=.
При любом множество B(X)={Xi : Xi £ X}={1,2,3,4,5,6} =X. Тогда
Тогда
F(X)=P1+ p2+ p3+ p4+ p5+ p6=1.
Заметим, что при переходе от одного интервала к другому множество B(X) расширяется на одно значение и от пустого множества переходит к множеству всех возможных значений X={1,2,3,4,5,6}.
Все вычисления можно объединить в формулу
. (2.6)
Пример 2.4. Построим функцию распределения для появления числа гербов при трех подбрасываниях монеты (Пример 2.1).
Решение. Ряд распределения был найден в Примере 2.1.
ξ | 0 | 1 | 2 | 3 |
Обозначим через X множество всех возможных значений этой случайной величины X = { 0, 1, 2, 3 }. Заметим, что множество B(X) при любом X Является подмножеством X. Числа из множества X Разбивают числовую ось на интервалы (-¥,0), [0,1), [1,2), [2,3), [3,+¥).
Числа из множества X Разбивают числовую ось на интервалы (-¥,0), [0,1), [1,2), [2,3), [3,+¥).
Пусть X любое число из интервала (-¥
Возьмем любое XÎ[0,1). Множество B(X) содержит значение 0:
B(X) ={0} и F(X)= P0 =.
Возьмем XÎ[1,2). Множество B(X) ={0,1}, и F(X) = P0+ P1= .
Для всех XÎ[2,3) множество B(X) ={0,1,2}, и F(X)=P0+ P1+P2= .
Для всех XÎ[3,¥) множество B(X)={0,1,2,3}=X . Отсюда следует
F(X)= P0+ P1+P2+P3= .
Запишем полученные значения функции распределения на отдельных интервалах в виде формулы
.
Построим график функции распределения F(X) дискретной случайной
Величины
F(X)
1
0 1 2 3 X
| < Предыдущая | Следующая > |
|---|
|
⇐ ПредыдущаяСтр 5 из 8Следующая ⇒ Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает значения, зависящие от случая. Случайные величины принято обозначать прописными буквами латинского алфавита: X, Y, Z, …, либо буквами греческого алфавита: x, h, q, …, а их значения – строчными буквами латинского алфавита: x, y, z. Дискретной называется случайная величина Х, которая в результате эксперимента Е может принимать только определенные изолированные друг от друга значения. Примеры дискретных случайных величин: число студентов в группе, успешно сдавших экзамен по математике; число клиентов банка, своевременно возвративших кредит; число звонков, поступивших в службу такси в течение часа, и т. д. Случайные величины, возможные значения которых непрерывно заполняют некоторый (конечный или бесконечный) промежуток числовой оси, называются непрерывными. Множество возможных значений непрерывных случайных величин является несчетным множеством. Примеры непрерывных случайных величин: время безотказной работы оборудования после очередного ремонта; время простоя клиента магазина в очереди; масса израсходованного автомобилем бензина на одном и том же расстоянии; отклонение размера изделия от номинала – являются непрерывными случайными величинами.
Закон распределения случайной величины Законом распределения дискретной случайной величины называется соответствие между значениями этой величины и их вероятностями Закон распределения дискретной случайной величины может быть задан таблично или аналитически (то есть с помощью формул). Очевидно, что для полного описания исследуемого вероятностного эксперимента (то есть для исчерпывающего задания характеризующей его случайной величины) недостаточно задать только пространство элементарных событий W. К этому необходимо добавить также: а) для дискретной случайной величины – правило, сопоставляющее каждому возможному значению случайной величины хi вероятность того, что случайная величина
;
б) для непрерывной случайной величины – правило, позволяющее поставить в соответствие любой измеримой области DX возможных значений случайной величины X вероятность попадания значения случайной величины в эту область:
.
Дадим общее определение: законом распределения случайной величины X называется любое соотношение, устанавливающее связь между возможными значениями этой случайной величины и соответствующими им вероятностями.
Ряд распределения Пусть X – дискретная случайная величина, а x1, x2, x3,… – ее значения. Совокупность всех элементарных событий, на которых X принимает фиксированное значение xi, образует событие X = xi. Простейшим способом задания закона распределения дискретной случайной величины является ряд распределения. Это таблица, в первой строке которой указаны возможные значения случайной величины x1, x2, x3, …, а во второй – соответствующие им вероятности p1, p2, p3,…, где pi = P(X = xi) – вероятность того, что в результате эксперимента случайная величина X примет значение xi:
Так как события (X = x1), (X = x2), … – несовместны, и их объединение представляет собой все пространство элементарных событий, то сумма вероятностей рi равна 1:
.
Графическое изображение ряда распределения может быть представлено одним из двух способов: в виде столбцовой диаграммы и в виде многоугольника распределения. Столбцовая диаграмма строится следующим образом: для каждого возможного значения случайной величины восстанавливается перпендикуляр к оси абсцисс, на котором откладывается вероятность данного значения. При построении многоугольника распределения по оси абсцисс откладываются возможные значения случайной величины, по оси ординат – соответствующие им вероятности, и полученные соседние точки соединяются отрезками.
Функция распределения Универсальным способом задания закона распределения, пригодным как для дискретных, так и для непрерывных случайных величин, является функция распределения.
Функцией распределения случайной величины X называется функция F(x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x, то есть
F(x) = P(X < x). Основные свойства функции распределения F(x): 1Так как по определению F(x) равна вероятности события, все возможные значения функции распределения принадлежат отрезку [0; 1]:
0 £ F(x) £ 1.
2Если , то , то есть F(x) – неубывающая функция своего аргумента. 3Вероятность того, что случайная величина примет значение, принадлежащее полуинтервалу [a, b), равна приращению функции распределения на этом интервале: P(a £ X < b) = F(b) – F(a). 4Если все возможные значения случайной величины принадлежат отрезку [a, b], то F(x) = 0, при x £ a; F(x) = 1, при x > b.
Функция распределения дискретных случайных величинможет быть определена по формуле . Если известен ряд распределения дискретной случайной величины, легко вычислить и построить ее функцию распределения. Продемонстрируем, как это делается на примере 23. В общем случае, функция распределения F(x) дискретной случайной величины X есть разрывная ступенчатая функция, непрерывная слева, скачки которой происходят в точках, соответствующих возможным значениям х1, х2, … случайной величины X и равны вероятностям p1, p2, … этих значений. Функция распределения непрерывных случайных величин.Теперь можно дать более точное определение непрерывных случайных величин: случайная величина X называется непрерывной, если ее функция распределения F(x) при всех значениях x непрерывна и, кроме того, имеет производную всюду, за исключением, может быть, отдельных точек. Из непрерывности функции F(x) следует, что вероятность каждого отдельного значения непрерывной случайной величины равна нулю. Так как вероятность каждого отдельного значения непрерывной случайной величины равна 0, свойство 3 функции распределения для непрерывной случайной величины будет иметь вид P(a £ X < b) = P(a £ X £ b) = P(a < X £ b) = P(a < X < b) = F(b) – F(a).
2.2.3 Функция плотности распределения вероятностей Плотностью распределения вероятностей непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке:
f(x) = F ¢(x).
По своему смыслу значения функции f(x) пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки x. Функция плотности распределения f(x), как и функция распределения F(x), является одной из форм задания закона распределения, но она применима только для непрерывных случайных величин. Функцию плотности распределения вероятностей f(x) еще называют дифференциальной функцией распределения, тогда как функцию распределения F(x) называют, соответственно, интегральной функцией распределения. График функции плотности распределения f(x) называется кривой распределения. Рассмотрим свойства, которыми обладает функция плотности распределения непрерывной случайной величины.
Свойство 1.Плотность распределения вероятностей – неотрицательная функция: f(x) ³ 0
(геометрически: кривая распределения лежит не ниже оси абсцисс).
Свойство 2. ; (геометрически: эта вероятность равна площади криволинейной трапеции, ограниченной кривой f(x), осью Ох и прямыми x = a и x = b). Свойство 3. (геометрически: площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице). В частности, если все возможные значения случайной величины принадлежат отрезку [a, b], то Свойство 4.Функция распределения F(x) может быть найдена по известной функции плотности распределения следующим образом: . ⇐ Предыдущая12345678Следующая ⇒ Читайте также: |
Дискретные и непрерывные случайные величины.

По своей физической природе случайные величины могут быть детерминированными и случайными.
Дискретной называют случайную величину, отдельные значения которой можно перенумеровать (число изделий, количество деталей – бракованных и годных и т.п.).
Непрерывной называют случайную величину, возможные значения которой заполняют некоторый промежуток (отклонение размера изготовленной детали от номинала, погрешность измерения, величина отклонения формы детали, высота микронеровностей и т.п.).
Случайная величина не может характеризоваться каким-то одним значением. Для неё необходимо указать множество возможных значений и вероятностные характеристики, заданные на этом множестве.
В том случае, если случайное событие выражается в виде числа, можно говорить о случайной величине. Случайной называют величину, которая в результате испытания примет одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Выпадение некоторого значения случайной величины Х это случайное событие: Х = хi. Среди случайных величин выделяют дискретные и непрерывные случайные величины.
Дискретной случайной величиной называется случайная величина, которая в результате испытания принимает отдельные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным. Примеры дискретной случайной величины: запись показаний спидометра или измеренной температуры в конкретные моменты времени.
Непрерывной случайной величиной называют случайную величину, которая в результате испытания принимает все значения из некоторого числового промежутка. Число возможных значений непрерывной случайной величины бесконечно. Пример непрерывной случайной величины: измерение скорости перемещения любого вида транспорта или температуры в течение конкретного интервала времени.
Любая случайная величина имеет свой закон распределения вероятностей и свою функцию распределения вероятностей. Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом x > X. Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.
Прежде, чем дать определение функции распределения, рассмотрим переменные, которые её определяют. Пусть задано некоторое х – действительное число и получена случайная величина X, при этом x > X. Требуется определить вероятность того, что случайная величина Х будет меньше этого фиксированного значения х.
Функцией распределения случайной величины Х называется функция F(х), определяющая вероятность того, что случайная величина Х в результате испытания примет значение меньшее значения х, то есть:
| F (х) = Р(Х < х ). |
где х – произвольное действительное число.
Случайная величина (непрерывная или дискретная) имеет численные характеристики:
Математическое ожидание М (Х). Эту характеристику можно сравнивать со средним арифметическим наблюдаемых значений случайной величины Х.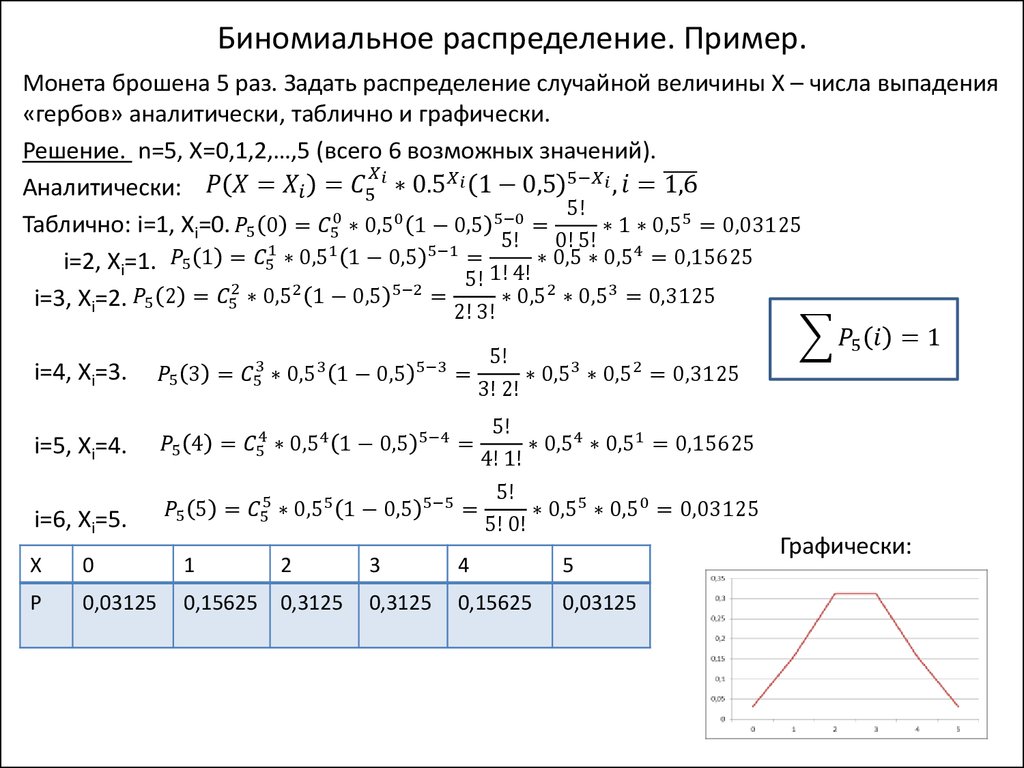
Дисперсия D(X). Это характеристика отклонения случайной величины Х от математического ожидания.
Среднее квадратическое отклонение σ(Х) для дискретной и непрерывной случайной величины Х – это корень квадратный из ее дисперсии:
Случайная величина характеризуется в теории вероятностей законом ее распределения. Этот закон устанавливает связь между возможными значениями случайной величины и соответствующими этим значениям вероятностям их появления. Существует две формы описания закона распределения случайной величины — дифференциальная и интегральная. Причем, в метрологии в основном используется дифференциальная форма — закон распределения плотности вероятностей случайной величины.
Дифференциальный закон распределенияхарактеризуетсяплотностью распределения вероятностей f(x) случайной величиных. Вероятность Р попадания случайной величины в интервал от х1 до х2при этом дается формулой:
Графически эта вероятность представляет собой отношение площади под кривой f(x) в интервале от х1 до х2 к общей площади, ограниченной всей кривой распределения. Как правило, площадь под всей кривой распределения вероятностей нормируют на единицу.
Как правило, площадь под всей кривой распределения вероятностей нормируют на единицу.
В данном случае представлено распределение непрерывной случайной величины. Кроме них существуют и дискретные случайные величины, принимающие ряд определенных значений, которые можно пронумеровать.
Интегральный закон распределения случайной величины представляет собой функцию F(x), определяемую формулой
Вероятность, что случайная величина будет меньше х1 дается значением функции F(х) при х = х1 :
Хотя закон распределения случайных величин является их полной вероятностной характеристикой, нахождение этого закона является довольно трудной задачей и требует проведения многочисленных измерений. Поэтому на практике для описания свойств случайной величины используют различные числовые характеристики распределений. К ним относятся моменты слу-чайных величин: начальные и центральные, которые представляют собой некоторые средние значения. При этом если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения – то центральными.
При этом если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения – то центральными.
Начальный момент k-го порядка определяется формулой:
Наибольший практический интерес представляет начальный момент первого порядка — математическое ожидание случайной величины m1 (k=1):
Математическое ожидание определяет положение центра группирования случайной величины, вокруг которого наблюдается ее рассеяние. Экспериментальной оценкой математического ожидания при многократных измерениях является среднее арифметическое значение измеряемой величины.
Центральный момент k-го порядка определяется формулой:
Особую роль играет центральный момент второго порядка. Он называется дисперсией D случайной величины и характеризует рассеяние отдельных значений этой величины:
На практике чаще используется среднее квадратическое отклонение σ (СКО) случайной величины, определяемое формулой:
Дрейф нуля в усилителях постоянного тока (УПТ). Самопроизвольное изменение напряжения на выходе при отсутствии напряжения на входе – входного сигнала.
Самопроизвольное изменение напряжения на выходе при отсутствии напряжения на входе – входного сигнала.
Дата добавления: 2016-06-15; просмотров: 20376; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Математическое ожидание дискретной случайной величины
Математическим ожиданием (средним значением) случайной величины X, заданной на дискретном вероятностном пространстве, называется числоm=M[X]=∑xipi, если ряд сходится абсолютно.
Назначение сервиса. С помощью сервиса в онлайн режиме вычисляются математическое ожидание, дисперсия и среднеквадратическое отклонение (см. пример). Кроме этого строится график функции распределения F(X).
- Шаг №1
- Шаг №2
- Видеоинструкция
Укажите количество данных
Если данные представлены в виде корреляционной таблицы, то необходимо воспользоваться этим сервисом. Полученное решение сохраняется в файле Word и Excel.
Полученное решение сохраняется в файле Word и Excel.
Свойства математического ожидания случайной величины
- Математическое ожидание постоянной величины равно ей самой: M[C]=C, C – постоянная;
- M[C•X]=C•M[X]
- Математическое ожидание суммы случайных величин равно сумме их математических ожиданий: M[X+Y]=M[X]+M[Y]
- Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: M[X•Y]=M[X]•M[Y], если X и Y независимы.
Свойства дисперсии
- Дисперсия постоянной величины равна нулю: D(c)=0.
- Постоянный множитель можно вынести из-под знака дисперсии, возведя его в квадрат: D(k*X)= k2D(X).
- Если случайные величины X и Y независимы, то дисперсия суммы равна сумме дисперсий: D(X+Y)=D(X)+D(Y).
 2D(Y) + 0 = 81*9 + 64*6 = 1113
2D(Y) + 0 = 81*9 + 64*6 = 1113
Алгоритм вычисления математического ожидания
Свойства дискретных случайных величин: все их значения можно перенумеровать натуральными числами; каждому значению сопоставить отличную от нуля вероятность.- Поочередно умножаем пары: xi на pi.
- Складываем произведение каждой пары xipi.
Например, для n = 4: m = ∑xipi = x1p1 + x2p2 + x3p3 + x4p4
Функция распределения дискретной случайной величины ступенчатая, она возрастает скачком в тех точках, вероятности которых положительны.Пример №1.
xi 1 3 4 7 9 pi 0.  1
10.2 0.1 0.3 0.3
Математическое ожидание находим по формуле m = ∑xipi.
Математическое ожидание M[X].
M[x] = 1*0.1 + 3*0.2 + 4*0.1 + 7*0.3 + 9*0.3 = 5.9
Дисперсию находим по формуле d = ∑x2ipi — M[x]2.
Дисперсия D[X].
D[X] = 12*0.1 + 32*0.2 + 42*0.1 + 72*0.3 + 92*0.3 — 5.92 = 7.69
Среднее квадратическое отклонение σ(x).
σ = sqrt(D[X]) = sqrt(7.69) = 2.78Пример №2. Дискретная случайная величина имеет следующий ряд распределения:
Найти величину a, математическое ожидание и среднее квадратическое отклонение этой случайной величины.Х -10 -5 0 5 10 р а 0,32 2a 0,41 0,03 
Решение. Величину a находим из соотношения: Σpi = 1
Σpi = a + 0,32 + 2a + 0,41 + 0,03 = 0,76 + 3a = 1
0.76 + 3a = 1 или 0.24=3a, откуда a = 0.08Пример №3. Определить закон распределения дискретной случайной величины, если известна её дисперсия, причем х1<x2<x3<x4
x1=6; x2=9; x3=x; x4=15
p1=0,3; p2=0,3; p3=0,1; p4=0,3
d(x)=12,96Решение.
Здесь надо составить формулу нахождения дисперсии d(x):
d(x) = x12p1+x22p2+x32p3+x42p4-m(x)2
где матожидание m(x)=x1p1+x2p2+x3p3+x4p4
Для наших данных
m(x)=6*0,3+9*0,3+x3*0,1+15*0,3=9+0. 1x3
1x3
12,96 = 620,3+920,3+x320,1+1520,3-(9+0.1x3)2
или-9/100 (x2-20x+96)=0
Соответственно надо найти корни уравнения, причем их будет два.
x3=8, x3 =12
Выбираем тот, который удовлетворяет условию х1<x2<x3<x4
x3=12Закон распределения дискретной случайной величины
x1=6; x2=9; x3=12; x4=15
p1=0,3; p2=0,3; p3=0,1; p4=0,3Вычислить математическое ожидание онлайн. Дискретные случайные величины
Случайной величиной называют переменную величину, которая в результате каждого испытания принимает одно заранее неизвестное значение, зависящее от случайных причин. Случайные величины обозначают заглавными латинскими буквами: $X,\ Y,\ Z,\ \dots $ По своему типу случайные величины могут быть дискретными и непрерывными .

Дискретная случайная величина — это такая случайная величина, значения которой могут быть не более чем счетными, то есть либо конечными, либо счетными. Под счетностью имеется ввиду, что значения случайной величины можно занумеровать.
Пример 1 . Приведем примеры дискретных случайных величин:
а) число попаданий в мишень при $n$ выстрелах, здесь возможные значения $0,\ 1,\ \dots ,\ n$.
б) число выпавших гербов при подкидывании монеты, здесь возможные значения $0,\ 1,\ \dots ,\ n$.
в) число прибывших кораблей на борт (счетное множество значений).
г) число вызовов, поступающих на АТС (счетное множество значений).
1. Закон распределения вероятностей дискретной случайной величины.
Дискретная случайная величина $X$ может принимать значения $x_1,\dots ,\ x_n$ с вероятностями $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$. Соответствие между этими значениями и их вероятностями называется законом распределения дискретной случайной величины .
 Как правило, это соответствие задается с помощью таблицы, в первой строке которой указывают значения $x_1,\dots ,\ x_n$, а во второй строке соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$.
Как правило, это соответствие задается с помощью таблицы, в первой строке которой указывают значения $x_1,\dots ,\ x_n$, а во второй строке соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$.$\begin{array}{|c|c|}
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end{array}$Пример 2 . Пусть случайная величина $X$ — число выпавших очков при подбрасывании игрального кубика. Такая случайная величина $X$ может принимать следующие значения $1,\ 2,\ 3,\ 4,\ 5,\ 6$. Вероятности всех этих значений равны $1/6$. Тогда закон распределения вероятностей случайной величины $X$:
$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline\hline
\end{array}$Замечание . Поскольку в законе распределения дискретной случайной величины $X$ события $1,\ 2,\ \dots ,\ 6$ образуют полную группу событий, то в сумме вероятности должны быть равны единице, то есть $\sum{p_i}=1$.
 n_{i=1}{p_ix_i}=1\cdot {{1}\over {6}}+2\cdot {{1}\over {6}}+3\cdot {{1}\over {6}}+4\cdot {{1}\over {6}}+5\cdot {{1}\over {6}}+6\cdot {{1}\over {6}}=3,5.$$
n_{i=1}{p_ix_i}=1\cdot {{1}\over {6}}+2\cdot {{1}\over {6}}+3\cdot {{1}\over {6}}+4\cdot {{1}\over {6}}+5\cdot {{1}\over {6}}+6\cdot {{1}\over {6}}=3,5.$$Можем заметить, что $M\left(X\right)$ заключено между наименьшим ($1$) и наибольшим ($6$) значениями случайной величины $X$.
Пример 4 . Известно, что математическое ожидание случайной величины $X$ равно $M\left(X\right)=2$. Найти математическое ожидание случайной величины $3X+5$.
Используя вышеуказанные свойства, получаем $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\cdot 2+5=11$.
Пример 5 . Известно, что математическое ожидание случайной величины $X$ равно $M\left(X\right)=4$. Найти математическое ожидание случайной величины $2X-9$.
Используя вышеуказанные свойства, получаем $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\cdot 4-9=-1$.
3. Дисперсия дискретной случайной величины.
Возможные значения случайных величин с равными математическими ожиданиями могут по-разному рассеиваться вокруг своих средних значений.
 2D\left(X\right)=4D\left(X\right)=4\cdot 3=12$.
2D\left(X\right)=4D\left(X\right)=4\cdot 3=12$.4. Функция распределения дискретной случайной величины.
Способ представления дискретной случайной величины в виде ряда распределения не является единственным, а главное он не является универсальным, поскольку непрерывную случайную величину нельзя задать с помощью ряда распределения. Существует еще один способ представления случайной величины — функция распределения.
Функцией распределения случайной величины $X$ называется функция $F\left(x\right)$, которая определяет вероятность того, что случайная величина $X$ примет значение, меньшее некоторого фиксированного значения $x$, то есть $F\left(x\right)=P\left(X
Свойства функции распределения :
- $0\le F\left(x\right)\le 1$.
- Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$, равна разности значений функции распределения на концах этого интервала: $P\left(\alpha
- $F\left(x\right)$ — неубывающая.

- ${\mathop{lim}_{x\to -\infty } F\left(x\right)=0\ },\ {\mathop{lim}_{x\to +\infty } F\left(x\right)=1\ }$.
Пример 9 . Найдем функцию распределения $F\left(x\right)$ для закона распределения дискретной случайной величины $X$ из примера $2$.
$\begin{array}{|c|c|}
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end{array}$Если $x\le 1$, то, очевидно, $F\left(x\right)=0$ (в том числе и при $x=1$ $F\left(1\right)=P\left(X
Если $1
Если $2
Если $3
Если $4
Если $5
Если $x > 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)+P\left(X=6\right)=1/6+1/6+1/6+1/6+1/6+1/6=1$.
Итак, $F(x)=\left\{\begin{matrix}
0,\ при\ x\le 1,\\
1/6,при\ 1 1/3,\ при\ 2 1/2,при\ 3 2/3,\ при\ 4 5/6,\ при\ 4 1,\ при\ x > 6.
\end{matrix}\right. $
$Как уже известно, закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.
Математическое ожидание, как будет показано далее, приближенно равно среднему значению случайной величины. Для решения многих задач достаточно знать математическое ожидание. Например, если известно, что математическое ожидание числа выбиваемых очков у первого стрелка больше, чем у второго, то первый стрелок в среднем выбивает больше очков, чем второй, и, следовательно, стреляет лучше второго. Хотя математическое ожидание дает о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения задач, подобных приведенной и многих других, знание математического ожидания оказывается достаточным.

§ 2. Математическое ожидание дискретной случайной величины
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть случайная величина X может принимать только значения х 1 , х 2 , …, х п , вероятности которых соответственно равны р 1 , р 2 , . . ., р п . Тогда математическое ожидание М (X ) случайной величины X определяется равенством
М (X ) = х 1 р 1 + х 2 р 2 + … + x n p n .
Если дискретная случайная величина X принимает счетное множество возможных значений, то
М (Х )=
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Замечание. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. Рекомендуем запомнить это утверждение, так как далее оно используется многократно. В дальнейшем будет показано, что математическое ожидание непрерывной случайной величины также есть постоянная величина.
Пример 1. Найти математическое ожидание случайной величины X , зная закон ее распределения:
Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:
M (X )= 3* 0, 1+ 5* 0, 6+ 2* 0, 3= 3, 9.
Пример 2. Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.
Решение. Случайная величина X — число появлений события А в одном испытании — может принимать только два значения: х 1 = 1 (событие А наступило) с вероятностью р и х 2 = 0 (событие А не наступило) с вероятностью q = 1 —р.
 Искомое
математическое ожидание
Искомое
математическое ожиданиеM (X )= 1* p + 0* q = p
Итак, математическое ожидание числа появлений события в одном испытании равно вероятности этого события. Этот результат будет использован ниже.
§ 3. Вероятностный смысл математического ожидания
Пусть произведено п испытаний, в которых случайная величина X приняла т 1 раз значение х 1 , т 2 раз значение х 2 ,…,m k раз значение x k , причем т 1 + т 2 + …+т к = п. Тогда сумма всех значений, принятых X , равна
х 1 т 1 + х 2 т 2 + … + х к т к .
Найдем среднее арифметическое всех значений, принятых, случайной величиной, для чего разделим найденную сумму на общее число испытаний:
= (х 1 т 1 + х 2 т 2 + .
 .. + х к т к )/п,
.. + х к т к )/п, = х 1 (m 1 / n ) + х 2 (m 2 / n ) + … + х к (т к /п ). (*)
Заметив, что отношение m 1 / n — относительная частота W 1 значения х 1 , m 2 / n — относительная частота W 2 значения х 2 и т. д., запишем соотношение (*) так:
= х 1 W 1 + x 2 W 2 + .. . + х к W k . (**)
Допустим, что число испытаний достаточно велико. Тогда относительная частота приближенно равна вероятности появления события (это будет доказано в гл. IX, § 6):
W 1 p 1 , W 2 p 2 , …, W k p k .

Заменив в соотношении (**) относительные частоты соответствующими вероятностями, получим
x 1 p 1 + х 2 р 2 + … + х к р к .
Правая часть этого приближенного равенства есть М (X ). Итак,
М (X ).
Вероятностный смысл полученного результата таков: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.
Замечание 1. Легко сообразить, что математическое ожидание больше наименьшего и меньше наибольшего возможных значений. Другими словами, на числовой оси возможные значения расположены слева и справа от математического ожидания. В этом смысле математическое ожидание характеризует расположение распределения и поэтому его часто называют центром распределения.
Этот термин заимствован из механики: если массы р 1 , р 2 , .
 .., р п расположены
в точках с абсциссами x 1 , х 2 , …, х n ,
причем
.., р п расположены
в точках с абсциссами x 1 , х 2 , …, х n ,
причем
то абсцисса центра тяжестиx c =
.Учитывая, что
= M (X ) и
получим М (Х ) = х с .Итак, математическое ожидание есть абсцисса центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы — их вероятностям.
Замечание 2. Происхождение термина «математическое ожидание» связано с начальным периодом возникновения теории вероятностей (XVI — XVII вв.), когда область ее применения ограничивалась азартными играми. Игрока интересовало среднее значение ожидаемого выигрыша, или, иными словами, математическое ожидание выигрыша.
Математическое ожидание
Дисперсия непрерывной случайной величины X , возможные значения которой принадлежат всей оси Ох, определяется равенством:
Назначение сервиса .
 Онлайн калькулятор предназначен для решения задач, в которых заданы либо плотность распределения f(x) , либо функция распределения F(x) (см. пример). Обычно в таких заданиях требуется найти математическое ожидание, среднее квадратическое отклонение, построить графики функций f(x) и F(x) .
Онлайн калькулятор предназначен для решения задач, в которых заданы либо плотность распределения f(x) , либо функция распределения F(x) (см. пример). Обычно в таких заданиях требуется найти математическое ожидание, среднее квадратическое отклонение, построить графики функций f(x) и F(x) .Инструкция . Выберите вид исходных данных: плотность распределения f(x) или функция распределения F(x) .
Задана плотность распределения f(x) Задана функция распределения F(x)Задана плотность распределения f(x):
Задана функция распределения F(x):
Непрерывная случайна величина задана плотностью вероятностей
(закон распределения Релея – применяется в радиотехнике). Найти M(x) , D(x) .Случайную величину X называют непрерывной , если ее функция распределения F(X)=P(X Функция распределения непрерывной случайной величины применяется для вычисления вероятностей попадания случайной величины в заданный промежуток:
P(α причем для непрерывной случайной величины не имеет значения, включаются в этот промежуток его границы или нет:
P(α Плотностью распределения непрерывной случайной величины называется функция
f(x)=F’(x) , производная от функции распределения.
Свойства плотности распределения
1. Плотность распределения случайной величины неотрицательна (f(x) ≥ 0) при всех значениях x.
2. Условие нормировки:Геометрический смысл условия нормировки: площадь под кривой плотности распределения равна единице.
3. Вероятность попадания случайной величины X в промежуток от α до β может быть вычислена по формуле
Геометрически вероятность попадания непрерывной случайной величины X в промежуток (α, β) равна площади криволинейной трапеции под кривой плотности распределения, опирающейся на этот промежуток.
4. Функция распределения выражается через плотность следующим образом:Значение плотности распределения в точке x не равно вероятности принять это значение, для непрерывной случайной величины речь может идти только о вероятности попадания в заданный интервал. Пусть }
Дискретные случайные величины, их числовые характеристики и функция распределения.
Величина, которая в зависимости от случая, может принимать те или другие числовые значения называется случайной.
 Примерами случайной величины являются: размер выигрыша, который выпал на билет лотереи; количество зерен в случайно взятом колосе; количество очков при бросании кубика; результат измерения длины, массы, времени и т.д.
Примерами случайной величины являются: размер выигрыша, который выпал на билет лотереи; количество зерен в случайно взятом колосе; количество очков при бросании кубика; результат измерения длины, массы, времени и т.д.Случайные величины обозначаются заглавными буквами латинского алфавита X, Y, Z, а их значения – малыми буквами (с индексами) – x, y, z.
Величина, которая может принимать только конечное или счетное множество значений, называется дискретной.
Законом распределения дискретной случайной величины называется соответствие между значениями , , ,… этой величины и их вероятностями , , ,…
Закон распределения дискретной случайной величины может быть задан таблично или аналитически.
Универсальным способом задания случайной величины X является задание её функции распределения, которая определяется равенством: , где x – любое действительное число.
Значение функции распределения в точке x равно вероятности события, состоящего в том, что случайная величина примет значение меньше, чем x.

Свойства функции распределения.
1. Все значения функции распределения F(x) принадлежат отрезку [0; 1], т.е.
2. Функция F(x) неубывающая, т.е. если
3. Функция F(x) в точке x0 непрерывна слева, т.е.
4. Если функция распределения F(x) задана, то вероятность события вычисляется по формуле
5.
Если дискретная СВ Х принимает конечное множество значений х1, х2, … , хn соответственно с вероятностями р1, р2, … , рn, то ее закон распределения определяется формулой ,
Этот закон можно задать таблицей:
X x1 x2 x3 … xn P p1 p2 p3 … pn Для наглядности закон распределения дискретной СВ изображают графически, для чего в прямоугольной декартовой системе координат строят точки (xi,pi) и соединяют их последовательно отрезками прямых.
 Полученная при этом ломаная линия называется многоугольником (полигоном) распределения СВ Х.
Полученная при этом ломаная линия называется многоугольником (полигоном) распределения СВ Х.—————————————————————————————————————-
Дискретные СВ. Стр 1.
Закон распределения полностью характеризует случайную величину. Кроме того, в теории вероятностей широко используются некоторые «типичные» значения, которые характеризуют случайную величину суммарно. Эти числа, описывающие некоторые характерные черты распределения, называются числовыми характеристиками.
Математическое ожидание характеризует среднее значение случайной величины, вокруг которого группируются все ее значения.
Термин «математическое ожидание» связан с начальным периодом развития теории вероятностей, когда она развивалась на примерах и задачах азартных игр, и игрока интересовал средний выигрыш, т.е. среднее значение ожидаемого выигрыша.
Для дискретных случайных величин математическое ожидание М(х) равно сумме произведений всех возможных значений величины X на соответствующие вероятности:
Для обозначения математического ожидания используются и другие символы:а, .

Свойства математического ожидания.
1) Значение математического ожидания случайной величины Х заключено между ее наименьшим и наибольшим значениями.
2) Математическое ожидание постоянной величины равно этой постоянной:
3) Постоянный множитель можно выносить за знак математического ожидания:
4) Математическое ожидание алгебраической суммы конечного члена случайных величин равно алгебраической сумме их математических ожиданий:
5) Математическое ожидание произведения конечного числа независимых случайных величин равно произведению их математических ожиданий:
Дисперсией D(X) дискретной случайной величины X называется математическое ожидание квадрата отклонения случайной величины X от ее математического ожидания: Дисперсия является мерой рассеивания значений СВ относительно её математического ожидания.

Дисперсию удобно вычислять по формуле:
Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю:
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
3) Дисперсия алгебраической суммы нескольких независимых СВ равна сумме их дисперсий:
Средним квадратическим (стандартным) отклонением случайной величины X называется корень квадратный из дисперсии:
—————————————————————————————————————-
Дискретные СВ. Стр 2.
Пример 1. По мишени стреляют один раз с вероятностью попадания 0,6. Случайная величина X – число попаданий. Найти закон распределения этой случайной величины.
Решение. Очевидно, X может принимать только два значения: 1 и 0, причем их вероятности равны соответственно 0,6 и 0,4.
 Действительно, при выстреле возможны два исхода: попадание (тогда X=1) и промах (тогда X=0). Тогда:
Действительно, при выстреле возможны два исхода: попадание (тогда X=1) и промах (тогда X=0). Тогда:X P 0,6 0,4 Пример 2.Дискретная случайная величина X задана законом распределения:
X P 0,2 0,1 0,5 0,2 Построить многоугольник распределения.
Решение. Построим прямоугольную систему координат, причем по оси абсцисс будем откладывать возможные значения xi, а по оси ординат – соответствующие вероятности Построим точки M1(1; 0,2), M2(2; 0,1), M3(4; 0,5), M4(6; 0,2).
 Соединив эти точки отрезками прямых, получим искомый многоугольник распределения.
Соединив эти точки отрезками прямых, получим искомый многоугольник распределения.Пример 3. Найти функцию распределения дискретной случайной величины Х из примера 2.
Решение. Используя данные из таблицы, получим функцию распределения:
График функции F(x) представлен на рисунке:
—————————————————————————————————————-
Дискретные СВ. Стр 3.
Пример 4. В денежной лотерее разыгрывается 1 выигрыш в 1000 денежных единиц, 10 выигрышей по 100 денежных единиц и 100 выигрышей по 1 денежной единице при общем числе билетов 10000. Найти закон распределения случайного выигрыша X для владельца одного лотерейного билета и математическое ожидание выигрыша X.
Решение. Возможные значения для X: Вероятности их будут: Следовательно, закон распределения выигрыша X может быть задан таблицей:
X P 0,9889 0,01 0,001 0,0001 Найдем математическое ожидание выигрыша X.
 Используя полученную таблицу, имеем:
Используя полученную таблицу, имеем:Пример 5. Случайная величина X задана законом распределения:
X P 0,2 0,2 0,3 0,1 0,2 Найти D(X).
Решение. Имеем:
Задачи для самостоятельного решения.
№1.Пусть случайная величина X – число очков, выпавших при подбрасывании игральной кости. Найдите закон распределения случайной величины X.
№2. Дискретная случайная величина X задана законом распределения:
X P 0,2 0,1 0,4 0,3 Постройте полигон распределения.

№3. Дискретная случайная величина задана законом распределения:
X P 0,2 0,1 0,4 0,3 Найдите функцию распределения и постройте ее график.
№4. Найдите дисперсию случайной величины X, заданной законом распределения:
X –1 P 0,2 0,3 0,5 №5. Производятся 2 выстрела с вероятностями попадания в цель, равными p1=0,4; p2=0,3. Найдите математическое ожидание общего числа попаданий.
№6. Вероятность того, что студент сдаст экзамен на «5» равна 0,2; на «4» – 0,4.
 Определите вероятность получения им оценок «3» и «2», если известно, что М(Х)=3,7. Дискретная случайная величина X – оценка, полученная студентом на экзамене.
Определите вероятность получения им оценок «3» и «2», если известно, что М(Х)=3,7. Дискретная случайная величина X – оценка, полученная студентом на экзамене.—————————————————————————————————————-
Дискретные СВ. Стр 4.
№7. Рассматривается работа трех функционирующих независимо друг от друга технических устройств (ТУ). Вероятности безопасной работы в течение заданного времени для каждого из ТУ соответственно равны 0,6; 0,7; 0,75. Рассматривается случайная величина Х – число ТУ, проработавших безотказно в течение времени t. Построить ряд распределения и полигон распределения этой случайной величины, найти функцию распределения и построить ее график. Вычислить числовые характеристики данной СВ.
№8. Вероятность успешной сдачи данного экзамена для каждого из четырёх студентов равна 0,8. СВ Х – число студентов, успешно сдавших экзамен.
 Построить ряд распределения и полигон распределения этой случайной величины, найти функцию распределения и построить ее график. Вычислить числовые характеристики данной СВ.
Построить ряд распределения и полигон распределения этой случайной величины, найти функцию распределения и построить ее график. Вычислить числовые характеристики данной СВ.№9. В коробке 7 карандашей, из которых 4 красных. Из этой коробки наудачу извлекают 3 карандаша. Найдите закон распределения случайной величины X, равной числу красных карандашей в выборке. Вычислить числовые характеристики данной СВ.
Домашнее задание к практической работе №6.
№1. Разыгрываются две вещи стоимостью по 5 денежных единиц и одна вещь стоимостью 30 денежных единиц. Составьте закон распределения выигрышей для человека, купившего один билет из 50.
№2. Дискретная случайная величина X задана законом распределения:
X P 0,5 0,2 0,3 Найдите функцию распределения F(X), постройте ее график.

№3. Найдите дисперсию случайной величины X, заданной таблицей распределения:
X P 0,1 0,6 0,3 №4. По одному и тому же маршруту в один и тот же день совершают полёт три самолёта. Каждый самолёт с вероятностью 0,7 может произвести посадку по расписанию. Для случайного числа самолётов, отклонившихся от расписания, составить ряд распределения. Найти функцию распределения и числовые характеристики.
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам…
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования…
Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? — задался я вопросом.
 ..
..Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
10 примеров случайных величин в реальной жизни
Случайная величина — это переменная, возможные значения которой являются результатами случайного процесса.
Существует два типа случайных величин:
- Дискретные : могут принимать только счетное число различных значений, таких как 0, 1, 2, 3, 50, 100 и т. д.
- Непрерывный : Может принимать бесконечное количество возможных значений, таких как 0,03, 1,2374553 и т. д.
В этой статье мы поделимся 10 примерами случайных величин в различных реальных ситуациях.
Пример 1: количество проданных товаров (дискретное)Одним из примеров дискретной случайной величины является количество товаров, проданных в магазине в определенный день.

Используя исторические данные о продажах, магазин может создать распределение вероятностей, которое показывает, насколько вероятно, что они продают определенное количество товаров в день.
Например:
Количество позиций Вероятность 0 .004 1 .023 2 .065 . . . . . . Вероятность того, что они продадут 0 товаров, равна 0,004, вероятность того, что они продадут 1 товар, равна 0,023 и т. д.
Пример 2: Количество покупателей (дискретное) это количество покупателей , которые входят в магазин в данный день.Используя исторические данные, магазин может создать распределение вероятностей, которое показывает, насколько вероятно, что определенное количество покупателей войдет в магазин.
Например:
Пример 3: Количество дефектных изделий (дискретное)Количество клиентов Вероятность 0 .  01
011 .03 2 .04 . . . . . . Другим примером дискретной случайной величины является количество дефектных изделий , произведенных за партию определенным заводом-изготовителем.
Используя исторические данные о дефектных продуктах, завод может создать распределение вероятностей, которое показывает, насколько вероятно, что определенное количество продуктов в данной партии будет дефектным.
Например:
Пример 4. Количество дорожно-транспортных происшествий (дискретное)Количество дефектных изделий Вероятность 0 .44 1 .12 2 .02 . . . . . . Другим примером дискретной случайной величины является число дорожно-транспортных происшествий , которые произошли в определенном городе в данный день.

Используя исторические данные, полицейское управление может создать распределение вероятностей, которое показывает, насколько вероятно, что определенное количество несчастных случаев произойдет в определенный день.
Например:
Пример 5: Количество хоум-ранов (дискретное)Количество дорожно-транспортных происшествий Вероятность 0 .22 1 .45 2 .11 . . . . . . Другим примером дискретной случайной величины является число хоум-ранов , совершенных определенной бейсбольной командой в игре.
Используя исторические данные, спортивные аналитики могут создать распределение вероятностей, которое показывает, насколько вероятно, что команда забьет определенное количество хоумранов в данной игре.

Например:
Пример 6. Время марафона (непрерывное)Количество хоумранов Вероятность 0 .31 1 .39 2 .12 . . . . . . Одним из примеров непрерывной случайной величины является время марафона данного бегуна.
Это пример непрерывной случайной величины, поскольку она может принимать бесконечное число значений.
Например, бегун может пробежать марафон за 3 часа 20 минут 12,0003433 секунды. Или они могут пробежать марафон за 4 часа 6 минут 2,28889 секунды и т. д.
В этом сценарии мы могли бы использовать историческое время марафона для создания распределения вероятностей, которое сообщает нам вероятность того, что данный бегун финиширует между определенным интервалом времени.
Пример 7: Процентная ставка (непрерывная)
Другим примером непрерывной случайной величины является процентная ставка кредитов в определенной стране.
Это непрерывная случайная величина, поскольку она может принимать бесконечное число значений. Например, процентная ставка по кредиту может составлять 3,5%, 3,765555%, 4,00095% и т. д.
процентная ставка в пределах определенного интервала.
Пример 8: Вес животного (непрерывный)Другим примером непрерывной случайной величины является вес определенного животного, например собаки.
Это непрерывная случайная величина, поскольку она может принимать бесконечное число значений. Например, собака может весить 30,333 фунта, 50,340999 фунта, 60,5 фунта и т. д. две разные суммы.
Пример 9: Высота растения (непрерывно)Другим примером непрерывной случайной величины является высота определенного вида растения.

Это непрерывная случайная величина, поскольку она может принимать бесконечное число значений. Например, растение может иметь высоту 6,5555 дюйма, 8,95 дюйма, 12,32426 дюйма и т. д.
В этом случае мы могли бы собрать данные о высоте этого вида растений и создать распределение вероятностей, которое говорит нам о вероятности случайно выбранное растение имеет высоту между двумя разными значениями.
Пример 10: Пройденное расстояние (непрерывно)Другим примером непрерывной случайной величины является расстояние, пройденное определенным волком в сезон миграции.
Это непрерывная случайная величина, поскольку она может принимать бесконечное число значений. Например, волк может пройти 40,335 миль, 80,5322 миль, 105,59 миль и т. д. путешествовать в пределах определенного интервала расстояния.
Дополнительные ресурсыВ следующих руководствах представлена дополнительная информация о переменных в статистике:
Знакомство со случайными величинами
Что такое i. i.d. Случайные переменные?
i.d. Случайные переменные?
Что такое уровни независимой переменной?Просмотреть все сообщения Zach
Дискретные случайные величины » Биостатистика » Колледж общественного здравоохранения и медицинских профессий » Университет Флориды
- Обозначение
- Раздел План
- Распределения вероятностей
- Гистограммы вероятностей
- Область гистограммы вероятности
- Поиск вероятностей
- Ключевые слова
- Среднее значение дискретной случайной величины
- Дисперсия и стандартное отклонение дискретной случайной величины
CO-6: Применять основные понятия вероятности, случайных вариаций и широко используемых статистических распределений вероятностей.
Видео: Дискретные случайные величины (всего 22:40)
Начнем с дискретных случайных величин: переменных, возможные значения которых представляют собой список различных значений.
 Чтобы определиться с обозначениями, давайте еще раз посмотрим на пример с подбрасыванием монеты:
Чтобы определиться с обозначениями, давайте еще раз посмотрим на пример с подбрасыванием монеты:Правильная монета подбрасывается дважды.
- Пусть случайная величина X будет количеством решек, которые мы получим в этом случайном эксперименте.
- В этом случае возможные значения, которые может принимать X, равны
- 0 (если получится ЧЧ),
- 1 (если получить HT или TH),
- и 2 (если получим ТТ).
Обозначение
Если мы хотим найти вероятность события «выпадение 1 решки», мы напишем: P(X = 1)
Если мы хотим найти вероятность события «выпадение 0 решек », мы напишем: P(X = 0)
В общем, мы будем писать: P(X = x) или P(X = k) для обозначения вероятности того, что дискретных случайная величина X получает значение x или k соответственно.
Многие учащиеся предпочитают второе обозначение, поскольку отслеживание разницы между X и x может привести к путанице.

- Здесь X представляет случайную величину, а x или k обозначают интересующее значение в текущей задаче (0, 1 и т. д.).
- Обратите внимание, что для случайных величин мы будем использовать заглавную букву, а для значения мы будем использовать строчную букву.
План раздела
Способ организации этого раздела о дискретных случайных величинах очень похож на то, как мы организовали наше обсуждение одной количественной переменной в модуле исследовательского анализа данных.
Он будет разделен на четыре секции.
- Сначала мы обсудим вероятность распределения дискретной случайной величины, способы ее отображения и способы ее использования для нахождения интересующих вероятностей.
- Затем мы перейдем к разговору о среднем значении и стандартном отклонении дискретной случайной величины, которые являются мерами центра и разброса ее распределения.
- Мы завершим эту часть обсуждением специального и очень распространенного класса дискретных случайных величин:0009 биномиальная

Распределения вероятностей
LO 6.12: Используйте распределение вероятностей для дискретной случайной величины, чтобы найти вероятность интересующих событий.
Когда мы научились находить вероятности, применяя базовые принципы, мы обычно сосредоточивались только на одном конкретном исходе или событии, например на вероятности выпадения ровно одной решки при двукратном подбрасывании монеты или вероятности выпадения пятерки при двойном подбрасывании. кубик брошен.
Теперь, когда мы освоили решение отдельных вероятностных задач, мы приступим к рассмотрению общей картины, рассматривая все возможные значения дискретной случайной величины вместе с их соответствующими вероятностями.
Этот список возможных значений и вероятностей называется распределением вероятностей случайной величины.
Комментарии:
- В разделе Исследовательский анализ данных этого курса мы часто рассматривали распределение выборочных значений в наборе количественных данных.
 Мы бы отображали значения с помощью гистограммы и суммировали их, сообщая их среднее значение.
Мы бы отображали значения с помощью гистограммы и суммировали их, сообщая их среднее значение. - В этом разделе, когда мы рассматриваем распределение вероятностей случайной величины, мы рассматриваем все ее возможные значения и их общие вероятности появления.
- Таким образом, мы имеем в виду всю совокупность значений переменной. Когда мы отображаем их с помощью гистограммы или суммируем их со средним значением, они представляют совокупность значений, а не выборку.
- Различие между выборкой и совокупностью является важным понятием в статистике, потому что конечная цель состоит в том, чтобы сделать выводы о неизвестных значениях для совокупности на основе того, что наблюдается в выборке.
В следующих примерах мы иногда будем иллюстрировать, как создается распределение вероятностей.
Мы делаем это, чтобы продемонстрировать полезность правил вероятности, которые мы обсуждали ранее, и ясно проиллюстрировать, как можно создавать распределения вероятностей.
Поскольку мы больше сосредоточены на методах, основанных на данных, вам часто будет даваться распределение вероятностей, основанное на данных, в отличие от построения теоретического распределения вероятностей на основе подбрасывания монет или подобных классических вероятностных экспериментов.
Вспомните наш первый пример, когда мы ввели понятие случайной величины. В этом примере мы бросили монету дважды.
ПРИМЕР: Двойное подбрасывание монеты
Каково распределение вероятностей X, где случайная величина X – это количество решек, выпавших при двух подбрасываниях правильной монеты?
Прежде всего заметим, что, поскольку монета честная, каждый из четырех исходов HH, HT, TH, TT в выборочном пространстве S равновероятен, и поэтому каждый имеет вероятность 1/4.
(В качестве альтернативы можно применить принцип умножения, чтобы найти вероятность каждого исхода 1/2 * 1/2 = 1/4.)
X принимает значение 0 только для исхода HH , поэтому вероятность того, что X = 0, равна 1/4.
X принимает значение 1 для исходов HT или TH . По принципу сложения вероятность того, что X = 1, равна 1/4 + 1/4 = 1/2.
Наконец, X принимает значение 2 только для исхода TT , поэтому вероятность того, что X = 2, равна 1/4 .
Распределение вероятностей случайной величины X легко представить в виде таблицы:
значение х».
Способ интерпретации этой таблицы:
- X принимает значения 0, 1, 2 и P(X = 0) = 1/4, P(X = 1) = 1/2, P(X = 2) ) = 1/4.
Обратите внимание, что события типа (X = x) подчиняются установленным ранее принципам вероятности и дадут нам способ систематического исследования поведения случайных величин.
В частности, теперь будут сформулированы первые два принципа в контексте вероятностных распределений случайных величин.
Любое распределение вероятностей из дискретных случайных переменных должно удовлетворять:
Распределение вероятностей для двух подбрасываний монеты было достаточно просто построить сразу.
Для более сложных случайных экспериментов обычно сначала составляют таблицу всех результатов и их вероятностей, а затем используют принцип сложения, чтобы сжать эту информацию в фактическую таблицу распределения вероятностей.
ПРИМЕР: Трижды подбрасывание монеты
Монета подбрасывается три раза. Пусть случайная величина X будет количеством решек.
Найдите распределение вероятностей X.
Мы будем следовать тем же рассуждениям, что и в предыдущем примере:
Сначала мы указываем 8 возможных исходов в S вместе с числом и вероятностью этого исхода.
- Поскольку все они равновероятны, вероятность каждого из них равна 1/8.
- В качестве альтернативы, согласно принципу умножения, каждая конкретная последовательность из трех лицевых сторон монеты имеет вероятность 1/2 * 1/2 * 1/2 = 1/8.
Затем мы выясняем, каково значение X (количество решек) для каждого возможного исхода.
Далее, мы используем принцип сложения, чтобы утверждать, что
- P(X = 1) = P(HHT или HTH или THH) = P(HHT) + P(HTH) + P(THH) = 1 /8 + 1/8 + 1/8 = 3/8.

- Аналогично, P(X = 2) = P(HTT или THT или TTH) = 3/8.
Результирующее распределение вероятностей:
В предыдущих двух примерах нам нужно было самим указать распределения вероятностей, исходя из физических обстоятельств ситуации.
В некоторых случаях распределение вероятностей может быть задано формулой.
Такая формула должна согласовываться с ограничениями, налагаемыми законами вероятности, так что вероятность каждого исхода должна быть между 0 и 1, а вероятности всех возможных исходов должны в сумме равняться 1.
Мы увидим это с биномиальным распределением.
Гистограммы вероятностей
Мы научились отображать распределение значений выборки для количественной переменной с помощью гистограммы, в которой горизонтальная ось представляет диапазон значений в выборке.
- Вертикальная ось представляет частоту или относительную частоту (иногда в процентах) выборочных значений, встречающихся в этом интервале.

- Ширина каждого прямоугольника на гистограмме представляет собой интервал или часть возможных значений количественной переменной.
- Высота каждого прямоугольника была частотой (или относительной частотой) для этого интервала.
Точно так же мы можем отобразить распределение вероятности случайной величины с помощью гистограммы вероятности.
- Горизонтальная ось представляет диапазон всех возможных значений случайной величины
- Вертикальная ось представляет вероятности этих значений.
Вот пример гистограммы вероятности.
(Такие вероятности не всегда увеличиваются, просто в этом примере они таковы).
Площадь гистограммы вероятности
Обратите внимание, что каждый прямоугольник на гистограмме имеет ширину 1 единицу. Высота каждого прямоугольника — это вероятность его появления.
Таким образом, площадь каждого прямоугольника равна основанию, умноженному на высоту, что для этих прямоугольников равно 1, умноженному на его вероятность для каждого значения X.
Это означает, что для вероятностных распределений дискретных случайных величин сумма площадей все прямоугольники равны сумме всех вероятностей. Общая площадь = 1 .
Для распределений вероятностей дискретных случайных величин это эквивалентно тому свойству, что сумма всех вероятностей должна равняться 1,
Учитесь на практике: Распределения вероятностей
Поиск вероятностей
Мы видели, как создаются распределения вероятностей. Теперь пришло время использовать их для поиска вероятностей.
ПРИМЕР: Смена специальности
Случайная выборка выпускников была опрошена непосредственно перед выпуском. Был задан один вопрос:
Сколько раз вы меняли специальность?
Результаты отображаются в виде распределения вероятностей.
Используя это распределение вероятностей, мы можем ответить на такие вероятностные вопросы, как:
Какова вероятность того, что случайно выбранный выпускник сменил специальность более одного раза?
Это можно записать как P(X > 1).
Мы можем найти эту вероятность, добавив соответствующие отдельные вероятности в распределение вероятностей.
- Р(Х > 1)
- = Р(Х = 2) + Р(Х = 3) + Р(Х = 4) + Р(Х = 5)
- = 0,23 + 0,09 + 0,02 + 0,01
- = 0,35
Как вы только что видели в этом примере, нам нужно обратить внимание на формулировку вероятностного вопроса.
Ключевые слова, которые подсказали нам, какие значения использовать для X, — это больше, чем .
Следующее поясняет и укрепляет ключевых слов и их значения.
Ключевые слова
Давайте начнем с некоторых повседневных ситуаций, используя не менее и не более .
Предположим, кто-то сказал вам: «Мне нужно, чтобы вы написали не менее 10 страниц для курсовой работы».
- Что это значит?
- Это означает, что 10 страниц — это наименьший объем, который вы собираетесь написать.

- Другими словами, вы напишете 10 или более страниц курсовой работы.
- Это то же самое, что сказать: « не менее 10 страниц».
- Так, например, написав 9страниц было бы неприемлемо.
С другой стороны, предположим, вы думаете о том, сколько детей у вас будет. Вы хотите не более 3 детей .
- Это означает, что трое детей — это максимум, что вы хотите иметь.
- Другими словами, у вас будет 3 или менее
- Это то же самое, что сказать: « не более 3 детей».
- Так, например, вы бы не хотели иметь 4 детей.
В следующей таблице приведен список некоторых ключевых слов, которые необходимо знать.
Предположим, что случайная величина X имеет возможные значения от 0 до 5.
| Ключевые слова | Значение | Символы | Значения для X |
|---|---|---|---|
| более 2 | строго больше 2 | Х > 2 | 3, 4, 5 |
| не более 2 | 2 или менее | Х ≤ 2 | 0, 1, 2 |
| менее 2 | строго меньше 2 | Х < 2 | 0, 1 |
| не менее 2 | 2 или более | Х ≥ 2 | 2, 3, 4, 5 |
| не менее 2 | 2 или более | Х ≥ 2 | 2, 3, 4, 5 |
| не более 2 | 2 или менее | Х ≤ 2 | 0, 1, 2 |
| ровно 2 | 2, не больше и не меньше, только 2 | Х = 2 | 2 |
Прежде чем мы перейдем к следующему разделу о средних значениях и дисперсиях распределения вероятностей, давайте еще раз вернемся к примеру с изменением основных характеристик:
ПРИМЕР.
 вы думаете, что было бы необычно менять специальность 2 или более раз?
вы думаете, что было бы необычно менять специальность 2 или более раз?Ответ :
- P(X ≥ 2) = 0,35.
- Итак, в 35% случаев студент меняет специальность 2 и более раз.
- Это означает, что в этом нет ничего необычного.
Вопрос : Как вы думаете, было бы необычно менять специальность 4 или более раз?
Ответ :
- P(X ≥ 4) = 0,03.
- Итак, в 3% случаев студент меняет специальность 4 и более раз.
- Это означает, что это довольно необычно.
Мы можем ответить даже на более сложные вопросы, используя наши правила вероятности!
Вопрос : Какова вероятность смены специальности только один раз при хотя бы одном изменении специальности.
Ответ :
- P(X = 1 | X ≥ 1) = P(X = 1 И X ≥ 1)/P(X ≥ 1) [с использованием правила вероятности 7]
- = P(X = 1)/P(X ≥ 1) [поскольку единственным исходом, удовлетворяющим одновременно X = 1 и X ≥ 1, является X = 1]
- = (0,37)/(0,37+0,23+0,09+0,02+0,01) = 0,37/0,72 = 0,5139.

- Таким образом, среди студентов, которые меняют специальность, 51% этих студентов меняют специальность только один раз.
После того, как мы узнаем о средних значениях и стандартных отклонениях, у нас будет другой способ ответить на эти вопросы.
Среднее дискретной случайной величины
LO 6.13: Найти среднее значение, дисперсию и стандартное отклонение дискретной случайной величины.
В разделе Исследовательский анализ данных (EDA) мы отобразили распределение одной количественной переменной с помощью гистограммы и дополнили ее числовыми показателями центра и разброса.
Здесь мы делаем то же самое.
- Отображаем распределение вероятностей дискретной случайной величины с помощью таблицы, формулы или гистограммы.
- И дополнить его числовыми показателями центра и разброса распределения вероятностей.
Эти меры представляют собой среднее и стандартное отклонение случайной величины .
Этот раздел будет посвящен внедрению этих мер. Как и прежде, мы начнем с числового измерения центра, среднего. Давайте начнем с повторного рассмотрения примера, который мы видели в EDA.
ПРИМЕР: Кубок мира по футболу
Напомним, что мы использовали следующие данные из 3 турниров Кубка мира (всего 192 игры), чтобы представить идею средневзвешенного значения .
Мы добавили в нашу таблицу третий столбец с относительными частотами.
| всего # голов/игра | частота | относительная частота |
|---|---|---|
| 0 | 17 | 17/192 = 0,089 |
| 1 | 45 | 45/192 = 0,234 |
| 2 | 51 | 51/192 = 0,266 |
| 3 | 37 | 37/192 = 0,193 |
| 4 | 25 | 25/192 = 0,130 |
| 5 | 11 | 11/192 = 0,057 |
| 6 | 3 | 3 / 192 = 0,016 |
| 7 | 2 | 2 / 192 = 0,010 |
| 8 | 1 | 1/192 = 0,005 |
Среднее значение для этих данных:
Распределив деление на 192, мы получим:
Обратите внимание, что среднее значение равно количеству голов за игру, умноженному на его относительную частоту.
Поскольку мы обычно записываем относительные частоты в виде десятичных дробей, мы можем видеть, что:
Среднее количество голов за игру =
- 0(0,089) + 1(0,234) + 2(0,266) + 3(0,193) + 4(0,130) + 5(0,057) + 6(0,016) + 7(0,010) + 8(0,005)
= 2,36 , округленное до двух знаков после запятой.
В исследовательском анализе данных мы использовали среднее выборки количественных значений — их среднее арифметическое — чтобы сообщить центру их распределение. Мы также видели, как использовалось средневзвешенное значение, когда у нас была таблица частот. Эти частоты можно изменить на относительные частоты.
Таким образом, мы, по сути, используем подход относительной частоты для нахождения вероятностей. Мы можем использовать это, чтобы найти среднее или центр распределения вероятностей для дискретной случайной величины , которое будет средневзвешенным значением ее значений; чем более вероятно значение, тем больший вес оно получает.
Как всегда, важно различать конкретную выборку наблюдаемых значений переменной и абстрактную совокупность всех значений, принимаемых случайной величиной в долгосрочной перспективе.
В то время как мы обозначали среднее значение выборки как x-bar, теперь мы обозначаем среднее значение случайной величины, используя греческую букву mu с нижним индексом для используемой нами случайной величины.
Давайте посмотрим, как это делается, на конкретном примере.
ПРИМЕР: Производственная линия Ксавьера
Производственная линия Ксавьера производит различное количество дефектных деталей в час, с вероятностями, показанными в этой таблице:
Сколько дефектных деталей обычно производится за час на производственной линии Ксавьера? Если мы суммируем возможные значения X, каждое из которых взвешено со своей вероятностью, мы имеем
Вот общее определение среднего значения дискретной случайной величины:
В общем, для любой дискретной случайной величины X с распределением вероятностей
Среднее значение случайной величины говорит нам о ее «долгосрочном» среднем значении.
Хотя « ожидаемое значение » является распространенным и даже предпочтительным термином в области статистики, это выражение может несколько ввести в заблуждение, поскольку во многих случаях случайная величина не может фактически равняться своему ожидаемому значению.
Например, среднее количество голов в футбольном матче чемпионата мира по футболу равно 2,36. Но мы никогда не можем ожидать, что в какой-либо одной игре будет забито 2,36 гола, поскольку невозможно забить долю гола. Скорее, 2,36 — это долгосрочное среднее значение всех футбольных матчей чемпионата мира.
В случае с производственной линией Ксавьера среднее количество дефектных деталей, производимых за час, равно 1,8. Но фактическое количество дефектных деталей, произведенных в любой данный час, никогда не может равняться 1,8, поскольку оно должно принимать целые числовые значения.
Чтобы лучше понять среднее значение случайной величины, давайте расширим пример с дефектными деталями:
ПРИМЕР: Производственные линии Ксавьера и Ива
Вспомним распределение вероятностей случайной величины X, представляющей количество дефектных деталей в час производства производственной линии Ксавьера.
Количество дефектных деталей, производимых каждый час производственной линией Ива, является случайной величиной Y со следующим распределением вероятностей:
Посмотрите на оба распределения вероятностей. И X, и Y принимают одинаковые возможные значения (0, 1, 2, 3, 4).
Однако они сильно различаются по способу распределения вероятности между этими значениями.
Обучение на практике: Сравнение вероятностных распределений #1
Понял ли я это?: Среднее значение дискретной случайной величины
Дисперсия и стандартное отклонение дискретной случайной величины
LO nd: LO nd: LO nd: LO nd 60,099 дисперсия и стандартное отклонение дискретной случайной величины.
В исследовательском анализе данных мы использовали среднее значение выборки количественных значений (их среднее арифметическое, x-bar), чтобы указать центр их распределения, и стандартное отклонение (s), чтобы указать типичное расстояние значений выборки от их среднее значение.
Мы описали центр распределения вероятностей для случайной величины, сообщив ее среднее значение, которое мы обозначили греческой буквой мю.
Теперь мы хотели бы установить сопутствующую меру распространения .
Наша мера разброса по-прежнему будет сообщать о типичном расстоянии значений от их средних значений, но для того, чтобы отличить разброс совокупности всех значений случайной величины от разброса (ов) выборочных значений, мы будем обозначать стандарт отклонение случайной величины X с греческой строчной буквой « сигма » и используйте нижний индекс, чтобы напомнить нам, что представляет собой интересующая переменная (в более поздних задачах может быть более одной):
Мы также будем фокусироваться чаще чем раньше, на квадрат стандартного отклонения, называемого дисперсия , потому что некоторые важные правила, которые нам нужно использовать, относятся к дисперсии, а не к стандартному отклонению.
ПРИМЕР: Производственная линия Ксавьера
Напомним, что количество дефектных деталей, производимых каждый час на производственной линии Ксавьера, является случайной величиной X со следующим распределением вероятностей:
быть 1,8.
Очевидно, что это среднее значение может варьироваться: в некоторые часы производится всего 0 дефектных деталей, тогда как в другие часы производится целых 4.
Насколько обычно число дефектных деталей отличается от среднего значения 1,8?
Как и для разброса выборочных значений, мы измеряем разброс случайной величины, вычисляя квадратный корень из среднего квадрата отклонения от среднего.
Теперь «среднее» — это средневзвешенное значение, где соответственно больший вес придается более вероятным значениям случайной величины.
Начнем с дисперсии или среднего квадрата отклонения от среднего, а затем возьмем квадратный корень, чтобы найти стандартное отклонение:
Как интерпретировать стандартное отклонение X?
- Производственная линия Xavier производит в среднем 1,80 бракованных деталей в час.
- Количество дефектных деталей меняется от часа к часу; обычно (или в среднем) он примерно на 1,21 отличается от среднего значения 1,80.

Вот формальное определение:
В общем, для любой дискретной случайной величины X с распределением вероятности
дисперсия от X определена как
. Существует также «сокращенная» формула, которая быстрее для ручного расчета. В приведенной ниже формуле мы опустили нижний индекс для переменной в обозначении. В этом сокращенном варианте нам просто нужно
- квадратных X,
- умножить на вероятность этого X,
- , затем суммируйте эти значения.
- Из этого результата вычитаем квадрат среднего, чтобы найти дисперсию.
Стандартное отклонение — квадратный корень из дисперсии
Я понял?: Стандартное отклонение дискретной случайной величины
переменная.
Учись на практике: Сравнение вероятностных распределений #2
ПРИМЕР: Производственные линии Ксавьера и Ива
Вспомните распределение вероятностей случайной величины X, представляющей количество дефектных деталей в час, производимых производственной линией Ксавьера, и распределение вероятностей случайной величины Y, представляющей количество бракованных деталей в час, производимых производственной линией Ива:
Внимательно посмотрите на оба распределения вероятностей. И X, и Y принимают одинаковые возможные значения (0, 1, 2, 3, 4).
И X, и Y принимают одинаковые возможные значения (0, 1, 2, 3, 4).
Однако они сильно различаются по способу распределения вероятности между этими значениями. Ранее мы видели, что это влияет на средние значения:
Теперь мы хотим понять, как различные распределения вероятностей влияют на их стандартные отклонения.
Напомним, что стандартное отклонение случайной переменной может быть интерпретировано как типичное (или долгосрочное среднее ) расстояние между значением X и его средним значением .
Учись на практике: Сравнение вероятностных распределений #3
Итак, в 75% случаев Y будет принимать значение (3), очень близкое к своему среднему значению (2,7), а X будет принимать значение (2) что близко к среднему (1,8) гораздо реже — всего в 25% случаев.
Таким образом, долгосрочное среднее расстояние между значениями Y и их средним значением будет намного меньше долгосрочного среднего расстояния между значениями X и их средним значением.
Следовательно,
На самом деле у нас есть
Таким образом, мы можем сделать следующий вывод:
Производственная линия Ива производит в среднем 2,70 бракованных деталей в час.
Количество дефектных деталей меняется от часа к часу; обычно (или в среднем) он составляет примерно 0,85 от 2,70.
Вот гистограммы для производственных линий:
Когда мы сравниваем распределения, распределение, в котором более вероятно обнаружение значений, которые дальше от среднего, будет иметь большее стандартное отклонение .
Аналогичным образом, распределение, в котором менее вероятность нахождения значений, далеких от среднего, будет иметь меньшее стандартное отклонение.
Я понял?: Стандартное отклонение дискретной случайной величины #2
Комментарий:
Как мы уже говорили ранее, использование среднего значения и стандартного отклонения дает нам еще один способ оценить, какие значения случайной величины являются необычными.
Для достаточно симметричных распределений любые значения случайной величины, находящиеся в пределах 2 или 3 стандартных отклонений от среднего, будут считаться обычными (не необычными).
Для любого распределения необычно, чтобы значения выходили за пределы 3 или 4 стандартных отклонений — в зависимости от вашего определения «необычного».
ПРИМЕР: Производственная линия Ксавьера — необычная или нет?
Еще раз взглянем на распределение вероятностей для производственной линии Ксавьера:
Будет ли считаться необычным наличие 4 дефектных деталей в час?
Мы знаем, что среднее значение равно 1,8, а стандартное отклонение равно 1,21.
Обычные значения находятся в пределах 2 (или 3) стандартных отклонений от среднего.
- 1,8 – 2(1,21) = -0,62 и
- 1,8 + 2(1,21) = 4,22.
Это дает нам интервал от -0,62 до 4,22.
Поскольку у нас не может быть отрицательного числа дефектных деталей, интервал, по существу, составляет от 0 до 4,22.
Поскольку число 4 находится внутри этого интервала, оно считается обычным. Таким образом, это , а не .
Будет ли считаться необычным отсутствие дефектных деталей?
Ноль находится в пределах 2 стандартных отклонений от среднего значения, поэтому отсутствие дефектных деталей не считается необычным.
Следующее задание укрепит эту идею.
Учись на практике: Необычно или нет?
Случайная величина
Что такое случайная величина?
Случайная переменная — это переменная, значение которой неизвестно, или функция, которая присваивает значения каждому результату эксперимента. Случайные переменные часто обозначаются буквами и могут быть классифицированы как дискретные, то есть переменные, имеющие определенные значения, или непрерывные, то есть переменные, которые могут принимать любые значения в непрерывном диапазоне.
Случайные переменные часто используются в эконометрическом или регрессионном анализе для определения статистических взаимосвязей между собой.
Ключевые выводы
- Случайная величина — это переменная, значение которой неизвестно, или функция, которая присваивает значения каждому результату эксперимента.
- Случайная величина может быть либо дискретной (имеющей определенные значения), либо непрерывной (любое значение в непрерывном диапазоне).
- Использование случайных величин наиболее распространено в теории вероятностей и статистике, где они используются для количественной оценки результатов случайных событий.
- Аналитики рисков используют случайные величины для оценки вероятности наступления неблагоприятного события.
Что такое случайная величина?
Понимание случайной величины
В теории вероятности и статистике случайные величины используются для количественной оценки результатов случайного события и, следовательно, могут принимать множество значений. Случайные переменные должны быть измеримыми и обычно представляют собой действительные числа. Например, буква X может обозначать сумму чисел, выпавших после броска трех игральных костей. В этом случае X может быть 3 (1 + 1 + 1), 18 (6 + 6 + 6) или где-то между 3 и 18, поскольку наибольшее число на кубике — 6, а наименьшее — 1.
Например, буква X может обозначать сумму чисел, выпавших после броска трех игральных костей. В этом случае X может быть 3 (1 + 1 + 1), 18 (6 + 6 + 6) или где-то между 3 и 18, поскольку наибольшее число на кубике — 6, а наименьшее — 1.
Случайная величина отличается от алгебраической переменной. Переменная в алгебраическом уравнении — это неизвестная величина, которую можно вычислить. Уравнение 10 + x = 13 показывает, что мы можем рассчитать конкретное значение для x, равное 3. С другой стороны, случайная величина имеет набор значений, и любое из этих значений может быть результирующим результатом, как показано в примере. кости выше.
В корпоративном мире случайные переменные могут быть присвоены таким свойствам, как средняя цена актива за определенный период времени, окупаемость инвестиций через определенное количество лет, предполагаемая скорость оборота в компании в течение следующих шести месяцев, и т. д. Аналитики риска назначают случайные переменные моделям риска, когда хотят оценить вероятность возникновения неблагоприятного события. Эти переменные представлены с использованием таких инструментов, как таблицы анализа сценариев и чувствительности, которые менеджеры по управлению рисками используют для принятия решений, касающихся снижения рисков.
Эти переменные представлены с использованием таких инструментов, как таблицы анализа сценариев и чувствительности, которые менеджеры по управлению рисками используют для принятия решений, касающихся снижения рисков.
Типы случайных величин
Случайная величина имеет распределение вероятностей, которое представляет вероятность появления любого из возможных значений. Предположим, что случайная величина Z — это число на верхней грани игральной кости при однократном броске. Таким образом, возможные значения для Z будут 1, 2, 3, 4, 5 и 6. Вероятность каждого из этих значений равна 1/6, поскольку все они с одинаковой вероятностью будут значением Z.
Например, вероятность выпадения 3 или P (Z = 3) при бросании кости равна 1/6, так же как и вероятность выпадения 4, 2 или любого другого числа на всех шести гранях кости. умереть. Обратите внимание, что сумма всех вероятностей равна 1.
Случайная величина может быть как дискретной, так и непрерывной.
Дискретные случайные величины
Дискретные случайные величины принимают счетное число различных значений. Рассмотрим эксперимент, в котором монету подбрасывают три раза. Если X представляет собой количество раз, когда монета выпадает орлом, то X является дискретной случайной величиной, которая может принимать только значения 0, 1, 2, 3 (от отсутствия орла в трех последовательных бросках монеты до всех орлов). Никакое другое значение для X невозможно.
Рассмотрим эксперимент, в котором монету подбрасывают три раза. Если X представляет собой количество раз, когда монета выпадает орлом, то X является дискретной случайной величиной, которая может принимать только значения 0, 1, 2, 3 (от отсутствия орла в трех последовательных бросках монеты до всех орлов). Никакое другое значение для X невозможно.
Непрерывные случайные величины
Непрерывные случайные величины могут представлять любое значение в пределах заданного диапазона или интервала и могут принимать бесконечное число возможных значений. Примером непрерывной случайной величины может быть эксперимент, включающий измерение количества осадков в городе за год или среднего роста случайной группы из 25 человек.
Опираясь на последнее, если Y представляет собой случайную величину для среднего роста случайной группы из 25 человек, вы обнаружите, что результирующий результат является непрерывной величиной, поскольку рост может быть 5 футов, или 5,01 фута, или 5,0001 фута. бесконечное число возможных значений высоты.
бесконечное число возможных значений высоты.
Пример случайной величины
Типичным примером случайной величины является результат подбрасывания монеты. Рассмотрим распределение вероятностей, при котором исходы случайного события не равновероятны. Если случайная величина Y — это количество выпавших орлов при подбрасывании двух монет, то Y может быть равно 0, 1 или 2. Это означает, что при подбрасывании двух монет у нас может не быть орла, может быть один орел или оба орла.
Однако две монеты приземляются четырьмя разными способами: TT, HT, TH и HH. Следовательно, P(Y=0) = 1/4, поскольку у нас есть один шанс не выпасть орла (т. е. две решки [TT] при подбрасывании монеты). Точно так же вероятность выпадения двух орлов (HH) также равна 1/4. Обратите внимание, что получение одной головы с вероятностью может произойти дважды: в HT и TH. В этом случае P (Y=1) = 2/4 = 1/2.
Что такое дискретная случайная величина?
Дискретная случайная величина — это тип случайной величины, которая имеет счетное число различных значений, которые могут быть присвоены ей, например, при подбрасывании монеты.
Что такое непрерывная случайная величина?
Непрерывная случайная величина обозначает любое количество в определенном диапазоне или наборе точек и может отражать бесконечное число потенциальных значений, таких как среднее количество осадков в регионе.
Что такое смешанная случайная величина?
Смешанная случайная величина объединяет элементы как дискретных, так и непрерывных случайных величин.
Как определить случайную величину?
Случайная величина — это величина, значение которой априори неизвестно, или же ей присваивается случайное значение на основе какого-либо процесса генерации данных или математической функции.
Почему важны случайные величины?
Случайные величины создают распределения вероятностей на основе экспериментов, наблюдений или какого-либо другого процесса генерации данных. Таким образом, случайные переменные позволяют нам понять мир вокруг нас на основе выборки данных, зная вероятность того, что конкретное значение произойдет в реальном мире или в какой-то момент в будущем.
Практический результат
Случайные величины, будь то дискретные или непрерывные, являются ключевым понятием в статистике и экспериментировании. Поскольку они случайны с неизвестными точными значениями, они позволяют нам понять распределение вероятностей этих значений или относительную вероятность определенных событий. В результате аналитики могут проверять гипотезы и делать выводы о природном и социальном мире вокруг нас.
Урок Видео: Дискретные случайные величины
Стенограмма видео
В этом видео мы потренируемся определение дискретных случайных величин и использование функций распределения вероятностей и столики к ним.
Начнем с того, что
термин дискретная случайная величина означает. Переменная означает, что это
величина, которая может принимать различные значения. Случайное означает, что взятое значение
определяется исходом случайного события или эксперимента. Или можно сказать, что это зависит от
элемент случайности. Ключевая часть здесь — это слово
дискретный, что означает, что может быть взят только конечный набор определенных значений. Мы называем этот набор значений
диапазон дискретной случайной величины. Например, количество голов.
наблюдаемое при подбрасывании двух монет было бы примером дискретного случайного
переменная. Его диапазон будет набором
значения ноль, один, два, поскольку у нас может быть ноль, один или два орла. Это конечное или счетное множество
значений, и поэтому 𝑋 количество орлов при подбрасывании двух монет является дискретным
случайная переменная.
Или можно сказать, что это зависит от
элемент случайности. Ключевая часть здесь — это слово
дискретный, что означает, что может быть взят только конечный набор определенных значений. Мы называем этот набор значений
диапазон дискретной случайной величины. Например, количество голов.
наблюдаемое при подбрасывании двух монет было бы примером дискретного случайного
переменная. Его диапазон будет набором
значения ноль, один, два, поскольку у нас может быть ноль, один или два орла. Это конечное или счетное множество
значений, и поэтому 𝑋 количество орлов при подбрасывании двух монет является дискретным
случайная переменная.
Давайте теперь рассмотрим, что мы подразумеваем под
функция распределения вероятностей дискретной случайной величины, и предположим, что мы
есть дискретная случайная величина 𝑋, областью значений которой является множество значений 𝑥 единица, 𝑥
два, до 𝑥 𝑛. Теперь важно отметить
здесь соглашение, которому мы следуем. Мы используем заглавные или прописные буквы
для представления самой переменной. И мы используем строчные буквы для
представлять значения в своем диапазоне. Теперь предположим, что у нас также есть функция
𝑓 такое, что 𝑓 из 𝑥 𝑖 равно вероятности того, что наша случайная величина 𝑋
принимает значение 𝑥 𝑖 для 𝑖 равно единице, двум, вплоть до 𝑛. Те для всех значений 𝑥 𝑖 в
диапазон нашей дискретной случайной величины капитала 𝑋. Тогда эта функция 𝑓 — это то, что мы
назовем функцию распределения вероятностей дискретной случайной величины 𝑋.
Теперь важно отметить
здесь соглашение, которому мы следуем. Мы используем заглавные или прописные буквы
для представления самой переменной. И мы используем строчные буквы для
представлять значения в своем диапазоне. Теперь предположим, что у нас также есть функция
𝑓 такое, что 𝑓 из 𝑥 𝑖 равно вероятности того, что наша случайная величина 𝑋
принимает значение 𝑥 𝑖 для 𝑖 равно единице, двум, вплоть до 𝑛. Те для всех значений 𝑥 𝑖 в
диапазон нашей дискретной случайной величины капитала 𝑋. Тогда эта функция 𝑓 — это то, что мы
назовем функцию распределения вероятностей дискретной случайной величины 𝑋.
Очень часто представляют
функция распределения вероятностей в виде таблицы со значениями в диапазоне, указанном в
первая строка и значения функции распределения вероятностей 𝑓 из 𝑥 заданы
во-вторых. Более неформально мы можем думать о
функция распределения вероятностей дискретной случайной величины просто как
набор всех значений, которые может принимать переменная, вместе с соответствующими им
вероятности. Одна важная особенность а
распределение вероятностей таково, потому что дискретная случайная величина может принимать только
значения в его диапазоне и никакие другие значения, сумма всех вероятностей в
функция распределения вероятностей должна быть равна единице.
Одна важная особенность а
распределение вероятностей таково, потому что дискретная случайная величина может принимать только
значения в его диапазоне и никакие другие значения, сумма всех вероятностей в
функция распределения вероятностей должна быть равна единице.
В качестве примера вероятности
функция распределения, предположим, что мы рассматриваем этот счетчик. Мы можем представить 𝑋 как
дискретная случайная величина, представленная числом, полученным, когда спиннер
закрученный. Этот спиннер имеет восемь равных
секции, три из них помечены цифрой один, одна помечена цифрой
два, два помечены цифрой три, а последние два помечены
Номер четыре. Это означает, что ассортимент нашего
дискретная случайная величина 𝑋 представляет собой набор значений один, два, три, четыре, поскольку они
единственные значения, которые может принимать 𝑋.
Мы можем записать вероятность функция распределения для этой дискретной случайной величины, которая, как вы помните, имеет значения в диапазоне в его первой строке и соответствующие вероятности в второй. Значения в диапазоне, как мы уже сказано: раз, два, три и четыре. В нем было восемь равных секций. нашего счетчика, поэтому все наши вероятности будут дробями со знаменателями восемь. Три секции имеют номер один на них одна секция имеет номер два, а две секции имеют номера три и четыре. Вероятность трех и четыре из двух восьмых можно было бы упростить до одной четверти, если бы мы захотели.
Итак, мы записали
функция распределения вероятностей для нашей дискретной случайной величины 𝑋. У нас есть набор всех значений в
его диапазон в верхнем ряду и соответствующие вероятности во втором. Обратите внимание, что сумма всех
вероятности в нашей функции распределения вероятностей действительно равны единице. Это ключевое свойство вероятности
Функции распределения полезны при определении того, является ли данная функция
может быть функцией распределения вероятностей, как мы увидим в нашем следующем примере.
Это ключевое свойство вероятности
Функции распределения полезны при определении того, является ли данная функция
может быть функцией распределения вероятностей, как мы увидим в нашем следующем примере.
Может ли функция в данной таблице быть функцией распределения вероятностей?
Теперь то, что у нас есть, безусловно
похоже, что это может быть функция распределения вероятностей. В верхней строке таблицы мы
иметь счетный набор значений, который может быть диапазоном дискретного случайного
переменная. И в нижнем ряду у нас есть несколько
десятичные значения, которые могут быть соответствующими вероятностями. Для того, чтобы проверить, является ли это
действительно может представлять собой функцию распределения вероятностей, нам нужно посмотреть на
вероятности поближе. И мы должны помнить, что сумма
всех вероятностей в функции распределения вероятностей должна быть равна
один.
Глядя на вторую строку таблицы и, по сути, глядя только в середину на значения в первую очередь, мы можем увидеть что сумма этих значений 0,43 и 0,69 является значением больше единицы. Конечно, если мы затем просуммируем все четыре значения, мы получаем еще большее значение 1,65. Это означает, что это не может быть функция распределения вероятностей, как если бы дискретная случайная величина могла принимать каждое значения ноль, один, четыре и пять с этими связанными вероятностями будут иметь общая вероятность больше единицы, что невозможно. Итак, наш ответ — нет.
Теперь рассмотрим пример в который нам нужен для вычисления пропущенной вероятности в распределении вероятностей.
Пусть 𝑋 обозначает дискретную случайную
переменная, которая может принимать значения два, шесть, семь и восемь. Учитывая, что вероятность 𝑋
равно двум равно вероятности 𝑋 равно шести, что на три больше 22, и
вероятность 𝑋 равна семи четырем одиннадцатым, найти вероятность 𝑋 равна
восемь. Дайте ответ в виде дроби.
Дайте ответ в виде дроби.
Начнем с представления информация, которую мы получили в несколько ином формате. Мы можем использовать таблицу для отображения этого функция распределения вероятностей. В верхнем ряду у нас будет четыре значения в диапазоне этой дискретной случайной величины, которые равны двум, шести, семи и восемь. Во второй строке мы заполним вероятности, которые нам дали: три больше 22 для двух и шести и четырех больше 11 на семь. Нам не хватает одного из вероятности: вероятность того, что 𝑋 равно восьми. И это значение, которое мы просили найти.
Для этого нам нужно вспомнить, что
сумма всех вероятностей в функции распределения вероятностей должна быть
равна единице, потому что дискретная случайная величина может принимать значения только в пределах своей
диапазон. Таким образом, мы можем составить уравнение
а затем подставьте три вероятности, данные нам в вопросе. Думая о четырех старше 11 как о
эквивалентная дробь восемь на 22, тогда мы имеем уравнение 14 на 22 плюс
вероятность 𝑋 равна восьми равна единице. Вычитание 14 из 22 из каждого
стороне, а затем упрощая 14 на 22 до семи на 11, мы получаем, что вероятность
𝑋 равно восьми равно одному минус семь больше 11, что равно четырем больше 11.
Думая о четырех старше 11 как о
эквивалентная дробь восемь на 22, тогда мы имеем уравнение 14 на 22 плюс
вероятность 𝑋 равна восьми равна единице. Вычитание 14 из 22 из каждого
стороне, а затем упрощая 14 на 22 до семи на 11, мы получаем, что вероятность
𝑋 равно восьми равно одному минус семь больше 11, что равно четырем больше 11.
Итак, используя тот факт, что сумма всех вероятностей в функции распределения вероятностей должна быть равна один, мы нашли недостающую вероятность. Вероятность того, что 𝑋 равно восемь — это четыре одиннадцатых.
Теперь рассмотрим аналогичный, но немного более сложный пример, в котором все вероятности в нашей вероятности распределение выражено алгебраически.
Функция в данной таблице функция вероятности дискретной случайной величины 𝑋. Найдите значение 𝑎.
Обратите внимание, что каждая вероятность в
эта функция распределения вероятностей была выражена через переменную
𝑎, значение которого нас попросили найти. Чтобы сделать это, нам нужно
напомним ключевой факт, что сумма всех вероятностей вероятности
функция распределения должна быть равна единице. Таким образом, мы можем составить уравнение
используя четыре значения во второй строке нашей таблицы. Три 𝑎 плюс восемь 𝑎 в квадрате плюс
четыре 𝑎 в квадрате плюс восемь 𝑎 равно единице. Это упрощается до 12𝑎 в квадрате.
плюс 11𝑎 равно единице. И затем вычитая один из каждого
стороны, мы видим, что у нас есть квадратное уравнение 12𝑎 в квадрате плюс 11𝑎 минус один равно
равен нулю.
Чтобы сделать это, нам нужно
напомним ключевой факт, что сумма всех вероятностей вероятности
функция распределения должна быть равна единице. Таким образом, мы можем составить уравнение
используя четыре значения во второй строке нашей таблицы. Три 𝑎 плюс восемь 𝑎 в квадрате плюс
четыре 𝑎 в квадрате плюс восемь 𝑎 равно единице. Это упрощается до 12𝑎 в квадрате.
плюс 11𝑎 равно единице. И затем вычитая один из каждого
стороны, мы видим, что у нас есть квадратное уравнение 12𝑎 в квадрате плюс 11𝑎 минус один равно
равен нулю.
Это уравнение можно решить за
различные способы. Но самый простой способ для этого
конкретный квадратичный будет решать факторингом. С небольшим испытанием и
ошибкой или, возможно, используя разложение по группам, мы видим, что эти квадратичные факторы как
12𝑎 минус один умножить на 𝑎 плюс один. Затем мы следуем обычному методу для
решение квадратного уравнения факторингом. Примем каждый множитель по очереди равным
нуля и решить полученное линейное уравнение, получив два значения 𝑎: 𝑎 равно единице
двенадцатая и 𝑎 равна отрицательной единице.
Затем мы следуем обычному методу для
решение квадратного уравнения факторингом. Примем каждый множитель по очереди равным
нуля и решить полученное линейное уравнение, получив два значения 𝑎: 𝑎 равно единице
двенадцатая и 𝑎 равна отрицательной единице.
Итак, у нас есть две возможности для
значение 𝑎, оба правильных корня этого квадратного уравнения. Но только одно значение имеет смысл в
контекст этой проблемы. Если мы вернемся к нашему столу, мы
см., например, вероятность того, что 𝑋 равна нулю, равна трем 𝑎. Если мы используем значение одна двенадцатая,
тогда это становится тремя двенадцатыми или одной четвертью. Но если мы используем отрицательное значение
один, это дает минус три. Помните, что вероятности должны
всегда быть между нулем и единицей, поэтому у нас не может быть вероятности отрицательного
три. Это означает, что значение 𝑎 равно
отрицательный, хотя и является правильным решением квадратного уравнения, не является
правильно в контексте этой задачи как значение 𝑎.
Мы можем проверить, является ли это значение одна двенадцатая верна при подсчете всех вероятностей. Три 𝑎 дают три двенадцатых, что эквивалентно 36 на 144. И таким же образом мы можем найти вероятности в виде дробей со знаменателем 144 для восьми 𝑎 в квадрате, четырех 𝑎 в квадрате и восемь 𝑎. Когда мы суммируем эти четыре значения вместе мы действительно получаем 144 вместо 144 или одного, и, таким образом, это подтверждает, что наша ценность из 𝑎 правильно. Тогда значение 𝑎 равно единице двенадцатый.
В этом примере мы выделили
еще одна ключевая особенность функций распределения вероятностей, заключающаяся в том, что все
индивидуальные вероятности должны быть между нулем и единицей. Итак, мы включим это в наш
определение функции распределения вероятностей, когда мы вернемся к ней позже. Далее, однако, давайте рассмотрим, как мы
могут сами написать функцию распределения вероятностей из словесного описания
дискретная случайная величина.
Два мальчика и две девочки ранжированы по их баллам на экзамене. Предположим, что нет двух одинаковых оценок и что все возможные ранжирования равновероятны. Найдите распределение вероятностей случайной величины 𝑋, выражающей наивысший рейтинг, достигнутый девушкой, для Например, 𝑋 равно двум, если лучший ученик — мальчик, а второй — студентка — девушка.
Итак, у нас четверо студентов и они будут ранжированы в соответствии с их баллами на экзамене. Нам нужно начать с перечисления всех разными способами мы можем разместить этих двух мальчиков и двух девочек на четырех позициях. Теперь заметьте, что нам все равно, какой девочка или какой мальчик находится в каждой позиции, только является ли человек в каждом ранге мальчиком или девушка.
Давайте начнем с девушки.
первая позиция. Затем мы можем поместить другую девушку в
позиция вторая, позиция третья или позиция четвертая. Каждый раз оставшиеся два пробела
оба должны быть заполнены мальчиками. Если бы вместо этого у нас был мальчик
в первой позиции, то таким же образом второй мальчик мог быть либо в
вторая позиция, третья позиция или четвертая позиция. И в каждом случае оставшиеся два
обе должности будут заполнены девушками. Итак, мы видим, что у нас есть шесть возможных
заказ двух девочек и двух мальчиков. Помните, каждый раз, когда мы не
интересно, какой это мальчик или какая девочка. Вопрос говорит нам, что все
возможные ранжирования равновероятны, что означает, что вероятность, связанная
с каждым из этих порядков составляет одну шестую.
Каждый раз оставшиеся два пробела
оба должны быть заполнены мальчиками. Если бы вместо этого у нас был мальчик
в первой позиции, то таким же образом второй мальчик мог быть либо в
вторая позиция, третья позиция или четвертая позиция. И в каждом случае оставшиеся два
обе должности будут заполнены девушками. Итак, мы видим, что у нас есть шесть возможных
заказ двух девочек и двух мальчиков. Помните, каждый раз, когда мы не
интересно, какой это мальчик или какая девочка. Вопрос говорит нам, что все
возможные ранжирования равновероятны, что означает, что вероятность, связанная
с каждым из этих порядков составляет одну шестую.
Дискретная случайная величина 𝑋
нас интересует наивысший рейтинг, достигнутый девушкой. В каждом из первых трех случаев
на первом месте стоит девушка, поэтому значение 𝑋 равно единице. В четвертом случае девушки
на третьей и четвертой позициях, таким образом, самый высокий рейтинг, достигнутый девушкой, значение
из 𝑋, это три. В пятом случае девушки находятся в
вторая и четвертая позиции, поэтому самый высокий рейтинг равен двум. А в шестом случае девушки
были на втором и третьем местах. Снова высший рейтинг
два. Эти значения в последнем столбце
задайте диапазон нашей дискретной случайной величины 𝑋. Он может принимать значения один, два или
три.
В пятом случае девушки находятся в
вторая и четвертая позиции, поэтому самый высокий рейтинг равен двум. А в шестом случае девушки
были на втором и третьем местах. Снова высший рейтинг
два. Эти значения в последнем столбце
задайте диапазон нашей дискретной случайной величины 𝑋. Он может принимать значения один, два или
три.
Затем нам нужно заполнить
ассоциированные вероятности. Помните, значение один появляется
трижды, поэтому его общая вероятность равна трижды одной шестой. Это три шестых, что может быть
упрощено до половины. Значение два появляется дважды. Таким образом, его полная вероятность равна
две шестых, что упрощается до одной трети. И, наконец, значение только три
появляется один раз, поэтому его вероятность равна одной шестой. Итак, мы нашли вероятность
распределение случайной величины 𝑋. Значения в диапазоне равны единице,
два и три с соответствующими вероятностями половина, одна треть и
одна шестая.
В нашем последнем примере мы кратко подумайте, как отвечать на вопросы, где нас просят найти вероятность того, что дискретная случайная величина больше или меньше определенного значения.
Пусть 𝑋 обозначает дискретную случайную переменная, которая может принимать отрицательные значения два, два, четыре и пять. Учитывая, что вероятность 𝑋 равняется отрицательному значению два — 0,15, вероятность 𝑋 равняется двум — 0,43, а вероятность 𝑋 равна четырем равна 0,25, найдите вероятность 𝑋 больше двух.
В этом вопросе нам не задавали
определить вероятность того, что наша случайная величина равна определенному
значение, а скорее вероятность того, что оно больше заданного значения. Это может показаться немного запутанным
во-первых, но главное помнить, что дискретная случайная величина может принимать только
значения в своем диапазоне и никакие другие. Начнем с представления
информацию в вопросе с помощью таблицы. У нас есть значения в диапазоне
наша дискретная случайная величина в верхней строке и соответствующие вероятности в
второй ряд.
Начнем с представления
информацию в вопросе с помощью таблицы. У нас есть значения в диапазоне
наша дискретная случайная величина в верхней строке и соответствующие вероятности в
второй ряд.
Теперь у нас есть недостающий вероятность, вероятность того, что 𝑋 равно пяти, но об этом мы поговорим позже если необходимо. Мы хотим найти вероятность что 𝑋 больше двух. Теперь вспомним, что наш дискретный случайная величина может принимать значения только из своего диапазона. Чтобы 𝑋 было строго больше, чем два, это означает, что он должен принимать либо значение четыре, либо значение пять. Других значений он не может брать. Вероятность 𝑋 больше, чем два тогда равно сумме вероятности 𝑋 равно четырем и вероятности 𝑋 равно пяти.
Помните, мы не знаем
вероятность 𝑋 равна пяти, хотя мы можем легко вычислить ее, вспомнив, что
сумма всех вероятностей в распределении должна быть равна единице. Вместо этого можно использовать более простой способ.
следует напомнить, что вероятность 𝑋 больше двух будет равна единице минус
вероятность 𝑋 меньше или равна двум. Итак, вместо этого мы можем просто вычесть
вероятности того, что 𝑋 равняется минус двум и 𝑋 равняется двум из одного, одного
минус 0,15 и 0,43, что равно 0,42.
Вместо этого можно использовать более простой способ.
следует напомнить, что вероятность 𝑋 больше двух будет равна единице минус
вероятность 𝑋 меньше или равна двум. Итак, вместо этого мы можем просто вычесть
вероятности того, что 𝑋 равняется минус двум и 𝑋 равняется двум из одного, одного
минус 0,15 и 0,43, что равно 0,42.
Важно помнить, что дискретная случайная величина может принимать значения только из своего диапазона. Так что, если нас попросят о совокупном вероятности, поскольку мы были здесь, нам просто нужно рассмотреть, какие значения в диапазоне будут удовлетворить это.
Давайте теперь рассмотрим ключевые моменты
рассказывается в этом видео. Дискретная случайная величина – это
количество, значение которого определяется случайно, и оно может принимать только исчисляемое или
конечное число значений, которое мы называем его диапазоном. Распределение вероятностей
функция 𝑓 дискретной случайной величины представляет собой список или таблицу всех значений в
диапазон вместе с их соответствующими вероятностями. Распределение вероятностей
функция имеет два ключевых свойства. Во-первых, как и со всеми вероятностями,
каждая отдельная вероятность должна быть между нулем и единицей. И, во-вторых, сумма или общее количество
все вероятности в функции распределения вероятностей должны быть равны
один. Мы видели на примерах, как мы
можно записать функцию распределения вероятностей и как мы можем использовать эти
свойства для вычисления пропущенных значений или вероятностей.
Распределение вероятностей
функция 𝑓 дискретной случайной величины представляет собой список или таблицу всех значений в
диапазон вместе с их соответствующими вероятностями. Распределение вероятностей
функция имеет два ключевых свойства. Во-первых, как и со всеми вероятностями,
каждая отдельная вероятность должна быть между нулем и единицей. И, во-вторых, сумма или общее количество
все вероятности в функции распределения вероятностей должны быть равны
один. Мы видели на примерах, как мы
можно записать функцию распределения вероятностей и как мы можем использовать эти
свойства для вычисления пропущенных значений или вероятностей.
Дискретная случайная величина: значение и типы
Вы когда-нибудь играли в игру со стрельбой из лука и пытались узнать, сколько раз вы можете бросить стрелу, прежде чем поразите конкретную цель? Делая это, вы проверяете вероятности и исходы случайных событий. Мы можем выразить и описать результаты случайных событий с помощью случайных величин.
Мы можем выразить и описать результаты случайных событий с помощью случайных величин.
Дискретные случайные величины — это тип случайной величины, в которой значения заданы или конечны в интервале. Другими словами, значения являются исчисляемыми и имеют ограниченное число результатов. Примерами дискретных случайных величин являются, среди прочего, количество книг в пачке, количество кубиков сахара в коробке, количество коз в загоне и размер обуви человека. В этом уроке мы подробно узнаем о дискретных случайных величинах и их вероятностных распределениях.
Дискретная случайная величина — это переменная, которая может принимать только ограниченное число определенных счетных значений. Все значения в области определения случайной величины имеют связанные с ними вероятности. Эти вероятности должны суммироваться до 1, когда рассматриваются все возможные значения.
Дискретные случайные величины: типы распределения
Прежде всего, давайте вспомним понятие распределения. Распределение вероятности для дискретной случайной величины X представляет собой исчерпывающий набор каждого потенциального значения X вместе с вероятностью того, что X примет это значение в одном испытании эксперимента. Другими словами, дискретные распределения вероятностей используются для описания вероятностей, связанных со значениями дискретной случайной величины. Двумя распространенными типами дискретных случайных величин являются биномиальные случайные величины (с биномиальное распределение вероятностей) и геометрические случайные величины (с геометрическим распределением вероятностей ) .
Распределение вероятности для дискретной случайной величины X представляет собой исчерпывающий набор каждого потенциального значения X вместе с вероятностью того, что X примет это значение в одном испытании эксперимента. Другими словами, дискретные распределения вероятностей используются для описания вероятностей, связанных со значениями дискретной случайной величины. Двумя распространенными типами дискретных случайных величин являются биномиальные случайные величины (с биномиальное распределение вероятностей) и геометрические случайные величины (с геометрическим распределением вероятностей ) .
В этой статье мы рассматриваем только биномиальные и геометрические случайные величины, которые имеют отношение к курсу AP Statistics. Другие типы, которые не будут рассмотрены в этой статье, включают распределения Бернулли, мультиномиальное, гипергеометрическое и распределение Пуассона.
Биномиальные и геометрические распределения вероятностей дискретных случайных величин
Вероятностное распределение дискретной случайной величины относится к каталогу потенциальных значений этой дискретной случайной величины вместе с вероятностью того, что она примет это значение при одной попытке эксперимента.
Распределения дискретных случайных величин должны удовлетворять следующим двум условиям для данной дискретной случайной величины X:
Давайте рассмотрим пример того, что понимается под вероятностным распределением дискретной случайной величины.
Пусть X — количество выпадений орла при двукратном подбрасывании правильной монеты. Во-первых, постройте распределение вероятностей X. Во-вторых, найдите вероятность того, что выпадет хотя бы один орёл.
Решение:
Для этого выборочного пространства возможные значения X равны 0, 1 и 2. Потенциальные исходы имеют равные шансы произойти и следуют следующим образом:
S = {hh, ht, th, tt}.
То есть «hh» относится к результату двух орлов,
«ht» относится к результатам одного орла и одной решки и так далее.
Поскольку число наблюдаемых голов представлено X = 0:
X = 0 соответствует {tt}, без наблюдаемых голов
X = 1 соответствует {ht, th}, с 1 наблюдаемой головкой
X = 2 соответствует {hh}, с двумя наблюдаемыми орлами
Путем простого подсчета мы получаем вероятность каждого из этих трех событий, представленную дискретной переменной X. Таким образом:
Таким образом:
Таблица 1: Распределение вероятностей подбрасывания ярмарки Дважды монета
| x | 0 | 1 | 2 |
| P (x) | 0,25 | 0,50 | 0.25 |
Биномиальные случайные величины
Биномиальная случайная величина — это тип дискретной случайной величины, которую мы используем для выражения частоты определенного исхода (или события) на протяжении фиксированного числа экспериментальных испытаний. Биномиальная случайная величина выражается в рамках биномиального распределения.
Биномиальная случайная величина выражается в рамках биномиального распределения.
Для того чтобы дискретная случайная величина также была биномиальной случайной величиной, должны применяться следующие характеристики:
Количество испытаний заранее определено или исправлено .
Испытания независимы. (Результаты испытаний не влияют друг на друга.)
В каждом испытании могут быть только два исхода: «успех» или «неудача». Другими словами, конкретное интересующее событие либо произойдет, либо не произойдет. Этот тип результата также можно назвать «бинарным».
Любое данное испытание имеет такую же вероятность «успеха», как и другие в эксперименте.
Если дискретная случайная величина (X) классифицируется как биномиальная, ее можно использовать для подсчета количества успехов в n испытаниях. Это означает, что X имеет биномиальное распределение со следующими двумя параметрами:
Это означает, что X имеет биномиальное распределение со следующими двумя параметрами:
«n», который измеряет количество испытаний, и
«p», который измеряет вероятность успеха определенного события.
Например, давайте рассмотрим случайную выборку из 125 медсестер, выбранных из крупной больницы, в которой доля медсестер женского пола составляет 57%. Предположим, что X обозначает количество женщин-медсестер в выборке. В этом эксперименте есть 125 (n = 125) идентичных и независимых испытаний общей процедуры: выбор медсестры наугад. Для каждого испытания есть ровно два возможных исхода: «успех» (рассчитываемое нами событие, что медсестра — женщина) и «неудача» (не женщина). Наконец, вероятность успеха в любом испытании равна одному и тому же числу (p = 0,57). Поскольку доля медсестер составляет 57% женщин, случайный отбор, таким образом, дает 57%-ную вероятность выбора медсестры-женщины. Таким образом, X является биномиальной случайной величиной с параметрами n = 125 и p = 0,57.
Формула вероятности для биномиальной случайной величины
Если распределение описывается биномиальной случайной величиной, вы можете применить приведенную ниже формулу для расчета вероятности X:
где,
P = биномиальная вероятность = частота определенного исхода в рамках определенного числа испытаний
= количество комбинаций
p = вероятность успеха в одном испытании
q = вероятность неудачи в одном испытании
n = количество попыток
Предположим, что правильная монета подбрасывается 10 раз. Какова вероятность того, что выпадет 6 решек?
Решение
В эксперименте с подбрасыванием монеты можно получить два результата: орёл или решка. Следовательно:
- Вероятность выпадения решки составляет 50% (или 0,5) при данном броске.
- Количество испытаний, n = 10
- Частота исхода, x = 6
- Вероятность успеха в одном испытании, p = 0,5
- Вероятность неудачи в одном испытании, q = 0,5
Подставляя эти значения в формулу:
Геометрические случайные величины Эта концепция используется в нескольких сферах жизни, таких как анализ затрат и результатов в финансовых отраслях.

Экспериментальные условия, необходимые для геометрических случайных величин, очень похожи на условия для биномиальных случайных величин: и те, и другие классифицируют испытания как успешные или неудачные, и испытания должны быть независимыми с одинаковой вероятностью возникновения для каждого из них. Однако, в отличие от биномиальных случайных величин, количество испытаний для геометрических случайных величин заранее не фиксируется. Скорее, это зависит от количества последовательных неудач, которые происходят до достижения успеха.
Например, рассмотрим геометрическую случайную величину X = 3, которая представляет получение числа 3 в результате броска игральной кости. В этом эксперименте с геометрическими случайными величинами мы должны подсчитать, сколько раз игральная кость бросается до достижения значения 3 (X = 3) раз . Испытание, в котором выпадает 3, помечается как «успех», а любое испытание, в котором 3 не выпадает, помечается как «неудача». Поскольку это эксперимент с геометрическими случайными величинами, нам нужно получить только один успех, чтобы закончить его. Поскольку наблюдения независимы друг от друга, вероятность того, что X = 3 (при броске кости выпадет 3), будет равна 1/6 для каждого броска. Вероятность 1/6 объясняется тем, что у игральной кости шесть граней, что дает значения от 1 до 6.
Поскольку это эксперимент с геометрическими случайными величинами, нам нужно получить только один успех, чтобы закончить его. Поскольку наблюдения независимы друг от друга, вероятность того, что X = 3 (при броске кости выпадет 3), будет равна 1/6 для каждого броска. Вероятность 1/6 объясняется тем, что у игральной кости шесть граней, что дает значения от 1 до 6.
Формула вероятности для геометрической случайной величины
Если распределение описывается геометрической случайной величиной, вы можете применить приведенную ниже формулу для расчета вероятности X:
где 0 < p < 1 и x = 1 , 2, 3...
Представитель отдела маркетинга Национального театра случайным образом выбирает людей на случайной улице в Вашингтоне, округ Колумбия, пока не найдет человека, который был на последнем сеансе кино. Пусть p, вероятность того, что ему удастся найти такого человека, равна 0,20. И пусть X обозначает количество людей, которых он выбирает, пока не добьется своего первого успеха.
а. Какова вероятность того, что специалист по маркетингу должен выбрать 4 человека, прежде чем он найдет одного из пришедших на кинопоказ?
Решение:
Таким образом, существует приблизительно 10%-ная вероятность того, что представителю отдела маркетинга придется выбрать 4 человека, прежде чем он найдет того, кто посетит последний киносеанс.
Среднее значение, дисперсия и стандартное отклонение дискретных случайных величин
В этом разделе мы обсудим среднее значение, дисперсию и стандартное отклонение применительно к дискретным случайным величинам. Затем мы применяем эти концепции к примерной задаче.
Среднее
Среднее также известно как ожидаемое значение и относится к среднему значений. Для дискретных случайных величин среднее значение относится к среднему значению всех значений, присвоенных событиям, которые происходят в повторяющихся испытаниях эксперимента. Среднее значение дискретной случайной величины определяется следующим выражением:
Среднее значение дискретной случайной величины определяется следующим выражением:
Таким образом, среднее значение получается путем умножения каждого значения на вероятность его появления. Затем эти значения суммируются, чтобы получить среднее значение эксперимента.
Find the mean of the discrete probability distribution below:
x | -2 | 1 | 2 | 3.5 |
P(x) | 0,21 | 0,34 | 0,54 | 0,31 |
Раствор:
. Следующая форма.0004
→ µ = (-2) * 0,21 + (1) * 0,34 + (2) * 0,54 + (3,5) * 0,31
Таким образом, µ = 2,085
Дисперсия
Дисперсия измеряет, насколько разбросаны данные . Более конкретно, это средневзвешенное значение, измеряющее квадраты отклонений или вариаций каждого значения относительно среднего значения повторных испытаний эксперимента. Это определяется как:
Это определяется как:
Стандартное отклонение
Подобно дисперсии, стандартное отклонение также измеряет дисперсию данных. В частности, он измеряет величину, на которую каждое наблюдение отклоняется от означает . Чтобы вычислить стандартное отклонение дискретной случайной величины, просто возьмите квадратный корень из значения дисперсии.
A Дискретная случайная переменная x имеет следующее распределение вероятностей:
| x | -1 | 0 | 1 | 4 |
| 4 P (x) | 94494444444444444444444444444444444444444444444444444444444444444444444444449449444944944449004. α | 0,1 |
Определите следующее:
1. α
2. P (0)
3. P (X > 0)
4. P (X ≥ 0)
5. Среднее значение µ X
Среднее значение µ X
6. Дисперсия X
7. Стандартное отклонение X
Решение
1. Поскольку сумма всех вероятностей должна составлять 1, α = 1 – (0,2 + 0,5 + 0,1) = 0,2
2. Ссылаясь на таблицу, P (0) = 0,5
3. Еще раз из таблицы P (X > 0) = P (1) + P (4) = 0,2 + 0,1 = 0,3
4. Из таблицы P (X ≥ 0) = P ( 0) + Р (1) + Р (4) = 0,5 + 0,2 + 0,1 = 0,8
5. Используя формулу определения среднего µ:
µ = E(X) = ∑x P(x) = (-1) * 0,2 + (0) * 0,5 + (1) * 0,2 + ( 4) * 0,1 = 0,4
6. Используя значение µ, полученное с помощью формулы для дисперсии:
7. Используя рассчитанную дисперсию, мы можем получить стандартное отклонение, используя следующую формулу:
Дискретное случайное Переменная — ключевые выводы
- Дискретные случайные величины — это случайные величины, принимающие заданные или конечные значения в интервале.
 Значения могут быть исчисляемыми и иметь конечное число результатов.
Значения могут быть исчисляемыми и иметь конечное число результатов. Типы дискретных случайных величин: бернуллиевские, полиномиальные, биномиальные, геометрические, гипергеометрические и пуассоновские.
Список каждого потенциального значения дискретной случайной величины X вместе с вероятностью того, что X примет это значение в одной попытке эксперимента, представляет собой распределение вероятностей этой дискретной случайной величины X.
распределение вероятностей для биномиальной случайной величины определяется как:
Распределение вероятностей для геометрической случайной величины определяется как:
.
Дискретные распределения вероятностей для дискретных случайных величин — Криста Кинг Математика
Дискретные случайные величины и распределения вероятностей
Дискретная случайная величина – это переменная, которая может принимать только дискретные значения. Например, если вы дважды подбросите монету, вы можете получить орел только ноль раз, один раз или два раза. У вас не получается получить головы???1.5??? раз, или ???0,31??? раз. Количество орлов, которое вы можете получить, принимает дискретный набор значений: ???0???, ???1??? и ???2???. А непрерывная случайная величина , с другой стороны, может принимать любое значение в определенном интервале.
Например, если вы дважды подбросите монету, вы можете получить орел только ноль раз, один раз или два раза. У вас не получается получить головы???1.5??? раз, или ???0,31??? раз. Количество орлов, которое вы можете получить, принимает дискретный набор значений: ???0???, ???1??? и ???2???. А непрерывная случайная величина , с другой стороны, может принимать любое значение в определенном интервале.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
В распределениях вероятностей для всех случайных величин вероятности каждой из возможностей должны в сумме ???1???, или ???100\%???.
Например, если я дважды подброшу монету, я могу получить любой из следующих результатов:
???ЧЧ???
???HT???
???TH???
???ТТ???
Есть четыре возможных результата, и один из них, где я получаю ???0??? голов, значит вероятность выпадения ???0??? головки ???1/4???. В ???HT??? и ???TH??? Я получаю ???1??? Орел, значит вероятность выпадения ???1??? головы ???2/4???. В ???ХХ??? Я получаю???2??? Орел, значит вероятность выпадения ???2??? головки ???1/4???.
В ???HT??? и ???TH??? Я получаю ???1??? Орел, значит вероятность выпадения ???1??? головы ???2/4???. В ???ХХ??? Я получаю???2??? Орел, значит вероятность выпадения ???2??? головки ???1/4???.
Теперь мы можем сказать, что это правильное дискретное распределение вероятностей, потому что
???\frac14+\frac24+\frac14=1=100\%???
Тот факт, что правильное распределение вероятностей всегда дает в сумме ???100\%??? позволяет нам находить пропущенные значения в наших данных. Например, если бы вместо этого нам сказали, что в приведенной ниже таблице указана вероятность выпадения определенного количества орлов при двукратном подбрасывании монеты,
мы могли бы вычислить недостающее значение, вычитая известные вероятности из ???1.00???. Таким образом, мы могли бы сказать, что вероятность получить ровно ???2??? головы
???P(2\текст{головки})=1.00-0.25-0.50=0.25???
И тогда мы могли бы заполнить таблицу:
Имейте в виду, что мы часто используем заглавную ???X??? для представления дискретной случайной величины. Это означает, что, например, при двойном подбрасывании монеты мы могли бы назвать количество выпавших орлов как ???X???, а вероятность выпадения определенного количества орлов как ???P(X)???. И мы могли бы дать таблицу распределения вероятностей как
Это означает, что, например, при двойном подбрасывании монеты мы могли бы назвать количество выпавших орлов как ???X???, а вероятность выпадения определенного количества орлов как ???P(X)???. И мы могли бы дать таблицу распределения вероятностей как
Или мы могли бы взять ту же информацию и построить график распределения следующим образом:
Расчет дискретной вероятности на основе ожидаемых значений
Пройти курс
Хотите узнать больше о вероятности и статистике? У меня есть пошаговый курс для этого. 🙂
Учить больше
Ожидаемое значение Получив распределение вероятностей для дискретной случайной величины ???X???, мы можем вычислить ожидаемое значение ???E(X)???, т. е. означает ???X???. Способ, которым мы справляемся с дискретной переменной, заключается в «взвешивании» каждого значения.
е. означает ???X???. Способ, которым мы справляемся с дискретной переменной, заключается в «взвешивании» каждого значения.
Например, если мы хотим найти ожидаемое значение количества орлов, когда мы подбрасываем монету два раза, мы умножим каждое значение ???X??? на соответствующее значение ???P(X)???, а затем сложите их все вместе.
Таким образом, ожидаемое значение равно
???E(X)=\mu_X=0(0,25)+1(0,50)+2(0,25)???
???\mu_X=0+0.50+0.50???
???\mu_X=1???
Следовательно, в среднем мы ожидаем получить ???1??? Орел, когда мы бросаем монету два раза. Затем мы можем экстраполировать это, чтобы предположить, что, например, мы должны получить ???50??? Орел, когда мы подбрасываем монету ???100??? раз.
Тот факт, что правильное распределение вероятностей всегда дает в сумме 100 %, позволяет нам находить недостающие значения в наших данных. 92=0,50???
Мы также можем найти стандартное отклонение ???X???, ???\sigma_X???, которое представляет собой просто квадратный корень из дисперсии.




 (14)
(14)
 (15)
(15)

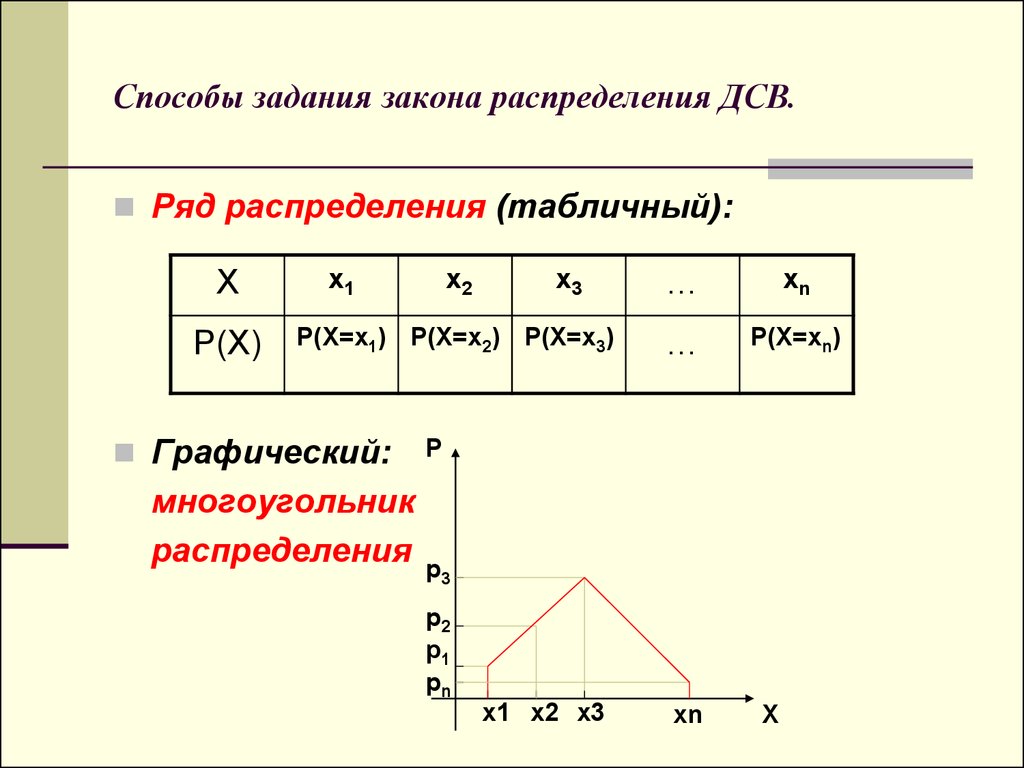 Вероятность попадания значения случайной величины на участок от a до b определяется по формуле
Вероятность попадания значения случайной величины на участок от a до b определяется по формуле 2D(Y) + 0 = 81*9 + 64*6 = 1113
2D(Y) + 0 = 81*9 + 64*6 = 1113
 1
1
 1x3
1x3
 Как правило, это соответствие задается с помощью таблицы, в первой строке которой указывают значения $x_1,\dots ,\ x_n$, а во второй строке соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$.
Как правило, это соответствие задается с помощью таблицы, в первой строке которой указывают значения $x_1,\dots ,\ x_n$, а во второй строке соответствующие этим значениям вероятности $p_1,\dots ,\ p_n$.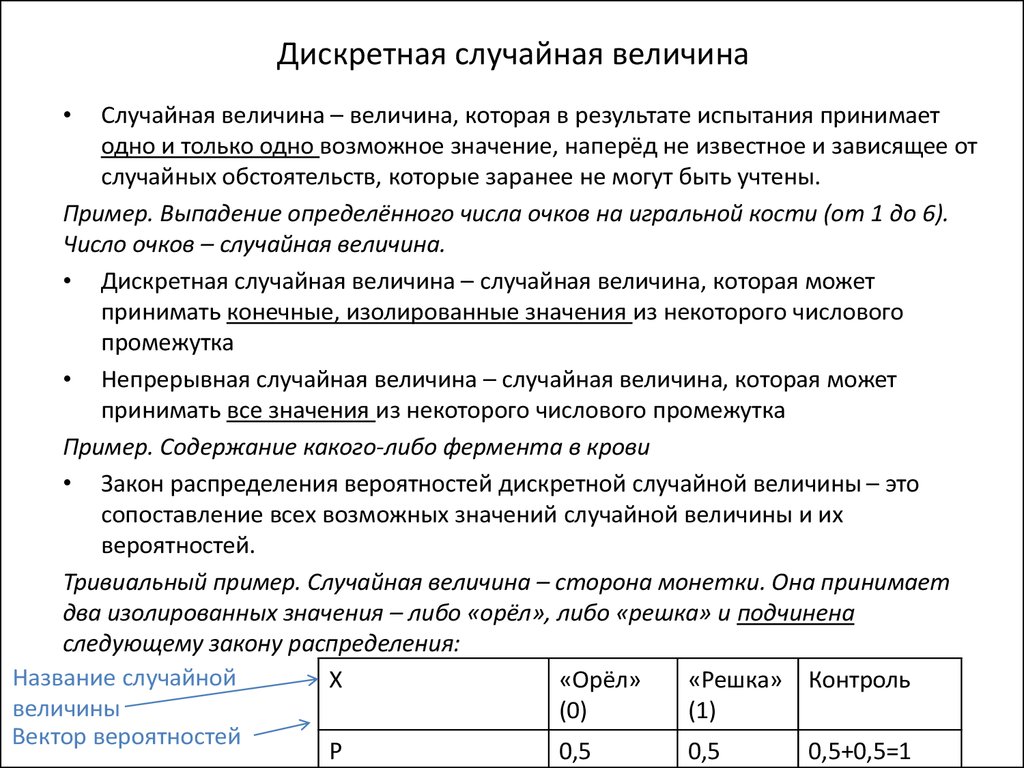 n_{i=1}{p_ix_i}=1\cdot {{1}\over {6}}+2\cdot {{1}\over {6}}+3\cdot {{1}\over {6}}+4\cdot {{1}\over {6}}+5\cdot {{1}\over {6}}+6\cdot {{1}\over {6}}=3,5.$$
n_{i=1}{p_ix_i}=1\cdot {{1}\over {6}}+2\cdot {{1}\over {6}}+3\cdot {{1}\over {6}}+4\cdot {{1}\over {6}}+5\cdot {{1}\over {6}}+6\cdot {{1}\over {6}}=3,5.$$ 2D\left(X\right)=4D\left(X\right)=4\cdot 3=12$.
2D\left(X\right)=4D\left(X\right)=4\cdot 3=12$.
 $
$

 Искомое
математическое ожидание
Искомое
математическое ожидание