Решение матричных уравнений онлайн
Назначение сервиса. Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
- Также решают
Инструкция. Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
Вид уравнения:A·X = B
X·A = B
A·X·B = C
Размерность матрицы А 12345678910 x 12345678910
Размерность матрицы B 12345678910 x 12345678910
Размерность матрицы C 12345678910 x 12345678910
где А,В,С — задаваемые матрицы, Х — искомая матрица.
A·X - B = C, то необходимо, сначала сложить матрицы C + B, и находить решение для выражения A·X = D, где D = C + B. Если задано выражение A*X = B2, то предварительно матрицу B надо возвести в квадрат.
Вместе с этим калькулятором также используют следующие:
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
Координаты вектора в базисе
По координатам вершин пирамиды найти
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление пределов
Вычисление интеграловРекомендуется также ознакомиться с основными действиями над матрицами.

Пример №1. Задание. Найти решение матричного уравнения
Решение. Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1:Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1·A·X·B·B-1 = A-1·C·B-1. Так как A·A-1 = B·B-1 = E и E·X = X·E = X, то X = A-1·C·B-1
Найдем обратную матрицу A-1.
Транспонированная матрица A
Обратная матрица A-1:
Найдем обратную матрицу B-1.
Транспонированная матрица BT:
Обратная матрица
| B-1 = -½ |
|
Матрицу X ищем по формуле: X = A-1·C·B-1
| X = — |
| * |
| -½ |
| = |
Ответ:
Пример №2.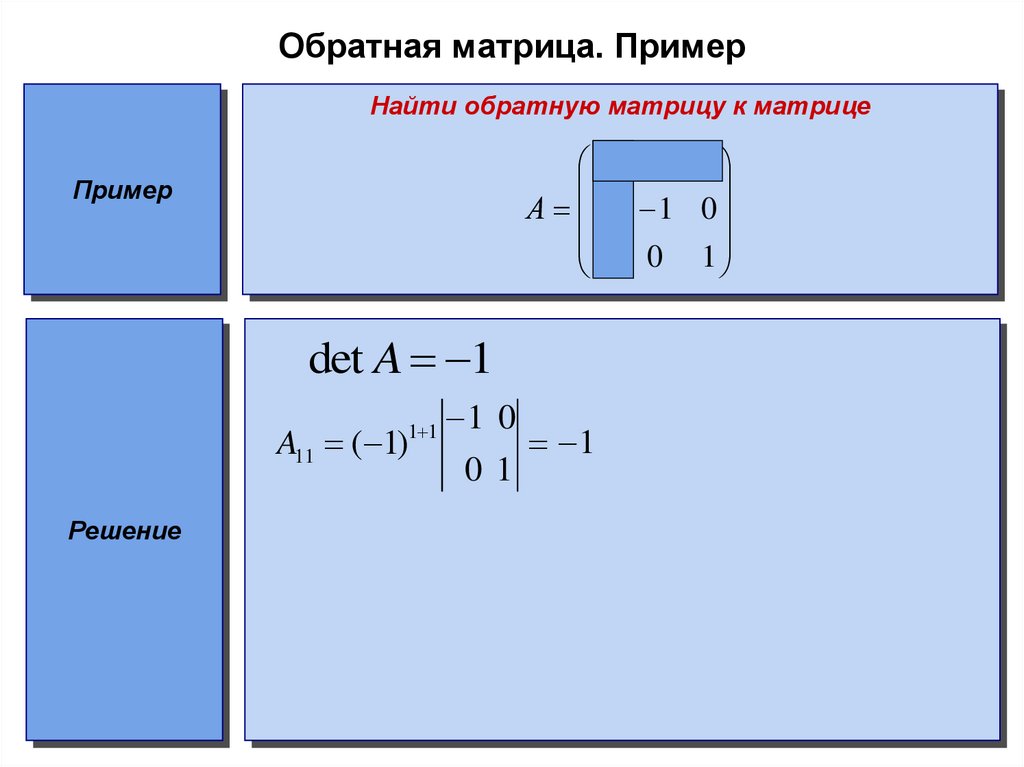 Задание. Решить матричное уравнение
Задание. Решить матричное уравнение
Решение. Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3. Задание. Найти решение матричного уравнения
Решение. Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1
Найдем обратную матрицу A-1.
Транспонированная матрица A
Обратная матрица A-1:
Матрицу X ищем по формуле: X = B·A-1
Ответ:
Пример №4. Задание. Решить матричное уравнение
Решение. Обозначим:
Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.
Найдем обратную матрицу A-1.
Транспонированная матрица AT:
Обратная матрица A-1:
Матрицу Х ищем по формуле: X = A-1·B
Ответ:
Обратная матрица — вычисление, основные понятия и определения с примерами решения и образцами выполнения
Содержание:
- Обратная матрица
- Свойства обратных матриц
- Системы n линейных уравнений с n неизвестными
- Теорема Кронекера — Капелли
- Решение систем n линейных уравнений с n неизвестными
- Обратная матница и её определение
Миноры первого порядка можно определить для любой (не только квадратной) матрицы. Матрица может иметь много миноров, причём некоторые из них могут равняться нулю, а другие — нет.
Матрица может иметь много миноров, причём некоторые из них могут равняться нулю, а другие — нет.
Высший порядок минора матрицы, который не равен нулю, называют рангом матрицы.
Пример.
а) Рассмотрим матрицу:
Матрица не имеет миноров третьего порядка, но имеет три минора второго порядка, которые равны нулю
Следовательно, ранг матрицы
б) Рассмотрим матрицу:
Минор 3-го порядка этой матрицы, то есть её определитель, равный нулю:
Рассмотрим миноры 2-го порядка:
Видим, что существует минор 2-го порядка, отличный от нуля. Следовательно,
Очевидно, что ранг матрицы не может превышать её порядок.
Ранги транспонированных матриц совпадают.
Можно доказать, что ранг матрицы равный максимально возможному числу её линейно независимых строк (столбцов). Так, в приведённом нами примере строки 1 -1 3 и 4 -1 5 дают в сумме строку 3 0 2, то есть строки матрицы линейно зависимы.
Матрица, ранг которой меньше её порядка, называется вырожденной матрицей (это матрица, определитель которой равен нулю).
Для невырожденных матриц (а такими могут быть только квадратные) вводят понятие обратной матрицы.
По аналогии с умножением чисел, обратной для матрицы А называют матрицу , если
Для матрицы А обратной будет матрица:
где алгебраические дополнения элементов матрицы А.
Замечание.
1. Алгебраические дополнения элементов рядов матрицы стоят в соответственных столбцах, то есть проведена операция транспонирования.
2. Если в уравнении выполнять одинаковые элементарные преобразования строк матриц А и Е до тех пор, пока матрица А не преобразуется в единичную, то уравнение примет вид где преобразованная единичная матрица. Потому, что получим , то есть обратная матрица — это преобразованная единичная.
Свойства обратных матрицПоследнее свойство легко доказывается. Действительно, согласно свойствам определителей известно, что
Действительно, согласно свойствам определителей известно, что
Пример 1. Найти матрицу, обратную к матрице А:
Решение.
а) Установить, не будет ли вырожденной матрица А; для этого вычислим
Определитель отличный от нуля, поэтому для матрицы А существует
б) Вычислить алгебраические дополнения соответствующих элементов матрицы А:
в) Запишем матрицу М, составленную из алгебраических дополнений элементов матрицы А:
г) Запишем обратную матрицу транспонировав матрицу М:
д) Необходимо проверить правильность выполнения операции, то есть проверить, что
Следовательно, обратная матрица найдена правильно.
Пример 2. Найти обратную матрицу для матрицы А:
Решение. Запишем параллельно матрицы А и Е и выполним над ними одинаковые элементарные преобразования, направленные на преобразование матрицы А в единичную:
— умножим первый ряд матриц А и Е на три и отнимем от второго ряда соответствующей матрицы:
— сложим вторые ряды матриц А и Е с первыми:
— умножим вторые ряды на
В результате приведённых выше преобразований из единичной матрицы Е мы получили матрицу, обратную матрице А:
Проверим правильность нахождения обратной матрицы, вычислив её согласно схеме, приведённой в примере 1:
— вычислим определитель матрицы
— вычислим алгебраические дополнения элементов матрицы А:
— сложим матрицу М, составленную из алгебраических дополнений и транспонируем её:
— запишем обратную матрицу для матрицы А:
Как видим, матрицы совпадают.
Определение. Линейным уравнением с n неизвестными называют уравнения вида:
где коэффициенты уравнения; неизвестные; свободный член.
В курсе средней школы рассматривали линейные уравнения с одним, двумя и тремя неизвестными. Это уравнения:
Геометрически эти уравнения изображают точку на числовой прямой, прямую на площади, площадь в пространстве.
Решением линейного уравнения считают совокупность значений неизвестных этого уравнения, которые преобразуют его в истинную тождественность.
Системой линейных уравнений называют два или более уравнений, которые решаются совместно. Это означает, что решением системы будут те решения её уравнений, которые удовлетворяют все уравнения системы. (сечение решений уравнений системы).
В общем виде система m линейных уравнений имеет вид:
где неизвестные; коэффициенты систем; свободные члены.
Систему можно представлять как произведение матриц:
Такую запись системы называют матричной формой записи.
Если ввести обозначения
то систему можно записать в виде матричного равенства:
Система называется однородной, если все свободные члены равны нулю (АХ=0).
Системы называется квадратной, если n=m (количество равенств и количество неизвестных равны).
Не каждая система имеет решения, например система состоящая из следующих уравнений:
решений не будет иметь.
Система называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет ни одного решения.
Если совместная система имеет только одно решение, то она называется определённой.
Однородная система всегда совместная, она имеет так называемое тривиальное решение
Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг матрицы, составленной из её коэффициентов меньше чем число n её столбцов.
Квадратная однородная система имеет нетривиальное решение, только тогда когда определитель матрицы, составленной из её коэффициентов равен нулю.
Вопрос совместимости системы линейных уравнений полностью решается следующей теоремой.
Теорема Кронекера — КапеллиДля того, чтобы система была совместимой, необходимо и достаточно чтобы ранг основной матрицы А совпадал с рангом расширенной матрицы (матрица А, к которой присоединён столбец свободных чисел).
Доказательство. Рассмотрим матрицы А и :
Минор, который определяет ранг матрицы А входит в матрицу , следовательно ранг матрицы или равен матрице А, или на единицу больше него.
Необходимость. Если система А совместимая, то существуют значения неизвестных которые и являются решениями. Подставив эти значения в систему, получим m тождеств, из которых видно, что последний столбец матрицы является суммой всех последних столбцов, взятых вместе с коэффициентами (линейной комбинацией столбцов матрицы А). Определитель, у которого столбцы линейно зависимы равен нулю. Следовательно, ранг матриц совпадает.
Определитель, у которого столбцы линейно зависимы равен нулю. Следовательно, ранг матриц совпадает.
Достаточность. Пусть ранги матриц А и совпадают. Это значит, что количество линейно независимых столбцов у этих матриц одинаковое. Потому, что матрицы отличаются только последним столбцом матрицы , существуют числа , такие, что сумма столбцов матрицы А взятых вместе с этими числами, равна столбцу свободных членов из системы . Следовательно, числа являются решениями системы.
Теорема доказана.
Отметим, что совместная система имеет единое решение тогда и только тогда, когда ранг матрицы А равен числу неизвестных.
Пример 1. Установить совместимость системы:
Решение. Ранг матрицы, составленной из коэффициентов системы равен 2. Ранг расширенной матрицы равен 3, поскольку
Ответ: система несовместима.
Пример 2. Установить совместимость системы:
Решение. Ранг матрицы, составленной из коэффициентов системы равен 2, то есть равен числу коэффициентов. Ранг расширенной матрицы 2. Следовательно, система совместима и имеет единое решение.
Ранг матрицы, составленной из коэффициентов системы равен 2, то есть равен числу коэффициентов. Ранг расширенной матрицы 2. Следовательно, система совместима и имеет единое решение.
Ответ: система совместима.
Пример 3. Установить совместимость системы:
Решение. Ранг матрицы, составленной из коэффициентов системы 2. Ранг расширенной матрицы 2.
Ответ: система совместима.
Решение систем n линейных уравнений с n неизвестными1. Матричный метод. Одним из способов решения систем линейных уравнений является её умножение на обратную матрицу.
Пусть дана система6
АХ=В.
Умножим правую и левую части на А-1:
А-1(АХ)=А-1В или (А-1А)Х=А-1В.
Потому что, А-1А=Е, получим
Х=А-1В.
Нахождение обратной для матриц высоких порядков достаточно сложное, поэтому матричный метод используют довольно редко.
Пример 1. Решить систему:
Решение.
а) Запишем систему в матричной форме:
б) Вычислим определитель матрицы А:
в) Запишем обратную матрицу А-1:
Обратная матрица найдена правильно, поскольку
г) Вычислим произведение матрицы А-1В:
Ответ: х=2, у=1, z=3.
2. Метод Крамера. Пусть дана система (запишем в виде матричного уравнения) n линейных уравнений с n неизвестными
где определитель матрицы матрица, составленная из алгебраических дополнений элементов матрицы А:
Как видим, полученные выражения для элементов матрицы Х — это разложения элементов i-ой строки некоторого определителя, а именно:
где определитель матрицы А, а определитель матрицы, в которой столбец коэффициентов, которые стоят при заменён на столбец свободных членов (матрица В).
Если , то система будет иметь единое решение.
Если , то система или неопределённая, или несовместимая. Система будет несовместимой (не будет иметь ни одного решения), если хотя бы один из .
Если же, и , то система будет иметь множество решений (неопределённая)
Пример. Найти решения системы:
Решение.
а) Вычислим определитель матрицы А:
б) Вычислим определитель . Для этого первый столбец матрицы А заменим на столбец свободных членов (матрицей В) и для получения матрицы вычислим определитель:
в) Вычислим определители . Для этого заменим соответствующие столбцы матрицы А на столбец свободных членов и вычислим определители полученных матриц:
г) Найдём значения неизвестных
Ответ:
3. Метод Гаусса. Суть метода Гаусса заключается в последовательном изъятии неизвестных из уравнения системы. Поясним на примере системы трёх уравнений:
Разделим коэффициенты первого уравнения на . Получим систему:
Получим систему:
Если теперь последовательно перемножить первое уравнение на коэффициенты и отнять соответственно от второго и третьего уравнения системы, то получим:
Неизвестное х мы изъяли из второго и третьего уравнения системы.
Изымем таким же способом у: разделим второе уравнение на , а потом, умножив на , отнимем от третьего. Получим:
Из третьего уравнения находим z, со второго — у, с третьего — х.
Алгоритм можно применять к системам более высоких порядков.
На практике, при непосредственном вычислении удобно использовать расширенную матрицу системы:
которую с помощью элементарных преобразований приводят к виду:
Пример 1. Решить систему уравнений:
Решение. Коэффициент системы равен 1, поэтому выпишем расширенную матрицу:
Умножим первую строку на 2 и отнимем от второй:
а потом умножим первую строку на 3 и отнимем от третьей:
Продолжим изымать переменные со второго и третьего уравнений системы (со второй и третьей строки расширенной матрицы). Коэффициент равен 1, поэтому просто умножим вторую строку на 5 и отнимем от третьей:
Коэффициент равен 1, поэтому просто умножим вторую строку на 5 и отнимем от третьей:
Система свелась к виду:
Из третьего уравнения системы находим z=1, подставив найденное значение во второе уравнение системы найдём у= -2, а из первого уравнения — х=3.
Ответ: х=3, у= -2, z=1.
Пример2. Решить систему уравнений:
Решение. Выпишем расширенную матрицу системы:
Разделим первую строку системы на коэффициент . Получим:
Умножим первую строку матрицы последовательно на 4 и 2 и отнимем соответственно от второй и третьей строк:
Разделим третью строку полученной матрицы на . Получим:
Умножим вторую строку матрицы на и отнимем её от третьей строки:
Начальная система свелась к виду:
Из третьего уравнения получим z=1, со второго — у=1, с первого х=1.
Ответ: х=1, у=1, z=1.
Обратная матница и её определениеКвадратная матрица называется обратной квадратной матрице если выполняется условие где единичная матрица. Квадратная матрица называется невырожденной или неособенной, если ее определитель отличен от нуля. Если определитель матрицы равен нулю, она называется вырожденной или особенной.
Квадратная матрица называется невырожденной или неособенной, если ее определитель отличен от нуля. Если определитель матрицы равен нулю, она называется вырожденной или особенной.
Всякая невырожденная квадратная матрица
имеет единственную обратную матрицу
где алгебраическое дополнение элемента матрицы . (Алгебраическое дополнение элементов каждой строки матрицы записаны в столбец с тем же номером).
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Чтобы найти матрицу, обратную данной, необходимо:
1) вычислить определитель данной матрицы; 2) найти алгебраические дополнения ее элементов 3) составить матрицу из алгебраических дополнений взятых в том же порядке, что и элементы в матрице 4) в матрице поменять ролями строки и столбцы, записать матрицу каждый элемент матрицы разделить на определитель матрицы Рангом матрицы называется наивысший из порядков ее миноров, отличных от нуля.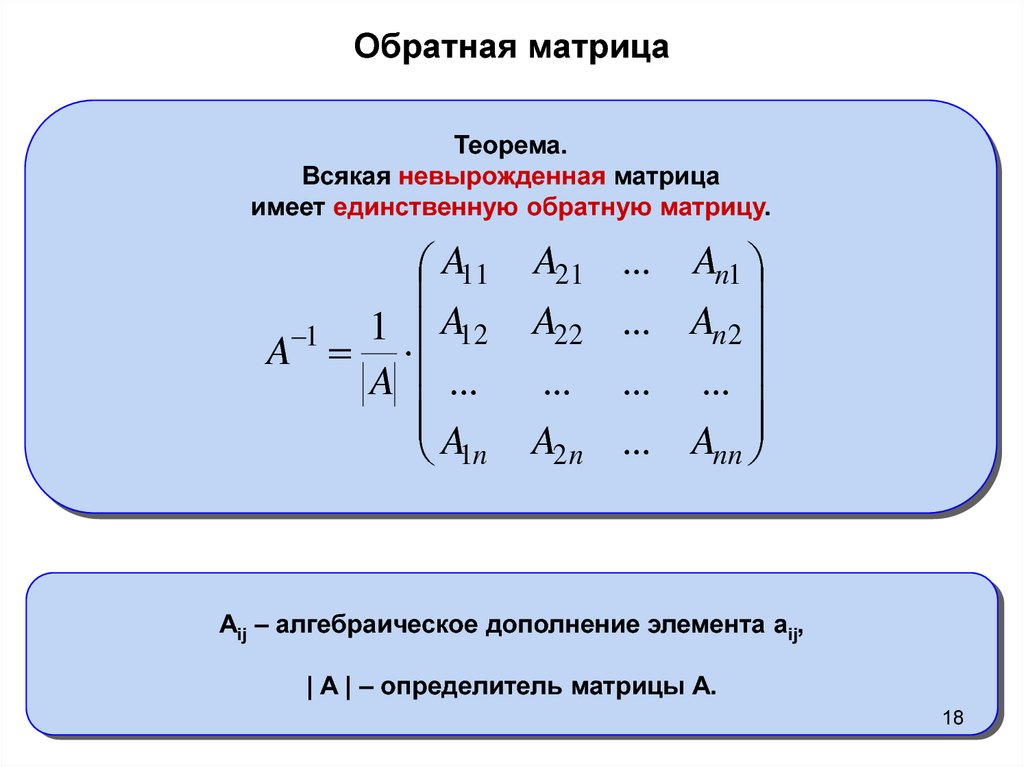 Ранг матрицы обозначается так: или .
Ранг матрицы обозначается так: или .
Возможно вам будут полезны данные страницы:
Производная сложной функции примеры решений |
Скалярное произведение векторов примеры решения |
Определенный интеграл примеры решений |
Область определения функции примеры решения |
Примеры с решением
Пример 1.
Найти матрицу, обратную матрице
Вычисляем определитель матрицы
Поскольку то матрица имеет обратную. В данном случае
Составляем матрицы:
Находим матрицу обратную матрице
Следовательно
Замечание. Формула (1.9) при принимает вид так как Последняя формула для означается следующее: чтобы найти матрицу, обратную квадратной матрице второго порядка, необходимо в исходной матрице поменять местами элементы главной диагонали, изменить знаки элементов второй диагонали, полученную матрицу умножить на число, обратное определителю исходной матрицы.
Пример 2.
Выяснить, существуют ли обратные матрицы для матриц
Вычисляем определители матриц.
Поскольку то матрица имеет обратную. Так как то не существует матрицы, обратной матрице
Пример 3.
Выяснить, при каких значениях существуют матрицы, обратные для матриц
Вычисляем определители матриц.
Так как при то матрица имеет обратную при всех значениях кроме Поскольку при т.е. при то матрица имеет обратную при всех значениях кроме значений
Пример 4.
Найти матрицу, обратную матрице
Вычисляем определитель матрицы
Так как то существует матрица обратная матрице
Вычисляем алгебраические дополнения элементов матрицы
Составляем матрицы и
В соответствии с формулой (1.9), которая при принимает вид:
получаем обратную матрицу .
Квадратная матрица имеет обратную, если определитель.
Пример 5.

Выяснить, существуют ли обратные матрицы для матриц
Вычисляем определители матриц
Поскольку то матрица не имеет обратной. Так как то существует матрица, обратная матрице
Пример 6.
Выяснить, при каких значениях существуют матрицы, обратные матрицам
Вычисляем определители матриц
Так как при то матрица, обратная для матрицы существует при всех значениях кроме Поскольку при то матрица, обратная матрицей, существует при всех значениях кроме значений
Пример 7.
Найти ранг матрицы
Определитель этой матрицы равен нулю, так как содержит пропорциональные строки. Все определители второго порядка также равны нулю, в чем можно убедиться непосредственно. Матрица содержит элементы, отличные от нуля. Наивысший порядок миноров, отличных от нуля, равен единице, следовательно, ранг матрицы равен единице:
Так называемая теорема об обратимой матрице является основным результатом в линейной алгебре, которая связывает существование обратной матрицы с рядом других эквивалентных свойств. |
Матрица , обладающая обратным называется неособо, или обратимым. Когда мы умножаем матрицу на ее обратную, мы получаем матрицу идентичности.
Замечание.
Ранг матрицы не меняется при элементарных преобразованиях. Умножим первую строку на (-2) и прибавим ко второй; умножим первую строку на (-3) и прибавим к третьей:
Из последней матрицы видно, что ее ранг равен единице, значит, ранг исходной матрицы также равен единице.
Пусть квадратная матрица порядка, а единичная матрица того же порядка.
Определение Матрица называется обратной для квадратной матрицы если
Из этого определения следует, что обратная матрица будет квадратной матрицей того же порядка, что и матрица
Обратная матрица для матрицы обозначается Таким образом, если, конечно, существует
Из определения обратной матрицы следует, что матрица в свою очередь является обратной для матрицы т.е.
Про матрицы и
можно говорить, что они обратны друг другу или взаимно обратны.
Определение Матрица называется невырожденной, если определитель этой матрицы отличен от нуля: в противном случае матрица называется вырожденной.
Теорема Если матрица имеет обратную, то эта матрица является невырожденной:
Доказательство. Пусть обратная матрица для матрицы . Тогда откуда, согласно свойству 8 определителей получим
1. Из полученного равенства следует, что и что
Теорема доказана.
Верно и обратное утверждение:
Теорема Всякая невырожденная матрица
имеет обратную матрицу причем
где алгебраические дополнения элементов матрицы .
Доказательство.
Докажем, что матрица определенная формулой в самом деле является обратной для матрицы Для этого следует доказать равенства Обозначим и вычислим элемент
матрицы согласно формуле
Так как
то следовательно,
это значит, что матрица единичная: Таким образом, равенство доказано. Точно так же доказывается и равенство Теорема доказана.
Точно так же доказывается и равенство Теорема доказана.
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Как видим, операция транспонирования может применяться как в начале, над исходной матрицей, так и в конце, над полученными алгебраическими дополнениями.
Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Определение 1: матрица называется вырожденной, если её определитель равен нулю.
Определение 2: матрица называется невырожденной, если её определитель не равен нулю.
Матрица «A» называется обратной матрицей , если выполняется условие A*A-1 = A-1 *A = E (единичной матрице).
Квадратная матрица обратима только в том случае, когда она является невырожденной.
Схема вычисления обратной матрицы:
1) Вычислить определитель матрицы «A», если ∆ A = 0, то обратной матрицы не существует.
2) Найти все алгебраические дополнения матрицы «A».
3) Составить матрицу из алгебраических дополнений (Aij )
4) Транспонировать матрицу из алгебраических дополнений (Aij )T
5) Умножить транспонированную матрицу на число, обратное определителю данной матрицы.
6) Выполнить проверку:
На первый взгляд может показаться, что это сложно, но на самом деле всё очень просто. Все решения основаны на простых арифметических действиях, главное при решении не путаться со знаками «-» и «+», и не терять их.
А теперь давайте вместе с Вами решим практическое задание, вычислив обратную матрицу.
Задание: найти обратную матрицу «A», представленную на картинке ниже:
Решаем всё в точности так, как это указано в план-схеме вычисления обратной матрицы.
1. Первое, что нужно сделать, это найти определитель матрицы «A»:
Пояснение:
Мы упростили наш определитель, воспользовавшись его основными функциями. Во первых, мы прибавили ко 2 и 3 строке элементы первой строки, умноженные на одно число.
Во первых, мы прибавили ко 2 и 3 строке элементы первой строки, умноженные на одно число.
Во-вторых, мы поменяли 2 и 3 столбец определителя, и по его свойствам поменяли знак перед ним.
В-третьих, мы вынесли общий множитель (-1) второй строки, тем самым, снова поменяв знак, и он стал положительным. Также мы упростили 3 строку также, как в самом начале примера.
У нас получилась треугольный определитель, у которого элементы ниже диагонали равны нулю, и по 7 свойству он равен произведению элементов диагонали. В итоге мы получили ∆ A = 26, следовательно обратная матрица существует.
А11 = 1*(3+1) = 4
А12 = -1*(9+2) = -11
А13 = 1*1 = 1
А21 = -1*(-6) = 6
А22 = 1*(3-0) = 3
А23 = -1*(1+4) = -5
А31 = 1*2 = 2
А32 = -1*(-1) = -1
А33 = 1+(1+6) = 7
3. Следующий шаг — составление матрицы из получившихся дополнений:
5. Умножаем эту матрицу на число, обратное определителю, то есть на 1/26:
6. Ну а теперь нам просто нужно выполнить проверку:
Ну а теперь нам просто нужно выполнить проверку:
В ходе проверки мы получили единичную матрицу, следовательно, решение было выполнено абсолютно верно.
2 способ вычисления обратной матрицы.
1. Элементарное преобразование матриц
2. Обратная матрица через элементарный преобразователь.
Элементарное преобразование матриц включает:
1. Умножение строки на число, не равное нулю.
2. Прибавление к любой строке другой строки, умноженной на число.
3. Перемена местами строк матрицы.
4. Применяя цепочку элементарных преобразований, получаем другую матрицу.
А-1 = ?
1. (A|E) ~ (E|A-1 )
2. A-1 * A = E
Рассмотрим это на практическом примере с действительными числами.
Задание: Найти обратную матрицу.
Решение:
Выполним проверку:
Небольшое разъяснение по решению:
Сперва мы переставили 1 и 2 строку матрицы, затем умножили первую строку на (-1).
После этого умножили первую строку на (-2) и сложили со второй строкой матрицы. После чего умножили 2 строку на 1/4.
Заключительным этапом преобразований стало умножение второй строки на 2 и прибавлением с первой. В результате слева у нас получилась единичная матрица, следовательно, обратная матрица — это матрица справа.
После проверки мы убедились в правильности решения.
Как вы видите, вычисление обратной матрицы — это очень просто.
В заключении данной лекции хотелось бы также уделить немного времени свойствам такой матрицы.
Алгоритм решения обратной матрицы. Как найти обратную матрицу. Нахождение обратной матрицы методом присоединённой матрицы
Уголок строительства и ремонта. Только полезные советы » Бассейн » Алгоритм решения обратной матрицы. Как найти обратную матрицу. Нахождение обратной матрицы методом присоединённой матрицы
Для обратной матрицы существует уместная аналогия с обратным
числом. Для каждого числа a , не равного нулю, существует такое число b , что произведение a и b равно единице: ab = 1
. Число b называется обратным для числа b . Например, для числа 7 обратным является число 1/7,
так как 7*1/7=1.
Для каждого числа a , не равного нулю, существует такое число b , что произведение a и b равно единице: ab = 1
. Число b называется обратным для числа b . Например, для числа 7 обратным является число 1/7,
так как 7*1/7=1.
Обратной матрицей , которую требуется отыскать для данной квадратной матрицы А , называется такая матрица
произведение на которую матрицы А справа является единичной матрицей, т.е,
. (1)
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Нахождение обратной матрицы — задача, которая чаще решается двумя методами:
- методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц
(складывать строки, умножать строки на одно и то же число и т.
 д.).
д.).
Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной , несингулярной ), если её определитель не равен нулю, и особенной (или вырожденной , сингулярной ), если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
Нахождение обратной матрицы методом исключения неизвестных Гаусса
Первый шаг для нахождения обратной матрицы методом исключения неизвестных Гаусса —
приписать к матрице A единичную матрицу того же порядка, отделив их вертикальной чертой. Мы
получим сдвоенную матрицу .
Умножим обе части этой матрицы на ,
тогда получим
Мы
получим сдвоенную матрицу .
Умножим обе части этой матрицы на ,
тогда получим
,
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась единичная матрица, тогда в правой части на месте единичной матрицы автоматически получится обратная матрица. Матрица A в левой части преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы
найти обратную матрицу.
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим
.
Разделим третью строку на 8, тогда
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
.
Переставим местами вторую и третью строку, тогда окончательно получим:
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица . Таким образом:
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
В результате должна получиться обратная матрица. (2+1) = -1.
(2+1) = -1.
В результате вы получите матрицу дополнений, теперь транспонируйте ее. Транспонирование — это операция, симметричная относительно главной диагонали матрицы, столбцы и строки меняются местами. Таким образом, вы нашли присоединенную матрицу A*.
Способы нахождения обратной матрицы. Рассмотрим квадратную матрицу
Обозначим Δ = det A.
Квадратная матрица А называется невырожденной, или неособенной , если ее определитель отличен от нуля, и вырожденной, или особенной , если Δ = 0.
Квадратная матрица В есть для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е — единичная матрица того же порядка, что и матрицы А и В.
Теорема . Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Обратная матрица матрице А, обозначается через А — 1 , так что В = А — 1 и вычисляется по формуле
, (1)
где А i j — алгебраические дополнения элементов a i j матрицы A. .
.
Вычисление A -1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A -1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример 1 . Для матрицы найти A -1 .
Решение. Находим сначала детерминант матрицы А
значит, обратная матрица существует и мы ее можем найти по формуле: , где А i j (i,j=1,2,3) — алгебраические дополнения элементов а i j исходной матрицы.
Откуда .
Пример 2 . Методом элементарных преобразований найти A -1 для матрицы: А= .
Решение. Приписываем к исходной матрице справа единичную матрицу того же порядка: . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы: ~
. К третьему столбцу прибавим первый, а ко второму — первый, умноженный на -2: . Из первого столбца вычтем удвоенный второй, а из третьего — умноженный на 6 второй; . Прибавим третий столбец к первому и второму: . Умножим последний столбец на -1: . Полученная справа от вертикальной черты квадратная матрица является обратной матрицей к данной матрице А. Итак,
.
1.
Находим определитель исходной матрицы.
Если
,
то матрица-
вырожденная и обратной матрицыне
существует. Если,
то матрицаневырожденная
и обратная матрица существует.
2. Находим матрицу , транспонированную к.
3. Находим алгебраические дополнения элементов и составляем из них присоединенную матрицу.
4. Составляем обратную матрицу по формуле .
5. Проверяем правильность вычисления обратной матрицы , исходя из ее определения:.
Пример. Найти матрицу, обратную данной: .
Р е ш е н и е.
1) Определитель матрицы
.
2) Находим алгебраические дополнения элементов матрицы и составляем из них присоединенную матрицу :
3) Вычисляем обратную матрицу:
,
4) Проверяем:
№4 Ранг матрицы. Линейная независимость строк матрицы
Для решения и исследования ряда математических и прикладных задач важное значение имеет понятие ранга матрицы.
В матрице размеромвычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы-го порядка, где. Определители таких подматриц называютсяминорами -го порядка матрицы .
Например,
из матриц
можно
получить подматрицы 1, 2 и 3-го порядка.
Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначение:или.
Из определения следует:
1) Ранг матрицы не превосходит меньшего из ее размеров, т.е..
2) тогда и только тогда, когда все элементы матрицы равны нулю, т.е..
3) Для квадратной матрицы n-го порядка тогда и только тогда, когда матрица- невырожденная.
Поскольку непосредственный перебор всех возможных миноров матрицы , начиная с наибольшего размера, затруднителен (трудоемок), то пользуются элементарными преобразованиями матрицы, сохраняющими ранг матрицы.
Элементарные преобразования матрицы:
1) Отбрасывание нулевой строки (столбца).
2) Умножение всех элементов строки (столбца) на число .
3) Изменение порядка строк (столбцов) матрицы.
4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
5)
Транспонирование матрицы.
Определение. Матрица , полученная из матрицыпри помощи элементарных преобразований, называется эквивалентной и обозначаетсяА В .
Теорема. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ее ранга не представляет труда.
Матрица называется ступенчатой если она имеет вид:
Очевидно, что ранг ступенчатой матрицы равен числу ненулевых строк , т.к. имеется минор-го порядка, не равный нулю:
.
Пример. Определить ранг матрицы с помощью элементарных преобразований.
Ранг матрицы равен количеству ненулевых строк, т.е. .
№5Линейная независимость строк матрицы
Дана матрица размера
Обозначим строки матрицы следующим образом:
Две строки называются равными , если равны их соответствующие элементы. .
Введем операции умножения строки на число и сложение строк как операции, проводимые поэлементно:
Определение. Строка
называется
линейной комбинацией строкматрицы,
если она равна сумме произведений этих
строк на произвольные действительные
числа(любые
числа):
Строка
называется
линейной комбинацией строкматрицы,
если она равна сумме произведений этих
строк на произвольные действительные
числа(любые
числа):
Определение. Строки матрицы называютсялинейно зависимыми , если существует такие числа , не равные одновременно нулю, что линейная комбинация строк матрицы равна нулевой строке:
Где . (1.1)
Линейная зависимость строк матрицы обозначает, что хотя бы 1 строка матрицы является линейной комбинацией остальных.
Определение. Если линейная комбинация строк (1.1) равна нулю тогда и только тогда, когда все коэффициенты , то строкиназываютсялинейно независимыми .
Теорема о ранге матрицы . Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные строки (столбцы).
Теорема
играет принципиальную роль в матричном
анализе, в частности, при исследовании
систем линейных уравнений.
№6 Решение системы линейных уравнений снеизвестными
Системы линейных уравнений находят широкое применение в экономике.
Система линейных уравнений спеременными имеет вид:
,
где () — произвольные числа, называемыекоэффициентами при переменных и свободными членами уравнений , соответственно.
Краткая запись: ().
Определение. Решением системы называется такая совокупность значений , при подстановке которых каждое уравнение системы обращается в верное равенство.
1) Система уравнений называется совместной , если она имеет хотя бы одно решение, и несовместной , если она не имеет решений.
2) Совместная система уравнений называется определенной , если она имеет единственное решение, и неопределенной , если она имеет более одного решения.
3)
Две системы уравнений называются равносильными (эквивалентными ) ,
если они имеют одно и то же множество
решений (например, одно решение).
9. Обратная матрица
Вместо операции деления матриц вводится понятие обратной матрицы.
Обозначается обратная матрица , то есть .
Очевидна аналогия с числами: для числа 2 число ½ есть обратное, так как . Именно поэтому матрица, обратная к А, обозначается .
Теорема «Необходимое и достаточное условие существования обратной матрицы». Для того чтобы квадратная матрица имела обратную матрицу , необходимо и достаточно, чтобы определитель матрицы был не равен нулю.
Правило нахождения обратной матрицы
0) Смотрим, является ли матрица квадратной. Если нет, то обратной матрицы не существует; если квадратная, то переходим к пункту 1.
1) Вычисляем определитель матрицы :
если он не равен нулю, то обратная матрица
существует: ; если
равен нулю, то обратной матрицы нет.
2) Для каждого элемента матрицы вычисляем его алгебраическое дополнение .
3) Составляем матрицу из алгебраических дополнений, которая затем транспонируем: .
4) Каждый элемент матрицы делим на определитель : Получаем матрицу, обратную данной.
10. Нахождение обратной матрицы для матриц второго порядка
Пример 10. Дана матрица . Найти обратную матрицу.
Решение.
Проверка. Убедимся, что найдена действительно обратная матрица. Найдем произведение матриц и .
11. Свойства обратной матрицы
1. , где А и В – невырожденные квадратные матрицы одинакового порядка.
2. .
3. .
.
4. .
Контрольные вопросы
Дайте определение матрицы и укажите ее виды.
Как проводятся линейные операции над матрицами — сложение матриц, умножение на число?
Даны матрицы . При каких условиях на определены матрицы ?
Как умножить матрицу на матрицу? Запишите условие, которому должны удовлетворять первая и вторая матрицы-сомножители.
Как найти любой элемент произведения матриц?
Даны матрицы . При каких условиях на определены матрицы ?
Запишите свойства суммы и произведения матриц.
Какая матрица называется транспонированной к данной? Составьте матрицу и транспонируйте ее. Какова ее размерность? Запишите свойства операции транспонирования.

Какая матрица называется единичной? Нулевой? Приведите примеры.
Запишите элементы матрицы и элементы матрицы .
Что называется определителем второго порядка?
Как вычислить определитель третьего порядка?
Как вычислить определитель 3 порядка по правилу треугольников?
Что называется алгебраическим дополнением элемента определителя? Приведите примеры для определителей 2 и 3 порядков.
Напишите разложения определителя третьего порядка по элементам произвольной строки и произвольного столбца.
Сформулируйте основные свойства определителей.
В каком случае определители равны нулю? Приведите примеры.
Представьте определитель в виде суммы двух определителей.
 <-1>=left( egin 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end
<-1>=left( egin 3/13 & -5/26 & 1/26 \ 4/13 & 1/13 & -8/13 \ -6/13 & -3/26 & 37/26 end
ight)$.Найти матрицу, обратную матрице $A=left( egin 6 & -5 & 8 & 4\ 9 & 7 & 5 & 2 \ 7 & 5 & 3 & 7\ -4 & 8 & -8 & -3 end
ight)$.Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Чтобы найти обратную матрицу, для начала нужно вычислить определитель матрицы $A$. Лучше всего в данной ситуации это сделать с помощью разложения определителя по строке (столбцу). Выбираем любую строку или столбец и находим алгебраические дополнения каждого элемента избранной строки или столбца.
Например, для первой строки получим:
Определитель матрицы $A$ вычислим по следующей формуле:
А далее продолжаем находить алгебраические дополнения:
Матрица из алгебраических дополнений: $A^*=left(egin556 & -300 & -536 & -112\ -77 & 50 & 87 & 4 \ -93 & 50 & 83 & 36\ 473 & -250 & -463 & -96end
ight)$. <-1>=left( egin 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end
<-1>=left( egin 139/25 & -77/100 & -93/100 & 473/100 \ -3 & 1/2 & 1/2 & -5/2 \ -134/25 & 87/100 & 83/100 & -463/100 \ -28/25 & 1/25 & 9/25 & -24/25 end
ight)$.Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Продолжаем разговор о действиях с матрицами. А именно – в ходе изучения данной лекции вы научитесь находить обратную матрицу. Научитесь. Даже если с математикой туго.
Что такое обратная матрица? Здесь можно провести аналогию с обратными числами: рассмотрим, например, оптимистичное число 5 и обратное ему число . Произведение данных чисел равно единице: . С матрицами всё похоже! Произведение матрицы на обратную ей матрицу равно – единичной матрице, которая является матричным аналогом числовой единицы. Однако обо всём по порядку – сначала решим важный практический вопрос, а именно, научимся эту самую обратную матрицу находить.

Что необходимо знать и уметь для нахождения обратной матрицы? Вы должны уметь решать определители. Вы должны понимать, что такое матрица и уметь выполнять некоторые действия с ними.
Есть? Тогда поехали дальше. А хотя… ехать могут все, если что-то не знаете, я буду ставить нужную ссылку по ходу объяснений.
Существует два основных метода нахождения обратной матрицы:
с помощью алгебраических дополнений и с помощью элементарных преобразований.Сегодня мы изучим первый, более простой способ.
Начнем с самого ужасного и непонятного. Рассмотрим квадратную матрицу . Обратную матрицу можно найти по следующей формуле:
, где – определитель матрицы , – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Понятие обратной матрицы существует только для квадратных матриц, матриц «два на два», «три на три» и т.д.

Обозначения: Как вы уже, наверное, заметили, обратная матрица обозначается надстрочным индексом
Начнем с простейшего случая – матрицы «два на два». Чаще всего, конечно, требуется найти обратную матрицу для матрицы «три на три», но, тем не менее, настоятельно рекомендую изучить более простое задание, для того чтобы усвоить общий принцип решения.
Найти обратную матрицу для матрицы
Решаем. Последовательность действий удобно разложить по пунктам.
1) Сначала находим определитель матрицы.
Если с пониманием сего действа плоховато, ознакомьтесь с материалом Как вычислить определитель?
Важно! В том случае, если определитель матрицы равен НУЛЮ – обратной матрицы НЕ СУЩЕСТВУЕТ.
В рассматриваемом примере, как выяснилось, , а значит, всё в порядке.
2) Находим матрицу миноров .
Для решения нашей задачи не обязательно знать, что такое минор, однако, желательно ознакомиться со статьей Как вычислить определитель.

Матрица миноров имеет такие же размеры, как и матрица , то есть в данном случае .
Дело за малым, осталось найти четыре числа и поставить их вместо звездочек.Возвращаемся к нашей матрице
Сначала рассмотрим левый верхний элемент:
Как найти его минор?
А делается это так: МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:
Оставшееся число и является минором данного элемента, которое записываем в нашу матрицу миноров:
Рассматриваем следующий элемент матрицы :
Мысленно вычеркиваем строку и столбец, в котором стоит данный элемент:
То, что осталось, и есть минор данного элемента, который записываем в нашу матрицу:
Аналогично рассматриваем элементы второй строки и находим их миноры:
Готово.– матрица миноров соответствующих элементов матрицы .
3) Находим матрицу алгебраических дополнений .
Это просто.
 В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:
В матрице миноров нужно ПОМЕНЯТЬ ЗНАКИ у двух чисел:
Именно у этих чисел, которые я обвел в кружок!– матрица алгебраических дополнений соответствующих элементов матрицы .
4) Находим транспонированную матрицу алгебраических дополнений .
Что такое транспонирование матрицы, и с чем это едят, смотрите в лекции Действия с матрицами.
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
5) Ответ.
Вспоминаем нашу формулу
Всё найдено!Таким образом, обратная матрица:
Ответ лучше оставить в таком виде. НЕ НУЖНО делить каждый элемент матрицы на 2, так как получатся дробные числа. Более подробно данный нюанс рассмотрен в той же статье Действия с матрицами.
Как проверить решение?
Необходимо выполнить матричное умножение либо
Проверка:
Получена уже упомянутая единичная матрица – это матрица с единицами на главной диагонали и нулями в остальных местах.

Таким образом, обратная матрица найдена правильно.
Если провести действие , то в результате тоже получится единичная матрица. Это один из немногих случаев, когда умножение матриц перестановочно, более подробную информацию можно найти в статье Свойства операций над матрицами. Матричные выражения. Также заметьте, что в ходе проверки константа (дробь) выносится вперёд и обрабатывается в самом конце – после матричного умножения. Это стандартный приём.
Переходим к более распространенному на практике случаю – матрице «три на три»:
Найти обратную матрицу для матрицы
Алгоритм точно такой же, как и для случая «два на два».
Обратную матрицу найдем по формуле: , где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
1) Находим определитель матрицы.
Здесь определитель раскрыт по первой строке.Также не забываем, что , а значит, всё нормально – обратная матрица существует.

2) Находим матрицу миноров .
Матрица миноров имеет размерность «три на три» , и нам нужно найти девять чисел.
Я подробно рассмотрю парочку миноров:
Рассмотрим следующий элемент матрицы:
МЫСЛЕННО вычеркиваем строку и столбец, в котором находится данный элемент:Оставшиеся четыре числа записываем в определитель «два на два»
Этот определитель «два на два» и является минором данного элемента. Его нужно вычислить:
Всё, минор найден, записываем его в нашу матрицу миноров:Как вы, наверное, догадались, необходимо вычислить девять определителей «два на два». Процесс, конечно, муторный, но случай не самый тяжелый, бывает хуже.
Ну и для закрепления – нахождение еще одного минора в картинках:
Остальные миноры попробуйте вычислить самостоятельно.Окончательный результат:
– матрица миноров соответствующих элементов матрицы .То, что все миноры получились отрицательными – чистая случайность.

3) Находим матрицу алгебраических дополнений .
В матрице миноров необходимо СМЕНИТЬ ЗНАКИ строго у следующих элементов:
В данном случае:
– матрица алгебраических дополнений соответствующих элементов матрицы .4) Находим транспонированную матрицу алгебраических дополнений .
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
5) Ответ:
Проверка:
Таким образом, обратная матрица найдена правильно.
Как оформить решение на чистовик? Примерный образец чистового оформления задания можно найти на странице Правило Крамера. Метод обратной матрицы в параграфе, где идет речь о матричном методе решения системы линейных уравнений. По существу, основная часть упомянутой задачи – и есть поиск обратной матрицы.
Нахождение обратной матрицы для матрицы «четыре на четыре» не рассматриваем, так как такое задание может дать только преподаватель-садист (чтобы студент вычислил один определитель «четыре на четыре» и 16 определителей «три на три»).
 В моей практике встретился только один такой случай, и заказчик контрольной работы заплатил за мои мучения довольно дорого =).
В моей практике встретился только один такой случай, и заказчик контрольной работы заплатил за мои мучения довольно дорого =).В ряде учебников, методичек можно встретить несколько другой подход к нахождению обратной матрицы, однако я рекомендую пользоваться именно вышеизложенным алгоритмом решения. Почему? Потому что вероятность запутаться в вычислениях и знаках – гораздо меньше.
Иногда обратную матрицу требуется найти методом Гаусса-Жордана, но второй способ доступен для студентов с приличной техникой элементарных преобразований.
Автор: Емелин Александр
(Переход на главную страницу)
Профессиональная помощь по любому предмету – Zaochnik.com
Что значит найти обратную матрицу?
Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a, не равного нулю, существует такое число b, что произведение a и b равно единице: ab = 1 .
 Число b называется обратным для числа b. Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.
Число b называется обратным для числа b. Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица
,
произведение на которую матрицы А справа является единичной матрицей, т.е,
. (1)Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Нахождение обратной матрицы — задача, которая чаще решается двумя методами:
- методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).
Для особо любознательных существуют и другие методы, например, метод линейных преобразований.
 На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или вырожденной, сингулярной), если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)
Для неособенной квадратной матрицы А обратной является матрица
, (2)
где — определитель матрицы А, а — матрица, союзная с матрицей А.

Союзной с квадратной матрицей A называется матрица того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы , транспонированной относительно матрицы A. Таким образом, если
то
и
Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A, на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно.
 В противном случае начать процесс решения снова.
В противном случае начать процесс решения снова.Пример 1. Для матрицы
найти обратную матрицу.
Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А . Находим по правилу треугольников:
Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу , транспонированную относительно матрицы A:
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:
Следовательно, матрица , союзная с матрицей A, имеет вид
Замечание. Порядок вычисления элементов и транспонирования матрицы может быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать матрицу алгебраических дополнений.
 В результате должны получиться те же элементы союзной матрицы.
В результате должны получиться те же элементы союзной матрицы.Применяя формулу (2), находим матрицу, обратную матрице А:
Нахождение обратной матрицы методом исключения неизвестных Гаусса
Первый шаг для нахождения обратной матрицы методом исключения неизвестных Гаусса — приписать к матрице A единичную матрицу того же порядка, отделив их вертикальной чертой. Мы получим сдвоенную матрицу . Умножим обе части этой матрицы на , тогда получим
,
и .
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась единичная матрица, тогда в правой части на месте единичной матрицы автоматически получится обратная матрица. Матрица A в левой части преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы.
 В этом случае дальнейшее нахождение обратной матрицы прекращается.
В этом случае дальнейшее нахождение обратной матрицы прекращается.Пример 2. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим
.
Разделим третью строку на 8, тогда
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
.

Переставим местами вторую и третью строку, тогда окончательно получим:
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица . Таким образом:
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
.
В результате должна получиться обратная матрица.
Пример 3. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим
.
Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет.
 Дальнейшее нахождение обратной марицы прекращаем.
Дальнейшее нахождение обратной марицы прекращаем.Нахождение обратной матрицы методом линейных преобразований
Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот, системе линейных уравнений соответствует некоторая матрица.
Поэтому существует метод линейных преобразований для нахождения обратной матрицы. Для решения задач нам будет достаточно знать, что линейное преобразование — это система линейных уравнений, вид которой будет приведён ниже в алгоритме.
Алгоритм нахождения обратной матрицы методом линейных преобразований
1. Для данной невырожденной матрицы A составить линейное преобразование — систему линейных уравнений вида
,
где a ij — элементы матрицы A.
2. Решить полученную систему относительно y — найти для предыдущего линейного преобразование обратное линейное преобразование
,
в котором A ij — алгебраические дополнения элементов матрицы A, Δ — определитель матрицы A.
 Внимание! Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки — в столбце, а для элементов столбца — в строке.
Внимание! Алгебраические дополнения располагаются как в транспонированной матрице, то есть для элементов строки — в столбце, а для элементов столбца — в строке.3. Находим коэффициенты при y: , которые и будут элементами матрицы, обратной для матрицы A.
4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.
Наиболее наблюдательные могли заметить, что по сути метод линейных преобразований — это тот же метод алгебраических преобразований (союзной матрицы), но с другой формой записи. Для кого-то метод линейных преобразований может оказаться более удобным как более компактный.
Пример 4. Найти обратную матрицу для матрицы
.
Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю, следовательно, обратная матрица существует.
Для данной матрицы записываем линейное преобразование:
.
Находим линейное преобразование, обратное предыдущему, для этого потребуется находить алгебраические дополнения (урок откроется в новом окне).
 Запишем обратное линейное преобразование:
Запишем обратное линейное преобразование:Коэффициенты при иксах в обратном линейном преобразовании — это элементы обратной матрицы для матрицы A. Таким образом нашли обратную матрицу:
Найти обратную матрицу самостоятельно, а затем посмотреть решение
Пример 5. Найти обратную матрицу для матрицы
.
обратная матрица
Сначала прочтите наше введение в матрицы.
Что такое обратная матрица?
Точно так же, как число , число имеет обратную…
… матрица имеет обратную :
Обратное число (примечание: 1 8 также может быть записано как 8 -1 )
Мы пишем A -1 вместо 1 A потому что мы не делим на матрицу!
Обратная матрицаЕсть и другие сходства:
, когда мы умножим номер на его взаимный , мы получаем 1 :
8 × 1 8 = 1
, когда мы умножьте матрицу на его
Идентификационная матрица (что похоже на «1» для матриц):
A × A -1 = I
То же самое, когда сначала идет инверсия:
1 8 × 8 = 1
А -1 × А = I
Матрица идентичности
Мы только что упомянули «Матрицу личности».
. Это матричный эквивалент числа «1»:
Это матричный эквивалент числа «1»:I =
100 010 001
Идентификационная матрица 3×3
- Это «квадрат» (имеет такое же количество строк, как и столбцов),
- У него 1 с по диагонали и 0 с везде.
- Его символ — заглавная буква I .
Матрица идентичности может быть размером 2×2 или 3×3, 4×4 и т. д.
Определение
Вот определение:
Обратное к A равно A -1 только тогда, когда:
AA -1 = A -1 A = I
Иногда обратного нет вообще.
(Примечание: запись AA -1 означает A умножить на A -1 )
Матрица 2×2
Хорошо, а как вычислить обратное?
Ну, для матрицы 2×2 обратное:
−1 = 1 ad−bc
d−b −ок
Другими словами: поменять местами a и d, поставить отрицательных чисел перед b и c, и разделить все на ad-bc .

Примечание: ad-bc называется определителем.
Давайте попробуем пример:
−1 = 1 4×6−7×2
6−7 −24
= 1 10
6−7 −24
=
0,6−0,7 −0,20,4
Откуда мы знаем, что это правильный ответ?
Помните, должно быть верно, что: AA -1 = I
Итак, давайте проверим, что произойдет, если мы умножим матрицу на обратную:
0,6−0,7 −0,20,4
=
4×0,6+7×−0,24×−0,7+7×0,4 2×0,6+6×−0,22×−0,7+6×0,4
=
2,4−1,4−2,8+2,8 1,2−1,2−1,4+2,4
И, эй!, мы получаем Матрицу Личности!
Так и должно быть.Должно быть верно и , что: A -1 A = I
Почему бы тебе не попробовать их умножить? Посмотрите, получите ли вы также матрицу идентичности:
0,6−0,7 −0,20,4
=
Зачем нужна инверсия?
Потому что с матрицами мы не делить ! Серьезно, нет понятия деления на матрицу.

Но мы можем умножить на обратное , что даст то же самое.
Представьте, что мы не можем делить на числа…
… и кто-то спрашивает: «Как мне разделить 10 яблок с двумя людьми?»
Но мы можем взять обратное от 2 (что равно 0,5), поэтому мы ответим:
10 × 0,5 = 5
Каждый из них получил по 5 яблок.
То же самое можно сделать с матрицами:
Допустим, мы хотим найти матрицу X, и мы знаем матрицы A и B:
XA = B
Было бы неплохо разделить обе части на A (чтобы получить X=B/A), но помните, что мы можем’ t разделить .
Но что, если мы умножим обе части на A -1 ?
XAA -1 = BA -1
И мы знаем, что AA -1 = I, поэтому:
XI = BA -1
Мы можем удалить I (по той же причине мы можем удалить I можно удалить «1» из 1x = ab для чисел):
X = BA -1
И у нас есть ответ (при условии, что мы можем вычислить A -1 )
В этом примере мы очень внимательно следили за правильным умножением, потому что в случае с матрицами важен порядок умножения.
 AB почти никогда не равен BA.
AB почти никогда не равен BA.Пример из жизни: автобус и поезд
Группа совершила поездку на автобусе по цене 3 доллара США за ребенка и 3,20 доллара США за взрослого на общую сумму 118,40 долларов США.
Они взяли поезд обратно по 3,50 доллара за ребенка и 3,60 доллара за взрослого, всего 135,20 доллара.
Сколько детей и сколько взрослых?
Во-первых, давайте настроим матрицы (будьте внимательны, чтобы строки и столбцы были правильными!):
Это точно так же, как в примере выше:
ХА = В
Итак, чтобы решить это, нам нужно обратное «А»:
33,5 3.23.6
−1 = 1 3×3,6−3,5×3,2
3,6−3,5 −3,23
=
−98,75 8−7,5
Теперь у нас есть обратное, которое мы можем решить, используя:
Х = БА -1
=
118,4 135,2
−98,75 8−7,5
=
118,4×−9 + 135,2×8118,4×8,75 + 135,2×−7,5
Было 16 детей и 22 взрослых!
Ответ появляется почти как по волшебству.
 Но он основан на хорошей математике.
Но он основан на хорошей математике.Подобные расчеты (но с использованием гораздо более крупных матриц) помогают инженерам проектировать здания, используются в видеоиграх и компьютерной анимации для придания трехмерности и во многих других местах.
Это также способ решения систем линейных уравнений.
Расчеты выполняются компьютером, но люди должны понимать формулы.
Заказ важен
Скажем, что мы пытаемся найти «X» в этом случае:
AX = B
Это отличается от приведенного выше примера! X теперь после A.
С матрицами порядок умножения обычно меняет ответ. Не думайте, что AB = BA, это почти никогда не верно.
Итак, как решить эту задачу? Используя тот же метод, но поместив A -1 впереди:
A -1 AX = A -1 B
И мы знаем, что A -1 A= I, поэтому:
IX = A -1 B
Мы можем удалить I:
X = A -1 B
И у нас есть ответ (при условии, что мы можем вычислить A -1 )
Почему бы нам не попробовать наш пример с автобусом и поездом, но с данными, настроенными таким образом.

Это можно сделать и так, но мы должны быть осторожны при настройке.
Вот как это выглядит, когда AX = B:
33,2 3.53.6
=
118,4 135,2
Выглядит так аккуратно! Я думаю, что предпочитаю это так.
Также обратите внимание, как строки и столбцы меняются местами в
(«Транспонированные») по сравнению с предыдущим примером.Чтобы решить это, нам нужно обратное «А»:
33,2 3.53.6
−1 = 1 3×3,6−3,2×3,5
3,6−3,2 −3,53
=
−98 8,75−7,5
Это похоже на инверсию, которую мы получили раньше, но
Transposed (строки и столбцы меняются местами).Теперь мы можем решить, используя:
Х = А -1 В
=
−98 8,75−7,5
118,4 135,2
=
−9×118,4 + 8×135,2 8,75×118,4 − 7,5×135,2
Тот же ответ: 16 детей и 22 взрослых.

Итак, матрицы — мощная штука, но их нужно правильно настроить!
Обратное может не существовать
Прежде всего, чтобы получить обратную матрицу, она должна быть «квадратной» (одинаковое количество строк и столбцов).
Но также и определитель не может быть равен нулю (иначе мы закончим делением на ноль). Как насчет этого:
−1 = 1 3×8−4×6
8−4 −63
= 1 24−24
8−4 −63
24−24? Это равно 0, а 1/0 не определено .
Дальше идти нельзя! Эта матрица не имеет обратной.Такая матрица называется «Singular»,
что происходит только тогда, когда определитель равен нулю.И это имеет смысл… посмотрите на числа: вторая строка просто удваивает первую строку, и не добавляет никакой новой информации .
И определитель 24−24 позволяет нам узнать об этом факте.

(Представьте, что в нашем примере с автобусом и поездом цены в поезде были ровно на 50% выше, чем в автобусе: так что теперь мы не можем понять никаких различий между взрослыми и детьми. Должно быть что-то, что отличало бы их друг от друга. )
Большие матрицы
Инверсия 2×2 равна просто … по сравнению с более крупными матрицами (например, 3×3, 4×4 и т. д.).
Для таких больших матриц есть три основных метода вычисления обратной величины:
- Обратная матрица с использованием элементарных операций над строками (Гаусса-Жордана)
- Обратная матрица с использованием миноров, кофакторов и адьюгата
- Используйте компьютер (например, Matrix Calculator)
Заключение
- Инверсия A равна A -1 только тогда, когда AA -1 = A -1 A = I
- Чтобы найти обратную матрицу 2×2: поменять местами a и d, поставить отрицательных чисел перед b и c и разделить все на определитель (ad-bc).

- Иногда вообще нет обратного
Инверсия матрицы 2×2
ПоискВ этом уроке мы будем иметь дело только с Квадратные матрицы 2×2 . Я подготовил пять (5) рабочих примеров, чтобы проиллюстрировать процедуру решения или поиска обратной матрицы с использованием метода формул .
Чтобы дать вам общее представление, две матрицы являются обратными друг другу, если их произведение равно единичной матрице . Единичная матрица размером 2 × 2 — это матрица с нулями везде, но с единицами по диагонали. Похоже на это.
Важно знать, как матрица и обратная матрица связаны результатом их произведения. Итак,
- Если матрица A 2 × 2 является обратимой и умножается на обратную (обозначается символом A −1 ), результирующим произведением является матрица идентичности, которая обозначается I. Чтобы проиллюстрировать эту концепцию, см. схему ниже.

- На самом деле, я могу поменять порядок или направление умножения между матрицами A и A −1 , и я все равно получу единичную матрицу I. Это означает, что обратимые матрицы коммутативны.
Как найти обратную матрицу? Формула довольно проста. Пока вы следуете ему, не должно быть никаких проблем. Вот так.
Дана матрица A
Обратная ей вычисляется по формуле
где \color{red}{\rm{det }}\,A читается как определитель матрицы A.
Несколько замечаний о формула:
- Элементы \color{blue}a и \color{blue}d из матрицы A меняются местами или меняются местами в формуле.
- Элементы \color{blue}b и \color{blue}c из матрицы A остаются на своих текущих позициях, однако их знаки меняются местами. Другими словами, поместите отрицательные символы перед элементами b и c.
- Так как \color{red}{\rm{det }}\,A – это просто число, то \large{1 \over {{\rm{det }}A}} также является числом, которое скалярный множитель на матрицу
См.
 мой отдельный урок о скалярном умножении матриц.
мой отдельный урок о скалярном умножении матриц.Примеры поиска обратной матрицы 2×2
Пример 1: Найдите обратную матрицу 2×2 ниже, если она существует.
Формула требует от нас найти определитель данной матрицы. Вы помните, как это сделать? Если нет, то все в порядке. Просмотрите приведенную ниже формулу, чтобы найти определитель матрицы 2 × 2.
Итак, определитель матрицы A равен
Чтобы найти обратную, мне просто нужно подставить значение {\rm{det}}A = — 1 в формулу и выполнить некоторую «реорганизацию» элементов, и, наконец, выполнить скалярное умножение.
- Вот снова формула для нахождения обратной матрицы 2×2. Теперь давайте найдем обратную матрицу A. получаем матрицу идентичности.
Поскольку умножение в обоих направлениях дает матрицу идентичности, то мы гарантируем, что обратная матрица, полученная с помощью формулы, является правильным ответом!
Пример 2: Найдите обратную матрицу 2×2 ниже, если она существует.

Сначала найдите определитель матрицы B.
Во-вторых, подставьте значение det B = 1 в формулу, а затем реорганизуйте элементы матрицы B, чтобы они соответствовали формуле.
Я предоставляю вам проверить, что
Другими словами, матричное произведение B и B −1 в любом направлении дает матрицу идентичности.
Пример 3: Найдите обратную матрицу ниже, если она существует.
Это отличный пример, потому что определитель не равен ни +1, ни -1, что обычно приводит к тому, что обратная матрица имеет рациональные или дробные элементы. Должен признать, что большинство задач, которые учителя задают ученикам на обратную матрицу 2×2, похожи на эту.
Шаг 1 : Найдите определитель матрицы C.
- Формула для нахождения определителя
- Ниже показано анимированное решение для вычисления определителя матрицы C
Шаг 2 : Определитель матрицы C равен −2.
 Подставьте значение в формулу, а затем упростите, чтобы получить обратную матрицу C.
Подставьте значение в формулу, а затем упростите, чтобы получить обратную матрицу C.Шаг 3 : Проверьте правильность вычисленной обратной матрицы, выполнив умножение левых и правых матриц, чтобы получить единичную матрицу.
Да, умножение матриц работает в обоих случаях, как показано ниже.
Первый случай:
Второй случай:
Пример 4: Найдите обратную матрицу ниже, если она существует.
В наших предыдущих трех примерах нам удалось найти обратную заданную матрицу 2 х 2. Я не хочу, чтобы у вас сложилось впечатление, что все матрицы 2 х 2 имеют обратные.
В этом примере я хочу показать, когда данная матрица 2 х 2 не имеет обратной. Как это происходит?
Если еще раз просмотреть формулу, то очевидно, что такая ситуация может иметь место, когда определитель данной матрицы равен нулю, поскольку 1 разделить на ноль не определено . Таким образом, неопределенный термин, распределенный по каждому элементу матрицы, не имеет никакого смысла.

Вернемся к задаче на нахождение определителя матрицы D.
Следовательно, обратной матрицы D не существует потому что определитель матрицы D равен нулю. Это наш окончательный ответ!
Пример 5: Найдите обратную матрицу ниже, если она существует.
Шаг 1 : Найдите определитель матрицы E.
Шаг 2 : Реорганизуйте элементы матрицы E, чтобы они соответствовали формуле, и подставьте найденное значение определителя матрицы E. Распределите значение \large{1 \over {{\rm{det}}E }} к элементам матрицы E, затем упростите, если это возможно.
Шаг 3 : Подтвердите свой ответ, проверив, что вы получили матрицу идентичности в обоих сценариях.
Первый сценарий:
Второй сценарий:
Вам также может быть интересно:
Обратная функция абсолютного значения
Обратная постоянная функция
Обратно от экспоненциальной функции
Обратная линейная функция
.
 Функция
ФункцияНайти обратную матрицу
Результаты обучения
- Проверить, что умножение матрицы на обратную дает 1. 9{-1}[/latex] соответствует идентификационной матрице . Единичная матрица представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули во всех остальных местах. Мы идентифицируем матрицы идентичности как [latex]{I}_{n}[/latex], где [latex]n[/latex] представляет размерность матрицы. Приведенные ниже уравнения представляют собой единичные матрицы для матрицы [latex]2\text{}\times \text{}2[/latex] и матрицы [latex]3\text{}\times \text{}3[/latex] , соответственно.
[латекс]{I}_{2}=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 0\\ \hfill 0& \hfill & \hfill 1\end{array}\ справа][/латекс] 9{-1}[/latex] уникален. Мы рассмотрим два метода нахождения обратной матрицы [latex]2\text{}\times \text{}2[/latex] и третий метод, который можно использовать как для [latex]2\text{} матрицы \times \text{}2[/latex] и [latex]3\text{}\times \text{}3[/latex].
 {-1}[/латекс], мультипликативная обратная матрица [латекс]А[/латекс].
{-1}[/латекс], мультипликативная обратная матрица [латекс]А[/латекс].Пример: демонстрация того, что матрица идентичности действует как 1
Учитывая матрицу A , покажите, что [latex]AI=IA=A[/latex].
[latex]A=\left[\begin{array}{cc}3& 4\\ -2& 5\end{array}\right][/latex]Показать решение
Как: Имея две матрицы, показать, что одна из них является мультипликативной, обратной другой [латекс]B[/латекс] порядка [латекс]n\times n[/латекс] умножить на [латекс]АВ[/латекс]. 9{-1}[/латекс].
Пример: демонстрация того, что матрица
A является мультипликативно обратной матрице BПокажите, что данные матрицы являются мультипликативно обратными друг другу.
[латекс]A=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 5\\ \hfill -2& \hfill & \hfill -9\end{array}\right],B =\left[\begin{array}{rrr}\hfill -9& \hfill & \hfill -5\\ \hfill 2& \hfill & \hfill 1\end{array}\right][/latex]
Показать решение
Попробуйте
Покажите, что следующие две матрицы являются обратными друг другу.
[латекс]A=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill 4\\ \hfill -1& \hfill & \hfill -3\end{array}\right],B =\left[\begin{array}{rrr}\hfill -3& \hfill & \hfill -4\\ \hfill 1& \hfill & \hfill 1\end{array}\right][/latex]
Показать решение
Нахождение обратной мультипликативной матрицы с помощью умножения матриц
Теперь мы можем определить, являются ли две матрицы обратными, но как найти обратную для заданной матрицы? Поскольку мы знаем, что произведение матрицы и ее обратной является единичной матрицей, мы можем найти обратную матрицу, составив уравнение, используя умножение матрицы на .
Пример. Нахождение обратной мультипликативной матрицы с помощью умножения матриц
Используйте умножение матриц, чтобы найти обратную заданную матрицу.
[латекс]A=\left[\begin{array}{rrr}\hfill 1& \hfill & \hfill -2\\ \hfill 2& \hfill & \hfill -3\end{array}\right][/ латекс]
Показать решение
Нахождение мультипликативной инверсии путем увеличения тождества
Другой способ нахождения мультипликативной инверсии 9{-1}[/латекс].
Например, задано
[латекс]A=\left[\begin{array}{rrr}\hfill 2& \hfill & \hfill 1\\ \hfill 5& \hfill & \hfill 3\end{array}\ right][/latex]
дополнить [latex]A[/latex] идентификатором
[latex]\left[\begin{array}{rr}\hfill 2& \hfill 1\\ \hfill 5& \hfill 3 \end{массив}\text{ }|\text{ }\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 0& \hfill 1\end{массив}\right][/latex]
Выполнить операций со строками с целью превратить [латекс]А[/латекс] в личность.
- Переключить строку 1 и строку 2.
[латекс]\left[\begin{array}{rr}\hfill 5& \hfill 3\\ \hfill 2& \hfill 1\end{array}\text{ }|\ text{ }\begin{array}{rr}\hfill 0& \hfill 1\\ \hfill 1& \hfill 0\end{array}\right][/latex] - Умножить строку 2 на [латекс]-2[/латекс] и добавить к строке 1.
[латекс]\left[\begin{array}{rr}\hfill 1& \hfill 1\\ \hfill 2& \hfill 1\ end{массив}\text{ }|\text{ }\begin{array}{rr}\hfill -2& \hfill 1\\ \hfill 1& \hfill 0\end{массив}\right][/latex] - Умножить строку 1 на [латекс]-2[/латекс] и добавить к строке 2.

[латекс]\left[\begin{array}{rr}\hfill 1& \hfill 1\\ \hfill 0& \hfill -1 \end{массив}\text{ }|\text{ }\begin{array}{rr}\hfill -2& \hfill 1\\ \hfill 5& \hfill -2\end{массив}\right][/latex] - Добавить строку 2 к строке 1.
[латекс]\left[\begin{array}{rr}\hfill 1& \hfill 0\\ \hfill 0& \hfill -1\end{array}\text{ }|\text { }\begin{массив}{rr}\hfill 3& \hfill -1\\ \hfill 5& \hfill -2\end{массив}\right][/latex] 9{-1}=\left[\begin{array}{rrr}\hfill 3& \hfill & \hfill -1\\ \hfill -5& \hfill & \hfill 2\end{array}\right][/latex]Нахождение мультипликативной обратной матрицы 2×2 с помощью формулы
Когда нам нужно найти мультипликативную обратную матрицы [латекс]2\х2[/латекс], мы можем использовать специальную формулу вместо использования матричное умножение или увеличение на единицу.
Если [латекс]А[/латекс] представляет собой матрицу [латекс]2\умножить на 2[/латекс], например 9{-1}=\frac{1}{ad-bc}\left[\begin{array}{rrr}\hfill d& \hfill & \hfill -b\\ \hfill -c& \hfill & \hfill a\end {array}\right][/latex]
, где [latex]ad-bc\ne 0[/latex].
 Если [latex]ad-bc=0[/latex], то [latex]A[/latex] не имеет обратного.
Если [latex]ad-bc=0[/latex], то [latex]A[/latex] не имеет обратного.Пример: использование формулы для нахождения мультипликативной обратной матрицы
AИспользуйте формулу для нахождения мультипликативной обратной матрицы
[latex]A=\left[\begin{array}{cc}1& -2\ \ 2& -3\конец{массив}\право][/латекс]
Показать раствор
Попробуйте
Используйте формулу, чтобы найти обратную матрицу [латекс]А[/латекс]. Проверьте свой ответ, дополнив единичную матрицу.
[latex]A=\left[\begin{array}{cc}1& -1\\ 2& 3\end{array}\right][/latex]
Показать решение
Пример: нахождение обратной матрицы, если она существует
Найдите обратную матрицу, если она существует, данной матрицы.
[латекс] A=\left[\begin{массив}{cc}3& 6\\ 1& 2\end{массив}\right][/latex]
Показать раствор
Нахождение мультипликативной обратной матрицы 3×3
К сожалению, у нас нет формулы, похожей на формулу для матрицы [latex]2\text{}\times \text{}2[/latex], чтобы найти обратная матрица [latex]3\text{}\times \text{}3[/latex].
 Вместо этого мы дополним исходную матрицу единичной матрицей и используем операций со строками , чтобы получить обратную.
Вместо этого мы дополним исходную матрицу единичной матрицей и используем операций со строками , чтобы получить обратную.Дана матрица [latex]3\text{}\times \text{}3[/latex]
[latex]A=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1 \\ 2& 4& 1\end{массив}\right][/latex]
дополнить [latex]A[/latex] единичной матрицей
[latex]A|I=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end {array}\text{ }|\text{ }\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right][/latex]
Чтобы начать, мы пишем расширенную матрицу с единицей справа и [латекс]А[/латекс] слева. Выполнение элементарных операций со строками так, чтобы единичная матрица 9Слева появится 0015, справа мы получим обратную матрицу . Мы найдем обратную этой матрице в следующем примере.
Как: Имея матрицу [латекс]3\умножить на 3[/латекс], найдите обратную
- Запишите исходную матрицу, дополненную единичной матрицей справа.

- Используйте элементарные операции со строками, чтобы идентификатор отображался слева.
- То, что получается справа, является обратной исходной матрицей. 9{-1}A=I[/латекс].
- Запишите исходную матрицу, дополненную единичной матрицей справа.
Пример: нахождение обратной матрицы 3 × 3
Для заданной матрицы [latex]3\times 3[/latex] [latex]A[/latex] найти обратную.
[латекс]A=\left[\begin{array}{ccc}2& 3& 1\\ 3& 3& 1\\ 2& 4& 1\end{массив}\right][/latex]
Показать решение
Попробуйте
Найдите обратную матрицу [латекс]3\умножить на 3[/латекс].
[латекс]A=\left[\begin{array}{ccc}2& -17& 11\\ -1& 11& -7\\ 0& 3& -2\end{массив}\right][/latex]
Показать раствор
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Обратная матрица
Горячая математика Мультипликативная обратная квадратная матрица называется ее обратной матрицей. Если матрица
А
имеет обратное, то
А
говорят, что неособый или обратимый. А единственное число матрица не имеет обратной. Чтобы найти обратную квадратную матрицу
А
, нужно найти матрицу
А
−
1
такое, что произведение
А
а также
А
−
1
является единичной матрицей.
Если матрица
А
имеет обратное, то
А
говорят, что неособый или обратимый. А единственное число матрица не имеет обратной. Чтобы найти обратную квадратную матрицу
А
, нужно найти матрицу
А
−
1
такое, что произведение
А
а также
А
−
1
является единичной матрицей.
Другими словами, для каждой квадратной матрицы А невырожденной существует обратная матрица со свойством, что А А − 1 знак равно А − 1 А знак равно я , куда я является единичной матрицей соответствующего размера.
Вы можете использовать любой из следующих методов, чтобы найти обратную квадратную матрицу.
Способ 1:
Позволять
А
быть
н
×
н
матрица.
1. Напишите дважды увеличенную матрицу [ А | я н ] .
2. Применяя элементарные операции со строками, запишите матрицу в сокращенной строчно-эшелонной форме.
3. Решите, является ли матрица А обратимо (несингулярно).
4. Если А можно привести к единичной матрице я н , тогда А − 1 — матрица справа от преобразованной расширенной матрицы.
5. Если А нельзя свести к единичной матрице, то А единственное число.
Способ 2:
Вы можете использовать следующую формулу при нахождении обратной н × н матрица.
Если
А
является невырожденной матрицей, существует обратная, которая задается формулой
А
−
1
знак равно
1
|
А
|
(
прил. А
)
, куда
|
А
|
является определителем матрицы.
А
)
, куда
|
А
|
является определителем матрицы.
Пример :
Находить А − 1 , если он существует. Если А − 1 не существует, пишите в единственном числе.
А знак равно [ 1 2 1 1 ]
Шаг 1:
Напишите дважды увеличенную матрицу [ А | я н ] .
[ А | я ] знак равно [ 1 2 1 0 1 1 0 1 ]
Шаг 2:
Примените элементарные операции со строками, чтобы записать матрицу в сокращенной форме строки-эшелона.
[ 1 2 1 0 0 1 1 − 1 ] р 2 знак равно р 1 − р 2 [ 1 0 − 1 2 0 1 1 − 1 ] р 1 знак равно − 2 р 2 + р 1 [ 1 0 − 1 2 0 1 1 − 1 ] знак равно [ я | А − 1 ]
Система имеет решение.
Следовательно, А обратим и А − 1 знак равно [ − 1 2 1 − 1 ]
Обратная квадратная матрица
6.3 — Обратная квадратная матрицаРеальные числа
При работе с действительными числами уравнение ax=b может быть решено относительно x путем деления обоих стороны уравнения на a, чтобы получить x = b / a, если a не равно нулю. Поэтому казалось бы логичным что при работе с матрицами можно взять матричное уравнение AX=B и разделить оба стороны на A, чтобы получить X=B/A.
Однако это не сработает, потому что…
Разделения матрицы НЕТ!
Хорошо, скажете вы. Вычитание определялось сложением, а деление определялось с помощью
умножение. Так что вместо деления я просто умножу на обратное. Вот как это
должно быть сделано.
Вот как это
должно быть сделано.
Обратная матрица
Итак, что такое обратная матрица?
Ну, в действительных числах обратным любому действительному числу и было число 9.0012 a -1 , так что a умножить на a -1 равно 1. Мы знали, что для действительного числа обратным числом является величина, обратная число, если число не равно нулю.
Обратной квадратной матрицей A, обозначаемой A -1 , является матрица так что произведение А и A -1 — матрица идентичности. Матрица идентичности, которая получается будет того же размера, что и матрица A. Ничего себе, есть а много общего там между действительными числами и матрицами. Это хорошо, правильно — ты не хочу это должно быть что-то совершенно другое.
А(А -1 ) = I или А -1 (А) = I
Однако есть пара исключений. Прежде всего, A -1 делает
не означает 1/А. Помните: «Матричного деления не существует!» Во-вторых, A -1 делает
не значит взять обратное значение каждого элемента
в матрице А.
Требования для инверсии
- Матрица должна быть квадратной (одинаковое количество строк и столбцов).
- Определитель матрицы не должен быть равен нулю (определители описаны в разделе 6.4). Это вместо того, чтобы действительное число не было нулем, чтобы иметь обратное, определитель не должен быть нулем, чтобы иметь обратную.
Квадратная матрица, имеющая обратную, называется обратимой или невырожденной . Матрица, которой нет есть инверсия называется единственного числа .
Матрица не обязательно должна иметь обратную, но если она есть, то обратная матрица уникальна.
Трудный путь поиска обратного
Обратная матрица A будет удовлетворять уравнению A(A -1 ) = I.
- Присоедините единичную матрицу справа от исходной матрицы так, чтобы
у вас есть A на левой стороне и единичная матрица на правой стороне. Это
будет выглядеть так [ A | я].

- Уменьшение строки (я предлагаю использовать поворот) матрицы пока левая сторона не станет матрицей идентичности. Когда левая сторона — это Личность матрица, правая сторона будет обратным [ I | А -1 ]. Если вы не можете чтобы получить единичную матрицу в левой части, то матрица вырождена и не имеет обратного.
- Возьмите расширенную матрицу с правой стороны и назовите ее обратной.
Быстрый способ найти обратную матрицу 2×2
Обратная матрица 2×2 может быть найдена с помощью …
- Переключатель элементов на главной диагонали
- Возьмем два противоположных элемента
- Разделите все значения на определитель матрицы (так как мы не говорил об определителе, для системы 2×2 это произведение элементов главной диагонали минус произведение двух других элементов).
Пример ярлыка
Давайте возьмем исходную матрицу
| 7 | -2 | ||
| 3 | 5 |
Шаг 1, переключение элементов на главной диагонали будет включать в себя переключение
5 и 7.
| 5 | -2 | ||
| 3 | 7 |
Шаг 2, возьмите противоположные два других элемента, но оставьте их там, где они есть.
| 5 | 2 | ||
| -3 | 7 |
Шаг 3, найдите определитель и разделите на него каждый элемент. Определитель это произведение элементов главной диагонали минус произведение элементы вне главной диагонали. Это означает, что определитель этой матрицы равен 7(5) — (-3)(2) = 35 + 6 = 41. Делим каждый элемент на 41.
Матрица, обратная исходной, равна …
| 5/41 | 2/41 | ||
| -3/41 | 7/41 |
Теперь, вы говорите, подождите минутку — вы сказали, что матричного деления не было. Разделения по матрице нет. Вы можете умножать или делить матрицу на
скаляр (действительное число) и определитель
является скаляром.
Разделения по матрице нет. Вы можете умножать или делить матрицу на
скаляр (действительное число) и определитель
является скаляром.
Использование калькулятора
Теперь, когда вы знаете, как найти матрицу идентичности вручную, давайте поговорим о практичности. Калькулятор сделает это за вас.
Вход в матрицу
- Нажмите клавишу Matrix (прямо под клавишей X). На TI-83+ вам понадобится чтобы поразить 2 й Матрица.
- Стрелка в подменю Правка.
- Выберите матрицу для работы. У вас есть пять на выбор с TI-82 и десять на выбор. выбрать из с TI-83. Как правило, вы будете использовать [A]. Старайтесь не использовать [E] для неуказанные причины, которые будут указаны, если вы возьмете конечную математику.
- Введите количество строк, нажмите клавишу ввода, затем введите количество столбцов, а затем войти.
- Теперь вы вводите каждый элемент в матрицу, читая слева направо и сверху вниз. Нажимать
вводите после каждого числа.
 Вы можете использовать клавиши со стрелками для перемещения, если вы допустили ошибку.
Вы можете использовать клавиши со стрелками для перемещения, если вы допустили ошибку. - Выйти (режим 2 и ), когда вы закончите ввод всех цифр.
Использование матриц
Всякий раз, когда вам нужно получить доступ к созданной вами матрице, просто нажмите клавишу Matrix и выберите соответствующую матрицу. Я бы посоветовал вам начать использовать Матрицу 1, Матрицу 2 и т. д. вместо Матрица, стрелка вниз, ввод. Это пойдет быстрее, и вы будете много делать с этими матрицами. 9(-1).
Возможно, вам придется использовать клавиши со стрелками вправо или влево, чтобы прокрутить всю матрицу, чтобы записать ее. вниз. По возможности давайте точные ответы.
Один из способов дать точные ответы — заставить калькулятор преобразовать десятичные дроби в дроби.
ты. В конце концов, дроби действительно ваши друзья (и я серьезно говорю об этом здесь). Вы можете иметь
Калькулятор преобразует десятичную дробь в дробь, нажав Math, Enter, Enter.
Кроме того, если вы получите ответ вроде 1.2E-12, шансы действительно хорошо, что число равно нулю, и это из-за неточностей в калькуляторе что вы получаете этот ответ. Преобразовать число до нуля.
Зачем нужна была инверсия?
Я так рад, что вы спросили об этом.
Одним из основных применений инверсий является решение системы линейных уравнений. Вы можете записать систему в матричной форме как AX = B.
Теперь предварительно умножьте обе части на обратную А. Убедитесь, что вы соответствуете этим два условия.
- Вы должны поместить обратную матрицу рядом с матрицей. То есть потому что инверсии должны быть рядом друг с другом (очень свободно математически, но вернемся к функциям), чтобы отменить друг друга.
- Если
вы умножаете, помещая что-то перед левой стороной (предварительно умножая),
он должен идти впереди правой стороны. Если вы положите что-то позади
(после умножения) левая сторона, она должна идти за правой стороной.

Умножение матриц НЕ является коммутативным!
A -1 (AX) = A -1 (B) … предварительно умножить с обеих сторон по A -1
(A -1 A) X = A -1 B … использовать ассоциативный свойство перегруппировывать факторы
I X = A -1 B … при умножении инверсий вместе они становятся идентификационной матрицей
X = A -1 B … единичная матрица похожа на умножение на 1.
Если AX = B, то X = A -1 B
Итак, вы со своим обычным цинизмом спрашиваете: «Вы только что решили другое уравнение, что это как-то связано?»
Решение систем линейных уравнений
Рассмотрим систему линейных уравнений
3x + 2y - 5z = 12 х - 3у + 2г = -13 5х - у + 4г = 10
Запишите коэффициенты в матрицу A.
| х | г | по | ||
|---|---|---|---|---|
| 3 | 2 | -5 | ||
| 1 | -3 | 2 | ||
| 5 | -1 | 4 |
Запишите переменные в матрицу X.
| х | ||
| и | ||
| по |
Запишите константы в матрицу B.
| 12 | ||
| -13 | ||
| 10 |
Убедитесь, что AX = B
Этот шаг на самом деле не нужен, но я хотел показать вам, что эта штука действительно работает.
AX будет (3×3) × (3×1) = 3×1 матрица. Матрица B также является матрицей 3 × 1, поэтому по крайней мере размеры правильно заниматься.
Вот A раз X.
| 3 | 2 | -5 | х | 3x + 2y — 5z | ||||||||
| 1 | -3 | 2 | и | = | 1x — 3 года + 2z | |||||||
| 5 | -1 | 4 | по | 5х — 1г + 4з |
Обратите внимание, что это левая часть системы уравнений. B — правая часть, поэтому мы добились равенства. Ууууу! Ты можешь написать
система линейных уравнений при AX = B.
B — правая часть, поэтому мы добились равенства. Ууууу! Ты можешь написать
система линейных уравнений при AX = B.
Итак, если вы можете записать систему линейных уравнений в виде AX=B, где A — коэффициент матрица, X — переменная матрица, а B — правая часть, можно найти решение системы через Х = А -1 Б.
Поместите матрицу коэффициентов в [A] на калькуляторе, а правая рука стороной в [B].
Если вы попросили калькулятор найти обратный коэффициент матрица, это даст вам это для A -1
| 5/44 | 3/88 | 1/8 | ||
| -3/44 | -37/88 | 1/8 | ||
| -7/44 | -13/88 | 1/8 |
Вы могли бы сделать это, а затем умножить это на B, но было бы проще просто
ввести целое выражение в калькулятор и сразу получить ответ. Даже то, что показано ниже, требует больше работы, чем необходимо.
Даже то, что показано ниже, требует больше работы, чем необходимо.
Х = А -1 В = …
| х | 5/44 | 3/88 | 1/8 | 12 | 191/88 | |||||||||||
| и | = | -3/44 | -37/88 | 1/8 | -13 | = | 519/88 | |||||||||
| по | -7/44 | -13/88 | 1/8 | 10 | 111/88 |
Итак, x = 191/88, y = 519/88 и z = 111/88. Это было бы настоящим
боль
решить вручную.
Это было бы настоящим
боль
решить вручную.
Это просто, почему бы нам всегда так не делать?
Основная причина в том, что это не всегда работает.
- Инверсии существуют только для квадратных матриц. Это означает, что если вы не то же самое количество уравнений в качестве переменных, то вы не можете использовать этот метод.
- Не каждая квадратная матрица имеет обратную. Если матрица коэффициентов A сингулярный (не имеет обратного), то решения может не быть или может быть много решений, но мы не можем сказать, что это такое.
- Инверсию очень сложно найти вручную. Если у вас есть калькулятор, это не так плохо, но помните, что калькуляторы не всегда дают вам ответ, который вы находясь в поиске.
Как найти обратную матрицу (формула и примеры)
Мы объясним, что такое обратная матрица и как ее найти. Вы изучите формулы для вычисления обратной матрицы 2 × 2 и обратной матрицы 3 × 3. Также вы увидите несколько решенных примеров. И, наконец, поясним свойства обратной матрицы.
И, наконец, поясним свойства обратной матрицы.
Содержание
Что является обратной матрицей?
Определение обратной матрицы следующее:
обратная матрица — это матрица, умножение которой на исходную матрицу дает единичную матрицу, независимо от порядка умножения матриц.
Таким образом, пусть A — квадратная матрица, обратная матрица A обозначается A -1 и удовлетворяет условию:
A·A -1 =I
A -1 ·A=I
Где I — единичная матрица.
Когда можно инвертировать матрицу?
Самый простой способ определить обратимость матрицы — вычислить ее определитель:
- Если определитель матрицы не равен нулю, матрица обратима .
- Если определитель матрицы равен 0, матрица не может быть инвертирована . В таком случае матрица является сингулярной или вырожденной.
Как найти обратную матрицу 2×2
Формула для нахождения обратной матрицы 2×2 выглядит следующим образом:
Как видите, инвертировать матрицу размерности 2×2 очень просто: вам нужно только решить определитель матрицы (|A|) , поменяйте местами элементы на главной диагонали и поменяйте знак элементов на побочной диагонали.
Пример
Мы собираемся вычислить обратную следующую квадратную матрицу 2×2:
Сначала возьмем определитель матрицы 2×2:
Теперь применим формулу обратной матрицы:
И умножим матрицу на дробь:
Итак, обратная матрица А:
3 Как видите, инвертирование 90 матрица с этой формулой очень быстрая, но ее можно использовать только для матриц 2×2.
Практика
Задача 1
Инвертировать следующую размерную матрицу 2×2:
См. решение
Во-первых, вычисляем определитель матрицы:
Во-вторых, используем формулу для нахождения обратной матрицы:
Следовательно, обратная матрица A:
2
Задача 2
Найдите обратную следующую матрицу 2-го порядка:
См. решение
Сначала вычислим определитель матрицы:
Затем воспользуемся формулой обратной0003
и, наконец, мы выполняем умножение:
Задача 3
Выполните матрицу инверсии следующего 2 × 2 -размерной матрицы:
See 2 × 2 Diferension Matrix:
. определитель матрицы А:
определитель матрицы А:
Теперь применим формулу для вычисления обратной матрицы А:
И решим произведение дроби на матрицу:
Как найти обратную матрицу 3×3
Формула для вычисления обратной матрицы 3×3 выглядит следующим образом:
Где: матрица A.
Далее мы увидим, как вычислить обратную матрицу 3×3, шаг за шагом решая упражнение:
Пример
Найдите обратную матрицу следующая матрица 3×3:
Чтобы определить обратную матрицу, мы должны применить следующую формулу:
Следовательно, мы должны вычислить определитель матрицы и убедиться, что он отличен от 0. Таким образом, мы вычисляем определитель матрицы матрица 3×3 с использованием расширения кофактора:
Определитель матрицы не равен 0, поэтому матрица обратима.
Следовательно, подставив значение определителя в формулу, обратная матрица будет:
Теперь нам нужно вычислить сопряженную матрицу A. Для этого мы должны заменить каждый элемент матрицы A его кофактором, чтобы получить матрицу кофакторов, а затем транспонировать матрицу кофакторов.
Для этого мы должны заменить каждый элемент матрицы A его кофактором, чтобы получить матрицу кофакторов, а затем транспонировать матрицу кофакторов.
Помните, что формула для вычисления кофактора i, j матрицы выглядит следующим образом:
Где M ij — минор i, j матрицы, то есть определитель, полученный в результате удаления i -я строка и j-й столбец матрицы.
Таким образом, кофакторы элементов матрицы A:
. матрицы А по ее кофактору:
И транспонируем матрицу кофактора, чтобы найти сопряженную матрицу:
Таким образом, подставляем сопряженную матрицу в формулу обратной матрицы:
И, наконец, мы умножаем каждый член матрицы на дробь:
После того, как мы увидели, как вычислить обратную матрицу 3×3, вы можете попрактиковаться в решении следующих упражнений. шаг за шагом, чтобы полностью понять концепцию.
Практика
Задача 4
Обратим следующую матрицу размерности 3×3 методом сопряженной матрицы:
См. решение
Формула обратной матрицы:
Сначала найдем определитель матрицы, используя разложение на кофакторы:
Определитель отличен от нуля, поэтому матрицу можно инвертировать.
После того, как мы решили определитель, мы находим кофактор каждого элемента матрицы A:
Теперь мы выплатим элементы COFACTOR MATRIX. по его кофактору:
и мы транспонируем кофакторную матрицу, чтобы получить соединение матрицы A:
Таким образом, инвертированная матрица:
Проблема 5
Найти внедрение. 3-го порядка по алгоритму сопряженной матрицы:
См. решение
Формула для нахождения обратной матрицы 3-го порядка выглядит следующим образом:
Итак, сначала мы должны вычислить определитель матрицы проверить обратимость матрицы:
Определитель матрицы A равен нулю, поэтому матрица необратима , другими словами, обратной матрицы A не существует.
Задача 6
Выполните преобразование следующей матрицы размерности 3×3 методом сопряженных матриц:
См. решение
Для обращения матрицы 3×3 необходимо применить следующую формулу :
Сначала вычислим определитель матрицы 3×3:
Определитель отличен от нуля, поэтому матрицу можно инвертировать.
После того, как мы решили определитель, мы находим кофакторы всех элементов матрицы A:
Теперь мы вычисляем. элемент матрицы A своим кофактором:
Транспонируем матрицу кофакторов, чтобы найти сопряженную матрицу:
и мы применяем формулу обратной матрицы 3 × 3:
Свойства по обратной матрице
. Обратная матрика имеет следующую характеристику:
. обратная матрица единственна. То есть, если матрица обратима, существует только одна обратная матрица.
- Инверсия обратной матрицы приводит к исходной матрице:
- Обратное умножение матриц равно произведению обратных матриц, но с изменением порядка их умножения.
- Сначала трансформировать матрицу, а затем найти обратную матрицу — это то же самое, что сначала вычислить обратную матрицу, а затем транспонировать ее.
- Определитель обратной матрицы равен обратной величине определителя исходной матрицы.
- Если матрица обратима, то для скалярного умножения справедливо следующее уравнение:
Решение системы уравнений с обратной матрицей
Теперь вам может быть интересно… для чего нужна обратная матрица? Он действительно для чего-то используется?
Ну, одно из применений обратной матрицы — решение систем линейных уравнений. Давайте посмотрим на примере, как это сделать:
Систему уравнений можно выразить с помощью матриц:
Мы можем проверить, что эти матрицы соответствуют системе уравнений, перемножив матрицы, так как мы получили бы два уравнения системы.

 Пусть дана неособенная матрица n -го порядка:
Пусть дана неособенная матрица n -го порядка:
 е,
е, 

 Тогда получим
Тогда получим
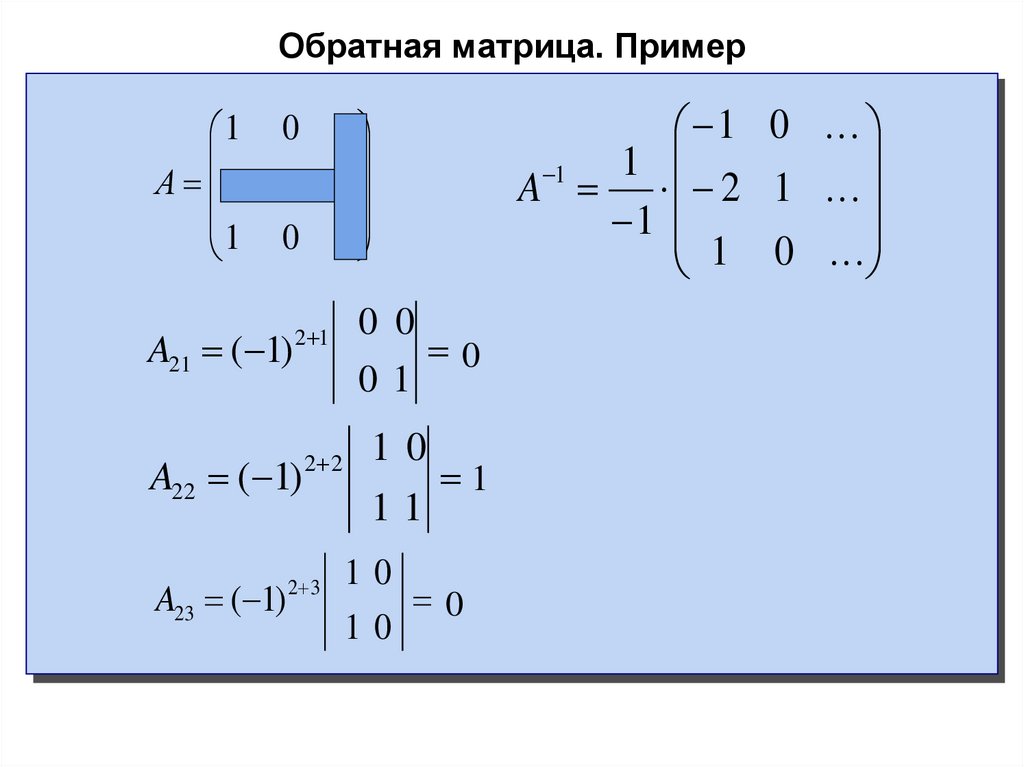
 Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.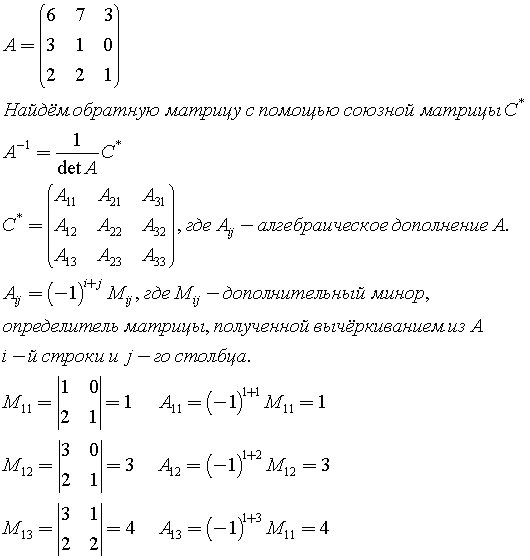 пример 1)
пример 1)
 Результаты вычислений оформляются в отчете формата Word
и в формате Excel
(т.е. имеется возможность проверить решение). см. пример оформления .
Результаты вычислений оформляются в отчете формата Word
и в формате Excel
(т.е. имеется возможность проверить решение). см. пример оформления .