Периметр равностороннего треугольника — формула и примеры нахождения » Kupuk.net
В задачах по математике иногда приходится находить суммарное значение всех сторон равностороннего треугольника, формула периметра которого немного отличается от других фигур. Чтобы разбираться в материале, нужно ознакомиться с формулировками основных определений, а также доказать теорему практическим путем.
Общие сведения
Изучение любой фигуры, процесса или явления всегда начинается с определений. Треугольником называется геометрическое тело, состоящее из трех, не лежащих на одной прямой, вершин. Прямая — совокупность бесконечного количества точек, лежащих в одной плоскости и проходящих без искажений.
Вершина — точка, образованная сторонами треугольника. Периметр — суммарное значение всех сторон любой фигуры. Высота — отрезок, проведенный из любой вершины на сторону, которая является противоположной, под углом в 90 градусов.
Медиана — часть прямой, проведенной из вершины, но не под прямым углом, а соединяющая ее с серединой противолежащей стороны. Биссектриса — прямая, делящая угол на 2 равных величины.
Биссектриса — прямая, делящая угол на 2 равных величины.
Виды треугольников
Треугольники классифицируются по углам и сторонам. На основании первого критерия можно выделить несколько типов фигур:
В первом случае у фигуры все углы острые, т. е. градусная мера каждого не должна превышать 90 градусов. Если хотя бы один из них эквивалентен 90, треугольник является прямоугольным. Однако когда градусная мера одного из них превышает 90, он принадлежит к третьему типу.
Треугольники классифицируются еще и по сторонам. Распределение на группы происходит по такому принципу:
Равнобедренный треугольник можно считать прямоугольным и тупоугольным.
Кроме того, равносторонняя фигура всегда является остроугольной. Далее необходимо перейти к доказательству теоремы о периметре.
Теорема о периметре
Каждому ученику известна формула периметра треугольника для 3 класса. Она является довольно примитивным соотношением, и применяется в абсолютно другом виде в старших классах и высших учебных заведениях. Математики предлагают рассмотреть доказательство теоремы о периметре правильного треугольника. Ее формулировка имеет следующий вид: периметр треугольника равен утроенному произведению одной из его сторон, когда фигура является правильной.
Доказывается утверждение очень просто. Для этого необходимо использовать следующий алгоритм:
Можно найти и другое доказательство теоремы, в которой используется прямоугольник. В фигуре нужно провести диагонали, а затем по формуле Пифагора выразить боковые стороны. Однако процесс доказательства утверждения является более сложным.
У каждой теоремы есть какие-либо следствия. Они позволяют существенно оптимизировать вычисления при решении задач. Далее необходимо рассмотреть полезные формулы.
Полезные формулы
Для вычисления различных параметров треугольника применяются определенные формулы. Кроме того, вводится новая величина, которая называется полупериметром. Она обозначается литерой «р» и составляет половину от периметра, т. е. р=Р/2. Специалисты рекомендуют использовать следующие формулы (если известны исходные параметры):
 (½) сантиметров.
(½) сантиметров.Таким образом, для решения задач по геометрии необходимо знать теорему о периметре и формулы для расчетов различных параметров равностороннего треугольника.
Периметр равностороннего треугольника — формула и примеры нахождения
В задачах по математике иногда приходится находить суммарное значение всех сторон равностороннего треугольника, формула периметра которого немного отличается от других фигур. Чтобы разбираться в материале, нужно ознакомиться с формулировками основных определений, а также доказать теорему практическим путем.
Содержание
- Общие сведения
- Виды треугольников
- Теорема о периметре
- Полезные формулы
- Пример решения задачи
Общие сведения
Изучение любой фигуры, процесса или явления всегда начинается с определений. Треугольником называется геометрическое тело, состоящее из трех, не лежащих на одной прямой, вершин. Прямая — совокупность бесконечного количества точек, лежащих в одной плоскости и проходящих без искажений.
Прямая — совокупность бесконечного количества точек, лежащих в одной плоскости и проходящих без искажений.
Вершина — точка, образованная сторонами треугольника. Периметр — суммарное значение всех сторон любой фигуры. Высота — отрезок, проведенный из любой вершины на сторону, которая является противоположной, под углом в 90 градусов.
Медиана — часть прямой, проведенной из вершины, но не под прямым углом, а соединяющая ее с серединой противолежащей стороны. Биссектриса — прямая, делящая угол на 2 равных величины.
Виды треугольников
Треугольники классифицируются по углам и сторонам. На основании первого критерия можно выделить несколько типов фигур:
В первом случае у фигуры все углы острые, т. е. градусная мера каждого не должна превышать 90 градусов. Если хотя бы один из них эквивалентен 90, треугольник является прямоугольным. Однако когда градусная мера одного из них превышает 90, он принадлежит к третьему типу.
Однако когда градусная мера одного из них превышает 90, он принадлежит к третьему типу.
Треугольники классифицируются еще и по сторонам. Распределение на группы происходит по такому принципу:
Равнобедренный треугольник можно считать прямоугольным и тупоугольным. Кроме того, равносторонняя фигура всегда является остроугольной. Далее необходимо перейти к доказательству теоремы о периметре.
Теорема о периметре
Каждому ученику известна формула периметра треугольника для 3 класса. Она является довольно примитивным соотношением, и применяется в абсолютно другом виде в старших классах и высших учебных заведениях. Математики предлагают рассмотреть доказательство теоремы о периметре правильного треугольника. Ее формулировка имеет следующий вид: периметр треугольника равен утроенному произведению одной из его сторон, когда фигура является правильной.
Ее формулировка имеет следующий вид: периметр треугольника равен утроенному произведению одной из его сторон, когда фигура является правильной.
Доказывается утверждение очень просто. Для этого необходимо использовать следующий алгоритм:
Можно найти и другое доказательство теоремы, в которой используется прямоугольник. В фигуре нужно провести диагонали, а затем по формуле Пифагора выразить боковые стороны. Однако процесс доказательства утверждения является более сложным.
У каждой теоремы есть какие-либо следствия.
(½) сантиметров.
Таким образом, для решения задач по геометрии необходимо знать теорему о периметре и формулы для расчетов различных параметров равностороннего треугольника.
Предыдущая
ГеометрияВнутренние односторонние углы — теория, правило и свойства
После нахождения периметра равнобедренного треугольника. Периметр и площадь треугольника
Периметром треугольника , как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: см
Формула расчета периметра равнобедренного треугольника будет выглядеть так:
Формула расчета периметра равностороннего треугольника :
Пример расчета периметра равностороннего треугольника.
Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по
теореме Пифагора . К примеру, если известны длины катетов, то можно найти гипотенузу по формуле: Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.
Дан треугольник с катетами a =b =5 см. Найти периметр. Для начала найдем недостающую сторону с . см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле:
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле.Периметр – это сумма всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.
Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это проистекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и проистекает формула периметра:
P=2a+b, где b-это основание треугольника, a-значение боковой стороны.
Рис. 1. Равнобедренный треугольник
Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. Рассмотри несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра.
Задача 1
- В равнобедренном треугольнике основание равно 6, а высота, проведенная к этому основанию, равна 4.
2}=\sqrt{9+16}=\sqrt{25}=5$$
Найдем периметр: P=AC+AB*2=6+5*2=16
Задача 2
- В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам. нужно найти периметр треугольника.
Рис. 3. Рисунок к задаче 2
Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)={BH\over AB}={1\over2}$$ — синус 30 градусов является табличным значением.
Выразим нужную сторону:
$$AB={{BH\over {1\over 2}}} =BH*2=10*2=20$$
Через котангенс найдем значение AH:
$$ctg(BAH)={AH\over BH}={1\over\sqrt{3}}$$
$$AH={BH\over\sqrt{3}}=10*\sqrt{3}=17,32$$ — получившееся значение округлим до сотых.
Найдем основание:
AC=AH*2=17,32*2=34,64
Теперь, когда все требуемые значения найдены, определим периметр:
P=AC+2*AB=34,64+2*20=74,64
Задача 3
- В равнобедренном треугольнике ABC известна площадь, которая равна $$16\over\sqrt{3}$$ и острый угол при основании в 30 градусов.
Найти периметр треугольника.
Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.
Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
Площадь: $$S={1\over 2}*AC*BH={1\over 2}*2a*h=ah$$
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято.
2}=4,62$$Подставим значения в формулу периметра:
P=AB*2+AH*2=4,62*2+4*2=17,24
Что мы узнали?
Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.
Тест по теме
Оценка статьи
Средняя оценка: 4.4 . Всего получено оценок: 83.
Любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
P = a + b + c
где P — это периметр треугольника, a , b и c — его стороны.
Можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
P = 2a + b
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.
Можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
P = 3a
где P — это периметр равностороннего треугольника, a — любая из его сторон.
Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом . Рассмотрим треугольник ABC :
Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:
В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения.
Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:
Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2 . Общая формула для нахождения площади треугольников будет выглядеть так:
S = ah a 2 где S — это площадь треугольника, a — его основание, h a — высота, опущенная на основание a .
Предварительные сведения
Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон.
Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
Определение 1
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Определение 2
Точки в рамках определения 1 будем называть вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.
В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.
Определение 4
Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.
Определение 5
Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.
Определение 6
Треугольник будем называть равносторонним, если все его стороны равняются друг другу.
Все виды этих треугольников Вы можете видеть на рисунке 2. Как найти периметр разностороннего треугольника?
Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.
Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.
Пример 1
Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.
$P=34+12+11=57$ см
Ответ: $57$ см.
Пример 2
Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.
Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда
$α=10$ По правилу вычисления периметра разностороннего треугольника, получим
$P=10+8+6=24$ см
Ответ: $24$ см.
Как найти периметр равнобедренного треугольника?
Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+β=2α+β$
Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.
Пример 3
Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.
По рассмотренному выше примеру, видим, что
$P=2\cdot 12+11=35$ см
Ответ: $35$ см.
Пример 4
Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.
Рассмотрим рисунок по условию задачи:
Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.
По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда
По правилу вычисления периметра равнобедренного треугольника, получим
$P=2\cdot 10+12=32$ см
Ответ: $32$ см.
Как найти периметр равностороннего треугольника?
Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+α=3α$
Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.
Пример 5
Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.
По рассмотренному выше примеру, видим, что
$P=3\cdot 12=36$ см
Предварительные сведения
Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
Определение 1
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Определение 2
Точки в рамках определения 1 будем называть вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.
В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.
Определение 4
Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.
Определение 5
Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.
Определение 6
Треугольник будем называть равносторонним, если все его стороны равняются друг другу.
Все виды этих треугольников Вы можете видеть на рисунке 2.
Как найти периметр разностороннего треугольника?
Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.
Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.
Пример 1
Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.
$P=34+12+11=57$ см
Ответ: $57$ см.
Пример 2
Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.
Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда
$α=10$ По правилу вычисления периметра разностороннего треугольника, получим
$P=10+8+6=24$ см
Ответ: $24$ см.
Как найти периметр равнобедренного треугольника?
Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+β=2α+β$
Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.
Пример 3
Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.
По рассмотренному выше примеру, видим, что
$P=2\cdot 12+11=35$ см
Ответ: $35$ см.
Пример 4
Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.
Рассмотрим рисунок по условию задачи:
Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.
По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда
По правилу вычисления периметра равнобедренного треугольника, получим
$P=2\cdot 10+12=32$ см
Ответ: $32$ см.
Как найти периметр равностороннего треугольника?
Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+α=3α$
Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.
Пример 5
Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.
По рассмотренному выше примеру, видим, что
$P=3\cdot 12=36$ см
Как найти периметр равнобедренного треугольника через высоту
Периметр треугольника
Так как изначально периметр для любой фигуры – это сумма длин всех ее сторон, то периметр треугольника найти проще всего, зная все три стороны: P=a+b+c . Для равнобедренного треугольника формула периметра будет выглядеть несколько иначе в силу того, что две из сторон у него конгруэнтны, то есть равны по значению: P=2a+b . С равносторонним треугольником все еще незатейливей – у него все три стороны одинаковые, поэтому периметр будет равен утроенной стороне: P=3a .
Для треугольников, обладающих особыми свойствами, как например, вышеупомянутые равнобедренный и равносторонний треугольники, могут быть выведены и другие формулы. Например, периметр равнобедренного треугольника можно найти и через высоту. Высота в данном случае делит основание пополам, исходя из чего можно найти неизвестную сторону по теореме Пифагора из получившихся прямоугольных треугольников.
Если дана боковая сторона, то половина основания будет равна , а само основание, соответственно, . Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим . Если дано основание, то по той же теореме Пифагора находим боковую сторону . Формула периметра равнобедренного треугольника через основание и высоту тогда принимает вид .
Найти периметр равностороннего треугольника становится возможным, уже зная одну лишь высоту. Используя теорему Пифагора, выражаем сторону треугольника через высоту . Подставляем в формулу периметра равностороннего треугольника и получаем
Периметр прямоугольного треугольника можно найти, зная две стороны из трех. Если известны два катета a и b , то гипотенуза c по теореме Пифагора равна , и периметр получается . Если дана гипотенуза и один из катетов, формула периметра прямоугольного треугольника принимает уже другой вид:
Формула периметра равнобедренного треугольника
Периметр равнобедренного треугольника ABC , длины сторон которого соответственно равны: боковые стороны AB = BC = a , основание AC = b вычисляется по формуле:
Периметр равнобедренного треугольника вычисляется по формуле:
\( P_ = a + b + c = 2 \cdot a + b\)
где a,b,c – стороны равнобедренного треугольника.
Основные понятия, справедливые для треугольников
- Сумма углов треугольника равна 180°.
- Высота – это отрезок перпендикуляра, опущенного из вершины на противоположную сторону.
- Центр описанной окружности лежит на пересечении медиатрис.
- Медиатриса – это перпендикулярна прямая, проходящая через середину стороны.
- Центр вписанной окружности лежит на пересечении биссектрис углов.
- Биссектриса угла делит угол на две равные части.
- Медиана – это отрезок, соединяющий вершину с серединой противоположной стороны.
- Медианы пересекаются в центре тяжести, который делит каждую медиану в отношение 2:1.
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты.
Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.Периметр равнобедренного треугольника
Периметр – это сумма длин всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.
Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это вытекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и вытекает формула периметра:
P=2a+b, где b – это основание треугольника, a – значение боковой стороны.
Рис. 1. Равнобедренный треугольник
Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон.
Рассмотрим несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра.
Задача 1
- В равнобедренном треугольнике основание равно 6, а высота, проведенная к этому основанию, равна 4. Необходимо найти периметр фигуры.
Рис. 2. Рисунок к задаче 1
Высота равнобедренного треугольника, проведенная к основанию, является также медианой и биссектрисой. Это свойство очень часто используется при решении задач, связанных с равнобедренными треугольниками.
Треугольник АВС высотой ВM делится на два прямоугольных треугольника: АВM и ВСM. В треугольнике АВM катет ВM известен, катет АM равен половине основания треугольника АВС, так как ВM является медианой, биссектрисой и высотой. По теореме Пифагора найдем значение гипотенузы АВ.
Найдем периметр: P=AC+AB*2=6+5*2=16
Задача 2
- В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам.
нужно найти периметр треугольника.
Рис. 3. Рисунок к задаче 2
Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)==$$ – синус 30 градусов является табличным значением.
Выразим нужную сторону:
Через котангенс найдем значение AH:
$$AH=>=10*\sqrt=17,32$$ – получившееся значение округлим до сотых.
Теперь, когда все требуемые значения найдены, определим периметр:
Задача 3
- В равнобедренном треугольнике ABC известна площадь, которая равна $$16\over\sqrt$$ и острый угол при основании 30 градусов. Найти периметр треугольника.
Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных.
Попробуем решить по-другому.
Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято.
Подставим полученное значение в формулу площади.
Подставим значение a в формулу площади и определим значение высоты:
Через теорему Пифагора найдем боковую сторону треугольника:
Подставим значения в формулу периметра:
Что мы узнали?
Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.
Как найти периметр равностороннего треугольника с высотой? – Обзоры Вики
Итак, чему равен периметр равностороннего треугольника, высота которого равна 4 √ 3? Периметр треугольника = 3 × Сторона = 3 (4√3) = 12√3 см.
Дополнительно При нахождении периметра равностороннего треугольника можно ли найти периметр только одной известной длины стороны, объясните? Периметр любого многоугольника равен сумма длин его сторон. В равностороннем треугольнике все стороны равны (имеют одинаковую длину). Таким образом, если длина стороны равностороннего треугольника равна 2, периметр равен 2+2+2, потому что все его стороны равны 2.
Чему равен периметр равностороннего треугольника, высота которого равна 3.
46 см? Следовательно, периметр равностороннего треугольника равен 6 см.
Чему равен периметр равностороннего треугольника с высотой 24?
Формула высоты равностороннего треугольника: -a√3/2=24, поэтому сторона треугольника 24.2/√3=48.100/173 (значение √3), следовательно, сторона a равна 27.74, а теперь периметр треугольника треугольник 3а=3.27.
Как найти периметр с высотой? Периметр — это сумма всех сторон фигуры, чтобы получить одну длину. Итак, для нахождения периметра используется формула основание + высота + основание + высота. Если основание 10 дюймов, а высота 5 дюймов, у вас будет: Периметр: 10 + 5 + 10 + 5 = 30 дюймов. Определить площадь прямоугольника с помощью умножения.
Какова высота формулы равностороннего треугольника? Формула для расчета высоты равностороннего треугольника дается как: высота равностороннего треугольника, ч = (√3/2)а, где а — сторона равностороннего треугольника.
Как насчет равностороннего треугольника с одинаковым периметром?
Поскольку стороны равностороннего треугольника равны, периметр равен равно 3а.
Также Каков периметр равностороннего треугольника с одной стороной, измеряющей 4×8 единиц? Поскольку треугольник равносторонний, все его стороны равны друг другу. Таким образом, периметр равен 3 (S), где S — длина стороны.
Как найти стороны равностороннего треугольника?
Формулы и расчеты для равностороннего треугольника:
Высота равностороннего треугольника ч = (1/2) * √3 * в. Углы равностороннего треугольника: A = B = C = 60° Стороны равностороннего треугольника: a = b = c.
Какая связь между периметром и длиной стороны равностороннего треугольника?
Следовательно, периметр равностороннего треугольника равен эквивалентно утроенной длине стороны треугольника.
Какова длина стороны и периметр равностороннего треугольника, высота которого равна 9 см * 1 точка?
а = {2 / (√3)} * 9см = (6√3)см ≈ 10.
392 см.
Чему равна площадь равностороннего треугольника? Площадь равностороннего треугольника равна √3/4 раза (сторона)2 равностороннего треугольника а периметр равностороннего треугольника в 3 раза больше стороны равностороннего треугольника.
Как найти периметр треугольника 30 60 90? периметр равен 30.05 д — сложение всех сторон дает результат perimeter = a + a√3 + 2a = a (3 + √3) ≈ 30.05 дюйма.
Как найти площадь равностороннего треугольника с высотой?
В общем, высота равностороннего треугольника равна √3 / 2, умноженной на сторону равностороннего треугольника. Площадь равностороннего треугольника равна 1/2 * √3s / 2 * s = √3s2/4.
Что такое формула равностороннего треугольника? Формула высоты равностороннего треугольника: ч = (1/2) * √3 * в. Углы равностороннего треугольника: A = B = C = 60 градусов. Стороны равностороннего треугольника: a равно b равно c.
Если периметр равностороннего треугольника равен 180 см, то его площадь будет равна?
Периметр △ABC=180 см.
Значит сторона равностороннего треугольника равна 60 см. Площадь равностороннего треугольника определяется как Площадь = √34 × 2 где х — сторона равностороннего треугольника. Следовательно, площадь треугольника равна 1558.84 см2.
Какова высота равностороннего треугольника со стороной 6 см? Ответ: Высота данного равностороннего треугольника равна 3√3 см.
Как найти периметр квадрата и равностороннего треугольника?
Как найти периметр треугольника и полукруга?
Чтобы найти периметр треугольника надо.
Находим периметр треугольника различными способами
Предварительные сведения
Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
Определение 1
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Определение 2
Точки в рамках определения 1 будем называть вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.
В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.
Определение 4
Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.
Определение 5
Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.
Определение 6
Треугольник будем называть равносторонним, если все его стороны равняются друг другу.
Все виды этих треугольников Вы можете видеть на рисунке 2.
Как найти периметр разностороннего треугольника?
Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.
Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.
Пример 1
Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.
$P=34+12+11=57$ см
Ответ: $57$ см.
Пример 2
Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.
Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда
$α=10$ По правилу вычисления периметра разностороннего треугольника, получим
$P=10+8+6=24$ см
Ответ: $24$ см.
Как найти периметр равнобедренного треугольника?
Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+β=2α+β$
Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.
Пример 3
Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.
По рассмотренному выше примеру, видим, что
$P=2\cdot 12+11=35$ см
Ответ: $35$ см.
Пример 4
Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.
Рассмотрим рисунок по условию задачи:
Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.
По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону.
Обозначим ее через $α$, тогда
По правилу вычисления периметра равнобедренного треугольника, получим
$P=2\cdot 10+12=32$ см
Ответ: $32$ см.
Как найти периметр равностороннего треугольника?
Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+α=3α$
Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.
Пример 5
Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.
По рассмотренному выше примеру, видим, что
$P=3\cdot 12=36$ см
В статье на примерах покажем, как находить периметр треугольника . Рассмотрим все основные случая, как найти периметры треугольников , даже когда не все значения сторон известны.
Треугольником называется простая геометрическая фигура состоящая из трех прямых линий пересекающих друг друга.
В которой точки пересечения прямых, называются вершинами, а прямые линии соединяющие их, называются сторонами.
Периметром треугольника называется сумма длин сторон треугольника. От того сколько мы имеем изначальных данных, для вычисления периметра треугольника, зависит каким из вариантов мы воспользуемся, для его вычисления.
Первый вариант
Если мы знаем длины сторон n, y и z треугольника, то периметр мы можем определить с помощью следующей формулы: в которой P — это периметр, n, y, z- стороны треугольникапериметр прямоугольника формула
P = n + y + z
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =8см. найти его периметр.
Пользуясь формулой получаем 10 + 10 + 8 = 28.
Ответ: Р = 28см.Для равностороннего треугольника находим периметр так — длина одной стороны умноженная на три. формула выглядит следующим образом:
Р = 3n
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =10см.найти его периметр.
Пользуясь формулой получаем 10 * 3 = 30
Ответ: Р = 30см.Для равнобедренного треугольника находим периметр так — к длине одной боковой стороны умноженной на два, прибавляем сторону основания
Равнобедренным треугольником называется простейший многоугольник у которого две боковые стороны равны, а третья сторона называется основанием.P = 2n + z
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =7см. найти его периметр.
Пользуясь формулой получаем 2 * 10 + 7 = 27.
Ответ: Р = 27см.
Второй вариант
Когда нам не известна длина одной стороны, но мы знаем величины длины двух других сторон и угла между ними, а периметр треугольника возможно найти только после того как мы узнаем длину третьей стороны. В этом случае неизвестная сторона будет равна корню квадратному из выражения в2 + с2 — 2 ∙ в ∙ с ∙ cosβP = n + y + √ (n2 + y2 — 2 ∙ n ∙ y ∙ cos α)
n, y — длины сторон
α — размер угла между известными нам сторонамиТретий вариант
Когда нам не известны стороны n и y, но мы знаем длину стороны z и величины прилегающих к ней.Периметр треугольника в этом случае мы сможем найти только тогда когда узнаем длины двух неизвестных нам сторон, определим их с помощью теоремы синусов, с помощью формулы
P = z + sinα ∙ z / (sin (180°-α — β)) + sinβ ∙ z / (sin (180°-α — β))
z — длина известной нам стороны
α, β — размеры известных нам угловЧетвертый вариант
Так же можно найти периметр треугольника по радиусу вписанному в его окружность и площади треугольника. Определяем периметр по формулеP = 2S / r
S — площадь треугольника
r — радиус вписанной в него окружностиМы с вами разобрали четыре разных варианта, как можно найти периметр треугольника.
Находить периметр треугольника в принципе не сложно. Если у вас появились какие то вопросы по статье, дополнения, то обязательно пишите их в комментариях.Кстати, на referatplus.ru вы можете скачать рефераты по математике бесплатно .
Одной из базовых геометрических фигур является треугольник. Он образуется при пересечении трех отрезков прямых.
Данные отрезки прямых формируют стороны фигуры, а точки их пересечения называются вершинами. Каждый школьник, изучающий курс геометрии, обязан уметь находить периметр этой фигуры. Полученное умение будет полезным для многих и во взрослой жизни, к примеру, пригодится студенту, инженеру, строителю,
Существуют разные способы найти периметр треугольника. Выбор необходимой для вас формулы зависит от имеющихся исходных данных. Чтобы записать данную величину в математической терминологии используют специальное обозначение – Р. Рассмотрим, что такое периметр, основные способы его расчета для треугольных фигур разных видов.
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Альтернативный вариант
В математических задачах все данные длины редко бывают известны.
В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольникеявляется наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла;
- медиана к основанию;
- высота треугольника;
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Полезное видео: задачи на периметр труегольника
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон.
Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
.
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
.
Расчет через высоту
Рассчитать периметр таких категорий, как равнобедренные и прямоугольные треугольники, можно через показатель их средней линии. Как известно, высота треугольника разделяет его основание пополам. Таким образом, она образует две прямоугольных фигуры. Далее, нужный показатель вычисляется при помощи теоремы Пифагора. Формула будет иметь следующий вид:
.
Если известна высота и половина основания, используя этот способ, вы получите нужное число без поиска остальных данных о фигуре.
Полезное видео: нахождение периметра треугольника
Периметр любого треугольника — это длина линии, ограничивающей фигуру. Чтобы его вычислить, нужно узнать сумму всех сторон этого многоугольника.
Вычисление по данным значениям длины сторон
Когда известны их значения, то сделать это несложно. Обозначив эти параметры буквами m, n, k, а периметр буквой P, получим формулу для вычисления: P = m+n+k. Задание: Известно, что треугольник имеет стороны длиной 13,5 дециметров, 12,1 дециметров и 4,2 дециметра.
Узнать периметр. Решаем: Если стороны данного многоугольника — a = 13,5 дм, b = 12,1 дм, c = 4,2 дм, то P = 29,8 дм. Ответ: P = 29,8 дм.
Периметр треугольника, который имеет две равные стороны
Такой треугольник называется равнобедренным. Если эти равные стороны имеют длину a сантиметров, а третья сторона — b сантиметров, то периметр легко узнать: P =b+2a. Задание: треугольник имеет две стороны по 10 дециметров, основание 12 дециметров. Найти P. Решение: Пусть боковая сторона a = c = 10 дм, основание b = 12 дм. Сумма сторон P = 10 дм + 12 дм + 10 дм = 32 дм. Ответ: P = 32 дециметра.
Периметр равностороннего треугольника
Если все три стороны треугольника имеют равное количество единиц измерения, он называется равносторонним. Еще одно название — правильный. Периметр правильного треугольника находят при помощи формулы: P = a+a+a = 3·a. Задача: Имеем равносторонний треугольный земельный участок. Одна сторона равна 6 метрам. Найти длину забора, которым можно обнести этот участок.
Решение: Если сторона этого многоугольника a= 6м, то длина забора P = 3·6 = 18 (м). Ответ: P = 18 м.
Треугольник, у которого есть угол 90°
Его называют прямоугольным. Наличие прямого угла дает возможность находить неизвестные стороны, пользуясь определением тригонометрических функций и теоремой Пифагора. Самая длинная сторона называется гипотенуза и обозначается c. Имеются еще две стороны, a и b. Следуя теореме, носящей имя Пифагора, имеем c 2 = a 2 + b 2 . Катеты a = √ (c 2 — b 2) и b = √ (c 2 — а 2). Зная длину двух катетов a и b, вычисляем гипотенузу. Затем находим сумму сторон фигуры, сложив эти значения. Задание: Катеты прямоугольного треугольника имеют длину 8,3 сантиметра и 6,2 сантиметра. Периметр треугольника нужно вычислить. Решаем: Обозначим катеты a = 8,3 см, b = 6,2 см. За теоремой Пифагора гипотенуза c = √ (8,3 2 + 6,2 2) = √ (68,89 + 38,44) = √107,33 = 10,4 (см). P = 24,9 (см). Или P = 8,3 + 6,2 + √ (8,3 2 + 6,2 2) = 24,9 (см). Ответ: P = 24,9 см. Значения корней брали с точностью до десятых.
Если нам известны значения гипотенузы и катета, то значение Р получим, вычислив Р=√ (c 2 — b 2) + b + c. Задача 2: Отрезок земельного участка, лежащий против угла в 90 градусов, 12 км, один из катетов — 8 км. За какое время можно обойти весь участок, если двигаться со скоростью 4 километра в час? Решение: если наибольший отрезок — 12 км, меньший b = 8 км, то длина всего пути составит P = 8 + 12 + √ (12 2 — 8 2) = 20 + √80 = 20 + 8,9 = 28,9 (км). Время найдем, разделив путь на скорость. 28,9:4 = 7,225 (ч). Ответ: можно обойти за 7,3 ч. Значение квадратных корней и ответа берем с точностью до десятых. Можно найти сумму сторон прямоугольного треугольника, если дана одна из сторон и значение одного из острых углов. Зная длину катета b и значение противолежащего ему угла β, найдем неизвестную сторону a = b/ tg β. Находим гипотенузу c = a: sinα. Периметр такой фигуры находим, сложив полученные значения. P = a + a/ sinα + a/ tg α, или P = a(1 / sin α+ 1+1 / tg α). Задание: В прямоугольном Δ АВС с прямым углом С катет ВС имеет длину 10 м, угол А — 29 градусов.
Нужно найти сумму сторон Δ АВС. Решение: Обозначим известный катет ВС = a = 10 м, угол, лежащий напротив него, ∟А = α = 30°, тогда катет АС = b = 10: 0,58 = 17,2 (м), гипотенуза АВ = c = 10: 0,5 = 20 (м). Р = 10 + 17,2 + 20 = 47,2 (м). Или Р = 10 · (1 + 1,72 + 2) = 47,2 м. Имеем: P = 47,2 м. Значение тригонометрических функций берем с точностью до сотых, значение длины сторон и периметра округляем до десятых. Имея значение катета α и прилежащего угла β, узнаем, чему равен второй катет: b = a tg β. Гипотенуза в таком случае будет равна катету, разделенному на косинус угла β. Периметр узнаем по формуле P = a + a tg β + a: cos β = (tg β + 1+1: cos β)·a. Задание: Катет треугольника с углом 90 градусов 18 см, прилежащий угол — 40 градусов. Найти P. Решение: Обозначим известный катет ВС = 18 см, ∟β = 40°. Тогда неизвестный катет АС = b = 18 · 0,83 = 14,9 (см), гипотенуза АВ = c = 18: 0,77 = 23,4 (см). Сумма сторон фигуры равна Р = 56,3 (см). Или Р = (1 + 1,3+0,83)*18 = 56,3 см. Ответ: P = 56,3 см.
Если известна длина гипотенузы c и какой-нибудь угол α, то катеты будут равны произведению гипотенузы для первого — на синус и для второго — на косинус этого угла. Периметр этой фигуры P = (sin α + 1+ cos α)*c. Задание: Гипотенуза прямоугольного треугольника АВ = 9,1 сантиметр, а угол 50 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим гипотенузу: AB = c = 9,1 см, ∟A= α = 50°, тогда один из катетов BC имеет длину a = 9,1 · 0,77 = 7 (см), катет АС = b = 9,1 · 0,64 = 5,8 (см). Значит периметр этого многоугольника равен P = 9,1 + 7 + 5,8 = 21,9 (см). Или P = 9,1·(1 + 0,77 + 0,64) = 21,9 (см). Ответ: P = 21,9 сантиметров.
Произвольный треугольник, одна из сторон которого неизвестна
Если мы имеем значения двух сторон a и c, и угла между этими сторонами γ, третью находим теоремой косинусов: b 2 = с 2 + a 2 — 2 ас cos β, где β — угол, лежащий между сторонами а и с. Затем находим периметр. Задание: Δ АВС имеет отрезок АВ длиной 15 дм, отрезок АС, длина которго 30,5 дм.
Значение угла между этими сторонами 35 градусов. Вычислить сумму сторон Δ АВС. Решение: Теоремой косинусов вычислим длину третей стороны. BC 2 = 30,5 2 + 15 2 — 2·30,5·15·0,82 = 930,25 + 225 — 750,3 = 404,95. BC = 20,1 см. P = 30,5 + 15 + 20,1 = 65,6 (дм).Имеем: P = 65,6 дм.
Сумма сторон произвольного треугольника, у которого длины двух сторон неизвестны
Когда знаем длину только одного отрезка и значение двух углов, можно узнать длину двух неизвестных сторон, пользуясь теоремой синусов: «в треугольнике стороны всегда пропорциональны значениям синусов противоположных углов». Откуда b = (a* sin β)/ sin a. Аналогично c = (a sin γ): sin a. Периметр в таком случае будет P = а + (а sin β)/ sin a + (a sin γ)/ sin a. Задание: Имеем Δ ABC. В нем длина стороны BC 8,5 мм, значение угла C — 47°, а угла B — 35 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим длины сторон BC = a = 8,5 мм, AC = b, AB = c, ∟ A = α= 47°, ∟B = β = 35°, ∟ C = γ = 180° — (47° + 35°) = 180° — 82° = 98°.
Из соотношений, полученных из теоремы синусов, находим катеты AC = b = (8,5·0,57): 0,73= 6,7 (мм), AB = c = (7 · 0,99): 0,73 = 9,5 (мм). Отсюда сумма сторон этого многоугольника равна P = 8,5 мм + 5,5 мм + 9,5 мм = 23,5 мм. Ответ: P = 23,5 мм. В случае, когда есть только длина одного отрезка и значения двух прилежащих углов, сначала вычисляем угол, противоположный известной стороне. Все углы этой фигуры в сумме имеют 180 градусов. Поэтому ∟A = 180° — (∟B + ∟C). Дальше находим неизвестные отрезки, используя теорему синусов. Задание: Имеем Δ ABC. Он имеет отрезок BC, равный 10 см. Значение угла B равно 48 градусов, угол C равен 56 градусов. Найти сумму сторон Δ ABC. Решение: Сначала найдем значение угла A, противолежащего стороне BC. ∟A = 180° — (48° + 56°) = 76°. Теперь с теоремой синусов вычислим длину стороны AC = 10·0,74: 0,97 = 7,6 (см). AB = BC* sin C/ sin A = 8,6. Периметр треугольника Р = 10 + 8,6 + 7,6 = 26,2 (см). Результат: P = 26,2 см.
Вычисление периметра треугольника с использованием радиуса окружности, вписанной в него
Иногда из условия задачи не известна ни одна сторона.
Зато есть значение площади треугольника и радиуса окружности, вписанной в него. Эти величины связаны: S = r p. Зная значение площади треугольника, радиуса r, можем найти полупериметр p. Находим p = S: r. Задача: Участок имеет площадь 24 м 2 , радиус r равен 3 м. Найти количество деревьев, которое нужно высадить равномерно по линии, ограждающей этот участок, если между двумя соседними должно быть расстояние 2 метра. Решение: Сумму сторон данной фигуры находим так: P = 2 · 24: 3 = 16 (м). Затем делим на два. 16:2= 8. Итого: 8 деревьев.
Сумма сторон треугольника в декартовых координатах
Вершины Δ АВС имеют координаты: A (x 1 ; y 1), B (x 2 ; y 2), C(x 3 ; y 3). Найдем квадраты каждой из сторон AB 2 = (x 1 — x 2) 2 + (y 1 — y 2) 2 ; ВС 2 = (x 2 — x 3) 2 + (y 2 — y 3) 2 ; АС 2 = (x 1 — x 3) 2 + (y 1 — y 3) 2 . Чтобы найти периметр, достаточно сложить все отрезки. Задание: Координаты вершин Δ ABC: B (3; 0), A (1; -3), C (2; 5). Найти сумму сторон этой фигуры. Решение: поставив значения соответствующих координат в формулу периметра, получим P = √(4 + 9) + √(1 + 25) + √(1 + 64) = √13 + √26 + √65 = 3,6 + 5,1 + 8,0 = 16,6.
Имеем: P = 16,6. Если фигура находится не на плоскости, а в пространстве, то каждая из вершин имеет три координаты. Поэтому формула суммы сторон будет иметь еще одно слагаемое.
Векторный метод
Если фигура задана координатами вершин, периметр можно вычислить, используя векторный метод. Вектор — отрезок, имеющий направление. Его модуль (длина) обозначается символом ǀᾱǀ. Расстояние между точками — это и есть длина соответствующего вектора, или модуль вектора. Рассмотрим треугольник, лежащий на плоскости. Если вершины имеют координаты А (х 1 ; у 1), М(х 2 ; у 2), Т (х 3 ; у 3), то длину каждой из сторон находим по формулам: ǀАМǀ = √ ((х 1 — х 2) 2 + (у 1 — у 2) 2), ǀМТǀ = √ ((х 2 — х 3) 2 + (у 2 — у 3) 2), ǀАТǀ = √ ((х 1 — х 3) 2 + (у 1 — у 3) 2). Периметр треугольника получим, сложив длины векторов. Аналогично находят сумму сторон треугольника в пространстве.
Периметром треугольника , как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.

Формула периметра треугольника выглядит так:Пример расчета периметра треугольника. Пусть дан треугольник со сторонами a = 4см, b = 6 см, c = 7 см. подставим данные в формулу: см
Формула расчета периметра равнобедренного треугольника будет выглядеть так:
Формула расчета периметра равностороннего треугольника :
Пример расчета периметра равностороннего треугольника. Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по теореме Пифагора . К примеру, если известны длины катетов, то можно найти гипотенузу по формуле:
Рассмотрим пример расчета периметра равнобедренного треугольника при условии, что мы знаем длину катетов в прямоугольном равнобедренном треугольнике.

Дан треугольник с катетами a =b =5 см. Найти периметр. Для начала найдем недостающую сторону с . см
Теперь посчитаем периметр: см
Периметр прямоугольного равнобедренного треугольника будет равен 17 см.В случае, когда известна гипотенуза и длина одного катета, можно найти недостающий по формуле:
Если в прямом треугольнике известна гипотенуза и один из острых углов, то недостающая сторона находится по формуле.Периметр равностороннего треугольника – формула, определение, примеры
Периметр равностороннего треугольника – это общая длина его границы. В геометрии равносторонний треугольник — это треугольник, у которого все три стороны равны. Общую длину границы треугольника можно вычислить, сложив длины всех его сторон. В этой статье мы научимся вычислять периметр равностороннего треугольника и его формулу с помощью решенных примеров.
1. Каков периметр равностороннего треугольника? 2. Периметр равностороннего треугольника Формула 3. Как найти периметр равностороннего треугольника? 4. Часто задаваемые вопросы о периметре равностороннего треугольника Каков периметр равностороннего треугольника?
Периметр равностороннего треугольника равен сумме трех его сторон. Треугольник считается равносторонним, если он обладает следующими основными свойствами:
- Все три стороны равны.
- Все три угла равны 60°
На приведенном ниже рисунке стороны треугольника PQR равны, т. е. PQ = QR = RP. При этом углы треугольника также равны. Следовательно, это равносторонний треугольник. Теперь периметр равностороннего треугольника = 3a (где «а» — сторона равностороннего треугольника)
Периметр равностороннего треугольника Формула
Основная формула, которая используется для вычисления периметра равностороннего треугольника: P = 3a , где «а» представляет одну сторону треугольника.
Поскольку все три стороны равностороннего треугольника равны, сумма равна а + а + а = 3а.
Несколько других формул, связанных с равносторонним треугольником, следующие:
- Иногда, когда даны стороны равностороннего треугольника, нам нужно найти его высоту, тогда мы используем формулу: Высота равностороннего треугольника = (√3a)/2
- В некоторых случаях нам нужно найти полупериметр равностороннего треугольника. Полупериметр равен половине периметра и рассчитывается по формуле Полупериметр = (а + а + а)/2 = 3а/2
Как найти периметр равностороннего треугольника?
Мы знаем, что формула периметра равностороннего треугольника равна 3а, где а = сторона равностороннего треугольника. Теперь давайте научимся применять формулу периметра равностороннего треугольника.
Пример: Найдите периметр равностороннего треугольника со стороной 9 единиц. Чему равен полупериметр этого треугольника?
Решение:
Дано: Сторона равностороннего треугольника = а = 9 единиц.
Периметр равностороннего треугольника = 3а. Подставляя значение a = 9в формуле = 3 × 9 = 27 единиц
Полупериметр равностороннего треугольника = 3a/2. Подставив значение a = 9 в формулу = (3 × 9)/2 = 27/2 = 13,5 единиц
Примечание: Полупериметр равностороннего треугольника равен половине периметра равностороннего треугольника.
Периметр равностороннего треугольника при заданной площади
Периметр равностороннего треугольника можно вычислить, если известна площадь треугольника. В этом случае сначала нужно найти длины сторон, с помощью которых можно вычислить периметр.
Пример: Если площадь равностороннего треугольника равна 56 квадратных единиц, найдем его периметр.
Решение: Мы знаем, что площадь равностороннего треугольника = (a 2 √3)/4. Итак, сторону можно вычислить, подставив значение площади в формулу.
Площадь = (a 2 √3)/4
56 = (a 2 √3)/4
a 2 = (56 × 4)/√3
5 90 единиц
Теперь можно вычислить периметр равностороннего треугольника, P = 3a = 3 × 11,37 = 34,11 единиц.
Периметр равностороннего треугольника при заданной высоте
Периметр равностороннего треугольника можно рассчитать, зная высоту (высоту) треугольника. В этом случае мы можем найти длину стороны треугольника по формуле: Высота равностороннего треугольника = (√3a)/2. Найдя длину стороны, можно легко вычислить периметр равностороннего треугольника.
Пример: Если высота равностороннего треугольника равна 6 единицам, найдите его периметр.
Решение: Мы знаем, что формула высоты равностороннего треугольника = (√ 3a)/ 2. Таким образом, длину стороны можно вычислить как , подставив в формулу значение высоты.
Высота = ( √ 3a)/2
6 = ( √ 3a)/2
a = (6 × 2)/ √ 3
A = 6,92 единицы
Теперь, периметр. равностороннего треугольника можно рассчитать, P = 3a = 3 × 6,92 = 20,76 единиц.
☛ Статьи по теме
- Периметр прямоугольного треугольника
- Периметр равнобедренного треугольника
- Периметр разностороннего треугольника
- Периметр треугольника
- Площадь равностороннего треугольника
- Формулы равностороннего треугольника
Примеры по периметру равностороннего треугольника
Пример 1: Вычислите периметр равностороннего треугольника, каждая сторона которого равна 10 дюймам.
Решение:
Периметр равностороннего треугольника = 3а, где а — сторона. Дано, а = 10 дюймов. Таким образом, периметр = 3 × 10 = 30 дюймов. Следовательно, периметр равностороннего треугольника равен 30 см.
Пример 2: Каков периметр равностороннего треугольника, каждая сторона которого равна 30 дюймов. Сможете ли вы найти высоту этого равностороннего треугольника?
Решение:
Используя формулу периметра равностороннего треугольника = 3а, где а — сторона. Дано а = 30 дюймов. Таким образом, периметр равностороннего треугольника = 3 × 30 = 90 дюймов, а высота равностороннего треугольника = (√3a)/2. Следовательно, высота равностороннего треугольника равна = (√3 × 30)/2 = 15√3 дюйма = .
Пример 3: Найдите периметр равностороннего треугольника, если его площадь равна 64√3 см. 4. Итак, длину стороны можно рассчитать, подставив в формулу значение площади.
Площадь = (a 2 √3)/4
64√3 = (a 2 √3)/4
a 2 = 64 × 4 = 256
5 единиц, следовательно . Теперь, когда мы знаем сторону треугольника, мы можем найти периметр равностороннего треугольника,
Периметр равностороннего треугольника = 3а, где а = 16 единиц. Таким образом, периметр равностороннего треугольника = 3 × 16 = 48 единиц
перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Практические вопросы по периметру равностороннего треугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о периметре равностороннего треугольника
Каков периметр равностороннего треугольника?
Общая длина границы равностороннего треугольника называется его периметром.
Периметр равностороннего треугольника можно вычислить, если известна длина его стороны. Например, если одна сторона равностороннего треугольника равна 5 единицам, периметр = 3 × сторона = 3 × 5 = 15 единиц.
Как найти периметр равностороннего треугольника?
Чтобы найти периметр равностороннего треугольника, нужно знать длину его стороны. Поскольку все стороны равностороннего треугольника равны по длине, периметр легко вычислить по длине одной из его сторон. Это значение можно подставить в формулу периметра равностороннего треугольника P = 3 × a; где «а» — длина стороны треугольника.
Как найти периметр равностороннего треугольника, зная площадь?
Если мы знаем площадь равностороннего треугольника, мы можем легко найти его периметр. В этом случае сначала нужно найти длины сторон, с помощью которых можно вычислить периметр. Например, если площадь равностороннего треугольника равна 48 квадратных единиц, найдем его периметр. Мы знаем, что площадь равностороннего треугольника = (a 2 √3)/4.
Теперь длину стороны можно рассчитать, подставив значение площади в формулу. 48 = (а 2 √3)/4. Решив это, мы получим «а» = 10,53. Теперь, используя эту длину стороны, можно вычислить периметр. Периметр = 3а = 3 × 10,53 = 31,59 единицы.
Как найти периметр равностороннего треугольника, зная высоту?
Периметр равностороннего треугольника можно вычислить, если известна высота (высота) треугольника. Здесь мы можем найти длину стороны треугольника с помощью формулы: Высота равностороннего треугольника = (√3a)/2, Найдя длину стороны, можно вычислить периметр равностороннего треугольника. Например, если высота равностороннего треугольника равна 8 единицам, найдем его периметр. Мы знаем, что высота равностороннего треугольника = (√3a)/2. Теперь давайте вычислим длину стороны, подставив значение высоты в формулу. 8 = 3а/2. Итак, а = 5,3 единицы. Теперь, используя эту длину стороны, можно вычислить периметр. Периметр = 3а = 3 × 5,3 = 15,9 единиц.
Найдите периметр равностороннего треугольника со стороной 9см.
Если сторона равностороннего треугольника равна 9 см, периметр можно рассчитать по формуле периметр = 3а, где а = длина стороны. Подставим значение «а» в формулу. Р = 3а = 3 × 9 = 27 см. Следовательно, периметр равностороннего треугольника со стороной 9 см равен 27 см.
Является ли равносторонний треугольник правильным многоугольником?
Да, равносторонний треугольник считается правильным многоугольником, потому что:
- Это треугольник, в котором все углы равны.
- Все стороны равны по длине.
Сколько сторон у равностороннего треугольника?
Равносторонний треугольник имеет три стороны. Длина каждой стороны равностороннего треугольника равна.
Чему равна сумма всех углов равностороннего треугольника?
Сумма всех углов равностороннего треугольника равна 180°. Каждый угол равен 60°. Соответственно, 60°+ 60°+ 60° = 180 градусов.
Сколько углов у равностороннего треугольника?
Равносторонний треугольник имеет три угла.
Все углы равны 60°. Сумма этих углов равна 180°.
Какая формула равностороннего треугольника?
Основная формула, используемая для вычисления периметра равностороннего треугольника, такова: P = 3a , где «а» представляет одну сторону треугольника. Формула, которая используется для нахождения площади равностороннего треугольника: Площадь равностороннего треугольника = (a 2 √3)/4, где «a» — одна сторона треугольника.
Как найти периметр равностороннего треугольника?
Равносторонний треугольник — это треугольник, у которого все три стороны равны и углы также равны. Значение каждого угла равностороннего треугольника составляет 60 градусов, поэтому он также известен как равносторонний треугольник. Равносторонний треугольник считается правильным многоугольником или правильным треугольником, так как углы равны и стороны также равны.
Например, в треугольнике ABC равны, т.е.
AB = BC = CA = a единиц.
Кроме того, ∠A, ∠B и ∠C = 60°
Свойства равностороннего треугольника
- Все три стороны равны.
- Все три угла равны 60 °
Периметр равностороннего треугольника
Полу периметра равенского треугольникаSemi Периметр по периметру ура равностороннего треугольника.
Другими словами, имеем
Полупериметр равностороннего треугольника =
Периметр равностороннего треугольника, если задана площадьПредположим, что a — сторона равностороннего треугольника.
Периметр равностороннего треугольника можно вычислить, используя его площадь, которая определяется как,
Теперь,
Мы знаем,
Периметр равностороннего треугольника = Сторона + Сторона + Сторона
Периметр равностороннего треугольника , P определяется выражением = 3 × a
Следовательно, значения a можно заменить на P/3.
Периметр равностороннего треугольника при заданной высотеПериметр равностороннего треугольника можно вычислить, зная высоту (высоту) треугольника.
Имеем,
Высота равностороннего треугольника =
После подстановки значений периметра равностороннего треугольника имеем,
Периметр равностороннего треугольника = Сторона + Сторона + Сторона
Периметр равностороннего треугольника = 3 × a
Следовательно,
Высота (или Высота) =
Примеры вопросов
Вопрос 1. Вычислите периметр равностороннего треугольника, если сторона треугольника √3 см.
Решение:
Здесь нам нужно найти периметр равностороннего треугольника
Нам известно, что сторона равностороннего треугольника равна 30√3 см
Как мы знаем, что
Формула периметра равностороннего треугольника
Периметр равностороннего треугольника = Сторона + Сторона + Сторона
Периметр равностороннего треугольника = 3 × a
где а — сторона равностороннего треугольника
Периметр равностороннего треугольника = 3 × 30√3
Периметр равностороннего треугольника = 90√3 см
Следовательно,
Периметр равностороннего треугольника равен 90√3 см.
Вопрос 2. Если сторона равностороннего треугольника равна 90 м, то найдите периметр и полупериметр треугольника?
Решение:
Здесь мы должны найти периметр и полупериметр равностороннего треугольника,
Первое нахождение периметра равностороннего треугольника
Нам известно, что сторона равностороннего треугольника равна 90 м
Формула периметра равностороннего треугольника
Периметр равностороннего треугольника = Сторона + Сторона + Сторона
Периметр равностороннего треугольника = 3 × a
Подстановка значения a в формулу
Периметр равностороннего треугольника = 3 × 90
Периметр равностороннего треугольника = 270 м
Дальнейшее нахождение полупериметра
Формула полупериметра равностороннего треугольника =
Где а — сторона равностороннего треугольника
Подставляя значение а в формулу
Полупериметр равностороннего треугольника =
Полупериметр равностороннего треугольника = 135 м
Следовательно,
Периметр равностороннего треугольника равен 270 м, а полупериметр равностороннего треугольника равен 135 м.
Вопрос 3. Считать, что площадь равностороннего треугольника равна 100√3 см 2 . Тогда вычислить его периметр?
Решение:
Здесь мы должны найти периметр равностороннего треугольника, используя его площадь
Формула площади равностороннего треугольника =
Площадь равностороннего треугольника = 100√3
100√3 =
A 2 =
A = √400
A = 20
Следовательно,
Сторона равенственного треугольника — 20 см
. равностороннего треугольника = сторона + сторона + сторона = 3а
Периметр равностороннего треугольника = 3 × 20
Периметр равностороннего треугольника = 60 см
Вопрос 4. Найдите периметр равностороннего треугольника, если высота треугольника составляет 35√3 м.
Решение:
Здесь нам нужно найти Периметр равностороннего треугольника высотой 35√3 м
Формула для вычисления периметра по высоте приведена ниже равностороннего треугольника
35√3 =
a =
a = 70 м
Далее находим периметр равностороннего треугольника
Периметр равностороннего треугольника = сторона + сторона + сторона = 3a
Периметр равностороннего треугольника = 3 × 70
Периметр равностороннего треугольника = 210 м
Вопрос 5.
Если сторона равностороннего треугольника равна 23 см, то найдите периметр и высоту равностороннего треугольника?
Решение:
Здесь мы должны найти периметр равностороннего треугольника
Нам известно, что сторона равностороннего треугольника равна 23 см
Поскольку мы знаем, что
Формула периметра равностороннего треугольника
Периметр равностороннего треугольника = сторона + сторона + сторона
Периметр равностороннего треугольника = 3 × a
где а — сторона равностороннего треугольника
Периметр равностороннего треугольника треугольник = 3 × 23
Периметр равностороннего треугольника = 69 см
Дальнейшее нахождение высоты треугольника
Высота =
Здесь а — сторона равностороннего треугольника
Подставляя значение a в формулу
Высота =
Высота = 11,5√3
Следовательно,
Периметр равностороннего треугольника равен 69 см, а высота равностороннего треугольника равна 11,5√3 см.
Калькулятор равностороннего треугольника
- Площадь и высота равностороннего треугольника
- Периметр равностороннего треугольника, радиус описанной и вписанной окружности
- Как я могу использовать калькулятор равностороннего треугольника?
- FAQ
Калькулятор равностороннего треугольника поможет вам в расчетах стандартных параметров треугольника. Независимо от того, ищете ли вы площадь равностороннего треугольника, его высоту, периметр, радиус описанной окружности или внутренний радиус, этот великолепный инструмент является надежным выбором. Прокрутите вниз, чтобы узнать больше о полезных формулах (например, для высоты равностороннего треугольника) и узнать, что такое равносторонний треугольник.
Что такое равносторонний треугольник?
Равносторонний треугольник, также называемый правильным треугольником, представляет собой треугольник, у которого все три стороны равны. Каковы другие важные свойства этой конкретной правильной формы?
- Все три внутренних угла равны друг другу, и все они равны 60°.
- Высоты, биссектрисы углов, биссектрисы перпендикуляров и медианы совпадают.
Равносторонний треугольник является частным случаем равнобедренного треугольника, у которого равны не только две, но и все три стороны.
Площадь и высота равностороннего треугольника
Формула площади правильного треугольника равна квадрату стороны, умноженному на квадратный корень из 3, деленный на 4:
площадь = (a² × √3)/4и уравнение для высота равностороннего треугольника выглядит следующим образом:
h = a × √3/2, гдеa— сторона треугольника.А знаете ли вы, откуда берутся формулы? Вы можете найти их по крайней мере двумя способами: вывести из теоремы Пифагора или с помощью тригонометрии.
1. Использование теоремы Пифагора
Базовая формула площади треугольника: сторона
a(основание), умноженная на высотуh, разделенная на 2:
площадь = (a × h) / 2Высота равностороннего треугольника разбивает равносторонний треугольник на два прямоугольных треугольника.
Один катет этого прямоугольного треугольника равен высоте, другой катет — половине стороны, а гипотенуза — стороне равностороннего треугольника.
(а/2)² + h² = а²После несложных преобразований получаем формулу высоты равностороннего треугольника:
ч = а × √3 / 2Подставив
чв первую формулу площади, получим уравнение площади равностороннего треугольника:
площадь = a² × √3 / 42. Использование тригонометрии
Начнем с тригонометрической формулы площади треугольника:
площадь = (1/2) × a × b × sin(γ), гдеγугол между сторонамиМы помним, что в равностороннем треугольнике все стороны и все углы равны, поэтому формула упрощается до:
площадь = 0,5 × a × a × sin(60°)Более того, мы знаем, что синус 60° равен √3/2, поэтому формула площади равностороннего треугольника:
площадь = (1/2) × a² × (√3/2) = a² × √3/4Высота равностороннего треугольника получена из определения синуса:
h / a = sin(60°)поэтомуh = a × sin(60°) = a × √3 / 2Периметр равностороннего треугольника, радиус описанной и вписанной окружности
Вы можете легко найти периметр равностороннего треугольника, сложив все стороны треугольника вместе.
У правильного треугольника все стороны равны, поэтому формула для периметра:
периметр = 3 × aКак найти радиус окружности, описывающей три вершины, и радиус вписанной окружности?
окружность_радиус = 2 × h / 3 = a × √3 / 3
incircle_radius = h / 3 = a × √3 / 6Как я могу использовать калькулятор равностороннего треугольника?
Возьмем пример из повседневной жизни: мы хотим найти все параметры знака доходности.
Введите данное значение в правильное поле . Предположим, у нас есть знак с длиной стороны 36 дюймов.
Калькулятор равностороннего треугольника быстро находит другие значения . Теперь мы знаем, что:
- Высота знака доходности 31,2 дюйма;
- Его площадь равна 561 кв. дюйму;
- Периметр: 108 дюймов;
- Радиус окружности составляет 20,8 дюйма; и
- Радиус вписанной окружности 10,4 дюйма
Оцените гибкость нашего инструмента .
Обновите калькулятор и введите другой параметр, например, периметр. Это тоже работает, разве это не круто?
Часто задаваемые вопросы
Как найти площадь равностороннего треугольника?
Чтобы найти площадь равностороннего треугольника, следуйте данным инструкциям:
Возьмите квадратный корень из 3 и разделите его на 4 .
Умножить на квадрат стороны на результат шага 1 .
Поздравляем! Вы вычислили площадь равностороннего треугольника.
Как найти высоту равностороннего треугольника?
Чтобы найти высоту равностороннего треугольника, выполните следующие действия:
Возьмите квадратный корень из 3 и разделите на 2 .
Умножьте результат шага 1 на длину стороны .
Вы получите высоту равностороннего треугольника.
Как найти периметр равностороннего треугольника со стороной 8 см?
Периметр данного треугольника равен 24 см . Чтобы вычислить периметр равностороннего треугольника, нам нужно умножить длину его стороны на 3 . Длина каждой стороны данного треугольника равна 8 см. Следовательно, его периметр будет равен 3 × 8 см = 24 см .
Может ли прямоугольный треугольник быть равносторонним?
Нет, прямоугольный треугольник не может быть равносторонним . Один из углов прямоугольного треугольника равен 90°. Так как сумма всех внутренних углов треугольника равна 180°, то два других угла прямоугольного треугольника всегда меньше 90°.
Согласно определению равносторонних треугольников все внутренние углы равны. Следовательно, прямоугольный треугольник никогда не может быть равносторонним.
Ханна Памула, кандидат наук
Сторона (a)
Высота (h)
Периметр
Радиус окружности
Радиус вписанной окружности
Посмотреть 18 подобных калькуляторов треугольников «equi» означает равный, равносторонний треугольник — это тот, в котором все стороны равны.
Внутренние углы любого заданного равностороннего треугольника имеют одну и ту же меру, то есть равны 60 градусам.
Треугольники делятся на три типа в зависимости от длины их сторон:
Разносторонний треугольник: Стороны и углы разностороннего треугольника не равны.
Равнобедренный треугольник: Равнобедренный треугольник имеет две равные стороны и два равных угла.
Равносторонний треугольник: Все стороны и углы равностороннего треугольника равны.
Площадь равностороннего треугольника
Область, ограниченная тремя сторонами равностороннего треугольника, определяется как площадь равностороннего треугольника. Выражается в квадратных единицах. Общие единицы, используемые для выражения площади равностороннего треугольника, это дюйм2, м2, см2 и ярд2 9.
0005
Ниже обсуждаются площадь формулы равностороннего треугольника, высота формулы равностороннего треугольника, периметр формулы равностороннего треугольника и полупериметр равностороннего треугольника.
Площадь равностороннего треугольника Формула
Площадь равностороннего треугольника — это площадь, которую он занимает в двумерной плоскости. Напомним, равносторонний треугольник можно определить как треугольник, в котором все стороны равны, а мера всех внутренних углов равна 60°. Итак, площадь равностороннего треугольника можно вычислить, если известна длина любой стороны треугольника.
Площадь, занимаемая сторонами равностороннего треугольника на плоскости, рассчитывается по формуле площади равностороннего треугольника.
Формула для вычисления площади треугольника с известным основанием и высотой:
Площадь = 1/2 × основание × высота равносторонний треугольник:
Площадь = √3/4 × (сторона)2 квадратные единицы
Периметр равностороннего треугольника Формула
Периметр треугольника равен сумме длин трех его сторон, независимо от того, равны они или нет.
Периметр равностороннего треугольника равен сумме трех его сторон.
P = 3a — основная формула для вычисления периметра равностороннего треугольника, где «a» обозначает одну из сторон треугольника. Сумма становится a + a + a = 3a, так как все три стороны равностороннего треугольника равны.
Height = √3a/ 2
Semi perimeter = (a + a + a)/2 = 3a/2
Formulas and Calculations for an Equilateral Triangle:
Perimeter of Equilateral Triangle : P = 3a
Полупериметр равностороннего треугольника Формула: s = 3a/2
Площадь равностороннего треугольника Формула: K = (1/4) * √3 * a2
Высота равностороннего треугольника Формула: h = (1/2) * √3 * a
Углы равностороннего треугольника: A = B = C = 60 градусов
Стороны равностороннего треугольника: a равно b равно c.
1. Зная сторону треугольника, найдите периметр, полупериметр, площадь и высоту.
2. По периметру треугольника найти сторону, полупериметр, площадь, высоту.
3. Зная полупериметр треугольника, найдите сторону, периметр, площадь и высоту.
4. Зная площадь треугольника, найдите сторону, периметр, полупериметр и высоту.
К известно; найти a, P, s и h.
a = √
(4/√3) ∗ k
(4/√3) ∗ k равно 2 * √
K/√ 3
2K/√ 3
2K/√ 3
2K/k Equals 2 * √
K/k equals 2 * √
K/k e equals 2 * √
K/k.
3
P = 3a
s = 3a / 2
- 80005
h = (1/2) * √3 * a
5. Зная высоту/высоту, найти сторону, периметр, полупериметр и площадь
Высота (h) известна; найти a, P, s и K. ) * √3 * a2
Решенные примеры
1. Примените формулу площади равностороннего треугольника и найдите площадь равностороннего треугольника, каждая сторона которого равна 12 дюймам.
Решение:
Стоя = 12 в
Применение равенственной формулы области треугольника,
Область = √3/4 × (сторона) 2
585858588 гг.)2
= 36√3 дюйма2
Ответ: площадь равностороннего треугольника 36√3 дюйма2
.
Решение:
Периметр = 3A
Полупериметр = 3A/ 2
, сторона A = 12 единиц
Теперь периметром уравненного треугового 12 = 36 единиц
И, полупериметр равностороннего треугольника равен:
36/2 = 18 единиц.
3. Предположим, у вас есть равносторонний треугольник со стороной 5 см. Чему будет равен периметр данного равностороннего треугольника?
Решение) Мы знаем, что формула периметра равностороннего треугольника равна 3а.
Здесь a = 5 см
Следовательно, периметр = 3 * 5 см = 15 см.
Значение, примеры, формулы и методы
Треугольники содержат специальные сегменты, такие как серединный перпендикуляр, медиана и высота. Когда вы думаете о высоте, вы можете думать об увеличении высоты горных хребтов; Однако термин высота также имеет место в геометрии и относится к высоте треугольника.
В этой статье мы подробно рассмотрим концепцию высот в треугольниках и связанные с ними термины. Мы научимся вычислять высоту по отношению к различным типам треугольников.
Что такое высота?
Перпендикулярный отрезок от вершины к противоположной стороне или линии, содержащей противоположную сторону, называется высотой треугольника.
Треугольники с высотой, StudySmarter Originals
Высота измеряется как расстояние от вершины до основания, поэтому она также известна как высота треугольника. Каждый треугольник имеет три высоты, и эти высоты могут лежать снаружи, внутри или на стороне треугольника.
Давайте посмотрим, как это может выглядеть.
Высоты с разными положениями, ck12.org
Свойства высоты
Вот некоторые свойства высоты:
- Высота образует угол на стороне, противоположной вершине.
- Расположение высоты изменяется в зависимости от типа треугольника.
- Поскольку треугольник имеет три вершины, он имеет три высоты.
- Точка пересечения этих трех высот называется ортоцентром треугольника.
Формула высоты для различных треугольников
Существуют различные формы формул высоты в зависимости от типа треугольника. Мы рассмотрим формулу высоты для треугольников в целом, а также конкретно для разносторонних треугольников, равнобедренных треугольников, прямоугольных треугольников и равносторонних треугольников, включая краткое обсуждение того, как эти формулы получены.
Общая формула высоты
Поскольку высота используется для нахождения площади треугольника, мы можем вывести формулу из самой площади.
Площадь треугольника, где b — основание треугольника, а h — высота/высота. Отсюда мы можем вывести высоту треугольника следующим образом:
Высота (h)
Для треугольника площадь равна длине основания. Найдите длину высоты этого треугольника.
Решение : Здесь нам даны площадь и основание треугольника. Таким образом, мы можем напрямую применить общую формулу, чтобы найти длину высоты.
Высота h.
Формула высоты для разностороннего треугольника
Треугольник, у которого все три стороны имеют разную длину, известен как разносторонний треугольник. Здесь для определения высоты используется формула Герона.
Формула Герона — это формула для нахождения площади треугольника на основе длины сторон, периметра и полупериметра.
Высота для разностороннего треугольника, StudySmarter Originals
Площадь треугольника (по формуле Герона)
Здесь s — полупериметр треугольника (т.
е. ), а x, y, z — длины сторон.
Теперь, используя общую формулу площади и приравняв ее к формуле Герона, мы можем получить высоту,
Площадь
Итак, высота для разностороннего треугольника:
В разностороннем треугольнике AD равна высота с основанием BC. Длины всех трех сторон АВ, ВС и АС равны 12, 16 и 20 соответственно. Периметр этого треугольника равен 48 см. Вычислите длину высоты AD.
Разносторонний треугольник с неизвестной высотой, StudySmarter Originals
Решение : Здесь приведены. Основание ВС имеет длину 16 см. Чтобы вычислить длину высоты, нам нужен полупериметр. Давайте сначала найдем значение полупериметра из периметра.
Полупериметр
Теперь мы можем применить формулу высоты, чтобы получить меру высоты.
Высота разностороннего треугольника
Итак, высота этого разностороннего треугольника равна 12 см.
Формула высоты для равнобедренного треугольника
Равнобедренный треугольник — это треугольник, две стороны которого равны.
Высота равнобедренного треугольника — это биссектриса этого треугольника с противоположной стороной. Мы можем вывести его формулу, используя свойства равнобедренного треугольника и теорему Пифагора.
Высота в равнобедренном треугольнике, StudySmarter Originals
Поскольку треугольник является равнобедренным, его стороны имеют длину x. Здесь мы используем одно из свойств равнобедренного треугольника, которое гласит, что высота делит его сторону основания пополам на две равные части.
Теперь, применяя теорему Пифагора, получаем:
Теперь, подставляя все значения данной стороны, получаем:
Следовательно, a высота равнобедренного треугольника — длины сторон, y — основание, а h — высота.
Найдите высоту равнобедренного треугольника, если основание равно, а длина двух равных сторон равна.
Равнобедренный треугольник с неизвестной высотой, StudySmarter Originals
Решение : Согласно формуле высоты для равнобедренного треугольника имеем.
Высота для равнобедренного треугольника:
Итак, высота для данного равнобедренного треугольника равна
Формула высоты для прямоугольного треугольника
Прямоугольный треугольник — это треугольник с одним углом как, и высота от одной из вершин относительно гипотенузы можно объяснить с помощью важного утверждения, называемого теоремой о высоте прямоугольного треугольника. Эта теорема дает формулу высоты для прямоугольного треугольника.
Высота прямоугольного треугольника, StudySmarter Originals
Сначала разберемся с теоремой.
Высота прямоугольного треугольника Теорема : Высота от вершины прямого угла до гипотенузы равна среднему геометрическому двух отрезков гипотенузы.
Доказательство : Из данной фигуры AC высота прямоугольного треугольника. Теперь, используя теорему подобия прямоугольного треугольника, мы получаем, что два треугольника и подобны.
Теорема подобия прямоугольного треугольника: Если из вершины прямого угла провести высоту к гипотенузе прямоугольного треугольника, то два новых образовавшихся треугольника подобны исходному треугольнику, а также подобны друг другу.
Следовательно, из приведенной выше теоремы мы можем получить формулу для высоты.
Высота прямоугольного треугольника, где x и y — длины по обе стороны от высоты, которые вместе составляют гипотенузу.
В данном прямоугольном треугольнике и Найдите длину высоты BD в данном треугольнике.
Прямоугольный треугольник с неизвестной высотой, StudySmarter Originals
Решение : Для вычисления высоты мы воспользуемся теоремой о высоте под прямым углом.
Высота прямоугольного треугольника:
Отсюда длина высоты прямоугольного треугольника равна
Примечание : Мы не можем использовать теорему Пифагора для вычисления высоты прямоугольного треугольника, так как предоставлено недостаточно информации. Итак, мы используем теорему о высоте прямоугольного треугольника, чтобы найти высоту.
Формула высоты для равностороннего треугольника
Равносторонний треугольник — это треугольник, у которого все стороны и углы соответственно равны.
Мы можем вывести формулу высоты, используя либо формулу Герона, либо формулу Пифагора. Высота равностороннего треугольника также считается медианой.
Высота равностороннего треугольника, StudySmarter Originals
Площадь треугольника (по формуле Герона)
И мы также знаем, что Площадь треугольника
Таким образом, используя оба приведенных выше уравнения, мы получаем:
Теперь периметр равностороннего треугольника треугольник 3x. Значит полупериметр и все стороны равны.
Высота для равностороннего треугольника: , где h — высота, а x — длина всех трех равных сторон.
Для равностороннего треугольника стороны XY, YZ и ZX равны по длине Рассчитайте длину высоты этого треугольника.
Равносторонний треугольник с неизвестной высотой, StudySmarter Originals
Решение : Здесь Теперь применим формулу высоты для равностороннего треугольника.
Высота для равностороннего треугольника:
Следовательно, для этого равностороннего треугольника длина высоты равна
Совпадение высот
В свойствах высоты мы обсуждали, что все три высоты треугольника пересекаются в точке, называемой ортоцентром.
Давайте разберемся с концепциями параллелизма и ортоцентрового положения в разных треугольниках.
Все три высоты треугольника совпадают; то есть они пересекаются в точке. Эта точка совпадения называется ортоцентром треугольника.
Мы можем вычислить координаты ортоцентра, используя координаты вершины треугольника.
Положение ортоцентра в треугольнике
Положение ортоцентра может варьироваться в зависимости от типа треугольника и высот.
Остроугольный треугольник
Ортоцентр остроугольного треугольника лежит внутри треугольника.
Ортоцентр остроугольного треугольника, StudySmarter Originals
Прямоугольный треугольник
Ортоцентр прямоугольного треугольника лежит на вершине прямого угла.
Ортоцентр прямоугольного треугольника, StudySmarter Originals
Тупоугольный треугольник
В тупоугольном треугольнике ортоцентр лежит вне треугольника.
Ортоцентр тупоугольного треугольника, StudySmarter Originals
Применение высоты
Вот несколько применений высоты в треугольнике:
- В первую очередь высота применяется для определения ортоцентра этого треугольника.
- Высоту также можно использовать для расчета площади треугольника.
Высота над уровнем моря — основные выводы
- Отрезок, перпендикулярный вершине к противоположной стороне (или линии, содержащей противоположную сторону), называется высотой треугольника.
- Каждый треугольник имеет три высоты, и эти высоты могут лежать снаружи, внутри или на стороне треугольника.
- Высота разностороннего треугольника:.
- Высота равнобедренного треугольника:.
- Высота прямоугольного треугольника:.
- Высота равностороннего треугольника:.
- Все три высоты треугольника совпадают; то есть они пересекаются в точке, называемой ортоцентром.
свойства равностороннего треугольника
Мастер 7 столбов школы успеха
Улучшение своих классов и снижение стресса
Common Core Standard 7.G.G.6
9Common Core 7.G.G.6
9Common Core 7.
9G.G.6
.
- Возьмем любой треугольник.
- Нарисуйте на сторонах этого треугольника равносторонние треугольники.
- Найдите центр этих трех равносторонних треугольников. (См. A, B, C)
- Соедините эти три центра, и они образуют равносторонний треугольник
Теорема Наполеона
Как найти периметр равностороннего треугольника видео..
Как найти периметр равностороннего треугольника?
Что такое периметр?
Каков периметр равностороннего треугольника со стороной 12 единиц?
Как найти периметр равностороннего треугольника, если известна только высота?
Если высота равностороннего треугольника равна 12 единицам, как найти периметр?
Related Sites
Triangles-Equilateral,Isosceles,Scalene
Constructing an Equilateral Triangle with a Compass
Pre-Algebra/Expressions,Equations,Integers
Pre-Algebra/Fractions,Percents
Algebra/Exponents,Equations,Radicals
Math Calculators
Geometry/Shapes
Geometry/SAT
Geometry/Plane
Good Study Habits
Геометрия/Основы
Задача 1.
Найдите периметр равностороннего треугольника со стороной, равной двенадцати единицам.
Шаг 1 . 3*12 = 36 единиц
Задача 2. Найти периметр равностороннего треугольника с высотой 12 единиц.
Шаг 1 . Найдите длину одной стороны. Высота создает треугольник 30-60-90. Высота становится длинной стороной треугольника 30-60-90.
Шаг 2 . Чтобы получить длину стороны, используйте
, что равно 12/√3
Для обзора 30-60-90 правил проверьте здесь
Шаг 3. 12/√3 = 4√3, который равен половине длины стороны равностороннего треугольника
Шаг 4. Чтобы получить всю длину, возьмите 2* 4√3 =8√3
Шаг 5. Теперь вы можете использовать 3 * длину стороны или 3* 8√3= 24√(3) единиц
Формула высоты равностороннего треугольника 0 906
Практические задачи с равносторонним треугольником
youtube.com/embed/haDCLQVHSGs?autoplay=0&color1=0x999999&color2=0xe8e8e8&wmode=transparent» allowfullscreen=»»>
Формула периметра равностороннего треугольника
Что такое равносторонний треугольник?
Свойства равностороннего треугольника
S = Длина боковой длины
Область из равностороннего треугольника
Уравновесительные триуулские формали
0035 Equilateral Formulas
0350035 Типы треугольников
Вы также можете насладиться …
Площадь треугольника
Внешние углы треугольников
Обнаружение площади треууурина
Все три сестра. Конгруэнтность просто означает, что они равны.
Все три угла также конгруэнтны, что также называется равноугольным.

Углы в равностороннем треугольнике в сумме составляют 180 градусов, и углы равны, поэтому мера угла равна 60 градусам.
Треугольники имеют три стороны и три угла, но что такое равносторонний треугольник ? В евклидовой геометрии особенности равностороннего треугольника заключаются в следующем.
s = длина стороны
Привет Добро пожаловать в MooMooMath.
Сегодня мы рассмотрим равносторонние треугольники. Я нарисовал два разных треугольника. Первый из них, который мы знаем, является равносторонним, потому что все три стороны отмечены конгруэнтными. Вы можете увидеть конгруэнтный символ (указывает на треугольник) или вы можете увидеть, что мера каждой стороны равна. Есть два способа показать, что разные стороны равны. На втором давайте посмотрим на него с точки зрения фактической меры углов. Мы знаем, что треугольник в сумме дает 180 градусов. Итак, если у нас есть три равных угла, мы возьмем их и разделим на три. Сто восемьдесят разделить на три равно шестидесяти. Следовательно, каждый из этих углов должен быть равен 60 градусам. Если три угла равны 60, то это равносторонний треугольник. Итак, давайте посмотрим на правила. Первое правило заключается в том, что все три стороны треугольника конгруэнтны, что означает, что они равны. Во-вторых, все три угла должны быть равны. Наконец, мера углов всегда будет 60 градусов. Надеюсь, это видео было полезным.

 Кроме того, равносторонняя фигура всегда является остроугольной. Далее необходимо перейти к доказательству теоремы о периметре.
Кроме того, равносторонняя фигура всегда является остроугольной. Далее необходимо перейти к доказательству теоремы о периметре. (½) сантиметров.
(½) сантиметров. Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
Когда все стороны фигуры равны, то их можно просто умножить на три. Допустим, дан правильный треугольник со стороной 5 см в таком случае: см
 2}=\sqrt{9+16}=\sqrt{25}=5$$
2}=\sqrt{9+16}=\sqrt{25}=5$$ Найти периметр треугольника.
Найти периметр треугольника.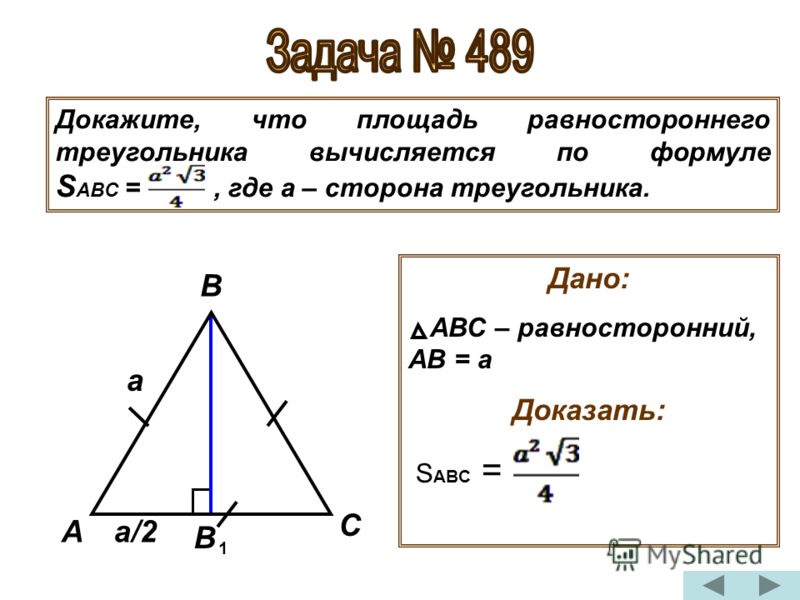
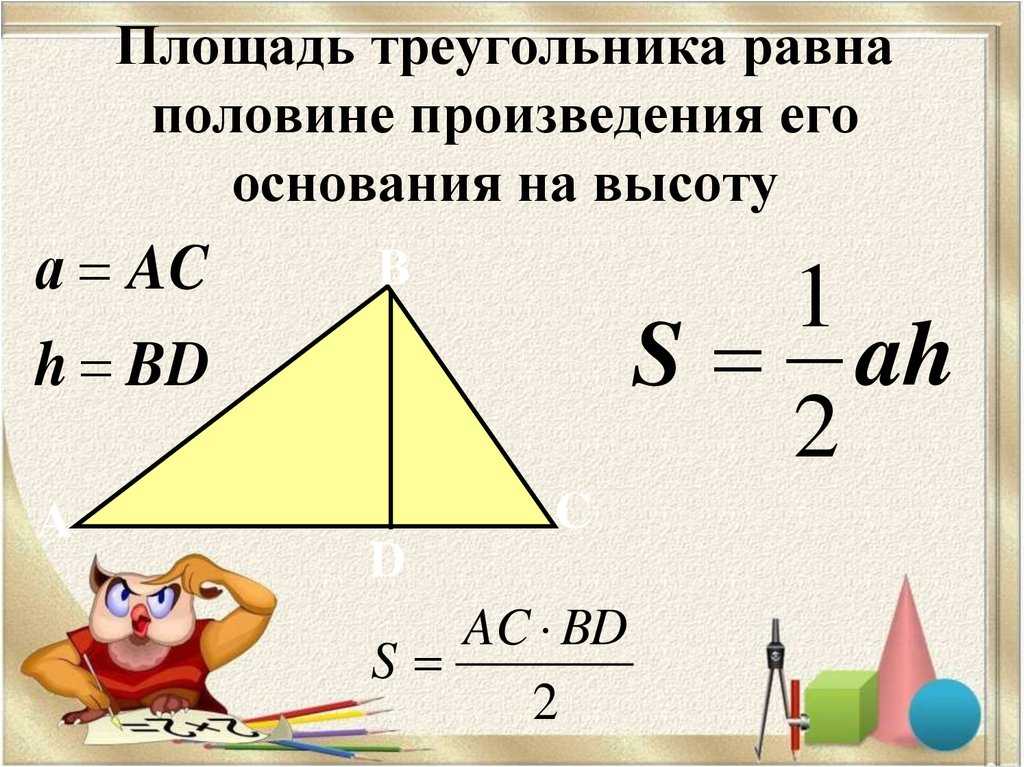
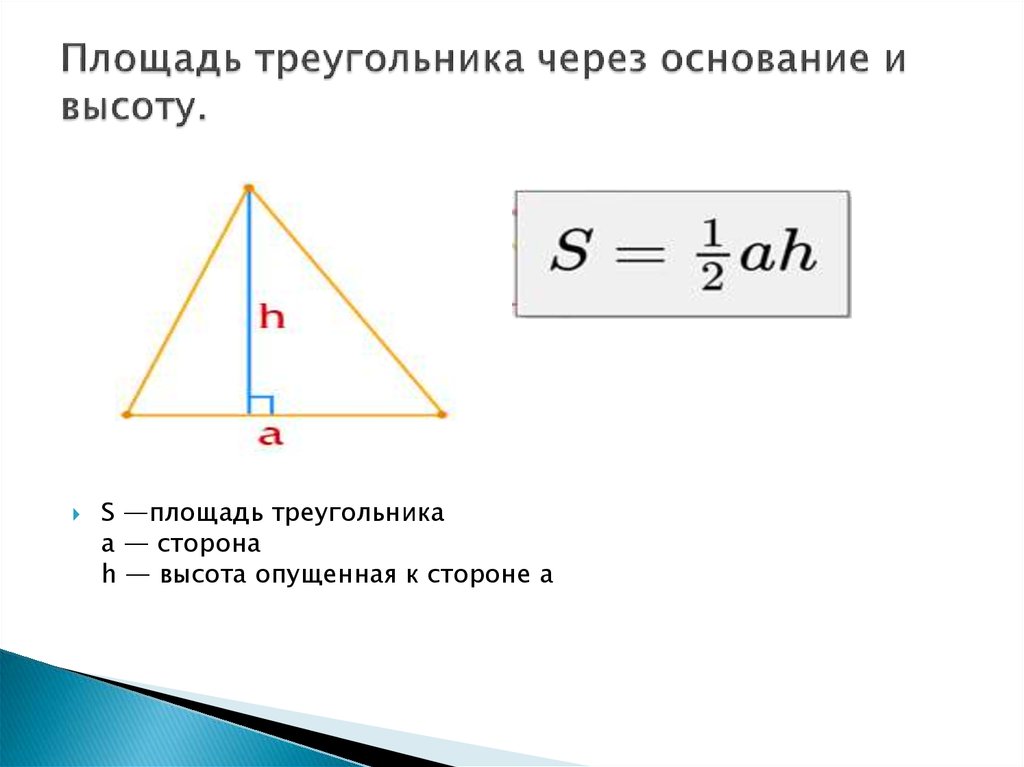 Значит для ΔABC площадь будет равна
Значит для ΔABC площадь будет равна Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
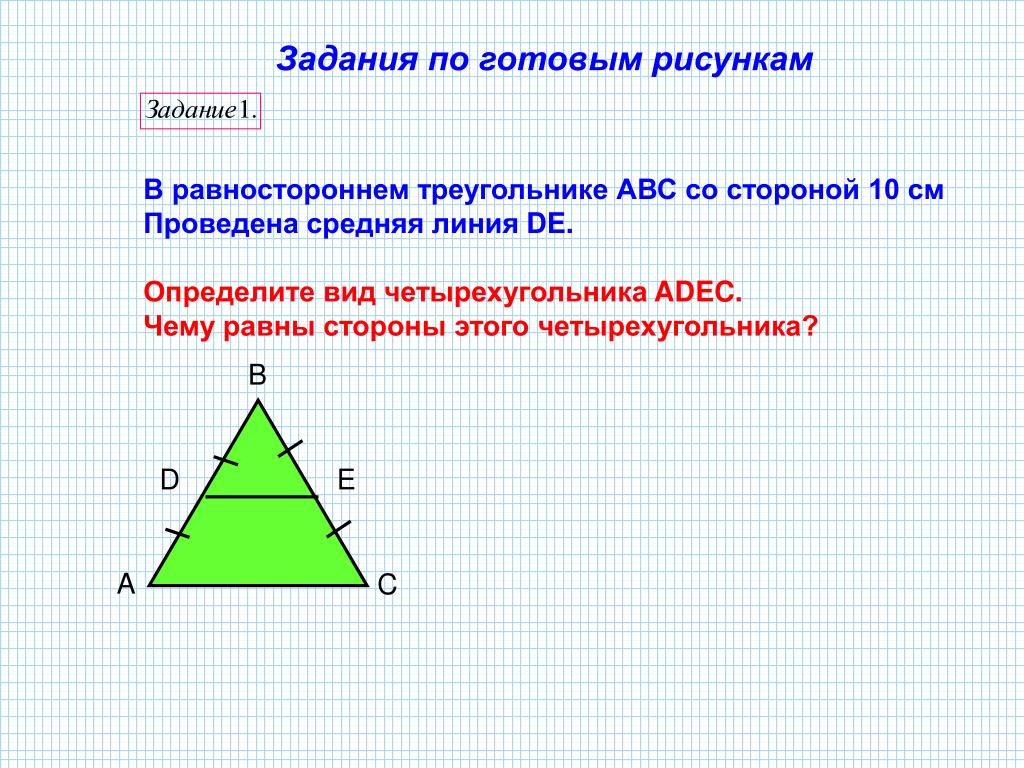
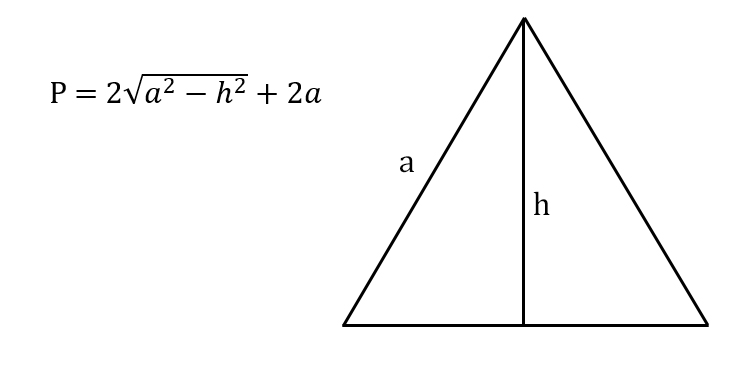

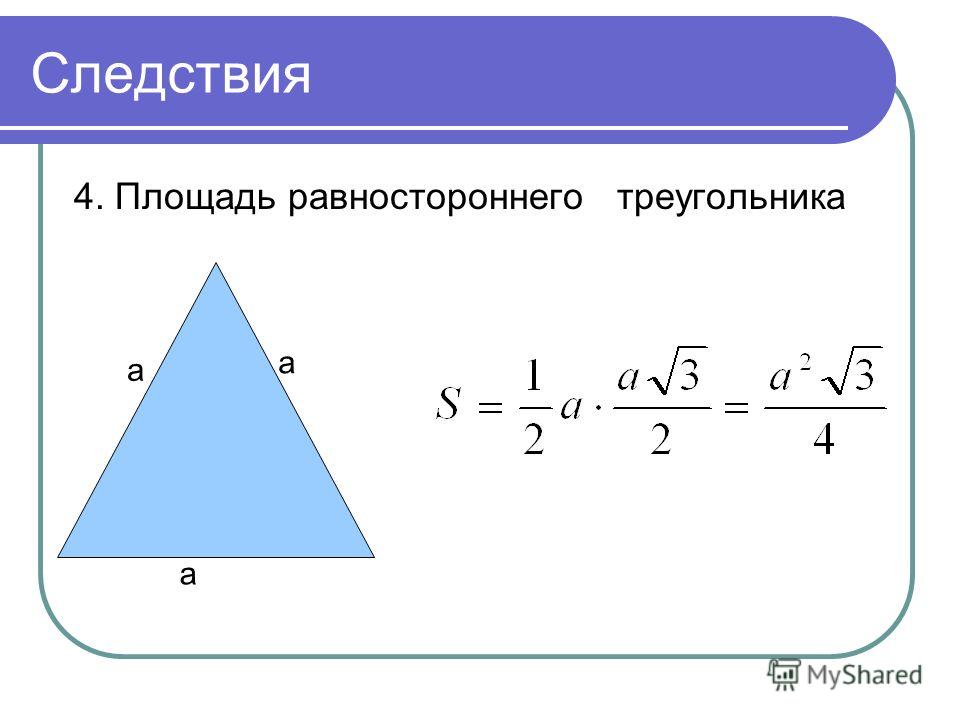

 Если дана боковая сторона, то половина основания будет равна , а само основание, соответственно, . Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим . Если дано основание, то по той же теореме Пифагора находим боковую сторону . Формула периметра равнобедренного треугольника через основание и высоту тогда принимает вид .
Если дана боковая сторона, то половина основания будет равна , а само основание, соответственно, . Подставив его в формулу для нахождения периметра равнобедренного треугольника, получим . Если дано основание, то по той же теореме Пифагора находим боковую сторону . Формула периметра равнобедренного треугольника через основание и высоту тогда принимает вид .
 Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте. Рассмотрим несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра.
Рассмотрим несколько задач на нахождение периметра равнобедренного треугольника. Задачи будем решать по мере возрастания сложности, это позволит лучше понять способ размышления, которому нужно следовать для нахождения периметра. нужно найти периметр треугольника.
нужно найти периметр треугольника. Попробуем решить по-другому.
Попробуем решить по-другому.
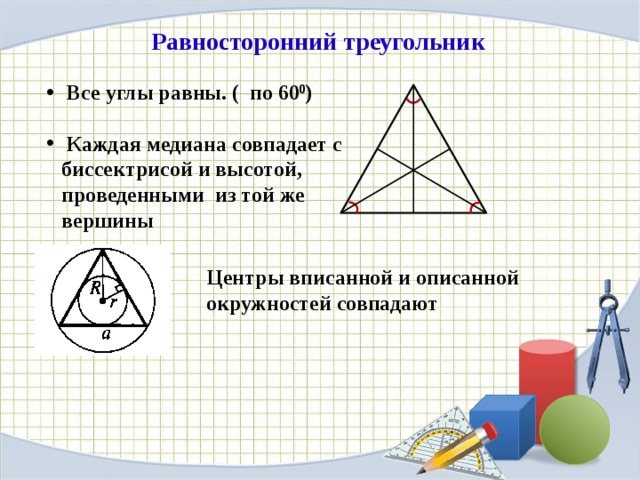 46 см? Следовательно, периметр равностороннего треугольника равен 6 см.
46 см? Следовательно, периметр равностороннего треугольника равен 6 см.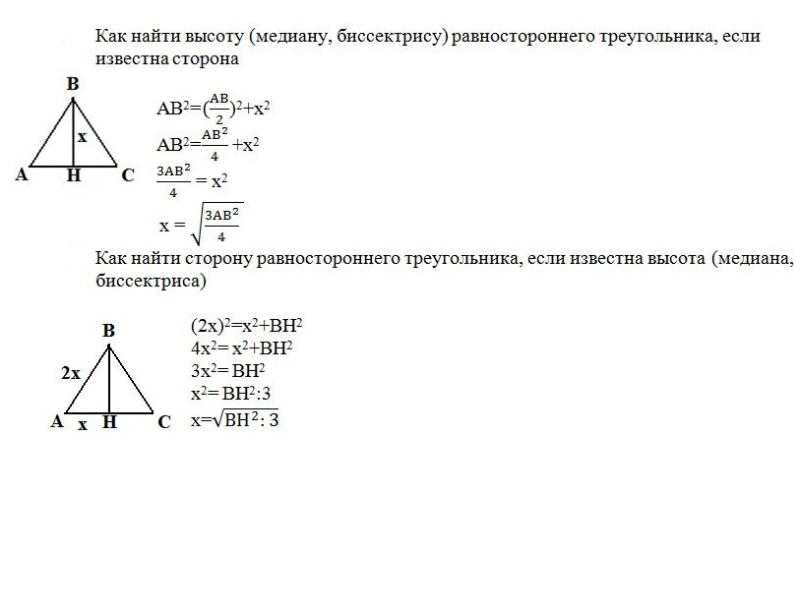
 392 см.
392 см. Значит сторона равностороннего треугольника равна 60 см. Площадь равностороннего треугольника определяется как Площадь = √34 × 2 где х — сторона равностороннего треугольника. Следовательно, площадь треугольника равна 1558.84 см2.
Значит сторона равностороннего треугольника равна 60 см. Площадь равностороннего треугольника определяется как Площадь = √34 × 2 где х — сторона равностороннего треугольника. Следовательно, площадь треугольника равна 1558.84 см2.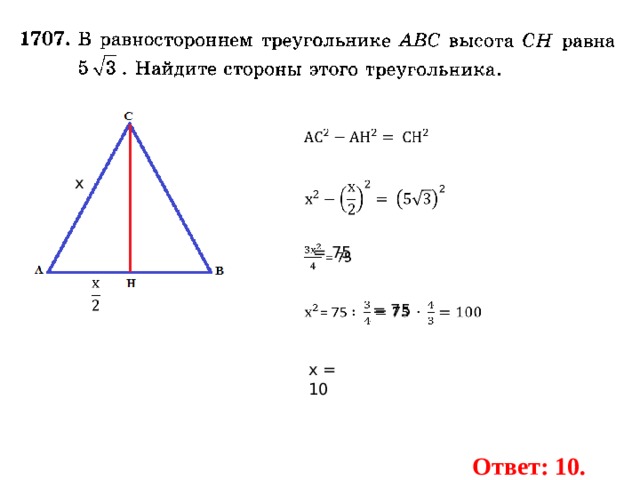 Находим периметр треугольника различными способами
Находим периметр треугольника различными способами

 Обозначим ее через $α$, тогда
Обозначим ее через $α$, тогда