Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тангенс tg x котангенс ctg x
Справочные данные по тангенсу (tg x) и котангенсу (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица тангенсов и котангенсов, производные, интегралы, разложения в ряды. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Геометрическое определение
Прямоугольный треугольник.|BD| – длина дуги окружности с центром в точке A.
α – угол, выраженный в радианах.
- Тангенс (tg α)
- – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине прилежащего катета |AB|.
- Котангенс (ctg α)
- – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине противолежащего катета |BC|.

, где n — целое.
, где n — целое.
Принятые обозначения
Тангенс
В западной литературе тангенс обозначается так:
.
Также приняты следующие обозначения:
;
;
.
Котангенс
В западной литературе котангенс обозначается так:
.
Также приняты следующие обозначения:
;
;
.
Графики функций тангенс, y = tg x, и котангенс, y = ctg x
Графики функций y=tg(x) и y=ctg(x).Свойства тангенса и котангенса
Периодичность
Функции y = tg x и y = ctg x периодичны с периодом π.
Четность
Функции тангенс и котангенс – нечетные.
Области определения и значений, возрастание, убывание
Функции тангенс и котангенс непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства тангенса и котангенса представлены в таблице (n — целое).
| y = tg x | y = ctg x | |
| Область определения и непрерывность | ||
| Область значений | –∞ < y < +∞ | –∞ < y < +∞ |
| Возрастание | – | |
| Убывание | – | |
| Экстремумы | – | – |
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | – |
Формулы
Выражения через синус и косинус
; ;
; ;
;
Формулы тангенса и котангенс от суммы и разности
Остальные формулы легко получить, например
Произведение тангенсов
Формула суммы и разности тангенсов
Таблица тангенсов и котангенсов
В данной таблице представлены значения тангенсов и котангенсов при некоторых значениях аргумента.
Выражения через комплексные числа
Выражения через гиперболические функции
;
;
Производные
; .
Производная n-го порядка по переменной x от функции :
.
Производная n-го порядка по переменной x от функции :
.
Вывод формул для тангенса > > >; для котангенса > > >
Интегралы
Разложения в ряды
Чтобы получить разложение тангенса по степеням x, нужно взять несколько членов разложения в степенной ряд для функций sin x и cos x и разделить эти многочлены друг на друга, . При этом получаются следующие формулы.
при .
при .
где Bn – числа Бернулли. Они определяются либо из рекуррентного соотношения:
;
;
где .
Либо по формуле Лапласа:
Обратные функции
Обратными функциями к тангенсу и котангенсу являются арктангенс и арккотангенс, соответственно.
Арктангенс, arctg
, где n — целое.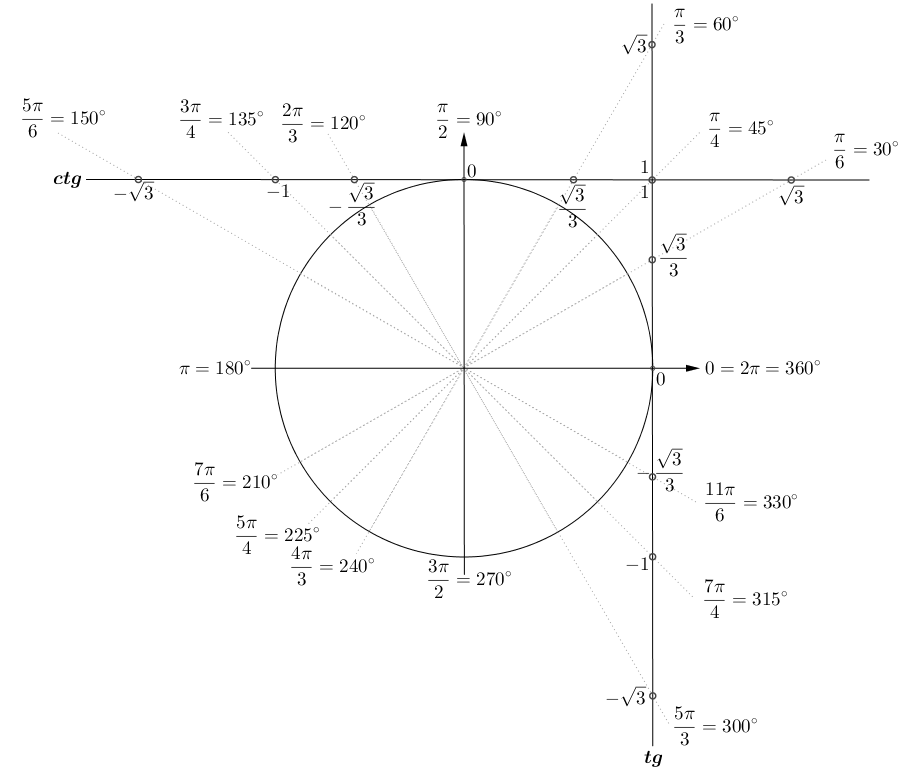
Арккотангенс, arcctg
, где n — целое.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Г. Корн, Справочник по математике для научных работников и инженеров, 2012.
Сумма тождеств: \[\begin{split}&\\&\sin{ \alpha}+\sin{\beta}=2\sin{\frac{\alpha +\beta}}{2}}\cos{\frac{\alpha -\beta}}{2}}\\\\\\ \\&\sin{\alpha}-\sin{\beta}=2\cos{\frac{\alpha+\beta}{2}}\sin{\frac{\alpha-\beta}{2}} \\\\\\\\&\ соз {\ альфа} + \ соз {\ бета} = 2 \ соз {\ гидроразрыва {\ альфа + \ бета} {2}} \ соз {\ гидроразрыва {\ альфа — \ бета {2}} \\\\\\\\&\cos{\alpha} -\cos{\beta}=-2\sin{\frac{\alpha +\beta}}{2}}\sin{ \frac{\alpha -\beta} {2}}\\\\\\\\&\text{tg}{\alpha}+\text{tg}{\beta}=\frac{\sin{\left ( \alpha +\beta \right )}}{\cos{\alpha}\cos{\beta}}\\\\\\\\&\text{tg}{\alpha}-\text{tg}{ \beta}=\frac{\sin{\left (\alpha -\beta \right)}}{\cos{\alpha}\cos{\beta}}\\\\\\\\&\text{ctg }{\alpha}+\text{ctg}{\beta}=\frac{\sin{\left (\beta +\alpha \right)}}}{\sin{\alpha}\sin{\beta}}\ \\\\\\\&\text{ctg}{\alpha}-\text{ctg}{\beta}=\frac{\sin{\left (\beta -\alpha \right)}}{\sin {\alpha}\sin{\beta}}\\\\\\\\&\cos{\alpha}+\sin{\alpha}=\sqrt{2}\sin{\left ( 45^\circ + \alpha \right )}=\sqrt{2}\cos{\left ( 45^\circ -\alpha \right )}\\\\\\\\&\cos{\alpha} -\sin{\alpha } = \ sqrt {2} \ cos {\ left ( 45 ^ \ circ + \ alpha \ right )} = \ sqrt {2} \ sin {\ left ( 45 ^ \ circ — \ alpha \ right )} \\\ \\конец{разделить}\] Идентификаторы продуктов: \[\begin{split}&\\&\sin{\alpha}\sin{\beta}=\frac{1}{2}\left [\cos{\left (\alpha -\ бета \ справа ) — \ соз {\ влево ( \ альфа + \ бета \ справа )}} \ справа ] \\\\\\& \ соз {\ альфа} \ соз {\ бета} = \ гидроразрыва {1} { 2}\left [\cos{\left (\alpha -\beta\right)+\cos{\left (\alpha +\beta \right)}} \right]\\\\\\&\sin{\ альфа} \ cos {\ бета} = \ гидроразрыва {1} {2} \ влево [ \ грех {\ влево ( \ альфа — \ бета \ вправо) + \ грех {\ влево ( \ альфа + \ бета \ вправо)} } \right ]\\\\\\\end{split}\] Другие формулы: 92{\alpha}=\cos{\left (\alpha +\beta\right)}\cos{\left (\alpha -\beta \right)}\\\\\end{split}\]
Предыдущий тема
Геометрия
Следующая тема
Предел последовательности
Онлайн калькулятор: Тригонометрические функции
Учеба Математика 070 Геометрия 9003 07070 07070 2 Этот онлайн-калькулятор вычисляет значения элементарных тригонометрических функций, таких как как sin, cos, tg, ctg, sec, cosec для угла, который может быть установлен в градусах, радианах или градах.
Тригонометрические функции представляют собой набор элементарных функций, связывающих углы треугольника с длинами сторон треугольника. Их также называют циклическими функциями. Смотрите картинку.
Тригонометрические функции: поле 0119 и получаем таблицу результатов. Угол может быть введен в градусах, радианах, градах, минутах или секундах. Единицы Градусы Радианы Минуты Секунды Точность вычислений Число знаков после запятой: 10 Файл очень большой.
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс 8008 косек — косеканс
версин — версин ( с синусоидой)
vercos — веркосинус (обратный косинус)
haversin — обратный синус
exsec — exsecant
excsc — exsecant3
Тригонометрические функции


 Шпаргалки. Детский сад, Школа. / / Тригонометрические функции тангенс и котангенс tg и ctg. Свойства. Основные формулы, формулы кратных и половинных аргументов, сложения, преобразования суммы в произведение, преобразования произведения в сумму
Шпаргалки. Детский сад, Школа. / / Тригонометрические функции тангенс и котангенс tg и ctg. Свойства. Основные формулы, формулы кратных и половинных аргументов, сложения, преобразования суммы в произведение, преобразования произведения в сумму Тригонометрические функции тангенс и котангенс tg и ctg:
Тригонометрические функции тангенс и котангенс tg и ctg: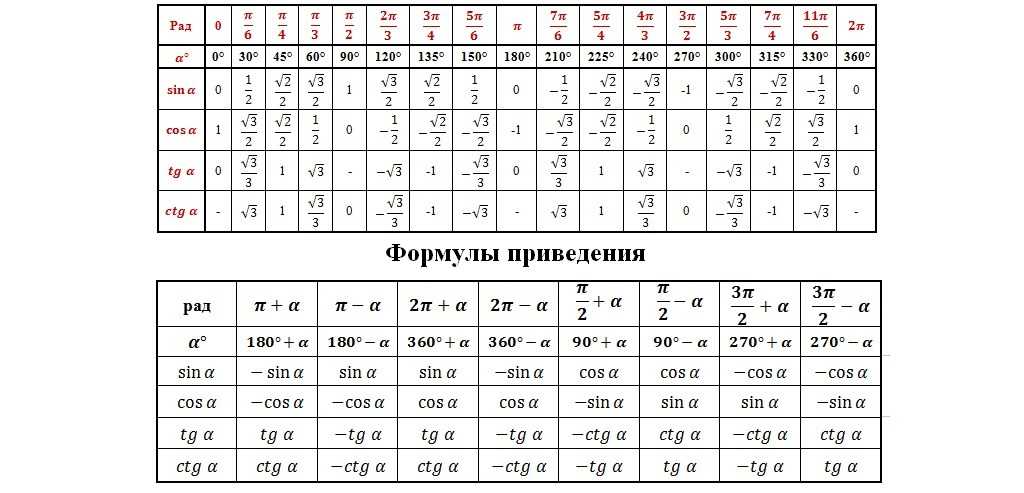 Введите свой запрос:
Введите свой запрос: