Ц из н по к формула: Число сочетаний — Онлайн калькуляторы

Как определить формулу вещества

Способов, как определить формулу вещества, достаточно много. Все зависит от исходных данных. Наиболее разнообразны подобные вычисления в органической химии. И это не удивительно, так как органических соединений значительно больше, чем неорганических.

Содержание:

1.Понятие простейшей и истинной формулы вещества

2.Массовая доля химического элемента: что означает и как высчитывается

3.Как определить формулу вещества по массовым долям элементов

4.Как определить формулу органического соединения:

4.1. по общей формуле вещества

4.2. по продуктам сгорания вещества

5. Как определить формулу вещества: комбинированные задачи

1.Понятие простейшей и истинной формулы вещества

В одних задачах на определение формулы вещества необходимо найти его простейшую формулу, а в других – истинную. В чем разница?

Простейшая, или иными словами, эмпирическая формула, указывает на соотношение атомов в молекуле (или в формульной единице, если речь идет о не ковалентном соединении).

Так, например: СН₂ – простейшая формула алкена – показывает, что на каждый 1 атом углерода приходится 2 водородных атома. То есть существует соотношение 1:2. Поэтому для нахождения простейшей (эмпирической) формулы вещества важно рассчитать количество вещества атомов, которые входят в его состав, то есть n(C) и n(H).

Истинная формула, или иначе молекулярная, отражает действительное количество атомов всех элементов в молекуле.

Например, для пропилена, относящегося к классу алкенов, истинная (молекулярная) формула будет C₃H₆. Она говорит о том, что молекула данного вещества включает 3 атома С и 6 атомов Н. Это вполне соответствует простейшей формуле, отвечающей соотношению атомов 1:2. Для нахождения истинной (молекулярной) формулы соединения требуется посчитать его относительную молекулярную (Mr) или молярную массу (M).  

2.

Массовая доля химического элемента: что означает и как высчитывается

Массовая доля – это отношение массы компонента системы к массе системы, выраженное в процентах или долях от единицы.

Ну, а теперь проще.

Молекула имеет массу. Все атомы в молекуле также имеют свои массы. Атомов одного химического элемента в молекуле может быть 1 или несколько. Важна масса всех атомов одного элемента. Если ее разделить на массу молекулы, то получится массовая доля этого элемента. Ее выражают либо в процентах, которые всегда меньше 100%, либо в долях от единицы, которые всегда меньше 1.

Массовая доля элемента обозначается греческой буквой «омега» — ω. И записывается, например, так: ω(Н), ω(Сl), ω(С) и т.д. и рассчитывается: 

Пример 1. Каковы массовые доли элементов в оксиде железа (III) Fe₂O₃.

3.Как определить формулу вещества по массовым долям элементов

Нахождение формулы вещества по массовым долям элементов применимо как к органическим, так и к неорганическим соединениям.

Пример 2. Сероуглерод содержит 15,8% углерода по массе. Какова  простейшая формула этого вещества?

Поскольку речь идет о массовых долях элементов, то необходимо знать массу вещества. В нашем случае – массу сероуглерода. В условии задачи о ней ничего не говорится. Поэтому допускаем, что масса вещества равна 100 г.

Почему 100 г? Это «круглое» число, и его использование облегчает все расчеты. Так как в итоге будем находить соотношения количеств веществ элементов, то какое-то особенное значение массы вещества не играет никакой роли.

Попробуйте ради эксперимента принять массу сероуглерода равной 23 г, 467 г и т.п. Результат будет один и тот же.

Допустим, что атомов углерода в молекуле х, а атомов серы – у. В таком случае формула вещества примет вид: С_хS_у.

Пример 3. Содержание углерода в углеводороде составляет 83,33%. Плотность паров соединения по водороду – 36. Какова молекулярная формула углеводорода?

Из данных задачи следует, что углеводород может находиться в газообразном состоянии, так как известна плотность его паров. Эта величина всегда требуется для нахождения молярной (относительной молекулярной) массы вещества. Как она находится и что это такое читайте подробнее здесь.

Чтобы не загромождать записи, массовую долю элементов будем считать не в процентах, а в долях от единицы.

Пусть вас не удивляет получившаяся простейшая формула. Ведь, исходя из определения простейшей формулы, на каждый 1 атом углерода приходится 2,4 атома водорода. Это всего лишь соотношение. Соединения с формулой СН_2,4 в принципе не существует. Не всегда простейшая и истинная формулы совпадают друг с другом.

А если полученная формула СН_2,4 вас все же смущает, вы можете решать задачу и вторым способом. Но это несколько более сложный способ, когда требуется составить и решить уравнение с двумя неизвестными.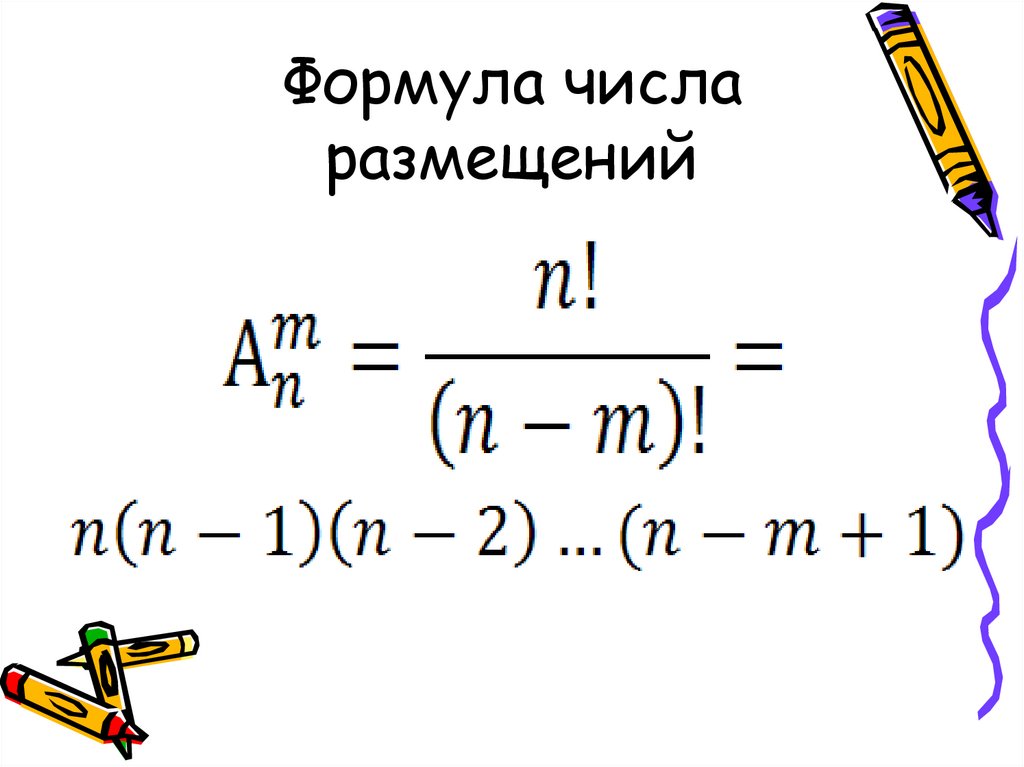

Не все химические вещества являются бинарными, то есть состоят из атомов двух химических элементов. Но в любом случае, алгоритм решения задачи тот же.

Пример 4. Некоторая кислота содержит водород (2,2%), иод (55,7%) и кислород (42,1%). Определите простейшую формулу этой кислоты.

4.Как определить формулу органического соединения

Определить формулу органического вещества можно не только зная массовые доли элементов в его составе.

4.1. Как определить формулу органического соединения

по общей молекулярной формуле вещества

Органические вещества сгруппированы по самостоятельным классам на основе общности строения и свойств. Каждый класс соединений характеризуется своей общей молекулярной формулой. Особенно это наглядно видно на примере углеводородов.

Если другие органические вещества рассматривать как их производные, в молекулы которых введена какая-либо функциональная группа, то и для них также можно составить общую молекулярную формулу.

К слову, метан СН₄ является представителем алканов, в молекулах которых на n атомов углерода и приходится 2n+2 атомов водорода. Алканы имеют общую молекулярную формулу, отражающую их состав: С_nH_2n+2.

Предельные одноатомные спирты можно рассматривать как производные алканов, в молекулах которых 1 атом водорода замещен на гидроксильную группа –ОН. Таким образом, их общая молекулярная формула такая: С_nH_2n+1ОН.

Ниже в таблице приведены общие молекулярные формулы основных классов органических соединений.

Разберем примеры решения задач с использованием общей молекулярной формулы вещества.

Пример 5. Плотность паров по воздуху некоторого алкана 4,414. Какова формула алкана?

4. 2. Как определить формулу органического соединения

по продуктам его сгорания

Это еще один распространенный тип задач на определение формулы органического соединения.

Необходимо запомнить и понять основные моменты:

— так как все органические вещества содержат  атомы С, Н, а также атомы О (кислородсодержащие соединения), то всегда при их сгорании выделяется углекислый газ СО₂ и образуется вода Н₂О;

— все углеродные атомы, входящие в состав органического соединения, окажутся в составе углекислого газа СО₂; следовательно, n(С) как в  соединении, так и в СО₂ – это одна и та же величина;

— все атомы водорода Н, которые имеются в составе вещества, перейдут в состав воды Н₂О; следовательно, n(Н) и в данном веществе, и в Н₂О – это одна и та же величина;

— при сгорании веществ, включающих в себя азот (например, амины), кроме СО₂ и Н₂О, образуется еще и N₂.

Разберем несколько примеров.

Пример 6. Сожгли 7,2 г углеводорода. Плотность его паров по водороду составляет 36. В результате реакции образовалось 22 г оксида углерода (IV)  и 10,8 г воды. Какова молекулярная формула соединения?

Пример 7. В результате сгорания 4,8 г органического соединения выделилось 3,36 л (н.у.) оксида углерода (IV) и образовалось 5,4 г воды. Плотность паров искомого соединения по кислороду равна 1. Вычислите молекулярную формулу вещества.

Пример 8. Результатом сжигания 0,31 г газообразного органического соединения, имеющего плотность  1,384 г/л, стало выделение 0,224 л (с.у.) оксида углерода (IV), 0,112 л азота и образование 0,45 г воды.  Вычислите молекулярную формулу этого вещества.

5. Как определить формулу вещества: комбинированные задачи

Наибольший интерес и некоторую трудность представляют комбинированные задачи, сочетающие в себе необходимость найти формулу соединения:

— используя приемы, применяемые в рассмотренных выше задачах;

— используя сведения не только о химических, но и физических свойствах вещества.

Вот несколько примеров.

Пример 9. Какова молекулярная формула предельного углеводорода,  при полном  сгорании 8,6 г которого выделилось 13, 44 л (н.у.) оксида углерода (IV).

В этой задаче:

1) известен класс вещества, поэтому возможно применить его общую молекулярную формулу;

2) речь идет о сгорании вещества, поэтому количество атомов в составе молекулы будем искать, используя данные о продукте сгорания – СО₂.

Пример 10. Алкен нормального строения содержит двойную связь при первом углеродном атоме. Образец этого алкена массой 0,7 г присоединил бром массой 1,6 г. Вычислите формулу алкена и назовите его.

В предлагаемых условиях:

1) известен класс вещества, следовательно, применим его общую молекулярную формулу;

2) речь идет об одном из химических свойств: способности алкенов присоединять галогены по месту разрыва двойной связи.

Пример 11. После полного сжигания в кислороде арена, имевшего массу 0,92 г, выделился оксид углерода (IV). Пропуская газ через избыток раствора щелочи Ca(OH)₂, получили 7 грамм осадка. Какова молекулярная формула арена?

В предлагаемой задаче:

1) известен класс вещества;

2) речь идет о сжигании соединения и образовании в качестве продукта горения углекислого газа, который при взаимодействии со щелочью Са(ОН)₂ привел к выпадению осадка известной массы.

Следующий пример очень характерен для задач, встречающихся в заданиях второй части ЕГЭ по химии.

Пример 12.  Некоторое соединение, образующее альдегид в реакции окисления, взаимодействует с избытком бромоводородной кислоты, образуя 9,84 г продукта (выход составляет 80% от теоретического), имеющего плотность паров  по Н₂ 61,5. Определите строение этого соединения, а также его массу, вступившую в реакцию?

В этой задаче:

1)  говорится о химических свойствах искомого соединения; анализируя их, приходим к выводу, что заданным веществом является предельный одноатомный спирт;

2) известна общая молекулярная формула предельных  одноатомных  спиртов;

3) более подробно говорится о взаимодействии заданного вещества с бромоводородной кислотой; спирт, реагируя с HBr, дает галогеналкан, для которого известны его масса, практический выход и относительная плотность по Н₂; именно от этих данных и нужно отталкиваться при решении данной задачи.

Итак, способов, как определить формулу вещества, действительно, множество. Мы рассмотрели лишь основные из них. Важно правильно уяснить понятия «простейшая формула вещества» и «истинная формула вещества», чтобы не путать их.

Чтобы самыми первыми узнавать о новых публикациях на сайте, присоединяйтесь к нашей группе ВКонтакте.

 

 

Одоризация газа — Что такое Одоризация газа ?

Этилмеркаптан С2Н5SН — наиболее распространенный одорант, бесцветная прозрачная жидкость

Одоризация — это придание природному газу специфического запаха с помощью специальных компонентов для своевременного обнаружения возможных утечек.

Природный газ не имеет цвета и запаха, что затрудняет обнаружение его утечек.
Добавление резкого и неприятного, предупреждающего запаха в природный газ упрощает обнаружение утечек.
Резкий запах должен ощущаться носом человека уже при небольшой объемной концентрации добавленного вещества, начиная с уровня от 20% нижнего порога образования взрывоопасной концентрации.  

Одоризация не изменяет физико-химические свойства природного газа.
Для этой цели используются одоранты — вещества:

• физиологически безвредные, 
• неагрессивные по отношению к металлам и материалам газовых сетей и приборов, 
• инертные к составным частям природного газа. 

Наиболее известны одоранты сернистых соединений:

• этилмеркаптан С₂Н₅SН — наиболее распространенный одорант, бесцветная прозрачная жидкость;
• метилмеркаптан; 
• пропилмеркаптан; 
• каптан; 
• сульфан. 



Типы одорантов

Тетрагидротиофен (THT) —  циклический сульфид.
Один из самых стойких к окислению от трубопроводов одорантов.
Имеет среднюю интенсивность запаха.
Формула: C₄H₈S
Молекулярная масса: 88. 172
Регистрационный номер химсоединения по классификации CAS: 

110-01-0
Относительная плотность: 1.000
Точка кипения: 115 — 124 °C
Точка замерзания: -96°C
Температура вспышки: -7 °C
Содержание серы: 36.37 (вес %)


Димитилсульфид (DMS) — характеризуется хорошей устойчивостью к окислению.
Запах схож с запахом чеснока. 
Обычно используется, как примесь к тетрагидротиофену.
Формула: C₂H₆S
Молекулярная масса: 62.135
Регистрационный номер химсоединения по классификации CAS 75-18-3
Относительная плотность 0.8
Точка кипения 37 °C
Точка замерзания -98°C
Температура вспышки -38 °C
Содержание серы 51.61 (вес %)

Этилмеркаптан (EM) — классический одорант, применяемый на территории РФ.


Норма одоризации газа составляет 16 г/1000м³
Формула C₂H₆S
Молекулярная масса 62.135
Регистрационный номер химсоединения по классификации CAS 75-08-1
Относительная плотность 0.839
Точка кипения 34 — 37 °C 31
Точка замерзания -148 -121°C
Температура вспышки -48 °C
Содержание серы 51.61 (вес %)

Метилакрилат (MA) и Этилакрилат (EA) — не серосодержащие одоранты, экологически чистые, но более дорогие.
Формула C₄H₆O и C₅H₈O₂
Молекулярная масса

86.0892 и 100.1158
Регистрационный номер химсоединения по классификации CAS 96-33-3 и 140-88-5
Относительная плотность 0. 9535 – 0.9574 0.9
Точка кипения 78 — 81 °C и 99 — 100 °C
Точка замерзания -75°C и -72°C
Температура вспышки -3 °C и 8.3 °C
Содержание серы (вес %) 32



Смеси одорантов

Делятся на 4 основные категории:
меркаптановые смеси; 
Меркаптан / алкилсульфидные смеси; 
Тетрагидротиофен / меркаптановые смеси; 
Смеси акрилатов (без серы). 
Смешивание одорантов  позволяет достичь или улучшить определенные свойства одоранта.

Одоранты, применяемые в России

этилмеркаптан. Из-за химической нестабильности окисляется в газопроводах с образованием дисульфида, который имеет меньшую интенсивность запаха;


смесь природных меркаптанов (СПМ), используемая с 1984 г, на большинстве газораспределительных станциях России. Производится в Оренбурге по ТУ 51-31323949- 94-2002. . Состав смеси: Этилмеркаптан < 44%,  Изопропилмеркаптан 31 %, Бутилмеркаптан 11%, Н-пропилмеркаптан 6 %, Трет-бутилмеркаптан  5 %, Н-бутилмеркаптан 1,5 %, Тетрогидротиофен  1,5 %.
Физико-химические свойства, которыми должны обладать одоранты:
• химическая стабильность, отсутствие реакции с газовыми компонентами; 
• высокое давление конденсации пара; 
• не должен оказывать коррозионного воздействия на технологическое оборудование в применяемых концентрациях; 
• стойкость и резкость запаха выше тяжелых гомологов метана; 
• не должен содержать воду, не должен окислять стенки газопроводов.
• Одоризацию проводят на газораспределительных станциях (ГРС) непосредственно перед подачей газа потребителям.

Одоризация — важная операция технологического процесса на ГРС, поскольку может предупредить утечку и связанные с ней аварийные ситуации. 
Специальные Блоки одоризации (БО) на ГРС обеспечивают подачу одоранта пропорционально расходу газа по установленным нормам.
Норма добавления реагента в природный газ: 16 г/1000 м³ (при температуре 0°С и давлении 760 мм.рт.ст.).
Годовое потребление одорантов — тысячи тонн.
Блоки одоризации на ГРС работают в ручном и автоматическом режимах.
Основные  типы БО на ГРС:

• капельные БО, где реагент подается в газопровод в виде капель или тонкой струи;
• барботажные БО, которые работают по принципу насыщения отведенного потока газа парами одоранта в барботажной камере и затем смешения его с основным потоком в газопроводе.

Хранение одорантов:

• на складах — в контейнерах заводского изготовления на открытых площадках;
• непосредственно на ГРС — в подземных или надземных металлических емкостях, связанных технологическими линиями с БО.

История

Впервые одоризацию газа, применив этилмеркаптан, для определения утечек в гидравлическом контуре использовал Фон Квальо в Германии в 1880^х гг.
Широкое внедрение техпроцесса одоризации началось в 1930

х гг. в Англии, когда после крупной аварии, произошедшей из-за утечки газа было разрушенное здание и погибло 319 человек. В результате этого несчастного случая, после Англии, проводить одоризацию газа начали в Канаде и США.
Ныне одоризация горючих газов применяется во всем мире.

N Формула выбора K — GeeksforGeeks

Комбинация описывается как процесс выбора одного, двух или нескольких элементов из заданной последовательности, независимо от порядка их появления. Если вы выберете два компонента из серии, которая содержит только два элемента, для начала порядок этих элементов не будет иметь значения.

Формула комбинации

При выборе r элементов из n элементов в последовательности число комбинаций равно

ⁿ C _k = 

Например, пусть n = 5 и r = 2, тогда количество способов выбрать два компонента из набора из пяти = ⁵ C ₂ = 5! / 2! (5 – 2)! = 10.

Стоит отметить, что если из набора n компонентов нужно получить r число комбинаций, и такие элементы могут повторяться, то

^n+r−1 C _r = ^n+r−1 C _n−1

Аналогичные задачи

Вопрос 1. Сколько двоичных строк длины 5 содержат ровно две единицы где-то в строке?

Решение:

Обратите внимание, что порядок битов в данном случае не важен, потому что нас интересует количество единиц в указанной строке, а не их порядок. Таким образом, нам нужно применить концепцию комбинаций, чтобы найти требуемое значение.

Здесь n = 5 и r = 2.

C(5, 2) = 

= 10

Итак, существуют 10-битные строки длины 5, содержащие ровно две единицы.

Вопрос 2. Найдите сколькими способами можно составить комиссию из пяти человек, если их нужно выбрать из группы из 7 мужчин и 6 женщин так, чтобы в ней было не менее 3 мужчин.

Решение:

По крайней мере три человека в комитете означает, что в комитете может быть ровно три, четыре или все пять человек.

Количество мероприятий, когда в комитете 3 мужчины и 2 женщины = ( ⁷ C ₃ × ⁶ C ₂ ) = 525

Количество мероприятий, когда в комитете 4 мужчины и 1 женщина комитет =  ( ⁷ C ₄ × ⁶ C ₁ ) = 210

Количество расстановок, когда все 5 человек входят в комитет = ( ⁷ C _{5 9002 = Всего договоренностей = 525 + 210 + 21}

= 756

Вопрос 3. Найдите количество расстановок букв в слове ВЕДУЩИЙ, при котором гласные всегда стоят вместе?

Решение:

Если гласные появляются вместе, они образуют в слове отдельную букву. Следовательно, у нас осталось 4 + 1 = 5 букв, которые можно расположить в 5! = 120 способов.

Более того, их 3! = 6 способов расположить гласные вместе.

Общее количество способов расположения букв = 120 × 6 = 720,

Вопрос 4. Найдите количество слов с 4 согласными и 3 гласными, которые можно составить из 8 согласных и 5 гласных.

Решение:

Количество способов выбора 4 согласно 10 = 700

Количество способов расположения 7 букв между собой = 7! = 5040

Количество слов, которые можно составить = 5040 × 700 = 3528000.

Вопрос 5. Сколько битовых строк длины 8 имеют одинаковое количество нулей и единиц?

Решение:

Вы выбираете из набора из восьми символов {1, 1, 1, 1, 0, 0, 0, 0} (что обычно дает 8! = 40320 вариантов, но у вас есть три одинаковых «1» и три одинаковых «0», что уменьшает количество вариантов до

= 

= 70-битных строк

Вопрос 6. Сколько 8-битных строк имеют по крайней мере два последовательных О или две последовательные единицы?

Решение:

8-битная строка может представлять все числа от 0 до 28 = 256.

Два последовательных нуля могут начинаться с позиции 1, 2, 3, 4, 5, 6 или 7.

Начиная с позиции 1: Строки вида [0 0 x x x x x x]

Оставшиеся 6 позиций можно расположить 26 = 64 способами.

Начиная с позиции 2: Строки вида [1 0 0 x x x x x x]

Оставшиеся 5 позиций можно расположить 25 = 32 способами.

Аналогичным образом количество позиций 3, 4, 5, 6 и 7 становится равным 32 каждая.

Количество способов = 64 + 32 + 32 + 32 + 32 + 32 + 32 + 32 – 10

= 246

Также количество строк, начинающихся с 2 последовательных единиц = 246

Таким образом, требуемое значение = 246 + 246 = 492

Вопрос 7. Сколько восьмибитных строк содержат не менее двух нулей подряд?

Решение:

Общее количество 8-битных строк (поскольку вы говорите о «строках», я предполагаю, что ведущие нули допустимы) = 256

Общее количество строк, где у нас нет последовательного 0S = ⁹ C ₀ + ⁸ C ₁ + ⁷ C ₂ + ⁶ C ₃ + ^{5 5 5 5 5 5 5 5 5 C ₃ + 5 5 6 C ₃ + + 6 C _{3 + + 6 C 3 + + 6 C 3 + + 6 C 3 .} C ₄}

= 55

Количество 8 -битных строк, где мы имеем последовательное 0 S = 256 — 55

= 201

Паскал, папская формула, формула биографии, биография

. Треугольник, формула Паскаля, биномиальная теорема и биномиальные разложения Формула Паскаля
Биномиальная теорема и биномиальные расширения

Треугольник Паскаля

n

C _r имеет математическую формулу: _n C _r n = 90! / (( n — r )! r !), см. теорему 6.4.1. Ваш калькулятор, вероятно, также имеет функцию расчета биномиальных коэффициентов. Но для малых значений проще всего определить значение нескольких последовательных биномиальных коэффициентов с помощью треугольника Паскаля:

n = 0	1
n = 1	1   1
n = 2	1   2   1
n = 3	1   3   3   1
n = 4	1   4   6   4   1
n = 5	1   5   10   10   5   1

Обратите внимание на симметрию, кроме начальной и конечной единиц, каждый член представляет собой сумму двух указанных выше членов.

Снова рассмотрим треугольник Паскаля, в котором каждое число получается как сумма двух соседних чисел в предыдущей строке. То, как записи построены в таблице, дает формулу Паскаля:

Теорема 6.6.1 Формула Паскаля top
Пусть n и r — положительные целые числа, и пусть r n . Затем

Пример 6.6.5 Получение новых формул из формулы Паскаля
Используйте формулу Паскаля, чтобы вывести формулу для _n +2C _r через _n C _{r 70017} , , , 0255 C _R — 1, _N C _R — 2, где N и R — это неотрицательные integers и 2 R 55555555555555555555555555555 года.
Решение: по формуле Паскаля

.

N

+ 2C _R = _{N + 1} C _{R — 1} + _N + 1C 7.

Снова применяя формулу Паскаля к каждому члену в правой части (RHS) этого уравнения,

N

+ 2C _R = _N C _{R — 2} + _N C _R —
6 — _{— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — . н} С _р ,

для всех неотрицательных целых чисел n и r таких, что 2 r n + 2,
Используйте эту формулу и треугольник Паскаля, чтобы убедиться, что ₅ C ₃ = 10.

5

С ₃ = ₃ С ₁ + 2( ₃ С ₂ ) + ₃ С 3

5

С ₃ = 3 + 2(3) + 1 = 10.

Можем ли мы использовать эту новую формулу для вычисления ₅ C ₄ ?

Теперь используйте эту формулу для вычисления значения ₇ C ₅ .

7

С ₅ = ₅ С ₃ + 2( ₅ С ₄ ) + ₅ С 5

7

С ₅ = 10 + 2(5) + 1 = 21.

Бином — многочлен, состоящий из двух членов. Быстрый метод возведения бинома в степень можно изучить, просто взглянув на шаблоны, связанные с биномиальными разложениями. Для начала рассмотрим разложение ( x + y ) ⁿ для нескольких значений n .

( х + у ) ⁰ = 1

( х + у ) ¹ = х + у

( х + у ) ² = х ² + 2 ху + у ² 9

( x + y ) ³ = x ³ + 3 x ² Y + 3 xy ^{29. 0015 + у 3}

( x + y ) ⁴ = x ⁴ + 4 x ³ y + 6 x ² y ² + 4 xy ³ + у ⁴

( x + y ) ⁵ = x ⁵ + 5 x ⁴ Y + 10 X 5 ^{3 Y + 10 X 3 Y + 10 x 3 Y + 10 x 3 Y + 10 x 3 Y + 10 X 3 Y0015 Y 2 + 10 x 2 Y 3 + 5 XY 4 + Y 59 5 + Y 59 5 9000}

999999999999999999999999999999. + Y 55 ^{5 + Y 55 5 + Y 559}

Мы можем сделать несколько замечаний:

1. В каждом расширении n + 1 член.
2. В каждом расширении x и y имеют симметричные роли. Степени x уменьшаются на 1 в последовательных условиях, тогда как степени y увеличиваются на 1.
3. Сумма степеней каждого члена равна n .
4. Биномиальные коэффициенты, _N C _R , где R является показателем второго термина, являются симметричными:
   ₅ C ₁ =
   ₅ C ₁ =
   _{. , 5 С 2 = 5 С 3 = 10.}

Попробуйте. ( х + с) ³ = х ³ + 3 x ² c + 3 x c ² + c ³ в отличие от более утомительного метода длинной руки:

							х	+	с
						*	х	+	с
							————————
								с x	с 2
						+	х 2	кс
							————————
							х 2	2 x в	с 2
						*	х	+	с
						———————————————
							x 2 в	2 x в 2	с 3
					+	х 3	2 x 2 в	xc 2
						———————————————
						x 3 + 3 x 2 с + 3 x c 2 + c 3

 

Биномиальное разложение разности так же просто, просто поменяйте знаки.
( x — y ) ³ = x ³ — 3 x ² Y + 3 XY 55 ²

555555555555555555555555555550 5555555555555555555555555555555550 555555555555555555555555555 — 55555555555550 гг.

В общем случае разложение бинома ( x + y ) ⁿ определяется биномиальной теоремой.
Теорема 6.7.1 Биномиальная теорема top

 Вы видите, как эта формула меняет знаки для расширения разности?

Пример 6.7.1 Подстановка в биномиальную теорему
Раскройте следующие выражения, используя биномиальную теорему:
a. ( а + б ) ⁵
б. ( х — 4 у ) ⁴ .
Решение а.

,

замены в значениях для биномиальных коэффициентов из треугольника Паскаля. A ³ B ² + 10 A ² B ³ + 5 AB ⁴ + B55555555555555555555555555555555555555555555555555555555555555555555555555555555555555н5н5а.

Решение б.
Учитывая, что для n = 4 коэффициенты равны 1, 4, 6, 4, 1, мы имеем

( x -4 y ) ⁴ = x ⁴ + 4 x ³ (-4 Y ) + 6 x 5555555555555555555555555555555555555555555555555555555555555555555559н. ) ² + 4 x (-4 y ) ³ + (-4 y ) ⁴

( х — 4 у ) ⁴ = x ⁴ — 16 x ³ y + 6 (16) x ² Y ² — 4 (64) x ² — 4 (64) 9

14

9. 9 9.9 9 ^9.9 9 9.9 9 2 9. 9 ² — 4 (64) ⁴

( x — 4 y ) ⁴ = x ⁴ — 16 x ³ y + 96 x ² y ² — 256 xy ³ + 256 у ⁴ .

Пример 6.7.3 Получение другого комбинаторного тождества из биномиальной теоремы
Используйте биномиальную теорему, чтобы показать, что

для всех целых чисел n ³ 0.

Решение: Поскольку 2 = (1 + 1) и 2 ⁿ = (1 + 1) ⁿ , применим к этому выражению биномиальную теорему.

начиная с 1 ^{n — r} = 1 и 1 ^р = 1.

Количество подмножеств множества
Теорема 5.3.6 Для всех целых чисел n ³ 0, если набор X имеет n элементов, то Power Set X , обозначенный P ( X ), имеет 2 ⁿ элементов.
Доказательство: Предположим, что S представляет собой набор из n элементов. Тогда каждое подмножество S имеет некоторое количество элементов k , где k находится в диапазоне от 0 до n .

No related posts.