Теоремы о равенстве треугольников: Первый признак равенства треугольников — урок. Геометрия, 7 класс.

Урок «Признак равенства треугольников по двум сторонам и углу между ними»

Обучающая: учащиеся «открывают» и доказывают первый признак равенства треугольников.

Оборудование: два треугольника из бумаги, линейка, проектор, компьютер с программой Power Point, презентация.

Действия учителя

Действия учащихся

— Какая фигура называется треугольником? — Какие треугольники называются равными? — Как установить равенство двух треугольников? — Все эти способы возможны, но они не всегда удобны, громоздки. А нет ли другого способа доказательства равенства двух треугольников? — Оказывается, равенство двух треугольников можно установить, не накладывая один треугольник на другой, а лишь сравнивая некоторые элементы этих фигур.

— Геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, соединенных отрезками, называется треугольником. — Два треугольника называются равными, если их можно совместить наложением. — Наложить один треугольник на другой, если они совместятся, то треугольники равны. Можно сравнить все стороны и углы одного треугольника со сторонами и углами другого. — ???

— Попробуем решить практическую задачу. Пусть надо измерить расстояние на местности от пункта А до пункта В, между которыми расположено озеро, поэтому с мерной лентой по прямой пройти нельзя. — На практике, для решения этой задачи поступают так: Выбирают некоторую точку С так, чтобы расстояние от точки С до точек А и В можно было измерить мерной лентой. Затем, на прямой АС отмечают точку К так, чтобы отрезок АС=СК, а на прямой ВС отмечают точку М так, чтобы отрезок ВС=СМ. Тогда на местности можно измерить расстояние МК, при этом утверждают, что оно равно искомому расстоянию между пунктами А и В. — Почему можно утверждать, что МК=АВ? Когда можно найти другие равные элементы в треугольниках? -Вероятно, DАВС=DМКС? — А каким свойством обладают равные треугольники? — Мы пока не знаем, равны наши треугольники или нет, DАВС=DМКС? Перечислите все равные элементы в этих треугольниках. — Итак, нам нужно установить равенство сторон АВ и МК, а равенство сторон следует из равенства треугольников. То есть, если мы докажем равенство треугольников, то равенство сторон будет доказано. Какова же цель урока? — Используя равенства каких элементов? — Сформулируйте цель урока. — Попробуем сформулировать утверждение, почему треугольники равны, по каким элементам? — Хорошо, если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. — Данное утверждение называется теоремой. Теорема – утверждение, которое необходимо доказать, а сами рассуждения называют доказательством. Сформулированную теорему называют первым признаком равенства треугольников или признаком равенства треугольников по двум сторонам и углу между ними. (С этого этапа каждое обоснование сопровождается слайдом с презентации) — Запишем в тетрадях тему. Признак равенства треугольников по двум сторонам и углу между ними. — Запишем формулировку теоремы. Теорема: Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. — Теорему можно назвать задачей, в которой есть условие, т.е. то, что дано и заключение, то, что необходимо доказать. — В теореме, начиная со слова если до слова то является условием теоремы. Прочитайте условие теоремы. — Все, что записано после слова то, называют заключением. Прочитайте заключение. — Запишем в тетрадях: Дано: — О каких фигурах идет речь? — Запишем в дано: DАВС иDА1В1С1 — О равенстве каких элементов говорится в условии? — Выберем эти стороны и найдем угол между этими сторонами. АВ=А1В1, АС=А1С1, ÐА=ÐА1. — Что нужно доказать? — Запишем: Доказать: DАВС=DА1В1С1 — Сделаем чертеж как на экране.   ІІ Исполнительский этап. 1. Нахождение способа доказательства теоремы. — Каким способом будем доказывать равенство треугольников? — Запишем: Доказательство (метод наложения) — С чего начнем проводить доказательство? С наложения каких элементов? (Если учащиеся говорят про стороны, то с помощью заготовленных треугольников можно показать, что не всегда такое наложение возможно, тогда остается только один вариант, когда доказательство начинаем проводить с наложения углов) — Посмотрим на экран, каким образом происходит наложение. 2. Проведение доказательства теоремы. — Запишем: 1. Т.к. ÐА=ÐА1, то DАВС можно наложить на DА1В1С1так, что луч АВ совместится с лучом А1В1 и луч АС совместится с лучом А1С1. — Какие элементы треугольника будем потом сравнивать? Что еще дано в условии? — Что произойдет с точками В и В1? — Посмотрим на экран, запишем: 2. Т.к. АВ=А1В1, то сторона АВ совместится со стороной А1В1 (точка В совместится с точкой В1). — О какой стороне еще говорится в условии? — Сделайте вывод о точках С и С1. — Посмотрим на экран, действительно ли совпадут эти точки? — Ваше утверждение верно, запишем: 3. Т.к. АС=А1С1, то сторона АС совместится со стороной А1С1  (точка С совместится с точкой С1). — Что произошло с концами отрезков ВС и В1С1? — Что теперь можно сказать про отрезки ВС и В1С1? — Правильно, запишем: 4. Т.к. концы отрезков ВС и В1С1 совместились, то сторона ВС совместится со стороной В1С1. — Что произошло с DАВС и DА1В1С1? — Молодцы, запишем: 5. DАВС совместился с DА1В1С1, значит DАВС=DА1В1С1. ІІІ Рефлексивно – оценочный этап. — Сформулируйте доказанную теорему. — Сверим доказанную теорему с теоремой в учебнике п.15, стр. 30 (Учебник по геометрии для 7 класса, автор  Атанасян). Прочитайте её, эту теорему мы только что доказали? Выделите условие и заключение теоремы. — Каким методом мы проводили доказательство? — С наложения каких элементов мы начали проводить доказательство? (Можно использовать для помощи слайд №6) — Равенство каких элементов еще использовали? — Что можно сказать про стороны ВС и В1С1? 1. Решение задач (устно). — Сколько пар соответственно равных элементов надо отыскать, чтобы доказать равенство треугольников по первому признаку? — Где должен лежать угол? 1. Докажите, что треугольники равны Учащиеся по рисунку отыскивают равные элементы и доказывают, что треугольники равны (Слайд 7, 8, 9), а потом проверяют верно они доказали или нет. 2. Дополните условия так, чтобы треугольники были равны по первому признаку. (Слайд 10, 11) 3. Докажите, что треугольники равны. (Слайд 12) — Достигли мы цели урока? — Какую теорему мы доказали? Сформулируйте её. — каким методом провели доказательство признака? 2. Домашнее задание. (Слайд 13) Домашнее задание:             Глава II, §1, п. 14-15 читать,                      выучить записи в тетради. 3. Контроль настроения. — С помощью сигнальных карточек покажите, каким стало ваше настроение к концу урока.

— Когда треугольники равны. — В равных треугольниках против соответственно равных сторон лежат равные углы, и наоборот, против равных углов, лежат равные стороны. — АС=СК, ВС=СМ – по построению, ÐАСВ=ÐМСК как вертикальные. — Доказать равенство треугольников. — Двух сторон и угла между ними. — Доказать равенство треугольников по двум сторонам и углу между ними. — Если в две стороны в одном треугольнике равны двум сторонам в другом и углы между этими сторонами в одном и в другом треугольнике равны, то такие треугольники равны. — О треугольниках. — О равенстве двух сторон и угла между этими сторонами. — Что DАВС=DА1В1С1 — Методом наложения. — АВ=А1В1 — Эти точки совпадут. — АС=А1С1 — Эти точки совпадут. — Концы отрезков ВС и В1С1 совпали. — ВС=В1С1 — Треугольники совпали, значит они равны. — Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. — «Если две стороны и угол между ними одного треугольника, соответственно равны двум сторонам и углу между ними другого треугольника» — это условие, то что дано. — «такие треугольники равны» — заключение, что требуется доказать. — Методом наложения. — С наложения углов. — Равенство сторон:  АВ=А1В1, то сторона АВ совместится со стороной А1В1, точка В совместится с точкой В1; — АС=А1С1, то сторона АС совместится со стороной А1С1 точка С совместится с точкой С1. /data/files/o1604343151.ppt (Презентация «Первый признак равенства треугольников»)- Они совпадут, значит эти стороны равны. — Три пары, две стороны и угол. — Между сторонами.

«Нестандартные признаки равенства треугольников» | Образовательная социальная сеть

МБУ ДО города Ростова-на-Дону «Дворец творчества детей и молодежи»

Донская академия наук юных исследователей им. Ю. А. Жданова

Математика

Тема: «Нестандартные теоремы о равенстве треугольников»

Автор работы:

Подгорный Максим, 7 кл.,

МБОУ СОШ № 3,

г. Сальск, Ростовская область

Руководитель:

Олейникова Людмила Александровна,

учитель математики,

МБОУ СОШ № 3,

г. Сальск, Ростовская область

г. Ростов-на-Дону

2017 год

Содержание

Введение………………………………………………………….………………3

Основная часть

Признаки равенства треугольников…………………………………………… 4

Нестандартные признаки равенства треугольников………………………….7

Заключение…………………………………………………………………… 10

Список литературы…………………………………………………………… 11

Приложение

Введение.

Актуальность:

Треугольник одна из основных фигур в планиметрии. Я много слышал от старшеклассников, что при подготовке к ЕГЭ им часто приходится доказывать равенство треугольников. И оказывается недостаточным знание основных признаков. Мне захотелось узнать, а можно ли доказать равенство треугольников по другим параметрам .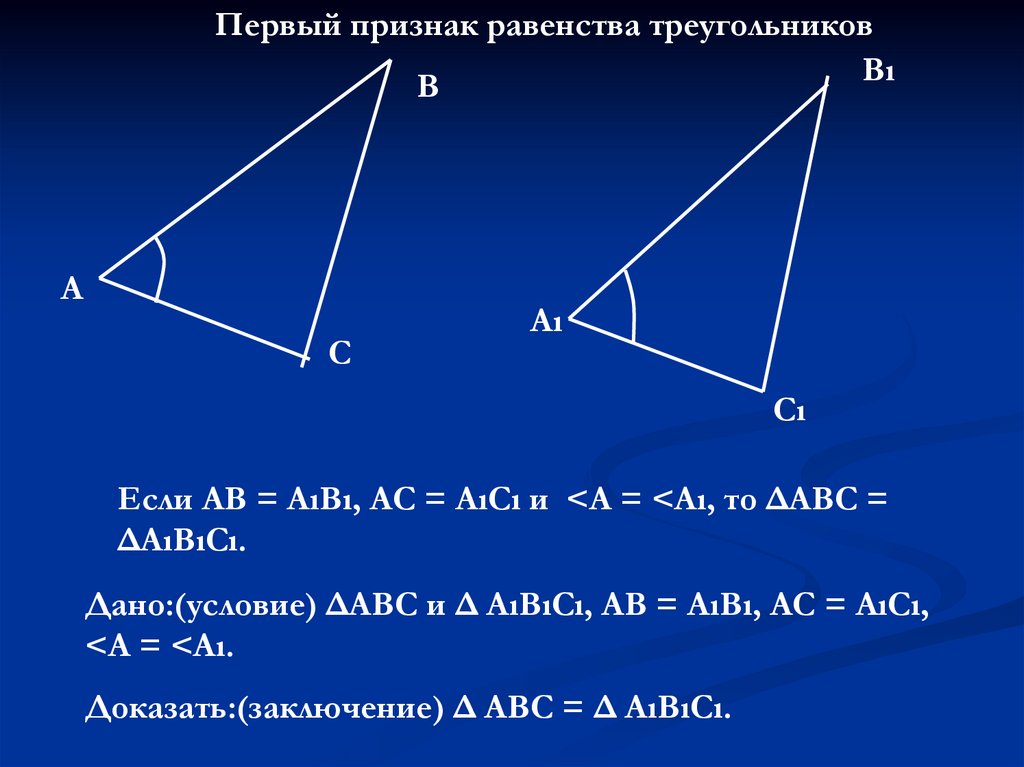 В учебнике геометрии, по которому обучаются ученики нашей школы ( авторы Л.С.Атанасян, В.Ф.Бутузов и др. Геометрия 7-9) рассматриваются всего 3 признака равенства треугольников. Я просмотрел учебно-методические комплекты других авторов. Но и в них для изучения предлагаются только три известные теоремы.

Гипотеза:

Возможно, ли сформулировать, кроме трех известных, другие признаки равенства треугольников?

Чтобы убедиться в том, что ответ на этот вопрос волнует не только меня, я провел социологический опрос среди учащихся 7-11 классов      см. приложение  1 ).

Мои предположения подтвердились. Большенство учеников знают только  три признака равенства треугольников.

Таким образом,  целью моего исследования стало отыскание новых признаков равенства треугольников.

Задачи :

       ΘИзучить литературу по исследуемой  теме.

       ΘУточнить количество признаков равенства треугольников.

       ΘПродемонстрировать своим одноклассникам и учащимся нашей  школы существование других признаков равенства треугольников  и возможности их доказательства.

Объект исследования :

Изучение признаков равенства  треугольников.

Предмет  исследования.  Треугольник, как одна из основных фигур в планиметрии.

Метод  исследования:  Теоретический ( изучение, анализ и синтез),системно-поисковый, практический (доказательство теорем ).

                     

Историческая справка

Треугольник является одной из центральных фигур всей геометрии.

При решении задач используют его самые разнообразные свойства.

Свойства треугольника широко применяют на практике: в архитектуре; при разработке чертежа здания, при планировке будущих квартир; в промышленности, при проектировании различных деталей, при изготовлении стройматериалов, при строительстве морских и авиа судов; в навигации для проложения правильного и максимально точного маршрута; в астрологии и астрономии треугольник является очень значимой фигурой; треугольники делают надежными конструкции высоковольтных линий электропередач и железнодорожных мостов.

Кроме того, много других сфер, где применяются различные свойства треугольника: начиная игру в бильярд, необходимо расположить шары в виде треугольника, для этого используют специальное приспособление; расстановка кеглей в игре Боулинг тоже в виде равностороннего треугольника; для составления красивых паркетов используются треугольники; устройство треугольника Паскаля: каждое число равно сумме двух расположенных над ним чисел (обвести треугольником три числа). Все элементарно, но сколько в этом таится чудес! Треугольник Паскаля компьютер перевёл на язык цвета.

Тему треугольника можно продолжать неограниченно.

Каких только треугольников нет на свете!

Существуют также переносные значения данной фигуры: например, правило «золотого треугольника» основано на психологии покупателя – найдя нужный ему товар, покупатель устремляется в кассу. Задача продавцов – заставить его задержаться в магазине подольше, расположив нужный покупателю товар в вершинах воображаемого треугольника, то есть «заякорить» покупателя. Чем больше площадь треугольника, тем более удачным можно назвать планировку магазина. В продуктовом магазине этими товарами-якорями являются гастрономия, молочная продукция, хлеб. Задняя торцевая стена торгового зала является вторым местом по значимости и именно там целесообразнее всего располагать товары-якоря – именно для того, что бы заставить покупателя пройти весь периметр магазина.

Широко известный Бермудский треугольник – это район в Атлантическом океане, в котором происходят якобы таинственные исчезновения морских и воздушных судов. Район ограничен линиями от Флориды к Бермудским островам, далее к Пуэрто-Рико и назад к Флориде через Багамы.

Поэтому изучение треугольника и всех его свойств – очень актуальная тема.

Цель данной работы – рассказать о признаках равенства треугольников, что является одним из важнейших их свойств.

Признаки равенства треугольников — это теоремы, на основании которых можно доказать, что некоторые треугольники равны.

В геометрии используются три признака равенства треугольников.

Данная тема практически изучена, так как на сегодняшний день существуют три признака равенства треугольников, доказываемых с помощью соответствующих теорем. 

В глубокой древности вместе с астрономией появилась наука – тригонометрия. Слово «тригонометрия» произведено от греческих «треугольник» и «меряю». Буквальное значение – «наука об измерении треугольников».

С помощью натянутых веревок длиной 3, 4 и 5 единиц египетские жрецы получали прямые углы при возведении храмов и т.п.

Искусство изображать предметы на плоскости с Древних времён привлекает к себе внимание человека, люди рисовали на скалах, стенах, сосудах и прочих предметах быта, различные орнаменты, растения, животных. Люди стремились к тому, чтобы изображение правильно отображало естественную форму предмета.

Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, очень много детских игрушек подобным предметам взрослого мира, обувь и одежда одного фасона выпускается различных размеров.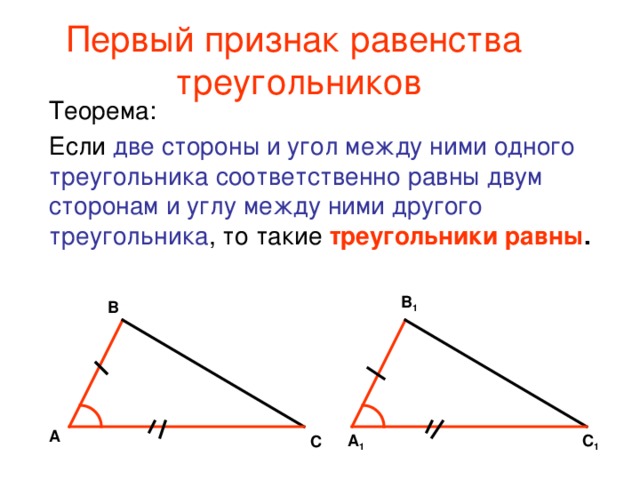 Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу и как утверждает Библия, создал их бог по своему образу и подобию.

Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались еще пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников).

Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Каким способом пользовался при этом Фалес, точно не известно.

Признаки  равенства  треугольников.

Начнем с определения. Треугольники  АВС  и  А1В1С1  называются равными, если их можно совместить наложением.

Треугольник состоит из  шести элементов: трех углов и трех сторон.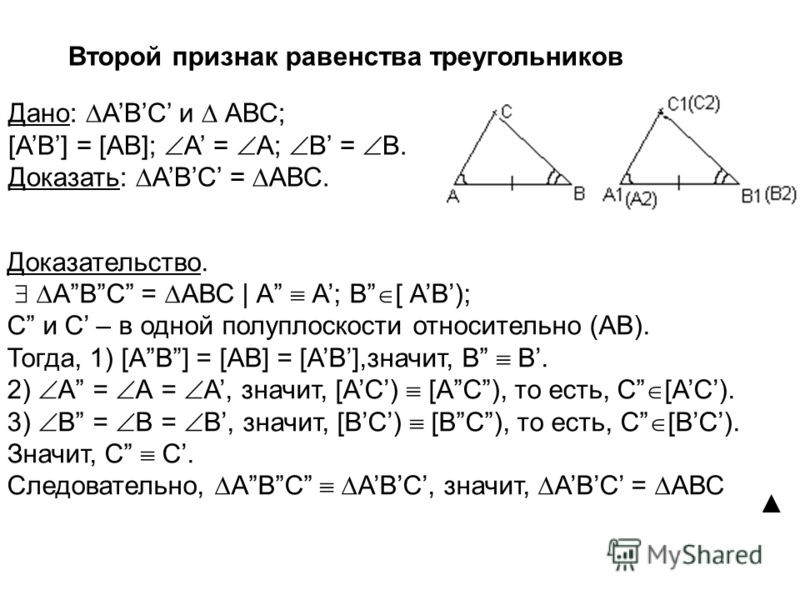

При этом возникает вопрос :   » Какое наименьшее количество элементов треугольника нужно взять для установления равенства   двух  треугольников ?»

Мы не сможем установить равенство двух треугольников по одному  элементу, потому что неизвестно :»Будут ли равны остальные элементы ?»

Так же невозможно установить равенство двух треугольников, используя два элемента  по причине нехватки информации для установления равенства.

Возможно установление равенства  двух треугольников, используя  три элемента. Но при этом возникает вопрос : «Какие именно три элемента нужно назвать, для установления равенства треугольников ?»

                                                                                   4

При изучении этого вопроса , я просмотрел школьные учебники геометрии различных авторов, а также словари и справочники. В учебниках за седьмой класс предложены к изучению только три признака равенства треугольников.

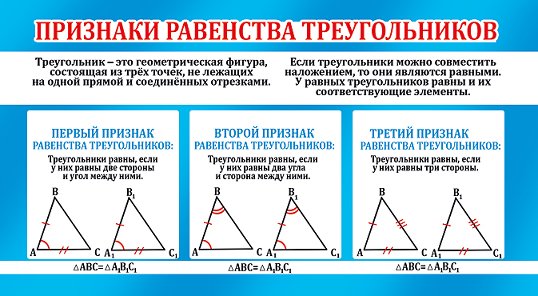
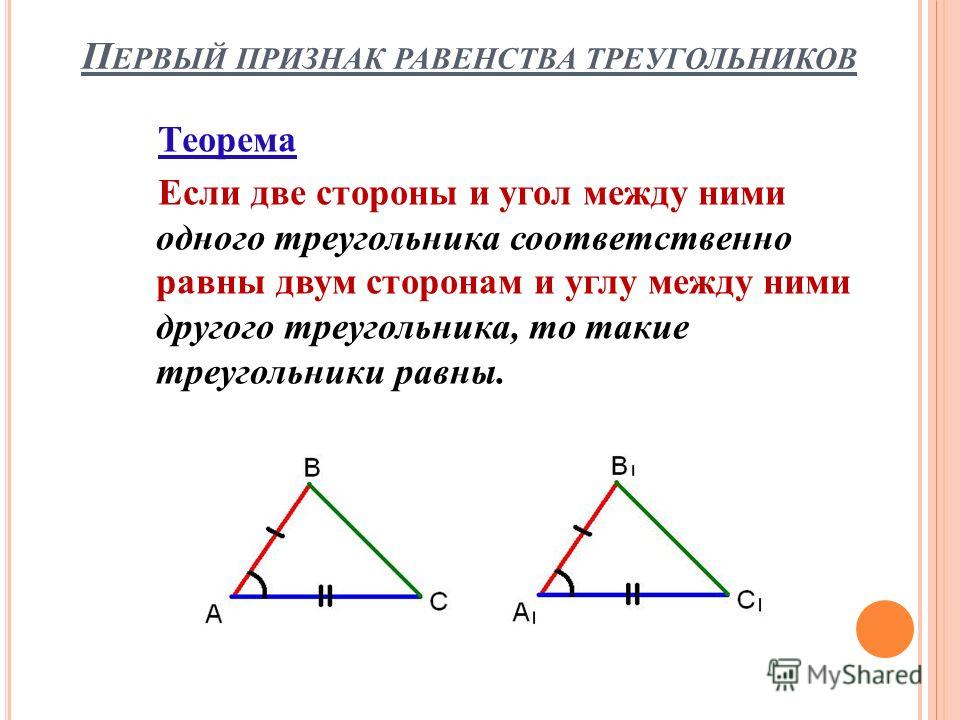
Θ1 Признак: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.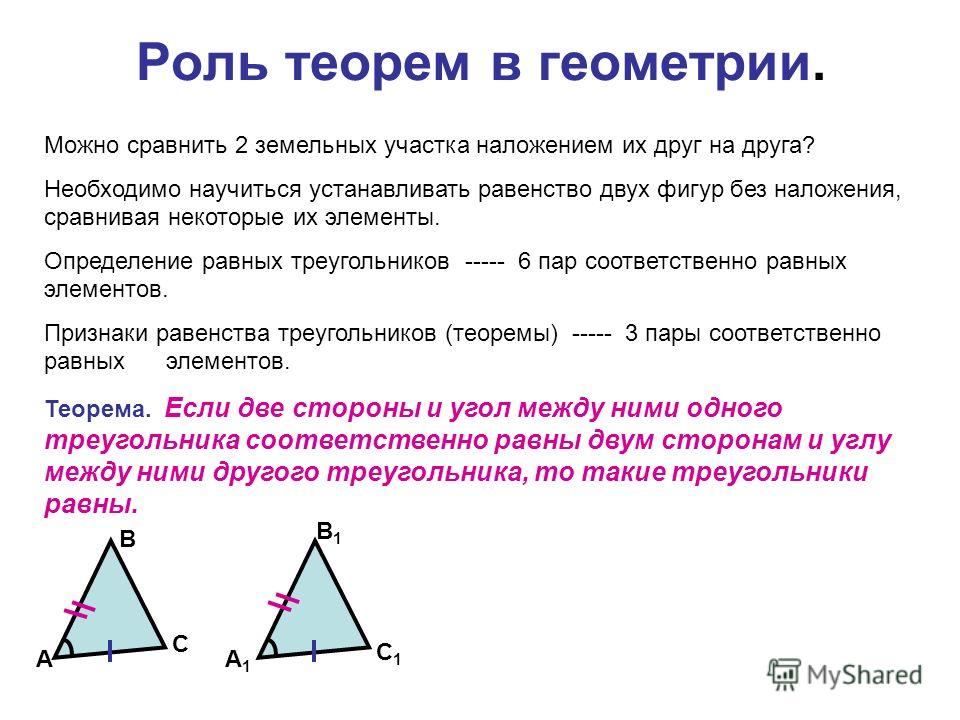 рис.1

Доказательство. Рассмотрим треугольники ABC и A1B1C1, (рис. 1) у которых АВ = A1B1, АС = A1C1 ∠ А = ∠ А1. Докажем, что ΔABC = ΔA1B1C1.

Так как ∠А = ∠А1, то треугольник ABC можно наложить на треугольник А1В1С1 так, что вершина А совместится с вершиной А1, а стороны АВ и АС наложатся соответственно на лучи А1В1 и A1C1. Поскольку АВ = A1B1, АС = А1С1, то сторона АВ совместится со стороной А1В1 а сторона АС — со стороной А1C1; в частности, совместятся точки В и В1, С и C1. Следовательно, совместятся стороны ВС и В1С1. Итак, треугольники ABC и А1В1С1 полностью совместятся, значит, они равны.

 А вот как в Древнем Египте применили первый признак равенства треугольников (по двум сторонам и углу между ними), создателем его также считается Фалес Милетский, для измерения высоты пирамиды: представим, что мы стоим перед огромной пирамидой, как же измерить её высоту? Ведь к ней не приложишь измерительные приборы! И тут на помощь Фалесу Милетскому приходит первый признак равенства треугольников: он подождал пока тень его точно совпадёт с его ростом, применил теорему, получилось, что высота пирамиды равна её тени (рис. 2).

Рис. 2

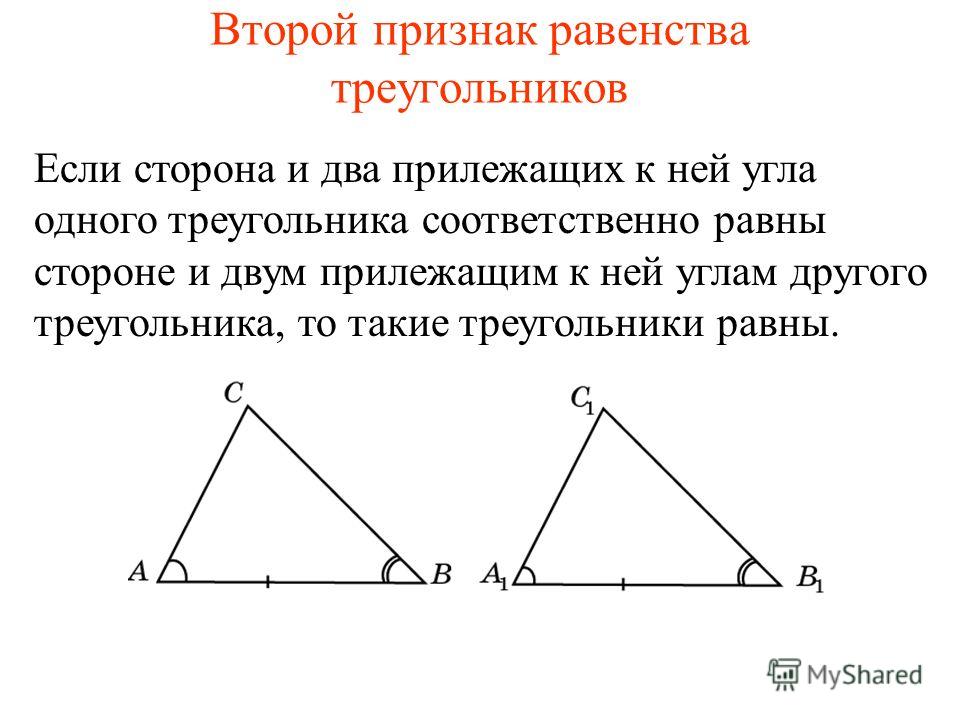
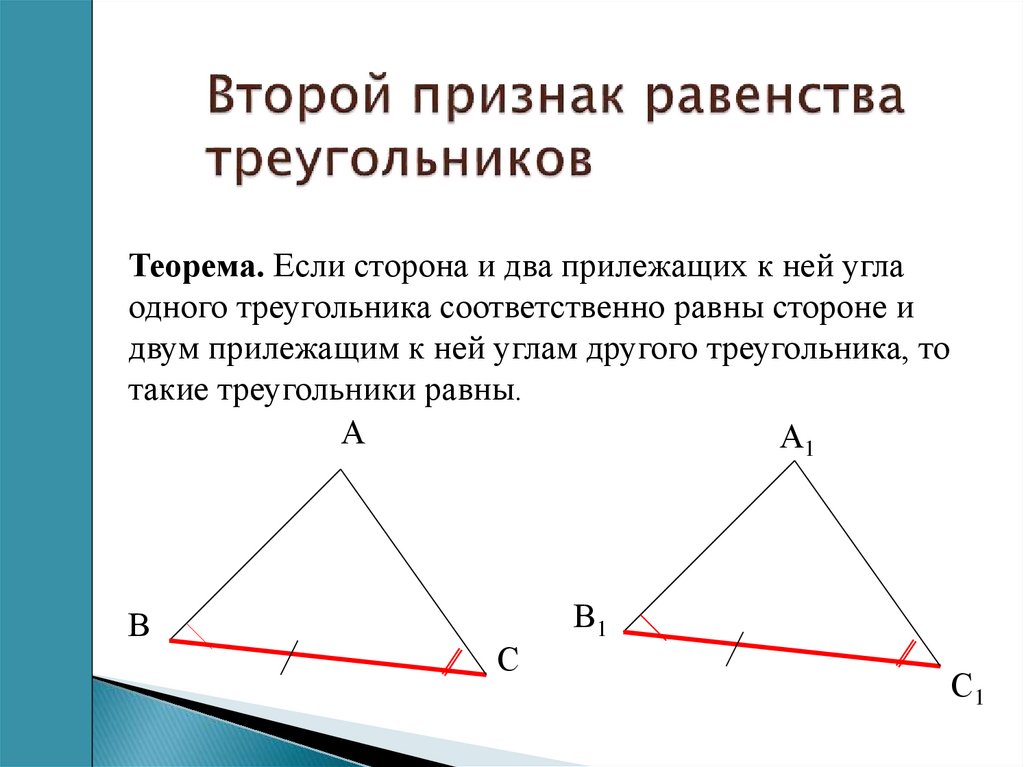
Θ2 Признак : Если сторона и два прилежащих к ней угла одного треугольника соответственно  равны стороне и двум прилежащим к ней углам другого треугольника, то такие  треугольники равны.

Доказательство: Если в △АВС и △А1В1С1 будут иметь место следующие равенства AB=А1В1, ∠BAC=∠B1A1C1, ∠АВС= ∠А1В1С1. Наложим друг на друга треугольники А1В1С1 и АВС таким образом, чтобы совпали равные стороны AB и А1В1 и углы, которые к ним прилегают. Как и в уже рассмотренном предыдущем примере, если это необходимо, треугольник А1В1С1 можно «перевернуть и приложить обратной стороной». Треугольники совпадут, следовательно, они могут считаться равными.

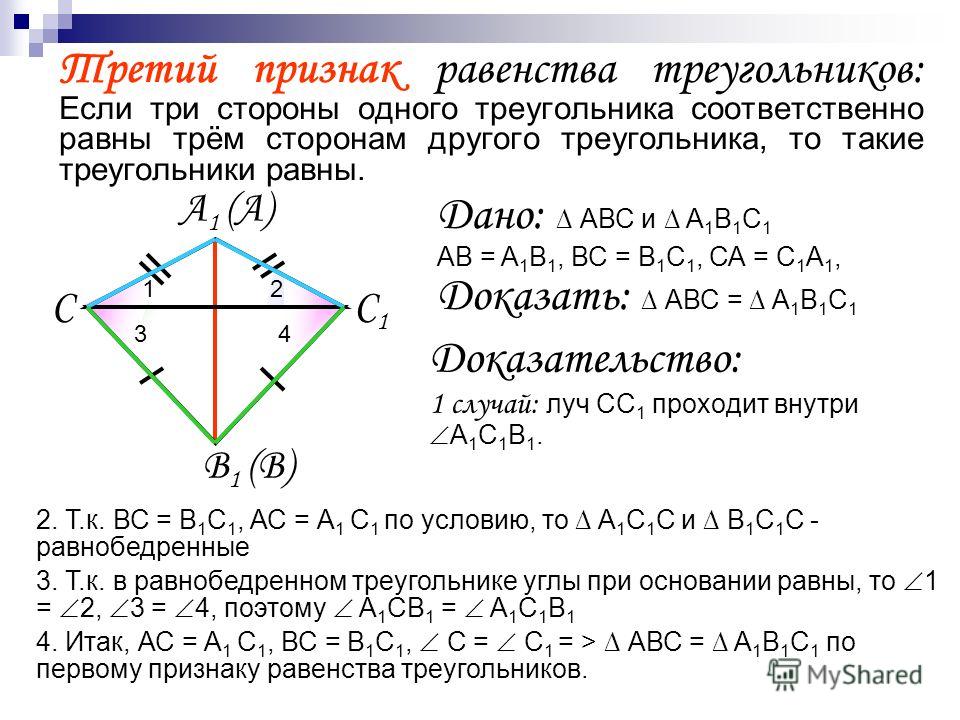
Θ3 Признак : Если три стороны  одного треугольника соответственно равны  трем сторонам другого треугольника, то такие треугольники равны. Доказательство:Пусть для △ABC и △A1B1C1 справедливы равенства А1В1=АВ, В1С1=ВС, С1А1=СА. Переместим треугольник А1В1С1 таким образом, что сторона А1В1 совпадет со стороной АВ, и вершины B1 и B, A1 и A, совпадут. Возьмем окружность с центром в A и радиусом AC, и вторую окружность с центром B и радиусом BC. Эти окружности пересекутся в двух симметричных относительно отрезка AB точках: точкой C и точкой C2. Значит, C1 после переноса треугольника A1B1C1 должна совпасть или с точками C, или с C2. Любом случае, это будет означать равенство △ABC=△A1B1C1, так как треугольники △ABC=△ABC2 равны (ведь эти треугольники являются симметричными относительно отрезка AB .

Это свойство – жесткость треугольника – широко используется на практике. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку; такой же принцип используется при установке кронштейна.

Свойство жесткости треугольника широко используют в практике при строительстве железных конструкций.

Из третьего признака равенства треугольников следует, что треугольник — жёсткая фигура. Потому, что: можно представим себе две рейки, у которых два конца скреплены гвоздем. Такая конструкция не является жёсткой, однако, сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними.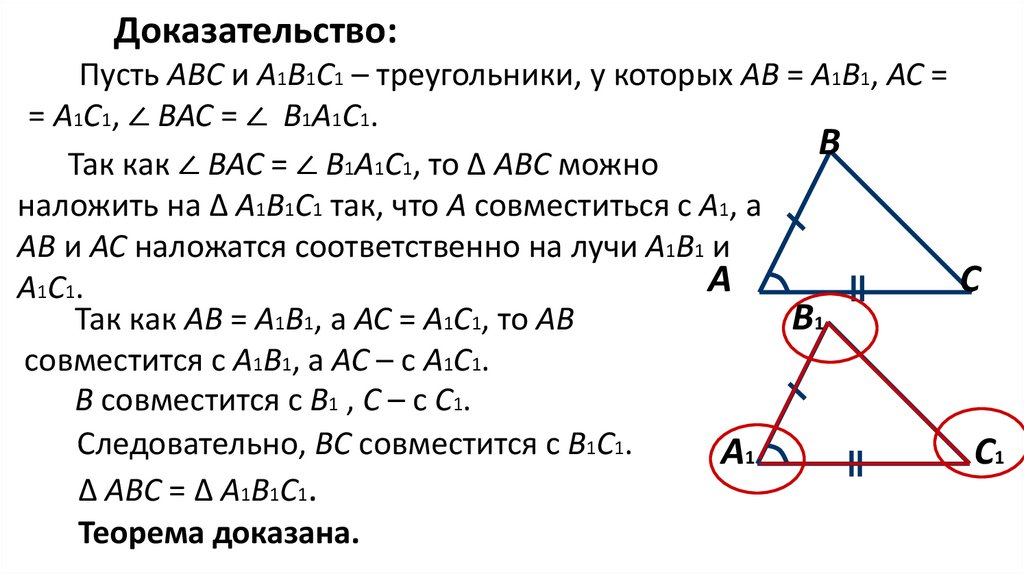 Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек . Полученная конструкция — треугольник — будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему

В справочнике по элементарной математике  М. Я. Выгодского я нашел еще один признак.

Θ4 Признак : Если две стороны и угол, лежащий против большей из них одного треугольника соответственно равны двум сторонам и углу, лежащему против большей из них другого треугольника, то такие треугольники равны.

 Докажу этот признак.

Дано : ΔABC , ΔA1B1C1 , AB=A1B1,AC=A1C1,∠B=∠B1

Доказать : ΔABC=A1B1C1.

Расположим треугольники так , как  на рисунке 1 . Соединим B и B1, тогда ΔАВВ1

-равнобедренный , значит ∠1=∠2.∠3=∠4 как остатки равных углов .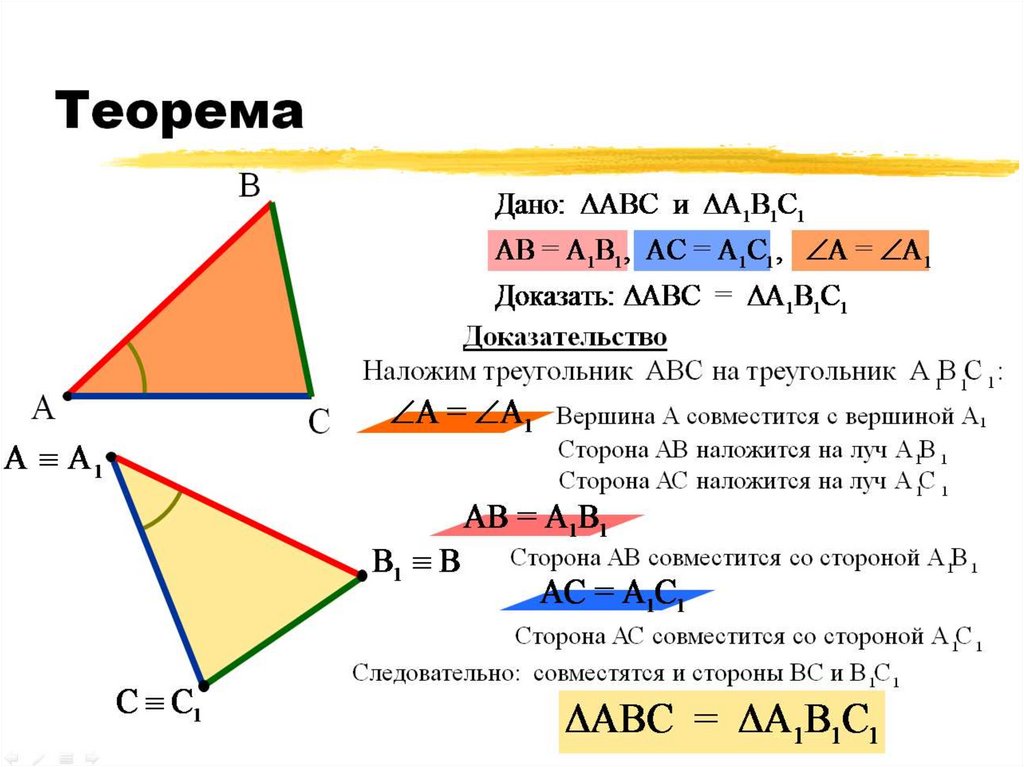

Получим ΔВСВ1- равнобедренный, отсюда ВС=В1С1. ΔАВС = ΔА1В1С1 по трем сторонам.

                                                                                 

Также в  школьном курсе рассматриваются  4  признака равенства прямоугольных треугольников :

Θ1. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.

Θ2. Если катет и прилежащий  к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого , то такие треугольники равны.

Θ3. Если гипотенуза и острый угол одного прямоугольного  треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники  равны.

Θ4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

                                                                                       

Я решил теоретическую базу по признакам равенства треугольников , довавив к сторонам и углам , используемым в класических признаках равенства треугольников , другие компоненты : биссектрису , медиану и высоту.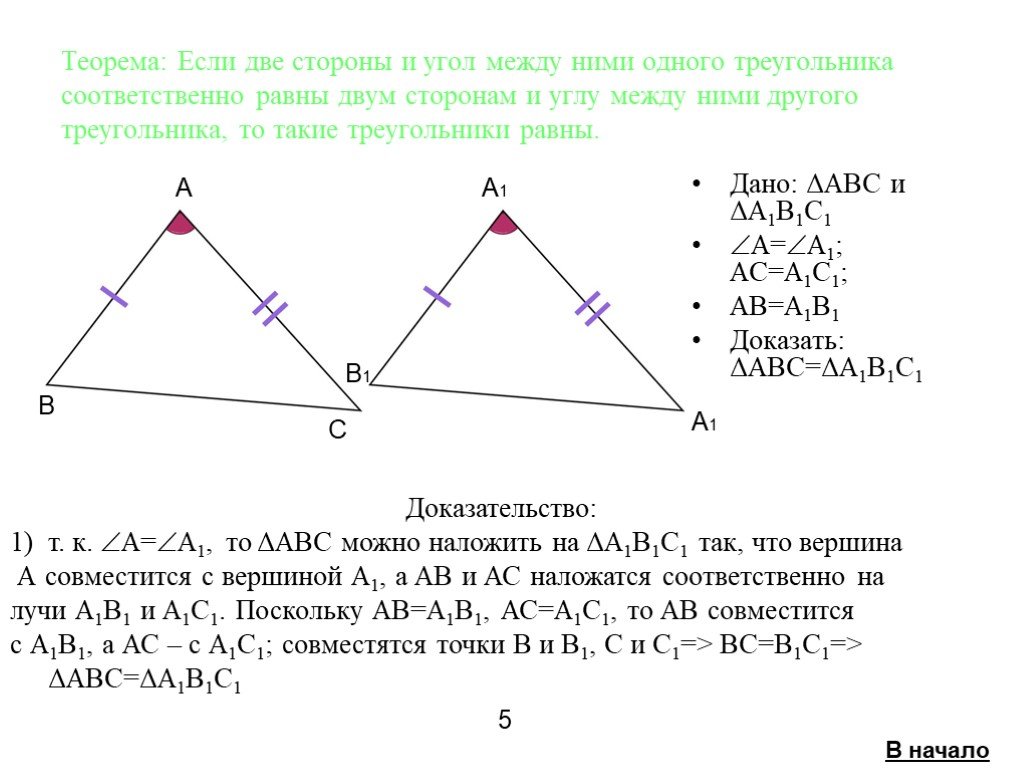

Нестандартные признаки равества треугольников.

1) По двум сторонам и высоте проведенной к одной из них .

Дано: AB=A1B1 , BC=B1C1 , AK=A1K1 ,

Доказать : ΔABC= ΔA1B1C1 .

Доказательство : ΔABK=ΔA1B1K1  по гипотенузе и катету , тогда ∠B=∠B1 и получим ΔABC= ΔA1B1C1  по первому признаку .

2) По двум сторонам и медиане , проведенной к одной из них

 

Дано: AB=A1B1 , BC=B1C1 , AK=A1K1 , AK и A1K1 — медианы.

Доказать : ΔABC= ΔA1B1C1 .

Доказательство :ΔABK=ΔA1B1K1  по трем сторонам , значит ∠B=∠B1  и ΔABC= ΔA1B1C1  по первому признаку.

3) По двум сторонам и высоте , проведенной из третьего угла.

Дано:∠ B=∠ B1 ,∠ C=∠ C1 , AK=A1K1 .

Доказать : ΔABC= ΔA1B1C1 .

Доказательство : ΔABK=ΔA1B1K1  по катету и острому углу , значит BK=B1K1 ,

ΔACK=ΔA1C1K1 по катету и острому углу , значит KC=K1C1 , а следовательно BC=B1C1  , а  ΔABC= ΔA1B1C1  по второму признаку.

4)По стороне и двум высотам , проведенным из углов , прилежащих к этой стороне .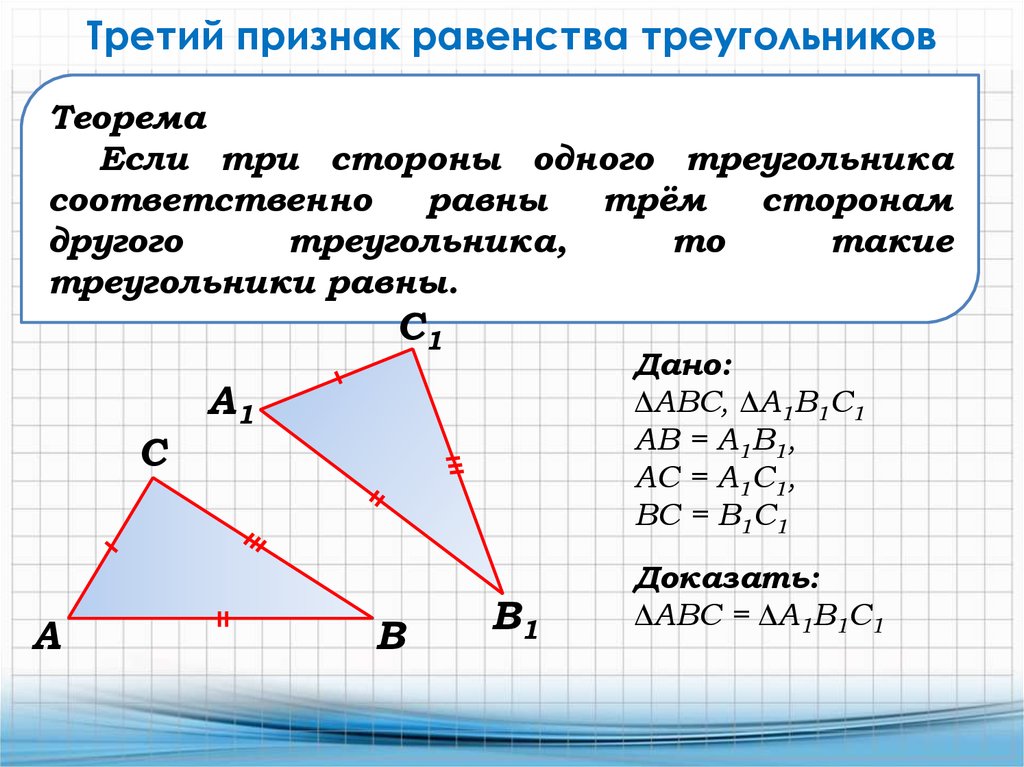

Дано: АС=А1С1, СМ=С1М1, АК=А1К1.

Доказать : ΔСC= ΔA1B1C1 .

Доказательство:  ΔAМC= ΔA1М1C1 по катету и гипотенузе , значит∠ А=∠А1  , а  ΔAКC= ΔA1К1C1 по катету и гипотенузе , значит∠ С=∠С1  .

Итак , ΔABC= ΔA1B1C1  по второму признаку .

 

5)По двум сторонам и высоте , проведеннойк третьей стороне .

Дано : АВ=А1В1,ВС=В1С1,ВК=В1К1.

Доказать : ΔABC= ΔA1B1C1 .

Доказательство:ΔABK=ΔA1B1K1  по гипотенузе и катету , значит AK=A1K1,

ΔBКC= ΔB1К1C1 по катету и гипотенузе, значит KC=K1C1 .

Итак ,ΔABC= ΔA1B1C1 по трем сторонам.

6)По стороне , одному из углов , прилежайщих к этой стороне и биссектрисе из этого угла.

Дано: АС=А1С1,  АК=А1К1,∠ А∠А1  .

Доказать : ΔABC= ΔA1B1C1 .

Доказательство: ΔКАС=ΔК1А1С1 по первому признаку , значит∠ С=∠С1  ,

ΔABC= ΔA1B1C1  по второму признаку.

7) По двум высотам и углу , из которого провдена одна из высот .

Дано : СМ=С1М1, АК=А1К1,∠ А∠А1  .

Доказать :  ΔABC= ΔA1B1C1 .

Доказательство : ΔAМC= ΔA1М1C1 по катету и острому углу,ΔКАС=ΔК1А1С1  по катету и гипотенузе ,ΔABC= ΔA1B1C1  по второму признаку.

Заключение.

    В  ходе исследования  я  выяснил, что помимо трех основных признаков равенства треугольников возможно указать немало других. Я  сформулировал и доказал равенство треугольников по медиане, высоте,  биссектрисе треугольника в сочетании со сторонами и углами треугольника, придерживаясь наличия трех элементов.   Теперь я могу рассказать учащимся нашей школы,  что существуют другие признаки равенства  треугольников.  Это позволит  выпускникам школы применить результаты моих исследований  при подготовке  к ОГЭ и ЕГЭ и легко решать геометрические  задачи на применение этих признаков.

Результат  моего   исследования :  Доказаны  несколько  признаков  равенства  треугольников, не изучаемых в школьном курсе  геометрии.

Список литературы

1. Выгодский М.Я. Справочник по элементарной математике.
2. Геометрия. 7-9 классы: учеб. Для общеобразоват. учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – 19-е изд. – М. : Просвещение, 2009.
3. Погорелов А. В. Геометрия: Учеб. Для 7-9 кл. общеобразоват. Учреждений. – 3-е издание. – М.: Просвещение, 2002.
4. . Энциклопедия «Аванта» по математике, Москва, 2004 г.
5. 2. «Википедия» — свободная энциклопедия.
6. 3. Глейзер Г.И. «История математики в школе», Москва, Просвещение, 1982 г.
7. 4. Гусева Т.М. Признаки подобия треугольников.- Москва, Первое сентября, приложение «Математика», 1999 г., №28
8. 5. Погорелов А.В. «Геометрия 7-9 классы», Москва, Просвещение, 2003 г.

Приложение 1

1.Как вы считаете, сколько существует признаков равенства треугольников?

А) 3 Б) более трех В) меньше трех

2. Хотели бы вы узнать новые признаки равенства треугольников?

А) да Б) нет

 

 

 

Правило поясняется картинками и примерами

Могут ли любые 3 длины сторон образовать треугольник?

Например, могу ли я создать треугольник из сторон длины.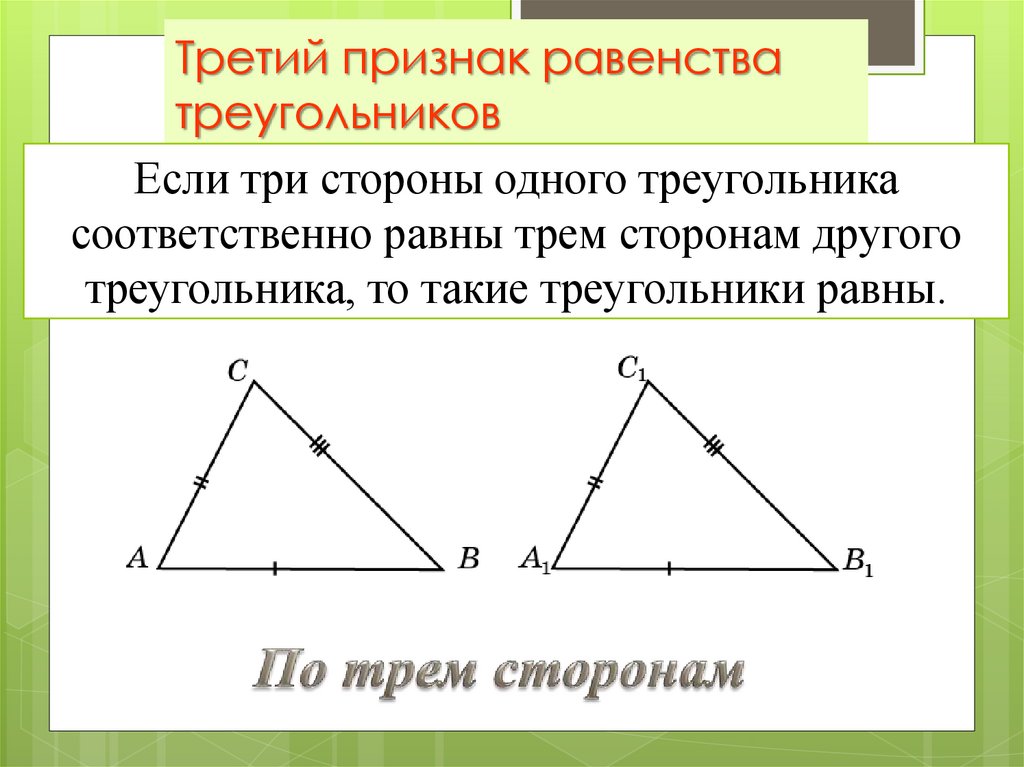 .. скажем, 4, 8 и 3?

Нет! На самом деле это невозможно!

Как вы можете видеть на рисунке ниже, невозможно создать треугольник, длина сторон которого равна 4, 8 и 3

Оказывается, есть некоторые правила, касающиеся длины сторон треугольников. Вы не можете просто составить 3 случайных числа и получить треугольник! Вы можете получить 3 строки, подобные тем, что изображены выше. нельзя соединить в треугольник.

Видео по теореме

Формула

Теорема о неравенстве треугольника утверждает, что сумма любых двух сторон треугольника должна быть больше, чем мера третьей стороны.

Примечание: Это правило должно выполняться для всех 3-х условий сторон.

Другими словами, как только вы узнаете, что сумма двух сторон меньше (или равна) меры третьей стороны, тогда вы знаете, что стороны не составляют треугольник.

Вы можете поэкспериментировать сами, используя наш бесплатный онлайн-калькулятор теоремы о неравенстве треугольника — который позволяет ввести любые три стороны и объясняет, как к ним применима теорема о неравенстве треугольника.

Должен ли я всегда проверять все 3 набора?

НЕТ!

Вам нужно только посмотреть, больше ли две меньшие стороны, чем наибольшая сторона!

Посмотрите на пример выше, проблема была в том, что 4 + 3 (сумма меньших сторон) не больше 10 (большая сторона)

Мы начнем использовать этот ярлык с практической задачи 2 ниже.

Интерактивная демонстрация теоремы

Интерактивная демонстрация ниже показывает, что сумма длин любых двух сторон треугольника должна превышает длину третьей стороны. Демонстрация также иллюстрирует, что происходит, когда сумма 1 пары сторон равняется длине третьей стороны — в итоге вы получите прямую линию! Вы не можете сделать треугольник!

В противном случае вы не можете создать треугольник с 3-х сторон.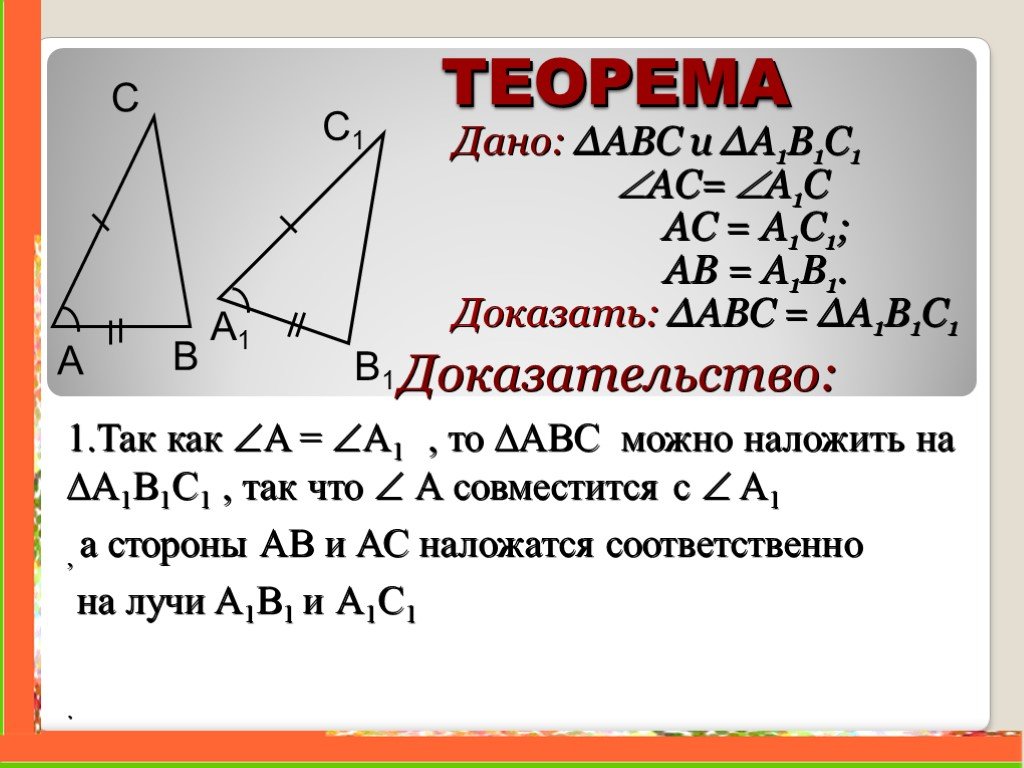

А + В > С

6 + 6 > 6

А + С > В

6 + 6 > 6

Б + С > А

6 + 6 > 6

Наведите курсор, чтобы начать демонстрацию

Практические задачи

Проблема 1

Может ли треугольник иметь длины сторон

• Сторона 1: 4
• Сторона 2: 8
• Сторона 3: 2

№

Используйте теорему о неравенстве треугольника и изучите все 3 комбинации сторон. Как только сумма любых двух сторон меньше третьей стороны то стороны треугольника не удовлетворяют теореме.

Проблема 2

Может ли треугольник иметь длины сторон

• Сторона 1: 5
• Сторона 2: 6
• Сторона 3: 7

Да

Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем большая сторона.

маленький + маленький > большой

потому что 5 + 6 > 7

Проблема 3

Может ли треугольник иметь длины сторон

• Сторона 1: 1,2
• Сторона 2: 3.1
• Сторона 3: 1,6

Нет

Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем большая сторона.

маленький + маленький > большой

потому что 1,2 + 1,6 $$\color{Red}{ \ngtr } $$ 3,1

Проблема 4

Может ли треугольник иметь длины сторон

• Сторона 1:6
• Сторона 2: 8
• Сторона 3: 15

Нет

Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем большая сторона.

маленький + маленький > большой

потому что 6 + 8 $$\color{Red}{ \ngtr } $$ 16

Больше похоже на Задача 1-4…

Проблема 4.1

Может ли треугольник иметь длины сторон

• Сторона 1: 5
• Сторона 2: 5
• Сторона 3: 10

Нет

Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем большая сторона.

маленький + маленький > большой

потому что 5 + 5 $$\color{Red}{ \ngtr } $$ 10

Проблема 4.2

Может ли треугольник иметь длины сторон

• Сторона 1: 7
• Сторона 2: 9
• Сторона 3: 15

Да

Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем большая сторона.

маленький + маленький > большой

потому что 7 + 9 > 15

Решайте задачи усерднее

Проблема 5

Две стороны треугольника имеют длины 8 и 4.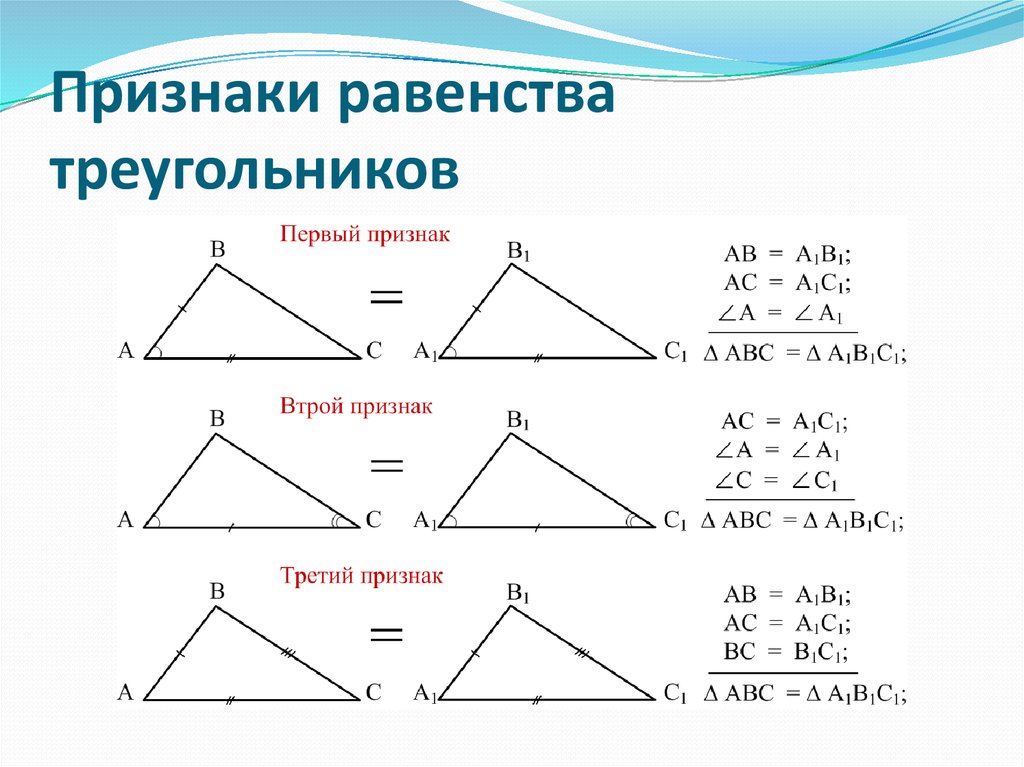 Найдите все возможные длины третьей стороны.

Вы можете использовать простую формулу, показанную ниже, для решения этих типов проблем:

разница $$< x <$$ сумма
$$8 -4 < x < 8+4 $$

Отвечать: $$4 < х < 12$$

Существует бесконечное количество возможных треугольников, но мы знаем, что сторона должна быть больше 4 и меньше 12.

Одно возможное решение

---

Вот пример треугольника, неизвестная сторона которого чуть больше 4:
.

Другое возможное решение

---

Вот пример треугольника, неизвестная сторона которого чуть меньше 12:
.

Проблема 6

Две стороны треугольника имеют длины 2 и 7. Найдите все возможные длины третьей стороны.

разница $$< x <$$ сумма
$$7 -2 < х < 7+2$$

Отвечать: $$5 < х < 9$$

Проблема 7

Две стороны треугольника имеют длины 12 и 5.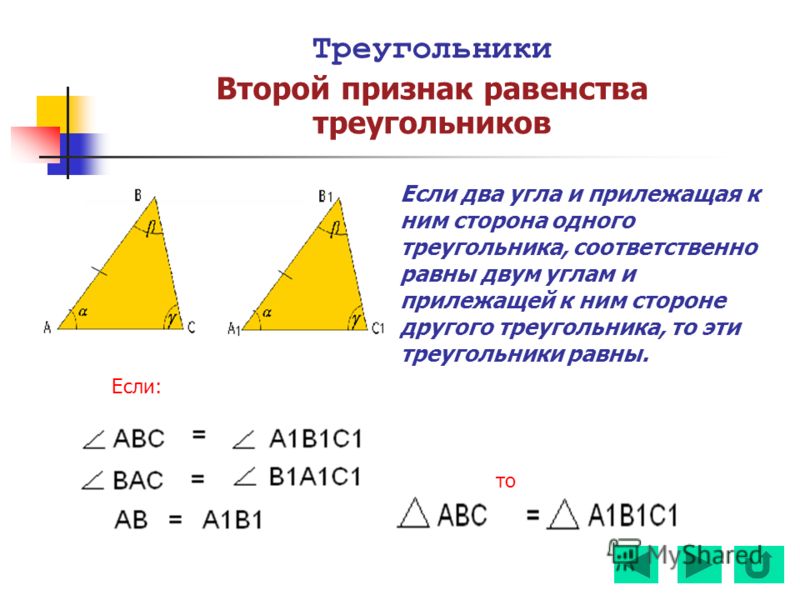 Найдите все возможные длины третьей стороны.

разница $$< x <$$ сумма
$12 -5 < x < 12 + 5$$

Отвечать: $$7 < х < 17$$

Расчет теоремы о неравенстве треугольника

Теорема о неравенстве треугольника – определение, формула, доказательство, примеры

LearnPracticeDownload

Теорема о неравенстве треугольника утверждает, что в треугольнике сумма длин любых двух сторон больше длины третьей стороны. Предположим, что a, b и c — длины сторон треугольника, тогда сумма длин сторон a и b больше, чем длина c. Точно так же b + c >

a и a + c > b. Если в любом случае заданные длины сторон не могут удовлетворить этим условиям, значит, треугольник с такими размерами построить невозможно.

1.	Что такое теорема о неравенстве треугольника?
2.	Формула теоремы о неравенстве треугольника
3.	Часто задаваемые вопросы по теореме о неравенстве треугольников

Что такое теорема о неравенстве треугольника?

Теорема о неравенстве треугольника гласит: «Сумма любых двух сторон треугольника больше его третьей стороны». Эта теорема помогает нам определить, можно ли нарисовать треугольник с заданными размерами или нет, не выполняя построения. Давайте разберемся в этом с помощью примера. Стороны треугольника ABC равны 6, 8 и 12 единицам.

Здесь AB = 6 единиц, BC = 8 единиц и CA = 12 единиц.

• Сумма сторон AB и BC равна 6 + 8 = 14 единиц и на 14 больше стороны CA (12 единиц).
• Сумма сторон ВС и СА равна 8 + 12 = 20 единиц и на 20 больше стороны АВ (6 единиц).
• Сумма сторон СА и АВ, равная 12 + 6 = 18 единиц и на 18 больше стороны ВС (8 единиц).

Таким образом, длины всех сторон удовлетворяют теореме о неравенстве треугольника. При этом не один, а все 3 случая должны удовлетворять теореме о неравенстве треугольника.

Возьмем другой пример. Проверим, удовлетворяет ли треугольник со сторонами 5 единиц, 3 единицы и 10 единиц теореме о неравенстве треугольника или нет.

Здесь

• 5 + 3 = 8 меньше 10
• 3 + 10 = 13, что больше 5
• 10 + 5 = 15, что больше 3

Мы видим, что два случая удовлетворяют теореме о неравенстве треугольника, но один случай не удовлетворяет. Это означает, что треугольника с такими длинами сторон не существует. Все три стороны должны удовлетворять теореме о неравенстве треугольника.

Формула теоремы о неравенстве треугольника

Прежде чем понять формулу, сначала нам нужно понять доказательство теоремы о неравенстве треугольника. Рассмотрим треугольник ABC, как показано ниже.

Продолжим сторону AB до точки D так, что AC = AD и △BDC образует прямоугольный треугольник с углом C.

Применяя свойство суммы углов к △BDC, получаем + ∠CBD + ∠BCD = 180°

∠BDC + ∠CBD + 90° = 180°

∠BDC + ∠CBD = 90°

Отсюда следует, что ∠BCD > ∠BDC.

Так как сторона, противоположная большему углу, длиннее, то BD > BC.

Отсюда следует:

BD > BC

AB + AD > BC

AB + AC > BC

Отсюда доказано.

Аналогично можно доказать, что AC + BC > AB и AB + BC > AC.

Итак, формула теоремы о неравенстве треугольника есть,

• AB + AC > BC
• АС + ВС > АВ
• АВ + ВС > АС

Связанные статьи о теореме о неравенстве треугольников

Ознакомьтесь со следующими статьями, чтобы узнать больше о теореме о неравенстве треугольников.

• Треугольник
• Неравенство треугольника
• Типы треугольников
• Площадь треугольника

 

Примеры теоремы о неравенстве треугольника

1. Пример 1: У Сьюзи есть три палки длиной 4 единицы, 8 единиц и 2 единицы. Используя теорему о неравенстве треугольника, выясните, может ли Сьюзи составить треугольник из этих палочек или нет?

   Решение: Треугольник, образованный данными палочками, должен удовлетворять теореме о неравенстве треугольника.

   Проверим, больше ли сумма двух сторон суммы третьей стороны.

   • 4 + 8 > 2 ⟹ 12 > 2 ⟹ ИСТИНА
   • 2 + 8 > 4 ⟹ 10 > 4 ⟹ ИСТИНА
   • 4 + 2 > 8 ⟹ 6 > 8 ⟹ ЛОЖЬ

   Итак, длины палочек не удовлетворяют теореме о неравенстве треугольника. Таким образом, Сьюзи не может составить треугольник из палочек заданной длины.

2. Пример 2: Рон хочет украсить свой треугольный флаг лентой. Две стороны флага составляют 8 единиц и 2 единицы. Используя теорему о неравенстве треугольника, узнайте, сколько ленты потребуется для третьей стороны?

   Решение: Используя теорему о неравенстве треугольника, мы можем сказать, что длина третьей стороны должна быть меньше суммы двух других сторон.

   Итак, третья сторона меньше 8 единиц + 2 единицы = 10 единиц.

   Также третья сторона не может быть меньше разницы между двумя другими сторонами.

   Итак, третья сторона больше 8 единиц — 2 единицы = 6 единиц.

   Таким образом, длина ленты может быть 7, 8 или 9 единиц.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по теореме о неравенстве треугольников

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по теореме о неравенстве треугольников

Что подразумевается под теоремой о неравенстве треугольников?

Теорема о неравенстве треугольника утверждает, что сумма любых двух сторон треугольника больше третьей стороны, и если сумма любых двух сторон треугольника не больше третьей стороны, это означает, что треугольник не существует.

Почему важна теорема о неравенстве треугольников?

Теорема о неравенстве треугольника важна для выяснения того, существует ли треугольник с данными тремя измерениями или нет. Как гласит теорема, сумма любых двух сторон должна быть больше измерения третьей стороны. Например, треугольник со сторонами 3 единицы, 4 единицы и 9 единиц не существует, поскольку он не удовлетворяет теореме о неравенстве треугольника.

• 3 + 4 > 9 ⟹ 7 > 9 ⟹ Ложь
• 4 + 9 > 3 ⟹ 13 > 3 ⟹ Верно
• 9 + 3 > 4 ⟹ 12 > 4 ⟹ Верно

Таким образом, используя теорему о неравенстве треугольника, мы можем сказать, что данные измерения не образуют треугольника.

Как теорема о неравенстве треугольников используется в реальной жизни?

Одним из примеров применения теоремы о неравенстве треугольника в реальной жизни является компания Engineers. Инженеры-строители используют теорему о неравенстве треугольника в реальной жизни. Так как их работа связана с геодезией, транспортом и градостроительством. С помощью теоремы о неравенстве треугольника вычисляют неизвестные длины и оценивают оставшуюся размерность.

Применяется ли теорема о неравенстве треугольников ко всем треугольникам?

Да, теорема о неравенстве треугольников применима ко всем треугольникам.