Найдем область определения…Алгебра Алимов 10-11 класс Упр 133 параграф 6 – Рамблер/класс
Найдем область определения…Алгебра Алимов 10-11 класс Упр 133 параграф 6 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Прив! Подскажете:
Найти область определения и множество значений функции, обратной к данной:
3) у = х3 — 1;
4) y = (x-1)3;
ответы
Хай! Да тут все просто:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
9 класс
11 класс
Химия
похожие вопросы 5
Алгебра.
9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство
Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)
ГДЗАлгебраАлимов Ш.А.Школа9 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Почему сейчас школьники такие агрессивные ?
Читали новость про 10 классника который растрелял ? как вы к этому относитесь
Новости10 классБезопасность
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос.
, шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
ГДЗЕГЭРусский языкЦыбулько И.П.
Введение в предметную область и диапазон — отношения и функции
Отношение — это набор или комбинация запрошенных наборов. Устроенная пара, обычно называемая точкой. Отношение — это группа пар входных и выходных значений, которая отображается в упорядоченной паре.
Это взаимосвязь между наборами данных.
Отношение = (Входное значение, Выходное значение)
Рассмотрим следующий пример отношения: Отношение между любимыми цветами учащихся и их именами.
(x, y) = (имя учащегося, любимый цвет)
Набор A = {(Розовый, Жениться), (Зеленый, Рон), (Красный, Стив), (Красный, Пол), (Розовый, Демон) }
Обратите внимание на набор: один и тот же цвет нравится более чем одному ученику.
Таким образом, они также позволяют одному входному значению иметь более одного соответствующего выходного значения.
Функция
Функция представляет собой набор упорядоченных пар, где каждый входной компонент имеет только ОДИН выходной компонент, связанный с ним.
Предыдущий пример отношения не является функцией, поскольку один и тот же цвет нравится более чем одному ученику.
Поскольку один и тот же вход связан с более чем одним выходом, он НЕ может быть функцией.
Примечание. Функция может иметь два входных значения, назначенных одному и тому же выходному значению, но НЕ может иметь два выходных значения, назначенных одному и тому же входному значению.
| — это функция | Не функция |
{1,5), (4,5)} | 9000 2 10101010101010101010111011111111111.10101010101010101110111011111111. , (5,4) } |
Интервал и его обозначение
Интервал — это подмножество, которое должно быть представлено на числовой строке.
Пример: Все действительные числа в диапазоне от 1 до 6 представляют собой интервал, подобный 2,5, 3, 4,567 и так далее до 6.
Включаем ли мы 1 и 6 в интервал?
Интервальная нотация — это метод составления подмножеств строки действительных чисел.
Пример : (0, 20], [1, 2], (4, 7), [4, 8), [-3, 0].
Типы интервалов
На числовой прямой есть два типа интервалов:
- Открытый интервал
- Закрытый интервал
Открытый интервал не включают конечные точки в набор. ( ) скобки представляют собой открытый интервал.
Пример: (4, 6), (6, 9), (-3, 2)
Замкнутый интервал включает в себя конечные точки в наборе.
Он представлен скобками [ ].
Пример: [3, 5], [-4, 0], [6, 9]
Пример – Установить A= {x : -4 < x <= 5 }. Здесь 4 не входит в набор, а 5 входит как x.
Итак, набор представлен как x = (-4,5].
Домен и диапазон
Домен — Все значения, которые входят в отношение или функцию, называются доменом.
Диапазон — все объекты ( output ), возникающие из отношения или функции, называются диапазоном.0003
Все используемые входные значения ( независимых значения ) формируют набор доменов.
Все используемые выходные значения ( зависимые значения ) формируют набор диапазонов.
Пример: Заданная функция: — f = 2x+1 , Найти домен, диапазон, если 1<=x<=5.
Решение:
Значения x лежат в диапазоне от 1 до 10.
Итак, домен равен {1, 2, 3, 4, 5} .
Значения f, полученные путем помещения элементов предметной области в функцию, будут находиться в диапазоне.
Итак, если x=1, то f = 2(1)+1 = 3,
, если x=2, то f = 2(2)+1 = 5,
, если x=3, то f = 2(3 )+1 =7,
, если x=4, то f = 2(4)+1 = 9,
, если x=5, то f = 2(5)+1 = 11.
Таким образом, диапазон равен { 3,5,7,9,11} .
Пример: Заданная функция:- F = x 2 -5 , Найти домен, диапазон?
Решение:
Значение x возводится в квадрат, а затем 5 вычитается из 5. Любое действительное число можно возвести в квадрат и из него вычесть 5, поэтому нет ограничений на область определения этой функции. Домен — это множество действительных чисел. Интервальная форма набора доменов будет (-∞,∞).
Пример: заданная функция:- F= (x+1)/(1-x), найти домен?
Решение:
Здесь знаменатель присутствует в функции , поэтому мы должны ограничить наш ввод, чтобы знаменатель не стал равным нулю.
Итак, мы находим значение x, где знаменатель будет равен нулю, приравнивая его к 0.
1 – x = 0
1 = x
x = 1
Итак, мы исключим 1 из нашего набора доменов. Набор доменов состоит из всех действительных чисел, кроме 1 . Интервальная форма набора доменов будет (-∞,1)∪(1,∞). где ∪ — символ объединения.
Итак, мы находим значение x, где знаменатель будет равен нулю, приравнивая его к 0.Домен и диапазон на графике
На графике координаты x (абсцисса) — это домен, а координаты y (ординаты) — диапазон.
Абсцисса — это значение домена, когда мы помещаем его в функцию, значение, которое мы получаем на выходе, будет лежать на оси Y.
Пример: На данном рисунке строка y=1 является функцией, в которой все значения x принадлежат набору доменов, и для каждого значения x мы получаем только 1 в качестве ответа. Итак, 1 — это диапазон.
Пример: Найдите область определения и область значений функции f(x) = x 2 , где -1
Решение:
Как указано в примере, x имеет ограничение от -1 до 1, поэтому область определения функции в интервальной форме равна (-1,1) .
Значения домена указаны по оси абсцисс, и, поскольку f является функцией x, значения f (ординаты), которые мы получаем, помещая значения по оси абсцисс, составят наш диапазон. Трудно найти значение y вручную для каждого x, поэтому будет легко, если мы нарисуем график и найдем диапазон (выход) функции.
Мы знаем, что выход является положительным значением для функции, включая 0 и исключая 1. Из графика мы можем сделать вывод, что диапазон функции в интервальной форме равен [0, 1).
Что такое совместный домен?Примечание: Поскольку значение x, для которого мы получаем 1 в качестве выхода, не включено в домен, поэтому мы не включаем 1 в диапазон.
Мы не используем скобки ‘[‘ или ‘]’ в домене, поскольку -1 и 1 не включены в значение x. И мы использовали «[» для 0, так как он включен в значения диапазона.
Набор, в котором элементы могут выходить на выходе, называется Содоменом.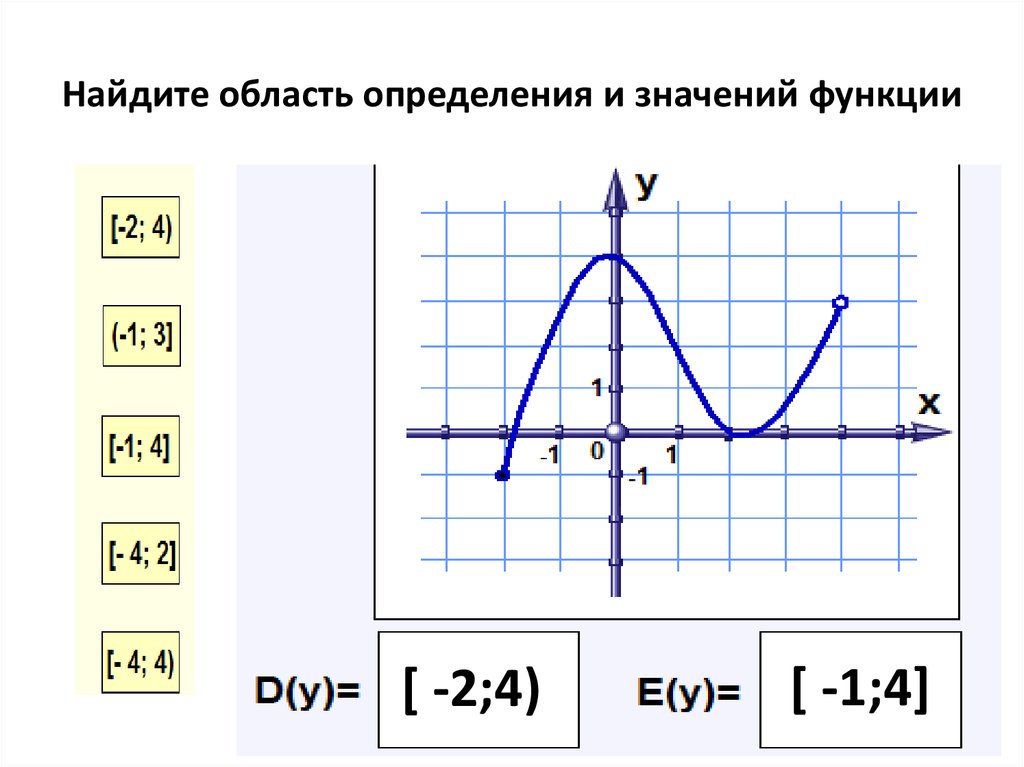
Элементы, которые являются выходным значением при вводе данных в функцию, образуют набор, называемый Range.
Все элементы, которые возможны в качестве выходных данных, но не являются результатом функций и элементов диапазона, вместе составляют набор, называемый Co-domain.
Пример: Дана функция y = 2x и если x>=1 , x<=7.
Важность совместного доменаТогда набор A = {1,2,3,4,5,6,7} является доменом,
набор B = {2,4,6,8,10,12,14} является диапазоном,
Набор C = {1,2,4,6,7,8,10,12,14,15} или {все действительные числа} является совместным доменом.
Является ли квадратный корень функцией? НЕТ, потому что когда мы ставим 16 на вход, мы получаем 4,-4 на выходе.
Мы знаем, что функция однозначна и мы не можем получить два значения из одного входа. Но если мы определим содомен как все положительные целые числа, тогда диапазон будет ограничен положительными целыми числами.
Следовательно, только 4 будут считаться выходными. Таким образом, квадратный корень будет функцией, если совместный домен определен или ограничен.
Совместный домен влияет на то, является ли данное отношение функцией или нет.
Отношение и функция на графике
Поскольку мы знаем, что координаты x являются доменом, а координаты y — диапазоном, то для любых значений x допускается только одно значение y, тогда будет рассматриваться только кривая или отношение как функция.
Проверка вертикальной линии для проверки функций: Если любая вертикальная линия может пересекаться с контуром отношения только в ОДНОЙ точке, то соединение вызывается как функция.
Если любая вертикальная линия пересекает любой график отношения более чем по одному значению, то это отношение нельзя назвать функцией.
Здесь, на рисунке ниже, линия (y=c), где c — любая константа, является функцией, поскольку любая вертикальная линия может пересекать горизонтальную линию только в одной точке.
Этот график параболы не рассматривается как функция, поскольку вертикальная линия пересекает этот график в двух точках.
Типы отношений
- Универсальные отношения
- Пустое соотношение
- Отношение идентификации
- Симметричная связь
- Отношение
- Рефлексивное отношение
- Транзитивное отношение
Рассмотрим множество A = {a, b, c}. Универсальными отношениями будут R, если R = {m, n}, где |m-n| ≥ 0.
Пустые отношения:
Отношение, в котором нет связи между любыми компонентами множества. Пустое отношение также называется недействительным отношением.
Предположим, что если множество A = {2, 3}, то отношение пустоты равно R = {m,n}, где |m-n| = 8.
Отношения тождества:
Отношение, в котором каждый компонент множества идентифицируется сам с собой
Рассмотрим множество A = {1,2,3}, отношение тождества будет I = {1,1}, {2,2}, {3,3}.
I = {(m,m), m ∈ A} Симметричные отношения:
Отношение является симметричным, если верно a=b, тогда b=a также верно. Связность R симметрична тогда и только тогда, когда (b, a) ∈ R истинно, когда (a,b) ∈ R.
R = {(1, 2), (2, 1)} множество симметричных отношений для множества A = {1, 2}.
Обратные отношения:
Обратное отношение возникает, когда набор имеет обратные пары другого набора.
Предположим, что если задать A = {(1,2),(3,4)}, то обратное соотношение будет R-1 = {(2,1), (4,3)}. R-1 = {(n, m): (m, n) ∈ R}
Рефлексивные отношения:
Отношение, в котором каждый компонент находится сам по себе.
Для набора A = {-1, 4}. Рефлексивное отношение = R = {(-1, -1), (4, 4), (-1, 4), (4, -1)}. (x,x) ∈ R
Переходные отношения:
Если (m,n) ∈ R, (n,p) ∈ R, то (m,p) ∈ R.
Рассмотрим aRb и bRc ⇒ aRc ∀ a, b, c ∈ A
Алгебраическое определение области определения функции
функция не определена.
Домен функции — это набор всех входных значений, для которых функция выдает результат. Область определения функции можно определить алгебраически, найдя значения x, которые делают функцию неопределенной.
2. Для этого приравняйте функцию к y и найдите x.
Домен — это набор всех возможных входных значений для функции. Чтобы найти область определения функции, установите функцию равной y и решите для x. Это даст вам набор всех значений x, для которых функция выдает реальное значение y.
3. Любые значения x, делающие функцию неопределенной, будут исключены из домена.
Домен функции — это набор всех входных значений, для которых функция выдает результат. Любые значения x, делающие функцию неопределенной, будут исключены из домена. Например, область определения функции f(x) = 1/x будет исключать любые значения x, которые приводят к делению на ноль.
4. В некоторых случаях может потребоваться использование квадратичной формулы для определения x.
Домен — это набор всех возможных входных значений для функции. В некоторых случаях может потребоваться использование квадратичной формулы для определения x. Квадратная формула — это математическая формула, используемая для нахождения корней квадратного уравнения.
5. Область определения функции также можно изобразить в виде графика, чтобы визуализировать, где определена функция.
Область определения функции — это набор всех входных значений, для которых функция выдает результат. Область определения функции также можно изобразить в виде графика, чтобы визуализировать, где функция определена. График области представляет собой визуальное представление входных и выходных данных функции.
Пожалуйста, внимательно прочитайте этот отказ от ответственности перед тем, как начать пользоваться сервисом. Используя эту услугу, вы подтверждаете, что вы полностью согласны и принимаете содержание этого заявления об отказе от ответственности.
Вы можете отказаться от использования сервиса, если не согласны с данным отказом от ответственности. Этот документ создается автоматически на основе общедоступного контента в Интернете, захваченного Платформой машинного обучения для ИИ. Авторские права на информацию в этом документе, такую как веб-страницы, изображения и данные, принадлежат их соответствующим авторам и издателям. Такой автоматически сгенерированный контент не отражает точку зрения или мнение Alibaba Cloud. Вы несете ответственность за определение законности, точности, подлинности, практичности и полноты содержания. Мы рекомендуем вам проконсультироваться со специалистом, если у вас есть какие-либо сомнения по этому поводу. Alibaba Cloud не несет ответственности за любые последствия использования вами контента без проверки. Если у вас есть отзывы или вы обнаружите, что в этом документе используется некоторый контент, в отношении которого у вас есть права и интересы, свяжитесь с нами по этой ссылке: https://www.alibabacloud.