Даны координаты вершин пирамиды abcd онлайн калькулятор: Аналитическая геометрия в пространстве онлайн

Площадь грани пирамиды

Задание. По координатам пирамиды найти все площади граней.

• Решение
• Видео решение

Решение получаем с помощью калькулятора.

1) Координаты векторов
Координаты векторов находим по формуле:
X = x_j — x_i; Y = y_j — y_i; Z = z_j — z_i
здесь X,Y,Z координаты вектора; x_i, y_i, z_i — координаты точки А_i; x_j, y_j, z_j — координаты точки А_j;
Например, для вектора AB
X = x₂ — x₁; Y = y₂ — y₁; Z = z₂ — z₁
X = -1-3; Y = 6-1; Z = 1-4
AB(-4;5;-3), AC(-4;0;2), AD(-3;3;-5), BC(0;-5;5), BD(1;-2;-2), CD(1;3;-7)

2) Модули векторов
Длина вектора a(X;Y;Z) выражается через его координаты формулой:

3) Угол между ребрами
Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле:

где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂
Найдем угол между ребрами AB и AC

4) Площадь грани
Площадь грани можно найти по формуле:
S=½·|a|·|b|·sin γ

Найдем площадь грани ABC
Найдем угол между ребрами AB и AC:


Площадь грани ABC

Найдем площадь грани ABD
Найдем угол между ребрами AB и AD:


Площадь грани ABD

Найдем площадь грани ACD
Найдем угол между ребрами AC и AD:


Площадь грани ACD

Найдем площадь грани BCD
Найдем угол между ребрами BC и BD:

Площадь грани BCD

5) Объем пирамиды
Объем пирамиды, построенного на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен:


Находим определитель матрицы
∆ = (-4)·(0·(-5)-3·2)-(-4)·(5·(-5)-3·(-3))+(-3)·(5·2-0·(-3)) = -70

7) Уравнение прямой
Прямая, проходящая через точки A₁(x₁; y₁; z₁) и A₂(x₂; y₂; z₂), представляется уравнениями:

Уравнение прямой AB

Уравнение прямой AC

Уравнение прямой BC

Уравнение прямой BD

Уравнение прямой CD

8) Уравнение плоскости
Если точки A₁(x₁; y₁; z₁

), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

Уравнение плоскости ABC

(x-3)(5·2-0·(-3)) — (y-1)((-4)·2-(-4)·(-3)) + (z-4)((-4)·0-(-4)·5) = 10x + 20y + 20z + 130 = 0
Уравнение плоскости ABD

(x-3)(5·(-5)-3·(-3)) — (y-1)((-4)·(-5)-(-3)·(-3)) + (z-4)((-4)·3-(-3)·5) = -16x — 11y + 3z-47 = 0
Уравнение плоскости ACD

(x-3)(0·(-5)-3·2) — (y-1)((-4)·(-5)-(-3)·2) + (z-4)((-4)·3-(-3)·0) = -6x — 26y — 12z-92 = 0
Уравнение плоскости BCD

(x+1)((-5)·(-2)-(-2)·5) — (y-6)(0·(-2)-1·5) + (z-1)(0·(-2)-1·(-5)) = 20x + 5y + 5z + 15 = 0

9) Уравнение плоскости, проходящей через точку перпендикулярно вектору
Уравнение плоскости, проходящей через точку M₀(x₀, y₀, z₀) перпендикулярно вектору N = (l,m,n), имеет вид:

l(x- x₀) + m(y- y₀) + n(z- z₀) = 0
-4(x — (-1)) + 5(y — 1) + (-3)(z — 6) = 0
-4x + 5y -3z + 9 = 0

10) Длина высоты пирамиды, проведенной из вершины A
Расстояние d от точки M₁(x₁;y₁;z₁) до плоскости Ax + By + Cz + D = 0 равно абсолютному значению величины:

11) Уравнение высоты пирамиды через вершину A
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:

12) Угол между прямой AB и плоскостью ABC
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле

13) Угол между плоскостью ABC и плоскостью ABD

Косинус угла между плоскостью A₁x + B₁y + C₁ + D = 0 и плоскостью A₂x + B₂y + C₂ + D = 0 равен углу между их нормальными векторами N₁(A₁, B₁, C₁) и N₂(A₂, B₂, C₂):

Нахождение элементов в пирамиде.

Контрольные онлайн



Образовательные онлайн сервисы: теория и практика

• Главная
• Примеры
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
• Видео-уроки
  • Математический анализ
  • Векторная алгебра и Аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование. Методы оптимизации
• Готовые работы
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
  • Другое
• Контакты

Полезные материалы:

• Учебники
• Справочники
• Онлайн калькуляторы

• Помощь в решении
• Онлайн занятия в Zoom

Нахождение элементов в пирамиде

Даны вершины пирамиды
  и точка .
   Найти:
   а) длину ребра ;
   б) косинус угла между рёбрами  и ;
   в) площадь грани ABC;
   г) объём пирамиды;
   д) уравнение прямой, на которой лежит ребро;
   е) уравнение прямой, на которой лежит высота  пирамиды, опущенная из вершины ;
Выяснить, лежат ли точки  и  по одну сторону плоскости грани
или по разные?

 Решение
а) Длину  найдём по формуле расстояния между двумя точками

б) Угол  между рёбрами и  будет равен углу между векторами  и
Введём в рассмотрение векторы  и  и найдём их координаты:



в) Площадь грани ABС (площадь треугольника АВС)
Введём в рассмотрение векторы  и  и найдём их координаты:
,
Найдём
Далее  и
г) Объём пирамиды
, ,
Найдём =

д) Прямая, на которой лежит ребро , проходит через точки  и . Запишем уравнение этой прямой, воспользовавшись уравнением прямой, проходящей через две точки  и :
Для решаемой задачи  или
е) Прямая, на которой лежит высота пирамиды , проходит через точку  перпендикулярно плоскости BCD. 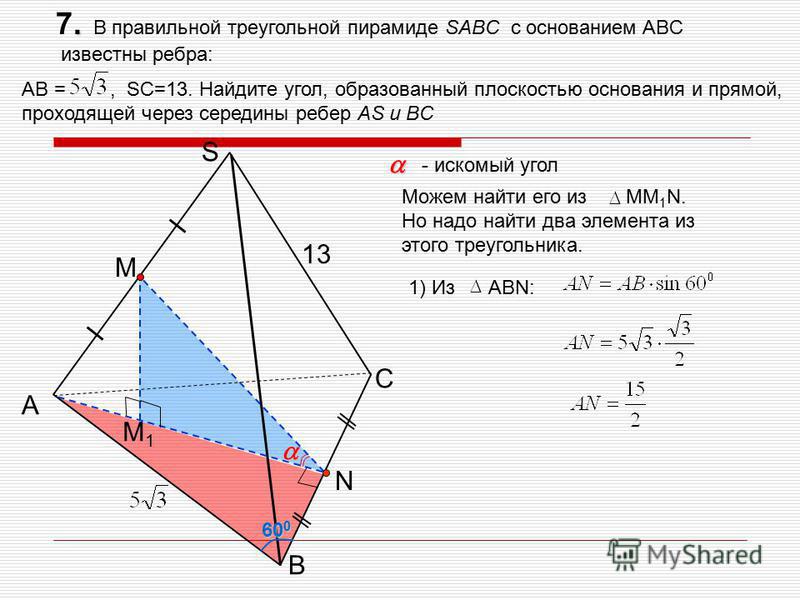Следовательно, нормальный вектор плоскости BCD будет являться направляющим вектором для прямой.
Уравнение плоскости BCD найдём, используя уравнение плоскости, проходящей через три заданные точки :
Для решаемой задачи это точки , ,  и, следовательно, уравнение  

,  ,  .
Вектор  является нормальным вектором плоскости , следовательно, этот вектор является направляющим вектором для прямой, проходящей через точку  перпендикулярно плоскости . Уравнение этой прямой
Выясним, лежат ли точки  и  по одну сторону плоскости грани  или по разные?

Найдём уравнение плоскости грани  как уравнение плоскости, проходящей через точку  и имеющей нормальный вектор :

.
Для решаемой задачи , а  найден в п. в) решаемой задачи. Следовательно, уравнение плоскости грани : или .
Для всех точек , лежащих на плоскости, будет выполняться равенство , для точек, лежащих по одну сторону плоскости, будет выполняться неравенство , для точек, лежащих по другую сторону плоскости, — неравенство .
Для точки  выполняется неравенство .
Для точки  выполняется неравенство .

   Следовательно, точки  и  лежат по одну сторону плоскости грани .



Задать вопрос
Заказать помощь

Отзывы

+7-911-7987704

vk.com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96.ru



DSQ: вычисление объема тетраэдра

Все математические ресурсы GMAT

22 диагностических теста 693 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

GMAT Math Help » Вопросы о достаточности данных » Геометрия » Прямоугольные тела и цилиндры » Тетраэдры » DSQ: Расчет объема тетраэдра

Пирамида 1 в трехмерном координатном пространстве имеет в качестве основания квадрат с вершинами в начале координат, , , и , и вершиной в точке ; Основанием пирамиды 2 является квадрат с вершинами в начале координат , , и , а вершина — в точке .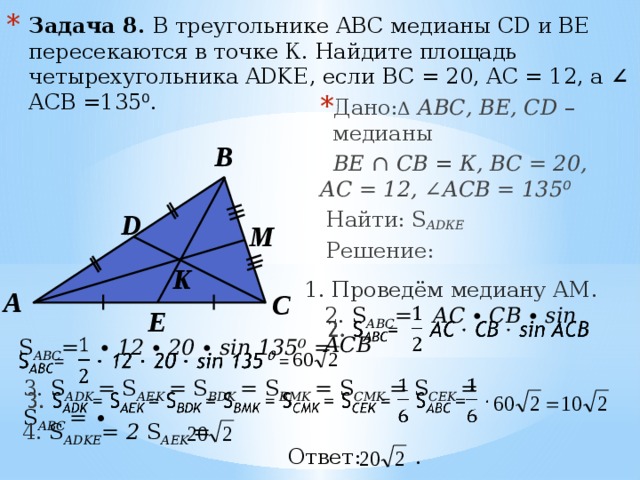 Все шесть переменных представляют собой положительные величины. Какая пирамида имеет больший объем?

Утверждение 1:   и 

Утверждение 2:   

Возможные ответы:

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно для ответа на вопрос.

ОБЕИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 1 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 2 НЕ достаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

Правильный ответ:

ТОЛЬКО Утверждение 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждение 1 НЕ достаточно, чтобы ответить на вопрос.

Пояснение:

Объем пирамиды равен одной трети произведения ее высоты на площадь основания. Две пирамиды имеют одинаковое основание, поэтому пирамида с большей высотой будет иметь больший объем (а если их высоты равны, то их объемы равны).

Пирамида 1 показана ниже:

Основание пирамиды находится в -плоскости, поэтому высота пирамиды – это расстояние по перпендикуляру от вершины  к этой плоскости; это -координата, . Основание пирамиды представляет собой квадрат со стороной 10, поэтому его площадь равна квадрату 10, или 100. Таким образом, объем пирамиды 1 

Аналогично, объем пирамиды 2 равен

. Задача требует от нас определить, какое из значений  и  больше.

Предположим, только оператор 1. Так как, мы можем умножить все выражения на , чтобы получить диапазон для объема Пирамиды 1:

Аналогично, поскольку мы можем умножить все выражения на 36, чтобы получить диапазон значений для объема пирамиды 2: определить наверняка, какая пирамида имеет больший объем.

Предположим, что используется только утверждение 2. Тогда из  и   легко следует, что

,

и, следовательно, Пирамида 2 имеет больший объем.

Сообщить об ошибке

Примечание. Рисунок НЕ выполнен в масштабе, но вы можете предположить  и .

На приведенном выше рисунке пирамида с прямоугольным основанием вписана внутрь прямоугольной призмы; его вершины . Каков объем пирамиды?

Утверждение 1: треугольник 30-60-90 имеет площадь.

Утверждение 2. Площадь равнобедренного прямоугольного треугольника равна 50.

Возможные ответы:

Утверждение 1 ОДНО ОДНО достаточно, чтобы ответить на вопрос, но ОДНО утверждение 2 НЕ достаточно, чтобы ответить на вопрос.

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ОБЕИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно, чтобы ответить на вопрос.

Правильный ответ:

ОБОИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

Объяснение:

Объем пирамиды составляет одну треть произведения высоты  и площади ее прямоугольного основания, то есть ; то есть

Предположим только утверждение 1. имеет площадь , которая равна половине произведения длины более короткого и более длинного катетов. Кроме того, по теореме 30-60-90, , поэтому, объединяя эти утверждения,

и .

Тем не менее, у нас нет возможности узнать, поэтому объем не может быть подсчитан.

Предположим, что используется только оператор 2. равнобедренный, значит ; опять же, поскольку площадь прямоугольного треугольника равна половине произведения длин его катетов,

Однако у нас нет возможности это выяснить.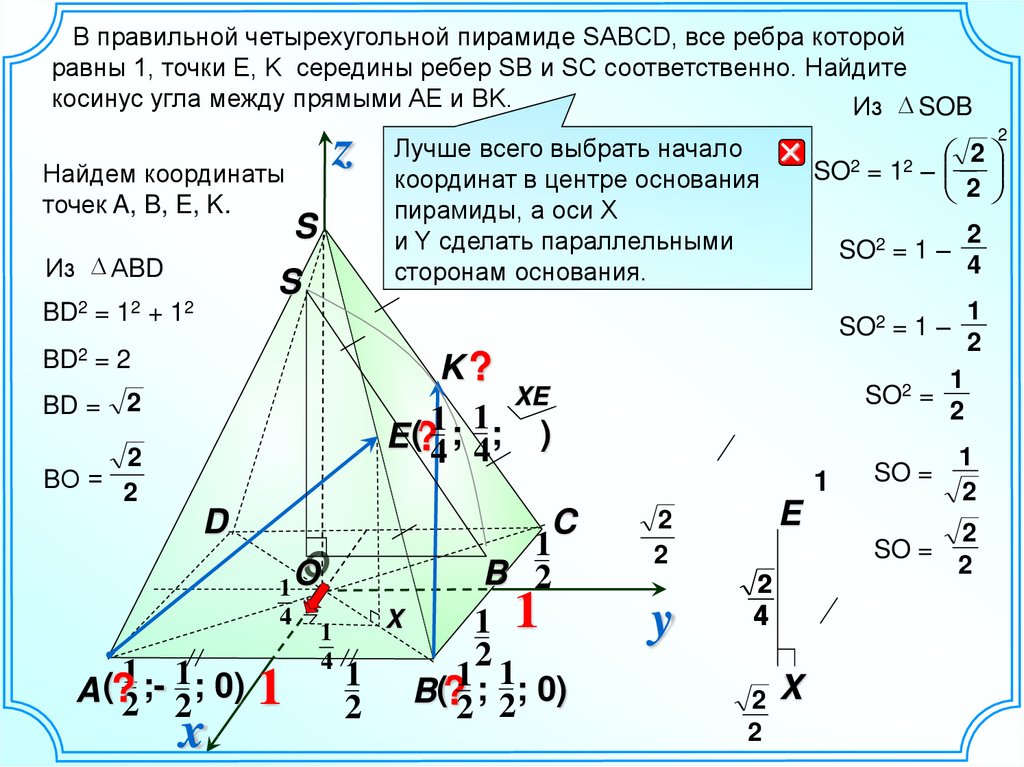

Два утверждения вместе дают все три из , , и , поэтому объем можно рассчитать как положительные значения . Каков объем твердого тела?

Утверждение 1: 

Утверждение 2: 

Возможные ответы:

ОБА утверждения ВМЕСТЕ достаточны для ответа на вопрос, но НИ ОДНОГО утверждения недостаточно для ответа на вопрос.

ТОЛЬКО Утверждения 1 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 2 НЕ достаточно, чтобы ответить на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно, чтобы ответить на вопрос.

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

Правильный ответ:

ТОЛЬКО Утверждение 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждение 1 НЕ достаточно, чтобы ответить на вопрос.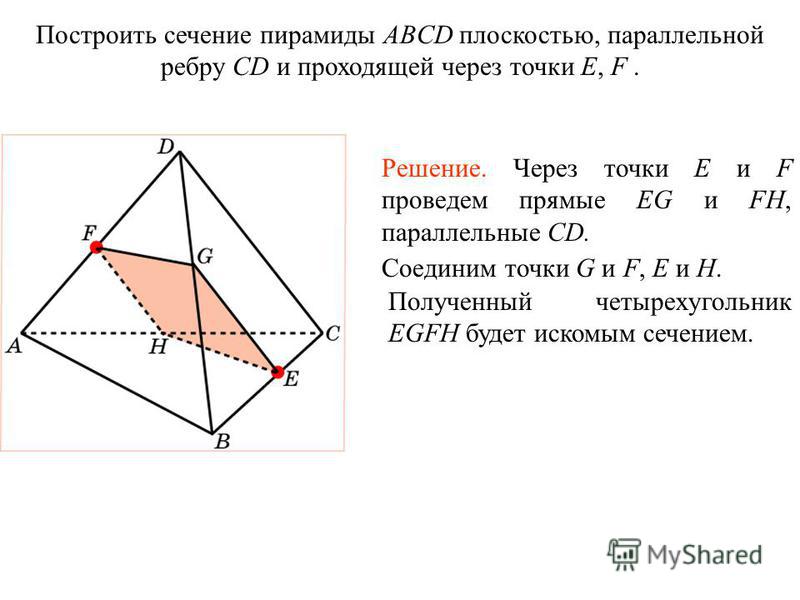

Пояснение:

 

Описанная фигура представляет собой треугольную пирамиду или тетраэдр в координатном трехмерном пространстве ниже.

Основание пирамиды можно рассматривать как треугольник с тремя известными координатами , и , а площадь его основания равна половине произведения длин его катетов, что составляет 

.

Объем пирамиды равен одной трети произведения площади ее основания, равной 48, и высоты, равной расстоянию по перпендикуляру от неизвестной точки до основания. Поскольку основание полностью находится в -плоскости, это расстояние является -координатой вершины, то есть . Следовательно, единственное, что нужно для определения объема пирамиды, это ; эта информация представлена ​​в Отчете 2, но не в Отчете 1.

Сообщить об ошибке

На приведенной выше диаграмме тетраэдр — треугольная пирамида — с вершинами показан внутри куба. Назовите объем тетраэдра.

Утверждение 1.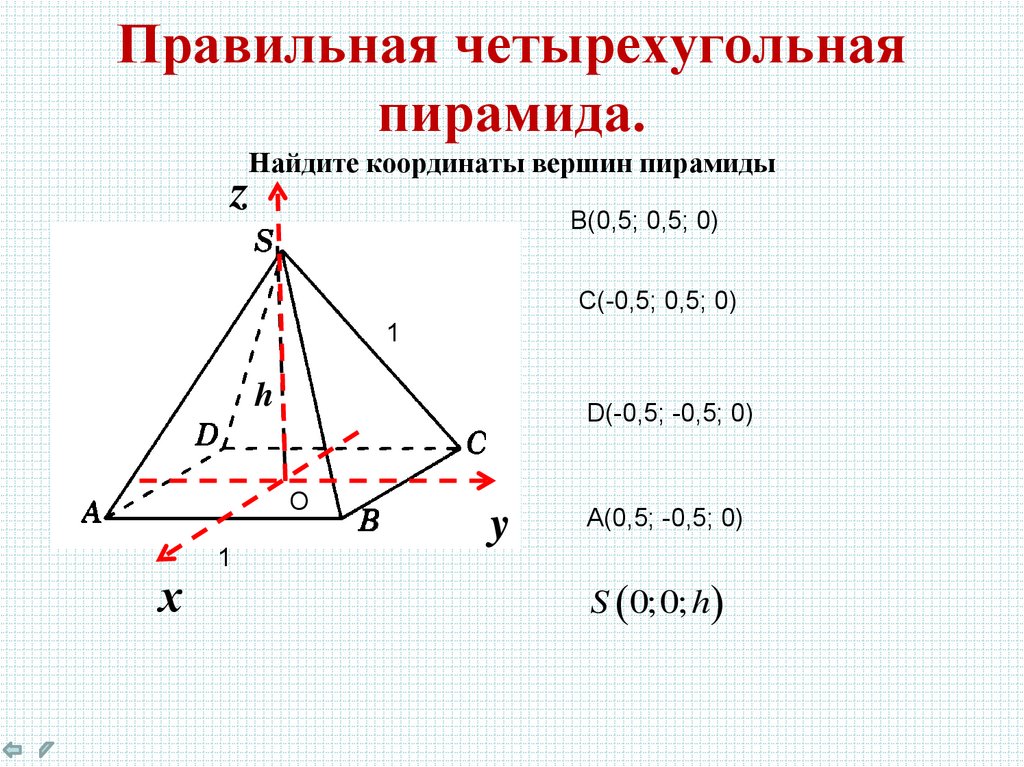 Периметр квадрата равен 16.

Утверждение 2. Площадь квадрата равна 8.

Возможные ответы:

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно, чтобы ответить на вопрос.

ОБЕИХ утверждений ВМЕСТЕ достаточно для ответа на вопрос, но НИ ОДНОГО утверждения НЕ достаточно для ответа на вопрос.

ТОЛЬКО Утверждения 1 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 2 НЕ достаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

Правильный ответ:

ОДНО ЛЮБОЕ утверждение достаточно для ответа на вопрос.

Объяснение:

Объем пирамиды составляет одну треть произведения высоты и площади ее основания, которое, в свою очередь, поскольку здесь треугольник прямоугольный, составляет половину произведения длин и  контуров.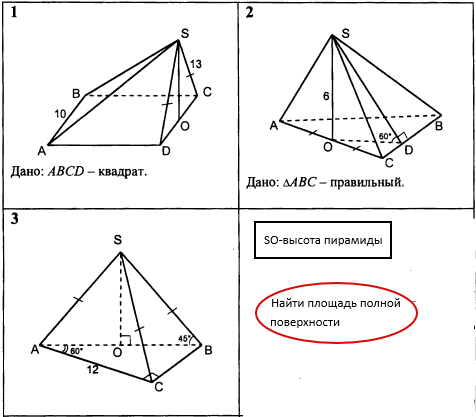 Поскольку призма на рисунке представляет собой куб, три длины равны, поэтому мы можем установить для каждой из них значение . Объем пирамиды равен

Следовательно, зная длину одного ребра куба, достаточно определить объем пирамиды.

Предположим, что используется только оператор 1. Поскольку периметр квадрата равен 16, каждая сторона квадрата и каждое ребро куба имеют одну четвертую эту меру, или 4.

Предположим только утверждение 2. имеет конгруэнтные ноги, каждая меры; так как его площадь равна 8,  можно найти следующим образом:

Из любого утверждения можно вычислить длину каждой стороны куба, а затем и объем пирамиды.

Сообщить об ошибке

Примечание: Рисунок выполнен НЕ в масштабе.

См. рисунок выше, на котором изображен тетраэдр или треугольная пирамида. Каков объем тетраэдра?

Утверждение 1: равнобедренный треугольник с площадью 64.

Утверждение 2: равносторонний треугольник с периметром 48. достаточно для ответа на вопрос.

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 1 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 2 НЕ достаточно, чтобы ответить на вопрос.

Правильный ответ:

ОБОИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

Объяснение:

Каждое выражение дает достаточно информации об одном треугольнике, чтобы определить его площадь, углы и длины сторон, но не дает никакой информации о трех других треугольниках, кроме одной стороны.

Предположим, что оба утверждения известны. является равнобедренным треугольником с площадью 64. Так как , мы можем найти эту общую длину стороны, используя формулу площади для треугольника, с этими длинами в качестве высоты и основания:

.

Это длина обоих слов  и .

По теореме 45-45-90, имеет длину, умноженную на это, или .

Так как  является равносторонним треугольником, . Так как  это прямоугольный треугольник, , и , треугольник также является равнобедренным, и ; по аналогичному аргументу, .

Объем пирамиды можно рассчитать. Его основание, которое конгруэнтно , имеет площадь 64, а его высота ; умножьте одну треть на их произведение, чтобы получить объем.

Сообщить об ошибке

Пирамида 1 в трехмерном координатном пространстве имеет в качестве основания квадрат с вершинами в начале координат, , , и , и вершиной в точке ; Основанием пирамиды 2 является квадрат с вершинами в начале координат , , и , а вершина — в точке . Все шесть переменных представляют собой положительные величины. Какая пирамида имеет больший объем?

Утверждение 1:  

Утверждение 2:  

Возможные ответы:

ОДНО Утверждение 1 достаточно, чтобы ответить на вопрос, но ОДНО Утверждение 2 НЕ достаточно, чтобы ответить на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно, чтобы ответить на вопрос.

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ОБЕИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

Правильный ответ:

ТОЛЬКО Утверждение 1 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждение 2 НЕ достаточно, чтобы ответить на вопрос.

Пояснение:

Объем пирамиды равен одной трети произведения ее высоты на площадь основания.

Пирамида 1 показана ниже:

Основание пирамиды находится на -плоскости, поэтому высота пирамиды – это расстояние по перпендикуляру от вершины  к этой плоскости; это -координата, . Основание пирамиды представляет собой квадрат со стороной 10, поэтому его площадь равна квадрату 10, или 100. Таким образом, объем пирамиды 1 равен

Аналогично, объем пирамиды 2 равен

Следовательно, задача спрашивает нас, какое количество из  к  больше.

Предположим, что используется только оператор 1. Если , то и

 

Так как , следует, что , и  — то есть Пирамида 2 имеет больший объем.

Утверждение 2 само по себе дает недостаточную информацию. Возьмем два набора значений и , которые в сумме дают 25:

Случай 1:

В этом случае пирамида 2 имеет большую высоту и большую площадь основания, поэтому легко следует, что пирамида 2 имеет больший объем .

Случай 2:

Тогда объем пирамиды 1 равен

, а объем пирамиды 2 равен

Это увеличивает объем Пирамиды 1.

Сообщить об ошибке

Примечание. Рисунок НЕ выполнен в масштабе, но вы можете предположить .

На приведенном выше рисунке пирамида с прямоугольным основанием вписана внутрь прямоугольной призмы; его вершины .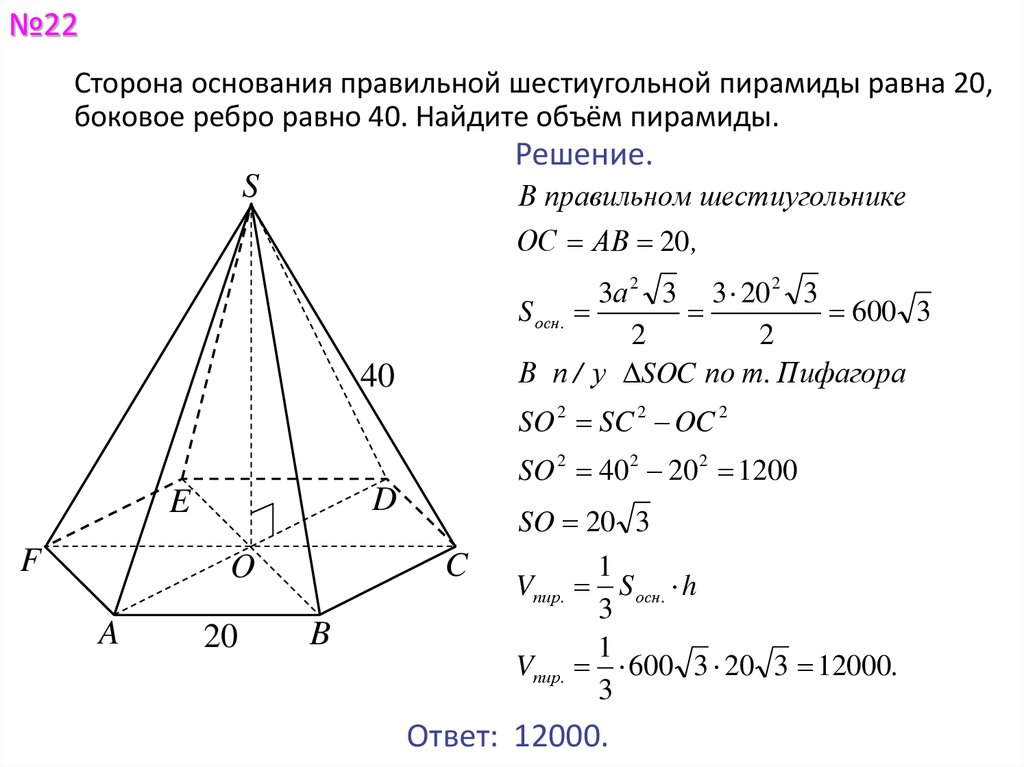 Каков объем пирамиды?

Утверждение 1. Гипотенуза треугольника 30-60-90 имеет длину 16.

Утверждение 2. Гипотенуза прямоугольного треугольника 45-45-90 имеет длину.

Возможные ответы:

ТОЛЬКО Утверждение 1 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждение 2 НЕ достаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно, чтобы ответить на вопрос.

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ОБЕИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

Правильный ответ:

ОБОИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

Объяснение:

Объем пирамиды составляет одну треть произведения высоты  и площади ее прямоугольного основания, то есть ; то есть

Предположим только утверждение 1. представляет собой треугольник 30-60-90 с гипотенузой длины 16. По теореме о треугольнике 30-60-90 длина короткого катета вдвое меньше, или 8, а длина длинного катета больше, чем длина , или . Однако определить длину  нельзя.

Предположим, что используется только оператор 2. представляет собой прямоугольный треугольник 45-45-90 с гипотенузой длины . По теореме 45-45-90 его ноги и каждая из них имеют длину, деленную на , что равно ; однако длину  нельзя определить.

Из двух утверждений вместе мы можем определить, что  и , и вычислить объем:

.

Сообщить об ошибке

Примечание. Рисунок выполнен НЕ в масштабе.

На приведенном выше рисунке показана прямоугольная призма с вписанной тетраэдр,  или треугольная пирамида с вершинами .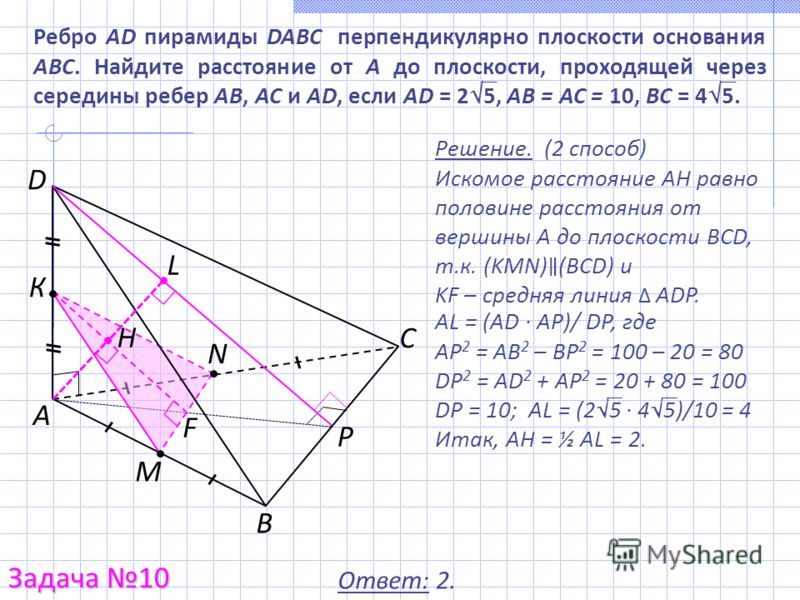 Каков объем тетраэдра?

Утверждение 1: Площадь равнобедренного прямоугольного треугольника 32.

Утверждение 2: 

Возможные ответы:

ОДНО Утверждение 1 достаточно, чтобы ответить на вопрос, но ОДНО Утверждение 2 НЕ достаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно, чтобы ответить на вопрос.

ОБЕИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

Правильный ответ:

ОБОИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

Объяснение:

Объем пирамиды составляет одну треть произведения высоты, то есть , и площади основания; это основание, будучи прямоугольным треугольником, равно половине произведения длин его катетов, или  и .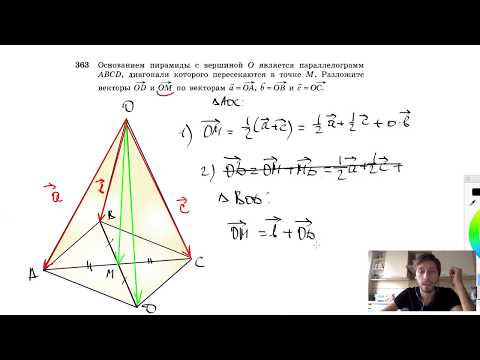 Следовательно,

или

Только из утверждения 1 мы знаем, что оно равнобедренное и имеет площадь 32; поэтому длину его общей ноги можно определить по формуле площади:

Следовательно, . Однако определить ничего нельзя.

Утверждение 2 само по себе не дает ни одной из трех искомых длин или какой-либо информации, необходимой для их поиска.

Однако заявление 2 вместе с информацией из заявления 1 можно использовать для поиска . Из Заявления 2,  и из Заявления 1, ; для нахождения можно использовать теорему Пифагора. Следовательно, можно найти все три из , и , и можно рассчитать объем пирамиды.

Сообщить об ошибке

Правильный тетраэдр — это тело с четырьмя гранями, каждая из которых представляет собой равносторонний треугольник.

Назовите объем правильного тетраэдра.

Утверждение 1. Каждое ребро имеет длину 8.

Утверждение 2. Каждая грань имеет площадь .

Возможные ответы:

ТОЛЬКО Утверждение 1 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждение 2 НЕ достаточно, чтобы ответить на вопрос.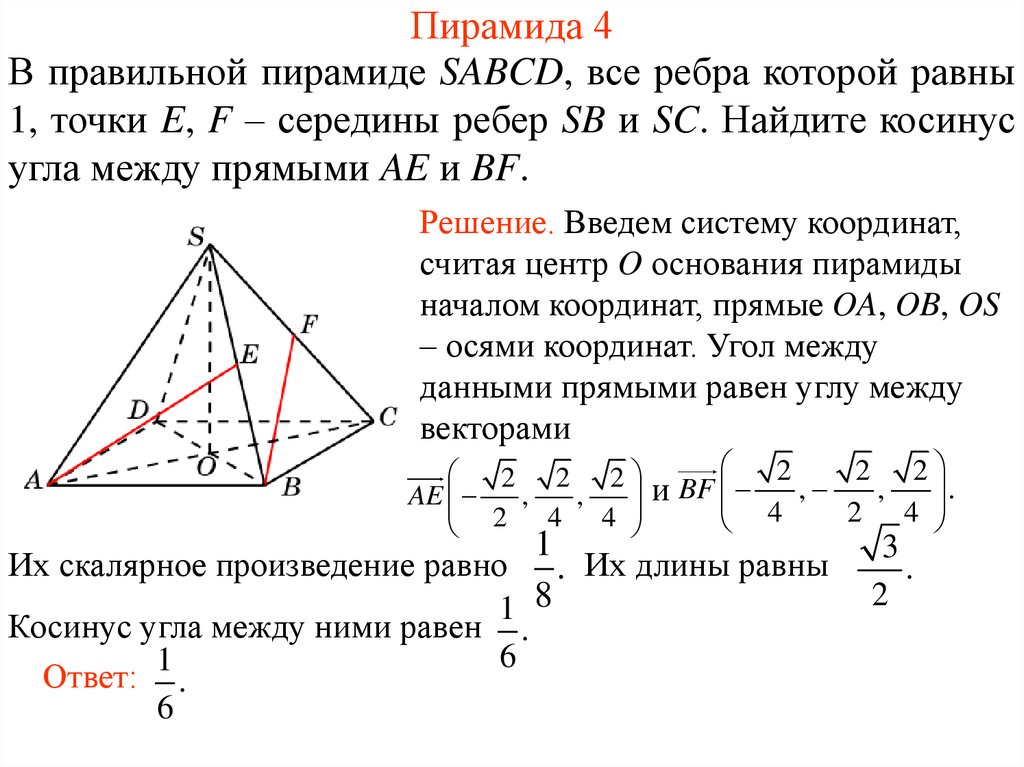

ОБЕИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

ОДНО ЛЮБОЕ утверждение достаточно, чтобы ответить на вопрос.

ТОЛЬКО Утверждения 2 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 1 НЕ достаточно, чтобы ответить на вопрос.

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

Правильный ответ:

ОДНО ЛЮБОЕ утверждение достаточно для ответа на вопрос.

Объяснение:

Формула объема правильного тетраэдра с учетом длины каждого ребра:

.

Заявление 1 предоставляет информацию в явном виде. Утверждение 2 дает средства для нахождения , так как если подставить вместо  в формуле равностороннего треугольника:

,

можно определить значение  .

Сообщить об ошибке

Примечание. Рисунок выполнен НЕ в масштабе.

На приведенном выше рисунке показана прямоугольная призма с вписанным тетраэдром ,  или треугольной пирамидой с вершинами. Каков объем тетраэдра?

Утверждение 1. Площадь прямоугольника 200.

Утверждение 2. Площадь прямоугольника 120. .

ОДНО ЛЮБОЕ утверждение достаточно для ответа на вопрос.

ТОЛЬКО Утверждения 1 достаточно, чтобы ответить на вопрос, но ТОЛЬКО Утверждения 2 НЕ достаточно, чтобы ответить на вопрос.

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

ОБЕИХ утверждений ВМЕСТЕ достаточно, чтобы ответить на вопрос, но НИ ОДНОГО утверждения недостаточно, чтобы ответить на вопрос.

Правильный ответ:

ОБА утверждения ВМЕСТЕ недостаточны для ответа на вопрос.

Объяснение:

Объем пирамиды составляет одну треть произведения высоты, то есть , и площади основания; это основание, будучи прямоугольным треугольником, равно половине произведения длин его катетов, или  и . Следовательно,

или

Нам нужно знать значения , , и , чтобы найти объем пирамиды. Мы показываем, что два утверждения дают недостаточную информацию, исследуя два сценария.

Случай 1:

Прямоугольник имеет площадь.

Прямоугольник имеет площадь .

Объем пирамиды

Случай 2:

Прямоугольник имеет площадь.

Прямоугольник имеет площадь.

Объем пирамиды равен

В каждом случае выполняются условия обоих утверждений, но объемы пирамид различаются.

Сообщить об ошибке

← Предыдущий 1 2 3 Следующий →

Уведомление об авторских правах

Все математические ресурсы GMAT

22 диагностических теста 693 практических теста Вопрос дня Карточки Learn by Concept

Калькулятор ортоцентра + онлайн-решатель с бесплатными шагами

Калькулятор ортоцентра — это бесплатный онлайн-калькулятор, который иллюстрирует пересечение трех высот треугольника.

Для всех треугольников ортоцентр служит ключевой точкой пересечения посередине. 9Положение 0019 ортоцентра прекрасно описывает тип изучаемого треугольника.

Что такое калькулятор ортоцентра?

Калькулятор ортоцентра — это онлайн-инструмент, используемый для расчета центроида или точки, где встречаются высоты треугольника.

Поскольку высота треугольника определяется как линия, проходящая через каждую его вершину и перпендикулярная другой стороне, существует три возможных высоты: по одной из каждой вершины.

Мы можем утверждать, что ортоцентр треугольника является местом, в котором последовательно пересекаются все три отметки.

Как использовать калькулятор ортоцентра

Вы можете использовать калькулятор ортоцентра , следуя этим подробным инструкциям, и калькулятор автоматически покажет вам результаты.

Шаг 1

Заполните соответствующее поле ввода тремя координатами (A, B и C) треугольника.

Шаг 2

Нажмите кнопку «Вычислить ортоцентр» , чтобы определить центр для заданных координат, а также отобразится полное пошаговое решение для калькулятора ортоцентра .

Как работает калькулятор ортоцентра?

Калькулятор ортоцентра использует два пересечения высот для расчета третьего пересечения. Согласно математике, ортоцентр треугольника — это точка пересечения, где сходятся все три высоты треугольника. Мы знаем, что существуют различные виды треугольников, включая разносторонние, равнобедренные и равносторонние треугольники.

Для каждого типа ортоцентр  будет отличаться. Ортоцентр расположен на треугольнике для прямоугольного треугольника, вне треугольника для тупоугольного треугольника и внутри треугольника для остроугольного треугольника.

Ортоцентр любого треугольника можно вычислить за 4 шага, которые перечислены ниже.

Шаг 1: Используйте следующую формулу для определения наклона сторон треугольника

Наклон линии $= \frac{y_2−y_1}{x_2−x_1}$

Шаг 2: Определите перпендикулярный наклон сторон, используя следующую формулу:

Перпендикулярный наклон линии $=− \frac{1}{Наклон линии}$

Шаг 3: Используя Следуя формуле, найдите уравнение для любых двух высот и их соответствующих координат: y−y1=m(x − x1)

Шаг 4: Решение уравнений для высоты (любые два уравнения высоты из шага 3)

Ортоцентр Свойства и мелочи

Некоторые интересные характеристики ортоцентра включают:

• Коррелирует с центром описанной окружности, центром вписанной стороны и центром тяжести равностороннего треугольника.
• Соотносится с прямоугольной вершиной прямоугольного треугольника.
• Для остроугольных треугольников лежит внутри треугольника.
• В тупоугольных треугольниках лежит вне треугольника.

Решенные примеры

Давайте рассмотрим несколько примеров, чтобы лучше понять Калькулятор ортоцентра .

Пример 1

Треугольник ABC имеет координаты вершин: A = (1, 1), B = (3, 5), C = (7, 2). Найдите его ортоцентр.

Решение

Найти уклон:

Уклон стороны AB \[ = \frac{(5 – 1) }{(3 – 1)} = 2 \]

Рассчитать уклон перпендикулярной линии:

Перпендикуляр наклон в сторону AB \[ = – \frac{1}{2} \]

Найдите уравнение прямой:

\[ y – 2 = – \frac{1}{2} (x – 7) \]

так

у = 5,5 – 0,5 (х)

Повторить для другой стороны, например, BC;

Боковой уклон БЛ \[= \frac{ (2 – 5) }{(7 – 3)} = – \frac{3}{4} \]

Перпендикулярный уклон в сторону БЛ \[= \frac{4 {3} \]

\[ y – 1 = \frac{4}{3} (x – 1) \] так \[ y = – \frac{1}{3} + \frac{4}{ 3} (x) \]

Решить систему линейных уравнений:

y = 5,5 – 0,5 . х

и
у = -1/3 + 4/3 . x 

Итак,

\[5,5 – 0,5 \times x = – \frac{1}{3} + \frac{4}{3} \times x \]

\[ \frac{35}{6} = x \times \frac{11}{6} \]

\[ x = \frac{35}{11} \приблизительно 3,182 \]

Подстановка x в любое уравнение даст нам:

\[ y = \frac{43}{11} \приблизительно 3,909 \]

Пример 2

Найдите координаты ортоцентра треугольника, вершины которого равны (2, -3) ( 8, -2) и (8, 6).

Решение

Даны точки A (2, -3) B (8, -2), C (8, 6) 
Теперь нам нужно поработать над наклоном переменного тока. Оттуда мы должны определить перпендикулярную линию через наклон B.
Наклон АС \[= \frac{(y2 – y1)}{(x2 – x1)}\]

Наклон АС \[= \frac{(6 – (-3))}{(8 – 2 )} \]
Наклон АС \[= \frac{9}{6} \]
Наклон АС \[= \frac{3}{2} \]

Наклон высоты BE \[= – \ frac{1}{наклон AC} \]
Наклон высоты BE \[ = – \frac{1}{(\frac{3}{2})} \]
Наклон высоты BE \[ = – \frac{2}{3} \]
Уравнение высоты BE задается как:
\[(y – y1) = m (x – x1) \]
Здесь B (8, -2) и $m = \frac{2}{3}$
\[ y – (-2) = (-\frac{2}{3})(x – 8) \]

3(у + 2) = -2 (х – 8)
3у + 6 = -2х + 16
2х + 3у -16 + 6 = 0
– 2х0 = 0

Теперь мы должны вычислить наклон BC.