Тригонометрические формулы треугольника: Тригонометрические функции острого угла прямоугольного треугольника — урок. Геометрия, 8 класс.

Тригонометрия формулы. Формулы суммы и разности тригонометрических функций.

• Альфашкола
• Статьи
• Формулы суммы и разности тригонометрических функций

Тригонометрия — это  измерение углов и сторон треугольников. Исторически сложилось так, что треугольный подход к тригонометрии является более ранним, чем круговой подход, который сейчас преподаётся в наших школах. Таким образом, первоначально была определена тригонометрия для определения отношений между элементами треугольника. В треугольнике есть шесть основных элементов: 3 стороны и 3 угла. Тригонометрия часто вызывает затруднение в решение тестовых задач по ЕГЭ.  Существует большое количество тригонометрических тождеств. 2 (α) — 1} {2ctg (α)}\)

 

Формулы разности и суммы:

\(sin (α + β) = sinα *cos β + cosα*sin β\)

\(cos (α + β) = cos α*cos β — sin α *sin β\)

\(sin (α — β) = sin α *cos β — cos α* sin β\)

\(cos (α — β) = cos α*cos β + sin α*sin β.\)

\(cos α + cos β = 2cos((α + β)/2) cos((α – β)/2)\)

\(cos α – cos β = 2sin((α + β)/2) sin((β – α)/2)\)

\(sin α + sin β = 2sin((α + β)/2) cos((α – β)/2)\)

\(sin α – sin β = 2sin((α – β)/2) cos((α + β)/2)\)

\(tg α + tg β = sin(α + β)/(cos α *cos β)\)

\(tg α – tg β = sin(α – β)/(cos α *cos β)\)

\(ctg α ± ctg β = sin(β ± α)/(sin α* sin β)\)

 

Тригонометрия — это методика поиска некоторых неизвестных элементов треугольника, если данные содержат достаточное количество измерений для однозначного определения поиска. Площадь треугольника можно найти из формулы \(s=\frac{a*b*sin(y)}{2}\)

Например, нам даны площадь и периметр треугольника, а нам нужно найти площадь описанной окружности.

Зная формулу \(S =\frac{ (a + b + c)r} {2 }.\), мы можем выразить \(r\) из формулы, подставив полученные значения.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Дмитрий Иванович Макаренко

Репетитор по математике

Стаж (лет)

Образование:

Харьковский педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Владислав Николаевич Серегин

Репетитор по математике

Стаж (лет)

Образование:

Московский государственный университет имени М. В.Ломоносова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Фёдор Владимирович Каузов

Репетитор по математике

Стаж (лет)

Образование:

Государственное образовательное учреждение высшего профессионального образования Ивановский государственный университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Предметы

• Математика
• Физика
• Химия
• Русский язык
• Английский язык
• Обществознание
• История России
• Биология
• География
• Информатика

Специализации

• Подготовка к ОГЭ по математике
• Подготовка к олимпиадам по химии
• Репетитор для подготовки к ОГЭ по физике
• Репетитор для подготовки к сочинению ЕГЭ по русскому
• Грамматика русского языка
• Подготовка к ОГЭ по английскому языку
• Английский язык для начинающих
• Репетитор по английскому для взрослых
• Репетитор для подготовки к ЕГЭ по истории
• Подготовка к ОГЭ по биологии

Похожие статьи

• Как складывать числа в столбик?
• О чем важно помнить, чтобы решать уравнения без труда
• Рациональные уравнения
• ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 3)
• ЕГЭ по математике, базовый уровень. Преобразование иррациональных выражений
• 5 советов по подготовке к ЕГЭ по математике
• Как подготовиться к самостоятельной по математике без напряга?
• Переезд в другой город на учебу: как освоиться в нем быстро и без стресса?

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Текст с ошибкой:

Расскажите, что не так

Определения тригонометрических функций в прямоугольном треугольнике

• Главная
• Справочник
• Тригонометрия
• Определения тригонометрических функций в прямоугольном треугольнике

• Графический метод запоминания
• Доказательство тригонометрической формулы для острого угла в прямоугольном треугольнике

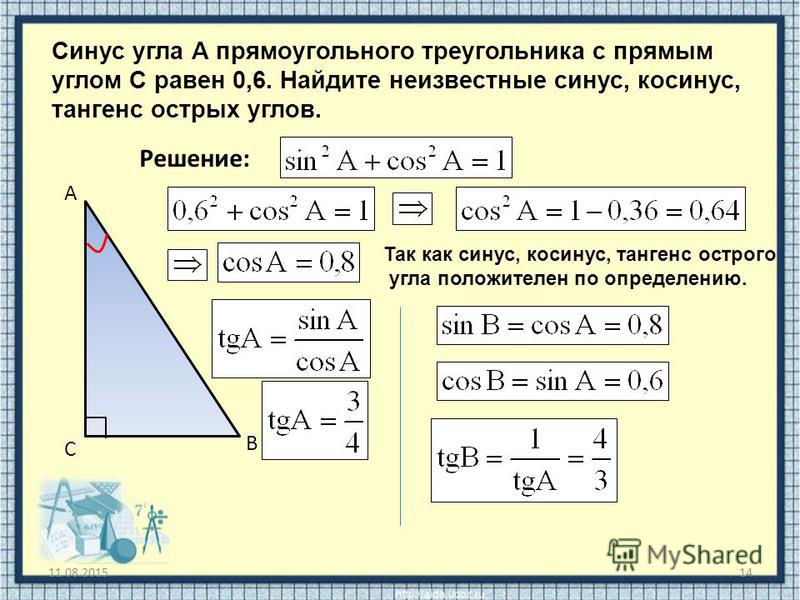
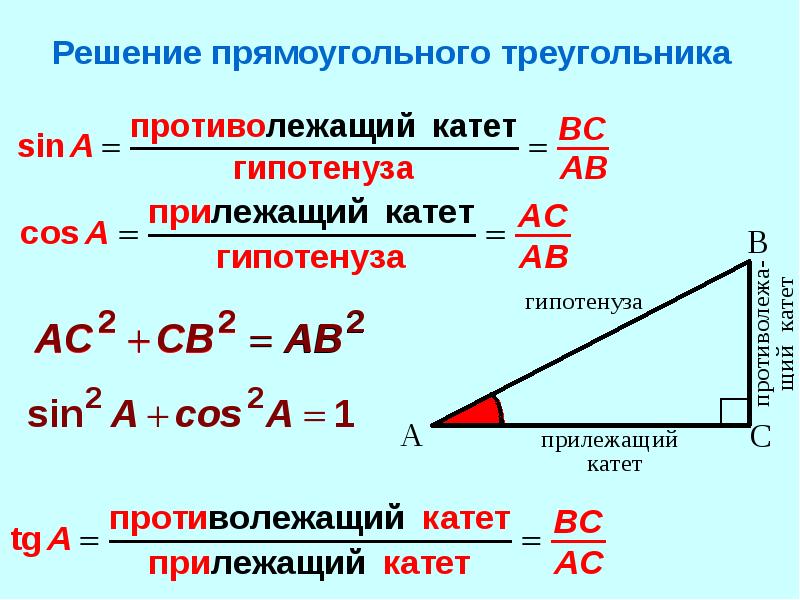
В прямоугольном треугольнике обозначим один острый угол буквой:

стороны и — катеты прямоугольного треугольника.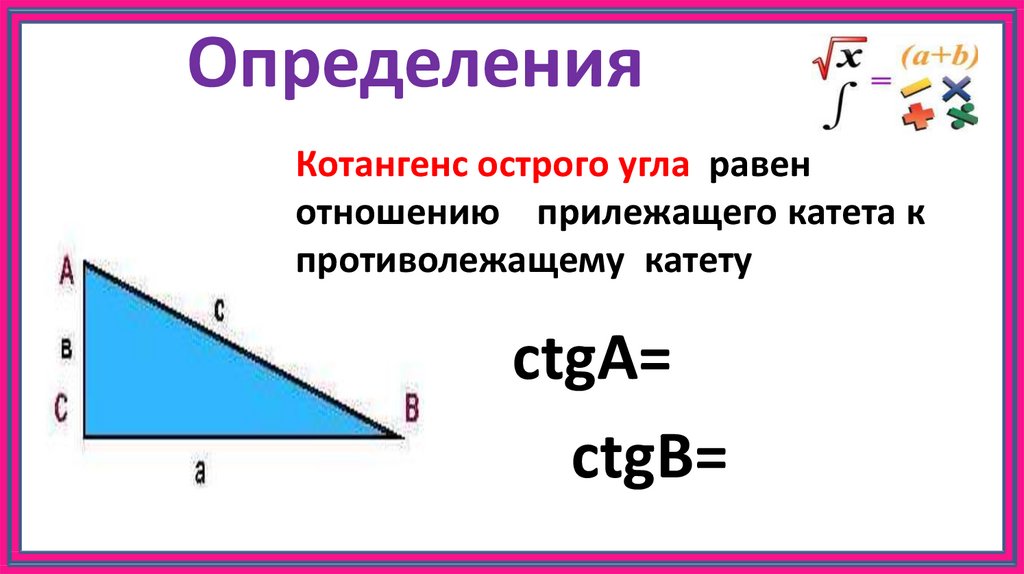
сторона — гипотенуза прямоугольного треугольника.

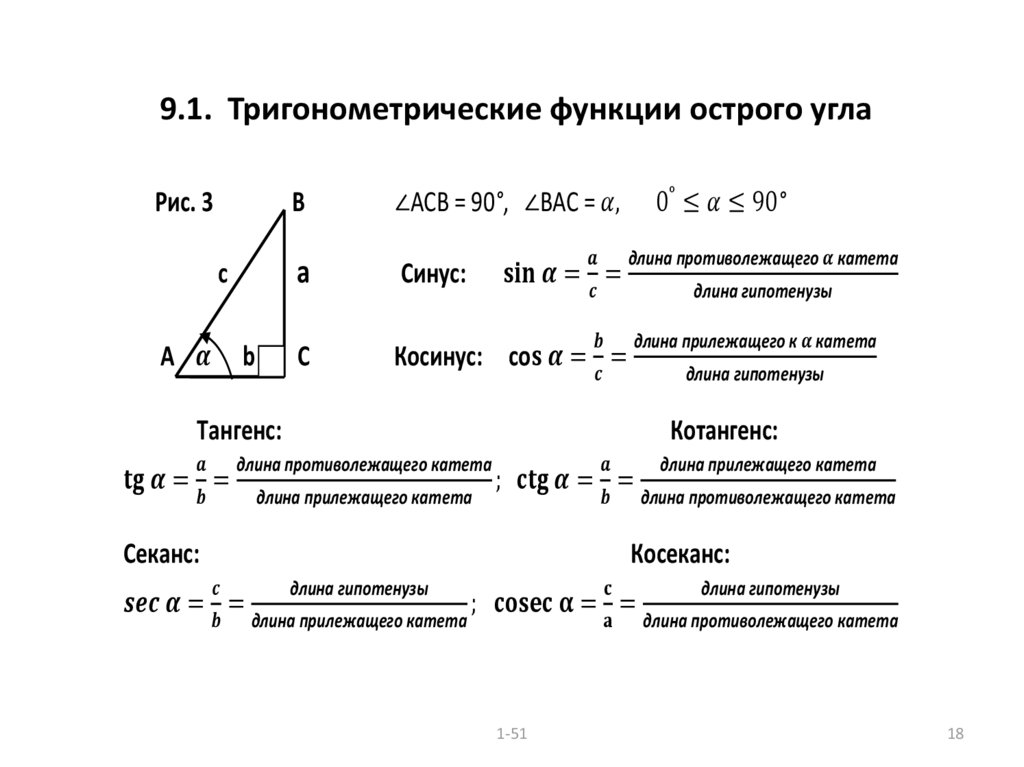
С указанными выше обозначениями у нас есть следующие определения тригонометрических функций:

или словами:

Графический метод запоминания

Чтобы вычислить синус острого угла в прямоугольном треугольнике:

• смотрим сначала в сторону, противоположную углу,
• затем к гипотенузе.

Чтобы вычислить косинус острого угла в прямоугольном треугольнике:

• сначала смотрим на основание прямоугольника,
• затем к гипотенузе.

Чтобы вычислить тангенс острого угла прямоугольного треугольника:

• смотрим сначала в сторону, противоположную углу,
• затем к основанию треугольника.

Чтобы вычислить котангенс острого угла в прямоугольном треугольнике:

• сначала смотрим на основание прямоугольника,
• затем в сторону, противоположную углу.

Доказательство тригонометрической формулы для острого угла в прямоугольном треугольнике

Возьмем любой прямоугольный треугольник и отметим в нем острый угол .

По определению тригонометрических функций мы знаем, что:

Следовательно: Из теоремы Пифагора мы знаем, что: Следовательно:

По определению тригонометрических функций мы знаем, что:

Следовательно: и: а также:

Когда мы знаем значение хотя бы одной тригонометрической функции, то с помощью приведенные выше формулы мы можем рассчитать значения всех остальных тригонометрических функций.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Тригонометрия Математика Тригонометрия Формулы Теория 8 класс 2367

Математика • Тригонометрия • Формулы • Теория • 8 класс

Вывести значения всех тригонометрических функций для выбранного угла .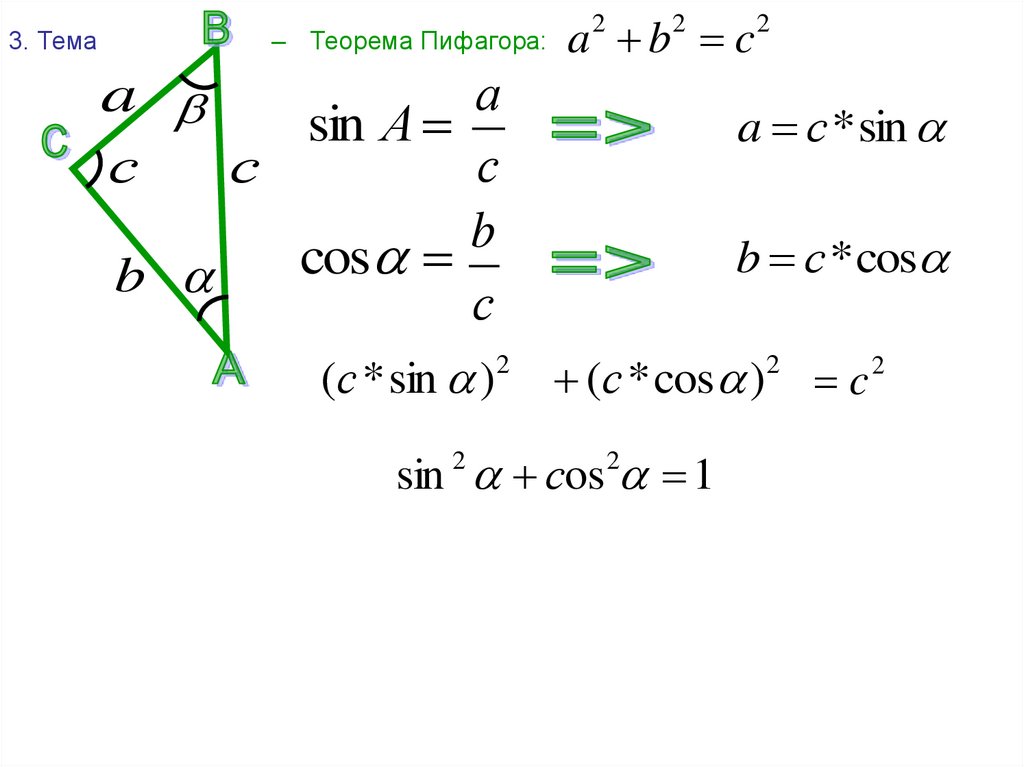

Непосредственно из рисунка мы читаем, что:

Уровень8 класс ПредметГеометрия СложностьПростая

Математика • Тригонометрия • Формулы • Теория • 8 класс

Вывести значения всех тригонометрических функций для выбранного угла .

Из данного рисунка мы читаем, что:

Уровень8 класс ПредметГеометрия СложностьПростая

Математика • Тригонометрия • Формулы • Теория • 8 класс

Вывести значения тригонометрических функций для угла выделенного на рисунке.

Непосредственно из рисунка мы читаем, что:

Уровень8 класс ПредметГеометрия СложностьПростая

Математика • Тригонометрия • Формулы • Теория • 8 класс

Вычислить значения тригонометрических функций для угла выделенного на рисунке.

Сначала мы должны вычислить длину гипотенузы . Мы используем теорему Пифагора: Затем:

Уровень8 класс ПредметГеометрия СложностьПростая

Математика • Тригонометрия • Формулы • Теория • 8 класс

Вычислить если известно, что .

Мы используем тригонометрические формулы:

Теперь мы вычисляем тангенс: Теперь мы вычисляем котангенс:

Уровень8 класс ПредметГеометрия СложностьПростая

Математика • Тригонометрия • Формулы • Теория • 8 класс

Вычислить если известно, что .

Мы используем тригонометрические формулы:

Теперь мы вычисляем тангенс: Теперь мы вычисляем котангенс:

Уровень8 класс ПредметГеометрия СложностьПростая

Математика • Тригонометрия • Формулы • Теория • 8 класс

Вычислить если известно, что .

Проще всего вычислить котангенс:

Теперь мы воспользуемся формулой для тангенса и составим систему уравнений с двумя неизвестными. Эти неизвестные, конечно, будут искать .

Z pierwszego równania możemy wyliczyć np. :

Теперь мы можем заменить синус на тригонометрическую единицу. В результате мы получим уравнение с одним неизвестным ( ):

Теперь мы вычислим синус, используя ранее обозначенную формулу:

Уровень8 класс ПредметГеометрия СложностьПростая

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

• Меры углов

  Для измерения углов используются градусы или радианы.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Соотношения между тригонометрическими функциями

  Знак тригонометрической функции в левой части должен совпадать со знаком правой части.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Периодичность тригонометрических функций

  Тригонометрические функции sin(x) и cos(x) являются периодическими, с наименьшим периодом равным 2*π. Тригонометрические функции tg(x) и ctg(x) являются периодическими, с наименьшим периодом равным π.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Четность и нечетность тригонометрических функций

  Четной называется функция, которая не меняет своего значения при изменении знака независимой переменной. Нечетной называется функция, которая меняет свое значение при изменении знака независимой переменной.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Тригонометрические функции суммы и разности углов

  Тригонометрические функции суммы и разности углов

  Тригонометрия Математика Тригонометрия Формулы Геометрия Теория

• Тригонометрические функции двойного, половинного и тройного аргументов

  Тригонометрические функции двойного, половинного и тройного аргументов

  Тригонометрия Математика Тригонометрия Формулы Геометрия Теория

• Соотношения между обратными тригонометрическими функциями

  Тригонометрия Математика Тригонометрия Формулы Теория

• Свойства обратных тригонометрических функций

  Названия обратных тригонометрических функций образуются следующим образом: приставка «арк-» (от латинского arc — дуга) + соответствующие им названия тригонометрических функций.

  Тригонометрия Математика Тригонометрия Формулы Теория

• Таблица степеней

  Таблицы по алгебре Математика Таблицы

• Сложение и вычитание векторов

  Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a. Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.

  Вектора Формулы Геометрия Алгебра Теория Обозначения

• Сколько грамм в ложке

  Масса и вес Масса Физика Теория Единицы измерения

• Калькулятор веса по росту и возрасту

  Калькуляторы веса и калорий Калькулятор Расчёт

• Что такое масса, вес нетто и вес брутто: в чем разница? Что больше: вес, масса нетто или брутто?

  Вес — это физическая величина, а именно сила, воздействующая на горизонтальную поверхность или вертикальную подвеску.

  Масса и вес Масса Физика Теория Единицы измерения

• Конвертер текста в юникод

  Конвертер для перевода любого текста (не только кириллицы) в Юникод.

  Работа с текстом Калькулятор Расчёт Конвертер Преобразовать Текст

• 1 mBTC это сколько BTC ? Чему равен 1 сатоши ? Что такое сатоши ?

  Bitcoin, Биткойн, часто Биткоин (от англ. bit — единица информации «бит», англ. coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.

  Разное Единицы измерения Деньги Справочник

• Что такое Ватт

  1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль.

  Электротехника Формулы Физика Теория Электричество

Объяснение урока: Нахождение площади треугольника с помощью тригонометрии

В этом объяснении мы научимся находить площадь треугольника с помощью длины двух сторон и синус прилежащего угла.

С самого начала нашего математического путешествия мы знали, как найти площадь треугольника, используя его основание и перпендикулярную высоту. Однако мы несколько ограничены этим методом, так как эти два измерения могут быть даны не всегда. В этом объяснителе мы расширим наши знания, введя тригонометрическую формулу для площадь треугольников, которую мы сейчас выводим.

Рассмотрим треугольник 𝐴𝐵𝐶, в котором мы знаем длины двух стороны 𝑎 и 𝑏 и мера угла между ними угол 𝐶. Мы называем это включенным или закрытый угол. Известная информация выделена жирным шрифтом на рисунке. ниже.

Чтобы применить обычную формулу площади треугольника, нам нужно знать длины его основания и высоты перпендикуляра. Проводим линию от вершина 𝐵, перпендикулярная основанию 𝐴𝐶, который мы обозначим как ℎ.

Площадь треугольника 𝐴𝐵𝐶 по обычной формуле равна площадь=𝑏ℎ2. Нам нужно подумать, как выразить перпендикулярная высота ℎ через известные длины сторон и известный угол. Рассмотрим треугольник 𝐵𝐶𝐷 на рисунке выше. Поскольку это прямоугольный треугольник, мы можем применить отношение синусов, чтобы выразить ℎ с точки зрения 𝑎 и 𝐶.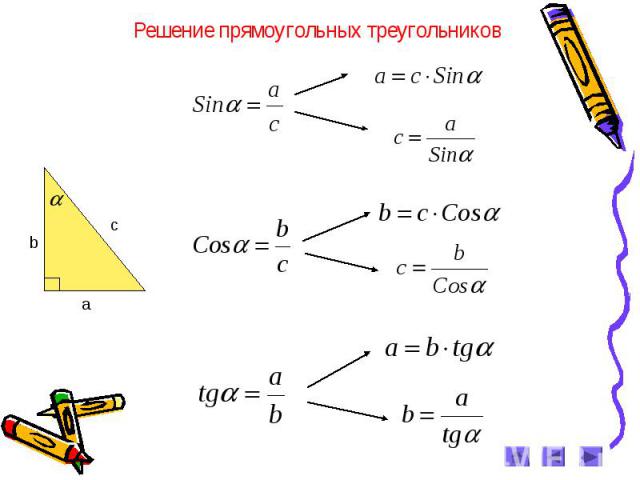 Вспоминая, что отношение синуса есть длина противоположного сторону разделить на длину гипотенузы, имеем синоффипсин𝐶=𝐶=ℎ𝑎.

Перестановка путем умножения на 𝑎 дает ℎ=𝑎𝐶.sin

Теперь мы выразили перпендикулярную высоту треугольника через сторону 𝑎 и угол 𝐶, оба из которых мы предполагали равными быть известным. Теперь мы можем подставить это выражение для ℎ в обычная формула площади треугольника для получения тригонометрической формулы areainsin=𝑏ℎ2=𝑏×𝑎𝐶2=12𝑎𝑏𝐶.

Определение: Тригонометрическая формула площади треугольников

Тригонометрическая формула площади треугольников Площадь=12𝑎𝑏𝐶, где 𝑎 и 𝑏 — длины двух сторон а 𝐶 — мера прилежащего угла.

Эта формула действительна как в градусах, так и в радианах и может применяться к любому треугольник. Можно было бы проработать процесс явно вычисление перпендикулярной высоты с использованием тригонометрии для каждого треугольника и затем применяя более простую формулу, но тригонометрическая формула сочетает в себе эти шаги для нас и, следовательно, более эффективным.

Важно отметить, что эту формулу можно применять всякий раз, когда мы знаем любое Две стороны треугольника и угол между ними. Для треугольника 𝐴𝐵𝐶 выше, мы могли бы эквивалентно выразить формулу как Площадь=12𝑏𝑐𝐴 или как Площадь=12𝑎𝑐𝐵.

Однако лучше не слишком беспокоиться о том, какие именно буквы используются и вместо этого понять, что они представляют с точки зрения относительного расположение сторон и угла.

Давайте теперь продемонстрируем, как применить эту формулу для вычисления площади треугольника, если даны длины двух сторон и мера заключенных между ними угол.

Пример 1. Использование тригонометрической формулы площади треугольников

𝐴𝐵𝐶 — треугольник, где 𝐵𝐶=15см, 𝐴𝐶=25см, и 𝑚∠𝐶=41∘. Найдите площадь 𝐴𝐵𝐶, ответив на три десятичные разряды.

Ответ

Полезно нарисовать треугольник 𝐴𝐵𝐶 как показано ниже (не в масштабе).

Из нашего эскиза видно, что информация, которую мы получили состоит из длин двух сторон треугольника и меру угла между ними. Напомним тригонометрическую формулу для площадь треугольника: площадь=12𝑎𝑏𝐶.

Замена боковых сторон по 15 см и 25 см и прилежащий угол 41∘ и оценка дает areasin=12×15×25×41=375412=123,01106…≈123,011,∘∘

Площадь треугольника 𝐴𝐵𝐶 с точностью до трех знаков после запятой равна 123,011 см ² .

В предыдущем примере нам были явно заданы длины двух сторон и их включенный угол. В других задачах нам может быть дан несколько иной набор Информация. Затем может потребоваться рассчитать необходимую длину и углы, использующие другие геометрические свойства, такие как сумма углов в треугольнике. Сейчас мы рассмотрим это на примере.

Пример 2. Использование тригонометрической формулы площади треугольников для нахождения площади треугольника.

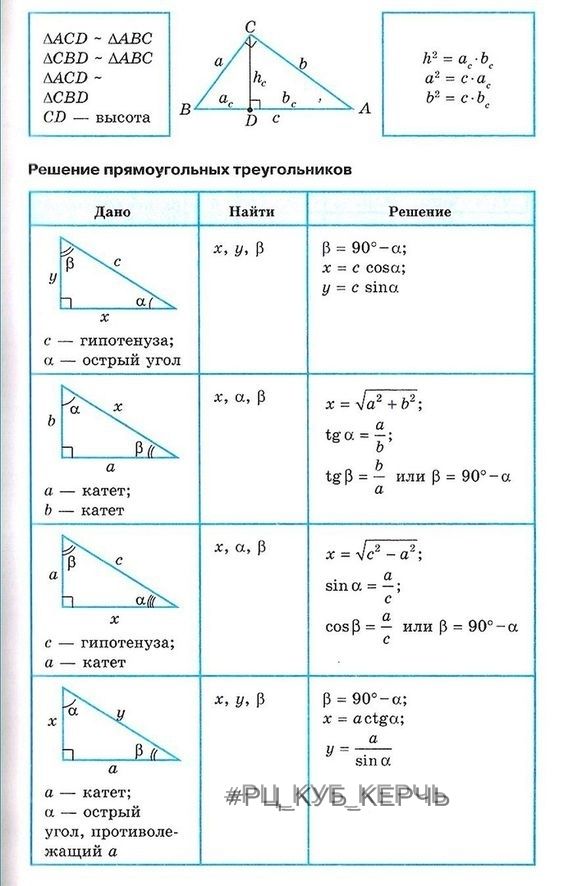an Isosceles Triangle

У равнобедренного треугольника две стороны длины 48 см и база углы 75∘. Найдите площадь треугольника, давая ответ с точностью до трех знаков после запятой. если необходимо.

Ответ

Начнем с рисования треугольника (не в масштабе). Напомним, что база Углы равнобедренного треугольника – это углы, образованные каждым из равных стороны с третьей стороны.

Теперь вспомним тригонометрическую формулу площади треугольника: площадь=12𝑎𝑏𝐶.

Нам известны длины двух сторон треугольника, и мы можем вычислить меру их прилежащего угла, угла 𝐶 на нашей диаграмме, используя сумму углов в треугольнике. Вычитая меры двух других углов из 180∘, получаем 𝑚∠𝐶=180−75−75=30.∘∘∘∘

Подставляя две длины сторон 48 см и включенный угол 30∘ в тригонометрическая формула площади треугольника и вычисление дает площади=12×48×48×30=12×48×48×12=576,∘

Поскольку это целое число, нет необходимости округлять ответ до трех.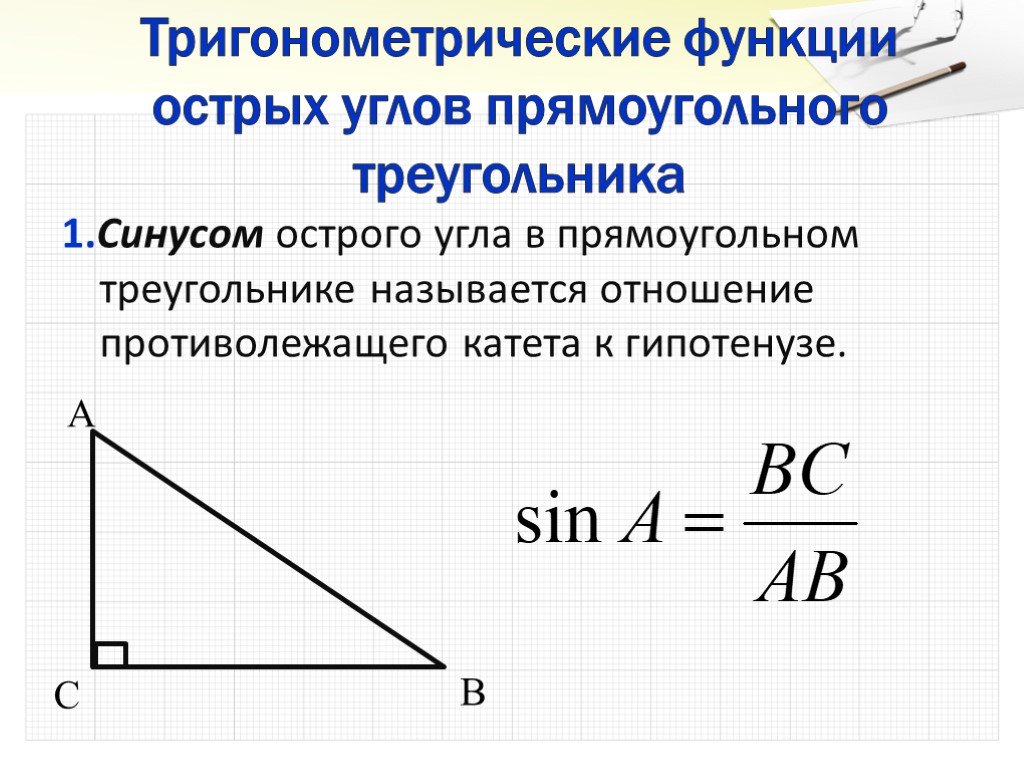 десятичные разряды.

Площадь треугольника 576 см ² .

В предыдущей задаче прилежащий угол был одним из специальных углов для в котором значения трех тригонометрических отношений могут быть точно выражены в в терминах частных и радикалов. Использование таких углов позволяет нам ответить такие проблемы, когда у нас нет доступа к калькулятору.

Теперь мы суммируем основные шаги, которые необходимо выполнить при применении тригонометрического формула площади треугольников.

Как вычислить площадь треугольника с помощью тригонометрической формулы

1. Определите пару длин сторон и угол между ними.
2. Может потребоваться рассчитать любое из этих значений, используя другую информацию дано в вопросе, например, используя сумму углов в треугольнике или углы на прямой.
3. Подставить значения в формулу areain=12𝑎𝑏𝐶, где 𝑎 и 𝑏 представляют длины сторон, а 𝐶 представляет угол между ними.

Мы также можем работать в обратном направлении, если дана площадь треугольника, длина одной стороны, и меру одного угла, чтобы определить длину второй стороны, которая заключает угол. Это потребует от нас составить и решить уравнение, так как мы продемонстрируем в нашем следующем примере.

Пример 3. Нахождение длины стороны треугольника по его площади, длине Сторона и мера угла

𝐴𝐵𝐶 — треугольник, где 𝐴𝐵=18см, 𝑚∠𝐵=60∘, а площадь треугольника 74√3 см ² . Найдите длину 𝐵𝐶, дающую ответ до двух знаков после запятой.

Ответ

Начнем с рисования треугольника 𝐴𝐵𝐶, используя информацию дано в вопросе.

Далее вспоминаем тригонометрическую формулу площади треугольника: площадь=12𝑎𝑏𝐶.

Напомним, что 𝑎 и 𝑏 обозначают длины любых двух сторон, а 𝐶 представляет угол между ними, поэтому для нашего треугольника мы можем выразить площадь, используя стороны 𝐴𝐵 и 𝐵𝐶 и прилежащий угол 60∘ как площади=12×𝐴𝐵×𝐵𝐶×60,∘

Заменив 74√3 на площадь и 18 на 𝐴𝐵 можно составить уравнение только с одним неизвестным: 74√3=12×18×𝐵𝐶×60. sin∘

Напомним, что sin60=√32∘ и решить наше уравнение для 𝐵𝐶 сначала сократив коэффициент √3 с каждой стороны, а затем изолируя 𝐵𝐶: 9×𝐵𝐶×√32=74√39𝐵𝐶2=74𝐵𝐶=74×29=16,444…≈16,44.

Длина 𝐵𝐶 до двух знаков после запятой 16,44 см.

Проблемы, которые мы видели до сих пор, были связаны с одним треугольником. Также можно применить тригонометрическую формулу для вычисления площадей составных фигур, включающих треугольники. Возможно, нам потребуется использовать другие навыки, такие как тригонометрия прямоугольного треугольника, чтобы вычислить недостающие длины, которые нам нужны, так как мы увидим в нашем следующем примере.

Пример 4. Нахождение площади сложной фигуры по тригонометрической формуле Площадь треугольников

Найдите площадь фигуры ниже, давая ответ с точностью до трех знаков после запятой. места.

Ответ

Составная фигура на рисунке состоит из двух треугольников, треугольник 𝐴𝐵𝐶 и треугольник 𝐴𝐶𝐷.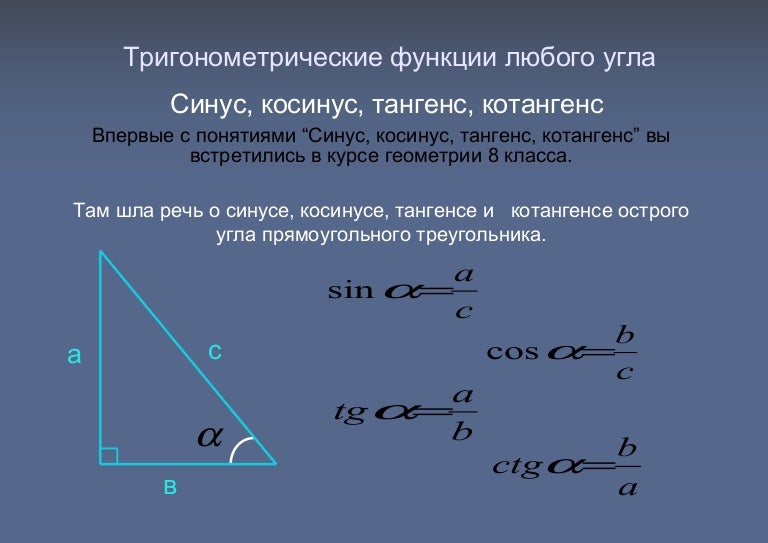 Давайте рассмотрим треугольник 𝐴𝐶𝐷 первый. Это равносторонний треугольник с длина борта 34 м и, следовательно, каждый из внутренних углов равен 60∘. Мы напоминаем о тригонометрическая формула площади треугольника: areain=12𝑎𝑏𝐶, где 𝑎 и 𝑏 представляют длины две стороны, а 𝐶 представляет угол между ними. В треугольнике 𝐴𝐶𝐷, длина каждой стороны равна 34 м и каждый угол 60∘, поэтому подставляя эти значения в формулу дает площадь треугольников sin𝐴𝐶𝐷=12×34×34×60=57860,∘∘

Напоминая, что sin60=√32∘, имеем площадьтреугольника𝐴𝐶𝐷=578×√32=289√3.

Далее рассмотрим треугольник 𝐴𝐵𝐶, который является прямым треугольник. Нам дана мера еще одного угла, и мы можем сделать вывод, что длина его гипотенузы 𝐴𝐶 равна 34 м. Чтобы подать заявку Тригонометрическая формула площади треугольника, нам сначала нужно вычислить длину второй стороны, заключающей угол 𝐶, сторона 𝐵𝐶.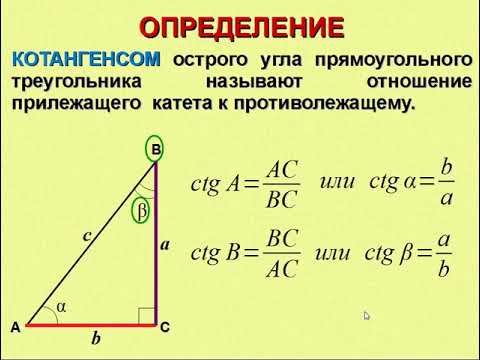

По отношению к углу 𝐶 сторона 𝐵𝐶 равна соседний. Применяя тригонометрию прямоугольного треугольника, мы имеем cosadjacenthypotenuse60==𝐵𝐶34.∘

Перестановка дает 𝐵𝐶=3460=34×12=17.cos∘

Теперь мы можем применить тригонометрическую формулу площади треугольников используя стороны 𝐵𝐶 и 𝐴𝐶 и включенные угол 𝐶: площадь треугольников в 𝐴𝐵𝐶=12×17×34×60=289√32,∘

Общая площадь сложной фигуры равна сумме площадей двух треугольники: общая площадьплощадьтреугольникаплощадьтреугольника=𝐴𝐶𝐷+𝐴𝐵𝐶=289√3+289√32=867√32=750,8440…≈750,844.

Площадь фигуры с точностью до трех знаков после запятой составляет 750,844 м ² .

В предыдущем примере мы применили тригонометрическую формулу для расчета площадь прямоугольного треугольника через длины двух его сторон и их включенный угол, который в данном случае не был прямым углом. это Интересно отметить, что произойдет, если мы применим тригонометрическую формулу, используя прямого угла и двух сторон, которые его заключают. Эти две стороны являются основой и перпендикулярная высота треугольника, как показано на рисунке ниже.

Применяя тригонометрическую формулу площади треугольника, получаем areain=12×𝑏×ℎ×90.∘

Учитывая, что sin90=1∘, это упрощается до площадь=12𝑏ℎ, что согласуется с обычной формулой площади треугольника с использованием его основание и перпендикулярную высоту. Таким образом, мы показали, что применительно к праву Таким образом, тригонометрическая формула сводится к формуле площади, которую мы уже знакомы.

Мы видели, как можно применить тригонометрическую формулу для площади треугольники для составных фигур, но его также можно применять для вычисления площади некоторых других геометрических фигур, таких как параллелограммы. Если такие фигуры можно разбить на треугольники, то при наличии необходимого множества информации, мы можем использовать эту формулу, чтобы найти их площадь как сумму площадей треугольников, которые они содержат.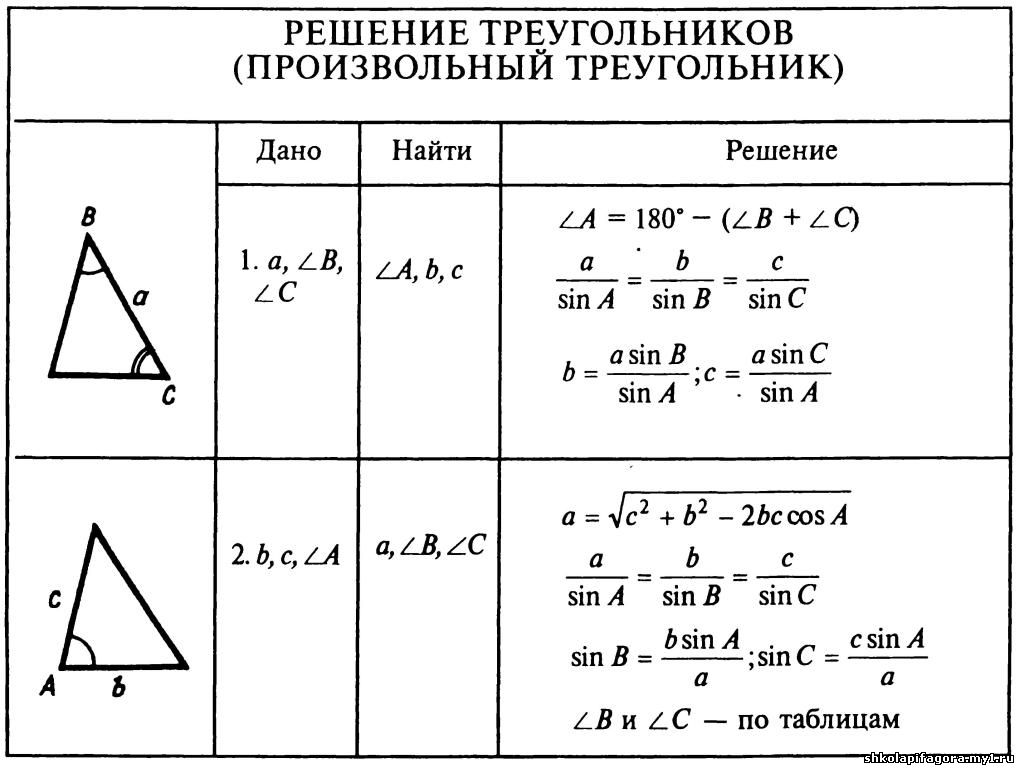 Теперь рассмотрим пример, в котором мы применяем эта формула для вычисления площади параллелограмма.

Пример 5. Нахождение площади параллелограмма по тригонометрической формуле Площадь треугольников

𝐴𝐵𝐶𝐷 — параллелограмм, где 𝐴𝐵=41см, 𝐵𝐶=27см, и 𝑚∠𝐵=159∘. Найдите площадь 𝐴𝐵𝐶𝐷, ответив на вопрос ближайший квадратный сантиметр.

Ответ

Начнем с рисования параллелограмма, как показано ниже.

Обычно при вычислении площади параллелограмма применяют формулу Areabaseperpendicularheight=×.

Однако нам не известна высота перпендикуляра этого параллелограмма. Вместо этого мы признаем, что, поскольку 𝐴𝐵𝐶𝐷 является параллелограммом, каждая из его диагоналей делит его на два равных треугольника. добавим диагональ 𝐴𝐶 к нашему эскизу.

Поскольку треугольники 𝐴𝐵𝐶 и 𝐴𝐷𝐶 равны, у них одинаковая площадь. Таким образом, площадь параллелограмма может быть вычисляется как удвоенная площадь треугольника 𝐴𝐵𝐶, в котором мы знать длины двух сторон и величину угла между ними.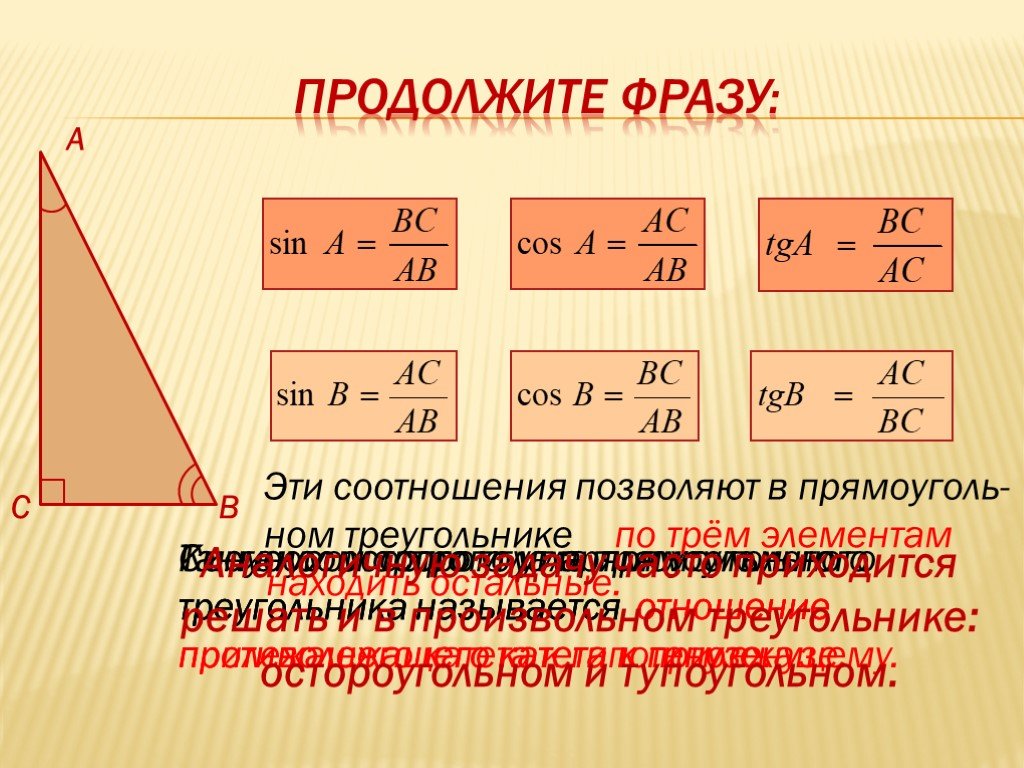 Мы можем Поэтому применим тригонометрическую формулу площади треугольника: площадь треугольников в𝐴𝐵𝐶=12×41×27×159.∘

Площадь параллелограмма вдвое больше: areaofsin𝐴𝐵𝐶𝐷=2×12×41×27×159.∘

Упрощение и оценка дает areaofsin𝐴𝐵𝐶𝐷=41×27×159=396,713…≈397,∘

Площадь 𝐴𝐵𝐶𝐷, с точностью до квадратный сантиметр, это 397 см ² .

Давайте закончим повторением некоторых ключевых моментов этого объяснения.

Ключевые точки

• Площадь любого треугольника можно вычислить, используя длины двух его стороны и синус угла между ними.
• Тригонометрическая формула площади треугольников: areain=12𝑎𝑏𝐶, где 𝑎 и 𝑏 — длины двух сторон а 𝐶 — мера прилежащего угла.
• При наличии площади треугольника и двух частей информации из длины сторон 𝑎 и 𝑏 и угол 𝐶 можно использовать тригонометрическую формулу для нахождения недостающего мера стороны или угла.
• Тригонометрическую формулу также можно использовать для вычисления площадей других геометрические фигуры или составные фигуры, которые можно разделить на треугольники.

Что такое тригонометрия? Определение, формулы и приложения

Тригонометрия — это раздел математики, который занимается изучением треугольников. Иногда его неофициально называют «триггер». В тригонометрии математики изучают отношения между сторонами и углами треугольников. Прямоугольные треугольники, которые представляют собой треугольники с одним углом в 90 градусов, являются ключевым предметом изучения в этой области математики.

Тригонометрия широко преподается в средних школах, как правило, учащимся младших классов. Тригонометрия основана на базовых математических понятиях, изученных в младших классах, и ориентироваться в ней может быть запутанным предметом. Преподаватели тригонометрии могут либо помочь учащимся лучше понять концепции тригонометрии, либо бросить им вызов мыслить нестандартно, в зависимости от их академического уровня и понимания тригонометрии. Читайте дальше, чтобы узнать больше об изобретении тригонометрии, о том, как лучше всего ее освоить, как репетиторы могут помочь и чем тригонометрия отличается от других математических предметов.

Что означает тригонометрия?

Слово тригонометрия происходит от греческих слов trigonon и metron, , которые означают «треугольник» и «мера» соответственно. Основы тригонометрии могут быть даже старше и, возможно, использовались в Древнем Египте. По сути, тригонометрия имеет дело с треугольниками и тем, как измерения сторон и углов треугольника соотносятся друг с другом.

Существует множество профессий, требующих использования тригонометрии, включая архитектора, космонавта, следователя на месте преступления, физика, геодезиста, инженера и многих других. Даже если вы не планируете делать карьеру ни в одной из этих областей, все равно важно понимать основные концепции тригонометрии. Тригонометрия является обязательным предметом в большинстве школьных округов, и если учащиеся не преуспевают по этому предмету, это может плохо отразиться на их общей успеваемости. Есть несколько причин, по которым тригонометрия в настоящее время преподается в школах, и множество способов, которыми тригонометрию можно использовать и применять в дальнейшей жизни.

Откуда взялась тригонометрия?

Тригонометрия имеет долгую историю, восходящую к древнему миру. Первоначально тригонометрия была связана с использованием основных функций для использования известного угла треугольника для вычисления остальных углов. Например, если бы были даны длины двух сторон треугольника и известна мера прилежащего угла, можно было бы вычислить третью сторону и два других угла. Тригонометрия и тогда, и сейчас в первую очередь сосредоточена на отношениях между углами треугольников.

Древние греки формализовали первые тригонометрические функции, начиная с Гиппарха из Вифинии, около 150 г. до н.э. Гиппарх рассматривал все типы треугольников, включая сферические треугольники, прямоугольные треугольники и плоские треугольники. Хотя интерес Гиппарха к тригонометрическим функциям в основном был связан с астрономией, в наше время тригонометрия может применяться во многих реальных ситуациях.

Для чего используется тригонометрия?

Как упоминалось ранее, тригонометрия часто используется в областях, связанных с физикой, химией и инженерией. Тригонометрия не только является теоретическим предметом, но и имеет множество практических применений. Инженеры во многих областях промышленности используют триггеры в ходе своей работы. Другие специалисты, которые могут использовать тригонометрию, включают геодезистов, архитекторов и пилотов. Как и Гиппарх более двух тысяч лет назад, тригонометрия используется в астрономии для измерения расстояния до ближайших звезд и расчета положения звезд. Тригонометрия также играет ключевую роль в спутниковых навигационных системах.

Одна из реальных проблем, которую можно решить с помощью правил тригонометрии, состоит в том, чтобы определить размеры вещей или пространств, которые трудно измерить напрямую. Например, тригонометрические функции можно использовать для расчета высоты гор, количества воды в озере и квадратных метров участка земли необычной формы. Тригонометрию можно использовать даже для точного измерения времени астрономами.

Тригонометрические концепции также используются в играх и музыке. Тригонометрия играет важную роль в разработке видеоигр, обеспечивая правильную работу игр. Он используется для написания программ, чтобы объекты в игре могли двигаться. Тригонометрию также можно использовать в процессе разработки персонажей, наборов и объектов для видеоигр. В музыке тригонометрия измеряет уровень или высоту звуковой волны или музыкальной ноты.

Таким образом, хотя тригонометрия, безусловно, является математической концепцией, ее можно применять ко многим различным областям и задачам за пределами математики. Все это реальные сценарии, в которых человек будет использовать тригонометрию, и они являются примерами того, почему важно научиться правильно применять тригонометрию.

Когда вы изучаете тригонометрию?

Поскольку тригонометрия может применяться в различных сферах деятельности, важно убедиться, что учащиеся хорошо понимают концепции тригонометрии. Тригонометрия основывается на базовых математических знаниях, которым обучают учащегося на протяжении всего обучения, включая понятия алгебры и геометрии. Поскольку тригонометрия объединяет понятия из разных математических предметов, существует определенный порядок, в котором эти предметы преподаются.

Обычно студенты изучают алгебру I, геометрию, а затем алгебру II или тригонометрию. В зависимости от штата некоторые школы предлагают учащимся выбор математического предмета, который они хотели бы изучать. Способность учащегося выбирать конкретный математический предмет также может зависеть от его успеваемости. Поскольку тригонометрия применяет понятия, преподаваемые в более ранних классах, и основывается на предыдущих знаниях, это может быть трудным предметом для изучения.

Можно ли выучить тригонометрию онлайн?

С появлением онлайн-обучения были достигнуты удивительные успехи в том, как функционируют виртуальные классы. Есть много способов, с помощью которых онлайн-обучение может помочь всем учащимся освоить тригонометрию. Используя образовательные приложения и программное обеспечение, учителя могут делиться экранами своих компьютеров и точно показывать, как решать математические задачи, точно так же, как они использовали бы доску или классную доску для решения задач для учащихся в классе.

Онлайн-занятия часто меньше, чем очные, что позволяет учителям сосредоточиться на помощи учащимся, которым нужна помощь в изучении конкретных понятий тригонометрии. Онлайн-образование значительно развилось за последние несколько лет и теперь предлагает безопасное пространство для всех типов учащихся и стилей обучения.

Тригонометрия сложна?

В то время как математика для некоторых является естественной, тригонометрия может быть запутанной темой для многих людей. Если учесть, что класс тригонометрии может включать в себя тригонометрические функции, тригонометрические значения, тригонометрические формулы и многое другое, то может быть сложно и запутанно держать все эти компоненты в чистоте. Лучший способ убедиться, что учащиеся правильно используют функции тангенса, синуса и косинуса, — это получить руководство от кого-то, кто хорошо разбирается в тригонометрии. Это может быть одноклассник, родитель, учитель или репетитор.

Даже если учащийся может выполнять алгебраические функции и хорошо разбирается в понятиях других разделов математики, у него могут возникнуть проблемы с некоторыми элементами тригонометрии, такими как тригонометрические отношения синус (sin), косинус (cos) и тангенс (загар). Независимо от того, учится ли студент в очном классе или в виртуальном классе, может быть очень полезно получить индивидуальную помощь от преподавателя. Таким образом, студенты могут получить немедленную обратную связь. Репетитор по тригонометрии может помочь учащимся чувствовать себя уверенно в новых понятиях, с которыми они сталкиваются, и может закрепить то, что они изучают, предоставляя дополнительную практику.

Чем могут помочь репетиторы по тригонометрии для учащихся

Тригонометрия может быть сложным предметом, особенно для людей, которые от природы не преуспевают в математике или естественных науках. Для родителей может быть трудно ожидать, что их дети преуспеют в каждом предмете. Стоит помнить, что существует много разных типов учащихся и много разных стилей обучения. Некоторые люди лучше всего учатся с визуальными эффектами, другие лучше всего учатся, слушая информацию, а некоторые люди лучше всего учатся, когда они могут читать и слушать инструкции для конкретной задачи. Некоторым учащимся может быть полезна помощь онлайн-репетитора по математике. Репетиторы также могут помочь учащимся, которые хорошо успевают, предлагая дополнительную практику перед подготовительными тестами в колледже или школьными экзаменами.

Многие компании, связанные с образованием, заявляют, что помогают студентам, но может быть трудно провести различие между компаниями, которые рассматривают молодых людей как знак доллара, и теми, которые искренне хотят, чтобы студенты преуспели. Также может быть сложно найти репетитора, который подходит для плотного графика семьи. К счастью, есть платформы, которые предлагают отличных онлайн-репетиторов, которые подбираются индивидуально для студентов через строгий процесс отбора. Одним из самых известных является Learner. Ученик фокусируется на предоставлении конкретных академических инструкций, адаптированных для каждого учащегося, а не на предоставлении общих уроков всем учащимся.

Учащийся настолько уверен, что сможет удовлетворить потребности своих клиентов в обучении, что имеет 100% гарантию удовлетворения без риска. Инновационная платформа Learner предлагает инструменты для совместной работы для повышения вовлеченности, показатели обратной связи, которые позволяют учащимся узнать, на каком уровне они находятся, и записи сеансов, чтобы учащиеся могли просмотреть их позже. и Learner работает на всех устройствах. Learner — один из многих веб-сайтов онлайн-обучения, но это одна из единственных платформ, которая использует персонализированное сопоставление с репетиторами мирового класса для ускоренного обучения.

Нужна помощь с тригонометрией? Поговорите с нашим академическим консультантом, чтобы подобрать лучшего онлайн-репетитора по математике уже сегодня!

Часто задаваемые вопросы о тригонометрии

Является ли тригонометрия геометрией?

Геометрия — это раздел математики, изучающий свойства и отношения точек, линий, поверхностей и тел, тогда как тригонометрия фокусируется исключительно на углах и треугольниках. Геометрию часто преподают в школах раньше, чем тригонометрию.

Является ли тригонометрия предварительным исчислением?

Тригонометрия является обязательным условием для прохождения курсов предварительного исчисления, поскольку в нем используются элементы тригонометрии, алгебры и аналитической геометрии.

Является ли Алгебра 2 тригонометрией?

Алгебра 2 не учит тем же математическим понятиям, что и тригонометрия. Алгебра 2 охватывает такие темы, как линейные уравнения, функции, квадратные уравнения, многочлены, радикальные выражения, неравенства, графики и матрицы. Тригонометрия, с другой стороны, связана с конкретными функциями углов и тем, как они применяются в вычислениях.

Что такое тригонометрические тождества?

Тригонометрические тождества — это равенства с участием тригонометрических функций. Они являются важными элементами в изучении треугольников. Тригонометрические тождества включают тождества Пифагора, формулы приведения и тождества кофункций. Часто научный калькулятор используется для решения тригонометрических задач, таких как тригонометрические тождества.

Что такое тригонометрические функции?

Тригонометрические функции описывают отношения между углами и сторонами треугольника. В современной математике существует шесть основных тригонометрических функций, также называемых тригонометрическими формулами: синус, тангенс, секанс, косинус, котангенс и косеканс. Эти функции описывают отношения сторон прямоугольных треугольников.

Что такое грех в тригонометрии?

Синус (sin), косинус (cos) и тангенс (tan) — три основные функции, используемые в тригонометрии. Они основаны на прямоугольных треугольниках. Синус одного угла прямоугольного треугольника равен отношению длины стороны треугольника, противолежащей углу, к длине гипотенузы треугольника.

Что такое Cos в тригонометрии?

Синус (sin), косинус (cos) и тангенс (tan) — тригонометрические функции, основанные на прямоугольных треугольниках. Косинусом угла прямоугольного треугольника называется отношение длины стороны, прилежащей к углу, к длине гипотенузы.

Что такое касательная функция в тригонометрии?

В прямоугольном треугольнике тангенс угла равен отношению противоположной стороны к прилежащей стороне этого угла.

Что такое теорема Пифагора?

Теорема Пифагора утверждает, что для прямоугольного треугольника квадрат длины гипотенузы равен сумме квадратов длин двух других сторон.

Работает ли тригонометрия с непрямыми углами?

Обычно курсы по тригонометрии в старших классах сосредоточены на применении тригонометрических функций, таких как синус, косинус и тангенс, к прямоугольным треугольникам (которые имеют один прямой угол). Более продвинутая тригонометрия колледжа может включать эти функции, а также применение тригонометрии к непрямым углам.

Что охватывают курсы по тригонометрии?

Курсы по тригонометрии обычно охватывают такие темы, как тождество Пифагора и использование тригонометрических функций, таких как синус и косинус, для решения прямоугольных треугольников.