Раскраски Умножение и Деление. Распечатай, реши и раскрась
На этой странице собраны задания, которые помогут школьникам в игровой форме проверить и закрепить свои знания по решению математических примеров на деление и умножение, одновременно с этим превращая черно-белую картинку в цветную. Чтобы узнать, каким цветом раскрасить деталь изображения, нужно решить пример.
Математические раскраски помогут детям думать самостоятельно, развить художественные навыки, память и логику. Их могут использовать учителя начальных классов на уроках в школе и родители, как дополнительную тренировку дома. Такая занимательная игра доставит детям больше удовольствия, чем обычное решение примеров.
Любую раскраску можно распечатать, наведя на неё курсор мышки и нажав на появившийся розовый значок принтера в верхнем правом углу картинки.
Математическая раскраска единорог. Только деление.Математическая раскраска деление в пределах 23.Раскраска Умножение от 55 до 696.

Раскраска умножение в пределах 24.Математическая раскраска умножение до 60.Крокодил с конфетойПавлин приглашает решить примеры с делением и умножением.Сказочная математическая раскраска с делением.
Раскрасьте с ребятами милого кенгуру на занятии.Король скачет не коне, а ребята-второклассники решают примеры и раскрашивают.Раскраска с примерами в несколько действий.Сказочная математическая раскраска с делением и умножением для 2 класса.Математическая раскраска для 2 класса с умножением и вычитанием в пределах 80.Черепашка предлагает подкрепить знания, решив примеры.Сложная раскраска из множества примеров четырехзначных чисел.Джин даёт непростые примеры ребятам.Раскраска для урока математики 2 класса.Математическая раскраска делениеСложная раскраска слоненка состоящего из множества примеров.Раскраска милой панды, где понадобятся знания математики.Математическая раскраска с примерами в пределах 300.
- Раскраски
Tags: Задания для детей
80
|
Главная » Сборники задач, заданий, самоучители » Тренировочные примеры по математике: 2-3 классы. Табличное умножение и деление. ФГОС
| ||||||||||||||||||||||||||
Учебное пособие: Пример задачи производительности CSP
Часть 1: Полный код
Часть 2: Видео
scrollTo(0,0)» src=»https://www.youtube.com/embed/SFE6zTCzouM?rel=0&showinfo=0″ frameborder=»0″ allowfullscreen=»»/>Часть 3: Письменный ответ
4
5 Предоставьте письменный ответ, который выполняет все три из следующих действий:
i. Описывает общую цель программы
ii. Описывает, какой функционал программы демонстрируется в видеоролике
iii. Описывает ввод и вывод программы, показанной в видео. Видео демонстрирует как викторины на умножение, так и на деление, в которых пользователя просят указать тип задачи, а затем дается 5 задач, на каждую из которых предоставляется возможность ответить, а результаты сообщаются.
Видео демонстрирует 2 разных входа и 3 разных выхода. Демонстрируемые входные данные просят пользователей выбрать тип проблемы, а затем дают предположение о проблемах. Три продемонстрированных вывода: вывод задачи, вывод результатов каждого предположения и вывод окончательной оценки в конце.
3Б.
Захватите и вставьте два сегмента кода программы, разработанные вами во время администрирования этой задачи, которые содержат список (или другой тип коллекции), используемый для управления сложностью вашей программы.
и. Первый сегмент программного кода должен показывать, как данные были сохранены в списке.
ii. Второй сегмент программного кода должен отображать данные в том же используемом списке, например создание новых данных из существующих данных или доступ к нескольким элементам в списке, как часть выполнения цели программы.
Затем предоставьте письменный ответ, содержащий все три пункта:
iii. Идентифицирует имя списка, используемого в этом ответе
iv. Описывает, что данные, содержащиеся в списке, представляют в вашей программе
v. Объясняет, как выбранный список управляет сложностью вашего программного кода, объясняя, почему ваш программный код не может быть написан или как он будет написан по-другому, если вы не использовал список
Первый сегмент кода:
first_number = [8, 12, 6, 20, 10]
второе_число = [2, 3, 3, 4, 5]
Второй сегмент кода:
print(first_number[i], end = " "),
если (тип == "М"):
распечатать("*", конец=" "),
правильно = первое_число[i] * второе_число[i]
еще:
распечатать("/", конец = ""),
правильно = первое_число[i] / второе_число[i]
печать (второе_число [я])
Программа использует два списка: first_number и second_number. В каждом списке хранятся значения, используемые в математических задачах. first_number хранит первое число в задаче, а second_number хранит второе число, которое является делителем для задач на деление.
В каждом списке хранятся значения, используемые в математических задачах. first_number хранит первое число в задаче, а second_number хранит второе число, которое является делителем для задач на деление.
Списки управляют сложностью двумя разными способами. Во-первых, используя списки вместо отдельных переменных, список может хранить все значения в одной переменной и использовать цикл для создания проблемы. Это также позволяет программе легко расширяться, устанавливая длину цикла в соответствии с длиной списков. Без списка программа должна была бы использовать отдельные переменные и записываться последовательно, а не в цикле.
Кроме того, благодаря сохранению определенных значений задачи программа может создавать задачи на деление, которые приводят к целочисленным ответам. Если бы программа генерировала случайные числа, было бы намного сложнее создавать задачи, которые приводили бы к целочисленным ответам.
3С.
Захватите и вставьте два сегмента кода программы, разработанные вами во время администрирования этой задачи, которые содержат разработанную учащимся процедуру, реализующую алгоритм, используемый в вашей программе, и вызов этой процедуры.
и. Первый сегмент программного кода должен быть разработанной студентом процедурой, которая:
• определяет имя процедуры и тип возвращаемого значения (при необходимости)
• содержит и использует один или несколько параметров, влияющих на функциональность процедура
• Реализует алгоритм, включающий определение последовательности, выборку и повторение
ii. Второй сегмент программного кода должен показывать, где в вашей программе вызывается процедура, разработанная учащимся.
Затем предоставьте письменный ответ, который выполняет оба следующих действия:
iii. Описывает в целом, что делает указанная процедура и как она влияет на общую функциональность программы
iv. Подробно объясняет, как работает алгоритм, реализованный в указанной процедуре. Ваше объяснение должно быть достаточно подробным, чтобы кто-то другой мог его воссоздать.
Первый сегмент кода:
по умолчанию вычислить(тип):
оценка = 0
для i в диапазоне (num_problems):
печать (первый_номер [я], конец = " "),
если (тип == "М"):
распечатать("*", конец=" "),
правильно = первое_число[i] * второе_число[i]
еще:
распечатать("/", конец = ""),
правильно = первое_число[i] / второе_число[i]
печать (второе_число [я])
answer = int(input("Введите ответ:"))
если ответ == правильный:
печатать("Верно!")
оценка += 1
еще:
print("Хорошая попытка!")
Распечатать()
обратный счет
Второй сегмент кода:
оценка = вычислить (тип) * 100 / количество_проблем
Выбранная функция способствует общему выполнению программы, выполняя вопросы викторины и возвращая количество правильных вопросов. Функция принимает тип вопросов в качестве входных данных, а затем возвращает количество правильных ответов в основную программу.
Функция принимает тип вопросов в качестве входных данных, а затем возвращает количество правильных ответов в основную программу.
Функция делает это, перебирая все значения в списке, чтобы создать проблему. Внутри цикла функция начинает с вывода первого числа задачи из списка first_number. Затем он использует оператор выбора, чтобы распечатать оператор и вычислить правильный ответ для задачи на деление или умножение на основе параметра проходов. Затем он выводит второе число из списка second_number и запрашивает у пользователя его предположение. Используя оператор выбора, он сравнивает правильный ответ с вводом пользователя и выводит результаты. Если ответ правильный, он также добавляется к переменной трекера, которая отслеживает количество правильных ответов. В конце цикла функция завершается, возвращая количество правильных ответов.
3D.
Предоставьте письменный ответ, который выполняет все три из следующих действий:
i. Описывает два вызова процедуры, указанной в письменном ответе 3c. Каждый вызов должен передавать разные аргументы, которые вызывают выполнение другого сегмента кода в алгоритме.
Описывает два вызова процедуры, указанной в письменном ответе 3c. Каждый вызов должен передавать разные аргументы, которые вызывают выполнение другого сегмента кода в алгоритме.
ii. Описывает, какие условия проверяются при каждом вызове процедуры
iii. Определяет результат каждого вызова
Два тестовых примера основаны на передаче разных входных данных для создания различных типов задач в функции (умножение или деление). Первый вызов будет передавать букву М. На основе этого вызова программа должна выбрать задачи на умножение для печати. Внутри цикла оператор выбора выполнит первую часть оператора выбора и напечатает задачу с помощью оператора *. Он также рассчитает ответ путем умножения значений из списков first_number и second_number. Результатом вызова будет вывод 5 задач на умножение и возврат количества правильных ответов.
Второй вызов пройдет букву D. На основе этого вызова программа должна выбрать задачу деления. Внутри цикла оператор выбора выполнит предложение else, поскольку D не равно M. В результате код напечатает оператор / и вычислит ответ, разделив значение first_number на значение second_number. Результатом вызова будет вывод 5 задач на деление и возврат количества правильных ответов.
В результате код напечатает оператор / и вычислит ответ, разделив значение first_number на значение second_number. Результатом вызова будет вывод 5 задач на деление и возврат количества правильных ответов.
6/6
Ряд 1:
Ответ заработал баллы для этой строки, отвечая всем шести критериям:
• Видео демонстрирует, как программа получает пользовательский ввод как для типа задачи, так и для ответов на задачу
• Целью программы является создание математической викторины и видео демонстрирует создание викторины на умножение и деление.
• Программа демонстрирует выходные данные, создавая задачи и отображая результаты каждой задачи и теста.
• Ввод и вывод описываются в ответе следующим образом: предположение для задач. Три продемонстрированных вывода: вывод задачи, вывод результатов каждого предположения и вывод окончательного результата в конце».
Строка 2:
Ответ заработал баллы для этой строки, отвечая всем трем критериям:
• Показаны два отдельных сегмента кода
• Имя списка описывается как first_number
• Состояние ответа какие значения хранятся в списке: «first_number хранит первое число в задаче»
Строка 3:
Ответ заработал балл за эту строку, отвечающую обоим критериям:
• Ответ включает два списка first_number и second_number и используются в цикле для создания нескольких задач
• Ответ объясняет, как он управляет сложностью, заявляя, что «список может хранить все значения в одной переменной и использовать цикл для создания проблемы». Он также объясняет, как программа должна быть написана без списка, заявляя: «Без списка программа должна была бы использовать отдельные переменные и писать последовательно, а не в цикле».
Он также объясняет, как программа должна быть написана без списка, заявляя: «Без списка программа должна была бы использовать отдельные переменные и писать последовательно, а не в цикле».
Строка 4:
Ответ заработал баллы для этой строки, отвечая обоим критериям:
• Ответ включает два отдельных сегмента кода, один из которых определяет функцию, вычисляемую с параметром типа, а другой вызывает эту функцию
• Ответ описывает, что делает процедура, заявляя: «Функция принимает тип вопросов в качестве входных данных, а затем возвращает количество правильных ответов обратно в основную программу», и описывает, как она относится к общей функции, заявляя: «Функция выбранная функция способствует общему выполнению программы, выполняя вопросы викторины и возвращая количество правильных вопросов».
Строка 5:
Ответ заработал баллы для этой строки, отвечая обоим критериям:
• Выбранный алгоритм включает в себя последовательность, выбор (два оператора if) и итерацию (для цикла решения задач)
• Ответ включает подробное объяснение того, как воссоздать алгоритм во втором абзаце 3C.
Строка 6:
Ответ зарабатывает баллы для этой строки, отвечая всем трем критериям:
• Описаны два разных вызова, M и D. Для каждого описан сегмент кода, который выполняется. Например, «Внутри цикла оператор выбора выполнит первую часть оператора выбора и напечатает задачу с помощью оператора *».
• Для каждого вызова описывается тестируемое состояние. «Два тестовых примера основаны на передаче разных входных данных для создания различных типов задач в функции (умножение или деление)».
• Результат каждого вызова описывается в ответе: «Результатом вызова будет вывод 5 задач на умножение и возврат количества правильных ответов».
Оператор по модулю Python и деление по полу
В дополнение к обычным операторам сложения, вычитания, умножения и деления, стандартная библиотека Python включает некоторые арифметические операторы, с которыми вы, возможно, менее знакомы. В этом посте я расскажу о модуле ( % ) и этажное деление ( // ), а также некоторые распространенные ловушки, связанные с ними.
Что делают деление по модулю и полу?
Модуль по модулю
Оператор по модулю используется для выполнения евклидова деления. Вы почти наверняка узнали о евклидовом делении в школе, даже если не знали, как оно называется.
При выполнении евклидова деления вы начинаете с делимого (число, которое вы хотите разделить) и делителя (число, на которое нужно разделить делимое). Допустим, 10 и 3 .
В так называемом «стандартном делении» результатом 10/3 является повторяющееся 3,333 или 3 и треть. В евклидовом делении нас не интересуют числа после запятой. Нам важен целочисленный результат деления (в данном случае 3 ), который называется частным . Сумма, оставшаяся после деления, называется 9.0017 остаток , что в данном случае равно 1 .
Чтобы дать вам еще один пример, 11 / 3 дает нам частное 3 и остаток 2 .
В Python оператор по модулю просто возвращает остаток:
>>> 10 % 3
1
>>> 11 % 3
2
Поэтажное деление
Поэтажное деление также используется для выполнения евклидова деления, но, в отличие от оператора по модулю, деление по этажам дает частное , а не остаток.
Рассмотрим пару примеров:
>>> 10 // 3
3
>>> 9 // 2
4
Мы можем создать небольшую функцию для вывода полного результата евклидова деления, например:
def euclidean_division(x, y):
частное = х // у
остаток = х % у
print(f"{частное} остаток {остаток}")
euclidean_division(10, 3) # 3 остаток 1
euclidean_division(11, 3) # 3 остаток 2
Однако есть проблема. Что происходит, когда мы вызываем нашу функцию с отрицательными числами?
>>> евклидов_дивизион (10, -3)
-4 остаток -2
Это выглядит неправильно. -3 , умноженное на -4 , равно 12 , что больше, чем 10 . В результате мы должны были получить
В результате мы должны были получить -3 остаток 1 . Так что же происходит?
Это ошибка деления пола
Картина, которую я нарисовал для вас ранее о евклидовом делении, не совсем точна. Для положительных целых чисел деление по полу и по модулю работает точно так же, как евклидово деление, но все становится сложнее, когда дело доходит до отрицательных чисел.
Это связано с округлением. Если мы посмотрим на документацию Python для арифметических операторов, мы найдем подсказку о том, что происходит:
[T] он результат [деления пола] является результатом математического деления с применением функции «пола».
Итак, давайте посмотрим на документацию по функции floor .
Возвращает нижний предел x, наибольшее целое число, меньшее или равное x.
И вот в чем проблема. -4 считается менее повторяющимся, чем -3,333 . Это левее на числовой прямой. Это означает, что деление этажа всегда будет округляться от нуля для отрицательных чисел и до нуля для положительных чисел.
Это означает, что деление этажа всегда будет округляться от нуля для отрицательных чисел и до нуля для положительных чисел.
>>> 10 // 3
3 # 3,333 раунда в ноль
>>> 10 // -3
-4 # -3,333 раунда от нуля
>>> 9 // 2
4 # 4,5 раунда в ноль
>>> 9 // -2
-5 # -4,5 раунда до нуля
Так в чем проблема с модулем?
Мы выяснили, почему мы получаем неожиданные результаты от деления на пол и отрицательных чисел, но наш остаток также оказался не таким, как мы ожидали. Так почему же?
Оказывается, деление по модулю и деление на пол являются тесно связанными операторами, о которых вы могли прочитать, если немного заглянули в документацию. Модульное и напольное деление связаны следующим тождеством: x = (x // y) * y + (x % y) .
Это означает, что результат деления этажа напрямую влияет на результат операции по модулю. Мы можем изменить вышеприведенное так: (х % у) = х - (х // у) * у .
Давайте попробуем один из наших предыдущих примеров, 10 % -3 :
10 % -3 = 10 - (-3) * (10 // -3)
10 % -3 = 10 - (-3) * (-4) # Помните, здесь деление пола округляется от нуля
10 % -3 = 10 - 12
10 % -3 = -2
И мы получаем точно такой же результат, как и раньше: 10 % -3 = -2 .
Несколько заключительных замечаний
В этом заключительном разделе я просто хочу упомянуть еще несколько интересных вещей о делении по модулю и полу. Однако, прежде чем я углублюсь в это, я думаю, важно отметить, что реализация деления по полу и по модулю в Python не является ошибкой. Однако я считаю важным понимать, когда и как такие реализации отличаются от нашего интуитивного понимания, потому что тогда мы сможем использовать эту реализацию как инструмент, и она перестанет быть источником, возможно, неприятных ошибок.
Преобразование типов
Одна из интересных особенностей деления на пол в Python заключается в том, что оно не обязательно производит число с плавающей запятой. Фактически, во всех наших примерах результатом было целое число. Это полностью отличается от стандартного деления в Python, которое всегда дает число с плавающей запятой.
Оператор по модулю работает так же, возвращая целое число, если оба операнда были целыми числами.
Если любой из операндов является числом с плавающей запятой, деление по модулю и по полу даст число с плавающей запятой.
Использование чисел с плавающей запятой
Хотя все примеры в этом посте были целыми числами, вполне возможно использовать числа с плавающей запятой для любого операнда, и они работают точно так же, они просто дают число с плавающей запятой.
Пример из документации: 3,14 % 0,7 , что даст 0,34 .
Комплексные числа
Комплексные числа — это числа с действительной и мнимой частями. Здесь их стоит отметить только потому, что ни модульное деление, ни деление на пол не могут принимать комплексное число в качестве операнда. Попытка использовать комплексное число для деления на пол или операций по модулю приведет к повышению Ошибка типа .
Резюме
- Для положительных чисел деление по полу и по модулю работает как евклидово деление, получая частное и остаток соответственно.
- Для отрицательных чисел обе операции дадут несколько неожиданные результаты.
- Полное деление всегда округляется от нуля для отрицательных чисел, поэтому
-3,5 округляется до -4 , но к нулю для положительных чисел, поэтому 3,5 округляется до 3 .

 В каждом списке хранятся значения, используемые в математических задачах. first_number хранит первое число в задаче, а second_number хранит второе число, которое является делителем для задач на деление.
В каждом списке хранятся значения, используемые в математических задачах. first_number хранит первое число в задаче, а second_number хранит второе число, которое является делителем для задач на деление.
 Функция принимает тип вопросов в качестве входных данных, а затем возвращает количество правильных ответов в основную программу.
Функция принимает тип вопросов в качестве входных данных, а затем возвращает количество правильных ответов в основную программу.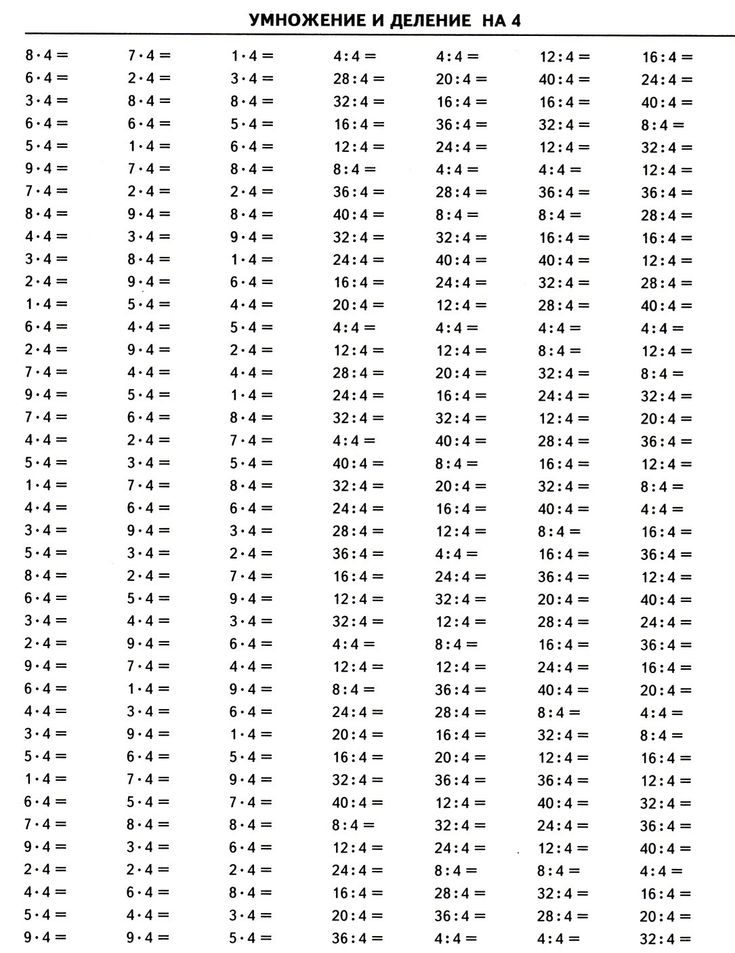 Описывает два вызова процедуры, указанной в письменном ответе 3c. Каждый вызов должен передавать разные аргументы, которые вызывают выполнение другого сегмента кода в алгоритме.
Описывает два вызова процедуры, указанной в письменном ответе 3c. Каждый вызов должен передавать разные аргументы, которые вызывают выполнение другого сегмента кода в алгоритме. 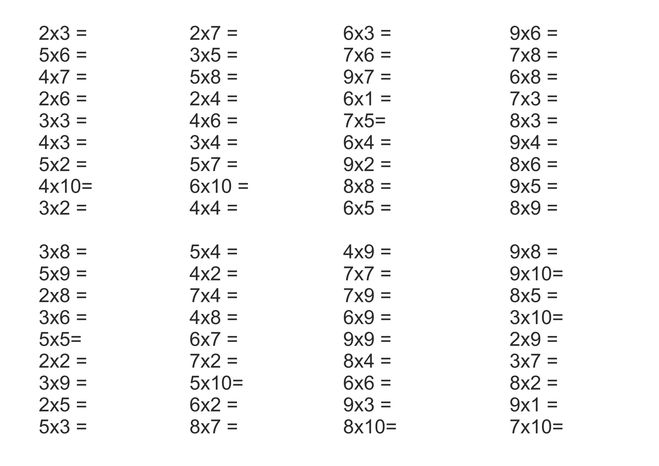 В результате код напечатает оператор / и вычислит ответ, разделив значение first_number на значение second_number. Результатом вызова будет вывод 5 задач на деление и возврат количества правильных ответов.
В результате код напечатает оператор / и вычислит ответ, разделив значение first_number на значение second_number. Результатом вызова будет вывод 5 задач на деление и возврат количества правильных ответов.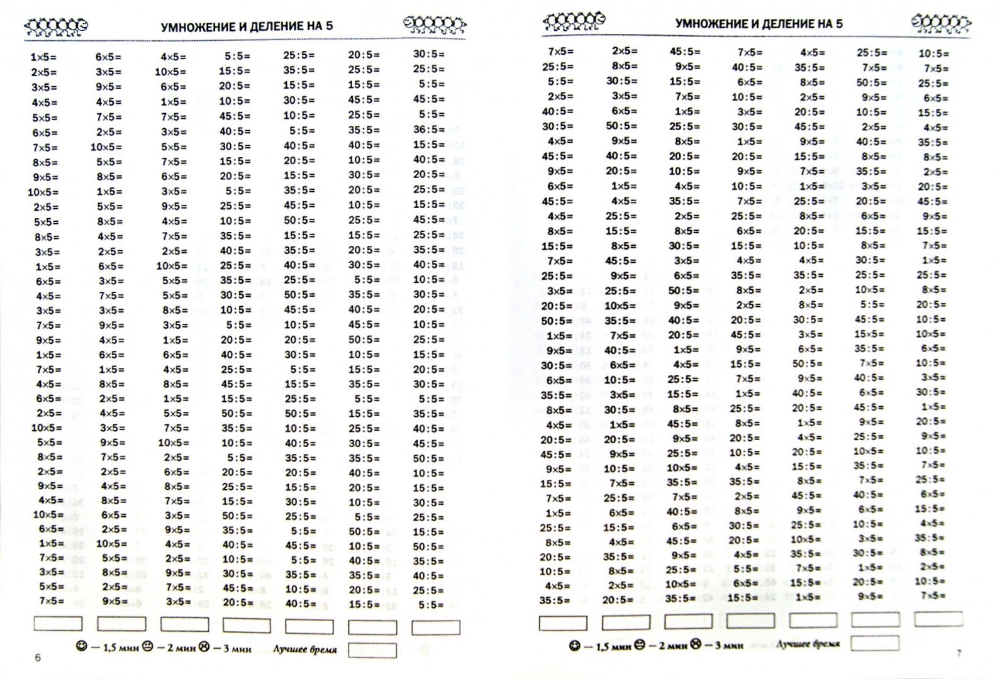 Он также объясняет, как программа должна быть написана без списка, заявляя: «Без списка программа должна была бы использовать отдельные переменные и писать последовательно, а не в цикле».
Он также объясняет, как программа должна быть написана без списка, заявляя: «Без списка программа должна была бы использовать отдельные переменные и писать последовательно, а не в цикле».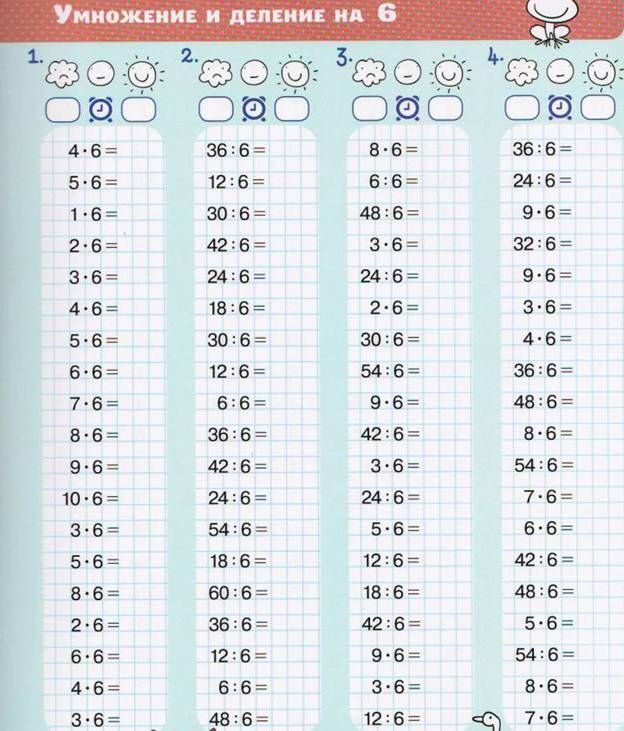
% ) и этажное деление ( // ), а также некоторые распространенные ловушки, связанные с ними.
10 и 3 . 10/3 является повторяющееся 3,333 или 3 и треть. В евклидовом делении нас не интересуют числа после запятой. Нам важен целочисленный результат деления (в данном случае 3 ), который называется частным . Сумма, оставшаяся после деления, называется 9.0017 остаток , что в данном случае равно 1 . 11 / 3 дает нам частное 3 и остаток 2 .
-3 , умноженное на -4 , равно 12 , что больше, чем 10 . В результате мы должны были получить
В результате мы должны были получить -3 остаток 1 . Так что же происходит? floor . -4 считается менее повторяющимся, чем -3,333 . Это левее на числовой прямой. Это означает, что деление этажа всегда будет округляться от нуля для отрицательных чисел и до нуля для положительных чисел.
Это означает, что деление этажа всегда будет округляться от нуля для отрицательных чисел и до нуля для положительных чисел. x = (x // y) * y + (x % y) . (х % у) = х - (х // у) * у . 10 % -3 : 10 % -3 = -2 .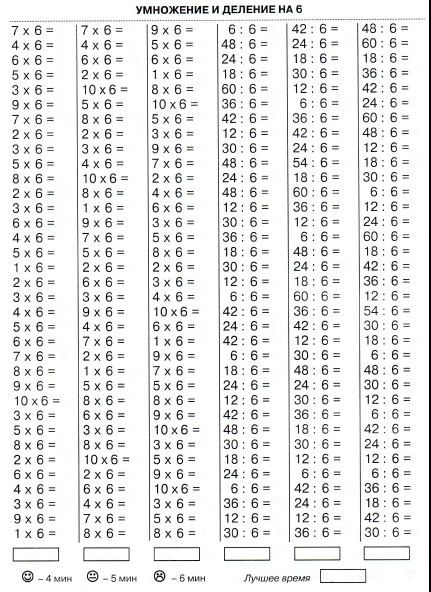
3,14 % 0,7 , что даст 0,34 . Ошибка типа . -3,5 округляется до -4 , но к нулю для положительных чисел, поэтому 3,5 округляется до 3 .

 Табличное умножение и деление. ФГОС» из жанра Сборники задач, заданий, самоучители
Табличное умножение и деление. ФГОС» из жанра Сборники задач, заданий, самоучители Web-мастеринг.
Web-мастеринг. Табличное умножение и деление. ФГОС
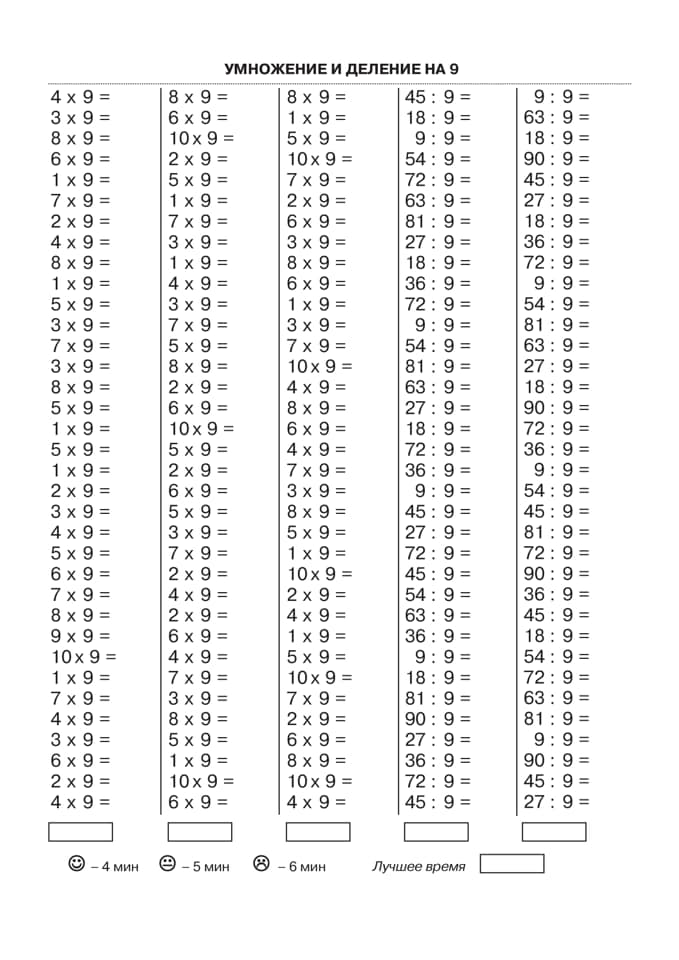
Табличное умножение и деление. ФГОС В книге представлен материал, который позволит, с одной стороны, за короткое время выучить таблицу умножения, с другой — эффективно тренировать устойчивость внимания, оперативную память детей, умение сосредоточиться. Дети, работая с пособием, научатся быстро и правильно умножать и делить числа, выполнять обратные математические операции с натуральными числами. Для учителя данный материал является хорошим инструментом диагностики причин затруднений каждого ученика. Пособие является необходимым дополнением к учебникам по математике, рекомендованным Министерством образования и науки Российской Федерации и включённым в Федеральный перечень учебников.
В книге представлен материал, который позволит, с одной стороны, за короткое время выучить таблицу умножения, с другой — эффективно тренировать устойчивость внимания, оперативную память детей, умение сосредоточиться. Дети, работая с пособием, научатся быстро и правильно умножать и делить числа, выполнять обратные математические операции с натуральными числами. Для учителя данный материал является хорошим инструментом диагностики причин затруднений каждого ученика. Пособие является необходимым дополнением к учебникам по математике, рекомендованным Министерством образования и науки Российской Федерации и включённым в Федеральный перечень учебников.