Метод искусственного базиса это: Недопустимое название — Циклопедия

Метод искусственного базиса решения задач линейного программирования

Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.

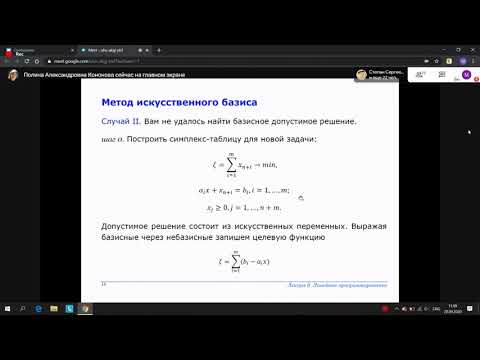
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М — достаточно большое положительное число.

В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.

В процессе решения М-задачи Искусственные векторы выходят из базиса, в результате чего будет получен опорный план. В противном случае исходная задача неразрешима.

2. Постановка задачи линейного программирования

При откорме, каждое животное должно получить не менее 9 ед. белка, 8 ед. протеина, и 10 ед. углеводов. Для составления рациона используется 2 вида корма, состав которых приведён в таблице. Стоимость 1 кг. Первого составляет 4 ден. ед., а второго 6 ден. ед..

Составьте дневной рацион питательности, имеющий минимальную стоимость.

Таблица 2 Состав питательных веществ в кормах

Питательное вещество	Содержание вещества
	Корм 1	Корм 2
Белок	3	1
Углеводы	1	2
Протеин	1	6

2. Построение математической модели задачи

Практически во всех науках о природе, живой и неживой, об обществе, построение и использование моделей является мощным орудием познания. Реальные объекты и процессы бывают столь многообразны и сложны, что лучшим способом изучения часто является построение модели, отражающей лишь какую-то часть реальности.

В любом случае модель строится с целью узнать про объект что-либо новое или сохранить об объекте информацию, которая может стать недоступной в будущем.

Как правило, процесс изучения, связанный с использованием моделей и называемый моделированием не заканчивается созданием одной модели. Построив модель и получив с её помощью, какие-либо результаты, соотносят их с реальностью, и если это соотношение даёт неудовлетворительные результаты, то в построенную модель вносят коррективы или даже создают другую модель. В случае достижения хорошего соответствия с реальностью выясняют границы применения модели. Это очень важный вопрос, он решается путём сравнения модели с оригиналом путём сравнения предсказаний, полученных с помощью компьютерной модели. Если это сравнение даёт удовлетворительные результаты, то модель принимают на вооружение, если нет, приходится создавать другую модель.

Математическое моделирование относится к классу знакового моделирования, при этом модели могут создаваться из любых математических объектов, чисел, функций, уравнений, графиков, графов.

Практически во всех науках построение и использование моделей является мощным орудием познания.

Цель задачи заключается в нахождение рациона питания, который бы восполнял минимальный набор питательных веществ. При минимальных денежных затратах.

Пусть число килограммов корма 1-го вида, ачисло килограмм корма 2-го вида необходимых для составления рациона.

Цель задачи: Минимизировать расход, при соблюдение нормы рациона.

Следовательно,

Состав питательных веществ в рационе не должен быть меньше необходимой дневной нормы. Отсюда следует система неравенств:

Метод искусственного базиса (Симплекс-метод) — Пример 1

Целевая функция:
1X₁+5X₂+4X₃-3X₄→max
Условия:
2X₁+7X₂+1X₃+0X₄≤5
1X₁+4X₂+2X₃+8X₄=6
-1X₁+0X₂+2X₃+5X₄=9
Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных. Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные. Тогда система запишется в виде:
2X₁+7X₂+1X₃+0X₄+X5=5
1X₁+4X₂+2X₃+8X₄+R1=6
-1X₁+0X₂

+2X₃+5X₄+R2=9
Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции. Так как нам необходимо найти максимум целевой функции, то в таблицу заносятся коэффициенты с противоположным знаком
Так как среди исходного набора условий были равенства, мы ввели искуственные переменные R. Это значит, что в симплекс таблицу нам необходимо добавить дополнительную строку M, элементы которой расчитываются как сумма соответствующих элементов условий-равенств (тех которые после приведения к каноническому виду содержат искусственные переменные R) взятая с противоположным знаком.
Из данных задачи составляем исходную симплекс таблицу.

	X1	X2	X3	X4	Своб член
F	-1	-5	-4	3	0
X5	2	7	1	0	5
R1	1	4	2	8	6
R2	-1	0	2	5	9
M	0	-4	-4	-13	-15

Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение. В строке M имеются отрицательные элементы, это означает что полученое решение не оптимально. Определим ведущий столбец. Для этого найдем в строке M максимальный по модулю отрицательный элемент – это -13 Ведущей строкой будет та для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является R1, а ведущий элемент: 8.

	X1	X2	X3	Своб член
F	-1.375	-6.5	-4.75	-2.25
X5	2	7	1	5
X4	0. 125	0.5	0.25	0.75
R2	-1.625	-2.5	0.75	5.25
M	1.625	2.5	-0.75	-5.25

В строке M имеются отрицательные элементы, это означает что полученое решение не оптимально. Определим ведущий столбец. Для этого найдем в строке M максимальный по модулю отрицательный элемент – это -0.75 Ведущей строкой будет та для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X4, а ведущий элемент: 0.25.

	X1	X2	X4	Своб член
F	1	3	19	12
X5	1. 5	5	-4	2
X3	0.5	2	4	3
R2	-2	-4	-3	3
M	2	4	3	-3

В столбце свободных членов и в строке F нет отрицательных элементов. Выполнение алгоритма на этом завершено, однако не все искусственные переменные (R) были исключены из базиса (условия исходной задачи не совместны).

   

Подробнее

Аппроксимация. Основные понятия. Сфера применения. Понятие о методе наименьших квадратов

Курсовая работа, Высшая математика

Выполнил: user986395

симплекс метод ( метод искусственного базиса)

Решение задач, Логистика

Выполнил: Nolu27

Так же вы можете купить уже выполненные похожие работы. Для удобства покупки работы размещены на независимой бирже. Подробнее об условиях покупки тут.

 

Исследование операций — Искусственная переменная в основе двухфазного метода линейного программирования

$\begingroup$

Предположим, у нас есть следующая проблема: $$Z = 3 x_{1} + 2 x_{2} + 3 x_{3} \to max$$ $$\begin{case} 2 x_{1} + x_{2} + x_{3} = 4 \\ x_{1} + 3 x_{2} + x_{3} = 12 \\ 3 x_{1} + 4 x_{2} + 2 x_{3} = 16 \\ x_{1}, x_{2}, x_{3} \geq 0 \end{cases}$$

Я пытаюсь решить это с помощью двухфазный метод. Я знаю, что нам нужно избавиться от искусственных переменных в базе на Фазе 1.

Но в данном случае это невозможно. В связи с этим здесь просто убрана искусственная переменная, несмотря на то, что она есть в базе!

Есть ли для этого какая-то причина?

• линейное программирование
• операции-исследования
• симплекс-метод
• двухфазный симплекс

$\endgroup$

$\begingroup$

У вас не будет проблем, если вы пропустите одно из ограничений. Вы можете (должны) сделать это, поскольку три ограничения линейно зависимы. Вы получите нулевую строку, если вычтете ограничение $1$ и ограничение $2$ из ограничения $3$. Вот вывод калькулятора, если второе ограничение было опущено.

$$Z = 3 x_{1} + 2 x_{2} + 3 x_{3} \to \textrm{max}$$

$$ 2 x_{1} + x_{2} + x_{3 } = 4$$ $$3 x_{1} + 4 x_{2} + 2 x_{3} = 16 $$ $$x_{1}, x_{2}, x_{3} \geq 0 $$

$\endgroup$

$\begingroup$

Суть в том, что искусственная переменная, застрявшая в базисе, имеет значение 0, что означает, что (а) решение допустимо и (б) ограничения линейно зависимы (поэтому вы не можете вывести искусственную переменную из основа). Как отметил @callculus42, вы можете удалить ограничение (обычно вы выбираете то, которое содержит искусственную переменную) и работать с уменьшенной проблемой.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

линейное программирование — Почему мы вводим искусственную переменную в двухфазный симплексный метод?

спросил 4 года 5 месяцев назад

Изменено 3 года, 9 месяцев назад

Просмотрено 6к раз

$\begingroup$

В двухфазном симплексном методе мы используем искусственные переменные, когда наше ограничение больше или равно некоторой константе. Я просто хочу знать, какова цель этих искусственных переменных?

• линейное программирование

$\endgroup$

7

$\begingroup$

Я получил ответ из другого источника. Это проясняет все мое замешательство.

Общая идея двухэтапных методов заключается в создании вспомогательной задачи с очевидным начальным решением (которое может быть невозможным для исходной задачи) с целью устранения неразрешимых задач. Если оптимальное вспомогательное решение устраняет недопустимости, то значения переменных вспомогательного решения из исходной задачи можно использовать для начала фазы 2 с базовым допустимым решением.

Искусственные переменные в фазе 1 введены для того, чтобы мы могли сделать исходные переменные задачи небазисными и установить их равными нулю, даже если это может оказаться невыполнимым для исходной задачи. Искусственные переменные принимают результирующие невозможности и являются базовыми в начале фазы 1. Цель фазы 1 состоит в том, чтобы свести эти переменные к нулю, после чего исходные переменные задачи допустимы, а текущая база состоит из исходных переменных задачи. (В случае вырождения может потребоваться некоторая незначительная очистка.