Действие с векторами: Действия над векторами /qualihelpy

Векторы и действия над векторами

Оглавление:

• Сложение векторов
• Вычитание векторов
• Умножение вектора на число
• Скалярное произведение векторов
• Онлайн-курс «Математика 10+11 100 баллов»

Стандартное определение: «Вектор — это направленный отрезок». Обычно этим и ограничиваются знания выпускника о векторах. Кому нужны какие-то «направленные отрезки»?

А в самом деле, что такое векторы и зачем они?

Прогноз погоды. «Ветер северо-западный, скорость 18 метров в секунду». Согласитесь, имеет значение и направление ветра (откуда он дует), и модуль (то есть абсолютная величина) его скорости.

Величины, не имеющие направления, называются скалярными. Масса, работа, электрический заряд никуда не направлены. Они характеризуются лишь числовым значением — «сколько килограмм» или «сколько джоулей».

Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.

Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения направлено к поверхности Земли, а величина его равна 9,8 м/с². Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.

Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B.  Конечный результат — его перемещение из точки A в точку B, то есть перемещение на вектор .

Теперь понятно, почему вектор — это направленный отрезок. Обратите внимание, конец вектора — там, где стрелочка. Длиной вектора называется длина этого отрезка. Обозначается: или .

До сих пор мы работали со скалярными величинами, по правилам арифметики и элементарной алгебры. Векторы — новое понятие. Это другой класс математических объектов. Для них свои правила.

Когда-то мы и о числах ничего не знали. Знакомство с ними началось в младших классах. Оказалось, что числа можно сравнивать друг с другом, складывать, вычитать, умножать и делить. Мы узнали, что есть число единица и число ноль.
Теперь мы знакомимся с векторами.

Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.

А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1. Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.

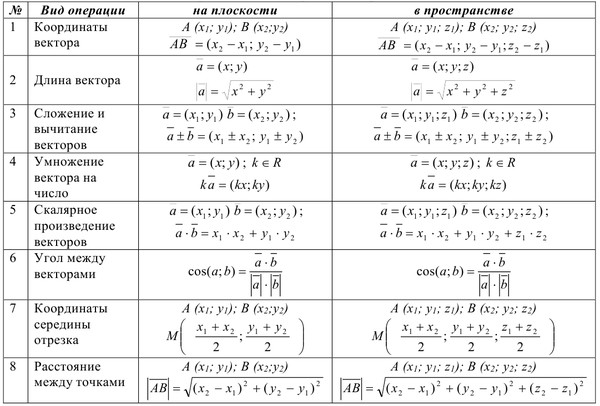
Удобнее всего работать с векторами в прямоугольной системе координат — той самой, в которой рисуем графики функций. Каждой точке в системе координат соответствуют два числа — ее координаты по x и y, абсцисса и ордината.
Вектор также задается двумя координатами: .

Здесь в скобках записаны координаты вектора — по x и по y.
Находятся они просто: координата конца вектора минус координата его начала.

Если координаты вектора заданы, его длина находится по формуле

к оглавлению ▴

Сложение векторов

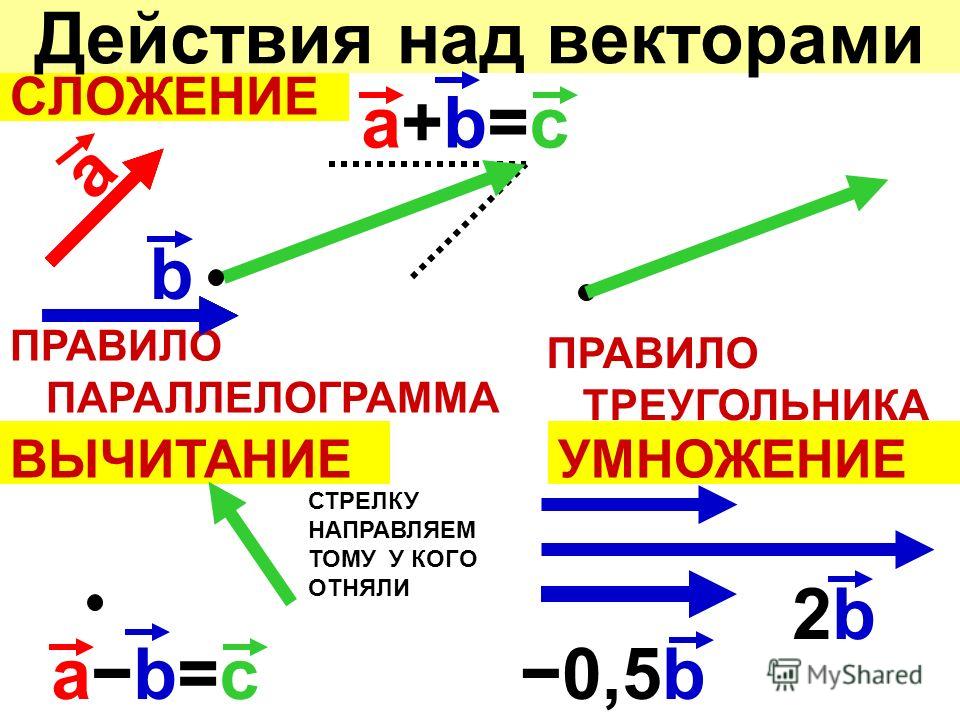
Для сложения векторов есть два способа.

1. Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов. и

Помните басню про лебедя, рака и щуку? Они очень старались, но так и не сдвинули воз с места. Ведь векторная сумма сил, приложенных ими к возу, была равна нулю.

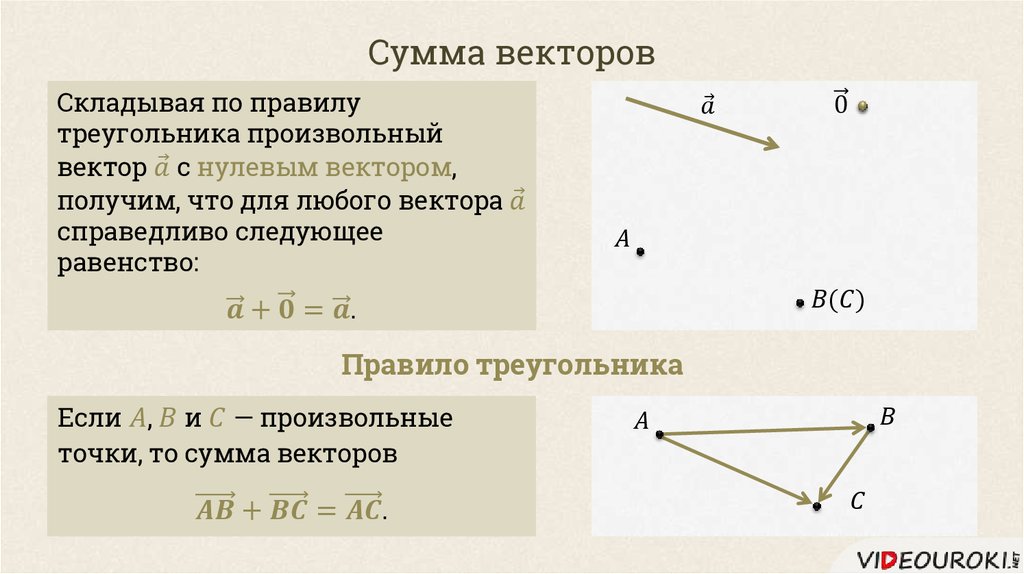
2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .

По тому же правилу можно сложить и несколько векторов. Пристраиваем их один за другим, а затем соединяем начало первого с концом последнего.

Представьте, что вы идете из пункта А в пункт В, из В в С, из С в D, затем в Е и в F. Конечный результат этих действий — перемещение из А в F.

При сложении векторов и получаем:

;

.

к оглавлению ▴

Вычитание векторов

Вектор направлен противоположно вектору . Длины векторов и равны.

Теперь понятно, что такое вычитание векторов.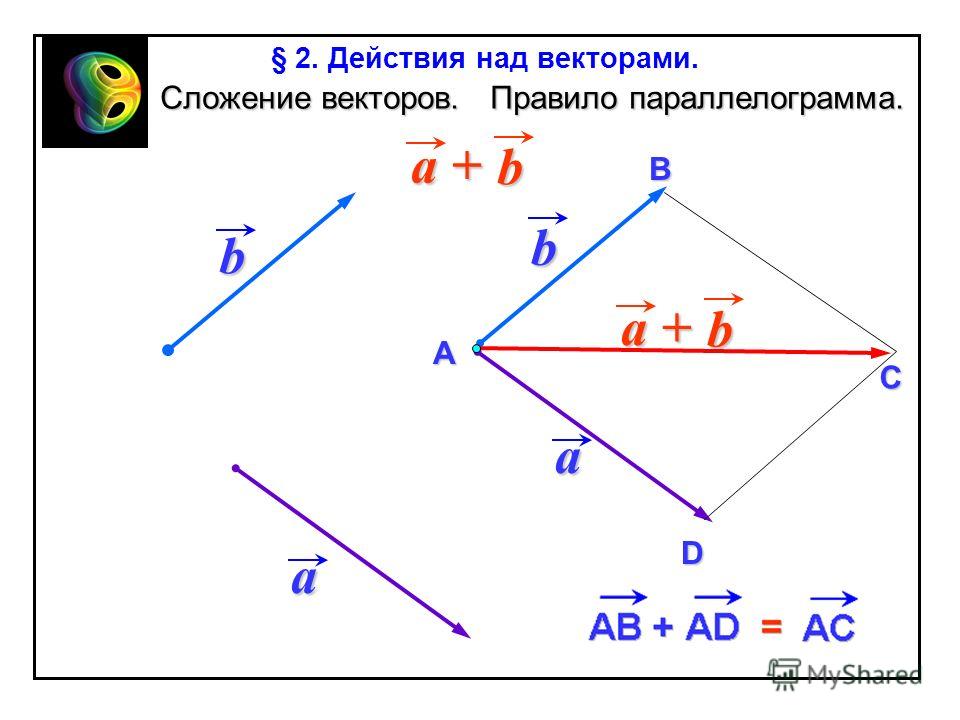 Разность векторов и — это сумма вектора и вектора .

к оглавлению ▴

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.

к оглавлению ▴

Скалярное произведение векторов

Векторы можно умножать не только на числа, но и друг на друга.

Скалярным произведением векторов называется произведение длин векторов на косинус угла между ними.

Обратите внимание — перемножили два вектора, а получился скаляр, то есть число. Например, в физике механическая работа равна скалярному произведению двух векторов — силы и перемещения:

.

Если векторы перпендикулярны, их скалярное произведение равно нулю.
А вот так скалярное произведение выражается через координаты векторов и :

.

Из формулы для скалярного произведения можно найти угол между векторами:

.

Эта формула особенно удобна в стереометрии. Например, в задаче 14 Профильного ЕГЭ по математике нужно найти угол между скрещивающимися прямыми или между прямой и плоскостью. Часто векторным методом задача 14 решается в несколько раз быстрее, чем классическим.

В школьной программе по математике изучают только скалярное произведение векторов.
Оказывается, кроме скалярного, есть еще и векторное произведение, когда в результате умножения двух векторов получается вектор. Кто сдает ЕГЭ по физике, знает, что такое сила Лоренца и сила Ампера. В формулы для нахождения этих сил входят именно векторные произведения.

Векторы — полезнейший математический инструмент. В этом вы убедитесь на первом курсе вуза.

---

к оглавлению ▴

Онлайн-курс «Математика 10+11 100 баллов»

— Теория: учебник Анны Малковой + 70 ч. видеоразборов.
— 144 ч. мастер-классов: 8 онлайн мастер-классов с Анной Малковой в месяц.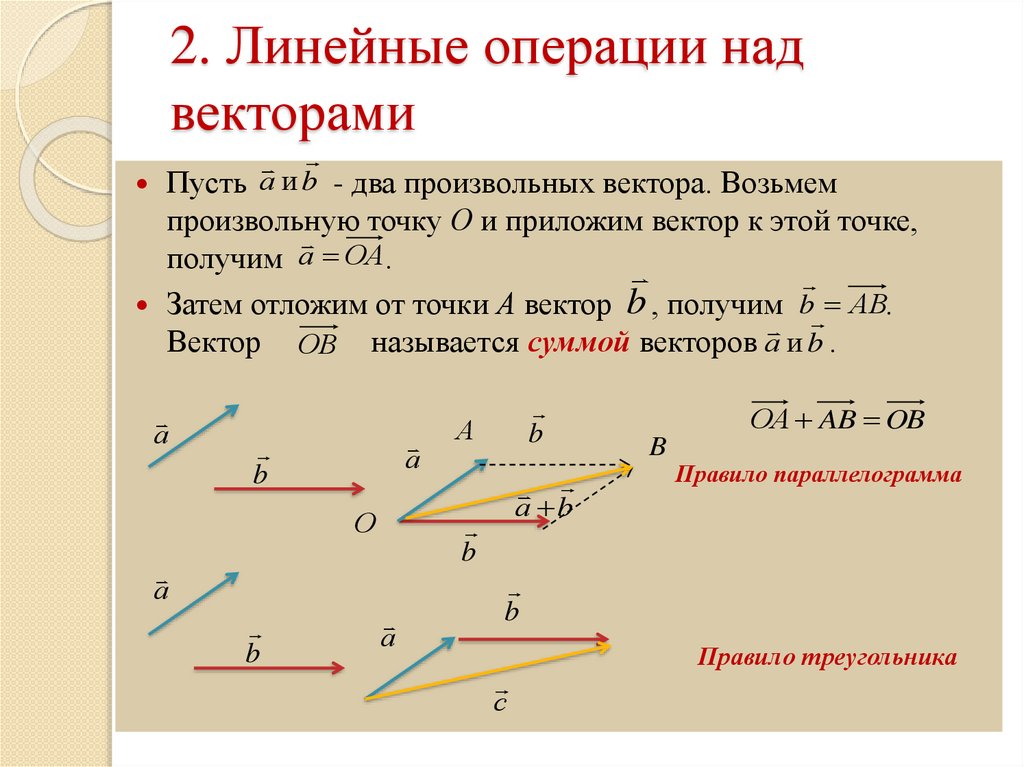
— Тренажер для отработки задач ЕГЭ (800+ задач): автоматическая + ручная проверки.
— Связь с Анной Малковой (чаты и почта).
— 9 репетиционных ЕГЭ: ежемесячно.
— Контроль: страница личных достижений учащегося, отчеты родителям.
— Личный кабинет.

ПОДРОБНЕЕ

---

Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Векторы наu0026nbsp;ЕГЭ поu0026nbsp;математике. Действия над векторами» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 08.04.2023

умножение, сложение векторов по правилу многоугольника

Прежде чем приступить к тематике статьи, напомним основные понятия.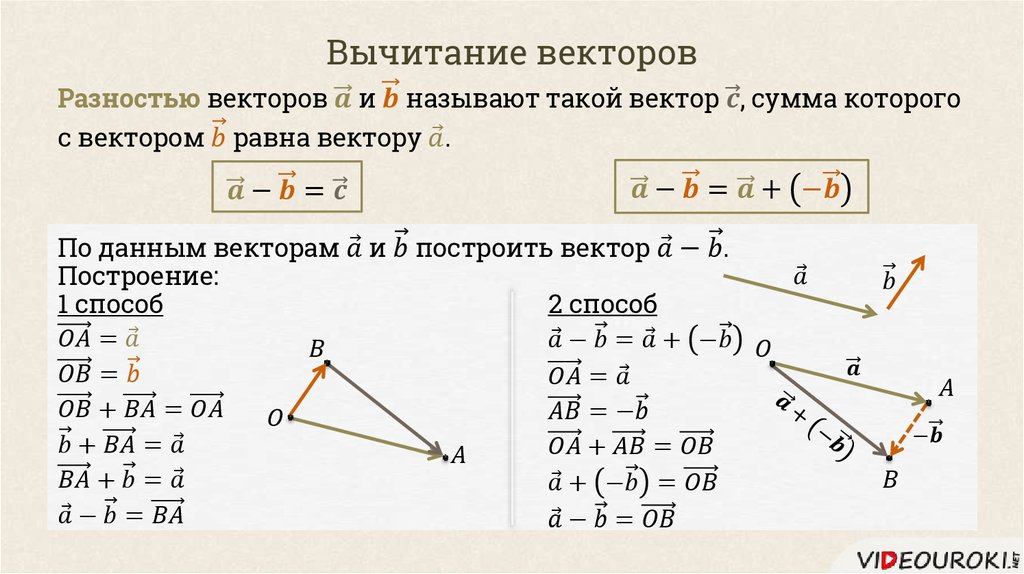

Определение 1

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Определение 2

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Определение 3

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Определение 4

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Сложение двух векторов

Определение 5

Исходные данные: векторы a→ и b→ . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор AB→, равный вектору а→; из полученной точки undefined – вектор ВС→, равный вектору b→.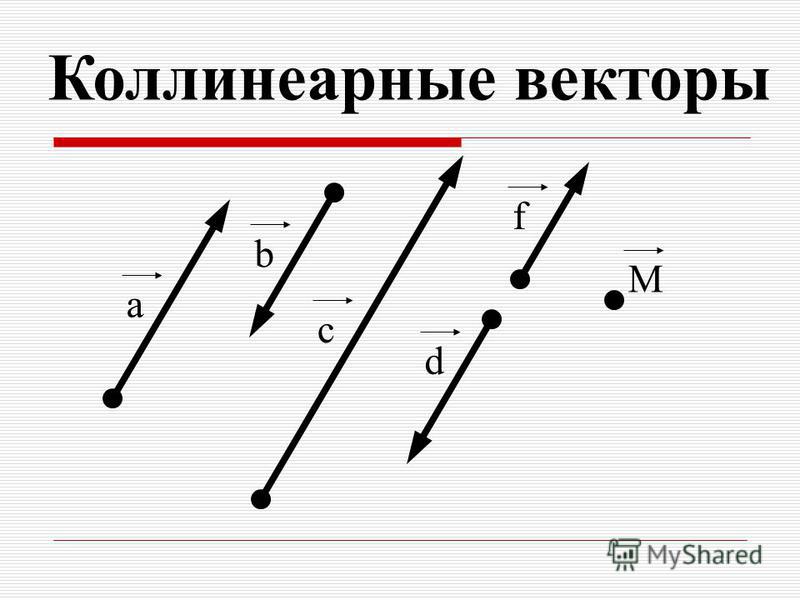 Соединив точки undefined и C, получаем отрезок (вектор) АС→, который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

— для неколлинеарных векторов:

— для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

Определение 6

Исходные данные: векторы a→ , b→, c→,d→. Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a→; затем от конца полученного вектора откладывается вектор, равный вектору b→; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B, а полученный отрезок (вектор) AB→ – суммой всех исходных данных.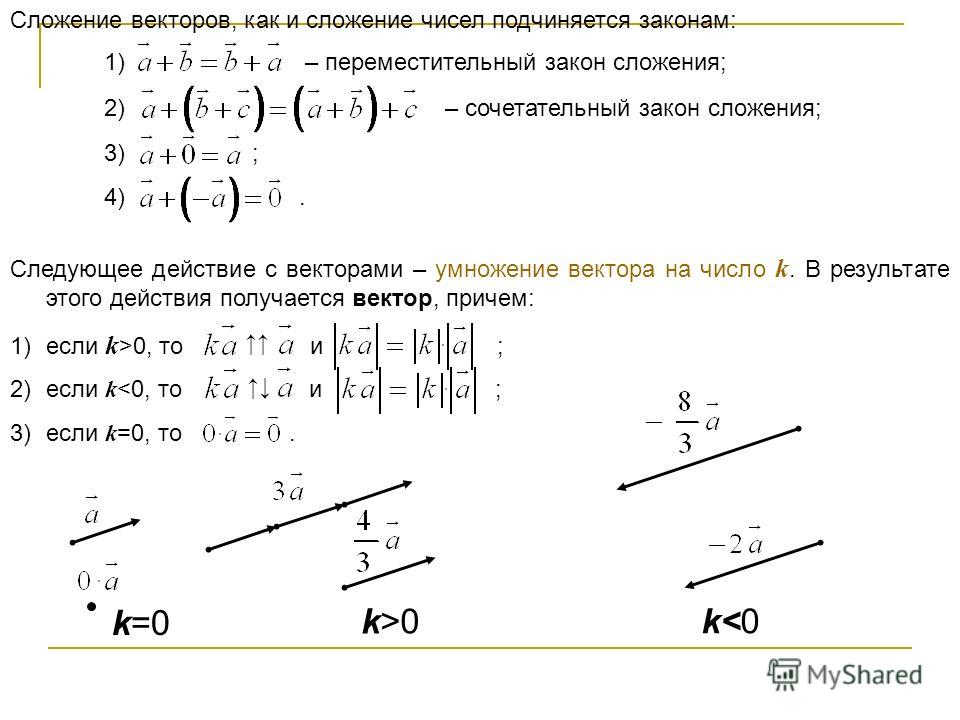 Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Определение 7

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a→и b→есть сумма векторов a→ и — b→.

Умножение вектора на число

Определение 8

Чтобы произвести действие умножения вектора на некое число k, необходимо учитывать следующие правила:
— еслиk>1, то это число приведет к растяжению вектора в k раз;
— если 0<k<1, то это число приведет к сжатию вектора в 1k раз;
— если k<0, то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
— если k=1, то вектор остается прежним;
— если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

Исходные данные:
1) вектор a→и число k=2;
2) вектор b→и число k=-13.

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a→, b→, c→и произвольные действительные числа λ и μ.

1. Свойство коммутативности: a⇀+b→=b→+a→ .
   
2. Свойство ассоциативности: (a→+b→)+c→=a→+(b→+c→) .
   
3. Свойство использования нейтрального элемента по сложению (нулевой вектор 0→ ⃗). Это очевидное свойство: a→+0→=a→
4. Свойство использования нейтрального элемента по умножению (число, равное единице): 1·a→=a→. Это очевидное свойство, не предполагающее никаких геометрических преобразований.
5. Любой ненулевой вектор a→ имеет противоположный вектор -a→ и верным является равенство: a→+(-a→)=0→. Указанное свойство — очевидное.
6. Сочетательное свойство операции умножения: ( λ · µ ) · a→ = λ · ( µ·a→ ).
   Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
7. Первое распределительное свойство (очевидно): ( λ + µ ) · a→ = λ ·a→ + µ · a→.
8. Второе распределительное свойство: λ · (a→ +b→) = λ ·a→ + λ · b→ .
   Геометрически это свойство определяется подобием треугольников:
   

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Пример 1

Задача: упростить выражение a→-2·(b→+3·a→)

Решение
— используя второе распределительное свойство, получим: a→-2·(b→+3·a→)=a→-2·b→-2·(3·a→)
— задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a→-2·b→-2·(3·a→)=a→-2·b→-(2·3)·a→=a→-2·b→-6·a→
— используя свойство коммутативности, меняем местами слагаемые:a→-2·b→-6·a→=a→-6·a→-2·b→
— затем по первому распределительному свойству получаем:a→-6·a→-2·b→=(1-6)·a→-2·b→=-5·a→-2·b→Краткая запись решения будет выглядеть так:a→-2·(b→+3·a→)=a→-2·b→-2·3·a→=5·a→-2·b→
Ответ: a→-2·(b→+3·a→)=-5·a→-2·b→

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Операции над n-мерными векторами

Следующая статья

Векторное пространство

• Векторное произведение
• Векторное пространство
• Векторы на плоскости и в пространстве
• Геометрическая фигура угол
• Деление отрезка в заданном соотношении
• Все темы по математике

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Все предметы

Узнать подробнее

задача обьемная Электротехника

• Вид работы:

  Контрольная работа

• Выполнена:

  26 декабря 2022 г.

• Стоимость:

  800 руб

Заказать такую же работу

Теория вероятностей

• Вид работы:

  Онлайн-помощь

• Выполнена:

  23 декабря 2022 г.

• Стоимость:

  2 600 руб

Заказать такую же работу

Расчет электропривода ленточного конвейера

• Вид работы:

  Курсовая работа

• Выполнена:

  16 декабря 2022 г.

• Стоимость:

  12 000 руб

Заказать такую же работу

Раскрыть выполнение трудовых действий согласно Профессионального стандарта Работник по исследованию скважин

• Вид работы:

  Доклад

• Выполнена:

  29 октября 2022 г.

• Стоимость:

  2 100 руб

Заказать такую же работу

Электротехника задач там где дано задачи делать только те которые указаны напротив таблицы с моими данными

• Вид работы:

  Контрольная работа

• Выполнена:

  26 октября 2022 г.

• Стоимость:

  3 400 руб

Заказать такую же работу

Техническое обслуживание и ремонт стен перекрытий перегородок крыш

• Вид работы:

  Реферат

• Выполнена:

  18 сентября 2022 г.

• Стоимость:

  1 800 руб

Заказать такую же работу

Смотреть все работы по электротехнике

Линейная алгебра

. Почему действие группы в векторном пространстве полиномов естественно является левым действием?

Задавать вопрос

спросил 11 лет, 1 месяц назад

Изменено 11 лет, 1 месяц назад

Просмотрено 2к раз 9{-1}г)$). *).$ Может быть, этот функтор двойного пространства что-то объясняет?

• линейная алгебра
• теория групп
• теория представлений

$\endgroup$

2

$\begingroup$

Действие, определенное здесь, относится к функциям , то есть к $P$, а не к векторам $z$. Напишите $R=g_2\cdot P$. Тогда $(g_1\cdot R)(z)=R(zg_1)$. Добавьте к этому тот факт, что $R(x)=P(xg_2)$ для любого вектора $x$. Здесь $x=zg_1$, поэтому мы получаем, что $$ (g_1\cdot(g_2\cdot P))(z)=(g_1\cdot R)(z)=R(zg_1)=(g_2\cdot P)(zg_1)=P((zg_1)g_2). $$

Другой способ увидеть это состоит в том, чтобы понять, что $g\cdot P$ — это функция, полученная путем составления $\rho_g:z\mapsto zg$ с $P$ справа (т. е. впереди $P$). Так $$ g\cdot P = P \circ \rho_g. $$ Поэтому $$ g_1\cdot(g_2\cdot P)=g_1\cdot(P\circ\rho_{g_2})=(P\circ\rho_{g_2})\circ\rho_{g_1}.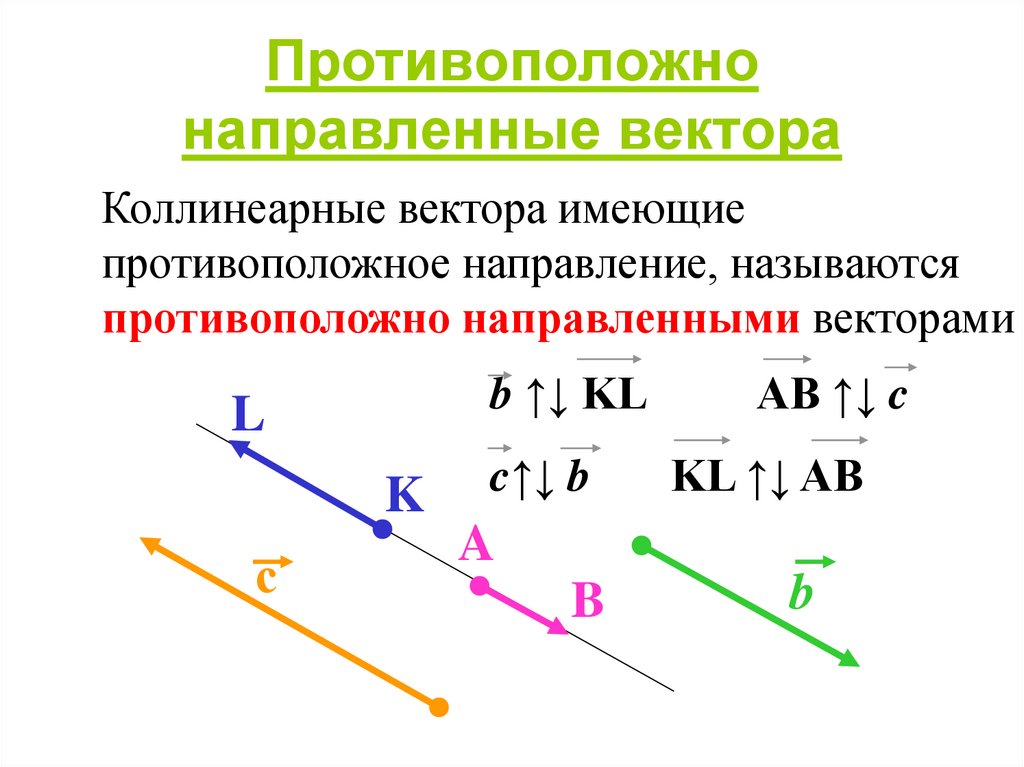 $$ В силу ассоциативности композиции эта последняя композиция тогда $$ P\circ(\rho_{g_2}\circ\rho_{g_1})=P\circ\rho_{g_1g_2}=(g_1g_2)\cdot P. $$ Здесь $\rho_{g_2}\circ\rho_{g_1}=\rho_{g_1g_2}$, потому что $$(\rho_{g_2}\circ\rho_{g_1})(z)=\rho_{g_2}(\rho_{g_1}(z))=\rho_{g_2}(zg_1)=(zg_1)g_2= z(g_1g_2)=\rho_{g_1g_2}(z). $$ 9*)$ из $G$-представления $V$, что дает интересующее вас действие на кольце многочленов.

$\endgroup$

8

общая теория относительности — действие 1-формы на продвижение вперед и назад вектора

Задавать вопрос

спросил 9{‘v}}\omega_{\mu}$.

Чтобы прояснить ситуацию, пожалуйста, найдите отрывок из заметок, которые я читаю: [отрывок]

• общая теория относительности
• дифференциальная геометрия

$\endgroup$

3

$\begingroup$

Я не уверен, что вы подразумеваете под «доказательством» определения.