Разложение факториала и гамма-функции в конечный знакочередующийся ряд
Шишкин Геннадий Петрович, кандидат педагогических наук, доцент кафедры естественнонаучных и общетехнических дисциплин,филиалФГБО ВПО «Московский государственныйиндустриальныйуниверситет»в г. Кирове, г. Киров[email protected]
Шишкин Андрей Геннадьевич,аспирант кафедры общей и экспериментальной физики, младший научный сотрудник Учебнонаучного радиофизического центра ФГБОУ ВПО «Московский государственный педагогический университет», г. Москва [email protected]
Разложение факториала и гамма –функциив конечный знакочередующийся ряд
Аннотация.В статье предлагается к рассмотрению тождество, разработанное авторами, выражающее факториал, с последующим обобщением на гамма –функцию для непрерывных значений аргумента. Получено оригинальное разложение единицы в числовой конечный знакочередующийся ряд.Ключевые слова: конечные разности, конечный знакочередующийся ряд,факториал, гаммафункция.
Раздел:(03) философия; социология; политология; правоведение; науковедение.
Известно, чтоконечные разности с шагом x1 для степенной функции y= xn, заданной для nна множестве натуральных чисел, имеют вид [1]. Таблица 1y= x2y= x3y= x4y= x5…y= xn2y=2!3y=3!4y=4!5y=5!…ny=n!
Выпишем конечные разности для произвольных значений xпо степеням2; 3; 4;…n, в общем виде и, раскрывая скобки, получим:
x2[x2–(x1)2] –[(x1)2–(x2)2] = x2–2(x1)2+ (x2)2= 2!
x3{[x3–(x1)3] –[(x1)3–(x2)3]} –{[(x1)3
(x2)3] –[(x2)3
[(x3)3]} =
= x3–3(x1)3+ 3(x2)3–(x3)3= 3!
x4x4–4(x1)4+ 6(x2)4–4(x3)4+ (x4)4= 4!…………………………………………………………………………………….xnCn0xn−Cn1(x−1)n+Cn2(x−2)n−⋯+(−1)nCnm(x−m)n+⋯=n!
где m 0; 1; 2;… n.Последнюю конечную разность общего вида можно записать как
(1)Легко видеть (достаточно раскрыть скобки), что полученные конечные разности являются тождествами справедливыми для любых х. Следовательно, можно взять x= n. Тогда получим:
,
или
(2)или
==(3)где m 0; 1; 2;… n.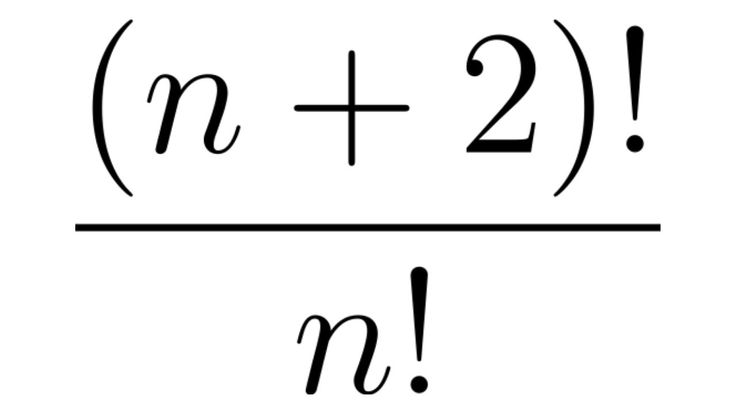
Тождества (1) и (2) справедливы для . Для целочисленных nряд обрывается при n= mи мы получаем конечный знакочередующийся ряд.Рассмотрим конечный знакочередующийся ряд (1), выражающий факториал
для дробных n 0.В таком случае следует перейти к гамма –функции, которая, как известно, является обобщением факториала. Получим приближенное равенство
Г(݊+1)≅∑(−1)(݊−݉)=⌊⌋=0(4)
Здесь удобнее заменить nна х, полагая, что х непрерывная переменная
Г(+1)≅∑(−1)(−݉)=⌊⌋=0(5)
Запишем ряд (5), как приближение гаммафункции, в развернутом виде
Г(+1)≅−(−1)+
+
(6)
Здесь, как и в (5), m=⌊x⌋
Вычисления по формуле (6) проводятся по схеме [2]:Таблица 2Значения аргументаЗначения функции Г(х1) по формуле (6)0≤x≤11≤x≤2−(−1)
2≤x≤3
m1≤x≤m
Как показывает численное исследование [3], конечный ряд (6) дает хорошее приближение для Г(х1), если х > 0 и не является целым числом. Таблица 3xГ(+)≅∑(−)=⌊⌋=(−)Г(x1)0110.20.
Из таблицы видно, что расчетные значения по формуле (6) несколько отличаются от точных значений гамма –функции. Следует заметить, что с ростом значения аргумента х отличия уменьшаются. Так для промежутка 1≤x≤2 имеются отличия в основном во втором знаке после запятой, а для промежутка 2≤x≤3, только в третьем. Для целочисленных значений аргумента х совпадения точные.На графике (рис.1) представлена кривая, составленнаяпо результатам вычислений по формуле (6) согласно схеме [2]. График гаммафункции [1], включающей и отрицательные значения аргумента, представлен на рис. 2. Гаммафункция в частности может быть представлена эйлеровым интегралом 2го рода [1].Г()=∫−1݁−݀∞0
Рис.1.Кривая результатов.
Формула (6)
Рис.2.График гаммафункций
Если в формуле (1) провести сокращение на n!, то получим тождествоТождество (7) справедливо для любых xи. Тождество (7) при х nибудет иметь вид1 = ,или после сокращения
1=∑(−1)(−)−1!(−−1)!.=−1=0(8)Отсюда, например, при n1=3, n24 и n37 получим соответственно
320!2!−221!1!+12!0!=1, 430!3!−331!2!+232!1!−133!0!=1, 760!6!−661!5!+562!4!−463!3!+364!2!−265!1!+166!0!=1
Может представлять интерес с точки зрения аддитивной проблемы теории чисел.Рассмотрим тождество (3) для целочисленных n≤ 0. В результате получим бесконечные числовые ряды:Г(0) () = ,Г(1) = () = ,Г(2) = () = ,………………………………………………………….Г(х)
(9)для х ≤ 0.
Все ряды вида (9) расходятся, что соответствует полюсам гаммафункции (рис.2).
Ссылки на источники1.Математический энциклопедический словарь. М. «Советская энциклопедия». 1988 г.
GennadyShishkin, Candidate of Pedagogic Sciences, Associate Professor at the chair of Natural sciences and engineering disciplines, branch of Moscow State Industrial University in Kirov, Kirov
shgp45@mail.
ru
Andrey Shishkin, PhDstudent,junior scientific researcher,Radiophysics Laboratory, Moscow State Pedagogical University, [email protected]
Factorial and gamma function expansion in a finite alternating seriesAbstract. The authorspropose to consider the identity expressing factorial, followed by an extension to the gamma function for continuous values of the argument. Original expansion units in numerical finite alternating series was obtained. Keywords: finite differences, finite alternating series, factorial, gamma function.
Рекомендовано к публикации:ГоревымП.М., кандидатом педагогических наук, главным редактором журнала «Концепт»
factorization – phrases
Sign in | English | Terms of Use
English ⇄ ChineseGermanJapaneseRussianUkrainianTerms for subject Mathematics containing factorization | all forms | exact matches only
| English | Russian |
| additive factorization | аддитивная факторизация |
| approximate factorization | приближённая факторизация |
| band factorization | ленточное разложение |
| big number factorization | факторизация целых (MichaelBurov) |
| big number factorization | факторизация целых чисел (MichaelBurov) |
| big number factorization | факторизация больших чисел (MichaelBurov) |
| block incomplete factorization | блочная неполная факторизация |
| canonical factorization | каноническая факторизация |
| Cholesky factorization | факторизация Холесского |
| Cholesky factorization | разложение Холецкого (decomposition) |
| complete factorization | полная факторизация |
| composite factorization | целочисленная факторизация (ssn) |
| composite factorization | факторизация составных целых чисел ( ssn) |
| composite factorization | составная факторизация |
| cyclotomic factorization | разложение на круговые многочлены |
| difference additive factorization | разностная аддитивная факторизация |
| difference factorization method | метод разностной факторизации |
| dominant factorization | доминирующая факторизация |
| double factorization | двойная факторизация |
| factorial factorization | факторизация факториала (разложение факториала на простейшие множители с степенями abakbot. ru) |
| factorization | фа́кторинг |
| factorization | представление в виде произведения |
| factorization | разложение на дроби |
| factorization | разделение на элементарные операции (сложного вычисления) |
| factorization | разложение на множители (Процесс разложения на множители состоит в представлении числа в виде произведения простых множителей.) |
| factorization | разложение (на множители) |
| factorization | факторизация (декомпозиция объекта (напр., числа, полинома или матрицы) в произведение других объектов или факторов, которые, будучи перемноженными, дают исходный объект wikipedia.org) |
| factorization criterion | факторизационный критерий |
| factorization criterion | критерий факторизации |
| factorization domain | область разложения (на множители) |
| factorization method | метод выделения множителей |
| factorization of a the polynomial | разложение многочлена |
| factorization of function | факторизация функции |
| factorization of graph | факторизация графа |
| factorization of group | факторизация группы |
| factorization of matrix | факторизация матрицы |
| factorization of transformation | разложение преобразования в композицию (преобразований) |
| factorization sequence | последовательность факторизации |
| factorization | факторизационная теорема |
| formal factorization | формальное разложение |
| incomplete LU-factorization | неполное LU-разложение (abab) |
| integer factorization | факторизация целых (MichaelBurov) |
| integer factorization | факторизация целых чисел (MichaelBurov) |
| integer factorization | факторизация больших чисел (MichaelBurov) |
| local factorization | локальная факторизация |
| LU-factorization | разложение LU матрицы |
| Neyman’s factorization theorem | теорема факторизации Неймана |
| no-fill factorization | без заполнения факторизация |
| no-fill factorization | факторизация без заполнения |
| non-negative matrix factorization | неотрицательное матричное разложение (klabukov) |
| partial factorization | частичная факторизация |
| polar factorization | полярное разложение |
| polynomial factorization | разложение многочлена (на множители) |
| prime factorization | разложение на простые множители |
| QR-factorization | разложение QR матрицы |
| Riesz factorization | факторизация Рисса |
| ring factorization | кольцевая факторизация |
| simple factorization | простая факторизация |
| spectral factorization | спектральное разложение |
| spectral factorization | разложение спектра на множители |
| spectrum factorization | разложение спектра на множители |
| spectrum factorization | спектральное разложение |
| standard factorization | стандартное разложение |
| the factorization A = LU is uniquely defined if | однозначно определён |
| this subroutine computes performs an LU-factorization of a general band matrix, using без артикля partial pivoting with row column interchanges | частичный выбор ведущего элемента |
| two-prime factorization | разложение на два простых множителя |
| unique factorization | однозначное разложение (на множители) |
| unique factorization domain | область с однозначным разложением на множители |
| unique factorization domain | факториальное кольцо (UFD wikipedia. org Andrey Truhachev) |
| unique factorization theorem | теорема о единственности разложения (числа на простые сомножители) |
Get short URL
2+\dotsb$
Тогда $f'(x)=f_1+2f_2x+\dotsb$.
И если расширение сосредоточено вокруг $x=0$, то \begin{align}f'(0)&=0 \\ f»(0)&=2f_2\\ f»'(0)&=3\cdot 2f_3.\\ \end{align}
Поэтому \начать{выравнивать} f_0&=f(0) \\ f_1&=\frac{f'(0)}{1} \\ f_2&=\frac{f»(0)}{2} \end{align}
И так далее. Отсюда и факториал?
Это совершенно ясно для полинома, но как насчет тригонометрической функции, такой как $\sin(x)$, кроме использования формулы Тейлора? 95$
Редактировать это непросто, но, надеюсь, видео поможет.
$\endgroup$
$\begingroup$
Похоже, вы уже согласны с тем, что термины $n!$ имеют смысл, когда вы говорите о многочленах.
2+cx+d$ вокруг точки $x=0$. По крайней мере, вы можете спросить, что их первая, вторая и третья производные совпадают при $x=0$. Итак: 95}{5!}$
$\endgroup$
Страница не найдена — а.и. решения
Страница не найдена
4500 Forbes Boulevard
Suite 300
Lanham, MD 20706
(301) 306-1756
Финансовый директор
Дебора Хикокс имеет более чем 35-летний профессиональный опыт в области финансов и бухгалтерского учета. Она обладает глубокими знаниями в области стратегического планирования, бухгалтерского учета и слияний и поглощений.
В 2010 году Дебора присоединилась к И.И. руководящая группа решений для обеспечения стратегического финансового и договорного руководства в поддержку искусственного интеллекта. цели роста решений. В партнерстве с высшим руководством Дебора разработала финансовое руководство, которое способствовало росту более чем на 300%.
Дебора является акционером a.i. решения.
До прихода в А.И. решений, Дебора возглавляла финансовый отдел в Analex Corporation, публичной компании. За время работы в Analex она поддержала получение венчурных инвестиций с Уолл-стрит для финансирования стратегии роста компании. Дебора была неотъемлемой частью завершения нескольких приобретений, приведших к продаже Analex компании Qinetiq, Северная Каролина.
Дебора получила степень магистра делового администрирования в Университете Джорджа Вашингтона. До этого она получила степень бакалавра наук в области бухгалтерского учета в Университете Мэриленда и впоследствии получила статус дипломированного бухгалтера.
Дебора руководила командами численностью до 50 человек и с энтузиазмом занимается наставничеством членов команд, продвигая образование и предоставляя возможности для профессионального развития. Несколько из ее бывших членов команды заняли руководящие финансовые должности в различных компаниях столичного округа Колумбия.
Жительница Чаттануги, штат Теннесси, Дебора любит проводить время на свежем воздухе со своим мужем и их тремя спасенными щенками.
Вице-президент по развитию бизнеса
Мариса Аче имеет более чем 33-летний профессиональный опыт в области проектирования и разработки ракет-носителей для космических аппаратов наблюдения Земли. Она обладает образцовым опытом и опытом в области развития бизнеса, операционных услуг и управления проектами.
В 2018 году Мариса была назначена вице-президентом по развитию бизнеса в компании a.i. решения. В этой роли Мариса возглавляет команду специалистов по стратегии, захвату, предложению и маркетингу в нескольких местах, чтобы поддерживать возможности операционных подразделений. Она отвечает за развитие деловых отношений, взаимодействие с директорами операционных подразделений компании для поддержки их деятельности по развитию бизнеса, поддержание потока возможностей и обеспечение соблюдения процесса развития бизнеса компании.
В 2016 году Мариса возглавила группу захвата, которая представила победившее предложение по крупнейшему на сегодняшний день контракту компании — интегрированной поддержке ракет-носителей одноразового использования 3 (ELVIS 3). Совсем недавно Мариса направила усилия на получение контракта Prototype Operations-I (POPS-I).
Мариса присоединилась к а.и. решения в 2002 году в качестве директора пусковых услуг в региональном офисе компании на мысе Канаверал, Флорида. Она руководила штатом из более чем 40 системных инженеров и ИТ-специалистов, ответственных за поддержку одноразовых ракет-носителей, обеспечение миссии и критически важные ИТ-услуги по нескольким крупным контрактам для клиентов. За время своего пребывания на посту директора Мариса увеличила подразделение пусковых услуг с девяти человек, поддерживающих один контракт в 2002 году, до 86 человек, поддерживающих пять контрактов в 2011 году. Мариса является акционером компании и входит в совет директоров в течение 9 лет.
0140 д.в. решения .
До прихода в a.i. решения , Мариса занимала несколько руководящих должностей в таких компаниях, как Science Application International Corporation (SAIC) и Boeing.
Мариса получила степень магистра наук в области маркетинга в Университете Джона Хопкинса и степень бакалавра наук в области аэрокосмической техники в Университете Южной Калифорнии. Она имеет ряд профессиональных сертификатов, от управления программами и бизнесом до оценки эффективности. Она является лауреатом нескольких наград за профессиональное мастерство, в том числе награды NASA Recognition Award и награды Office of Space Systems Development 9.0140 . Мариса является активным членом организации Women in Aerospace. Кроме того, Мариса является исполнительным вице-президентом Круглого стола космического бизнеса штата Мэриленд (MSBR) и членом Ассоциации подрядчиков Годдарда (GCA).
Мариса живет в Какао-Бич, Флорида, со своим мужем. Она любит проводить время со своими внуками и активна в своей церкви.
Директор по персоналу
Кристи Феннер имеет более чем 25-летний профессиональный опыт работы в качестве делового партнера отдела кадров, разрабатывая и реализуя стратегию в поддержку общего бизнес-планирования и стратегического управления организациями. Она разработала всестороннюю общую компенсацию, привлечение талантов и инновационные планы льгот, одновременно отстаивая широкомасштабное лидерство и инициативы по развитию карьеры.
В 2005 году Кристи присоединилась к ИИ. решения для критического согласования общего вознаграждения и эффективности талантов с бизнес-целями в AI. решения. Будучи одним из первых, кто внедрил связь между затратами на велнес и здравоохранение, она получила признание во всей отрасли. Она была отмечена в Wall Street Journal за создание рынка льгот, на котором сотрудники делают покупки для покрытия, известного сегодня как частная рыночная биржа. Бесстрашный разрушитель и сторонник разнообразия, справедливости и инклюзивности, Кристи служит ответственным за позитивные действия в И.
И. решения. В этой роли она защищает и контролирует усилия по вовлечению, внешнее партнерство и общую стратегию взаимодействия, чтобы обеспечить ИИ. Решения отражают постоянно растущее население STEM во всем мире. Кристи является акционером
д.в. решения
До прихода в a.i. решениях, Кристи был операционным директором-основателем компании Adams Communication Engineering Technology (ACET). Она успешно увеличила компанию с четырьмя сотрудниками, принадлежащую ветерану, до 100+ выпускников 8(a). После более чем двадцати лет работы ACET является многомиллионным поставщиком услуг в области разведки, обороны и федерального рынка ИТ.
Кристи имеет несколько профессиональных сертификатов и членство, включая активную роль в Исполнительной сети Общества менеджеров по персоналу и Национальной ассоциации афроамериканцев в области управления персоналом. Она выступает в различных качествах в качестве участника дискуссии, приглашенного докладчика и исполнительного участника круглого стола за свой опыт в качестве одного из первых, кто внедрил стратегии человеческого капитала и агента изменений в модернизации функций управления персоналом.
Кристи — выпускница Государственного университета Боуи, соучредитель и главный исполнительный директор everfourward, LLC — партнерства со своим мужем Дерриком Феннером, стремящегося поднять настроение малообеспеченным и недостаточно представленным в своем сообществе. Жительница Верхнего Мальборо, штат Мэриленд, она жена, мать четверых взрослых детей, сертифицированный инструктор по йоге и спортсменка на выносливость.
Гвендолин Э. Бойд присоединилась к AGB Search в 2017 году в качестве консультанта по поиску руководителей. Д-р Бойд – инженер и видный сторонник образования STEM (наука, технология, инженерия и математика). Ее описывают как динамичного и актуального лидера, плодовитого мотивационного оратора и мощного проповедника. С момента прихода в фирму она помогала в поиске высшего руководства:
- Университет Эдварда Уотерса (Флорида) – Президент
- Чикагский государственный университет – Президент
- Колледж Тугалу (MS) – Президент
Профессиональная карьера доктора Бойда, насчитывающая более трех десятилетий в лаборатории прикладной физики Университета Джона Хопкинса, была отмечена образцовым руководством и самоотверженными услугами в составе инженерных групп.
Бойд был прямым подчиненным президента Университета Джона Хопкинса и занимал пост председателя Совета руководителей разнообразия Джона Хопкинса с 2001 по 2014 год.
Доктор Бойд вернулась в свою альма-матер, Университет штата Алабама, в 2014 году, чтобы в течение трех лет проработать в качестве 14-й и первой женщины-президента ASU. Основные моменты ее президентства включали создание первой университетской программы получения степени инженера с одобрением степени бакалавра в области биомедицинской инженерии. Она и ее команда удалили университет из статуса предупреждения SACSCOC из-за предыдущей финансовой нестабильности. Самый большой класс первокурсников был задокументирован во время ее пребывания в должности.
Доктор Бойд является общепризнанным чемпионом в области образования, особенно в дисциплинах STEM. Она была назначена президентом Бараком Обамой и утверждена Сенатом в качестве попечителя Фонда стипендий Барри М. Голдуотера и передового опыта в области образования в 2009 году.
Позже она работала в Консультативной комиссии президента по передовому образованию для афроамериканцев в 2014 году.
Преподобный доктор Бойд — рукоположенный странствующий старейшина Афроамериканской методистской епископальной церкви. Она служит в составе служителей церкви Ebenezer AME в Форт-Вашингтоне, штат Мэриленд.
Доктор Бойд был избран с 2000 по 2004 год 22-м Национальным президентом Delta Sigma Theta Sorority Inc. Известный как «Президент по технологиям», Бойд помог внедрить технологии во все аспекты деятельности и управления женского общества. Ее четырехлетнее пребывание в должности включало преобразующие достижения, такие как запуск проекта SEE (Наука в каждом опыте), инициативы, финансируемой за счет гранта Национального научного фонда в размере 1,6 миллиона долларов, с целью продвижения математики и естественных наук для афроамериканских девочек средней школы. Она руководила деятельностью женского общества по защите гуманитарных и образовательных интересов в различных африканских странах.
В 2013 году Бойд был председателем празднования столетия женского общества, кульминацией которого стал съезд в Вашингтоне, округ Колумбия, который собрал более 40 000 участников со всего мира.
Доктор Бойд был удостоен четырех почетных докторских степеней; признание Конгресса; 32 «Ключи от города»; ключ от «штата Флорида»; объявление Дня Гвендолин Э. Бойд в восьми городах; награды за лидерство, и профессиональные награды, и профессиональные награды за ее достижения в области инженерии и высшего образования. Она является членом Столичного отделения Links, Inc., Вашингтонского отделения выпускников Delta Sigma Theta Sorority, Inc. и Leadership Greater Washington.
Доктор Бойд получила степень бакалавра наук. из Алабамского государственного университета по специальности математика и двойное дополнительное образование по физике и музыке. Она получила стипендию и стала первой афроамериканкой, получившей степень магистра наук. степень в области машиностроения Йельского университета.
Она заработала как M. Div. и Д. Мин. Дипломы Говардского университета.
Джеки Шмолл — вице-президент по требованиям и возможностям стратегического бизнес-подразделения Raytheon Space Systems компании Raytheon Intelligence & Space. В качестве руководителя по требованиям и возможностям Raytheon Space Systems Джеки отвечает за разработку и реализацию стратегий роста для Министерства обороны США и разведывательных сообществ, международной и гражданской космонавтики, а также рынков управления и контроля. Она обеспечивает критическое мышление для формирования и управления рыночными тенденциями, сохраняя при этом глубокое понимание клиентской среды.
До прихода в Raytheon Technologies Шмолл был генеральным директором и управляющим по прибылям и убыткам в космическом подразделении ISR в секторе космических систем в L3Harris Technologies в их сегменте космических и бортовых систем. Она отвечала за годовой объем продаж на сумму более 300 миллионов долларов США по нескольким сквозным контрактам на космические миссии для клиентов Министерства обороны США и разведки, что привело к росту на 50% в годовом исчислении в течение предыдущих двух лет.
Шмолл занял эту должность в 2020 году, подчиняясь президенту Space Systems. Подразделение ISR предоставляет высокопроизводительные комплексные космические решения для критически важных миссий в сокращенные сроки для клиентов National Security Space. Реконфигурируемые многоцелевые полезные нагрузки в рамках бизнеса обеспечивают гибкие решения для миссий на орбите для реагирующих спутников и размещенных полезных нагрузок.
Schmoll является членом Американского института аэронавтики и астронавтики и поддерживает Технический комитет по моделированию и симуляции. Она получила степень магистра делового администрирования и степень бакалавра аэрокосмической техники в Университете Мэриленда. В 2018 году она успешно завершила программу развития лидерских качеств L3Harris в Уортонской школе Университета Пенсильвании и была отмечена премией Space Coast Business 40 Under 40 Award в 2019 году.
Лиза — советник, консультант и спикер, работающая с руководителями высшего звена и отделами продаж по всему миру.
Она является автором пяти бестселлеров и популярным докладчиком. Известная своей искренностью и чувством юмора, Лиза была гуру продаж №4 в мире по версии Global Gurus.
Лиза вдохновила миллионы учащихся LinkedIn Learning курсами по продажам, лидерству и целеустремленности в работе. Ее работы также были представлены в Forbes, Fortune и The New York Times.
Полковник Спенсер является старшим советником ВВС в Управлении местного оборонного сообщества (OLDCC), полевой деятельности при Канцелярии министра обороны (OSD), отвечающей за оказание помощи правительствам штатов и местным органам власти в реагировании на последствия деятельности обороны. . До прихода в OEA полковник Спенсер был командиром 6-го отряда Центра развертывания и поддержки миссий ВВС, который служит единым штабом среднего уровня, поддерживающим комплексные объекты ВВС и экспедиционную поддержку на 177 базах. В этой должности она руководила 43 сотрудниками, обеспечивающими безопасность, аварийно-спасательные службы, связь, инженерные, логистические и финансовые услуги для восьми баз по всей стране с инфраструктурой стоимостью 55 миллиардов долларов, поддерживающей
гражданских и военных членов.
