«Деление с остатком » (5-й класс)
Класс: 5, математика
Тема: Деление с остатком.
Тип урока: Урок изучения нового материала.
Цели
Предметные: сформировать навыки выполнения деления с остатком, разъяснить связь между компонентами действия деления с остатком.
Личностные: развивать интерес к изучению темы и желание применить приобретённые знания и умения.
Метапредметные: формировать умение видеть математическую задачу в контексте проблемной ситуации, в окружающей жизни.
Планируемые результаты: Учащийся получит навык выполнения деления с остатком, получит представление о связи между компонентами действия деления с остатком.
Основные понятия: Остаток, неполное частное, делитель, делимое, правило нахождения делимого, деление нацело.
Ход урока
I. Организационный момент
II. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
— Решив примеры и заполнив таблицу, вы сумеете узнать тему урока.
На доске:
| |||||||||||||||||||||||||||||||||
|
— Прочитайте тему урока.
— Открыли тетради, записали число, тему урока.
III. Работа по теме урока
Решим устно.
1. Прочитайте выражения:
30 : 5
103 : 10
34 : 5
60 : 7
47 : 6
131 : 11
42 : 6
— На какие две группы их можно разделить? Выпишите и решите те, в которых деление с остатком.
2. Проверим.
Без остатка: | С остатком: | |
30 : 5 |
| 103 : 10 = 10 (ост 3) |
— Расскажите, как выполняли деление с остатком?
— Не всегда одно натуральное число делится на другое число. Но всегда можно выполнить деление с остатком.
— Что, значит, разделить с остатком? Чтобы ответить на этот вопрос, решим задачу.
В гости к бабушке пришли 4 внука. Бабушка решила угостить внуков конфетами. В вазочке было 23 конфеты. Сколько конфет достанется каждому внуку, если бабушка предложит поделить конфеты поровну?
— Давайте рассуждать.
— Сколько конфет у бабушки? (23)
— Сколько внуков пришло в гости к бабушке? (4)
— Что необходимо сделать по условию задачи? (Конфеты нужно разделить поровну, надо разделить 23 на 4; 23 делится на 4 с остатком; в частном получится 5, а в остатке 3.)
— Сколько же конфет достанется каждому внуку? (Каждому внуку достанется по 5 конфет, и в вазочке останется 3 конфеты.)
— Запишем решение.
Решение:
23 : 4=5 (ост 3)
— Как называется число, которое делят? (Делимым.)
— Что такое делитель? (Число, на которое делят.)
— Как называют результат деления с остатком? (Неполное частное.)
— Назовите делимое, делитель, неполное частное и остаток в нашем решении (23 — делимое, 4 — делитель, 5 — неполное частное, 3 – остаток. )
)
— Ребята, подумайте и запишите, как найти делимое 23, зная делитель, неполное частное и остаток?
— Проверим.
— Ребята, давайте сформулируем правило, как найти делимое, если известны делитель, неполное частное и остаток.
— Правило.
Делимое равно произведению делителя и неполного частного, сложенному с остатком.
а = вс + d, а — делимое, в — делитель, с — неполное частное, d — остаток.
— Когда выполняется деление с остатком, что мы должны помнить?
— Правильно, остаток всегда меньше делителя.
— А если остаток равен нулю, делимое делится на делитель без остатка, нацело.
IV. Закрепление изученного материала
— Найдите делимое, если:
А) неполное частное равно 7, остаток равен 3, а делитель 6.
Б) неполное частное равно 11, остаток равен 1, а делитель 9.
В) неполное частное равно 20, остаток равен 13, а делитель 15.
V. Работа с учебником
1. Работа над задачей.
2. Оформление решения задачи.
№ 516 (Задачу решает у доски ученик.)
20 х 10 : 18 = 11 (ост 2)
Ответ: 11 деталей по 18 кг можно отлить из 10 болванок, 2 кг чугуна останется.
№ 519 (Рабочая тетрадь, с. 52 №1.)
Первое задание выполняет ученик у доски. Второе и третье — ученики выполняют самостоятельно с самопроверкой.
Устно решаем задачи.
VI. Итог урока
— В вашем классе 17 учеников. Вас построили в шеренги. Получилось несколько шеренг из 5 учеников и одна неполная шеренга. Сколько получилось полных шеренг и сколько человек в неполной шеренге?
— Ваш класс на уроке физкультуры снова построили в шеренги. На этот раз получилось 4 одинаковых полных шеренг и одна неполная? Сколько человек в каждой шеренге? А в неполной?
Отвечаем на вопросы:
— Может ли остаток быть больше делителя? Может ли остаток быть равен делителю?
— Как найти делимое по неполному частному, делителю и остатку?
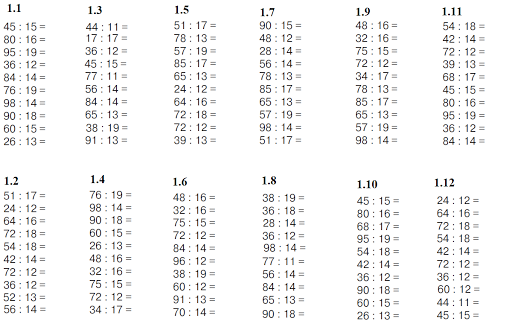
— Какие могут быть остатки при делении на 5? Приведите примеры.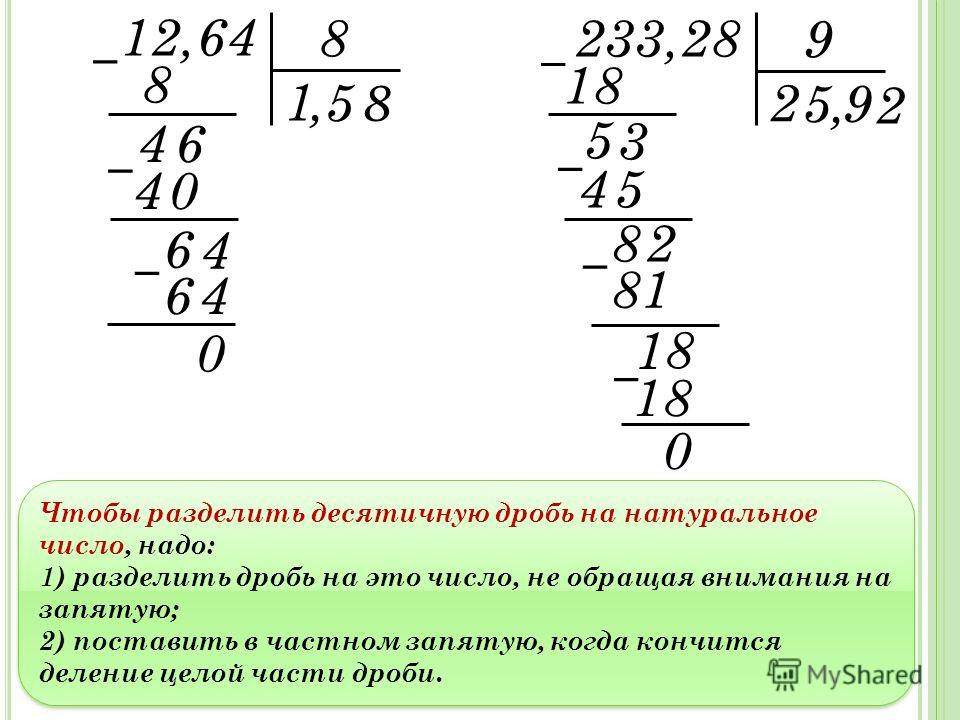
— Как проверить, верно ли выполнено деление с остатком?
— Оксана задумала число. Если это число увеличить в 7 раз и к произведению прибавить 17, то получится 108. Какое число задумала Оксана?
VII. Домашнее задание
Пункт 13, № 537, 538, рабочая тетрадь, с. 42, №4.
Список литературы
1. Математика : Учеб. для 5 кл. общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 9-е изд., стереотип. – М. : Мнемозина, 2017. – 384 с.: ил.
2. Математика. 5 класс. Рабочая тетрадь №1. натуральные числа / В.Н. Рудницкая. – 7-е изд. – М. : Мнемозина, 2017. – 87 с.: ил.
3. Чесноков А.С., Нешков К.И. Дидактические материалы по математике для 5 класса. – М. : Классикс Стиль, 2017. – 144 с.: ил.
Урок математики 5 класс по теме «Деление» / Открытый урок
Технологии: здоровьесбережение, развивающего обучения, самодиагностики и самокоррекции результатов.
Решаемые проблемы: при выполнении, каких заданий применяется деление?
Виды деятельности: работа у доски и в тетрадях, фронтальная работа с классом, самостоятельная работа с взаимопроверкой, контролирующая разноуровневая самостоятельная работа.
Планируемее результаты:
Предметные: систематизировать умения и навыки учащихся по теме «Деление натуральных чисел»
Метапредметные УУД:
Коммуникативные: формировать коммуникативные действия, направленные на структурирование информации по данной теме.
Регулятивные: определять новый уровень к самому себе как субъекту деятельности.
Ход урока
Сегодня у нас последний из 6-ти отведенных уроков по теме «Деление. —)
—)
Обменялись тетрадями с соседом по парте. Проверяем и ставим оценку.
III. Исправили ошибки. Отправляемся на поляну «Зеленой математики».
(Решаем устно задачи )
1.Из одного килограмма льна можно получить 40 километров нитей. Сколько килограммов льна потребуется для получения 28 000 километров нитей?
2. В Россию картофель завез Петр I в 1700 году. Сколько лет россияне знакомы с этим овощем?
3. В Таиланде и Малайзии существуют «обезьяньи школы», в которых учат обезьян собирать для людей кокосовые орехи. Обычный «выпускник» такой «школы» собирает 500 орехов в день, «отличник» — 800, а особо «одаренные» — 1400 орехов в день. Со скольких пальм соберет урожай каждый из «выпускников», если с одной пальмы можно снять 50 орехов? (10; 16; 28).
(Задания записаны на доске. Вычисления выполняется «змейкой», каждый учащийся выполняет одно действие)
12∙6 15∙5 14∙6
:8 :25 :21
+29 +28 +28
∙3 ∙3 ∙3
-58 -42 -43
+43 +44 +33
:4 :5 :6
+57 +52 +52
∙0 ∙0 ∙0
Заняли места в ракете.
 Определим параметры полета – скорость, время, расстояние. Решим задачу.
Определим параметры полета – скорость, время, расстояние. Решим задачу.Расстояние от Земли до планеты куда мы летим равно 90 млн. километров. Мы, посылаем световой сигнал, со скоростью 300 000 км/сек. Через сколько времени на планете узнают, что к ним прибудут гости? Сколько времени мы будем в пути, если скорость нашей ракеты 45 км/сек ?
V. «Волшебный сад». Цветок ромашка (на каждом лепестке вопрос о нахождении неизвестного компонента).
1. Как найти неизвестный множитель?
2. Как найти неизвестное делимое?
3. Как найти неизвестный делитель?
4. Как найти неизвестное слагаемое?
5. Как найти неизвестное уменьшаемое?
6. Как найти неизвестное вычитаемое?
(учащиеся выходят к доске по желанию, берут любой лепесток и отвечают на вопрос)
VI. Озеро Неизвестности.
Решить уравнения (у доски и в тетрадях)
1. 35х = 175
2. у : 35 = 18
3. (х – 12) ∙ 8 = 56.
VII. Дом невыученных уроков.
Разноуровневая самостоятельная работа.

1 уровень
1. Найдите значение выражения: 3 360 : 7 : 32.
2. Решите уравнения: а) 48х = 672,
в) 1 344 : у = 56.
2 уровень
1. Найдите значение выражения: 2 112 : 24 : 8.
2. Решите уравнения: а) х∙ 49 = 927 +935,
в) (148 – m ) ∙ 31 = 1 581.
3 уровень
1. Решите уравнения: а) 1 344 : z = 543 – 487,
в)992 : (130 — k) = 8.
2. Решите задачу. За 25 рабочих дней цех должен был выпустить 800 приборов. Однако каждый день цех выпускал на 8 приборов больше, чем планировалось. За сколько дней изготовили 800 приборов?
VIII. Возвращаемся домой. Путешествие завершено.
Подведение итогов.
Поднимите цветные карточки (зеленая – было интересно и все понятно; желтая – интересно, но не все понятно; красная – не интересно и непонятно).
Домашнее задание. Найти интересные примеры и задачи на деление.
Скачать публикацию
Фамилия | |||
71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 | 71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 |
Фамилия | Фамилия | ||
71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 | 71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 |
Фамилия | Фамилия | ||
71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 | 71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 |
Фамилия | Фамилия | ||
71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 | 71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 |
Фамилия | Фамилия | ||
71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 | 71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 |
Фамилия | Фамилия | ||
71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 | 71*11= 10 *311= 11*42 = 89*100= 451*0= 620*10= 1*413 = 659*1= 51*11= 66*3= | 29*9 74*99 65*999 72*9 84*99 62*999 |
Деление на 5 — Математика 3 класса
Деление означает разбиение числа на более мелкие равные группы.
На прошлом уроке вы научились делить числа на 4.
Теперь давайте научимся делить числа на 5. на 5:
1. Деление на группировка .
2. Деление на с повторным вычитанием .
3. Деление на умножение. (самый быстрый способ)
Вы можете использовать любой из этих способов! 🤗
👉 Разберем на примере.
15 ÷ 5 = ?
Метод 1: Группировка
Чтобы разделить число на 5 с помощью группировки, просто разделите его на 5 равных групп. Число в каждой группе является ответом.
Число в каждой группе является ответом.
Давайте попробуем!
Мы сделали 5 групп по 3 человека.
15 ÷ 5 = 3 ✅
Метод 2: Повторное вычитание
Чтобы разделить число на 5 с помощью многократного вычитания, вычтите из него 5 снова и снова, пока не получите 0. Число из
4
4 вычитания это ответ на задачу деления. Попробуем и этот метод! 😃
15 ÷ 5 = ?
Начните с 15 и вычтите 5 снова и снова.
Мы вычли 3 раза.
Итак,
15 ÷ 5 = 3
Отличная работа! 👏
Метод 3: Использование умножения
Быстро превратите любую задачу на деление в задачу на умножение , связанную с !
Если вы видите 15 ÷ 5 = ? , подумайте о диаграмме целой части:
Можете ли вы написать уравнение умножения для этой же диаграммы?
Да!
5 х ? = 15
Знаете ли вы, какое число, умноженное на 5, равно 15?
Отличная работа! Это 3.
Итак, вы узнали, что 15 ÷ 5 = 3.
Умножение и деление являются противоположностями друг друга. Как только вы знаете умножение, вы также знаете свое деление!
Другой пример
45 ÷ 5 = ?
Метод 1: Группировка
45 разделена на 5 групп по 9 элементов в каждой.
45 ÷ 5 = 9
Метод 2: Повторное вычитание
Мы можем вычесть 5 из 45 девять раз.
45 ÷ 5 = 9
Потрясающе!
Метод 3: Использование умножения
Чтобы вычислить 45 ÷ 5 = ? , подумайте о связанном с ним уравнении умножения:
5 x ? = 45
Ответ на оба уравнения один и тот же, потому что умножение и деление противоположны! 😺
Знаете ли вы, какое число умножить на 5 будет 45? Правильно, 9!
Итак, вы знаете, что 45 ÷ 5 = 9!
Обзор
Ниже приведен список фактов деления с делителем 5.
Запомните их!
5 ÷ 5 = 1
10 ÷ 5 = 2
15 ÷ 5 = 3
20 ÷ 4
25 ÷ 5 9004 9004
25 ÷ 5 9004 9004
25. 5 = 6
35 ÷ 5 = 7
40 ÷ 5 = 8
45 ÷ 5 = 9
50 ÷ 5 = 10
Отличная работа! Теперь вы знаете основные факты деления с делителем на 5!
Завершите практику, чтобы помочь вам запомнить.
Объяснение краткого деления и длинного деления
Мы работали с экспертами по начальной математике, чтобы создать руководство для родителей и новых учителей по короткому делению (включая метод автобусной остановки) и страшному длинному делению.
В этой статье мы объяснили все, что вам нужно знать, чтобы помочь вашему ребенку разобраться с этими сложными темами!
Неважно, короткое это деление или длинное, для многих детей и их родителей простое упоминание слова «Д» может вызвать мурашки по спине у многих юных математиков, но это не так. должно быть дело!
Здесь, в Third Space Learning, мы стремимся сделать математику доступной для всех, включая краткое и длинное деление…
В прошлом делению обучали без особого моделирования (с использованием физических предметов для облегчения представления математической задачи), поэтому неудивительно, что многим из нас это трудно и по сей день.
В настоящее время, когда дети проводят много времени в школе, понимая , как работает деление , а не просто запоминая метод, страх перед делением KS2 тает, но подведение итогов и поиск будут иметь большое значение, особенно если родители могут поддержка из дома.
Но прежде чем вы узнаете все, что вам нужно знать о дивизионах для детей, мы подготовили для вас краткий обзор дивизионов!
Этот блог является частью нашей серии блогов, предназначенных для учителей, школ и родителей, поддерживающих домашнее обучение.
Рабочие листы на деление в длинное число для 3-6 классов
Этот БЕСПЛАТНЫЙ ресурс содержит 3 готовых к использованию рабочих листа для вашего класса, которые помогут им со всеми аспектами деления в длинное число, от однозначных чисел до вычисления кратных!
Как учить делению:
Кратко о методах деления Мы знаем, насколько чертовски сложным может быть деление, поэтому давайте начнем с некоторых определений и повторим то, что вы, возможно, забыли со школы.
Что такое деление в математике? Деление — это операция, обратная умножению и заключающаяся в разделении на равные части или группы.
В начальной школе преподаются 3 метода деления, каждый из которых различается по сложности. Их:
Их:
- Разбиение на части
- Короткое деление (также известное как метод автобусной остановки)
- Длинное деление
Подробнее: Что такое деление?
Что такое фрагментация? Разбиение на части — это метод, используемый для деления больших чисел, которые нельзя разделить в уме.
При использовании метода фрагментации дети будут многократно вычитать делитель из делимого, пока не будет получен ответ. Например, 12 ÷ 3 можно решить, выполнив 12 – 3, чтобы получить 9., 9 – 3, чтобы получить 6, 6 – 3, чтобы получить 3, а затем 3 – 3, чтобы получить 0.
Когда все 3 вычитаются из 12, подсчитываются (4), становится ясно, что ответ 4.
Что такое короткое деление? Короткое деление — это быстрый и эффективный метод деления больших чисел.
После того, как ваш ребенок освоится с делением на фрагменты, он перейдет к короткому делению, так как его можно использовать для решения задачи на деление с очень большим делимым, выполнив ряд простых шагов.
Например:
В этом примере четыре дважды превращается в девять, а в остатке остается единица.
Этот остаток затем передается следующему числу (шесть), чтобы получилось 16. Четыре входит в число 16 четыре раза, так что при суммировании получается 24.
Что такое метод автобусной остановки?
Метод деления на автобусной остановке — это еще одно название для краткого деления. Он получил свое название от идеи, что делимое (число, которое вы хотите разделить) находится внутри автобусной остановки, а делитель ждет снаружи.
Учителя расходятся во мнениях относительно того, действительно ли это изображение полезно при изучении деления, поэтому в большинстве случаев мы просто будем называть его коротким делением.
Что такое длинное деление? Длинное деление — это метод, который используется при делении большого числа (обычно трех или более цифр) на двузначное (или большее) число. Он изложен аналогично методу автобусной остановки, который используется для короткого деления.
Взгляните на наш пример ниже, чтобы увидеть, как деление в длину объясняется наглядным примером.
Лучше всего это объяснить на примере – см. ниже.
У нас есть очень подробная статья, написанная для учителей на эту тему, которая может вам понравиться, если вы хотите более подробно изучить метод деления в KS2.
Терминология, которую необходимо знать при обучении делению
В наших блогах мы стараемся избегать слишком большого количества профессионального жаргона, но следующие три термина действительно важны для всех, кто занимается изучением деления.
- Дивиденд — это число, которое вы делите (число внутри «автобусной остановки»).
- Делитель — это число, на которое вы делите.
- Частное — это сумма, которую получает каждый делитель, т.е. ответ в большинстве случаев.
Хороший способ запомнить это делимое ÷ делитель = частное .
Части задачи на деление, помеченные для детей и родителей Изучив правильный словарный запас всех частей задачи на деление, ваш ребенок найдет многие элементы задачи на деление намного проще.
Что нужно знать моему ребенку о коротком и длинном делении в KS1 и KS2?
В связи с тем, что дети меняются из года в год на протяжении всей начальной школы, в кратком и длинном делении в блоге есть что рассказать, но чтобы помочь вам, мы разбили его по годам.
Как преподавать раздел
1-й год В 1-м классе раздел обычно называется , разделяя , и это делается с использованием конкретных предметов, таких как прилавки, кубики или даже продукты питания, такие как макароны.
Это помогает детям понять разделение как разделение между группами.
Ниже приведен простой пример.
Несколько простых задачек на деление для 1-го класса Возьмите математические манипуляторы или кубики, чтобы помочь юным ученикам решить эти задачки на деление.
Убедитесь, что вы не забыли использовать такие слова, как разделить и разделить повсюду, чтобы ваш ребенок познакомился с понятиями, где делитель — это количество групп, между которыми делится дивиденд.
Начните с 4 блоков. Разделите их на 2 равные группы.
Начните с 10 блоков. Разделите их на 2 равные группы.
Начните с 6 блоков. Разделите их на 3 равные группы.
Как преподавать деление Год 2 Во втором классе дети начинают более глубоко изучать принцип деления, а это означает, что вашему ребенку предстоит научиться еще кое-чему.
Ключевой концепцией, которую нужно понять и действительно освоить в этом возрасте, является 9 лет.0247 коммутативность .
Если вы изо всех сил пытаетесь вспомнить, что именно означает коммутативность, определение простое.
В математике свойство коммутативности утверждает, что порядок не имеет значения.
Умножение коммутативное ; вы можете поменять местами числа, и это не имеет значения.
2 x 3 = 6
3 x 2 = 6
Деление не является коммутативным . Если вы поменяете порядок чисел, это изменит ответ.
4 ÷ 2 = 2
2 ÷ 4 = 0,5
Деление и коммутативность во 2-м классе
В этом возрасте хорошо практиковаться в изучении таблиц умножения на 2, 5 и 10 с соответствующими фактами деления. Например:
Факт умножения:
2 x 5 = 10
Соответствующие факты деления:
10 ÷ 5 = 2
10 ÷ 2 = 5
обратное умножению, и они являются отличным примером того, почему коммутативность важна.
Если вашего ребенка устраивает разница между 10 ÷ 5 и 10 ÷ 2, даже после того, как он увидит, что 5 x 2 равно 2 x 5, он будет лучше подготовлен для комфортного перехода к короткому дивизиону KS2 и длинному KS2. разделение.
Как научить делению Год 3 В 3-м классе ваш ребенок сосредоточится на записи вычислений деления и решении основных задач на деление, связанных с пропущенными числами.
Здесь очень пригодится знание фактов умножения и деления, поэтому, как и в случае со 2-м классом, очень важно практиковать их со своим ребенком.
Эта проблема с пропущенными числами поможет вам понять, почему знание таблицы умножения значительно упрощает деление:
5 x 4 = 20
__ ÷ 5 = 4
20 ÷ __ = 5
Есть также два письменных метода деления, которые вводятся в этом возрасте, и они разбиты ниже.
Письменные методы деления для детей
Объяснение метода деления на фрагменты
Хотя этот метод немного медленнее, чем деление на автобусной остановке, он отлично подходит для развития умственных навыков, необходимых детям для более сложного деления в дальнейшем.
Как сделать разбиение на части метод деления Разбиение на части — это когда вы определяете, сколько раз одно число входит в другое число.
Вы вычисляете это путем многократного вычитания делителя (или кратных делителю) до тех пор, пока не получите ноль, чтобы увидеть, сколько раз делитель может войти в число, которое вы делите (делимое).
Разделение на фрагменты — это хороший способ познакомить вашего ребенка с некоторыми из основных понятий деления, и как только они с этим смирятся, они смогут перейти к методу деления на короткие фрагменты.
Объяснение метода короткого деления или метода деления на автобусной остановке Часто называется методом автобусной остановки из-за того, что при выводе на лист бумаги расчет имеет некоторое визуальное сходство с автобусной остановкой, этот метод короткого деления KS2 является одним из самых популярных методов, которым обучают в школах.
Этот метод быстрее, чем фрагментация, но важно, чтобы дети понимали, что они делают (а не просто следовали методу).
Это значительно облегчит деление на части в будущем, но рекомендуется убедиться, что ваш ребенок усвоил деление на фрагменты, прежде чем переходить к делению на короткие.
Как выполнить краткое деление В этом возрасте краткое деление будет включать однозначные делители и 3- или 4-значные делимые.
Слайд из третьего урока Space Learning 1-to-1, на котором ученики шаг за шагом проходят короткие деления. Сядьте вместе с ребенком и посмотрите на схему ниже, чтобы узнать названия и места для каждой части задачи на деление.
Они могут показаться очень незнакомыми, если вы привыкли выписывать суммы в строку, поэтому поработайте с ребенком, чтобы убедиться, что он знает свой делитель по делимому!
Как помочь ребенку разделить трех- или четырехзначное число на однозначное число Поскольку эти типы вопросов на деление составляют большинство вопросов на деление в 3-м классе, вот рисунок, в котором подробно показано, как разделить трех- или четырехзначное число число однозначным числом.
Как учить деление Год 4 В 4-м классе ваш ребенок будет использовать краткое деление (метод деления на автобусной остановке, описанный выше), чтобы делить числа до четырех цифр на двузначные числа.
Метод точно такой же, как и с однозначными цифрами, за исключением того, что первый шаг всегда включает группировку.
На этом этапе процесс деления становится гораздо более трудным, если ваш ребенок не выучил свою таблицу умножения наизусть, поэтому лучшее, что вы можете сделать для него, — это помочь ему выучить ее.
Им также нужно будет выбрать, какой остаток использовать в зависимости от вопроса, а некоторые распространенные вопросы будут связаны с реальными ситуациями, например, с разделением групп между автомобилями или предметами между ящиками.
Вопросы на деление с остатком Деление с остатком может быть сложной концепцией для понимания, когда дети впервые знакомятся как с коротким, так и с длинным делением, но важно, чтобы дети хорошо их понимали, поскольку они могут радикально измениться в зависимости от вопроса, который спрашивают.
Попрактикуйтесь в использовании пар множителей в 4-м классе, чтобы облегчить письменное деление Пары множителей — это два множителя (числа), которые при умножении вместе дают определенный продукт (результат).
Упражнения с парами факторов могут помочь вашему ребенку ускорить процесс деления, так как знание того, что 4 x 5 = 20, поможет ему, когда дело доходит до вычисления 20 ÷ 4 = _ .
Попросите ребенка найти как можно больше пар множителей для приведенного ниже числа. Почему бы не превратить это в игру?
Сядьте вместе со своим ребенком, возьмите ручку и лист бумаги и посмотрите, кто сможет вычислить наибольшее количество пар множителей для следующих чисел за минуту. Результаты могут быть ближе, чем вы думаете!
- 20
- 68
- 12
- 30
- 100
Read more: What is the highest common factor
How to teach division Year 5 By Year 5, your child должен уметь быстро мысленно уменьшать сумму вдвое или вчетверо.
Если им трудно, внедрение математики в реальный мир может помочь им справиться с половинками и четвертинками. Например, когда вы находитесь вне дома, спросите их, сколько будет стоить предмет, если он будет стоить половину, или сколько граммов будет в половине 1-килограммового мешка сахара.
Умение быстро делить на 2 (деление пополам) и 4 (четвертование) станет важной частью деления по мере того, как ваш ребенок будет учиться в школе, поэтому будет очень полезно, если он сможет научиться этому сейчас.
Сокращенное деление с десятичными знаками Сокращенное деление будет использоваться для чисел, содержащих десятичные дроби, впервые в 5-м классе.
Это означает, что самое время пересмотреть разрядность, чтобы ваш ребенок понял, как работают десятичные дроби.
Десятичные числа являются частями целого (аналогично дробям), но при делении десятичных дробей важно помнить, что столбцы разрядных значений уменьшаются в значении каждый раз, когда вы перемещаетесь вправо.
Пример деления с десятичными дробями Как научить делению Год 6 В 6-м классе ваш ребенок впервые познакомится со страшным делением на две части!
Однако хорошая новость заключается в том, что после того, как вы освоите деление на фрагменты и деление на короткие числа, деление на части будет совсем неплохим!
Когда дело доходит до деления в длинную форму для детей, важно не торопиться и поощрять их к аккуратному представлению своей работы, чтобы они могли легко замечать ошибки и работать над их исправлением.
Даже зная об этом, деление в длинное число все еще может быть пугающей перспективой для детей (и родителей!), поэтому взгляните на наш пример ниже, чтобы понять, как решить задачу деления в длинное число.
Вы учитель, который ищет поддержку в обучении делению в столбик? Ознакомьтесь с нашими идеями и советами по обучению делению в столбик, написанными опытными математиками-практиками.
Объяснение деления в длинное деление для детей В приведенном ниже примере показан самый популярный метод деления в длинное деление для детей, а также тот, с которым вы, возможно, знакомы еще со времен начальной школы.
Все, что вам нужно для выполнения вычисления 528 ÷ 24, это ручка, немного бумаги и ребенок, который хочет освоить этот метод!
После того, как вы попробуете ответить на несколько вопросов на деление на длинное деление (с вашей помощью для начала), ваш ребенок вскоре увидит, что этот метод может помочь ему понять, как решать задачи на деление на длинное деление, независимо от задействованных чисел, и окажется неоценимым. когда дело доходит до SAT.
когда дело доходит до SAT.
Как выполнить деление в длинное число: простой пошаговый метод деления в длинное число для использования в KS2 Не волнуйтесь, если процесс внедрения действительно займет некоторое время. Это длинная цепочка вещей, которые нужно запомнить, поэтому потребуется регулярная практика, чтобы запомнить этот метод. Ознакомьтесь с нашими вопросами о длинном делении и примерами длинного деления для получения дополнительной поддержки.
Просто запомните процесс: делить, умножать, вычитать, сводить; и повторить.
Тяжелая работа окупится в долгосрочной перспективе, поэтому стоит уделить время своему ребенку сейчас, чтобы убедиться, что деление в столбик хорошо объяснено на раннем этапе, чтобы уменьшить количество раз, когда вы услышите неизбежное:
» Мммммм… Как вы делаете деление в большую сторону…?»
Откуда мы знаем, когда делить и какой метод использовать? Различные вопросы на деление требуют разных методов деления для их решения, но вот краткое и простое руководство, которое покажет, какой метод и когда должен использовать ваш ребенок:
- Разбиение лучше всего подходит для небольших чисел и арифметики.

- Сокращенное деление отлично подходит для деления больших чисел на однозначные числа.
- Длинное деление удобно для деления больших чисел на числа, состоящие из 2 и более цифр.
Конечно, могут быть случаи, когда каждый из вышеперечисленных методов можно использовать в немного разных сценариях, но, как правило, этого должно быть достаточно, чтобы помочь вашему ребенку принять правильное решение.
Вопросы по разделу SAT для 6-го класса Когда придет время сдавать экзаменационные работы по математике, более чем вероятно, что вашему ребенку придется отвечать на некоторые вопросы по разделу.
Решение задач и рассуждения (бумаги 2 и 3) в 6-м классе могут быть сложными, когда речь идет о задачах на деление. Часто задачи требуют решения более чем одной операции, что может добавить элемент сложности в и без того напряженную обстановку, поэтому предложите ребенку обратить внимание на такие слова, как поделиться или группа , чтобы помочь ему идентифицировать что нужно сделать для решения проблемы.
Задачи на деление в задании 1 (арифметика) будут представлены в виде числовых предложений, и ваш ребенок должен будет продемонстрировать свое решение, если вопрос оценивается более чем в 1 балл.
Эти вопросы легко определить, потому что они будут использовать символы деления:
÷
или
, или они могут включать дроби.
Как правило, поощряйте ребенка к мысленному разделению там, где это возможно.
Хотя письменные методы отлично подходят для больших чисел, возможность мысленного деления даст им преимущество. Это означает, что когда они выполнят письменный метод, они смогут увидеть, является ли их ответ примерно правильным, путем оценки.
Помимо бесплатных печатных рабочих листов и вопросов на деление, вы также можете загрузить набор бесплатных вопросов SAT по делению и умножению, чтобы расширить свою практику.
Индивидуальные онлайн-уроки по математике, которым доверяют школы и учителя
Каждую неделю репетиторы-специалисты по математике Third Space Learning проводят еженедельные индивидуальные онлайн-уроки и математические вмешательства для тысяч детей начальной школы. С 2013 года мы помогли более 125 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.
С 2013 года мы помогли более 125 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.
Обучение математике для детей в возрасте от 5 до 12 лет, основанное на национальной учебной программе и проводимое в режиме онлайн
Стратегии 5-го класса
Вы боитесь преподавать дивизион каждый год? Я был в этом лагере. Мои ученики с трудом справились с делением, потому что им не хватало чувства числа и концептуального понимания. Однако, к счастью, я понял, что так быть не должно. Я могу использовать стратегии деления, которые не только подходят для развития, но и имеют смысл для моих учеников.
На самом деле, как только я отказался от стандартного алгоритма в качестве стратегии деления, мои ученики начали осваивать деление налево и направо. Кто-то все еще боролся? Да. К сожалению, ни одна из стратегий или советов, которыми я делюсь, не станет волшебной таблеткой, но они сделают деление доступным и концептуальным для ваших учеников.
Частичные частные с Easy Breezy Math
Частичные частные изменили правила игры для моих учеников. Частичные частные — это стратегия деления, в которой используется разбиение на фрагменты для многократного вычитания групп делителя более эффективным способом.
Но мне пришлось добавить леса для моих учеников. Мы называем этот каркас нашей «Легкой математикой». По сути, мы берем известные нам умножения и списываем их в сторону. Мы извлекаем из этих проблем, чтобы помочь нам решить проблему. Мы делаем это, потому что в начале года моим ученикам действительно не хватает понимания числа дивизий. Это также помогает им увидеть связь между умножением и делением.
В течение года они выйдут за рамки простой математики, разовьют чувство числа и начнут видеть закономерности.
Совет: напомните им, чтобы они складывали коэффициенты вертикально в их Easy Breezy Math. Иногда я даю своим ученикам доски специально для них, чтобы сделать их более увлекательными.
Для получения более подробной информации об этом методе деления и получения бесплатной помощи нажмите здесь.
Если эта стратегия для вас новая и вам нужно увидеть ее в действии, то посмотрите это видео.
Коробчатая модель или метод параллелепипеда с частичными частными
Коробчатая модель Разделение 1 было для меня новым год назад и работает лучше всего, когда учащиеся знакомы с использованием этого типа органайзера при умножении с частичными произведениями. Этот тип стратегии деления похож на частичные частные, но организован по-другому.
Если для вас это совершенно новое, посмотрите видео, в котором учитель и ее класс проходят этапы. Этот метод лучше всего «увидеть в действии», а не читать о нем.
Это видео длиннее, но оно отлично подходит для того, чтобы помочь учителям понять стратегию разделения и услышать язык, чтобы помочь ученикам понять его. Примечание. Часть работы What I Know совпадает с тем, что я называю Easy Breezy Math. »
Примечание. Часть работы What I Know совпадает с тем, что я называю Easy Breezy Math. »
Я настоятельно рекомендую представить эту стратегию (и вообще любую стратегию, но определенно эту) в контексте словесной задачи, чтобы помочь учащимся осмыслить стратегию и действительно понять, что происходит. Полезно называть делимое и делитель в зависимости от контекста.
Советы для обучающего отдела (с любой стратегией раздела)
1.) Представьте новые стратегии в увлекательном контексте или словесной задаче. Проходя этапы стратегии, пройдитесь по тому, что будет происходить в задаче.
2.) Если эти стратегии совершенно новые, то проведите день (или больше) с однозначными делителями, прежде чем переходить к двузначным. Это будет того стоить!
3.) Убедитесь, что учащиеся понимают цель Easy Breezy Math, если вы решите использовать эти леса. Кроме того, убедитесь, что они понимают, что это значит и как это работает (в нем представлены частичные частные, готовые для выбора учащимися).
4.) Научите учащихся проверять свои ответы умножением. Это поможет им в самооценке и позволит им обнаружить небольшие ошибки, которые они допускают при вычитании или других ошибках в вычислениях.
Как насчет традиционного алгоритма деления?
Поскольку в моем штате используется общее ядро, я не преподаю традиционный алгоритм деления в рамках моей учебной программы для пятого класса. Однако после государственного тестирования мы делаем превью по математике 6-го класса. В то время я постоянно преподаю традиционный алгоритм. К этому моменту года мои ученики хорошо понимают деление и намного лучше чувствуют числа. Это помогает им освоить алгоритм. Кроме того, я обнаружил, что многие учителя шестого класса ожидают от них знания традиционного алгоритма, поэтому я определенно не хочу, чтобы мои ученики отставали, когда они переходят в среднюю школу.
Нужно больше ресурсов для отдела?
БЕСПЛАТНЫЕ распечатки Division of the Day: нажмите здесь, чтобы получить бесплатный набор распечаток Division of the Day.






 Их:
Их:











 когда дело доходит до SAT.
когда дело доходит до SAT.» Мммммм… Как вы делаете деление в большую сторону…?»

Каждую неделю репетиторы-специалисты по математике Third Space Learning проводят еженедельные индивидуальные онлайн-уроки и математические вмешательства для тысяч детей начальной школы.
 С 2013 года мы помогли более 125 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.
С 2013 года мы помогли более 125 000 детей стать более уверенными в себе и способными к математике. Узнайте больше или запросите персональное предложение, чтобы рассказать нам о ваших потребностях и о том, как мы можем помочь.
Но мне пришлось добавить леса для моих учеников. Мы называем этот каркас нашей «Легкой математикой». По сути, мы берем известные нам умножения и списываем их в сторону. Мы извлекаем из этих проблем, чтобы помочь нам решить проблему. Мы делаем это, потому что в начале года моим ученикам действительно не хватает понимания числа дивизий. Это также помогает им увидеть связь между умножением и делением.

 Примечание. Часть работы What I Know совпадает с тем, что я называю Easy Breezy Math. »
Примечание. Часть работы What I Know совпадает с тем, что я называю Easy Breezy Math. »


 (синг)
(синг)

 Подведение итогов.
Подведение итогов.