Северо-Восточную и Юго-Восточную хорды соединят в Московский скоростной диаметр
Фото: Пресс-служба стройкомплекса
В Москве придумали практичное решение многих транспортных проблем. О новом дорожном проекте сообщил в своем блоге мэр столицы Сергей Собянин. По масштабу и важности это будет фактически МКАД, но в разы круче.
Что дает новая трасса
Диаметр свяжет десятки районов города и создаст в каждом из них комфортную транспортную реальность:
• между собой состыкуются крупнейшие вылетные магистрали — Дмитровское, Алтуфьевское, Ярославское, Щелковское шоссе, шоссе Энтузиастов, Рязанский и Волгоградский проспекты, Каширское и Варшавское шоссе;
• миллионы водителей смогут быстро и удобно ездить из одной части столицы в другую. По новой дороге через весь город, обогнув центр, можно будет пролететь без единого светофора за 40 (!) минут;
• время в пути сократится от 10 до 50 минут в зависимости от расстояния и времени суток. К примеру, по дороге в аэропорты «Шереметьево» и «Домодедово» можно будет сэкономить 20 — 25 минут;
• разгрузятся центральные улицы города, ТТК, МКАД, вылетные магистрали.
Свободнее станет и в метро, поскольку снова спокойно сядут за руль те, кто сейчас пользуется подземкой из-за пробок на дорогах;
• транзита грузового транспорта на диаметре не будет. Наконец исполнится давняя мечта столичных водителей — поездка по городу без простоев в глухих заторах, без тесных двухполосных улочек, без светофоров и без блокирующих дорогу тяжеловозов.
Фото: Пресс-служба стройкомплекса
Старт близко
Московский скоростной диаметр уже готов на 62%.
Дальше план такой:
•3-й квартал 2022 г. — достроят Северо-Восточную хорду (СВХ) в пределах МКАД. Для этого осталось протянуть 8 километров дорог с двумя эстакадами на участке от транспортной связки с Северо-Западной хордой (СЗХ) до Дмитровского шоссе.
•2023 г. — завершат СВХ в районе будущей трассы Москва — Казань, а также Юго-Восточную хорду, соединяющую шоссе Энтузиастов с Варшавским шоссе.
•4-й квартал 2023 г. — полноценный запуск движения по всему диаметру.
КСТАТИ
В конце 2023 года планируют построить еще один дорожный участок — от улицы Лухмановская до трассы М12 Москва — Нижний Новгород — Казань.
Его общая длина — 14,1 километра, в том числе 3 путепровода, 1 мост и 3 пешеходных перехода. Этот маршрут свяжет Московский скоростной диаметр с автомобильной дорогой федерального значения М12 Москва — Нижний Новгород — Казань.
Карта диаметра.Фото: Дмитрий ПОЛУХИН
Дорогу прокладывают одновременно на двух участках:
1 От Бусиновской развязки до трассы М12 Москва — Нижний Новгород — Казань (Северо-Восточная хорда).
Длина по прямой — 40 километров (строительная длина — 120 километров).
Сюда входят:
• 80 искусственных сооружений (38 километров), в том числе 65 эстакад, из них самая длинная эстакада в Европе — 2,5 километра на участке от МКАД до шоссе Энтузиастов, 1 тоннель, 6 мостов и 8 путепроводов;
•21 пешеходный переход.
Готовность — 82%.
2 От шоссе Энтузиастов до автодороги Солнцево — Бутово — Варшавское шоссе (Юго-Восточная хорда).
Длина по прямой — 28 километров (строительная длина — 98 километров).
Сюда входят:
•56 искусственных сооружений (22 километра), в том числе 35 эстакад, 4 тоннеля, 3 моста и 14 путепроводов;
•12 пешеходных переходов.
Готовность — 42%.
Продолжением диаметра станут:
•на севере — федеральная трасса М11 Москва — Санкт-Петербург;
•на востоке — строящаяся трасса М12 Москва — Казань;
•на юге — главная магистраль Новой Москвы Солнцево — Бутово — Варшавское шоссе
ВЫБИРАЕТЕ ВЫ!
В проекте «Активный гражданин» (на сайте ag.mos.ru и в мобильном приложении) желающие могут проголосовать за название будущей трассы. Власти гарантируют — как москвичи решат, так и будет. А значит, окончательное имя магистрали станет понятным и удобным для горожан. Участникам опроса нужно выбрать любой из двух пунктов — «Московский скоростной диаметр (МСД)» или «Хочу предложить свой вариант названия». Судя по комментариям в соцсетях, многим нравится первый вариант. Некоторые жители выдвигают и другие предложения, например, «Магистраль «Север — Юг» и «Главная московская автомагистраль».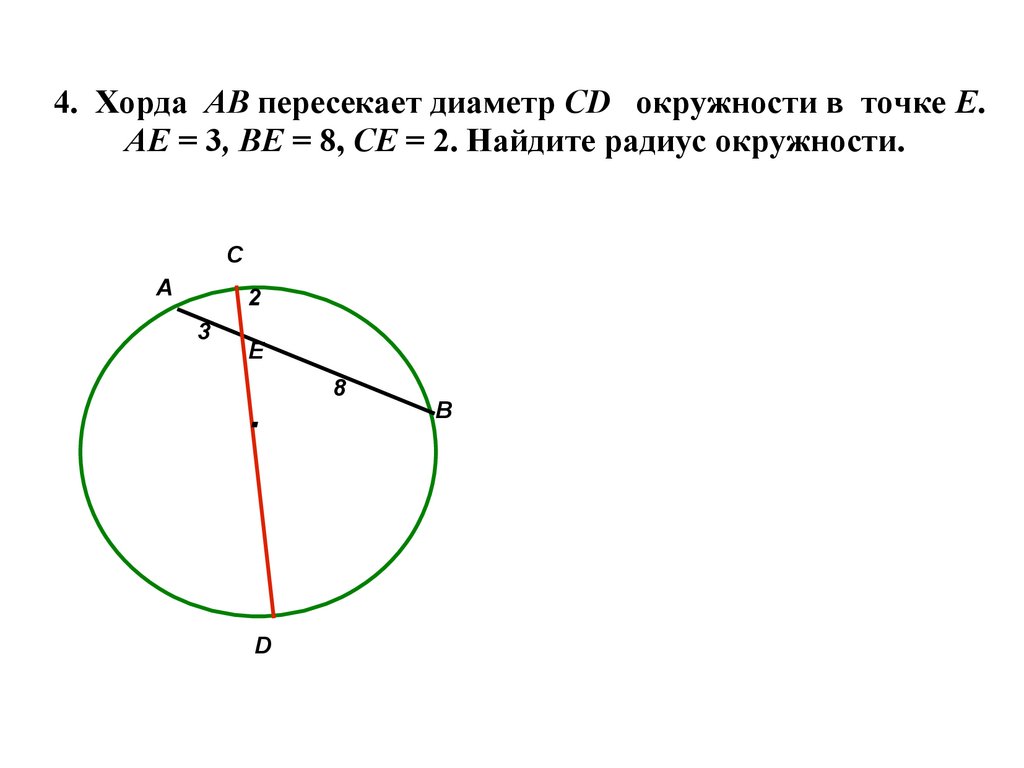
СКАЗАНО
«В Москве в завершающей стадии находится строительство двух крупнейших внеуличных магистралей — Северо-Восточной и Юго-Восточной хорды. При бесшовном соединении эти магистрали органически создают новую транспортную артерию — бессветофорный скоростной диаметр Москвы с юга до севера, от Симферопольского шоссе до платной магистрали на Санкт-Петербург. И с ответвлением до Некрасовки.
Поэтому мы приняли логичное решение объединить Северо-Восточную и Юго-Восточную хорды в новую городскую магистраль — под возможным названием Московский скоростной диаметр».
(Мэр Москвы Сергей СОБЯНИН — на сайте www.sobyanin.ru.)
Конспект урока геометрии в 5 классе «Линии в круге: радиус, диаметр, хорда»
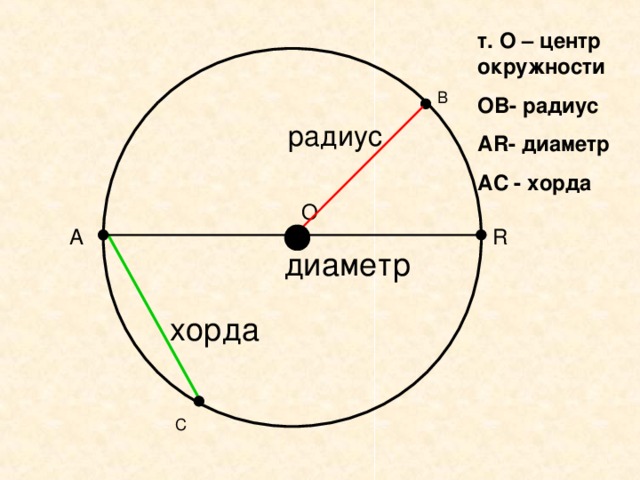
Тема: Линии в круге: радиус, диаметр, хорда.
Цели:
повторить и обобщить сформированные у школьников понятия радиуса, диаметра, хорды и окружности;
коррекция переключаемости внимания на основе упражнений;
воспитание настойчивости и терпения.
Оборудование: цветные карандаши (зеленый, красный, синий), кроссворд, модель круга и игра «Веселый круг» (каждому ученику), циркуль, карандаш, линейка, чертежный угольник, карточки с заданиями, образцы розеток.
Тип урока: повторительно-обобщающий.
Методы: наглядные и практические.
План урока:
1. Организационный момент.
2. Станция «Графическая»
3. Станция «Геометрический кроссворд»
4. Станция «Отрезки»
5. Станция «Физкультурная»
6. Станция «Построений»
7. Станция «Веселый круг»
8. Станция «Домашнее задание»
9. Станция «Итоговая».
Ход урока:
1. Организационный момент.
Внимание! Проверь, дружок,
Готов ли ты начать урок?
Все ли на месте, все ли в порядке –
Циркуль, книжка и тетрадка.
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку «5».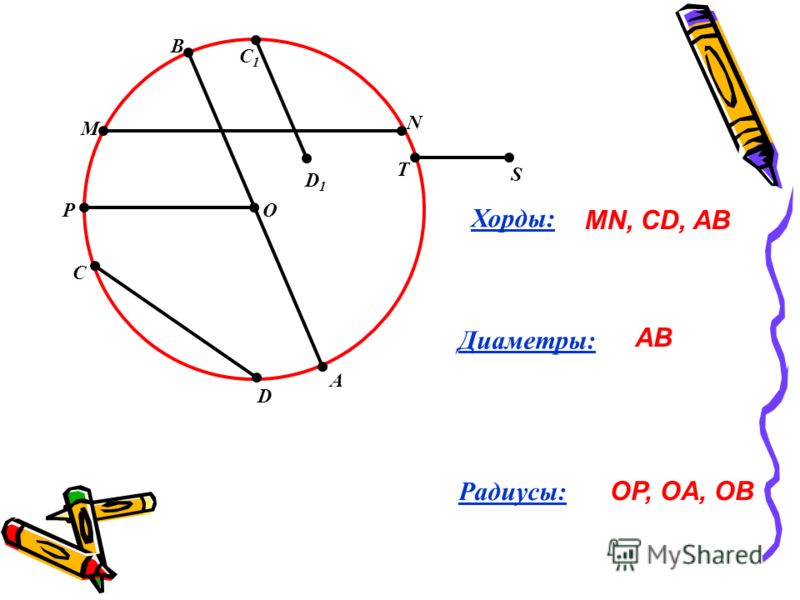
Будем отвечать активно,
Хорошо себя вести,
Чтобы гости дорогие
Захотели вновь прийти.
Есть у меня помощник лихой,
Он чертит круг одной ногой,
А другой – проткнул бумагу,
Уцепился и – ни шагу.
Что за друг у меня?
Отгадайте-ка, друзья! (циркуль)
Беседа о безопасной работе с циркулем.
Учитель: Я со своим помощником-циркулем приглашаю вас в путешествие по стране Геометрии. Тема урока: «Линии в круге: радиус, диаметр, хорда».
2. Станция «Графическая». На станции «Графической» мы будем строить дорожку при помощи циркуля. (Показать образцы дорожек.) Индивидуальная работа: хорошо успевающие учащиеся выполняют задание по замыслу, слабоуспевающие – по образцу.
3. Станция «Геометрический кроссворд».
По горизонтали: 1. Граница круга. 2. Отрезок, соединяющий точку окружности с ее центром.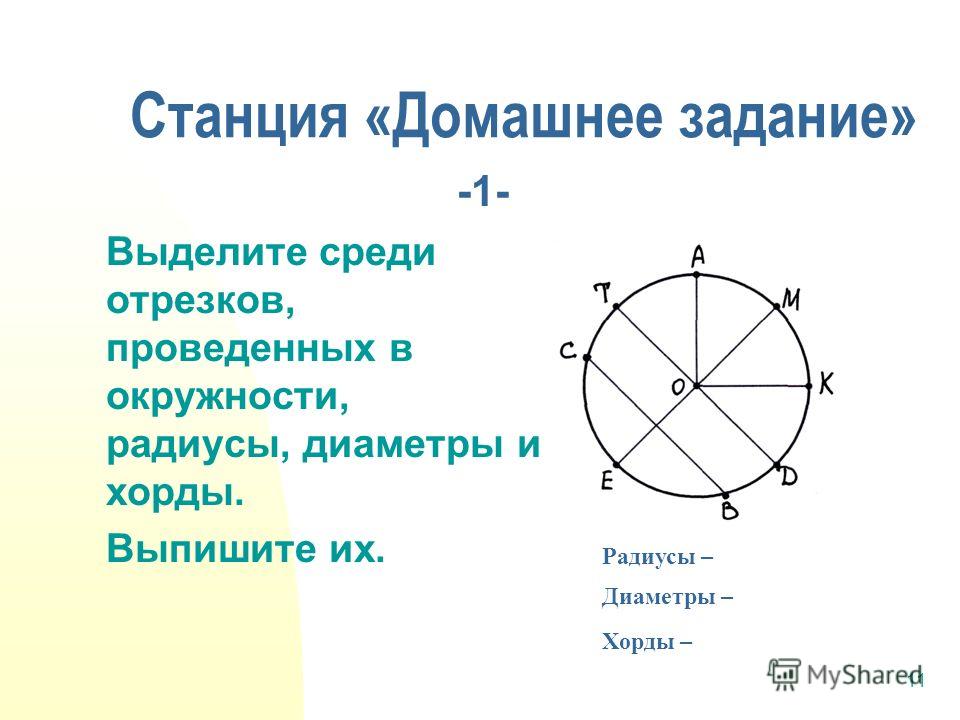
3. Незамкнутая кривая линия, часть окружности. 4. Отрезок, соединяющий две точки окружности и проходящий через ее центр.
По вертикали: 1. Отрезок, соединяющий две точки окружности.
4. Станция «Построений».
Задание 1. Определите, какие фигуры расположены внутри окружности. Чем являются стороны фигур? Начертите у себя в тетради такой же рисунок. Выпишите сначала все радиусы, затем хорды и диаметр.
Задание 2 выполняем по учебнику. С. 193, № 934. Начертите круг диаметром 4 см. Проведите в круге известные вам отрезки, обозначьте их буквами и подпишите названия.
Задание 3. Перегните модель круга по диаметру. Перегните модель круга так, чтобы линия сгиба была хордой.
5. Станция «Физкультурная».
Вы, наверное, устали?
Настало время отдыхать.
Предлагаю усталость
Физкультминуткой снять.
Мы проверили осанку
И свели лопатки.
Мы походим на носках,
А потом на пятках.
Упражнение для снятия утомления с глаз.
6. Станция «Отрезки».
Задание 1. Выделите среди отрезков, проведенных в окружности, красным карандашом радиусы, зеленым карандашом диаметры и синим – хорды. Сколько треугольников находится внутри окружности? Определите вид каждого треугольника.
Задание 2.Будет ли отрезок АВ диаметром окружности. Какое условие определения диаметра не выполняется?
7. Станция «Веселый круг». Из деталей игры «Веселый круг» смоделировать плоский предмет.
8. Станция «Домашнее задание».
1. Выделите среди отрезков, проведенных в окружности, радиусы, диаметры и хорды. Выпишите их.
Радиусы –
Диаметры –
Хорды –
2. Постройте розетку из окружностей.
Индивидуальная работа: Слабоуспевающие учащиеся выполняют несложную розетку по образцу. Остальные – по замыслу.
9. Станция «Итоговая».
Скоро прозвенит звонок
Пора заканчивать урок.
– О чем мы сегодня говорили на уроке?
– Все ли было понятно на уроке?
– Кто испытывал трудности?
– Что понравилось и запомнилось больше всего?
Урок составила и провела учитель математики ГБОУ Республики Марий Эл «Специальная (коррекционная) общеобразовательная школа-интернат для обучающихся, воспитанников с ограниченными возможностями здоровья VIII вида г. Козьмодемьянска»
Матвеева Ольга Вячеславовна
Дуги и хорды
На рисунке 1 окружность O имеет радиусы OA, OB, OC и OD. Если хорды AB и CD имеют одинаковую длину, можно показать, что Δ AOB ≅ Δ DOC. Таким образом, м ∠1 = м ∠2, что, в свою очередь, дает м = м . Это сформулировано как теорема.
Рисунок 1 Окружность с четырьмя радиусами и двумя хордами.
Теорема 78: В окружности, если две хорды равны по мере, то соответствующие им малые дуги равны по мере.
Обратное утверждение этой теоремы также верно.
Теорема 79: В окружности, если две малые дуги равны по мере, то их соответствующие хорды равны по мере.
Пример 1: Используйте рисунок 2 , чтобы определить следующее. (a) Если AB = CD и = 60°, найдите
Рисунок 2 Связь между равенством мер (не диаметральных) хорд и равенством мер соответствующих им малых дуг.
м = 60° (теорема 78)
GH = 8 (теорема 79)
Некоторые дополнительные теоремы о хордах в окружности приводятся ниже без пояснений. Эти теоремы могут быть использованы для решения многих типов задач.
Теорема 80: Если диаметр перпендикулярен хорде, то он делит хорду и ее дуги пополам.
На рис. 3, UT, диаметр QS перпендикулярен хорде QS. По теореме 80 QR = RS, м = м и м = м .
Рисунок 3 Диаметр, перпендикулярный хорде.
Теорема 81: В окружности, если две хорды равны по размеру, то они равноудалены от центра.
На рисунке 4, если AB = CD , то по теореме 81 OX = OY .
Рисунок 4 В окружности отношение между двумя хордами равно по размеру и равноудалено от центра.
Теорема 82: В окружности, если две хорды равноудалены от центра окружности, то эти две хорды равны по мере.
На рисунке 5, если OX = OY , то по теореме 82 AB = CD .
Пример 2: Используйте рисунок, чтобы найти x .
Рисунок 5 Окружность с двумя малыми дугами, равными по размеру.
Пример 3: Используйте рисунок 6, на котором м = 115°, м = 115° и BD = 10, чтобы найти AC .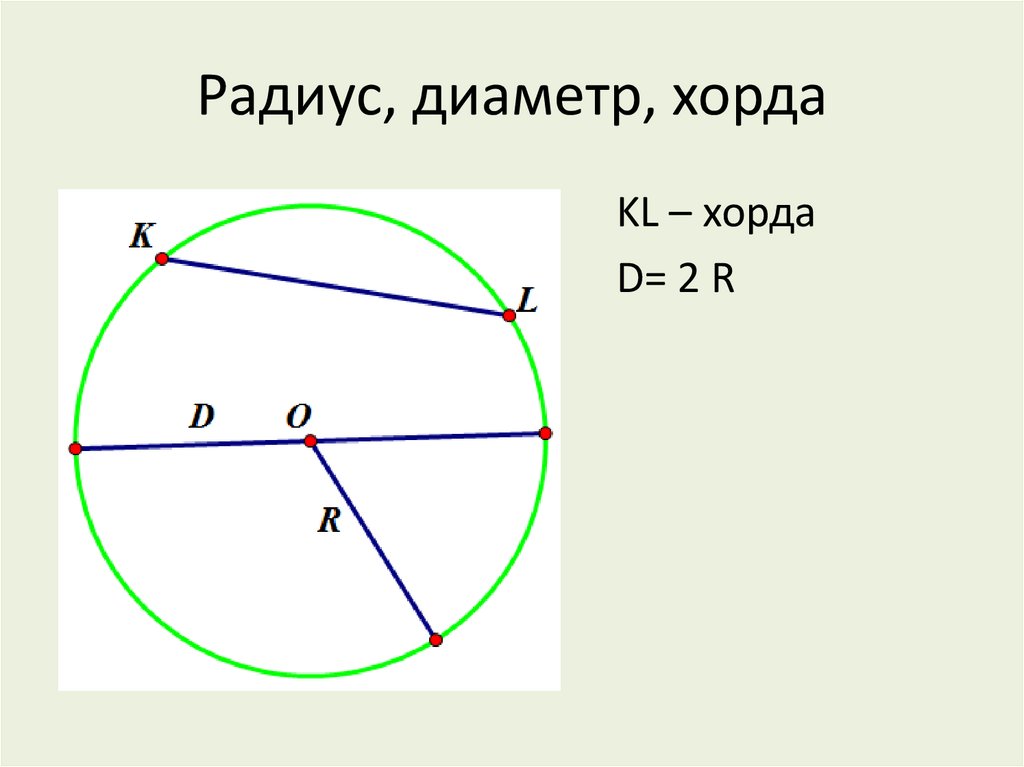
Рисунок 6 Окружность с двумя малыми дугами, равными по размеру.
Пример 4: Используйте Рисунок 7, в котором AB = 10, OA = 13 и M тий AOB = 55 °, чтобы найти OM , M и M .
Рисунок 7 Окружность с диаметром, перпендикулярным хорде.
Итак, ST ⊥ AB, а ST — диаметр. Теорема 80 говорит, что AM = BM . Поскольку AB = 10, то AM = 5. Теперь рассмотрим прямоугольный треугольник AMO . Поскольку OA = 13 и AM = 5, OM можно найти с помощью теоремы Пифагора.
Кроме того, Теорема 80 говорит, что м = м и м = м . С м ∠ AOB = 55°, тогда м = 55° и м = 305°. Следовательно, м = 27 ½ и м = 152 ½°.
Пример 5: Используйте рисунок 8, на котором AB = 8, CD = 8 и OA = 5, чтобы найти ON .
Рисунок 8 Окружность с двумя хордами равной длины.
По Теореме 81 , НА = ОМ . По Теорема 80 , AM = MB , поэтому AM = 4. OM теперь можно найти с помощью теоремы Пифагора или путем распознавания пифагорейской тройки. В любом случае OM = 3. Следовательно, ON = 3.
Задача о параллельных хордах
Задача о параллельных хордах
Задача о параллельных хордах
Если у нас есть круг, где мы знаем соответствующие длины двух параллельных хорд, и мы знаем расстояние друг от друга двух хорд, найдите радиус окружности.
Для удобства обозначений пусть длины двух хорд равны 2a и 2b , а расстояние друг от друга равно c .
Проблема, вероятно, требует обсуждения двух случаев:
Случай 1. Обе параллельные хорды лежат по одну сторону от центра окружности.
Случай 2. Центр окружности находится между двумя параллельными хордами.
Даны a , b и c , как определено на рисунке выше. Каково условие на a , b и c для определения того, находятся ли параллельные хорды по одну сторону от центра, или одна из них является диаметром, или они находятся по разные стороны от центра?
Расширение.
