Решение дифференциальных уравнений в полных дифференциалах
Студенты ВУЗ-ов частенько ищут информацию «Как найти решение уравнения в полных дифференциалах?». Из этого урока Вы получите полную инструкцию плюс готовые решения. Сначала краткое ознакомление — что такое уравнение в полных дифференциалах? Как искать решение уравнения на полный дифференциал?
Далее разбор готовых примеров, после которого возможно у Вас не останется вопросов по данной теме.
Определение 1. Уравнение вида M(x,y)dx+N(x,y)dx=0 называется уравнением в полных дифференциалах, если зависимость перед знаком равенства является полным дифференциалом некоторой функции двух переменных u(x,y), то есть справедливая формула
du(x,y)=M(x,y)dx+N(x,y)dx. (1)
Таким образом, первоначальное уравнение по содержанию означает равенство нулю полного дифференциала функции
du(x,y)=0.
Интегрируя дифференциал получим общий интеграл ДУ в виде
u(x,y)=С.
(2)
При вычислениях, как правило, постоянную возлагают равной нулю.
Пред вычислениями всегда возникает вопрос «Как проверить что заданное ДУ является уравнением в полных дифференциалах?»
На этот вопрос дает ответ следующее условие.
Необходимое и достаточное условие полного дифференциала
Необходимым и достаточным условием полного дифференциала является равенство между собой частных производных
(3)
При решении дифференциальных уравнений его проверяют в первую очередь, чтобы идентифицировать имеем ли уравнение в полных дифференциалах или возможно другое.
По содержанию это условие означает что смешанные производные функции равны между собой.
В формулах учитывая зависимости
(4)
необходимое и достаточное условие существования полного дифференциала можем записать в виде
Приведенный критерий и применяют при проверке уравнения на соответствие полному дифференциалу, хотя при изучении данной темы преподаватели не зададут Вам другого типа уравнений.
Алгоритм решения уравнения в полных дифференциалах
С обозначений (4) частных производных полного дифференциала функции следует, что u(x,y) мы можем найти интегрированием
Эти формулы дают выбор при вычислениях, поэтому для интегрирования выбирают ту частную производную, интеграл от которой легче найти на практике.
Далее второй важный момент — неопределенный интеграл представляет собой первообразную то есть «+ С», которую следует определить.
Поэтому, если интегрируем частную производную M(x,y) по «икс» то сталая зависит от y и наоборот — если интегрируем N(x,y) по y то сталая зависима от «икс».
Далее чтобы определить постоянную берут производную от u(x,y ) по другой переменной чем та, по которой производили интегрирование и приравнивают к второй частичной производной.
В формулах это будет выглядеть следующим образом
Как правило некоторые слагаемые упрощаются и получим уравнение на производную постоянной. Для первого из уравнений получим
Окончательно общий интеграл после определения постоянной имеет вид
В симметричной форме получим ответ и для другого уравнения.
Запись только на вид сложная, на самом деле на практике все выглядит значительно проще и понятнее. Проанализируйте следующие задачи на полные дифференциалы.
Готовые ответы на уравнение в полных дифференциалах
Пример 1. Решить дифференциальное уравнение
Решение:Левая часть уравнения является полным дифференциалом некоторой функции , поскольку выполняется условие
Отсюда записываем частную производную функции двух переменных от «икс»
и интегрированием находим ее вид
Чтобы доопределить постоянную находим частную производную функции по «y» и приравниваем со значением в уравнении
Подобные слагаемые в правой и левой части сокращаем, после чего постоянную находим интегрированием
Теперь имеем все величины для записи общего решения дифференциального уравнения в виде
Как можно убедиться, схема решения уравнений в полных дифференциалах не сложная и ее под силу выучить каждому.
Важное значение имеют множители при дифференциалах, поскольку их приходится интегрировать и дифференцировать чтобы найти решение.
Пример 2. (6.18) Найти интеграл дифференциального уравнения
Решение: По теории левая часть уравнения должна быть полным дифференциалом некоторой функции двух переменных u(x,y), при этом проверяем выполняется ли условие
Отсюда берем частную производную и через интеграл находим функцию
Вычисляем частную производную функции двух переменных по y и приравниваем к правой стороне дифференциального уравнения.
Производная выражается зависимостью
С учетом постоянной получили общий интеграл дифференциального уравнения в виде
На этом вычисления данного примера завершено.
Пример 3. (6.20) Решить дифференциальное уравнение
Решение: Левая часть уравнения будет полным дифференциалом некоторой функции двух переменных u(x; y) , если будет выполняться условие
Отсюда начинаем решать уравнения, а вернее интегрирование одной из частных производных
Далее находим производную от полученной функции по переменной y и приравниваем к правой стороне дифференциальной зависимости
Это позволяет найти константу, как функцию от y.
Если начинать раскрывать дифференциальную зависимость с правой стороны, то получим что константа зависит от x. Общее решение дифференциального уравнения при этом не изменится и для заданного уравнения имеет вид
На этом пример решен.
Пример 4. (6.21) Решить дифференциальное уравнение
Решение: Проверяем является ли полным дифференциалом некоторой функции u(x,y) выражение в левой стороне уравнения
Выписываем частную производную функции двух переменных и интегрированием восстанавливаем решение
Далее уточняем постоянную. Для этого вычисляем производную функции по y и приравниваем к значению в уравнении (выделено зеленым)
Отсюда, выражаем производную и интегрируем
Общее решение дифференциального уравнения можем записать формулой
Для закрепления тематики просим самостоятельно проверить что данные уравнения являются уравнениями в полных дифференциалах и решить их:
Здесь Вам и корневые функции, тригонометрические, экспоненты, логарифмы, одним словом — все что может ожидать Вас на модулях и экзаменах.
После этого Вам станет гораздо проще решать такого типа уравнения.
Из следующей статьи Вы познакомитесь с уравнениями вида
M(x,y)dx+N(x,y)dx=0
которые достаточно подобные уравнению в полных дифференциалах, однако в них не выполняется условие равенства частных производных. Их вычисляют поиском интегрирующего множителя, умножая на который приведенное уравнение становится уравнением в полных дифференциалах.
Полный дифференциал примеры решения. Уравнения в полных дифференциалах
В этой теме мы рассмотрим метод восстановления функции по ее полному дифференциалу, дадим примеры задач с полным разбором решения.
Бывает так, что дифференциальные уравнения (ДУ) вида P (x , y) d x + Q (x , y) d y = 0 могут содержать в левых частях полные дифференциалы некоторых функций. Тогда мы можем найти общий интеграл ДУ, если предварительно восстановим функцию по ее полному дифференциалу.
Пример 1
Рассмотрим уравнение P (x , y) d x + Q (x , y) d y = 0 . В записи левой его части содержится дифференциал некоторой функции U (x , y) = 0 .
Для этого должно выполняться условие ∂ P ∂ y ≡ ∂ Q ∂ x .
Полный дифференциал функции U (x , y) = 0 имеет вид d U = ∂ U ∂ x d x + ∂ U ∂ y d y . С учетом условия ∂ P ∂ y ≡ ∂ Q ∂ x получаем:
P (x , y) d x + Q (x , y) d y = ∂ U ∂ x d x + ∂ U ∂ y d y
∂ U ∂ x = P (x , y) ∂ U ∂ y = Q (x , y)
Преобразовав первое уравнение из полученной системы уравнений, мы можем получить:
U (x , y) = ∫ P (x , y) d x + φ (y)
Функцию φ (y) мы можем найти из второго уравнения полученной ранее системы:
∂ U (x , y) ∂ y = ∂ ∫ P (x , y) d x ∂ y + φ y » (y) = Q (x , y) ⇒ φ (y) = ∫ Q (x , y) — ∂ ∫ P (x , y) d x ∂ y d y
Так мы нашли искомую функцию U (x , y) = 0 .
Пример 2
Найдите для ДУ (x 2 — y 2) d x — 2 x y d y = 0 общее решение.
Решение
P (x , y) = x 2 — y 2 , Q (x , y) = — 2 x y
Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x:
∂ P ∂ y = ∂ (x 2 — y 2) ∂ y = — 2 y ∂ Q ∂ x = ∂ (- 2 x y) ∂ x = — 2 y
Наше условие выполняется.
На основе вычислений мы можем сделать вывод, что левая часть исходного ДУ является полным дифференциалом некоторой функции U (x , y) = 0 . Нам нужно найти эту функцию.
Так как (x 2 — y 2) d x — 2 x y d y является полным дифференциалом функции U (x , y) = 0 , то
∂ U ∂ x = x 2 — y 2 ∂ U ∂ y = — 2 x y
Интегрируем по x первое уравнение системы:
U (x , y) = ∫ (x 2 — y 2) d x + φ (y) = x 3 3 — x y 2 + φ (y)
Теперь дифференцируем по y полученный результат:
∂ U ∂ y = ∂ x 3 3 — x y 2 + φ (y) ∂ y = — 2 x y + φ y » (y)
Преобразовав второе уравнение системы, получаем: ∂ U ∂ y = — 2 x y . Это значит, что
— 2 x y + φ y » (y) = — 2 x y φ y » (y) = 0 ⇒ φ (y) = ∫ 0 d x = C
где С – произвольная постоянная.
Получаем: U (x , y) = x 3 3 — x y 2 + φ (y) = x 3 3 — x y 2 + C . Общим интегралом исходного уравнения является x 3 3 — x y 2 + C = 0 .
Разберем еще один метод нахождения функции по известному полному дифференциалу. Он предполагает применение криволинейного интеграла от фиксированной точки (x 0 , y 0) до точки с переменными координатами (x , y) :
U (x , y) = ∫ (x 0 , y 0) (x , y) P (x , y) d x + Q (x , y) d y + C
В таких случаях значение интеграла никак не зависит от пути интегрирования.
Мы можем взять в качестве пути интегрировании ломаную, звенья которой располагаются параллельно осям координат.
Пример 3
Найдите общее решение дифференциального уравнения (y — y 2) d x + (x — 2 x y) d y = 0 .
Решение
Проведем проверку, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x:
∂ P ∂ y = ∂ (y — y 2) ∂ y = 1 — 2 y ∂ Q ∂ x = ∂ (x — 2 x y) ∂ x = 1 — 2 y
Получается, что левая часть дифференциального уравнения представлена полным дифференциалом некоторой функции U (x , y) = 0 . Для того, чтобы найти эту функцию, необходимо вычислить криволинейный интеграл от точки (1 ; 1) до (x , y) . Возьмем в качестве пути интегрирования ломаную, участки которой пройдут по прямой y = 1 от точки (1 , 1) до (x , 1) , а затем от точки (x , 1) до (x , y) :
∫ (1 , 1) (x , y) y — y 2 d x + (x — 2 x y) d y = = ∫ (1 , 1) (x , 1) (y — y 2) d x + (x — 2 x y) d y + + ∫ (x , 1) (x , y) (y — y 2) d x + (x — 2 x y) d y = = ∫ 1 x (1 — 1 2) d x + ∫ 1 y (x — 2 x y) d y = (x y — x y 2) y 1 = = x y — x y 2 — (x · 1 — x · 1 2) = x y — x y 2
Мы получили общее решение дифференциального уравнения вида x y — x y 2 + C = 0 .
Пример 4
Определите общее решение дифференциального уравнения y · cos x d x + sin 2 x d y = 0 .
Решение
Проверим, выполняется ли условие ∂ P ∂ y ≡ ∂ Q ∂ x .
Так как ∂ (y · cos x) ∂ y = cos x , ∂ (sin 2 x) ∂ x = 2 sin x · cos x , то условие выполняться не будет. Это значит, что левая часть дифференциального уравнения не является полным дифференциалом функции. Это дифференциальное уравнение с разделяющимися переменными и для его решения подходят другие способы решения.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Определение: Уравнение вида
P(x,y)dx + Q(x,y)dy = 0, (9)
где левая часть представляет собой полный дифференциал некоторой функции двух переменных, называется уравнением в полных дифференциалах.
Обозначим эту функцию двух переменных через F(x,y). Тогда уравнение (9) можно переписать в виде dF(x,y) = 0, а это уравнение имеет общее решение F(x,y) = C.
Пусть дано уравнение вида (9).
Для того чтобы узнать, является ли оно уравнением в полных дифференциалах, нужно проверить, является ли выражение
P(x,y)dx + Q(x,y)dy (10)
полным дифференциалом некоторой функции двух переменных. Для этого необходимо проверить выполнение равенства
Допустим, что для данного выражения (10) равенство (11) выполняется в некоторой односвязной области (S) и, следовательно, выражение (10) является полным дифференциалом некоторой функции F(x,y) в (S).
Рассмотрим следующий способ нахождения этой первообразной. Необходимо найти такую функцию F(x,y), чтобы
где функция (у) будет определена ниже. Из формулы (12) тогда следует, что
во всех точках области (S). Теперь подберем функцию (у) так, чтобы имело место равенство
Для этого перепишем нужное нам равенство (14), подставив вместо F(x,y) ее выражение по формуле (12):
Произведем дифференцирование по у под знаком интеграла (это можно делать так как P(x,y) и — непрерывные функции двух переменных):
Так как по (11) , то, заменяя на под знаком интеграла в (16), имеем:
Проинтегрировав по у, найдем саму функцию (у), которая построена так, что выполняется равенство (14).
Используя равенства (13) и (14), видим, что
в области (S). (18)
Пример 5. Проверить, является ли данное дифференциальное уравнение уравнением в полных дифференциалах и решить его.
Это дифференциальное уравнение в полных дифференциалах. В самом деле, обозначая, убеждаемся в том, что
а это есть необходимое и достаточное условие того, что выражение
P(x,y)dx+Q(x,y)dy
является полным дифференциалом некоторой функции U(x,y). При этом — непрерывные в R функции.
Следовательно, чтобы проинтегрировать данное дифференциальное уравнение, нужно найти такую функцию, для которой левая часть дифференциального уравнения будет полным дифференциалом. Пусть такой функцией будет U(x,y), тогда
Интегрируя левую и правую части по x, получим:
Чтобы найти ц(y), используем тот факт, что
Подставляя найденное значение ц(y) в (*), окончательно получим функцию U(x,y):
Общий интеграл исходного уравнения имеет вид
Основные типы дифференциальных уравнений первого порядка (продолжение).
Определение: Линейным уравнением первого порядка называется уравнение вида
y» + P(x)y = f(x), (21)
где P(x) и f(x) — непрерывные функции.
Название уравнения объясняется тем, что производная y» — линейная функция от у, то есть если переписать уравнение (21) в виде y» = — P(x) +f(x), то правая часть содержит у только в первой степени.
Если f(x) = 0, то уравнение
yґ+ P(x) y = 0 (22)
называется линейным однородным уравнением. Очевидно, что однородное линейное уравнение является уравнением с разделяющимися переменными:
y» +P(x)y = 0; ,
Если f(x) ? 0, то уравнение
yґ+ P(x) y = f(x) (23)
называется линейным неоднородным уравнением.
В общем случае переменные в уравнении (21) разделить нельзя.
Уравнение (21) решается следующим образом: будем искать решение в виде произведения двух функций U(x) и V(x):
Найдем производную:
y» = U»V + UV» (25)
и подставим эти выражения в уравнение (1):
U»V + UV» + P(x)UV = f(x).
Сгруппируем слагаемые в левой части:
U»V + U = f(x). (26)
Наложим условие на один из множителей (24), а именно, предположим, что функция V(x) такова, что она обращает в тождественный нуль выражение, стоящее в квадратных скобках в (26), т.е. что она является решением дифференциального уравнения
V» + P(x)V = 0. (27)
Это уравнение с разделяющимися переменными, находим из него V(x):
Теперь найдем функцию U(x) такую, чтобы при уже найденной функции V(x) произведение U V было решением уравнения (26). Для этого надо, чтобы U(x) была решением уравнения
Это уравнение с разделяющимися переменными, поэтому
Подставляя найденные функции (28) и (30) в формулу (4), получаем общее решение уравнения (21):
Таким образом, рассмотренный метод (способ Бернулли) сводит решение линейного уравнения (21) к решению двух уравнений с разделяющимися переменными.
Пример 6. Найти общий интеграл уравнения.
Это уравнение не является линейным относительно y и y», но оно оказывается линейным, если считать искомой функцией x, а аргументом y.
Действительно, переходя к, получаем
Для решения полученного уравнения воспользуемся способом подстановки (Бернулли). Будем искать решение уравнения в виде x(y)=U(y)V(y), тогда. Получаем уравнение:
Выберем функцию V(y) так, чтобы. Тогда
Левые части дифференциальных уравнений вида иногда представляют собой полные дифференциалы некоторых функций. Если восстановить функцию по ее полному дифференциалу, то будет найден общий интеграл дифференциального уравнения. В этой статье опишем метод восстановления функции по ее полному дифференциалу, теоретический материал снабдим примерами и задачами с подробным описанием решения.
Левая часть дифференциального уравнения является полным дифференциалом некоторой функции U(x, y) = 0 , если выполняется условие .
Так как полный дифференциал функции U(x, y) = 0 есть , то при выполнении условия можно утверждать, что . Следовательно, .
Из первого уравнения системы имеем . Функцию можно найти, используя второе уравнение системы:
Так будет найдена искомая функция U(x, y) = 0
.
Рассмотрим пример.
Пример.
Найти общее решение дифференциального уравнения .
Решение.
В этом примере . Условие выполняется, так как
следовательно, левая часть исходного дифференциального уравнения представляет собой полный дифференциал некоторой функции U(x, y) = 0
. Наша задача сводится к отысканию этой функции.
Так как есть полный дифференциал функции U(x, y) = 0
, то . Интегрируем по x
первое уравнение системы и дифференцируем по y
полученный результат . С другой стороны, из второго уравнения системы имеем . Следовательно,
где С
– произвольная постоянная.
Таким образом, и общим интегралом исходного уравнения является .
Существует другой метод нахождения функции по ее полному дифференциалу. Он заключается во взятии криволинейного интеграла
от фиксированной точки (x 0 , y 0)
до точки с переменными координатами (x, y)
: . В этом случае значение интеграла не зависит от пути интегрирования. Удобно брать в качестве пути интегрирования ломаную, звенья которой параллельны осям координат.
Рассмотрим на примере.
Пример.
Найдите общее решение дифференциального уравнения .
Решение.
Проверим выполнение условия :
Таким образом, левая часть дифференциального уравнения представляет собой полный дифференциал некоторой функции U(x, y) = 0 . Найдем эту функцию, вычислив криволинейный интеграл от точки (1; 1) до (x, y) . В качестве пути интегрирования возьмем ломаную: первый участок ломаной пройдем по прямой y = 1 от точки (1, 1) до (x, 1) , вторым участком пути возьмем отрезок прямой от точки (x, 1) до (x, y) .
Определение 8.4. Дифференциальное уравнение вида
где
называется
уравнением в полных дифференциалах.
Заметим,
что левая часть такого уравнения есть
полный дифференциал некоторой функции
.
В общем случае, уравнение (8.4) можно представить в виде
Вместо уравнения (8.5) можно рассматривать уравнение
,
решение которого есть
общим интегралом уравнения (8.4). Таким
образом, для решения уравнения (8.
4)
необходимо найти функцию
.
В соответствии с определением уравнения
(8.4), имеем
(8.6)
Функцию
будем отыскивать, как функцию,
удовлетворяющую одному из этих условий
(8.6):
где — произвольная функция, не зависящая от.
Функция
определяется так, чтобы выполнялось
второе условие выражения (8.6)
(8.7)
Из
выражения (8.7) и определяется функция
.
Подставляя ее в выражение для
и получают общий интеграл исходного
уравнения.
Задача 8.3. Проинтегрировать уравнение
Здесь
.
Следовательно,
данное уравнение относится к типу
дифференциальных уравнений в полных
дифференциалах. Функцию
будем отыскивать в виде
.
С другой стороны,
.
В
ряде случаев условие
может не выполняться.
Тогда такие уравнения к рассматриваемому типу приводятся умножением на так называемый интегрирующий множитель, который, в общем случае, является функцией только или.
Если у некоторого уравнения существует интегрирующий множитель, зависящий только от , то он определяется по формуле
где отношение
должно быть только функцией.
Аналогично, интегрирующий множитель, зависящий только от , определяется по формуле
где
отношение
должно быть только функцией.
Отсутствие в приведенных соотношениях, в первом случае переменной , а во втором — переменной, являются признаком существования интегрирующего множителя для данного уравнения.
Задача 8.4. Привести данное уравнение к уравнению в полных дифференциалах.
.
Рассмотрим отношение:
.
Тема 8.2. Линейные дифференциальные уравнения
Определение
8.5 . Дифференциальное
уравнение
называется линейным, если оно линейно
относительно искомой функции,
ее производнойи не содержит произведения искомой
функции и ее производной.
Общий вид линейного дифференциального уравнения представляется следующим соотношением:
(8.8)
Если в соотношении (8.8) правая
часть
,
то такое уравнение называется линейным
однородным. В случае, когда правая часть
,
то такое уравнение называется линейным
неоднородным.
Покажем, что уравнение (8.8) интегрируется в квадратурах.
На первом этапе рассмотрим линейное однородное уравнение.
Такое уравнение является уравнением с разделяющимися переменными. Действительно,
;
/
Последнее соотношение и определяет общее решение линейного однородного уравнения.
Для
отыскания общего решения линейного
неоднородного уравнения применяется
метод вариации производной постоянной.
Идея метода состоит в том, что общее
решение линейного неоднородного
уравнения в том же виде, что и решение
соответствующего однородного уравнения,
однако произвольная постоянная
заменяется некоторой функцией
,
подлежащей определению. Итак, имеем:
(8.9)
Подставляя
в соотношение (8.8) выражения, соответствующие
и
,
получим
Подставляя последнее выражение в соотношение (8.9), получают общий интеграл линейного неоднородного уравнения.
Таким
образом, общее решение линейного
неоднородного уравнения определяется
двумя квадратурами: общего решения
линейного однородного уравнения и
частного решения линейного неоднородного
уравнения.
Задача
8.5. Проинтегрировать
уравнение
Таким образом, исходное уравнение относится к типу линейных неоднородных дифференциальных уравнений.
На первом этапе найдем общее решение линейного однородного уравнения.
;
На втором этапе определим общее решение линейного неоднородного уравнения, которое отыскивают в виде-
,
где
— функция, подлежащая определению.
Итак, имеем:
Подставляя соотношения для ив исходное линейное неоднородное уравнение получим:
;
;
.
Общее решение линейного неоднородного уравнения будет иметь вид:
.
Дифференциальное уравнение первого порядка в полных дифференциалах — это уравнение вида:
(1) ,
где левая часть уравнения является полным дифференциалом некоторой функции U(x, y)
от переменных x, y
:
.
При этом .
Если найдена такая функция U(x, y)
,
то уравнение принимает вид:
dU(x, y) = 0
.
Его общий интеграл:
U(x, y)
= C
,
где C
— постоянная.
Если дифференциальное уравнение первого порядка записано через производную:
,
то его легко привести к форме (1) . Для этого умножим уравнение на dx
.
Тогда .
В результате получаем уравнение, выраженное через дифференциалы:
(1) .
Свойство дифференциального уравнения в полных дифференциалах
Для того, чтобы уравнение (1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось соотношение:
(2) .
Доказательство
Далее мы полагаем, что все функции, используемые в доказательстве, определены и имеют соответствующие производные в некоторой области значений переменных x и y . Точка x 0 , y 0 также принадлежит этой области.
Докажем необходимость условия (2) .
Пусть левая часть уравнения (1) является дифференциалом некоторой функции U(x, y)
:
.
Тогда
;
.
Поскольку вторая производная не зависит от порядка дифференцирования, то
;
.
Отсюда следует, что .
Необходимость условия (2) доказана.
Докажем достаточность условия (2) .
Пусть выполняется условие (2) :
(2) .
Покажем, что можно найти такую функцию U(x, y)
,
что ее дифференциал:
.
Это означает, что существует такая функция U(x, y)
,
которая удовлетворяет уравнениям:
(3) ;
(4) .
Найдем такую функцию. Проинтегрируем уравнение (3) по x
от x 0
до x
,
считая что y
— это постоянная:
;
;
(5) .
Дифференцируем по y
считая, что x
— это постоянная и применим (2) :
.
Уравнение (4) будет выполнено, если
.
Интегрируем по y
от y 0
до y
:
;
;
.
Подставляем в (5) :
(6) .
Итак, мы нашли функцию, дифференциал которой
.
Достаточность доказана.
В формуле (6) , U(x 0
, y 0)
является постоянной — значением функции U(x, y)
в точке x 0
, y 0
.
Ей можно присвоить любое значение.
Как распознать дифференциальное уравнение в полных дифференциалах
Рассмотрим дифференциальное уравнение:
(1) .
Чтобы определить, является ли это уравнение в полных дифференциалах, нужно проверить выполнение условия (2) :
(2) .
Если оно выполняется, то это уравнение в полных дифференциалах. Если нет — то это не уравнение в полных дифференциалах.
Пример
Проверить, является ли уравнение в полных дифференциалах:
.
Решение
Здесь
,
.
Дифференцируем по y
,
считая x
постоянной:
.
Дифференцируем
.
Поскольку:
,
то заданное уравнение — в полных дифференциалах.
Методы решения дифференциальных уравнений в полных дифференциалах
Метод последовательного выделения дифференциала
Наиболее простым методом решения уравнения в полных дифференциалах является метод последовательного выделения дифференциала. Для этого мы применяем формулы дифференцирования, записанные в дифференциальной форме:
du ± dv = d(u ± v)
;
v du + u dv = d(uv)
;
;
.
В этих формулах u
и v
— произвольные выражения, составленные из любых комбинаций переменных.
Пример 1
Решить уравнение:
.
Решение
Ранее мы нашли, что это уравнение — в полных дифференциалах. Преобразуем его:
(П1) .
Решаем уравнение, последовательно выделяя дифференциал.
;
;
;
;
.
Подставляем в (П1) :
;
.
Ответ
Метод последовательного интегрирования
В этом методе мы ищем функцию U(x, y)
,
удовлетворяющую уравнениям:
(3) ;
(4) .
Проинтегрируем уравнение (3) по x
,
считая y
постоянной:
.
Здесь φ(y)
— произвольная функция от y
,
которую нужно определить. Она является постоянной интегрирования. Подставляем в уравнение (4) :
.
Отсюда:
.
Интегрируя, находим φ(y)
и, тем самым, U(x, y)
.
Пример 2
Решить уравнение в полных дифференциалах:
.
Решение
Ранее мы нашли, что это уравнение — в полных дифференциалах.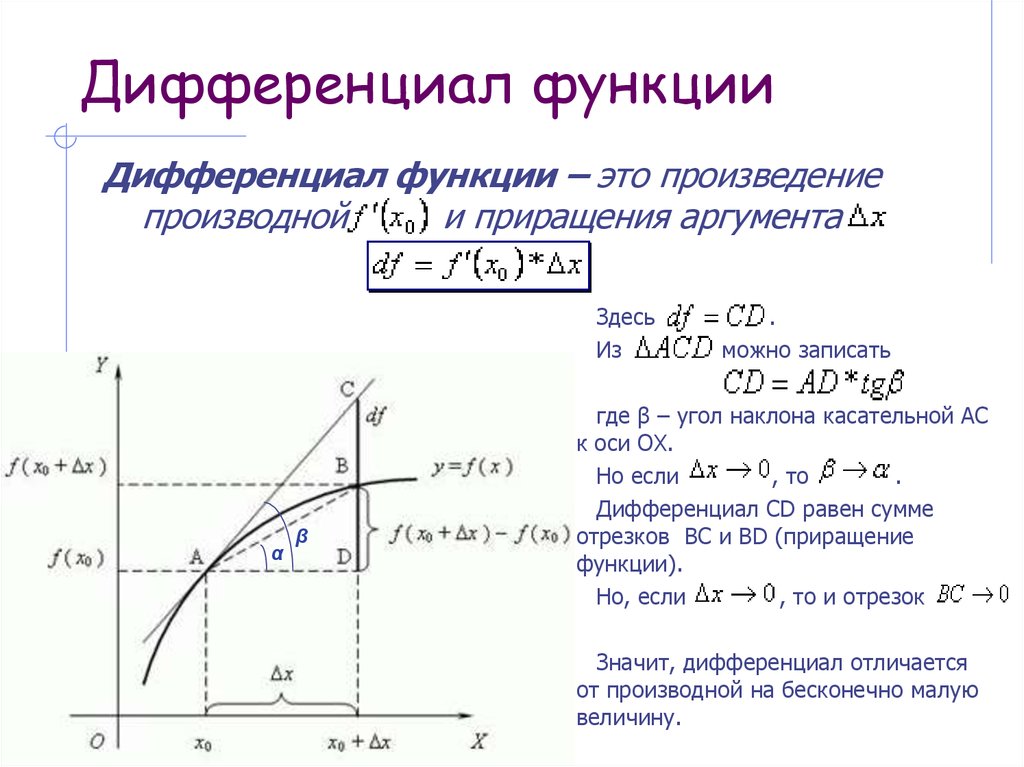
Введем обозначения:
,
.
Ищем Функцию U(x, y)
,
дифференциал которой является левой частью уравнения:
.
Тогда:
(3) ;
(4) .
Проинтегрируем уравнение (3) по x
,
считая y
постоянной:
(П2)
.
Дифференцируем по y
:
.
Подставим в (4) :
;
.
Интегрируем:
.
Подставим в (П2) :
.
Общий интеграл уравнения:
U(x, y)
= const
.
Объединяем две постоянные в одну.
Ответ
Метод интегрирования вдоль кривой
Функцию U
,
определяемую соотношением:
dU = p(x, y)
dx + q(x, y)
dy
,
можно найти, если проинтегрировать это уравнение вдоль кривой, соединяющей точки (x 0
, y 0)
и (x, y)
:
(7) .
Поскольку
(8) ,
то интеграл зависит только от координат начальной (x 0
, y 0)
и конечной (x, y)
точек и не зависит от формы кривой. Из (7) и (8) находим:
(9) .
Здесь x 0
и y 0
— постоянные.
Поэтому U(x 0
, y 0)
— также постоянная.
Пример такого определения U
был получен при доказательстве :
(6) .
Здесь интегрирование производится сначала по отрезку, параллельному оси y
,
от точки (x 0
, y 0
)
до точки (x 0
, y)
.
Затем интегрирование производится по отрезку, параллельному оси x
,
от точки (x 0
, y)
до точки (x, y)
.
В более общем случае, нужно представить уравнение кривой, соединяющей точки (x 0
, y 0
)
и (x, y)
в параметрическом виде:
x 1
= s(t 1)
;
y 1
= r(t 1)
;
x 0
= s(t 0)
;
y 0
= r(t 0)
;
x = s(t)
;
y = r(t)
;
и интегрировать по t 1
от t 0
до t
.
Наиболее просто выполняется интегрирование по отрезку, соединяющим точки (x 0
, y 0
)
и (x, y)
.
В этом случае:
x 1
= x 0 + (x — x 0)
t 1
;
y 1
= y 0 + (y — y 0)
t 1
;
t 0 = 0
;
t = 1
;
dx 1
= (x — x 0)
dt 1
;
dy 1
= (y — y 0)
dt 1
.
После подстановки, получается интеграл по t
от 0
до 1
.
Данный способ, однако, приводит к довольно громоздким вычислениям.
Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Решения дифференциального уравнения
по
Определение, порядок и степень, общее и частное решения дифференциального уравнения
Уравнение с производной одной или нескольких зависимых переменных, с одной или несколькими независимыми переменными, представляет собой дифференциальное уравнение (DE). Дифференциальные уравнения классифицируются по типу, порядку и линейности уравнения. Различают два основных типа дифференциальных уравнений: «обыкновенные» и «частные».
Дифференциальные уравнения с ОДНОЙ независимой переменной называются обыкновенными дифференциальными уравнениями.
Примеры:
Дифференциальные уравнения с двумя или более независимыми переменными называются уравнениями в частных производных.
Примеры:
порядок дифференциального уравнения – это порядок старшей производной дифференциального уравнения.
Например, y’ = 4 y — это дифференциальное уравнение первого порядка.
Уравнение дифференциального уравнения второго порядка S ” ( T ) = –32 имеет общее решение
S ( T ) = –16 T 2 + C 1 69 2 + C 1 6611 2 + C 1 661 2 + C 1 611 2 + C 1 6 t + C 2 Общее решение с” ( t ) = –32
, которое содержит две произвольные константы.
Следовательно, дифференциальное уравнение порядка n имеет общее решение с n произвольными константами.
Дифференциальное уравнение называется линейным, если между зависимыми переменными и их производными нет умножений.
Другими словами, все коэффициенты являются функциями независимых переменных. Дифференциальные уравнения, не удовлетворяющие определению линейных, являются нелинейными.
Решением дифференциального уравнения является функция, удовлетворяющая уравнению.
Общее решение: Решения, полученные интегрированием ДУ, называются общими решениями. Общее решение обыкновенного дифференциального уравнения порядка имеет произвольные константы. Например, дифференциация и замена показывают, что Y = E — 2 x — это решение дифференциального уравнения
Y ‘ + 2 y = 0.
Точно так же каждое решение этого дифференциального уравнения имеет вид
y = Ce – 2x Общее решение y ‘ + 2 y = 0
, где
5
– любое действительное число.
Частное решение — это решения, найденные путем подстановки конкретных значений произвольных констант в общие решения.
Частные решения дифференциального уравнения выводятся из начальных условий зависимой переменной или одной из ее производных для конкретных значений независимой переменной
Сингулярные решения: Решения, которые не могут быть выражены через общие решения, называются особыми решениями.
Аналитические решения ОДУ доступны для линейных ОДУ, а также для нескольких специальных классов нелинейных дифференциальных уравнений. Численный метод используется для получения графика или таблицы неизвестной функции
Например, дифференциальное уравнение второго порядка
s” ( t ) = –32, имеющее общее решение
S ( T ) = –16 T 2 + C 1 T + C 2 Общее решение S ” ( T ) = – 32
могут иметь следующие начальные условия.
s (0) = 80, s’ (0) = 64 Начальные условия
Здесь начальные условия дают частное решение0061 2 + 64 t + 80.
Частное решение
Для дифференциального уравнения xy’ – 3 y = 0 проверьте, что y =Cx 3906 решение. Затем найдите частное решение, определяемое начальным условием y = 2 при x = –3.
Решение:
Обратите внимание, что: y = Cx 3 является решением, потому что y’ = 3 Cx 2 и
XY ‘ — 3 Y = x (3 CX 2 ) — 3 ( CX 3 )
= 0.
3 )= 0,
. Классифицируйте следующие ДУ:ДУ имеет вид линейный , так как коэффициенты не являются функциями y и нет членов более высокой степени в y или его производных. является функцией т только .
Решить дифференциальное уравнение означает найти выражение для y через x или для A через t без производной.
Пожалуйста, поделитесь
примеров разделимых дифференциальных уравнений
примеров разделимых дифференциальных уравнений
| Математика 122 — Исчисление для биологии II | |
|---|---|---|
Государственный университет Сан-Диего — Последнее обновление этой страницы 15 июля 01 |
Разделимые дифференциальные уравнения. Примеры
- Основные примеры
- Изменяющийся во времени мальтузианский рост (Италия)
- Утечка воды из цилиндра
Эти рабочие примеры начинаются с двух основных отделяемых дифференциалов.
уравнения. Метод разделения переменных применяется к
рост населения в Италии и пример утечки воды из
цилиндр.
Пример 1: Решите следующие разделимые дифференциальные уравнения.
а. | б. |
Решение: а. Мы начните с разделения переменных и создания двух интегралов,
Интегралы оцениваются, давая
или
Это решено для y ( t ) дать
Вычислим произвольную константу C с использованием начального условия. Поскольку y (0) = 1, мы берем положительный квадратный корень. Таким образом, у нас есть
Отсюда следует, что 2 C = 5, значит решение
б. Как и в части а, мы начинаем с разделения переменных и создания
два интеграла.
Результат
Интеграл слева дает
, а интеграл справа требует разбиения на два интегралы, которые решаются следующим образом:
Обратите внимание, что мы добавляем произвольную константу к интегрированию на верно. Таким образом, мы имеем
Возводим в степень обе части приведенного выше уравнения, затем используем правила возведения в степень для получения
, где A = e C .
Далее подставляем начальное условие г (1) = 2 ( г = 2 и т = 1), поэтому
Это дает решение
Пример 2: За последние несколько десятилетий темпы роста Италии
скатитесь туда, где скоро стране не хватит даже рождений
(или иммиграции), чтобы заменить количество смертей в стране.
Таким образом, его популяция вскоре может начать сокращаться. Население
Италии в 1950 году был
47,1 млн, в
1970 г. было 53,7
миллионов, а в 1990 это было
56,8 млн.
а. Используйте данные 1950 и 1950 гг. 1990 г., чтобы найти мальтузианскую модель роста для населения Италии.
б. Рассмотрим неавтономную мальтузианскую модель роста, заданную дифференциальное уравнение
, где константы и и b определяются данные. Решите это дифференциальное уравнение с приведенными выше данными.
в. Если бы население Италии составляло 50,2 миллион в 1960 и 57,6 млн в 2000, затем используйте каждую из этих моделей для оценить численность населения в 1960 г. и 2000 и определить ошибку между модели и фактические значения переписи. Нарисуйте решения двух модели и точки данных с 1950 по 2000.
д. Определите, когда население Италии стабилизируется и начнет сокращаться
согласно неавтономной мальтузианской модели роста.
Решение: а. дифференциальное уравнение для мальтузианского роста имеет вид
Общее решение этой модели (для населения в миллионов) составляет
В 1990 году численность населения 56,8 млн, т. е.
Таким образом,
Отсюда следует, что
Решение мальтузианской модели роста:
б. Мы следуем конспектам лекций при решении неавтономных задач.
Мальтузианская модель роста.
Приведенная выше модель отделима
разделив обе стороны на P , оставив два
интегралов для решения:
Эти интегралы дают
для некоторой константы c . Этот означает, что есть три константы, которые нужно решить с данными дано в 1950 году, 1970 г. и 1990. Становится легче решать за константы, если мы сделаем перевод в 1950, поэтому запишите предыдущее уравнение в форма
, где константы b и c немного отличаются от предыдущее уравнение.
Используя исходные данные 1950 г., мы есть
Далее подставляем данные с 1970 года с ( t — 1950) = 20 и используя наше значение c = ln(47.1), поэтому
Аналогично, с данными 1990 г.
с ( т — 1950) = 40 и c = ln(47.
1), получаем
уравнение с неизвестными параметрами и и б
Это становится задачей решения двух линейных уравнений в двух неизвестные и и б . Если мы умножим уравнение с 1970 данных по -2, затем добавьте его в уравнение по данным 1990 г., то параметр b исчезает.
Отсюда следует, что
Подставив это значение a в любое из уравнений выше, получаем, что
Отсюда следует, что решение дается числом
.Возводя в степень приведенное выше решение, население Италии заданное неавтономной мальтузианской моделью роста, удовлетворяет
с. Ниже приведена таблица значений для каждой из моделей в 1960 и 2000 и связанные с ними ошибки, где население исчисляется миллионами. Значения для населения получается путем замены 1960 и 2000 г. на т в приведенных выше уравнениях.
Модель | 1960 | % Ошибка | 2000 | % Ошибка |
Италия Данные переписи | 50,2 | — | 57,6 | — |
Мальтузианский | 49,4 | 1,7% | 59,5 | 3,3% |
Неавтономный | 50,8 | 1,1% | 56,8 | 1,4% |
Процентная ошибка вычисляется по стандартной формуле, поэтому для 1960 оцениваем
Ниже приведен график двух моделей и данных.
Обе модели
достаточно близко к данным, но неавтономный мальтузианский рост
модель немного лучше соответствует данным.
д. Из наших расчетов выше мы имеем дифференциальное уравнение для неавтономной мальтузианской модели роста дается как
, где t в годах после 1950. Рост населения замедляется до ноль, поэтому население выравнивается, когда P ‘( t ) = 0. Это происходит, когда
Поскольку P ( t ) не равно нулю, нам нужно найти когда
, что происходит, когда
Отсюда следует, что неавтономная мальтузианская модель роста предсказывает
что население Италии стабилизировалось в
1995 (45
лет после 1950 г.
). Самые свежие данные
указывалось, что 2000 год был пиком
населения Италии, поэтому модель делает разумную работу
примерно выравнивание населения Италии.
Пример 3 (Закон Торричелли): Один из способов подачи воды в медленная скорость полива растительности заключается в том, чтобы поставить небольшое отверстие в дно цилиндрической емкости. Вода медленно вытекает через период времени, чтобы обеспечить расширенный полив. Вода, вытекающая из отверстие на дне резервуара с водой удовлетворяет требованиям Торричелли. закон.
Закон Торричелли: Скорость изменения объема воды, вытекающей из водохранилища ( В ) с отверстием в дне бака пропорциональна квадрату корень высоты воды над отверстием ( ч ). Математически это определяется дифференциалом уравнение:
Это уравнение получено с использованием фундаментальной физики с предположением
что сумма кинетической и потенциальной энергии системы
остается постоянным.
Ниже представлена схема течения воды из
цилиндр.
Поскольку мы рассматриваем цилиндрический резервуар с водой, объем воды в резервуаре равен площади поперечного сечения ( A ) цилиндра, умноженное на высота воды ( h ) с A остается постоянным и ч ( t ) меняется со временем (снижение). Таким образом,
Начиная с A является константой для цилиндр, у нас тот
Отсюда следует, что мы можем написать дифференциальное уравнение для потока воды из бака по уравнению
Предположим, что резервуар с 20 см
радиус начинается с высоты 144 см.
вода. При открытии отверстия вода начинает вытекать
удовлетворяющие закону Торричелли и орошающие опытный участок.
Предположим, что экспериментальное измерение дает константу к/А = 0,025 ч -1 .
а. Найдите высоту воды в водоеме в любой момент времени для этого экспериментальная система полива.
б. Определите, через какое время резервуар опустеет.
в. Каково среднечасовое количество воды (в см 3 /час) система орошения. Также найдите объем воды (в см 3 /час), который течет после 100 часов и 800 часы.
Решение:
а. Дифференциальное уравнение для высоты воды в резервуар записывается в следующем виде с использованием степени (1/2) для квадратного корня,
Это дифференциальное уравнение решается с помощью разделения техника переменных. Переменные разделены зависимой переменная h в интеграле по слева внизу и независимая переменная т в интеграле справа ниже. Таким образом, у нас есть два приведенных ниже интеграла для решения
Эти два интеграла легко решаются, что дает следующее уравнение
Это уравнение решается явно для ч ( т ) делением на 2 и возведения в квадрат обеих сторон, в результате чего уравнение
Далее используем начальное условие ч (0) = 144, чтобы найти константу С .
При начальном условии это
следует, что
или
С = 24.
Таким образом, решение дается уравнением
Дан график решения для высоты воды к
б. Резервуар пуст, когда ч ( t ) = 0. Таким образом, мы должны решить следующее:
Отсюда следует, что
или
т = 960 час
Резервуар опустеет через 960 часов или 40 дней.
в. Общий объем в резервуаре В = р(20) 2 144
= 57 600 р
= 180 956 см 3 , значит в среднем количество воды
поставлено на завод более 960
часов до того, как водохранилище опустеет, примерно
180 956/960 = 188,5
см 3 /час.
Для расчета количества воды, подаваемой в 100 часов и 800 часов, нам нужно использовать дифференциальное уравнение. Из информация о законе Торричелли, приведенная выше, объем воды вытекающая из водохранилища равна
с
так
Итак, нам нужно вычислить площадь поперечного сечения цилиндра A и определить высота воды при t = 100 и 800 час. площадь поперечного сечения удовлетворяет
Высота воды т = 100 и 800 часов дают
и
ч (800) = (12 — 0,0125(800)) 2 = (2,0) 2 = 4,0 см.
Объем, вытекающий из резервуара при т = 100 удовлетворяет
, в то время как объем, вытекающий из резервуара при т = 800 удовлетворяет
Отрицательный ответ в каждом из этих ответов для d V /d t указывает на то, что вода вытекает из резервуара.