Единичное круг — ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА ЧИСЛОВОГО АРГУМЕНТА — ЧИСЛА И ВЫРАЖЕНИЯ — АЛГЕБРА И НАЧАЛА АНАЛИЗА
Единичное круг — ОПРЕДЕЛЕНИЕ СИНУСА, КОСИНУСА, ТАНГЕНСА И КОТАНГЕНСА ЧИСЛОВОГО АРГУМЕНТА — ЧИСЛА И ВЫРАЖЕНИЯ — АЛГЕБРА И НАЧАЛА АНАЛИЗА — МАТЕМАТИКА. ПОЛНЫЙ ПОВТОРЮВАЛЬНИЙ КУРС. ПОДГОТОВКА К ВНЕШНЕМУ НЕЗАВИСИМОМУ ОЦЕНИВАНИЮ И ГОСУДАРСТВЕННОЙ ИТОГОВОЙ АТТЕСТАЦИИ
|
|
Содержание
Введение 3
Свойства тригонометрических функций на единичной окружности 4
Создание цифровой образовательной модели 5
Разработка внешнего интерфейса программы 5
Отрисовка основных элементов программы 6
Обеспечение реакции на управляющие кнопки 7
Организация пересчета значений функций 8
Тестирование получившейся программы 9
Заключение 11
Список литературы 12
Приложение 13
Введение
Образовательный
процесс в школьных учреждениях
несовершенен, усвояемость детьми
материала зависит не только от их
умственных способностей, но от качества
и способов подачи материала.
Программная среда Stratum 2000 позволяет разрабатывать как тестовые задания для проверки знаний ученика, так и интерактивные модели, позволяющие продемонстрировать учащимся учебный материал в понятной и интересной форме.
В данной работе поставлена цель: разработать интерактивную модель в среде Stratum, демонстрирующую определение тригонометрических функций (синуса, косинуса, тангенса и котангенса) на единичном круге.
Для достижения данной цели необходимо выполнять ряд задач:
1. Ознакомиться со средой моделирования и проектирования Stratum;
2. Ознакомиться с теоретической основой проекта;
3. Разработать модель единичного круга, реализовать вычисление и визуализацию значений тригонометрических функций:
создать единичный круг и радиус-вектор;
добавить элементы управления, определяющие отображаемую функцию и вид чертежа;
обеспечить изменение угла наклона радиус-вектора;
создать алгоритм пересчета значений, соответствующих выбранной функции и положению радиус-вектора;
протестировать разработанную модель.

Свойства тригонометрических функций на единичной окружности
Тригонометрический круг – основа тригонометрии. Он представляет собой окружность радиусом 1 с центром в начале координат. Тригонометрический круг позволяет нам:
пронаблюдать перевод градусов в радианы и наоборот;
найти значение синуса и косинуса;
убедиться, что синус и косинус принимают значения от -1 до 1;
увидеть, что синус и косинус – периодические функции с периодом 2π
вычислить тангенс и котангенс
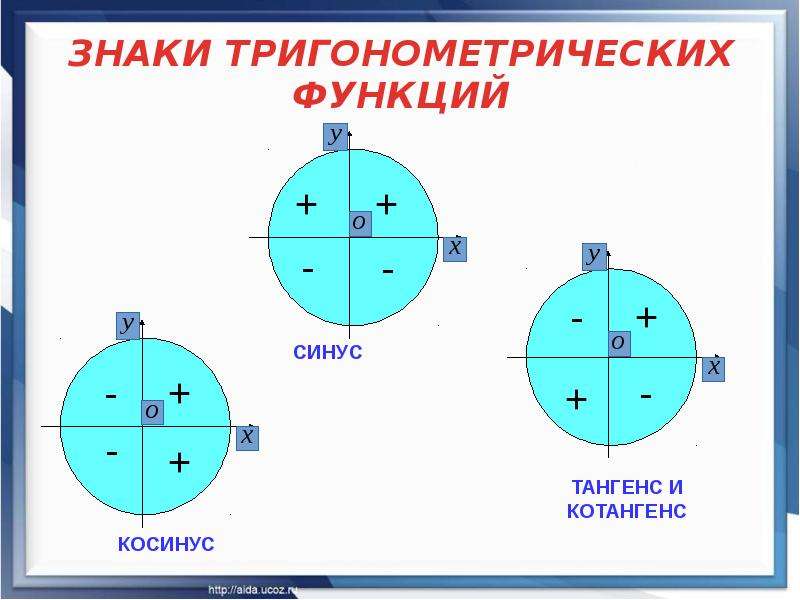
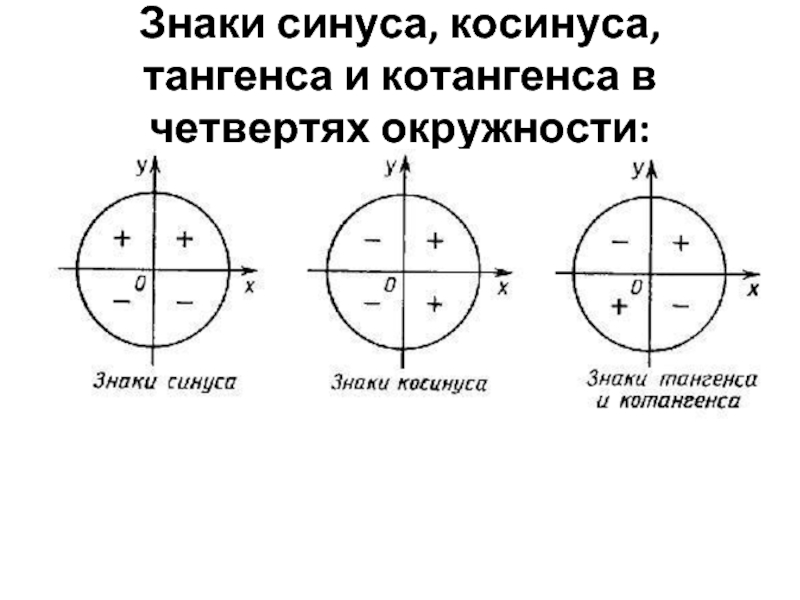
увидеть знаки у синуса и косинуса, а также вычислить знаки тангенса и котангенса
Отсчет
углов начинается от положительного
направления оси OX
и идет против часовой стрелки. Полный
круг составляет 360°. Точка
с координатами (1;0) соответствует углу
0°. Точка
с координатами (-1;0) соответствует углу
в 180°,
тока с координатами (0;1) – угол 90°,
а точка с координатами (0; -1) — 270°.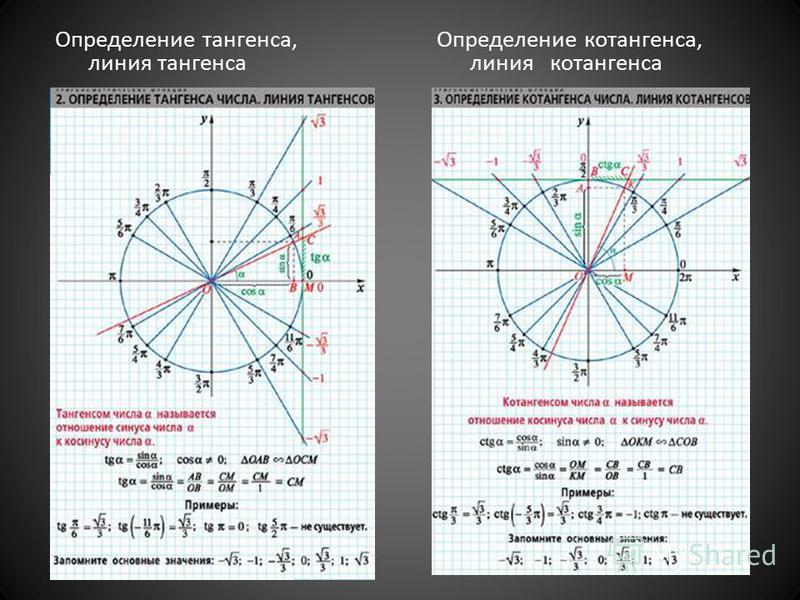
Косинусом угла называется абсцисса (то есть значение на оси OX, соответствующее данному углу α). Также косинус угла можно найти как отношение х к радиусу единичной окружности.
Для того, чтобы определить знак синуса или косинуса необходимо лишь поставить точку на окружности, соответствующую данному углу и посмотреть положительны или отрицательны у этой точки координаты.
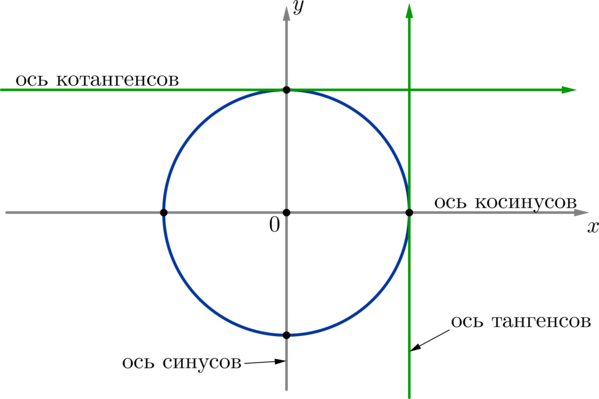
Тангенс – отношение синуса к косинусу. Касательная к окружности в точке (1;0) называется осью тангенса. Для того чтобы графически определить чему равен тангенс, необходимо провести луч через начало координат и точку, соответствующую данному углу, до пересечения с осью тангенса. Y – координата точки пересечения и будет являться значением тангенса.
Котангенс
– отношение косинуса к синусу.
Чтобы вычислить знаки тангенса или котангенса, необходимо найти знаки синуса и косинуса в данной точке и поделить их (для тангенса – синус на косинус, для котангенса – косинус на синус).
Тангенс окружности — Математика GCSE
Введение
Что такое касательная окружности?
Ключевые части круга, необходимые для этих теорем
Доказательство того, что если две касательные пересекаются, то они имеют одинаковую длину
Как использовать теоремы касательной
Тангенс окружности рабочий лист
Распространенные заблуждения
Практические вопросы касательной окружности
Касательная окружности Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое касательная окружности?
Ключевые части круга, необходимые для этих теорем
Доказательство того, что если две касательные пересекаются, то они имеют одинаковую длину
Как использовать теоремы касательной
Тангенс окружности рабочий лист
Распространенные заблуждения
Практические вопросы касательной окружности
Касательная окружности Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о теоремах о кругах, касающихся касательных окружности , включая их применение, доказательство и использование их для решения более сложных задач.
Существует также рабочих листов с теоремой о круге , основанных на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое касательная окружности?
Касательная окружности — это прямая линия, которая касается окружности окружности только в одной точке.
- Угол между касательной и радиусом равен 90 градусов .
- Касательные, пересекающиеся в одной точке, имеют одинаковую длину .
На диаграмме 1 выше касательная пересекает окружность в точке A, которая перпендикулярна (90 градусов) к радиусу окружности в этой точке (точка касания находится в точке A).
На диаграмме 2 две касательные встречаются с окружностью в двух разных точках ( B и D ) и пересекаются в точке A . Если точки B и D связаны хордой, то AB и AD имеют одинаковую длину, поэтому треугольник ABD равнобедренный. Если точки B и D соединяются с центром окружности C, они образуют воздушный змей ABCD. Это означает, что у нас есть две теоремы о круге:
Если точки B и D соединяются с центром окружности C, они образуют воздушный змей ABCD. Это означает, что у нас есть две теоремы о круге:
Равнобедренный треугольник
Воздушный змей
Что такое касательная окружности?
Ключевые части круга, необходимые для этих теорем
- радиус круга — это расстояние от центра до окружности круга. Радиус равен половине диаметра .
- Центр окружности — это точка, которая определяет середину окружности.
- Окружность окружности — это расстояние вокруг края окружности.
Доказательство того, что если две касательные пересекаются, то они имеют одинаковую длину
Чтобы доказать эту теорему, вам не нужно знать какую-либо другую теорему об окружности. Вам просто нужно быть уверенным с углами в треугольнике .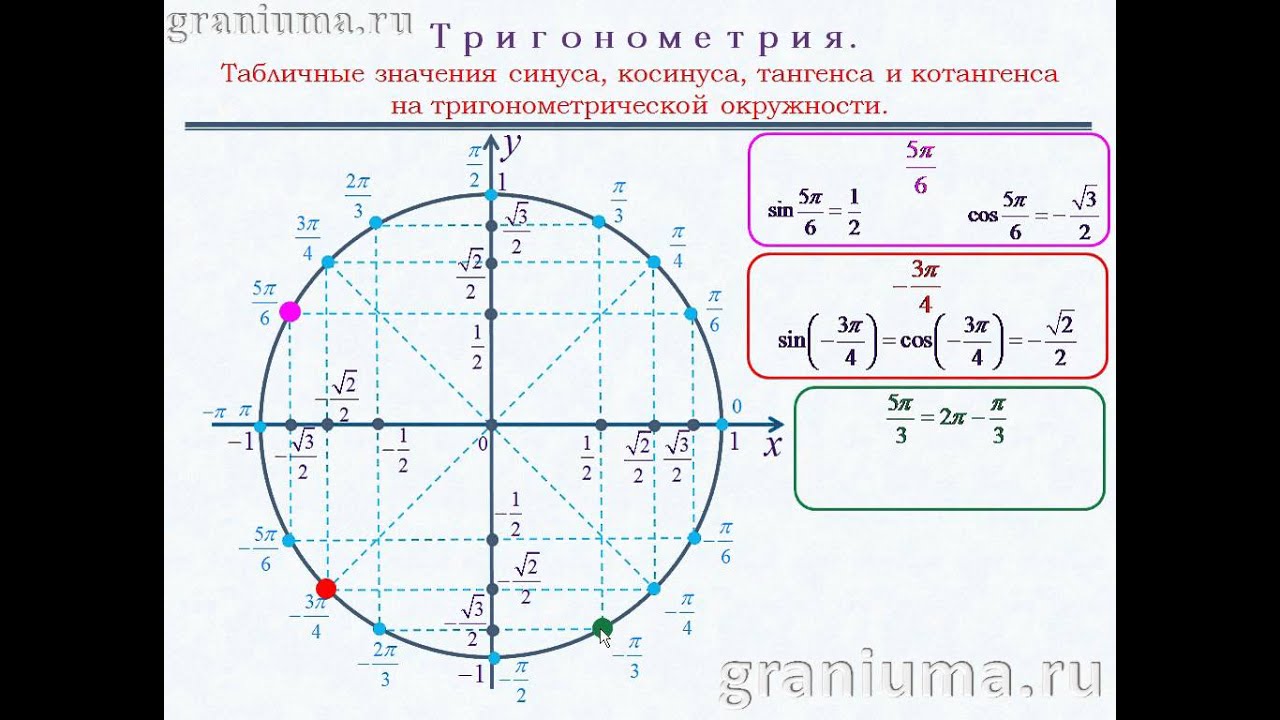 Вы также должны понимать конгруэнтность .
Вы также должны понимать конгруэнтность .
| Шаг | Схема | Описание |
| 1 | Сначала возьмем произвольную точку с меткой A (случайная точка в пространстве) вне круга. | |
| 2 | Точка А может быть соединена с окружностью двумя касательными. Одна линия касается окружности в точке B, другая касательная касается окружности в точке C. Нам нужно доказать, что длина AB=AC. Мы делаем это с помощью треугольников. | |
| 3 | Если мы соединим OA вместе, а затем соединим OB и OC, мы построим два треугольника. Если мы сможем доказать, что эти два треугольника равны, то AC будет равен AB. | |
| 4 | Углы OBA и OCA равны 90 градусов каждый, так как касательные пересекают окружность под углом 90 градусов. Это означает, что у нас есть два прямоугольных треугольника. Это означает, что у нас есть два прямоугольных треугольника. Мы также можем видеть, что поскольку OB и OC являются радиусами окружности, они должны быть одинаковой длины. | |
| 5 | Треугольники AOB и AOC прямые. У них одинаковая длина стороны AO, а другая длина стороны каждого треугольника равна радиусу окружности (OB=OC). Это означает, что два треугольника равны, поэтому AC = AB. Это означает, что касательные, пересекающиеся в одной точке, имеют одинаковую длину. |
Как использовать теоремы о касательной
Чтобы использовать касательную окружности:
- Найдите ключевые части окружности для теоремы.
- Используйте другие данные об углах, чтобы определить оставшиеся углы, образованные касательной.
- Используйте теорему о касательной, чтобы установить другой недостающий угол.
Как использовать теоремы о касательных
Рабочий лист касательной окружности
Получите бесплатный рабочий лист касательной окружности, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист касательной окружности
Получите бесплатный рабочий лист касательной окружности, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Касательная окружности примеры
Пример 1: стандартная диаграмма
Точки A , B и C находятся на окружности с центром O . DE — касательная в точке A. Вычислите величину угла BAD .
- Найдите ключевые части круга для теоремы .
Здесь имеем:
- Угол BCA = 52°
- AC диаметр
- DE тангенс
- Угол BAD = θ s) сделанный с касательной 9{\circ}\]
Пример 2: углы на одном отрезке
A, B, C и D — точки на окружности с центром O . AC и BD пересекаются в точке G. EF — касательная в точке C, параллельная BD.
 Вычислите величину угла BCF .
Вычислите величину угла BCF .Найдите ключевые части круга для теоремы .
Здесь имеем:
- Угол BDC = 48°
- AC диаметр
- EF тангенс 9{\circ}\]
- Угол BAC = 21°
- OC – радиус
- DE – касательная
- Угол BCE = θ
- Угол DCE = 80°
- OB — радиус
- AF — касательная
- Угол OBD = θ
- Угол ABC = 56°
- OA радиус
- DE тангенс
- Угол OAC = θ
- Угол BAD = 64°
- BC и CD радиусы
- EF и GH касательные
- Угол FPG = θ
- Угол между касательной и радиусом
- Теорема об альтернативных отрезках
- Угол в два раза больше или половина противоположного угла
Пример 3: углы в центре
Окружность с центром O имеет три точки на окружности: A, B и C. Касательная DE проходит через точку C. Вычислите величину угла BCE.
Найдите ключевые части круга для теоремы .
Здесь мы имеем:
Используйте другие углы, чтобы определить остальные углы (угол) сделано с касательной 9{\circ}\]
Пример 4: касательная окружности
B, C и D — точки на окружности с центром O . AE и AF касательные к окружности. Вычислите величину угла DBF.
Найдите ключевые части круга для теоремы .
Здесь мы имеем:
Используйте другие углы для определения остальных углов сделано с касательной .

Нам нужно найти способ вычисления угла OBD, так как этот угол, добавленный к θ, равен 90°. COBD — четырехугольник, поэтому, если мы сможем вычислить все углы внутри этого четырехугольника, мы сможем найти угол DBF.
ABOC является воздушным змеем, потому что касательных, пересекающихся в одной точке, равны , а две другие стороны OB и OC являются радиусами и, следовательно, имеют одинаковую длину. Прямая OA делит угол BOC пополам, поэтому можно утверждать, что угол COA = 72°, так как он такой же величины, как и угол AOB. Поскольку обе касательные пересекаются с радиусом в точке 90 градусов углы АСО и АВО также равны 90°.
Угол в центре в два раза больше угла на окружности , и так как угол в центре будет равен 144°(72+72=144), угол BDC равен половине этого угла и поэтому угол BDC = 72° .
Мы также можем вычислить величину угла OCE, потому что угол между касательной и радиусом равен 90° . Это означает угол OCD = 90 — 80 = 10°.

Так как углы вокруг точки в сумме составляют 360°, то можно сказать, что угол отражения BOC равен: 9{\circ}\]
Пример 5: теорема об альтернативных сегментах
Треугольник ABC вписан в окружность с центром O . DE — касательная в точке A. Вычислите величину угла OAC.
Найдите ключевые части круга для теоремы .
Здесь мы имеем:
Используйте другие углы, чтобы определить остальные углы сделано с касательной 9{\circ}\]
Пример 6: комплексная диаграмма
ABCD — наконечник стрелы, вписанный в окружность с центром C . Две касательные EF и GH пересекаются во внешней точке P. Вычислите величину угла FPG.
Найдите ключевые части круга для теоремы .
Здесь имеем:
Используйте другие данные об углах, чтобы определить оставшиеся углы, образованные касательной .

Угол в центре в два раза больше угла на окружности , поэтому угол BCD в два раза больше угла BAD. BCD = 128°.
Используйте теорему о касательной, чтобы установить другой недостающий угол .
Так как угол между касательной и радиусом равен 90° , теперь мы можем вычислить угол BPD, лежащий на прямой с FPG:
9{\circ}\]Распространенные заблуждения
Либо из-за просчета, либо из-за предположения, что угол между касательной и радиусом не равен 90°, потому что «это не похоже», это должно быть доказано.
Существуют случаи, когда теорема об альтернативных отрезках используется для описания угла при касательной или угла в альтернативном отрезке на окружности, но ни один из них не является верным. Возьмем пример 5 выше.
 Предполагается, что угол OAC равен 56°, тогда как угол CAE равен 56°.
Предполагается, что угол OAC равен 56°, тогда как угол CAE равен 56°.Воздушный змей, который образуется при встрече двух касательных, имеет два угла 90° и 90°, потому что они пересекаются с радиусом в 90° . Два других угла предполагаются двойными или половинными, тогда как в сумме они должны составлять 180° (это уникальный случай для вписанного четырехугольника).
Ниже приведен пример 4. Угол COB правильно равен 144°, так как 72×2=144°. Угол CAB ошибочно равен 144÷2 = 72°. Это неверно, потому что сумма углов в четырехугольнике должна составлять 360°, тогда как в форме ABOC всего 9 углов.{\circ} (угол в центре в два раза больше угла на окружности)
Касательная окружности Вопросы GCSE
1. (a) Окружность внизу имеет центр O . Треугольник АВС вписан в треугольник. Касательная DE проходит через точку A. ВС = АС. Вычислите размер угла x .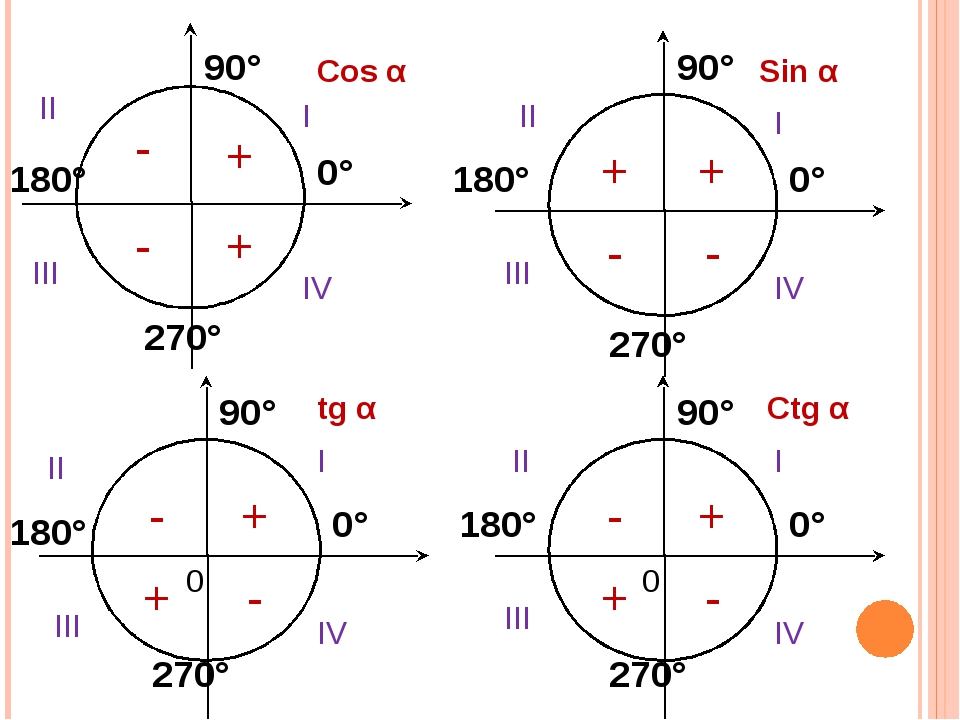 {\circ} 9{\ круг}
{\circ} 9{\ круг}
(1)
Учебный контрольный список
Теперь вы узнали, как:
- Применять и доказывать стандартные теоремы об углах, радиусах, касательных и хордах, а также использовать их для доказательства связанных результатов
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Объяснение урока: Касательные окружности
В этом объяснении мы узнаем, как использовать свойства касательных окружностей для нахождения недостающих углов или длин сторон.
Напомним, что касательной к окружности называется прямая, проходящая ровно через одну точку окружности. Линия не
войти в круг, но он просто проходит через периметр круга, как показано на диаграмме ниже.
Начнем с важной теоремы об угле между касательной и радиусом окружности.
Теорема: угол между касательной и радиусом окружности
Любая касательная к окружности перпендикулярна радиусу в точке касания.
Доказательство этой теоремы основано на том факте, что кратчайшее расстояние между прямой и точкой есть перпендикуляр расстояние между двумя объектами. Другими словами, кратчайший отрезок от точки до данной прямой должен пересекаться перпендикулярно линии.
Если прямая касается окружности, то любая точка прямой находится вне окружности, за исключением точки касания, лежащей на
круг. Мы знаем, что расстояние между центром окружности и внешней точкой окружности должно быть больше, чем
радиус окружности. С другой стороны, расстояние между центром окружности и точкой касания есть радиус
круга. Следовательно, радиус должен быть кратчайшим расстоянием между центром окружности и касательной, так как все
остальные точки касательной лежат вне окружности.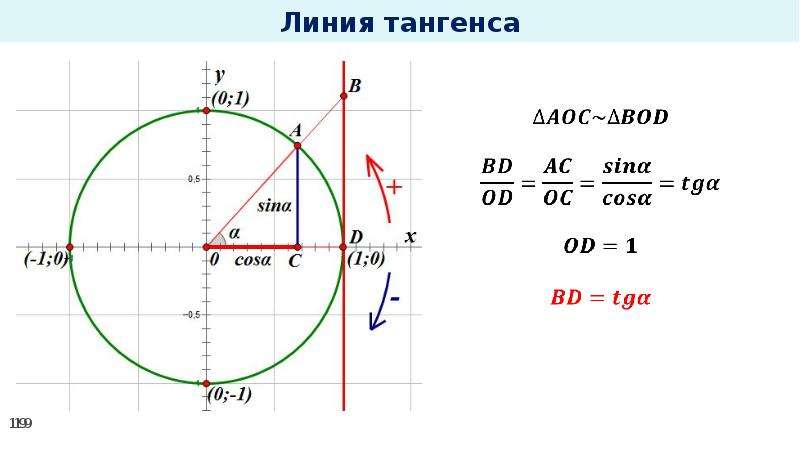 Поскольку радиус — это кратчайший отрезок, соединяющий центр
окружности касательной, она должна быть перпендикулярна касательной. Это доказывает теорему.
Поскольку радиус — это кратчайший отрезок, соединяющий центр
окружности касательной, она должна быть перпендикулярна касательной. Это доказывает теорему.
В нашем первом примере мы будем использовать эту теорему, чтобы найти неизвестную длину на диаграмме, включающей окружность и касательную.
Пример 1. Нахождение длины стороны прямоугольного треугольника по другой Длины двух сторон с использованием свойств касательных
Линия ⃖⃗𝐴𝐶 касается окружности с центром 𝑀 в точке точка 𝐴. Учитывая, что 𝐵𝑀=55см, 𝐴𝐶=96см, что такое 𝐵𝐶?
Ответ
Длина 𝐵𝐶, которую мы ищем, является длиной стороны в треугольнике 𝐴𝐵𝐶, поэтому начнем с определения угол в этом треугольнике. Мы можем определить ∠𝐵𝐴𝐶, вспомнив, что касательная к окружности перпендикулярна до радиуса в точке контакта.
Нам дано, что ⃖⃗𝐴𝐶 касается окружности с центром 𝑀 в точке 𝐴,
и мы можем видеть, что 𝑀𝐴 — это радиус окружности с центром в 𝑀, пересекающей
с касательной в точке касания.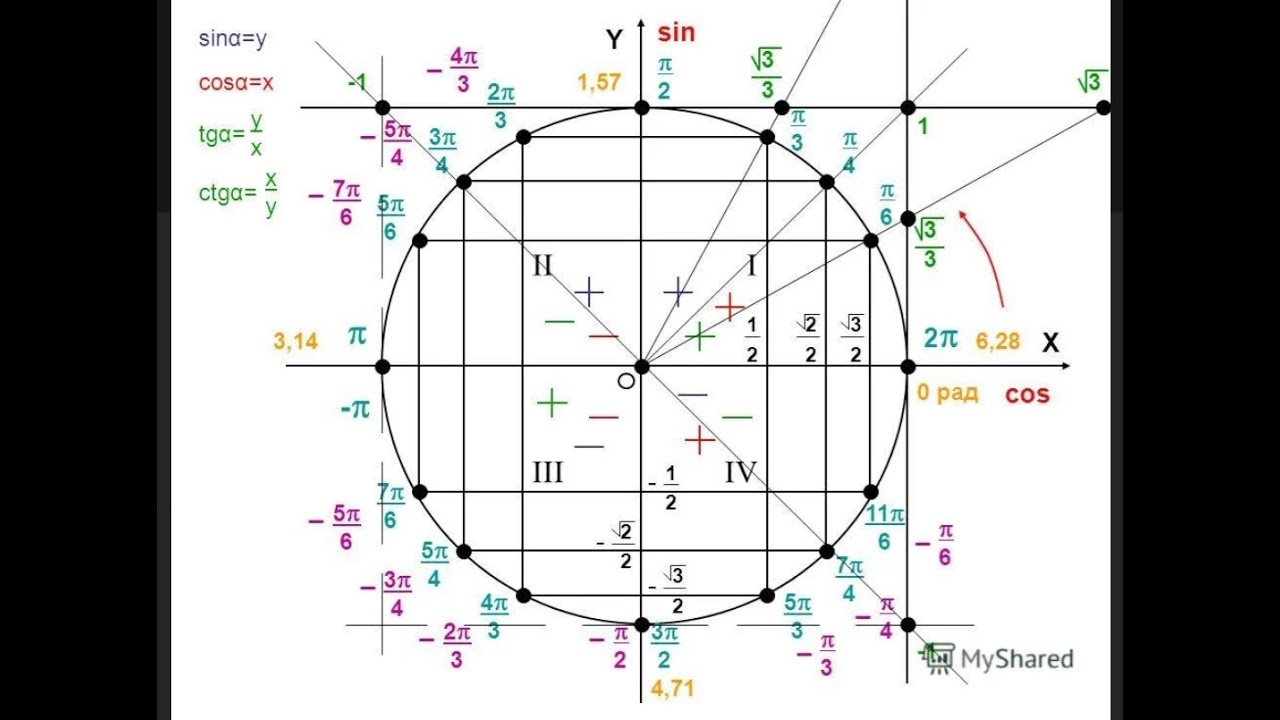 Это говорит нам о том, что угол ∠𝐶𝐴𝑀 прямой;
следовательно, треугольник △𝐶𝐴𝐵 прямоугольный.
Это говорит нам о том, что угол ∠𝐶𝐴𝑀 прямой;
следовательно, треугольник △𝐶𝐴𝐵 прямоугольный.
Длина искомой прямой 𝐵𝐶 есть гипотенуза прямоугольного треугольника. Используя теорему Пифагора, мы можем написать 𝐴𝐶+𝐴𝐵=𝐵𝐶.
Нам известна длина одной стороны этого треугольника, 𝐴𝐶=96см. Оставшаяся сторона 𝐴𝐵 — это диаметр окружности, который в два раза больше радиуса. Поскольку нам дано радиус 𝐵𝑀=55см, диаметр должен быть 55×2=110 см. Это ведет к 𝐴𝐵=110см. Подставляя эти значения в приведенное выше уравнение, у нас есть 96+110=𝐵𝐶𝐵𝐶=√96+110=146.
Следовательно, 𝐵𝐶=146см.
В предыдущем примере нам нужен был только тот факт, что касательная и радиус перпендикулярны, чтобы найти недостающую длину. В более сложных задачах геометрии нам может понадобиться использовать более одного геометрического свойства или теоремы, чтобы найти недостающее.
длины или углы. Наш следующий пример дополнительно потребует напоминания о свойстве серединного перпендикуляра к
аккорд.
Пример 2. Вычисление периметра составной фигуры с использованием свойств хорд и свойства касательных
На рисунке ниже 𝑀 — центр круга, 𝑀𝐵=15 см, 𝐴𝐵=20см, 𝑀𝐶=9см, и ⃖⃗𝐴𝐵 является касательной. Найдите периметр фигуры 𝐴𝐵𝐶𝑀.
Ответ
Напомним, что периметр четырехугольника равен сумме длин его сторон. Начнем с добавления заданных длин к диаграмме, а также выделить периметр, который мы хотим вычислить.
Мы видим, что две длины, 𝑀𝐶 и 𝐴𝐵, включенные в периметр, уже предоставлены. Следовательно, мы нужно получить длины 𝑀𝐴 и 𝐵𝐶.
Начнем с длины 𝐵𝐶. Из диаграммы видно, что 𝐶 — это середина
аккорда 𝐵𝐷. Напомним, что биссектриса хорды проходит через центр окружности. Так как 𝑀𝐶 делит пополам хорду 𝐵𝐷 и проходит через центр 𝑀
окружности, она должна быть серединным перпендикуляром к хорде. Это говорит нам о том, что ∠𝑀𝐶𝐵 — прямой угол;
следовательно, треугольник △𝑀𝐶𝐵 прямоугольный. Применяя к этому теорему Пифагора
треугольник, мы можем написать
𝐵𝐶+𝑀𝐶=𝑀𝐵.
Применяя к этому теорему Пифагора
треугольник, мы можем написать
𝐵𝐶+𝑀𝐶=𝑀𝐵.
Замена предоставленной длины 𝑀𝐶=9см и 𝑀𝐵=15см в это уравнение и решая выходы 𝐵𝐶+9=15𝐵𝐶=15−9=144𝐵𝐶=√144=12.
Это дает нам 𝐵𝐶=12см.
Далее найдем длину 𝑀𝐴. Напомним, что касательная к окружности перпендикулярна радиусу в точке контакт. На данной диаграмме ⃖⃗𝐴𝐵 является касательной к окружности, пересекающейся с радиусом 𝑀𝐵, поэтому угол ∠𝑀𝐵𝐴 должен быть прямым. Тогда мы можем применить пифагорейскую теорема к прямоугольному треугольнику 𝑀𝐵𝐴 написать 𝑀𝐵+𝐴𝐵=𝑀𝐴.
Нам дано 𝐴𝐵=20см и 𝑀𝐵=15 см, поэтому 15+20=𝑀𝐴𝑀𝐴=√15+20=25.
Это дает нам 𝑀𝐴=25см. Тогда по периметру фигуры 𝐴𝐵𝐶𝑀 𝑀𝐴+𝐴𝐵+𝐵𝐶+𝑀𝐶=25+20+12+9=66.cm
В предыдущих примерах мы применяли теорему о том, что касательная к окружности перпендикулярна радиусу в точке
контакта, чтобы найти недостающие длины. Другое приложение этой теоремы касается соотношения между длинами
двух касательных из одной точки.
Другое приложение этой теоремы касается соотношения между длинами
двух касательных из одной точки.
Теорема: длины двух касательных из внешней точки
Для данной внешней точки к окружности длины двух касательных из этой точки к окружности равны.
Чтобы доказать эту теорему, рассмотрим диаграмму, где 𝑀 — центр окружности, 𝐴 — внешняя точка, а 𝐴𝐵 и 𝐴𝐶 — две касательные к окружности с точками контакта 𝐵 и 𝐶.
Мы знаем, что касательные пересекаются ортогонально с радиусами, что говорит нам о ∠𝐴𝐶𝑀 и ∠𝐴𝐵𝑀 прямые углы, как показано на диаграмме. Длины 𝐴𝐶 и 𝐴𝐵 можно получить, используя теорему Пифагора о двух прямоугольных треугольниках △𝐴𝐶𝑀 и △𝐴𝐵𝑀: 𝐴𝐶+𝑀𝐶=𝐴𝑀,𝐴𝐵+𝑀𝐵=𝐴𝑀.
Поскольку правые части обоих уравнений одинаковы, мы можем приравнять левые части обоих уравнений, чтобы получить 𝐴𝐶+𝑀𝐶=𝐴𝐵+𝑀𝐵.
Мы также знаем, что стороны 𝑀𝐶 и 𝑀𝐵 имеют одинаковую длину,
так как они являются радиусами одной окружности. Следовательно, члены 𝑀𝐶 и 𝑀𝐵 в приведенном выше уравнении
нейтрализуют друг друга, что приводит к
𝐴𝐶=𝐴𝐵.
Следовательно, члены 𝑀𝐶 и 𝑀𝐵 в приведенном выше уравнении
нейтрализуют друг друга, что приводит к
𝐴𝐶=𝐴𝐵.
Это дает нам 𝐴𝐶=𝐴𝐵, что означает, что длины двух касательных 𝐴𝐶 и 𝐴𝐵 равны, как утверждается в теореме.
Рассмотрим пример, в котором мы используем эту теорему для нахождения недостающих длин в диаграмме, включающей две касательные к окружность из внешней точки.
Пример 3. Нахождение длин двух отрезков с использованием свойств касательных окружностей
Определить 𝐴𝑀 и 𝐴𝐵, округлив до сотых.
Ответ
На данной диаграмме 𝐴𝐶 и 𝐴𝐵 две касательные из внешней точки 𝐴 в окружность с центром в 𝑀. Напомним, что длины двух касательных из внешней точки к окружности равны. Следовательно, длины этих касательные должны быть равны. Поскольку нам дано 𝐴𝐶=10,73 см, мы также должны иметь 𝐴𝐵=10,73см.
Далее рассмотрим 𝐴𝑀. Напомним, что касательная к окружности перпендикулярна радиусу в точке
контакт. На диаграмме 𝐴𝐵 является касательной к окружности с центром в 𝑀,
а 𝑀𝐵 — радиус окружности. Следовательно,
∠𝐴𝐵𝑀 должен быть прямым углом. Это говорит нам о том, что △𝐴𝐵𝑀 — прямоугольный треугольник,
где 𝐴𝑀 — гипотенуза этого прямоугольного треугольника. Используя теорему Пифагора, мы можем написать
𝐴𝐵+𝐵𝑀=𝐴𝑀.
На диаграмме 𝐴𝐵 является касательной к окружности с центром в 𝑀,
а 𝑀𝐵 — радиус окружности. Следовательно,
∠𝐴𝐵𝑀 должен быть прямым углом. Это говорит нам о том, что △𝐴𝐵𝑀 — прямоугольный треугольник,
где 𝐴𝑀 — гипотенуза этого прямоугольного треугольника. Используя теорему Пифагора, мы можем написать
𝐴𝐵+𝐵𝑀=𝐴𝑀.
Замена 𝐴𝐵=10,73см и 𝐵𝑀=6 см в это уравнение дает 10,73+6=𝐴𝑀𝐴𝑀=√10,73+6=12,2936….
Округляя до сотых, 𝐴𝑀 и 𝐴𝐵 12,29 см и 10,73 см соответственно.
В следующем примере мы идентифицируем неизвестные константы на диаграмме, включающей две окружности, имеющие общие касательные.
Пример 4. Определение длины касательной к окружности путем решения двух линейных уравнений
Две окружности с центрами в точках 𝑀 и 𝑁 касаются друг друга снаружи. ⃖⃗𝐹𝐴 является общей касательной к ним в точке 𝐴 и
𝐵 соответственно, а ⃖⃗𝐹𝐶 является общей касательной к ним в точке 𝐶
и 𝐷 соответственно.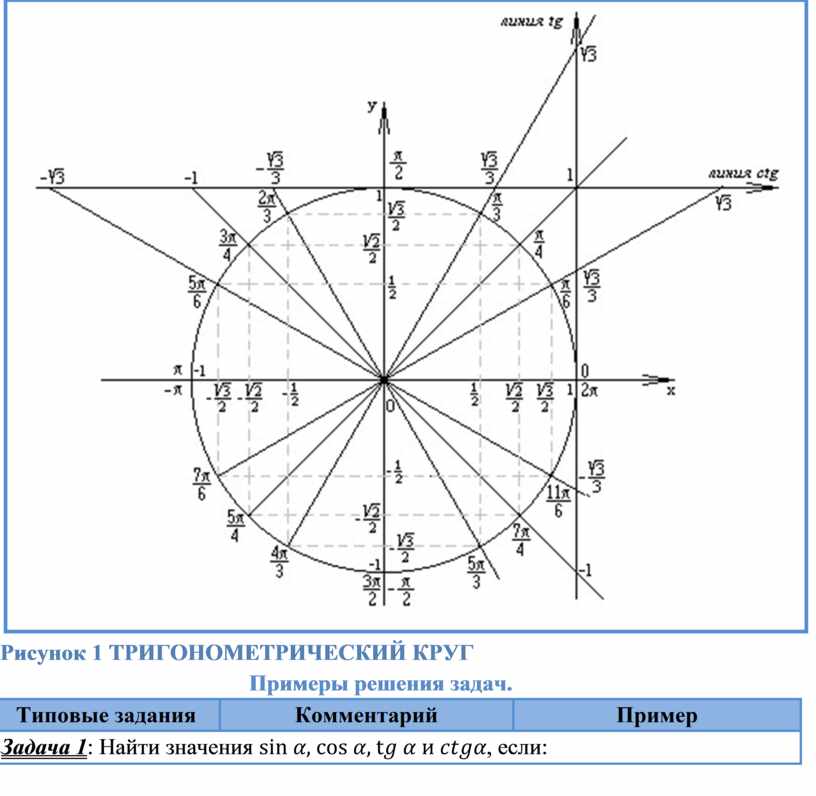 Учитывая, что 𝐴𝐵=11,01 см
и 𝐶𝐷=(𝑦−11,01) см,
найти 𝑥 и 𝑦.
Учитывая, что 𝐴𝐵=11,01 см
и 𝐶𝐷=(𝑦−11,01) см,
найти 𝑥 и 𝑦.
Ответ
Напомним, что длины двух касательных из внешней точки к окружности равны. Для окружности с центром в 𝑁, строки ⃖⃗𝐹𝐴 и ⃖⃗𝐹𝐶 касаются этой окружности в точках 𝐵 и 𝐷 соответственно. Следовательно, мы должны иметь 𝐹𝐵=𝐹𝐷, что означает 𝐹𝐵=12,31 см. Мы можем написать 𝑥−2=12,31, 𝑥=14,31, что приводит к
Далее рассмотрим круг с центром в 𝑀. Строки ⃖⃗𝐹𝐴 и ⃖⃗𝐹𝐶 касаются этой окружности в точках 𝐴 и 𝐶 соответственно. Следовательно, мы должны иметь 𝐹𝐴=𝐹𝐶. Нам дано 𝐴𝐵=11,01 см, и мы знаем, что 𝐹𝐵=12,31 см, значит 𝐹𝐴=𝐹𝐵+𝐴𝐵=12,31+11,01=23,32 см
Поскольку 𝐹𝐴=𝐹𝐶, мы знаем, что 𝐹𝐶=23,32 см. Поскольку 𝐹𝐶=𝐹𝐷+𝐶𝐷, мы можем заменить известные длины, чтобы написать 23,32=12,31+𝐶𝐷.
Это приводит к 𝐶𝐷=23,32−12,31=11,01.см
Также известно, что 𝐶𝐷=(𝑦−11,01)см; мы можем написать 𝑦−11,01=11,01, 𝑦=22,02, что приводит к
Таким образом, имеем 𝑥=14,31, 𝑦=22,02.
В предыдущих двух примерах мы применили тот факт, что две касательные из одной и той же точки к окружности имеют одинаковую длину, чтобы найти недостающие длины. Это свойство двух касательных приводит к ряду интересных геометрических теорем. В частности, мы рассмотрим две теоремы, которые следуют из этого свойства.
Теорема: Биссектриса угла, образованного двумя касательными, и центрального угла, образованного двумя радиусами Пересечение с касательными
Линия, соединяющая внешнюю точку с окружностью и центром окружности, делит пополам угол, образованный две касательные из точки к окружности и центральный угол, образованный двумя радиусами, пересекающимися с касательные.
Для доказательства этой теоремы рассмотрим следующую схему.
На диаграмме выше линии 𝐴𝐵 и 𝐴𝐶 являются двумя касательными
от внешней точки 𝐴 до окружности с центром в 𝑀. Мы знаем, что касательная пересекается с радиусом
перпендикулярно в точке касания, поэтому ∠𝐴𝐵𝑀 и ∠𝐴𝐶𝑀
прямые углы, как показано на схеме. Мы также знаем, что длины двух касательных, выходящих из одной
внешние точки равны, что говорит нам 𝐴𝐵=𝐴𝐶, как указано. Наконец, мы знаем, что радиусы одной и той же окружности имеют
равные длины; следовательно, 𝐵𝑀=𝐶𝑀, как указано.
Мы также знаем, что длины двух касательных, выходящих из одной
внешние точки равны, что говорит нам 𝐴𝐵=𝐴𝐶, как указано. Наконец, мы знаем, что радиусы одной и той же окружности имеют
равные длины; следовательно, 𝐵𝑀=𝐶𝑀, как указано.
Мы можем заключить, что △𝐴𝐵𝑀 и △𝐴𝐶𝑀 конгруэнтны, используя Критерий равенства сторона-угол-сторона. Это дает нам равенство соответствующих углов 𝑚∠𝐵𝑀𝐴=𝑚∠𝐶𝑀𝐴, значит, 𝑀𝐴 является биссектрисой ∠𝐵𝑀𝐶. Точно так же конгруэнтность этих треугольников также говорит нам 𝑚∠𝐵𝐴𝑀=𝑚∠𝐶𝐴𝑀, что говорит нам о том, что 𝑀𝐴 — это биссектриса ∠𝐵𝐴𝐶. Это доказывает приведенную выше теорему.
В следующем примере мы применим приведенную выше теорему вместе с двумя ранее введенными теоремами. найти меру угла.
Пример 5. Нахождение меры угла по свойствам касательных к окружности
Учитывая, что 𝑚∠𝑀𝐶𝐵=49∘, где 𝐴𝐵 и 𝐴𝐶 касаются окружности в 𝐵 и 𝐶 найдите 𝑚∠𝐵𝐴𝑀.
Ответ
Нам дано, что 𝐴𝐵 и 𝐴𝐶 касаются окружности
в 𝐵 и 𝐶. Напомним, что две касательные, выходящие из одной точки к окружности, имеют одинаковую длину,
что дает нам 𝐴𝐵=𝐴𝐶. Добавим на диаграмму указание на этот факт, а также на приведенный угол.
Напомним, что две касательные, выходящие из одной точки к окружности, имеют одинаковую длину,
что дает нам 𝐴𝐵=𝐴𝐶. Добавим на диаграмму указание на этот факт, а также на приведенный угол.
Напомним также, что касательная к окружности перпендикулярна радиусу в точке касания. В частности, это означает, что угол ∠𝐴𝐶𝑀 прямой. Мы можем вычислить 𝑚∠𝐴𝐶𝐵=𝑚∠𝐴𝐶𝑀−𝑚∠𝑀𝐶𝐵=90−49=41.∘∘∘
На диаграмме выше видно, что △𝐴𝐵𝐶 — равнобедренный треугольник потому что 𝐴𝐵=𝐴𝐶. Это значит, что 𝑚∠𝐴𝐵𝐶=𝑚∠𝐴𝐶𝐵=41.∘
Поскольку сумма внутренних углов треугольника составляет 180∘, мы можем написать 𝑚∠𝐵𝐴𝐶+𝑚∠𝐴𝐵𝐶+𝑚∠𝐴𝐶𝐵=180.∘
Подставляя два полученных угла, 𝑚∠𝐵𝐴𝐶+41+41=180.∘∘∘
Это приводит к 𝑚∠𝐵𝐴𝐶=98∘.
Наконец, чтобы получить 𝑚∠𝐵𝐴𝑀, нужно вспомнить, что линия, соединяющая внешнюю точку и центр
окружности является биссектрисой угла между двумя касательными, исходящими из точки. Это означает
𝑚∠𝐵𝐴𝑀=12𝑚∠𝐵𝐴𝐶=12×98=49.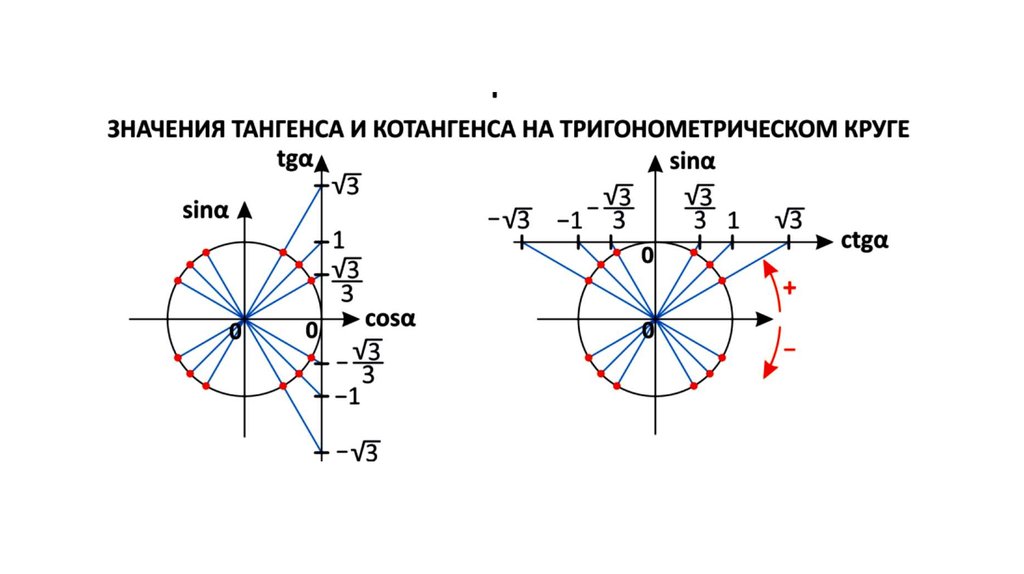 ∘∘
∘∘
Следовательно, 𝑚∠𝐵𝐴𝑀=49∘.
В предыдущем примере мы применили теорему, утверждающую, что линия, соединяющая центр окружности с внешней точка делит пополам угол, образованный двумя касательными из внешней точки, и центральный угол, образованный два радиуса до точек касания. Другое применение этой теоремы может привести к следующей теореме о перпендикулярных биссектрисах.
Теорема: Биссектриса перпендикуляра хорды, соединяющей точки касания двух исходящих касательных из внешней точки
Для данной внешней точки к окружности и двух касательных от этой точки к окружности линия, соединяющая внешнюю точка и центр окружности является серединным перпендикуляром хорды между точками контакта двух касательных.
Рассмотрим следующую диаграмму, где 𝑀 — центр круга, а ⃖⃗𝐴𝐵 и ⃖⃗𝐴𝐶 касательные в точках касания 𝐵 и 𝐶 соответственно.
Из предыдущей теоремы мы знаем, что 𝑀𝐴 — биссектриса угла
∠𝐵𝑀𝐶, что говорит нам о том, что 𝑚∠𝐵𝑀𝐷=𝑚∠𝐶𝑀𝐷
как указано на схеме.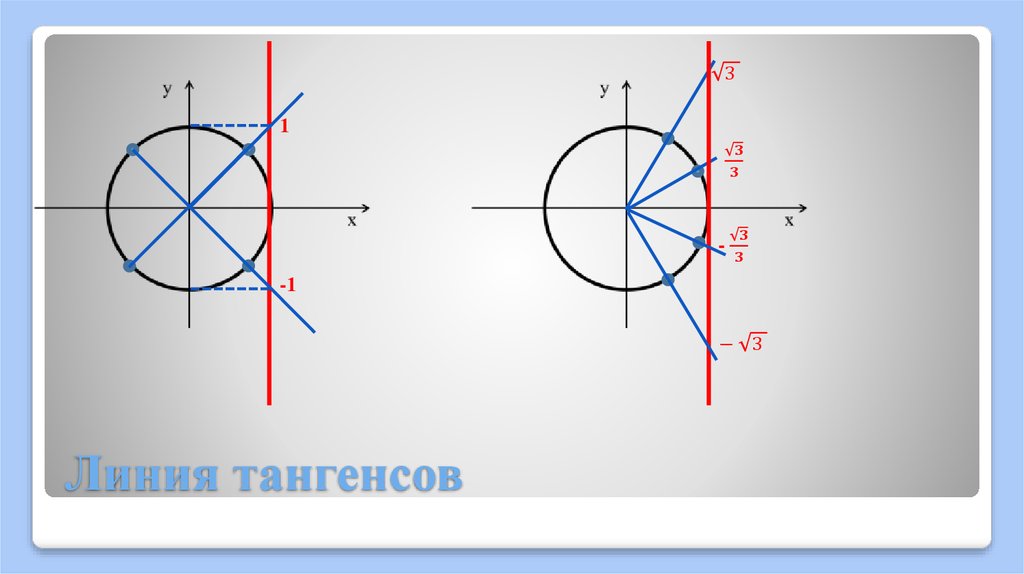 Мы также знаем, что 𝑀𝐵=𝑀𝐶, так как это радиусы одной и той же окружности. Кроме того,
сторона 𝑀𝐷 является общей для двух треугольников 𝑀𝐷𝐵 и 𝑀𝐷𝐶. По критерию равенства сторон треугольники 𝑀𝐷𝐵 и 𝑀𝐷𝐶 равны.
Мы также знаем, что 𝑀𝐵=𝑀𝐶, так как это радиусы одной и той же окружности. Кроме того,
сторона 𝑀𝐷 является общей для двух треугольников 𝑀𝐷𝐵 и 𝑀𝐷𝐶. По критерию равенства сторон треугольники 𝑀𝐷𝐵 и 𝑀𝐷𝐶 равны.
В частности, это означает, что 𝐵𝐷=𝐶𝐷, что означает, что 𝐷 является серединой аккорд 𝐵𝐶. Кроме того, поскольку 𝑚∠𝐵𝐷𝑀=𝑚∠𝐶𝐷𝑀 и эти углы в сумме составляют 180∘, оба эти угла должны быть прямыми. Это означает, что 𝑀𝐴 делит хорду 𝐵𝐶 пополам перпендикулярно. Это доказывает теорему.
Обратимся теперь к применению касательных к окружности в задачах с многоугольниками.
Определение: вписанные окружности и многоугольники
Окружность вписана в многоугольник, если каждая сторона многоугольника является касательной к окружности.
Многоугольник вписан в окружность, если многоугольник лежит внутри окружности и все вершины многоугольника лежат на окружности.
В следующем примере мы найдем площадь треугольника, вписанного в круг с другим меньшим кругом, вписанным
в треугольнике.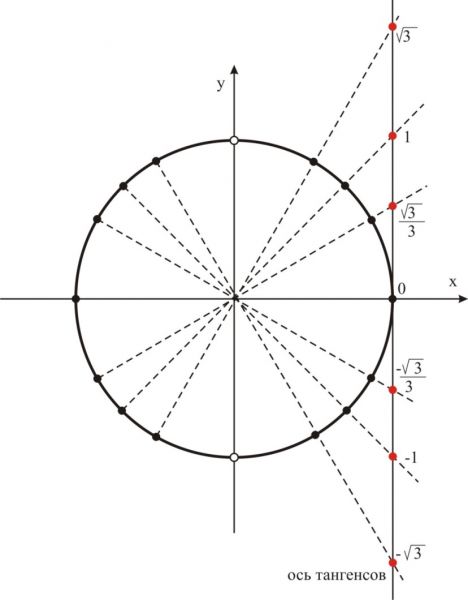
Пример 6. Нахождение площади треугольника по радиусам его описанной окружности и вписанной окружности
Показанные концентрические окружности имеют радиусы 16 см и 8 см. Найдите площадь треугольника с округлением до двух знаков после запятой.
Ответ
На данной диаграмме линии 𝐵𝐶, 𝐴𝐶, и 𝐴𝐵 касаются меньшего круга. Напомним, что линия, соединяющая внешнюю точку а центр окружности — биссектриса угла между двумя касательными, исходящими из точки. Следовательно, линии 𝑀𝐴, 𝑀𝐵 и 𝑀𝐶 являются биссектрисами углов ∠𝐶𝐴𝐵, ∠𝐴𝐵𝐶 и ∠𝐵𝐶𝐴 соответственно. Добавляем эти линии на схему.
Напомним также, что касательная к окружности перпендикулярна радиусу в точке касания. Таким образом, радиусы 𝑀𝑋, 𝑀𝑌 и 𝑀𝑍 меньшего круга пересекаются перпендикулярно касательным 𝐴𝐵, 𝐵𝐶 и 𝐶𝐴 соответственно. Теперь добавим эти линии на диаграмму.
На диаграмме выше наш треугольник 𝐴𝐵𝐶 разделен на шесть меньших прямоугольных треугольников.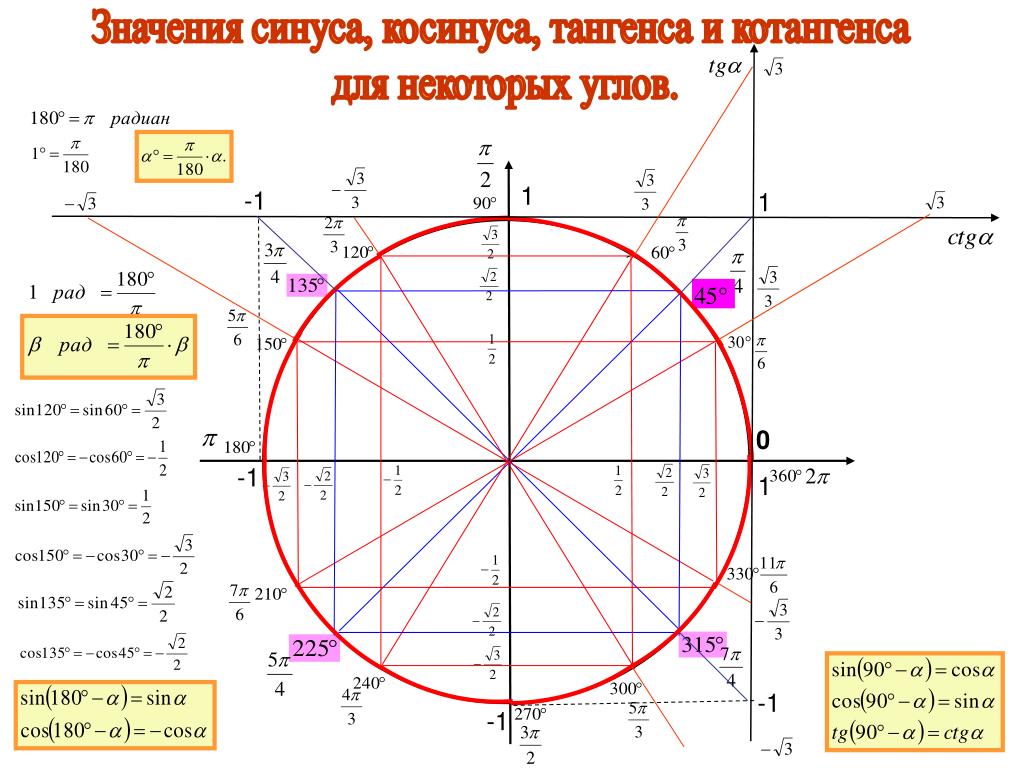 Мы утверждаем, что все шесть правильных
треугольники равны.
Мы утверждаем, что все шесть правильных
треугольники равны.
Чтобы доказать сравнение, сначала рассмотрим углы. Поскольку мы знаем, что 𝑀𝐴, 𝑀𝐵 и 𝑀𝐶 — биссектрисы угла ∠𝐶𝐴𝐵, ∠𝐴𝐵𝐶 и ∠𝐵𝐶𝐴 мы знаем, что пара углов при каждой вершине 𝐴, 𝐵 и 𝐶 имеют одинаковую меру. Дополнительно отметим что 𝑀𝐴, 𝑀𝐵 и 𝑀𝐶 – радиусы большей окружности; следовательно, они имеют одинаковую длину. Это говорит нам о том, что треугольники 𝑀𝐴𝐶, 𝑀𝐴𝐵 и 𝑀𝐵𝐶 равнобедренные, что означает, что пара углов, удаленных от центральной вершины 𝑀 в каждом из этих треугольников равны. Вместе это говорит нам о том, что все шесть меньших углов при вершинах 𝐴, 𝐵 и 𝐶 имеют одинаковую меру. Тогда каждый из шести меньших прямоугольных треугольников делит этот угол.
Поскольку сумма внутренних углов треугольника должна составлять 180∘, третьи углы
(угол при центральной вершине 𝑀) шести прямоугольных треугольников также должен иметь одинаковую меру. Наконец, повторное использование факта
что 𝑀𝐴, 𝑀𝐵 и 𝑀𝐶 равны
длин, все шесть меньших прямоугольных треугольников удовлетворяют критерию конгруэнтности угол-сторона-угол.
Наконец, повторное использование факта
что 𝑀𝐴, 𝑀𝐵 и 𝑀𝐶 равны
длин, все шесть меньших прямоугольных треугольников удовлетворяют критерию конгруэнтности угол-сторона-угол.
В частности, это означает, что площадь треугольника 𝐴𝐵𝐶 в шесть раз больше площади треугольника 𝐴𝑀𝑋, например. Найдем площадь прямоугольного треугольника 𝐴𝑀𝑋. Поскольку 𝑀𝑋 — это радиус меньшего круга, мы знаем, что 𝑀𝑋=8см. Мы должны найдите 𝐴𝑋, чтобы найти площадь этого треугольника. Применяя к этому треугольнику теорему Пифагора, мы можем написать 𝐴𝑋+𝑀𝑋=𝐴𝑀.
Мы знаем, что 𝑀𝑋=8см и 𝐴𝑀 радиус большего круга; следовательно, 𝐴𝑀=16см. Подставляя эти значения, 𝐴𝑋+8=16𝐴𝑋=16−8=192𝐴𝑋=√192.см
Вспоминая, что площадь треугольника равна половине произведения длины основания на высоту, площадь треугольника 𝐴𝑀𝑋 это 12×𝐴𝑋×𝑀𝑋=12×√192×8=4√192.см
Умножив эту площадь на 6, получим площадь треугольника 𝐴𝐵𝐶, округленную до сотых; то есть, 6×4√192=24√192=332,55 см
Давайте закончим повторением нескольких важных понятий из этого объяснения.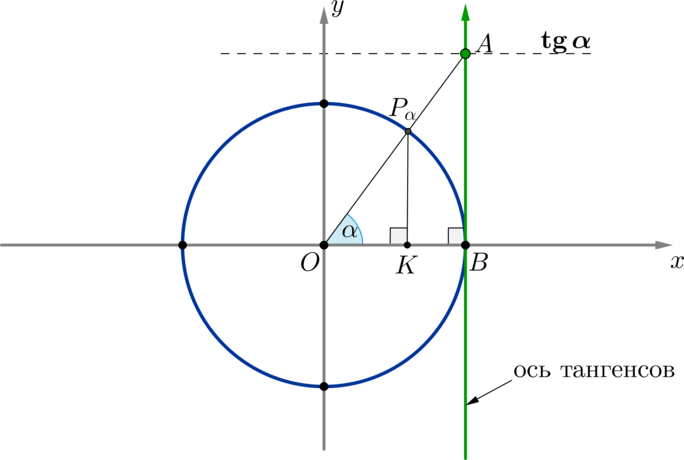

 ЧИСЛА И ВЫРАЖЕНИЯ
ЧИСЛА И ВЫРАЖЕНИЯ
 Вычислите величину угла BCF .
Вычислите величину угла BCF .

 Предполагается, что угол OAC равен 56°, тогда как угол CAE равен 56°.
Предполагается, что угол OAC равен 56°, тогда как угол CAE равен 56°.