Иррациональное число это что: Иррациональные числа — урок. Алгебра, 8 класс.

Содержание

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с.

Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной.

(Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.)

АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
2. Простые и составные числа. Признаки делимости.
3. Наибольший общий делитель и наименьшее общее кратное.
4. Целые числа. Рациональные числа.
5. Десятичные дроби. Представление рациональных чисел десятичными дробями.
6. Иррациональные числа. Действительные числа.
7. Действия с приближенными числами.
8. Числовая ось. Координаты точки на плоскости.
§ 2. Степени и корни
9. Степени с натуральными показателями.
10. Степени с целыми показателями.
11. Корни.
12. Степени с рациональными показателями. Степени с действительными показателями.
13. Алгоритм извлечения квадратного корня.
§ 3. Комплексные числа
14. Основные понятия и определения.
15. Рациональные действия с комплексными числами.
16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
17. Действия с комплексными числами, заданными в тригонометрической форме.

Формула Муавра.
18. Извлечение корня из комплексного числа.
Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
19. Алгебраические выражения. Одночлены и многочлены.
20. Формулы сокращенного умножения.
21. Бином Ньютона.
22. Разложение многочлена на множители.
23. Дробные алгебраические выражения.
§ 2. Иррациональные алгебраические выражения
24. Радикалы из алгебраических выражений.
25. Освобождение от иррациональности в знаменателе дроби.
Глава III. ЛОГАРИФМЫ
26. Определение и свойства логарифмов.
27. Логарифмы по различным основаниям. Модуль перехода.
§ 2. Десятичные логарифмы
28. Характеристика и мантисса десятичного логарифма.
29. Применение десятичных логарифмов к вычислениям.
Глава IV. ФУНКЦИИ И ГРАФИКИ
30. Величина. Числовые множества.
31. Определение функции.
32. График функции. Способы задания функций.
33. Элементарное исследование поведения функции.
34. Сложная функция.
35. Обратная функция.
36.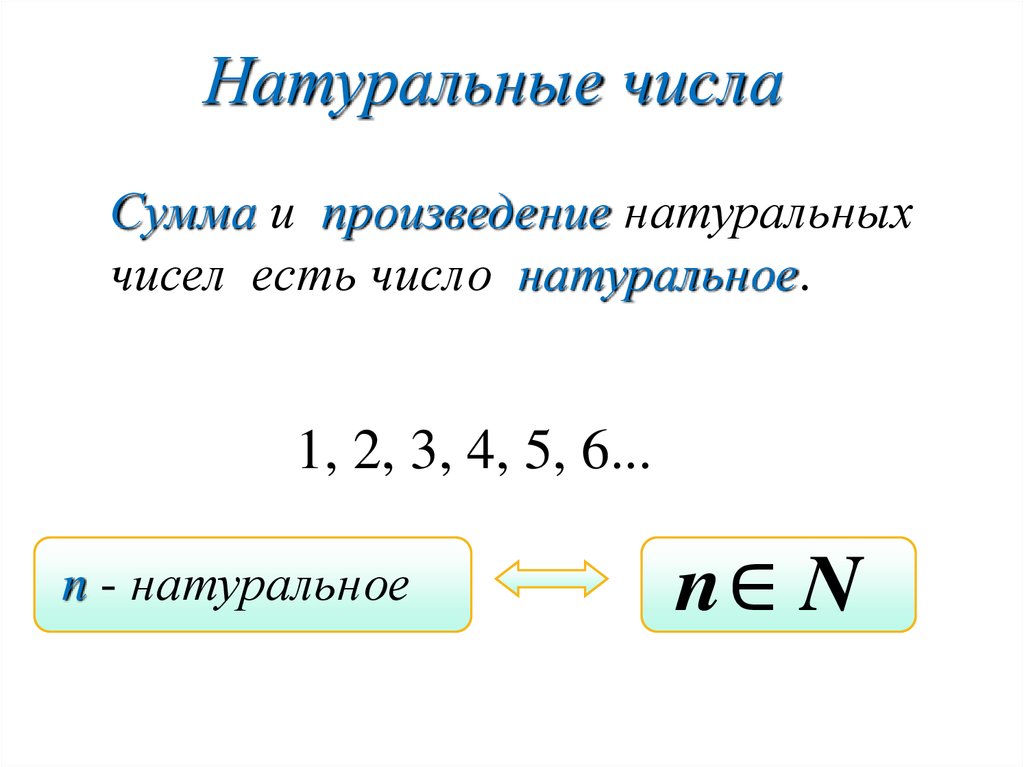

n.
41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени.
42. Показательная функция.
43. Логарифмическая функция.
§ 3. Преобразование графиков
44. Параллельный сдвиг графика.
45. График квадратного трех члена.
46. График дробно-линейной функции.
47. Преобразование симметрии. Сжатие и растяжение графика.
48. Построение графиков функций.
49. Сложение графиков.
§ 4. Некоторые сведения о рациональных функциях
50. Целые и дробные рациональные функции. Деление многочленов.
51. Схема Горнера. Теорема Безу.
52. Нули многочлена. Разложение многочлена на множители.
Глава V. УРАВНЕНИЯ
53. Уравнение. Корни уравнения.
54. Равносильные уравнения.
55. Системы уравнений.

56. Графическое решение уравнений.
§. 2. Алгебраические уравнения с одной неизвестной
57. Число и кратность корней.
58. Уравнения первой степени (линейные уравнения).
59. Уравнения второй степени (квадратные уравнения).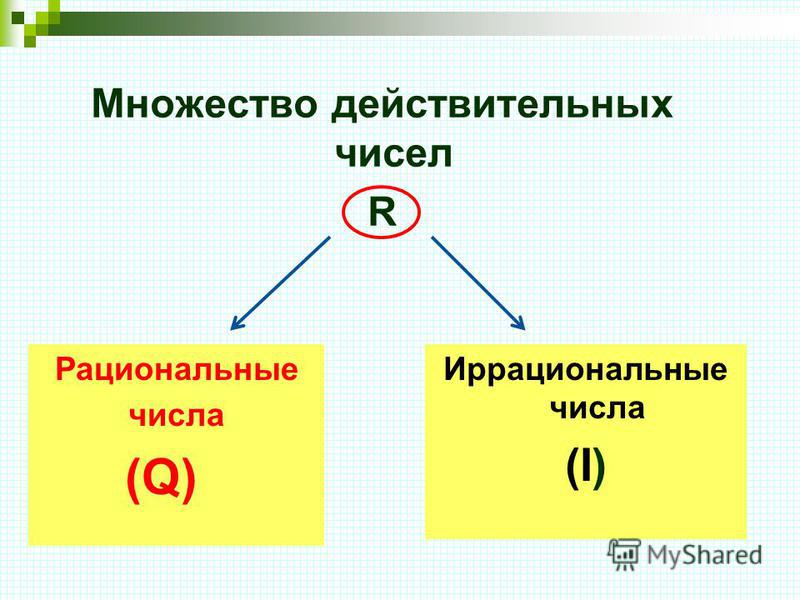

60. Формулы Виета. Разложение квадратного трехчлена на множители.
61. Исследование квадратного уравнения.
62. Уравнения высших степеней. Целые корни.
63. Двучленные уравнения.
64. Уравнения, сводящиеся к квадратным.
65. Возвратные уравнения.
§ 3. Системы алгебраических уравнений
66. Линейные системы.
67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными.
68. Системы, состоящие из уравнения второй степени и линейного уравнения.
69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней.
§ 4. Иррациональные, показательные и логарифмические уравнения
70. Иррациональные уравнения.
71. Показательные уравнения.
72. Логарифмические уравнения.
73. Разные уравнения. Системы уравнений.
Глава VI. НЕРАВЕНСТВА
74. Свойства неравенств. Действия над неравенствами.
75. Алгебраические неравенства.
§ 2. Решение неравенств
76. Множество решений неравенства.

Равносильные неравенства.
77. Графическое решение неравенств.
79. Квадратные неравенства.
80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х.
81. Иррациональные, показательные и логарифмические неравенства.
82. Неравенства с двумя неизвестными.
Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ
83. Числовая последовательность.
84. Предел числовой последовательности.
85. Бесконечно малые. Правила предельного перехода.
§ 2. Арифметическая прогрессия
86. Арифметическая прогрессия. Формула общего члена.

87. Свойства арифметической прогрессии.
88. Формула для суммы n членов арифметической прогрессии.
§ 3. Геометрическая прогрессия
89. Геометрическая прогрессия. Формула общего члена.
90. Свойства геометрической прогрессии.
91. Формулы для суммы n членов геометрической прогрессии.
92. Бесконечно убывающая геометрическая прогрессия.
Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
93. Вектор, проекция вектора.

94. Положительные углы и дуги, меньшие 360°.
95. Углы и дуги, большие 360°.
96. Отрицательные углы. Сложение и вычитание углов.
§ 2. Тригонометрические функции произвольного угла
97. Определение основных тригонометрических функций.
98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi.
§ 3. Соотношения между тригонометрическими функциями одного и того же угла
99. Основные тригонометрические тождества.

100. Вычисление значений тригонометрических функций по значению одной из них.
101. Значения тригонометрических функций некоторых углов.
§ 4. Четность, нечетность и периодичность тригонометрических функций
102. Четность и нечетность.
103. Понятие периодической функции.
104. Периодичность тригонометрических функций.
§ 5. Формулы приведения
105. Зависимость между тригонометрическими функциями дополнительных углов.
106. Формулы приведения.
Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ
§ 1.

Тригонометрические функции числового аргумента
108. Области определения и области изменения значений тригонометрических функций.
109. Некоторые неравенства и их следствия.
§ 2. Графики тригонометрических функций
110. Первоначальные сведения о таблицах тригонометрических функций.

111. Основные графики.
112. Примеры построения графиков некоторых других тригонометрических функций.
113. Дальнейшие примеры построения графиков функций.
Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
114. Расстояние между двумя точками на плоскости.
115. Косинус суммы и разности двух аргументов.
116. Синус суммы и разности двух аргументов.
117. Тангенс суммы и разности двух аргументов.
118. О формулах сложения для нескольких аргументов.
§ 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a
119. Тригонометрические функции двойного аргумента.
120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.

121. Тригонометрические функции половинного аргумента.
122. Выражение основных тригонометрических функций аргумента а через tg(a/2).
§ 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb
§ 4. Преобразование в произведение сумм вида
§ 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
127. Преобразование в произведение выражения a•sina + b•cosa.
128. Преобразование в произведение выражений a•sina+b и a•cosa+b
129. Преобразование в произведение выражения a•tga+b.
Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ
130. Функция у = arcsin x (арксинус).
131. Функция y = arccos x (арккосинус).
132. Функция y = arctg x (арктангенс).
133. Функция y = arcctg x (арккотангенс).
134. Пример.
§ 2. Операции над обратными тригонометрическими функциями
135. Тригонометрические операции.
136. Операции сложения (вычитания).
§ 3. Обратные тригонометрические операции над тригонометрическими функциями
137.

Функция у = arcsin (sin x).

138. Функция y = arctg (tg x).
Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
139. Уравнение sin х = а.
140. Уравнение cos х = a.
141. Уравнение tg x = a.
142. Уравнение ctg x = a.
143. Некоторые дополнения.
§ 2. Способ приведения к одной функции одного и того же аргумента
145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента.
146. Способ разложения на множители.
147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t.
§ 3. Некоторые частные приемы решения тригонометрических уравнений и систем
148. Введение вспомогательного аргумента.
149. Преобразование произведения в сумму или разность.
150. Переход к функциям удвоенного аргумента.
151. Решение уравнения типа…
152. Применение подстановок sinx ± соsx = y.
§ 4. Решение тригонометрических неравенств
154. Простейшие тригонометрические неравенства.

155. Примеры тригонометрических неравенств, сводящихся к простейшим.
Часть вторая. ГЕОМЕТРИЯ
156. Точка. Прямая. Луч. Отрезок.
157. Плоскость. Фигуры и тела.
160. Равенство фигур. Движение.
161. Равенство тел.
§ 2. Измерение геометрических величин
162. Сложение отрезков. Длина отрезка.
163. Общая мера двух отрезков.
164. Сравнительная длина отрезков и ломаных.
165. Измерение углов.
166. Радианная мера угла.
167. Измерение площадей.
168. Площадь прямоугольника. Объем прямоугольного параллелепипеда.
Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ
169. Перпендикуляр и наклонные.
170. Свойство перпендикуляра, проведенного к отрезку в его середине.
171. Параллельные прямые.
172. Углы, образованные двумя параллельными прямыми и секущей.
173. Углы с параллельными или перпендикулярными сторонами.
§ 2. Геометрические места точек. Окружность
174. Геометрическое место точек.
175. Свойство биссектрисы угла.

176. Окружность.
177. Взаимное расположение прямой и окружности. Касательная и секущая.
178. Хорда и диаметр. Сектор и сегмент.
179. Взаимное расположение двух окружностей.
§ 3. Основные задачи на построение
181. Деление отрезка пополам. Построение перпендикуляров.
182. Построение углов.
183. Другие задачи на построение.
Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ
184. Стороны и углы треугольника.
185. Биссектрисы треугольника. Вписанная окружность.
186. Оси симметрии сторон треугольника. Описанная окружность.
187. Медианы и выcоты треугольника.
188. Равенство треугольников.
189. Построение треугольников.
190. Равнобедренные треугольники.
191. Прямоугольные треугольники.
§ 2. Параллелограммы
192. Четырехугольники.
193. Параллелограмм и его свойства.
194. Прямоугольник.
§ 3. Трапеция
196. Трапеция.
197. Средняя линия треугольника.
198. Средняя линия трапеции.
199. Деление отрезка на равные части.

§ 4. Площади треугольников и четырехугольников
200. Площадь параллелограмма.
201. Площадь треугольника.
202. Площадь трапеции.
Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
203. Пропорциональные отрезки.
204. Свойства биссектрис внутреннего и внешнего углов треугольника.
§ 2. Подобное преобразование фигур (гомотетия)
205. Определение гомотетичных фигур.
206. Свойства преобразования подобия.
§ 3. Общее подобное соответствие фигур
207. Подобные фигуры.
208. Периметры и площади подобных треугольников.
209. Применение подобия к решению задач на построение.
Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ
210. Углы с вершиной на окружности.
211. Углы с вершиной внутри и вне круга.
212. Угол, под которым виден данный отрезок.
213. Четырехугольники, вписанные в окружность.
214. Пропорциональные отрезки в круге.
215. Задачи на построение.
§ 2. Метрические соотношения в треугольнике
216. Пропорциональные отрезки в прямоугольном треугольнике.

Теорема Пифагора.
218. Теорема синусов. Формула Герона.
217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов.
218. Теорема синусов. Формула Герона.
219. Радиусы вписанной и описанной окружностей.
§ 3. Решение треугольников
220. Таблицы функций.
221. Решение треугольников. Сводка основных формул.
222. Решение прямоугольных треугольников.
223. Решение косоугольных треугольников.
Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА
224. Выпуклые многоугольники.
225. Правильные многоугольники.
226. Соотношения между стороной, радиусом и апофемой.
227. Периметр и площадь правильного n-угольника.
228. Удвоение числа сторон правильного многоугольника.
§ 2. Длина окружности. Площадь круга и его частей
229. Длина окружности.
230. Площадь круга и его частей.
Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
231. Взаимное расположение двух прямых в пространстве.

232. Взаимное расположение прямой линии и плоскости.
233. Взаимное расположение двух плоскостей.
234. Свойства параллельных прямых и плоскостей.
235. Построения в стереометрии.
§ 2. Перпендикулярность прямых и плоскостей
236. Перпендикуляр к плоскости.
237. Перпендикуляр и наклонные.
238. Угол между прямой и плоскостью.
239. Связь между перпендикулярностью и параллельностью прямых и плоскостей.
240. Общий перпендикуляр двух скрещивающихся прямых.
§ 3. Двугранные и многогранные углы
241. Двугранный угол.
242. Взаимно перпендикулярные плоскости.
243. Трехгранные углы.
244. Многогранные углы.
§ 4. Многогранники
245. Многогранники.
246. Правильные многогранники.
Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА
247. Цилиндры и призмы.
248. Параллелепипеды.
249. Объемы призм и цилиндров.
250. Площадь боковой поверхности призмы.
251. Площадь поверхности цилиндра.
§ 2. Пирамида. Конус
252. Свойства пирамиды и конуса.

253. Объем пирамиды и конуса.
254. Площадь боковой поверхности правильной пирамиды и конуса.
255. Усеченный конус и усеченная пирамида.
§ 3. Шаровая поверхность. Шар
256. Шар и шаровая поверхность.
257. Объем шара и его частей.
258. Площадь поверхности шара и ее частей.
259. Понятие телесного угла.
Ответы к упражнениям
Приложения

Иррациональное число

Иррациональное число — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде обыкновенной дроби m n {displaystyle {frac {m}{n}}} , где m , n {displaystyle m,n} — целые числа, n ≠ 0 {displaystyle n eq 0} . Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.

Другими словами, множество иррациональных чисел есть разность I = R ∖ Q {displaystyle mathbb {I} =mathbb {R} ackslash mathbb {Q} } множеств вещественных и рациональных чисел.

О существовании иррациональных чисел (точнее отрезков, несоизмеримых с отрезком единичной длины), знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа 2 {displaystyle {sqrt {2}}} .

Иррациональными являются, среди прочих, отношение длины окружности к диаметру круга (число π), число Эйлера e, золотое сечение φ, квадратный корень из двух. Все квадратные корни натуральных чисел, кроме полных квадратов, иррациональны.

Иррациональные числа также могут рассматриваться через бесконечные непрерывные дроби.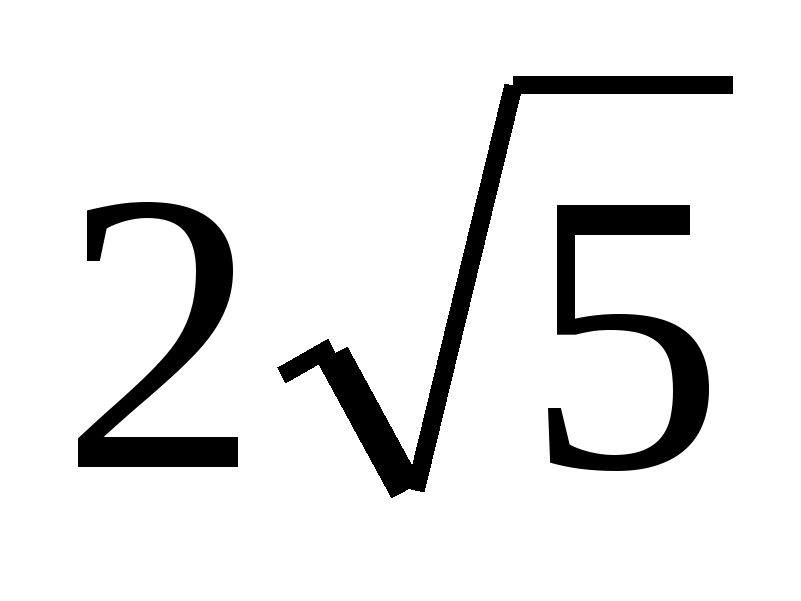 Следствием доказательства Кантора является то, что действительные числа не счётны, а рациональные — счётны, отсюда следует, что почти все действительные числа иррациональны.

Свойства

Сумма двух положительных иррациональных чисел может быть рациональным числом.
Иррациональные числа определяют дедекиндовы сечения во множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя различными числами имеется иррациональное число.

Алгебраические и трансцендентные числа

Каждое иррациональное число является либо алгебраическим, либо трансцендентным. Множество алгебраических чисел является счётным множеством. Так как множество вещественных чисел несчётно, то множество иррациональных чисел также несчётно.

Каждое вещественное трансцендентное число является иррациональным; алгебраическое число может быть как рациональным, так и иррациональным. .

Множество иррациональных чисел является множеством второй категории.

Иррациональные числа и непрерывные дроби

Иррациональное число представляются бесконечной непрерывной дробью. Пример, число e:

e = [ 2 ; 1 , 2 , 1 , 1 , 4 , 1 , 1 , 6 , 1 , … , 1 , 2 n , 1 , … ] . {displaystyle e=[2;1,2,1,1,4,1,1,6,1,ldots ,1,2n,1,ldots ].}

Квадратичным иррациональностям соответствуют периодические непрерывные дроби.

ϕ = 1 + 5 2 = [ 1 ; 1 , 1 , 1 , 1 , … ] . {x}} для любого рационального x ≠ 0 {displaystyle x eq 0}

Примеры доказательства иррациональности

Корень из 2

Допустим противное: 2 {displaystyle {sqrt {2}}} рационален, то есть представляется в виде дроби m n {displaystyle {frac {m}{n}}} , где m {displaystyle m} — целое число, а n {displaystyle n} — натуральное число.

Возведём предполагаемое равенство в квадрат:

2 = m n ⇒ 2 = m 2 n 2 ⇒ m 2 = 2 n 2 {displaystyle {sqrt {2}}={frac {m}{n}}Rightarrow 2={frac {m^{2}}{n^{2}}}Rightarrow m^{2}=2n^{2}} . {2}} невозможно. Значит, исходное предположение было неверным, и 2 {displaystyle {sqrt {2}}} — иррациональное число.

Двоичный логарифм числа 3

Допустим противное: log 2 ⁡ 3 {displaystyle log _{2}3} рационален, то есть представляется в виде дроби m n {displaystyle {frac {m}{n}}} , где m {displaystyle m} и n {displaystyle n} — целые числа. Поскольку log 2 ⁡ 3 > 0 {displaystyle log _{2}3>0} , m {displaystyle m} и n {displaystyle n} могут быть выбраны положительными. {m}} чётно, а правая часть получившегося равенства нечётна. Получаем противоречие.

См. раздел «Доказательство иррациональности» в статье «e».

История

Античность

Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (приблизительно 750—690 года до нашей эры) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.

Первое доказательство существования иррациональных чисел, а точнее существование несоизмеримых отрезков, обычно приписывается пифагорейцу Гиппасу из Метапонта (приблизительно 470 год до нашей эры). Нет точных данных о том, иррациональность какого числа была доказана Гиппасом. Согласно легенде он нашёл его, изучая длины сторон пентаграммы. Поэтому разумно предположить, что это было золотое сечение, так как это и есть отношение диагонали к стороне в правильном пятиугольнике.

Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.

Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара, оно было основано на теореме о том, что нечётное квадратное число делится на восемь с остатком один.

Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.

Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. Десятая книга «Начал» Евклида посвящена классификации иррациональных величин.

Средние века

Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сначала индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.

Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 «Начал» Евклида, персидский математик аль-Махани (ок. 800 года н. э.) исследовал и классифицировал квадратичные иррациональные числа и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:

Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких, как 10, 15, 20 — не являющихся квадратами.

В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввёл арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:

результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной.

Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счёл приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль-Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Аль-Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:

Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравнённая с единичной величиной составляет три пятых от неё, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней.

Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввёл современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π {displaystyle pi } , а также показали иррациональность некоторых значений тригонометрических функций. Джестадева привёл эти результаты в книге «Йуктибхаза».

Новое время

В XVII—XVIII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 году были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с работами Гейне, именно 1872 год принято считать годом рождения теории. Метод Вейерштрасса был полностью изложен Сальваторе Пинкерле в 1880 году, а Дедекинд получил дополнительную известность благодаря более поздней работе автора (1888) и одобрению Поля Таннери (1894). Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемыми) дедекиндовыми сечениями множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.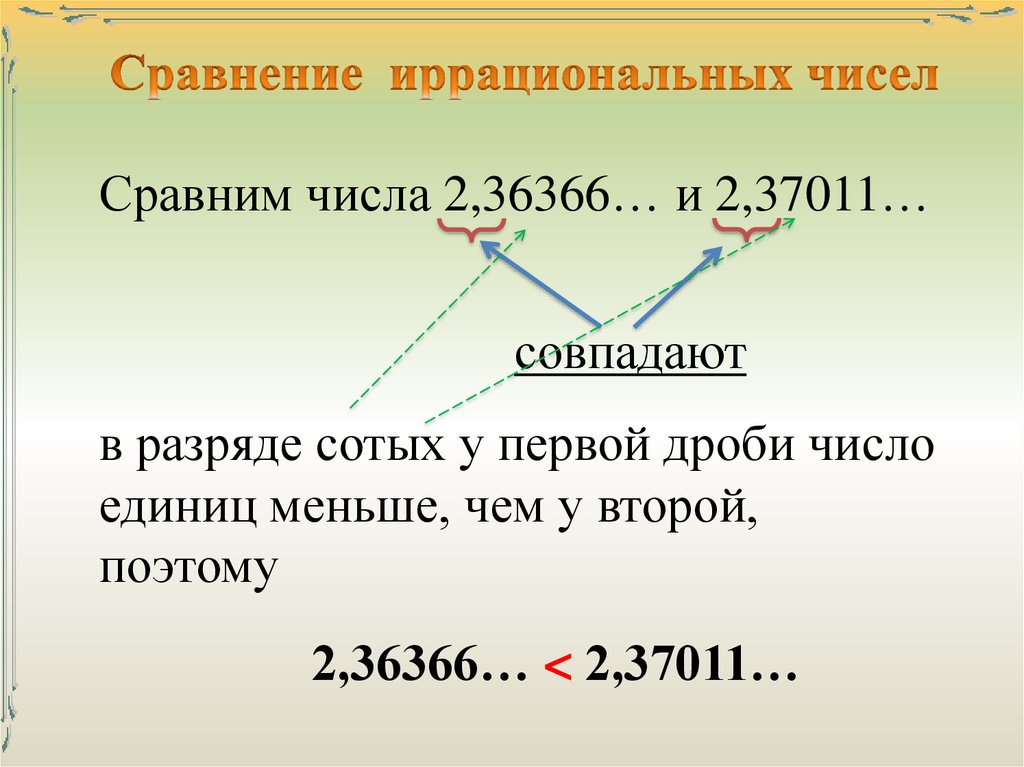 {2}} иррационально, откуда иррациональность π {displaystyle pi } следует тривиально (рациональное число в квадрате дало бы рациональное).

Существование трансцендентных чисел было доказано Лиувиллем в 1844—1851 годах. Позже Георг Кантор (1873) показал их существование, используя другой метод, и обосновал, что любой интервал вещественного ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность π {displaystyle pi } . Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом.

Видео-вопрос: определение иррационального числа, лежащего между двумя заданными рациональными числами

Стенограмма видео

Какое из следующих иррациональных чисел лежит между отрицательными семью и отрицательными тремя?

Итак, чтобы решить эту задачу, первое, что мы должны задать себе, это что такое иррациональное число? Ну, одно определение или определение, которое будет полезно для этого вопроса, заключается в том, что иррациональное число — это число, которое нельзя записать в виде простой дроби. Таким образом, мы можем использовать это, чтобы сразу исключить некоторые ответы.

Если мы посмотрим на Е, то увидим, что Е равно минус 11 больше двух. Но это уже фактически простая дробь. Таким образом, мы можем исключить это как наш ответ. И затем, если мы посмотрим на C, C равно минус пять. Ну, минус пять на самом деле не иррациональное число. И на самом деле вы можете записать это как простую дробь, потому что это может быть записано как минус пять на единицу. Так что в этом случае мы также можем исключить ответ C.

Итак, теперь у нас осталось три возможных ответа. Все три из них являются иррациональными числами. Так что их всех можно рассмотреть. Итак, чтобы действительно решить это сейчас, мы можем просто остановиться и подумать, ну, правильно, какие на самом деле будут наши параметры для наших значений?

Прежде всего, я начну с минимально возможного значения. Так каким же может быть наименьшее возможное значение? Что ж, мы знаем, что семь в квадрате равно 49. Итак, мы знаем, что нашим наименьшим возможным значением должен быть отрицательный корень 49, поскольку он говорит, что наше иррациональное число должно лежать между отрицательными семью и отрицательными тремя. Но если мы посмотрим на любой из ответов на самом деле ниже отрицательного 49, это означает, что да, опять же, мы можем фактически исключить один из наших ответов, потому что отрицательный корень 53 будет слишком низким значением. Итак, теперь мы можем исключить этот ответ.

Отлично! Итак, у нас осталось два ответа: либо отрицательный корень пять, либо отрицательный корень 29. Итак, давайте посмотрим, каким может быть максимально возможное значение. Итак, мы знаем, что три в квадрате равно девяти. Таким образом, максимально возможное значение — это отрицательный корень девять. Итак, еще раз, мы можем взглянуть на наши последние два ответа. Итак, при ближайшем рассмотрении мы видим, что на самом деле у нас не может быть ответа А, отрицательного корня пять, потому что на самом деле это слишком большой ответ, потому что отрицательный корень пять на самом деле больше, чем отрицательный корень девять. Следовательно, мы можем исключить ответ А. И мы можем сказать, что наш ответ будет D, отрицательный корень 29..

И мы можем просто проверить это. И чтобы проверить это, мы можем просто посмотреть на корень 29. И действительно, я думаю, мы посмотрим. Существуют ли два квадратных числа, между которыми было бы 29? И на самом деле мы видим, что да, есть, потому что 29 находится между 25 и 36. Таким образом, мы можем сказать, что корень 29 больше, чем корень 25, и меньше, чем корень 36. Таким образом, мы можем сказать, что корень 29 больше, чем пять , но меньше шести. Таким образом, мы можем сказать, что отрицательный корень 29 будет больше отрицательного числа шесть и меньше отрицательного числа пять. Таким образом, оно будет лежать между нашими значениями минус семь и минус три. Поэтому мы можем с уверенностью сказать, что отрицательный корень 29иррациональное число, лежащее между отрицательными семью и отрицательными тремя.

Иррациональное число Определение и значение

Основные определения
Тест
Примеры
Британский
Научный
Культурное слово

показывает уровень сложности

Сохрани это слово!

Показывает уровень сложности слова.

сущ. Математика.

число, которое не может быть точно выражено как отношение двух целых чисел.

ВИКТОРИНА

ТЫ ПРОШЕШЬ ИЛИ НАТЯНУСЬ НА ЭТИ ВОПРОСЫ ПО ГРАММАТИКЕ?

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Происхождение иррационального числа

Впервые записано в 1545–1555 гг.0005

Как использовать иррациональное число в предложении

Это потому, что иррациональных чисел намного больше, чем рациональных.
Тренер, возглавивший сборную США по математике, вернулся на вершину|Макс Дж. Леви|16 февраля 2021 г.|Журнал Quanta
Забавно, что вы не дали мне число — иррациональное число — на самом деле это самый распространенный тип числа.
Тренер, который вернул сборную США по математике на вершину|Макс Дж. Леви|16 февраля 2021 г.|Журнал Quanta
«Наши участники продолжают сталкиваться с рядом проблем, — сказала она.
Война республиканцев с Кале|Патриция Мерфи|7 января 2015|DAILY BEAST
Количество несогласных беспрецедентно для современной эпохи.
Демократы случайно спасли Бонера от республиканского переворота|Бен Джейкобс, Джеки Кусинич|6 января 2015 г.|DAILY BEAST

Руководящие принципы самаритянина написаны вокруг предположения, что самоубийство — это чисто иррациональный поступок, поступок, вызванный болезнью.
Сокрытие и озабоченные тролли: на самом деле, речь идет об этике в журналистике самоубийств|Артур Чу|3 января 2015|DAILY BEAST
Начиная с Теодора Рузвельта и Говарда Тафта, число посольств, возглавляемых профессиональными дипломатами, увеличилось.
Посольства США всегда выставлялись на продажу|Уильям О’Коннор|2 января 2015 г. |DAILY BEAST
Количество дипломатов было жалким (45 назначенцев в 1860 г.), как и количество выделяемых им денег.
Посольства США всегда выставлялись на продажу|Уильям О’Коннор|2 января 2015 г.|DAILY BEAST
Страна хорошо населена, так как в ней пятьдесят один город, около сотни городов-крепостей и множество деревень.
Путешествия Гулливера|Джонатан Свифт
У нас было шесть полевых орудий, но мы взяли только четыре, запряженных вдвое большим количеством лошадей.
Эдинбургский журнал Blackwood, № CCCXXXIX. Январь 1844 г. Том. LV.|Various
Существует ряд бацилл, называемых кислотоустойчивыми бациллами, которые окрашиваются так же, как туберкулезная палочка.
Руководство по клинической диагностике|Джеймс Кэмпбелл Тодд
Пятеро из них раньше учились у Листа, и молодые люди уже стали художниками перед публикой.
Музыкальное образование в Германии|Эми Фэй
Я не думаю, что среднее количество пассажиров на соответствующем маршруте в нашей стране может быть меньше двадцати.
Glances at Europe|Horace Greeley

Определения иррационального числа в Британском словаре

иррациональное число

существительное

любое действительное число, которое не может быть выражено как отношение двух целых чисел, например π — Полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Издатели 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012

Научные определения иррационального числа