Площадь поверхности и объем параллелепипеда: Найдите объем и площадь поверхности прямоугольного параллелепипеда если его измерения равны 8 см., 10 см.,…

Площадь поверхности параллелепипеда — формула и калькулятор

{S_{полн} = 2(ab+bc+ac)}

Найти площадь

полной поверхностибоковой поверхности

Длина a

ммсмдммкмдюймы (in)футы (ft)

Ширина b

ммсмдммкмдюймы (in)футы (ft)

Высота c

ммсмдммкмдюймы (in)футы (ft)

Результат в

мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)

Виджет

Ссылка на расчет

Сообщить об ошибке

Сохранить расчет

Печатать

Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.

В дополнение на сайте можно найти объем параллелепипеда.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.

Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.

Содержание:

1. калькулятор площади поверхности прямоугольного параллелепипеда
2. формула площади поверхности прямоугольного параллелепипеда
3. формула площади боковой поверхности прямоугольного параллелепипеда
4. примеры задач

Формула площади поверхности прямоугольного параллелепипеда

{S_{полн} = 2(ab+bc+ac)}

a

— длина прямоугольного параллелепипеда

b — ширина прямоугольного параллелепипеда

c — высота прямоугольного параллелепипеда

Формула площади боковой поверхности прямоугольного параллелепипеда

{S_{бок} = 2(ac+bc)}

a — длина прямоугольного параллелепипеда

b — ширина прямоугольного параллелепипеда

c — высота прямоугольного параллелепипеда

Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда

Задача 1

Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5. 2

Ответ: 126 см²

Как всегда ответ можно проверить с помощью калькулятора .

Параллелепипед, куб. Площади поверхностей. Объём

Урок 35. Подготовка к ЕГЭ по математике

В данном видеоуроке мы напомним, какую призму называют параллелепипедом. Вспомним, как находить площади боковой и полной поверхностей параллелепипеда и его объём. Повторим свойства параллелепипеда. Также на этом занятии мы поговорим о кубе.

Конспект урока «Параллелепипед, куб. Площади поверхностей. Объём»

Напомним, что призма, в основании которой лежит параллелограмм, называется параллелепипедом.

Стороны параллелограммов называются рёбрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра.

Например, грани  и  – противолежащие.

Грани, имеющие общее ребро, называются смежными. Например, грани  и  – смежные, ребро  у них общее.

Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его

боковыми рёбрами.

В нашем случае у параллелепипеда  грани  и  – его основания. Остальные же грани являются боковыми гранями.

Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий, противолежащие вершины, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.

Объединение боковых граней называется боковой поверхностью параллелепипеда, а объединение всех граней называется полной поверхностью параллелепипеда. Тогда площадью боковой поверхности параллелепипеда называется сумма площадей его боковых граней.

А площадью полной поверхности параллелепипеда называется сумма площадей всех его граней.

Параллелепипед обладает следующими свойствами:

1. Противолежащие грани параллелепипеда равны и лежат в параллельных плоскостях.

2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

3. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Объём параллелепипеда равен произведению площади основания на высоту.

Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Куб – это прямоугольный параллелепипед, все рёбра которого равны, то есть все грани которого – равные квадраты.

Диагональ куба с ребром  равна .

Объём куба равен , где  – ребро куба.

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задача первая. В основании прямого параллелепипеда лежит параллелограмм с основаниями  см и  см и острым углом . Боковое ребро параллелепипеда равно  см. Найдите площадь полной поверхности параллелепипеда.

Решение.

Задача вторая. Все грани параллелепипеда – ромбы с диагоналями  см и  см. Найдите площадь полной поверхности параллелепипеда.

Решение.

Задача третья. Найдите меньшую диагональ прямого параллелепипеда высотой  см
со сторонами основания  см и  см и углом между ними .

Решение.

Задача четвёртая. В прямоугольном параллелепипеде  ребро  см,  см. Найдите расстояние между диагональю параллелепипеда  и ребром .

Решение

.

Задача пятая. Две стороны основания параллелепипеда равны  см и  см, угол между ними . Боковое ребро равно  см и наклонено к основанию под углом .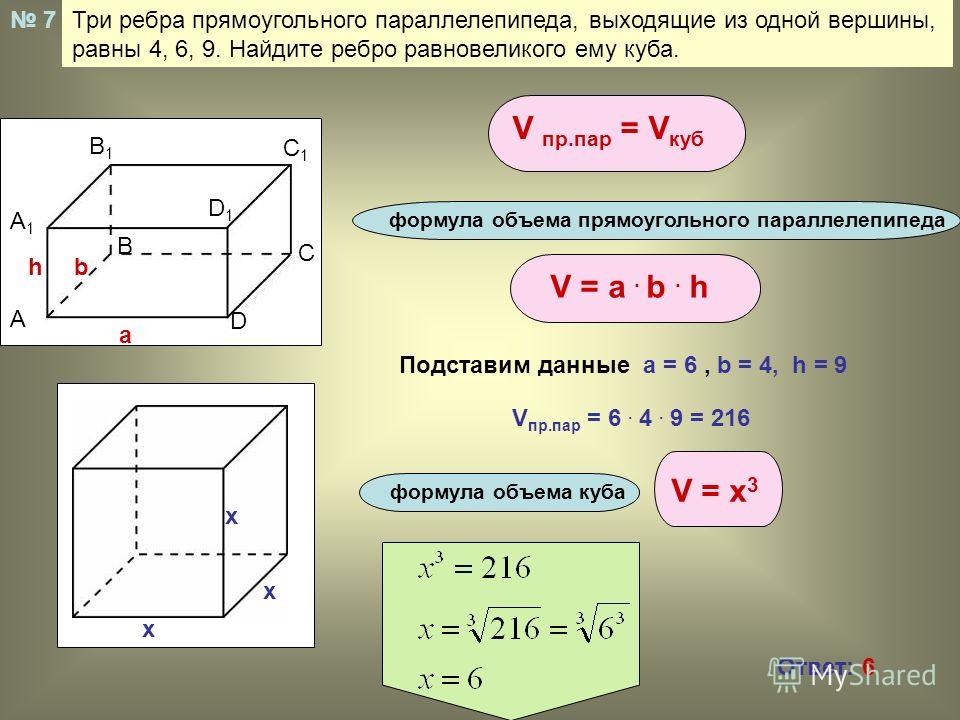 Найдите объём параллелепипеда.

Решение.

Задача шестая. Все грани параллелепипеда – ромбы с периметром равным  и острым углом . Найдите объём  параллелепипеда. В ответ запишите значение .

Решение.

Предыдущий урок 34 Призма. Площади поверхностей. Объём

Следующий урок 36 Пирамида. Площади поверхностей. Объём

Получите полный комплект видеоуроков, тестов и презентаций Подготовка к ЕГЭ по математике

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Отношение площади поверхности к объему призм — Krista King Math

Формулы площади поверхности и объема прямой прямоугольной призмы

Помните, что площадь поверхности прямой прямоугольной призмы дана в таблице:

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Формула площади поверхности прямоугольной призмы:

???A=2lw+2wh+2lh???

Объем прямоугольной призмы равен произведению длины на ширину и на высоту.

???V=lwh???

Отношение площади поверхности к объему

Отношение площади поверхности, ???S???, к объему, ???V???, может быть выражено как доля ???S/V ???, или преобразуется в десятичное число.

Как найти площадь поверхности прямоугольной призмы

Пройти курс

Хотите узнать больше о геометрии? У меня есть пошаговый курс для этого. 🙂

Узнать больше

Вычисление отношения площади поверхности к объему прямоугольной призмы

Пример

Вычисление отношения площади поверхности к объему прямоугольной призмы размером ???4\text{ см}??? высокий, ???\text{6 см}??? широкий и ???\text{8 см}??? длинный.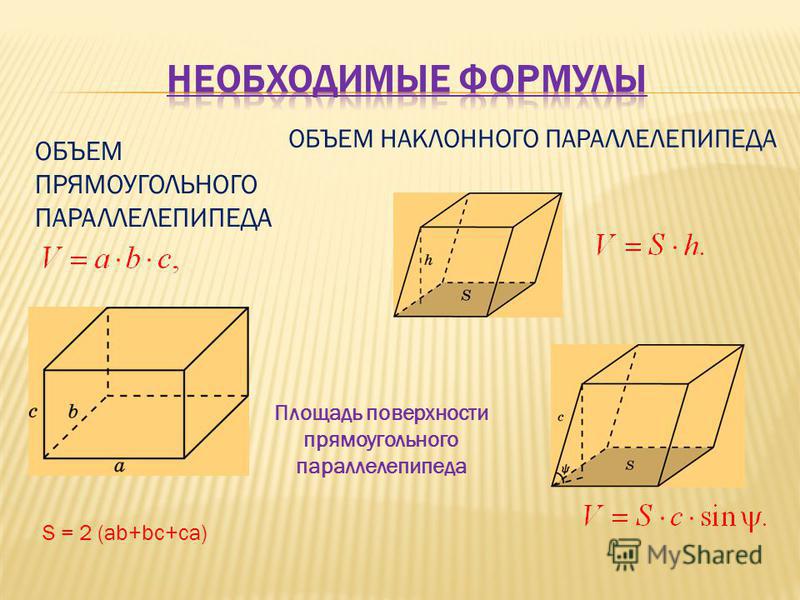 Выразите ответ в виде десятичной дроби с округлением до десятых.

Использовать ???A=2lw+2wh+2lh??? найти площадь поверхности.

???S=2\cdot 8\cdot 6+2\cdot 6\cdot 4+2\cdot 8\cdot 4???

???S=208???

Использовать ???V=lwh??? найти объем.

???V=8\cdot 6\cdot 4???

???V=192???

Теперь найдите отношение площади поверхности к объему.

???\frac{S}{V}=\frac{208}{192}=\frac{13}{12}???

При округлении десятичной дроби до ближайшей десятой отношение равно ???1.1???.

92???

Получить доступ к полному курсу геометрии

Начать

Изучение математикиКриста Кинг 27 сентября 2020 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, геометрия, трехмерная геометрия, трехмерная геометрия, призмы, прямоугольные призмы, площадь поверхности призм, объем призм, площадь поверхности до соотношение объемов

0 лайков

Параллелепипед Калькулятор площади и объема

Параллелепипед

Калькулятор площади и объема параллелепипеда онлайн: Вычислите объем и площадь параллелепипеда по трем его сторонам: длине, ширине и высоте. Введите в форму три неизвестных и нажмите кнопку РАСЧЕТ.

Содержание:

• Что такое параллелепипед?
• Характеристики Параллелепипеда
• Вычислить площадь параллелепипеда
• Рассчитайте объем параллелепипеда

Что такое параллелепипед?

Параллелепипед — это твердое тело, шесть граней которого являются параллелограммами. Для параллелограмма это то же, что куб для квадрата и прямоугольный кубоид для прямоугольника.

Характеристики параллелепипеда

Он имеет 6 сторон:

Две горизонтальные грани являются основаниями.

Остальные четыре грани называются «боковыми», совокупность четырех граней в сборе называется призматической поверхностью.

Имеет 8 вершин и 12 ребер: это ребра ограничивающих его граней, мы также говорим «пересечение двух плоскостей»

Что касается куба, то ребра, оканчивающиеся в одной вершине, перпендикулярны два на два, противоположные грани параллельны два на два и грани, имеющие общее ребро, перпендикулярны.

Каждая грань представляет собой прямоугольник, противоположные края одной и той же грани параллельны.

Две противоположные грани имеют одинаковую площадь;

Две противоположные кромки параллельны и имеют одинаковую длину.

Вычислить площадь параллелепипеда

Для вычисления площади, соответствующей поверхности параллелепипеда, достаточно сложить площади, соответствующие каждой из этих граней (формула вычисления площади прямоугольника), а именно:

Длина: a

Ширина: c

Глубина: b

2 грани, площадь которых равна a x b (верхняя и нижняя части параллелепипеда).

2 грани, площадь которых равна a x c (передняя и задняя грани параллелепипеда).

2 грани, площадь которых равна b x c (левая и правая стороны параллелепипеда).

Отсюда формула вычисления площади А параллелепипеда:

А = 2 (а х b + а х с + Ь х с)

Вычислите объем параллелепипеда

Объем параллелепипеда соответствует пространству, которое он занимает в окружающей среде.