Динамическое программирование онлайн: Динамическое программирование

alexxlab / / Разное

Содержание

Оптимальное распределение ресурсов методом динамического программирования. Уравнения Беллмана. Методы оптимальных решений

Краткая теория

Динамическое программирование (иначе — динамическое планирование) — это метод нахождения оптимальных решений в задачах с многошаговой (многоэтапной) структурой. Многие экономические процессы расчленяются на шаги естественным образом. Это все процессы планирования и управления, развиваемые во времени. Естественным шагом в них может быть год, квартал, месяц, декада, неделя, день и т. д. Однако метод динамического программирования может использоваться при решении задач, где время вообще не фигурирует; разделение на шаги в таких задачах вводится искусственно. Поэтому «динамика» задач динамического программирования заключается в методе решения.

В экономической практике встречается несколько типов задач, которые по постановке или способу решения относятся к задачам динамического программирования. Это задачи оптимального перспективного и текущего планирования во времени. Их решают либо путем составления комплекса взаимосвязанных статических моделей для каждого периода, либо путем составления единой динамической задачи оптимального программирования с применением многошаговой процедуры принятия решений. К задачам динамического программирования следует отнести задачи многошагового нахождения оптимума при размещении производительных сил, а также оптимального быстродействия.

Типичные особенности многошаговых задач.

1. Рассматривается система, состояние которой на каждом шаге определяется вектором . Дальнейшее изменение ее состояния зависит только от данного состояния  и не зависит от того, каким путем система пришла в него. Такие процессы называются процессами без последействия.

2. На каждом шаге выбирается одно решение , под действием которого система переходит из предыдущего состояния  в новое .

Это новое состояние является функцией состояния на начало интервала  и принятого в начале интервала решения  т. е.

 3. Действие на каждом шаге связано с определенным выигрышем (доходом, прибылью) или потерей (издержками), которые зависят от состояния на начало шага (этапа) и принятого решения.

4. На векторы состояния и управления могут быть наложены ограничения, объединение которых составляет область допустимых решений .

5. Требуется найти такое допустимое управление  для каждого шага , чтобы получить экстремальное значение функции цели за все  шагов.

Любую многошаговую задачу можно решать по-разному. Во-первых, можно считать неизвестными величинами щ и находить экстремум целевой функции одним из существующих методов оптимизации, т. е. искать сразу все элементы решения на всех  шагах. Отметим, что этот путь не всегда приводит к цели, особенно когда целевая функция задана в виде таблиц или число переменных очень велико.

Второй путь основан на идее проведения оптимизации поэтапно. Поэтапность отнюдь не предполагает изолированности в оптимизации этапов. Наоборот, управление на каждом шаге выбирается с учетом всех его последствий. Обычно второй способ оптимизации оказывается проще, чем первый, особенно при большом числе шагов. Идея постепенной, пошаговой оптимизации составляет суть метода динамического программирования. Оптимизация одного шага, как правило, проще оптимизации всего процесса в целом. Лучше много раз решать сравнительно простую задачу, чем один раз — сложную.

С первого взгляда идея может показаться тривиальной: если трудно оптимизировать сложную задачу, то следует разбить ее на ряд более простых. На каждом шаге оптимизируется задача малого размера, что уже нетрудно. При этом принцип динамического программирования вовсе не предполагает, что каждый шаг оптимизируется изолированно, независимо от других. Напротив, пошаговое управление должно выбираться с учетом всех его последствий.

Можно сформулировать следующие принципы, лежащие в основе динамического программирования: принцип оптимальности и принцип погружения.

Оптимальное управление на каждом шаге определяется состоянием системы на начало этого шага и целью управления. Или в развернутой форме: оптимальная стратегия обладает таким свойством, что, каковы бы ни были начальное состояние и начальные решения, последующие решения должны приниматься исходя из оптимальной стратегии с учетом состояния, вытекающего из первого решения. Этот принцип имеет довольно простую математическую интерпретацию, выражающуюся в составлении определенных рекуррентных соотношений (функциональных уравнений Р. Беллмана).

Природа задачи, допускающей использование метода динамического программирования не меняется при изменении количества шагов , т. е. форма такой задачи инвариантна относительно . В этом смысле всякий конкретный процесс с заданным числом шагов оказывается как бы погруженным в семейство подобных ему процессов и может рассматриваться с позиции более широкого класса задач.

Реализация названных принципов дает гарантию того, что решение, принимаемое на очередном шаге, окажется наилучшим относительно всего процесса в целом, а не узких интересов данного этапа. Последовательность пошаговых решений приводит к решению исходной -шаговой задачи.

Дадим математическую формулировку принципа оптимальности для задач с аддитивным критерием оптимальности (сепарабельная функция цели). Для простоты будем считать, что начальное  и конечное  состояния системы заданы. Обозначим через  значение функции цели на первом этапе при начальном состоянии системы  и при управлении , через  -соответствующее значение функции цели только на втором этапе, …., через  — на  этапе, …, через  — на -м этапе. Очевидно, что

Надо найти оптимальное управление  такое, что доставляет экстремум целевой функции при ограничениях .

Для решения этой задачи погружаем ее в семейство подобных. Введем обозначения. Пусть  — соответственно области определения для подобных задач на последнем этапе, двух последних и т.д.;  — область определения исходной задачи. Обозначим через

соответственно условно-оптимальные значения функции цели на последнем этапе, двух последних и т.д., на  последних и т.д., на всех  этапах.

Начинаем с последнего этапа. Пусть  — возможные состояния системы на начало -го этапа. Находим:

Для двух последних этапов получаем:

Аналогично:

 

…………………….

…………………….

Выражение (5) представляет собой математическую запись принципа оптимальности. Выражение (4) — общая форма записи  условно-оптимального значения функции цели для  оставшихся этапов.

Выражения (1)-(5) называются функциональными уравнениями Беллмана. Отчетливо просматривается их рекуррентный (возвратный) характер, т.е. для нахождения оптимального управления на  шагах нужно знать условно-оптимальное управление на предшествующих  этапах и т.д. Поэтому функциональные уравнения часто называются рекуррентными (возвратными) соотношениями Беллмана.

Пример решения задачи

Производственное объединение выделяет четырем входящим в него предприятиям кредит в сумме 100 млн.ден.ед. для расширения производства и увеличения выпуска продукции. По каждому предприятию известен возможный прирост  выпуска продукции (в денежном выражении) в зависимости от выделенной ему суммы . Для упрощения вычислений выделяемые суммы кратны 20 млн.ден.ед. При этом предполагаем, что прирост продукции на  предприятии не зависит от суммы средств, вложенных в другие предприятия, а общий прирост выпуска в производственном объединении равен сумме приростов, полученных на каждом предприятии объединения.

Требуется найти оптимальное решение распределения кредита между предприятиями, чтобы общий прирост выпуска продукции на производственном объединении был максимальным.  

Выделяемые средства , млн.ден.ед. Предприятие
№1 №2 №3 №4
Прирост выпуска продукции на предприятиях  млн.ден.ед.
20 10 12 11 16
40 31 24 36 37
60 42 36 45 46
80 62 52 60 63
100 76 74 77 80

Решение

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Динамическое программирование представляет собой многоэтапный поиск оптимального решения. Оптимизация многошагового процесса базируется  на принципе оптимальности Р. Беллмана.

Вычисления в динамическом программировании выполняются рекуррентно — оптимальное решение одной подзадачи используется в качестве исходных данных для поиска оптимального решения следующей подзадачи. Решив последнюю подзадачу, мы получим оптимальное решение исходной задачи.

Выделяемые средства
0 0 0 0 0
20 10 12 11 16
40 31 24 36 37
60 42 36 45 46
80 62 52 60 63
100 76 74 77 80

Шаг 1

В соответствии с вычислительной схемой динамического программирования рассмотрим сначала случай , т. е. предположим, что все имеющиеся средства выделяются на реконструкцию и модернизацию одного предприятия. Обозначим через  максимально возможный дополнительный доход на этом предприятии, соответствующий выделенной сумме . Каждому значению  отвечает вполне определенное (единственное) значение  дополнительного дохода, поэтому можно записать, что:

Шаг 2

Пусть теперь , т.е. средства распределяются между двумя предприятиями. Если второму предприятию выделена сумма , то дополнительный доход на нем составит . Оставшиеся другому предприятию средства  в зависимости от величины (а значит, и ) позволят увеличить дополнительный доход до максимально возможного значения . При этом условии общий дополнительный доход на двух предприятиях:

Шаг 3

Пусть теперь , т.е. средства распределяются между тремя предприятиями. Если третьему предприятию выделена сумма , то дополнительный доход на нем составит . Оставшиеся средства  в зависимости от величины (а значит, и ) позволят увеличить дополнительный доход до максимально возможного значения . При этом условии общий дополнительный доход на трех предприятиях:

 

Шаг 4

Пусть теперь , т.е. средства распределяются между четырьмя предприятиями. Если четвертому предприятию выделена сумма , то дополнительный доход на нем составит . Оставшиеся средства  в зависимости от величины (а значит, и ) позволят увеличить дополнительный доход до максимально возможного значения . При этом условии общий дополнительный доход на четырех предприятиях:

Составим сводную таблицу на основе расчетов:

Выделяемые средства
0 0 0 0 0
20 10 12 12 16
40 31 31 36 37
60 42 43 48 52
80 62 62 67 73
100 76 76 79 85

Ответ

Оптимальный план распределения между 4 предприятиями 100 единиц ресурса:

0 20 40 40

При этом суммарный прирост продукции достигнет максимальной величины, равной 85.

Онлайн-курс по олимпиадному программированию

24 января — 20 мая 2022

Онлайн-курс по олимпиадному программированию

Курс поможет развить компетенции в области программирования, подготовиться к олимпиадам, всероссийским и международным соревнованиям по информатике.

Регистрация закрыта

  • 7-11 класс
  • 14000
  • Онлайн-мероприятие

О курсе

Часто старшеклассники заинтересованы в более глубоком изучении языков программирования, чем может им предложить школьная подготовка. Регулярные онлайн-занятия по программированию от Университета Иннополис помогут развить компетенции в области программирования, подготовиться к олимпиадам, всероссийским и международным соревнованиям по информатике.  Занятия проходят 2 раза в неделю на платформе Zoom.

Стоимость курса

Указана стоимость обучения за весь полугодовой курс выбранной группы

14 000

Группа D – Начинающая


 Погружение в олимпиадное программирование

Желательно быть знакомым с вводом-выводом данных, переменными и арифметическими операциями в одном из языков программирования.

Основные темы:
— Условные операторы (if, else, elif)
— Циклы
— Массивы
— Символы и строки
— Функции и процедуры
— Рекурсия
— Сортировки
— Стек, очередь и дек
— Множества (set)
— Словари (dict)

Дополнительные темы:
— Теория графов
— Динамическое программирование
— Бинарный и тернарный поиски

Михаил Кусков
Студент Университета Иннополис
Достижения:
1. Призёр олимпиад школьников из перечня РСОШ по информатике и информационной безопасности 2017/2018 учебного года
2. Преподаватель Летней Школы Олимпиадной Подготовки Университета Иннополис 2020
3. Преподаёт в довузе Университета Иннополис с 2018 года

Когда: среда и пятница 18:30 – 20:30 по московскому времени
Язык программирования: Python 3
На основные темы будет по 2 занятия: теоретическое (рассказывается тема) и практическое (с решением задачек).
Базовые вещи по дополнительным темам рассказываются на последних 4-х занятиях.

Школьники, прошедшие данный курс будут иметь необходимый минимум знаний, который позволяет выбирать практически любое направление для продолжения обучения программированию.

Группа C – Продолжающая


 Базовые алгоритмы и структуры данных

Умение писать простейшие программы с условиями, циклами и массивам.

— Математика 1: Поиск делителей, факторизация, решето Эратосфена
— Математика 2: Алгоритм Евклида, бинарное возведение в степень
— Линейные структуры данных: cтек, очередь, дек, списки
— Сортировки и компараторы
— Динамическое программирование 1: числа Фибоначчи и префиксные суммы
— Динамическое программирование 2: восстановление ответа и двумерная динамика
— Динамическое программирование 3: задача о рюкзаке, НВП, НОП, расстояние по Левенштейну
— Графы 1: хранение и обходы
— Графы 2: топологическая сортировка и поиск цикла
— Бинарный и тернарный поиски
— Два указателя
— Очередь с приоритетом, множество и словарь (PQ, set, map)
— Графы 3: алгоритмы Дейкстры, Прима, Краскала, Флойда, Беллмана-Форда
— Строковые алгоритмы: префикс-функция, Z-функция, полиномиальное хэширование»

Анатолий Максудов
Тренер по спортивному программированию
Достижения:
1. Призёр олимпиад школьников из перечня РСОШ по информатике и математике 2014/2015 учебного года.
2. Автор и разработчик задач олимпиады Innopolis IT РОСТ 2019/2020 по информатике и индивидуальных туров по информатике олимпиады НТИ c 2017 по 2020.
3. С 2017-го года готовлю к олимпиадам по программированию. Офлайн на сборах и последний год онлайн на полугодовых курсах.
4. В 2020 запустил проект Miston Cats — командные стримы, где бывшие олимпиадники (ныне студенты или работающие программисты) решают олимпиады школьников и болтают о жизни.
Плейлист на YouTube: https://www.youtube.com/playlist?list=PLn4CTt5ibU6c-ykPIbX5OW6TuqxmDL3NK

Группу 1 ведёт Анатолий Максудов
Когда: среда и пятница 18:00 – 20:00 по московскому времени
Языки программирования: Python 3, Java, C++
На перечисленные темы будет по одному занятию. Каждое из таких тематических занятий состоит из теории и примера реализации алгоритма или структуры данных, а также разбора пары задач с олимпиад на данную тему.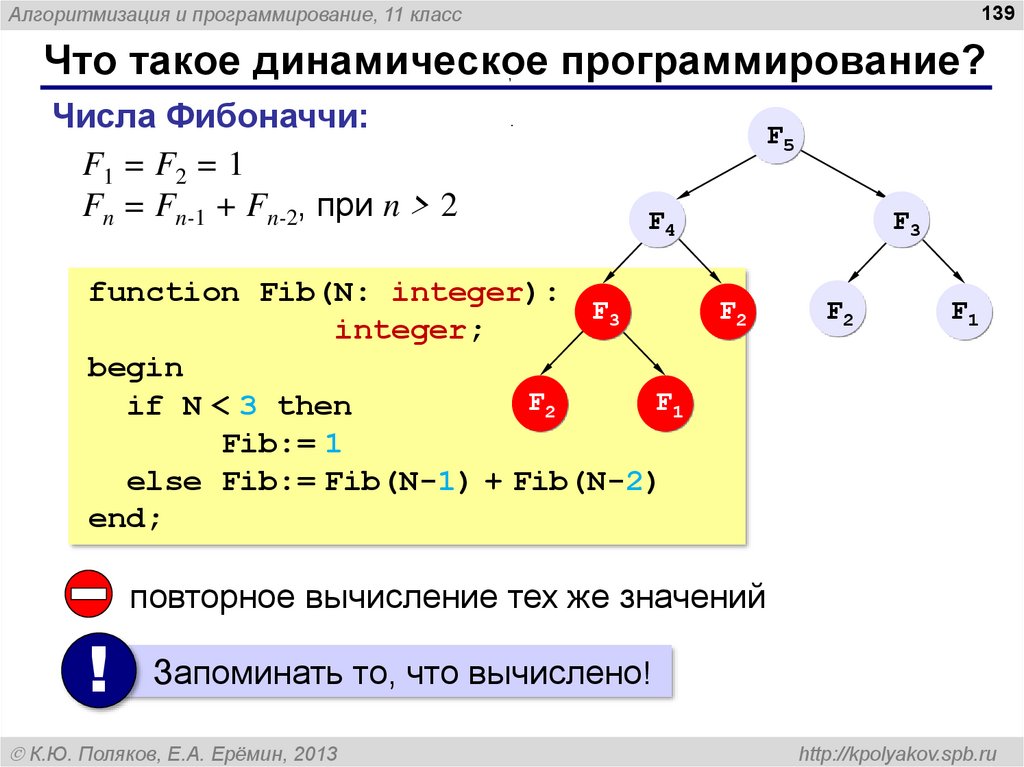 Раз в два-три занятия будет проводиться нетематическое занятие, состоящее из разбора «домашнего задания» — набора задач на изученные темы. Также во время занятий будут комментироваться ошибки в решениях и ответы на вопросы (при желании – в личных сообщениях). Занятия не привязаны к определенному языку программирования. Однако разбор большинства задач будет включать в себя написание решения задачи на одном из названных языков, в избранных случаях – на всех трёх сразу.

Прошедшие данный курс будут иметь базовые знания алгоритмов и структур данных, что позволит им лучше понимать и более эффективно реализовывать индустриальные проекты. А также поможет не упасть в грязь лицом на олимпиадах по программированию.

Группа B – Продвинутая


 Подготовка к ВсОШ и олимпиадам перечня РСОШ

Знание базовых алгоритмов и структур данных и желание достичь результатов на олимпиадах.

Основные темы:
— Какие бывают олимпиады по программированию и их особенности
— Задачи на реализацию и логическое мышление
— Динамическое программирование: краткий повтор тем группы C
— Динамическое программирование: задачи с олимпиад, Bitset
— Бинарный и тернарный поиски по ответу
— PQ, Set, Map, PBDS tree
— Графы: краткий повтор тем группы C
— Графы: поиск мостов и точек сочленения
— Система непересекающихся множеств (СНМ)
— Корневые оптимизации
— Дерево отрезков и дерево Фенвика
— LCA и разреженные таблицы
— Строковые алгоритмы: повтор тем группы C и префиксное дерево (бор)

Дополнительные темы:
— Интерактивные задачи и задачи с двойным запуском
— Алгоритм Ахо-Корасик
— Суффиксный массив
— Центроидная декомпозиция дерева
— Heavy-Light декомпозиция дерева»

Анатолий Максудов
Тренер по спортивному программированию
Достижения: 1. Призёр олимпиад школьников из перечня РСОШ по информатике и математике 2014/2015 учебного года.
2. Автор и разработчик задач олимпиады Innopolis IT РОСТ 2019/2020 по информатике и индивидуальных туров по информатике олимпиады НТИ c 2017 по 2020.
3. С 2017-го года готовлю к олимпиадам по программированию. Офлайн на сборах и последний год онлайн на полугодовых курсах.
4. В 2020 запустил проект Miston Cats — командные стримы, где бывшие олимпиадники (ныне студенты или работающие программисты) решают олимпиады школьников и болтают о жизни. Плейлист на YouTube: https://www.youtube.com/playlist?list=PLn4CTt5ibU6c-ykPIbX5OW6TuqxmDL3NK

Когда: воскресенье 14:00 – 18:00 по московскому времени
Языки программирования: Python 3, Java, C++

На основные темы будет по занятию. Иногда за занятие будет рассказываться сразу две темы. По каждой основной теме рассказывается теория с примерами реализации алгоритма или структуры данных, а также разбор пары задач с олимпиад на данную тему. Раз в три-четыре занятия будет проводиться нетематическое занятие, состоящее из разбора «домашнего задания» — набора задач на изученные темы.

Дополнительные темы рассказываются кратко на последних занятиях.
В начале занятия комментируются задачи, интересующие участников курса (например, с недавно прошедших олимпиад или других источников). Также во время занятий будут комментироваться ошибки в решениях домашних работ и ответы на вопросы (при желании – в личных сообщениях).
Занятия не привязаны к определенному языку программирования. Однако разбор большинства задач будет включать в себя написание решения задачи на одном из названных языков, в избранных случаях – на всех трёх сразу.Также обсуждение прошедших и предстоящих олимпиад с другими олимпиадниками, когда-либо проходившими этот курс, будет в отдельном чате.

Знает всё необходимое и даже больше об олимпиадах по программированию, алгоритмах и структурах данных, чтобы претендовать на дипломы ВсОШ и олимпиад перечня РСОШ.

Радиф Курбанов

Я занимаюсь олимпиадным программированием на регулярной основе с 2018 года. Азат Султанов и Анатолий Максудов — прекрасные педагоги.  Рекомендую занятия от Университета Иннополис, потому что они прокачают навык олимпиадного программирования, который, в свою очередь, поможет взять диплом олимпиады и поступить в желаемый вуз.

Никита Тимофеев

Записаться на регулярные занятия от Университета Иннополис мне посоветовали учителя. Мне стало интересно и в итоге на протяжении двух лет я изучал программирование и моделирование под руководством Ансата Абирова. Это позволило стать призером республиканской олимпиады.

Алексей Самойлов

Уже год я посещаю регулярные занятия по олимпиадному программированию. Мой педагог — Ансат Абиров, работаю с ним с удовольствием. Я получил полезный опыт и буду рекомендовать данные курсы, если в моем окружении появятся заинтересованные люди.

Тимур Набиуллин

С 2018 года я хожу на регулярные занятия Университета Иннополис по информатике. Мой педагог — Ансат Абиров, работать с ним было максимально комфортно, как по мне, все идеально. Регулярные занятия очень хорошо подтягивают знание предмета.

Андрей Хайрнасов

В прошлом учебном году я занимался олимпиадным программированием. Анатолий Максудов проводил курсы от Университета Иннополис прямо в моей школе, заниматься было очень комфортно. Я доволен полученным результатом — понимание алгоритмов улучшилось, этого достаточно. Было бы нереально за 11 класс стать всеросником, так как нужно больше опыта.

Мурат Мифтахов

Как-то я просматривал список доступных дополнительных занятий и увидел в нем прототипирование. Обучение по этому направлению вел Хани Хамед. Мне было очень интересно с ним работать и в итоге я занимался 2 года. Советую всем курсы Университета Иннополис по прототипированию, потому что для многих это будет новым опытом.

Алексей Ленсу

С октября 2019 года я хожу на курсы Университета Иннополис по информатике, которые ведет Ансат Абиров. Ему удалось заинтересовать меня информатикой, занятия оказались полезными и при случае я буду рекомендовать их своим знакомым.