Длина высоты треугольника по координатам: Даны вершины треугольника ABC. — примеры, решения

alexxlab / / Разное

х+у-2=0 9х-3у-4=0, координаты вершины А (2;2), составить уравнение сторон — Спрашивалка

Даны уравнения 2х высот треугольника АВС: х+у-2=0 9х-3у-4=0, координаты вершины А (2;2), составить уравнение сторон — Спрашивалка

В*

Виктория ***

  • сторона
  • треугольник
  • уравнение
  • высота
  • координата
  • вершина

Di

Diana

1. Т. к. координаты точки А не удовлетворяют ни одному из данных уравнений высот, то эти высоты проходят через точки В и С и перпендикулярны сторонам АВ и АС
2. Чтобы найти уравнения сторон АВ и АС нам достаточно найти хоть один вектор, перпендикулярный данным сторонам. Т. к. высоты перпендикулярны сторонам АВ и АС, то любой вектор, принадлежащий данной высоте перпендикулярен соответствующей стороне
3.

Найдем векторы, принадлежащие прямым:
х+у-2=0 и 9х-3у-4=0
Выразим:
x = 2 — y;
y = 3x — 4/3
Чтобы найти первую точку положим х = 0:
у = 2
у = -4/3
Итак мы нашли по одной точке на каждой из высот:
(0, 2) и (0, -4/3)
Найдем еще две точки. Для этого положим у = 0:
х = 2
х = 4/9
Итак мы нашли еще две точки на данных прямых:
(2, 0) и (4/9, 0)
Найдем координаты векторов, принадлежащих данным прямым (высотам) :
N1(2,-2) и N2(4/9, 4/3)
4. Теперь у нас есть все, чтобы найти уравнения прямых АВ и АС: т. е. векторы N1 и N2, перпендикулярные этим прямым и точка А, лежащая на данных прямых.
Строим общее уравнение прямых:
АВ: 2х — 2у + K = 0
AC: 4x/9 + 4y/3 + M = 0
Чтобы найти коэффициенты К и М подставим в уравнения координаты точки А:
4 — 4 + K = 0
K = 0
8/9 + 8/3 + M = 0
M = — 32/9
Окончательно получаем уравнения прямых АВ и АС:
AB: 2x — 2y = 0
AC: 4x/9 + 4y/3 — 32/9 = 0
Упростим уравнение стороны АС умножив его на 9:
4x + 12y — 32 = 0
5. Найдем точки В и С. Точка В находится на пересечении прямых 2x + 2y — 8 = 0 и х+у-2=0.
Решая совместно систему:
2x — 2y = 0
х+у-2=0.
Получим: х = 1, у = 1
Т. е. точка В имеет координаты (1, 1)
Аналогично из системы:
4x + 12y — 32 = 0
9х — 3у — 4 = 0
Найдем координаты точки С (1.2, 2.66)
6. Найдем каноническое уравнение прямой ВС. Для этого найдем координаты вектора ВС:
ВС (0.2, 1,66)
Используя координаты точки В и координаты вектора ВС построим уравнение стороны ВС:
(x — 1)/0.2 = (y — 1)/1.66
Вот и все. Уравнения всех трех сторон найдены.
Успехов!

Похожие вопросы

Как составить уравнение сторон треугольника. зная 1 высоту и 2 уравнения высот?

даны координаты вершин треугольника АВС А (1,-1) В (4,3) С (5,1) найти: 1)длина стороны АВ, 2) уравнение сторон АВ и ВС

Даны координаты вершин треугольника АВС: А (-6;1), В (2;4), С (2;2). Докажите что треугольник АВС- равнобедренный.

Стороны треугольника АВС заданы уравнениями: х+3у-7=0 (АВ) , 4х-у-2=0 (ВС) , 6х+8у-35=0 (АС).

4. Даны вершины треугольника АВС: А (-7; -2), В (-7; 4), С (5; -5). Найти: а) уравнение стороны АВ б) уравнение высоты С

Как найти координаты высоты треугольника зная координаты вершин?

Индивидуальные задания Даны координаты вершин треугольника АВС. Найти: 1) длину стороны АВ, 2) уравнения сторон АВ и АС

По координатам вершин треугольника АВС найти:

Найти координаты вершин треугольника, если даны уравнения двух сторон треугольника и двух высот:

даны вершины треугольника А (0; 1),В (6;5) С (12; -1).Составить уравнение высоты треугольника, проведенной из вершины C

Контрольные задания

Задача 1. Даны векторы ив некотором базисе трехмерного пространства. Показать, что векторыобразуют базис данного трехмерного пространства и найти координаты вектора в этом базисе.

    1. (1;2;3), (-1;3;2),(7;-3;5),(6;10;17).

    2. (4;7;8), (9;1;3),(2;-4;1),(1;-13;-13).

    3. (8;2;3), (4;6;10), (3;-2;1), (7;4;11).

    4. (10;3;1), (1;4;2),(3;9;2), (19;30;7).

    5. (2;4;1), (1;3;6),(5;3;1),(24;20;6).

    6. (1;7;3), (3;4;2),(4;8;5),(7;32;14).

    7. (1;-2;3), (4;7;2),(6;4;2),(14;18;6).

    8. (1;4;3), (6;8;5),(3;1;4),(21;18;33).

    9. (2;7;3), (3;1;8),(2;-7;4),(16;14;27).

    10. (7;2;1), (4;3;5),(3;4;-2),(2;-5;-13).

Задача 2. Даны векторы . Показать, что векторыобразуют базис четырехмерного пространства, и найти координаты векторав этом базисе.

2.1.

2.2.

2.3.

2. 4.

2.5.

2.6.

2.7.

2.8.

2.9.

2.10.

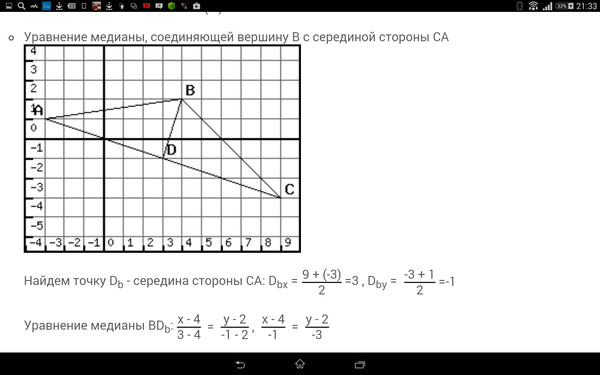
Задача 3. Даны вершины треугольника. Найти: 1) длину стороны; 2) внутренний уголв радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину; 4) уравнение медианы, проведенной через вершину; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины; 7) систему неравенств, определяющих треугольник. Сделать чертеж.

3.1. .

3.2. .

3.3. .

4.4. .

3. 5. .

3.6. .

3.7. .

3.8. .

3.9. .

3.10. .

Задача 4. Даны координаты вершин пирамиды А1А2А3А4. Найти:1)длину ребра А1А2; 2) угол между ребрами А1А2 и А1А4;3) угол между ребром А1А4 и гранью А1А2А3; 4) площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8)уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.

4.1. А1(4;2;5), А2(0;7;2), А3(0;2;7), А4 (1;5;0).

4.2. А1(4;4;10), А2(4;10;2), А3(2;8;4), А4 (9;6;4).

4.3. А1(4;6;5), А2(6;9;4), А3(2;10;10), А4 (7;5;9).

4.4. А1(3;5;4), А2(8;7;4), А3(5;10;4), А4 (4;7;8).

4.5. А1(10;6;6), А2(-2;8;2),

А3(6;8;9), А4 (7;10;3).

4.6. А1(1;8;2), А2(5;2;6), А3(5;7;4), А4 (4;10;9).

4.7. А1(6;6;5), А2(4;9;5), А3(4;6;11), А4 (6;9;3).

4.8. А1(7;2;2), А2(5;7;7), А3(5;3;1), А4 (2;3;7).

4.9. А1(8;6;4), А2(10;5;5), А3(5;6;8), А4 (8;10;7).

4.10. А1(7;7;3), А2(6;5;8), А3(3;5;8), А4 (8;4;1).

Задача 5 . Найти матрицу, обратную матрице

.

Проверить результат, вычислив произведение данной и обратной матриц.

Задача 6. Дана система линейных уравнений

Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления:

6. 1. 6.2.

6.3. 6.4.

6.5. 6.6.

6.7. 6.8.

6.9. 6.10.

Решения типовых задач

Задача 1. Даны векторы , , и в некотором базисе трехмерного пространства. Показать, что векторы образуют базис данного трехмерного пространства и найти координаты вектора в этом базисе.

Решение. Векторы образуют базис, если они линейно независимы. Составим векторное равенство

. Записывая в виде векторов – столбцов, получим

.

Задача свелась, таким образом, к решению системы

.

Решим систему методом Гаусса.

.

Итак, система приведена к виду

.

Полученная система имеет единственное нулевое решение: , т.е. векторы линейно независимы и, следовательно, составляют базис. Вектор можно представить в виде , т.е. координаты вектора в этом базисе . Для отыскания координат вектора решим систему линейных уравнений методом Гаусса:

.

.

Итак, система приведена к виду

.

Находим . т.е. вектор .

Задача 2. Даны векторы , , , и . Показать, что векторы образуют базис четырехмерного пространства, и найти координаты вектора в этом базисе.

Решение. Векторы образуют базис, если они линейно независимы. Составим векторное равенство . Записывая в виде векторов – столбцов, получим .

Задача свелась, таким образом, к решению системы

Решим систему методом Гаусса.

. Итак, система приведена к виду .

Полученная система имеет единственное нулевое решение: , т.е. векторы линейно независимы и, следовательно, составляют базис. Вектор можно представить в виде , т.е. координаты вектора в этом базисе . Для отыскания координат вектора решим систему линейных уравнений методом Гаусса:

.

.

Итак, система приведена к виду

.

Находим , т.е. вектор .

Задача 3. Даны вершины треугольника :. Найти: 1) длину стороны; 2) внутренний уголв радианах с точностью до 0,001; 3) уравнение высоты, проведенной через вершину; 4) уравнение медианы, проведенной через вершину; 5) точку пересечения высот треугольника; 6) длину высоты, опущенной из вершины; 7) систему неравенств, определяющих треугольник

Решение.

1) Длину стороны (длина вектора) находим как расстояние между двумя точками плоскостии:.

Поэтому

2) Угол — это угол между векторамии. Координаты этих векторов:,. Таким образом.

Таким образом, получаем

3) Составим уравнение стороны :, или. Угловой коэффициент стороныравен; следовательно, в силу условия перпендикулярности, угловой коэффициент высоты, проведенной из вершины, равен. Уравнение этой высоты имеет вид, получаем, или.

4) Пусть точка М середина стороны . Найдем ее координаты:

т..

Уравнение медианы находим с помощью уравнения прямой, проходящей через две данные точки:, получим.

5) Составим уравнение еще одной высоты треугольника . Например, выберем высоту, проведенную из вершины. Аналогично пункту 3) составим уравнение стороны:

.

Угловой коэффициент стороны равен; следовательно, в силу условия перпендикулярности, угловой коэффициент высоты, проведенной из вершины, равен. Уравнение этой высоты имеет вид, получаем, или. Поскольку мы ищем точку пересечения высот треугольника, то координаты этой точки должны удовлетворять системе уравнений;Таким образом, точка пересечения высот треугольникаимеет координаты

6) Найдем длину высоты, опущенной из вершины по формуле расстояния от точкидо прямой::. Таким образом

7) Стороны треугольника заданы уравнениями прямых:

: ; (см. пункт 3).

: ; (см. пункт 5).

: ;;.

Каждая из этих прямых делит координатную плоскость на две полуплоскости. Область треугольника лежит выше прямой, т.е. в полуплоскости, которая задается неравенством:. Прямаяделит координатную плоскость на две полуплоскости, нам необходима та, которая удовлетворяет неравенству:. Из двух полуплоскостей, которые разделяет прямая, выбираем ту, которая задается неравенством:.

Таким образом, область треугольника , определяется системой неравенств:

Задача 4. Даны координаты вершин пирамиды :

. Найти:

  1. длину ребра ;

  2. угол между ребрами и ;

  3. угол между ребром и гранью ;

  4. площадь грани ;

  5. объем пирамиды; 6) уравнение прямой ;

7) уравнение плоскости ;

8) уравнение высоты, опущенной из вершины на грань . Сделать чертеж.

Р

ешение.

𝛽

,𝐴-2.

  1. Длина ребра есть длина вектора , координаты которого Т.к. длина вектора находится по формуле , то .

  2. Угол между ребрами и есть угол между векторами

=(-1,5,1) и =(4-6;4-1;10-1)=(-2;3;9), поэтому

Отсюда

  1. Обозначим угол между ребром и гранью через , тогда , где — угол между вектором =(-2;3;9) и нормальным вектором плоскости , которым является, например, векторное произведение векторов и

Т. к. векторное произведение векторов =() и находится по формуле , то . Итак, . Найдем теперь угол

значит

или

4) Т.к. длина векторного произведения двух векторов равна площади параллелограмма, построенного на этих векторах, как на сторонах, то площадь S грани (площадь треугольника) найдем как половину площади параллелограмма, построенного на векторах и как на сторонах, т.е. как половину длины векторного произведения этих векторов.

Т.к. (см. пункт 3), то

5) Т.к. объем V треугольной пирамиды, построенной на векторах , находится по формуле , где — смешанное произведение векторов , то

. Найдем смешанное произведение векторов

и по формуле

:

(определитель вычислен по схеме треугольников). Итак, .

6) Т.к. уравнение прямой, проходящей через точку параллельно вектору имеет вид , то уравнение прямой найдем как уравнение прямой, проходящей через точку в направлении вектора : .

7) Т.к. уравнение плоскости, проходящей через точку перпендикулярно вектору имеет вид ( нормальный вектор плоскости), то уравнение плоскости найдем как уравнение плоскости, проходящей через точку с нормальным вектором (см. пункт 3):

или

8) Уравнение высоты, опущенной из вершины на грань , найдем как уравнение прямой, проходящей через точку в направлении вектора -нормального вектора плоскости (см. пункт 3): .

Задача 5. Найти матрицу, обратную матрице . Проверить результат, вычислив произведение данной и обратной матриц.

Решение. Определитель матрицы

, значит обратная матрица существует. Найдем матрицу , транспонированную к : . Найдем алгебраические дополнения всех элементов матрицы и составим из них присоединенную матрицу .

.

Найдем обратную матрицу :

.

Проверка:

.

.

Задача 6. Дана система линейных уравнений

Доказать её совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.

Решение. 1) Докажем совместность системы. Для этого вычислим ранг матрицы А исходной системы и ранг расширенной матрицы системы

Д

2

3

ля удобства вычислений элементарные преобразования будем производить с матрицей:

~ ~~

т.е. по теореме Кронекера-Капелли система совместна.

2) Решим систему методом Гаусса. Для этого матрицу приведем к диагональному виду:

тиии

3) Решим систему матричным способом. Для этого введем следующие матрицы и исходную систему запишем в матричном виде.

.

Вычислим обратную матрицу . Определитель матрицыА , значит обратная матрица существует. Затем, вычислив к каждому элементу матрицыА алгебраические дополнения, составим из них матрицу , транспонируем ееи находим обратную матрицу.

=

.

Ответ:

Координатная геометрия: вычисление высоты равностороннего треугольника

Задавать вопрос

спросил

Изменено 9 лет, 10 месяцев назад

Просмотрено 1к раз

$\begingroup$ 92$ — упрощение

$ x\sqrt3 = b $ — значит, это говорит о том, что высота точки C должна быть равна x\sqrt3 единицам.

Это дает мне конечный результат с координатами $(0, 2)$. Однако, честно говоря, это не кажется мне логичным… что я в основном говорю с этим результатом, так это то, что все равносторонних треугольников имеют высоту в две единицы. {\circ}$:

\begin{массив}{ccc} (-x,0)+2x(\cos 60, \sin 60) &=& (-x,0) + 2x(\tfrac{1}{2},\tfrac{\sqrt{3}}{2} ) \\\\ &=& (0,x\sqrt{3}) \end{array}

Если вам нужен «перевернутый» треугольник, пусть $C=(0,-x\sqrt{3})$.

$\endgroup$

2

$\begingroup$

Нарисуйте схему, и вы увидите, как получается треугольник.

В равностороннем треугольнике все стороны равны. Таким образом, гипотенуза прямоугольного треугольника равна $2x$. Пусть третья координата представлена ​​как $(0,c)$. Вы должны выяснить, почему координата $X$ точки $C$ равна $0$. 92$

Следовательно, $c$ = —-

Надеюсь, это будет полезно.

$\endgroup$

$\begingroup$

У вас есть базовые вершины вашего равностороннего треугольника в (-x, 0) и (x, 0), поэтому высота вашего треугольника лежит на оси y в том, что вы называете (0, b). Это делает основание любого из прямоугольных треугольников, которые вы используете $ \ x \ $ , но тогда гипотенуза вашего треугольника (сторона равностороннего треугольника) имеет длину $ \ 2x \ $ . Поэтому установка по теореме Пифагора должна быть 92 . $$

Вам нужно возвести в квадрат это 2x …

$\endgroup$

$\begingroup$

Поскольку координаты равностороннего треугольника выражены в виде $x$, ответ будет таким же, потому что он зависит от длины каждой стороны, верно?

На самом деле найти его не так уж сложно, но позвольте мне показать вам один прием и важную теорему, которые мы используем для решения этой задачи.

1), Высота любого равнобедренного треугольника – это медиана, биссектриса прилежащего угла и биссектриса перпендикуляра.

2), Равносторонний треугольник является частным случаем равнобедренного.

Это должно сказать вам, что высота, лежащая в вашем случае на оси $y$, будет не только перпендикулярна основанию, но и будет делить верхний угол пополам. Это образует треугольник 30-60-90, который вы, должно быть, изучали в геометрии.

Итак, если вы хотите найти высоту, просто используйте отношение $1$-$2$-$\sqrt{3}$.

Помогает ли это?

$\endgroup$

Математическая задача: Координаты — вопрос № 52091, геометрия

Координаты (5, 2) и (-6, 2) являются вершинами шестиугольника. Объясните, как найти длину отрезка, образованного этими концами. Какова длина сегмента?

Правильный ответ:

x =  11

Пошаговое объяснение:

A=(5,2) B=(−6,2)  Ay​=By​  x=∣Ax​−Bx​∣ =∣5−(−6)∣=11


Нашли ошибку или неточность? Не стесняйтесь

написать нам

. Спасибо!

Советы для связанных онлайн-калькуляторов

Вы хотите преобразовать единицы длины?
Теорема Пифагора является основой для калькулятора прямоугольного треугольника.

You need to know the following knowledge to solve this word math problem:

  • geometry
  • analytic geometry
  • line segment
  • planimetrics
  • Pythagorean theorem
  • polygon
Units of physical количество:
  • Длина
Оценка слов Проблема:
  • Практика для 13 -летних
  • Практика для 14 -летнего возраста

Мы призываем вас посмотреть этот урок.

  • Разделить отрезок
    Найти точку P на отрезке AB, такую, что |AP| = г |АВ|. Координаты конечных точек: A = (−2, 0, 1), B = (10, 8, 5), отношение r = 1/4.
  • Прямоугольный 3478
    В прямоугольной системе координат проведен отрезок AB с концами A [1;6] и B [5;2]. Центр симметрии является началом системы координат. Найдите координаты центра этого отрезка в этой проекции симметрии.
  • Сегмент
    Вычислите длину отрезка AB, если координаты конечных вершин равны A[10, -4] и B[5, 5].
  • Построить 8
    Построить задачу аналитической геометрии, где требуется найти вершины треугольника ABC: Вершинами этого треугольника являются точки A (1,7), B (-5,1) C (5, -11) ). В указанной задаче следует использовать понятия расстояния от точки до прямой, рати
  • Координаты 2
    Координаты вершин показанного треугольника: A(1,7), B(5,2) и C (5,7). Какова длина отрезка АВ в единицах?
  • Отрезок линии
    Для сегмента линии, конечными точками которого являются L[-1, 13] и M[18, 2], найдите значение x и y для точки, расположенной 4 над 7, расстояние от L до M.
  • Призма
    Длина, ширина и высота правой призмы равны 17, 11 и 11 соответственно. Какова длина самого длинного отрезка, концы которого являются вершинами призмы?
  • Координаты пересечения диагоналей
    В прямоугольной системе координат нарисован прямоугольник ABCD. Эти координаты определяют вершины прямоугольника. A = (2.2) B = (8.2) C = (8.6) D = (2.6) Найдите координаты пересечения диагоналей прямоугольника ABCD.
  • Центр
    В треугольнике ABC есть точка D[1,-2,6], являющаяся центром |BC|, и точка G[8,1,-3], являющаяся центром тяжести треугольник. Найдите координаты вершины A[x,y,z].
  • Координаты шестиугольника
    Дан правильный шестиугольник ABCDEF. Точка А имеет координаты [1; 3], а точка D имеет координаты [4; 7]. Вычислите сумму координат центра его описанной окружности.
  • Гаррет
    Гаррет и Джеффри планируют поиск сокровищ. Они решают разместить сокровище в точке, находящейся на расстоянии 5 единиц от оси x и трех единиц от оси y. Джеффри кладет сокровище в точку J с координатами (5,3), а Гаррет кладет одно 9.0040
  • Сара 4
    Сара и Джамал были партнерами по учебе на уроке математики и работали независимо друг от друга. Каждый из них стартовал в точке (−2, 5) и переместился на 3 единицы по вертикали в плоскости. Каждый ученик прибыл в разную конечную точку. Как это возможно? Объясните и перечислите хорду
  • BC
    Окружность k имеет центр в точке S = [0; 0].

    No related posts.

    • Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *