1.5.4 Разность множеств
Разностью множеств А и В называют множество, состоящее из тех и только тех элементов, которые принадлежат только множеству А и не принадлежат множеству В. Разность множеств1 А и В обозначается А\В. Формально определение разности множеств А и В можно записать в виде:
. 1.16
Примеры.
Пусть имеем А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}. Тогда А\В={4,8,16}, а B\A={1,2,7,17,30}.
A={a,b,c,d}; B={a,d,e,f,g}. В этом случае получаем: А\В={b,c} и B\A={e,f,g}.
Если как и ранее
множества А и В изобразить в виде точек
кругов А и В соответственно, то разность
множеств будет представляться так, как
это показано на рис. 1.3, где а) соответствует
разности А\В, b)- разности
B\A.
1.5.5 Симметрическая разность
Симметрической разностью множеств А и В называют множество, состоящее из объединения множеств разностей А\В и В\А. Симметрическая разность множеств А и В обозначается символом , т.е А В. Таким образом, по определению
. 1.17
Нетрудно убедиться, что . 1.18
Примеры.
Имеем: А={4,5,8,12,16,21}; B={1,2,5,7,12,17,21,30}. Тогда
А В={1,2,4,7,8,16, 17,30}.
A={a,b,c,d}; B={a,d,e,f,g}. В этом случае получаем А В={b,c,e,f,g}.
Графически симметричная разность множеств А и В может быть представлена как показано на рис. 1.4. Закрашенные области соответствуют симметрической разности множеств А и В.
1.5.6 Универсальное множество
Если
в некотором рассмотрении участвуют
только подмножества некоторого
фиксированного множеств I,
то это самое большое множество называют универсальным (или
полным) множеством.
В различных конкретных случаях роль универсального множества играют различные множества. Так, при рассмотрении студентов института универсальным (полным) множеством является вся совокупность студентов. Отдельные группы (факультеты) можно рассматривать как подмножества. В некоторых случаях универсальным множеством может являться и отдельная группа, в которой имеют место свои подмножества (отличники; студенты, проживающие в общежитии; юноши; девушки и т.п.).
Вполне очевидно, что для универсального множества справедливы следующие соотношения:
и 1.19
Универсальное
множество удобно изображать графически
в виде множества точек прямоугольника.
Различные области внутри прямоугольника
будут означать различные подмножества
универсального множества. Изображение
множества в виде областей в прямоугольнике,
представляющем универсальное множество,
называют диаграммой Эйлера-Венна.
1.5.7 Дополнение множества
Множество , определяемое из соотношения
1.20
называют дополнением множества А (до универсального множества I)
Графически дополнение множества А может быть представлено как показано на рис. 1.5.
Формальное определение дополнения множества А может быть записано как
1.21
Из определения дополнения множества следует, что А и не имеют общих элементов, т.е.
1.22
Кроме того, 1.23
Из
симметрии формул 1.22 и 1.23 следует, что
не только
является
дополнением А, но и А является дополнением
.
Но дополнение
есть .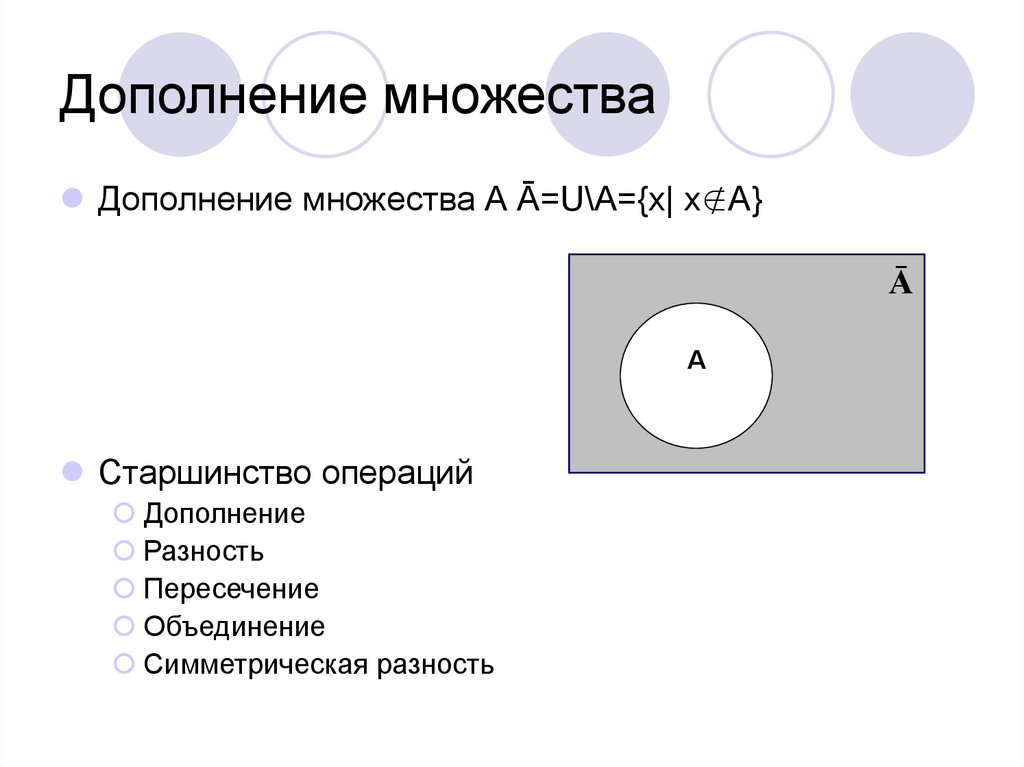
Таким образом 1.24
Рис. 1.5
С помощью операции дополнения удобно представить разность множеств:
= , т.е 1.25
SQL INTERSECT и EXCEPT — операторы для пересечения и разности результатов запросов
Навигация по уроку
- Операции пересечения и разности множеств в SQL
- Пересечение множеств: оператор SQL INTERSECT и его альтернативы
- Разность множеств: оператор SQL EXCEPT и его альтернативы
- Оператор SELECT
- Реляционная алгебра и её операции
| Назад | Содержание | Вперёд>>> |
Оператор SQL INTERSECT реализует операцию реляционной алгебры пересечение множеств, оператор SQL EXCEPT —
разность множеств.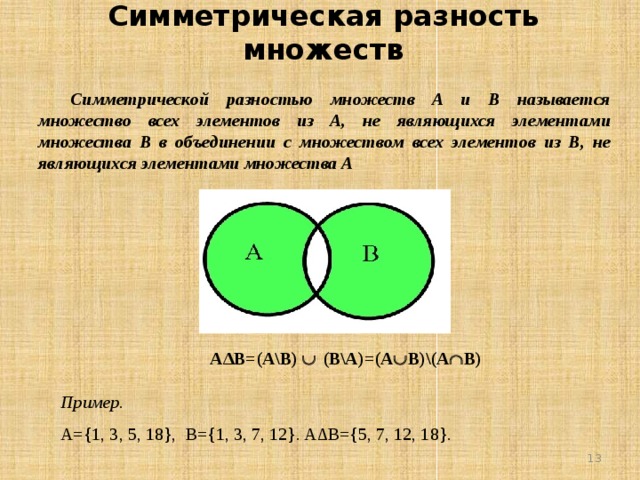
В виде множеств выступают результаты единичных запросов.
Таким образом, оператор SQL INTERSECT возвращает те и только те строки, которые возвращает и первый, и второй запросы. В свою очередь, оператор SQL EXCEPT возвращает те строки, которые возвращает первый запрос, и которых нет среди строк, возвращаемых вторым запросом.
Для того, чтобы были осуществлены операции пересечения и разности, запросы должны быть совместимы по объединению, то есть должны совпадать число столбцов, порядок их следования и их имена.
Оператор INTERSECT имеет следующий синтаксис:
SELECT ИМЕНА_СТОЛБЦОВ (1..N) FROM ИМЯ_ТАБЛИЦЫ INTERSECT SELECT ИМЕНА_СТОЛБЦОВ (1..N) FROM ИМЯ_ТАБЛИЦЫ
Оператор EXCEPT имеет следующий синтаксис:
SELECT ИМЕНА_СТОЛБЦОВ (1..N) FROM ИМЯ_ТАБЛИЦЫ EXCEPT SELECT ИМЕНА_СТОЛБЦОВ (1..N) FROM ИМЯ_ТАБЛИЦЫ
В этой конструкции единичные запросы могут иметь условия в секции WHERE, а могут не иметь их.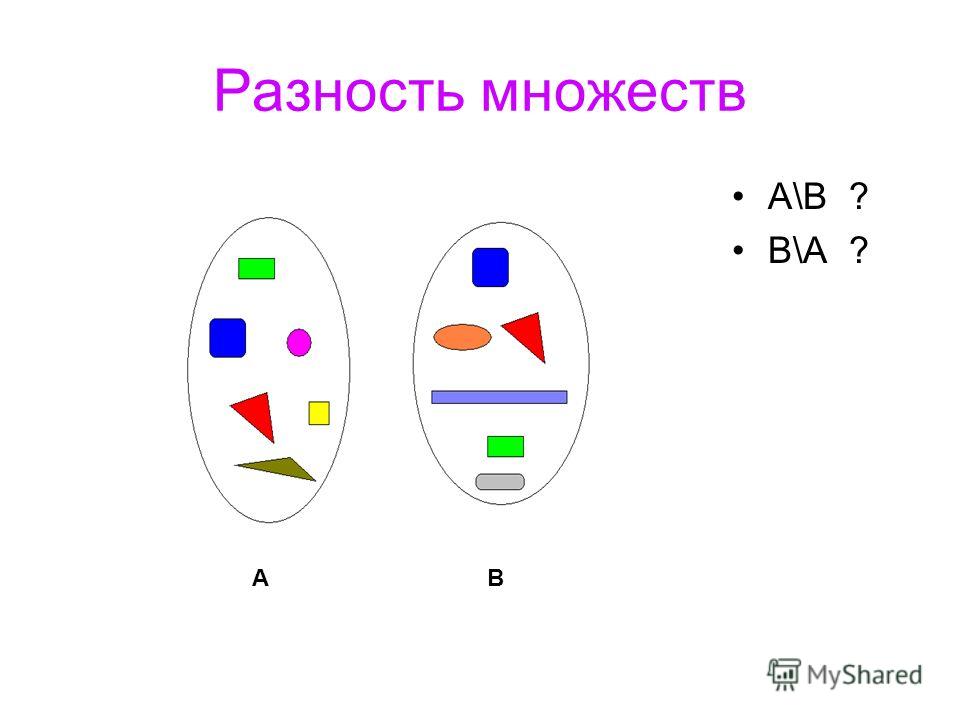
При помощи операторов INTERSECT и EXCEPT можно производить операции с запросами как к одной таблице,
так и к разным.
В примерах работаем с базой данных сети магазинов и таблицами SOLNYSHKO и VETEROK, содержащими данные о продуктах, которые имеются в магазинах с соответствующими названиями. Таблица SOLNYSHKO:
| Prod_ID | ProdName | Maker | Quantity |
| 1 | хлеб | AB | 100 |
| 2 | молоко | CD | 65 |
| 3 | мясо | EF | 75 |
| 4 | рыба | GH | 60 |
| 5 | сахар | IJ | 45 |
Таблица VETEROK:
| Prod_ID | ProdName | Maker | Quantity |
| 1 | хлеб | QW | 85 |
| 2 | молоко | LD | 70 |
| 3 | сыр | MV | 45 |
| 4 | масло | DG | 62 |
| 5 | рыба | LN | 55 |
Пересечением множеств A и B называется множество, состоящее их всех тех или только тех
элементов, которые принадлежат каждому из множеств A и B.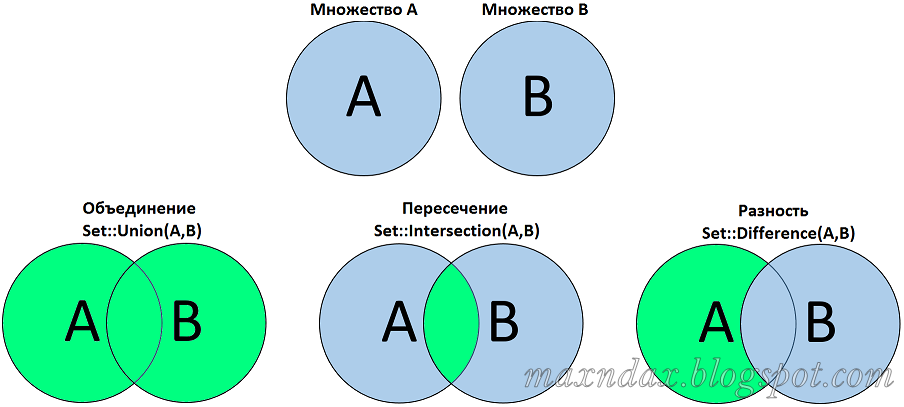
Больше об операциях над
множествами как над математическими объектами можно узнать из урока Множества и операции над множествами.
Пересечениями множеств могут служить носители одних и тех же имен в двух студенческих группах, овощи одних
и тех же наименований в двух корзинах и другие. Пересечением множеств является, наконец, набор товаров, которые имеются и в одном, и в другом магазинах.
Если вы хотите выполнить запросы к базе данных из этого урока на MS SQL Server, но эта СУБД не установлена на вашем компьютере, то ее можно установить, пользуясь инструкцией по этой ссылке.
Скрипт для создания базы данных магазинов, её таблиц и заполения таблиц данными — в файле по этой ссылке.
SELECT ProdName FROM Solnyshko INTERSECT SELECT ProdName FROM Veterok
Результатом выполнения запроса будет следующая таблица:
| ProdName |
| хлеб |
| молоко |
| рыба |
Во многих диалектах SQL, например, MySQL, оператор INTERSECT отсутствует.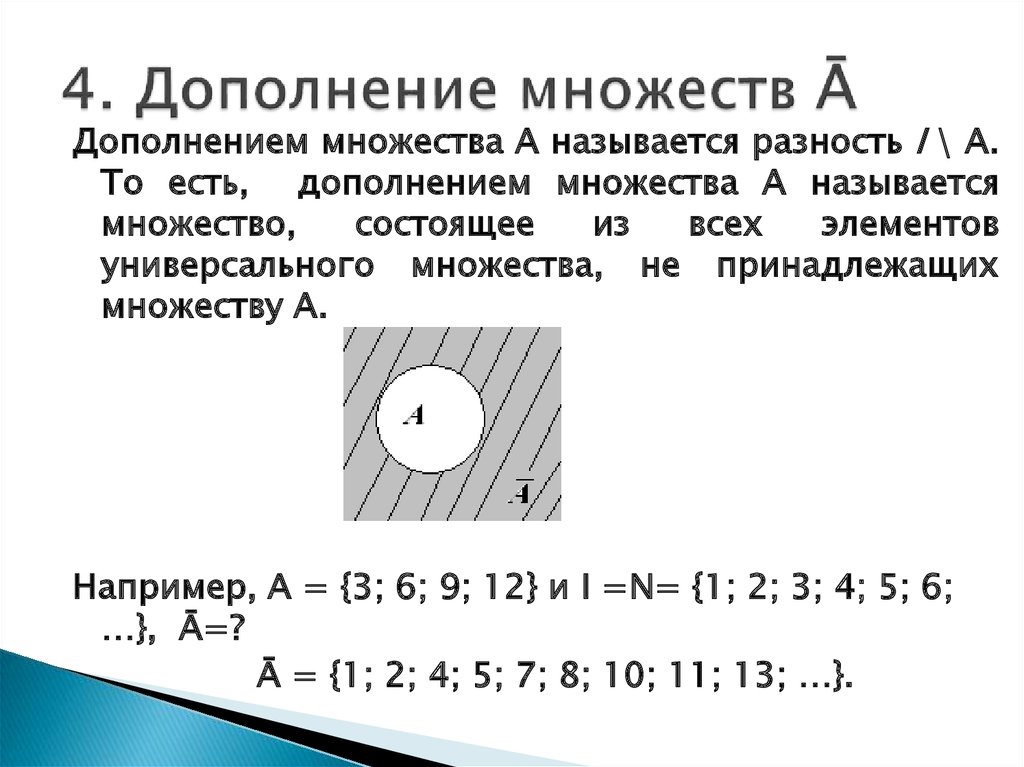
Но реализация операции
пересечения множеств возможна другими способами. Наиболее простой способ связан с использованием предиката EXISTS. В качестве альтернативы им можно
пользоваться и в MS SQL Server.
Пример 2. Вывести список продуктов, которые имеются и в мазазине Solnyshko, и в магазине Veterok. Использовать предикат SQL EXISTS. Пишем следующий запрос:
SELECT ProdName FROM Solnyshko AS name_soln WHERE EXISTS (SELECT ProdName FROM VETEROK WHERE ProdName=name_soln.ProdName)
Результатом выполнения запроса будет та же таблица, что и в примере 1:
| ProdName |
| хлеб |
| молоко |
| рыба |
- Аналогии между INTERSECT и EXISTS, EXCEPT и NOT EXISTS: более сложные примеры
Разностью множеств A и B называется множество состоящее из всех тех и только тех элементов
множества A, которые не являются элементами множества B.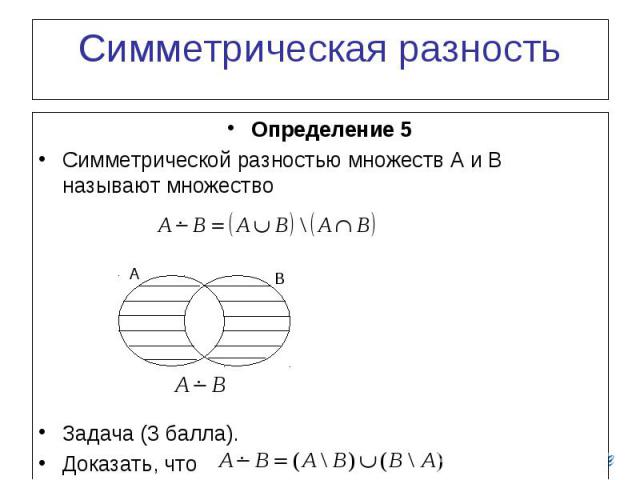
В частности, такое множество
может состоять из продуктов, которые имеются в одном из магазинов, но отсутствуют в другом магазине.
Пример 3. Вывести список продуктов, которые имеются в мазазине Solnyshko, и отсутствуют в магазине Veterok. Пишем следующий запрос с использованием оператора SQL EXCEPT:
SELECT ProdName FROM Solnyshko EXCEPT SELECT ProdName FROM Veterok
Результатом выполнения запроса будет следующая таблица:
| ProdName |
| мясо |
| сахар |
Во многих диалектах SQL, например, MySQL, оператор EXCEPT отсутствует. Наиболее простой альтернативный способ реализации разности множеств связан с использованием предиката EXISTS с отрицанием NOT, то есть NOT EXISTS. В качестве альтернативы им можно пользоваться и в MS SQL Server.
Пример 4. Вывести список продуктов, которые имеются в мазазине
SOLNYSHKO, и отсутствуют в магазине VETEROK.
Использовать предикат SQL NOT EXISTS. Пишем следующий запрос:
SELECT ProdName FROM Solnyshko AS name_soln WHERE NOT EXISTS (SELECT ProdName FROM Veterok WHERE ProdName=name_soln.ProdName)
Результатом выполнения запроса будет та же таблица, что и в примере 2:
| ProdName |
| мясо |
| сахар |
- Аналогии между INTERSECT и EXISTS, EXCEPT и NOT EXISTS: более сложные примеры
Поделиться с друзьями
| Назад | Содержание | Вперёд>>> |
Набор Разность между двумя и тремя наборами, свойства и примеры
Набор Разницу между двумя или тремя наборами можно понимать как разницу между данными наборами. Например, когда мы выполняем 8-3=5. Этот процесс понимается как получение разницы между двумя элементами. Точно так же в наборах, когда мы пишем X — Y = Z; это означает, что Z — это множество всех элементов X, которые не являются элементами Y.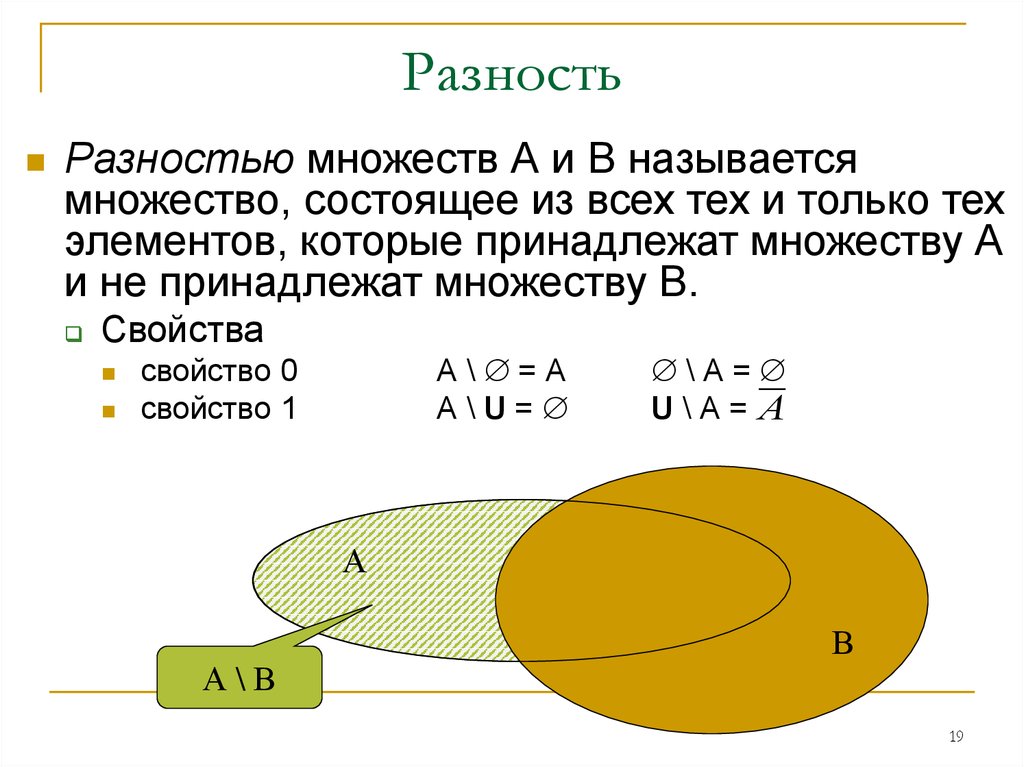
Другие операции с множествами — это объединение и пересечение множеств, дополнение множества.
Набор — это четко определенная группа чисел, объектов, алфавитов или любых элементов, заключенных в фигурные скобки, тогда как подмножество является частью набора. Диаграмма Венна использует перекрывающиеся круги или разные формы для представления логических ассоциаций между двумя или более конечными наборами элементов. Наборы подразделяются на отдельные типы, а именно: пустой набор, конечный набор, одноэлементный набор, эквивалентный набор, подмножества, набор мощности, универсальный набор, надмножество и бесконечный набор.
Определение разницы наборов: Разница наборов — это процесс получения разницы между двумя наборами.
Диаграммы Венна играют важную роль в теории множеств для изображения различных операций над множествами. В аналогичном подходе мы можем использовать Венна, чтобы показать разницу между двумя или тремя множествами. Рассмотрим приведенную ниже диаграмму:
На приведенной выше диаграмме Венна левый полумесяц (один с желтым цветом ) обозначает A – B, с другой стороны, правый полумесяц (один с розовый цвет) символизирует B – A.
Как найти разницу между двумя наборами?На приведенной выше диаграмме Венна мы увидели, как получить разность множеств с помощью диаграммы Венна. Давайте продолжим и узнаем больше о разнице между двумя наборами.
Если у нас два набора, скажем; установить P и Q, тогда P − Q в нотации построителя набора представлен следующим образом:
P – Q = {x : x ∈ P, и x ∉ Q}
На приведенной ниже диаграмме Венна показаны P – Q.
Результирующий набор получается удалением элементов P ∩ Q из P. Также читается как «P минус Q».
Аналогично, на приведенной ниже диаграмме Венна показано Q – P.
Результирующее множество получается удалением элементов P ∩ Q из Q. Символически записывается как Q – P и читается как «Q минус P».
Под заголовком выше мы увидели, как можно вычислить разницу между двумя множествами. Продолжение процесса позволяет нам понять разницу между тремя наборами. Если нам даны три непустых множества, скажем, P, Q и R, то P – Q – R можно представить на приведенной ниже диаграмме Венна.
Здесь P – Q – R ( фиолетовая область ) обозначает множество, включающее элементы P, которых нет в Q и R.
Симметричная разность между любыми двумя заданными множествами — это множество, включающее элементы, находящиеся либо в первом, либо во втором множестве, но не входящие в оба множества. Обратитесь к приведенной ниже диаграмме Венна, чтобы понять то же самое.
На приведенной выше диаграмме Венна P и Q представляют собой два множества. Симметричная разница между P и Q представлена обозначением P ∆ Q и изображается как P ∆ Q = (P – Q) U (Q – P).
Узнать о конечных и бесконечных множествах
Важные свойства разности множествНиже перечислены важные свойства разности множеств:
Свойство 1: = Y – X = ∅ т.е. пустое множество.
Свойство 2: Отличие непустого множества от пустого множества состоит в самом множестве, т. е. X – ∅ = X.
Свойство 3: набор. Математически выражается как X – X = ∅.
Свойство 4: Отличие множеств непустого множества от пустого приводит к пустому множеству, т. е. ∅ – X = ∅.
Свойство 5: Аналогично предыдущему свойству отличие множеств универсального множества от любого другого множества, скажем P, снова равно пустому множеству, т. е. P – U = ∅.
Свойство 6: Если мы вычтем надмножество из подмножества, результатом будет пустое множество. Математически выражается X – Y = ∅, если X ⊂ Y.
Свойство 7: Если P и Q два непересекающихся множества, т. е. они не содержат общих элементов, то P – Q = P и Q – P = Q.
Здесь указано, что:
P – Q = P, если P ∩ Q = ∅
Q – P = Q, если P ∩ Q = ∅
Установить разностный порядокустанавливает один раз. Там мы видели диаграмму Венна P – Q и Q – P. Совершенно ясно, что равнодействующая P – Q не равна Q – P, т.е. P – Q ≠ Q – P. Это, безусловно, имеет отношение к тому, что мы читал об общем расчете разницы, что 8 — 3 не тождественно 3 — 8.
Это свойство говорит о том, что при различии наборов следует обращать внимание на порядок наборов. Это указывает на то, что разность множеств некоммутативна.
Пример установки порядка разности: Если A = {2, 4, 6, 8, 10} и B = {4, 8, 12, 16, 20}.
A минус B=A – B={2, 6, 10} и B минус A=B – A={ 12, 16, 20}
Таким образом, из результатов мы можем утверждать, что A – B ≠ B – A.
Это также означает, что результат разности наборов будет другим, если мы изменим порядок двух наборов. 9c\) = U – P.
Это указывает на множество всех компонентов, которые имеются в универсальном множестве, но не являются компонентами множества P.
Разница между Set Intersection и Set Difference множества и разница между двумя множествами — две важные операции над множествами. Довольно просто провести различие между операциями пересечения и объединения. Но как отличить пересечения от различий между множествами?Давайте узнаем основную разницу между пересечением множеств и разницей множеств с помощью табличных данных ниже:
| Пересечение множеств | Разница множеств | 8 общие элементы или повторяющиеся элементы с множествами. | Различие между двумя наборами состоит в наборе элементов, состоящем из элементов одного набора, которых нет в другом наборе. |
| Для двух наборов скажем P и Q: \(P\cap{Q}=\{x:x\in{P}{\text{ and }}x\in{Q}\}\) | Для двух множеств скажем P и Q: P – Q = {x : x ∈ P, и x ∉ Q} |
| Пересечение двух множеств P и Q – это множество, состоящее из всех тех компонентов, которые являются общими для обоих наборов. Обозначается знаком «∩». | Разность между двумя множествами P и Q означает множество элементов, которые присутствуют в P, но не присутствуют в Q. Оно обозначается как P-Q. |
| Диаграмма Венна по пересечению наборов: | Диаграмма Венна различий в наборах: |
Решение: Даны данные: X = {2, 3, 5, 7, 9} и Y = {1, 3, 4, 5, 6, 7, 8}
Чтобы найти разницу X-Y, вычеркните все компоненты, имеющиеся как в X, так и в Y.
X-Y = {2, 3, 5, 7, 9}-{1, 3, 4, 5, 6, 7 , 8}
X-Y — набор оставшихся компонентов X. т. е. X-Y = {2, 9}.
Решено Пример 2: Рассмотрим два множества A={a, e, i, o, u} и B={a, b, c, d, e}. Получите A-B и B-A и начертите для них диаграмму Венна.
Решение: Дано:
A={a, e, i, o, u} и B={a, b, c, d, e}
A-B={a, e, i, o, u}-{a, b, c, d, e}={i, o, u}
B-A={a, b, c, d, e} -{a, e, i, o, u}={b, c, d}
Диаграмма Венна для того же:
Решенный пример 3: Если X = {5, 10, 15, 20, 25}, Y = {10, 20, 30, 40} и Z = {15, 30, 45, 60}, затем получите значение X – Y – Z.
Решение: Учитывая X = {5, 10, 15, 20, 25}
Y = {10, 20, 30, 40} и
Z = {15, 30, 45, 60}
X – Y – Z={5, 10, 15, 20, 25}-{10, 20, 30, 40}-{15, 30, 45, 60}
X – Y – Z={5, 25}
Подводя итоги статьи, можно констатировать, что различием между множествами X и Y в данном конкретном порядке является множество компонентов, которые присутствуют в множестве X, но отсутствуют в множестве Y , Разница между наборами X и Y обозначается символом X – Y или просто мы пишем это как X минус Y. Наконец, результат X минус Y не совпадает с Y минус X.
Мы надеемся, что выше статья о разнице наборов полезна для вашего понимания и подготовки к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о различиях наборов В. 1. Какие 4 операции над наборами?
ANS.1 4 важные операции наборов:
1. Союз наборов
2. Пересечение наборов
3. Дополнение наборов
4. Разница между наборами
Q .2 Что такое определение разности наборов?
Ответ 2 Разность множеств — это процесс получения разницы между двумя множествами.
Q.3 Что такое обозначение множества разностей?
Ответ 3 Если у нас есть два набора, скажем; установить P и Q, то P − Q в нотации построителя множеств представляется следующим образом: P – Q = {x : x ∈ P, и x ∉ Q}
Q.4 Что такое симметричная разность множеств?
Ответ 4 Симметричная разность между любыми двумя заданными множествами — это множество, включающее элементы, находящиеся либо в первом, либо во втором множестве, но не входящие в оба множества.
В.5 В чем разница между набором пересечений и набором разностей?
Ответ 5 Пересечение множества — это пересечение внутри двух или более заданных множеств, означающее общие элементы или повторяющиеся элементы с множествами.
Разность наборов — это разность между двумя наборами. Это набор элементов, состоящий из элементов одного набора, отсутствующих в другом наборе.
Скачать публикацию в формате PDF| Многоугольники: определение, классификация, формулы с изображениями и примерами |
| Четырехугольник: изучите определение, типы, формулы, периметр, площадь, стороны, углы на примерах! |
| Изучение производных правил и правил дифференцирования с доказательством и формулой |
| Производная 2x с доказательством и формулой |
| Производная формулы xsinx с доказательством по правилу произведения и первому принципу |
Симметричная разность между двумя наборами
следующий → ← предыдущая В этой статье мы собираемся обсудить симметричную разницу между двумя множествами. Надеюсь, эта статья поможет вам понять симметричную разницу между двумя множествами. Что такое симметричная разность?Другой вариант разности — симметричная разность. Предположим, что есть два множества, A и B. Симметричная разность между обоими множествами A и B — это множество, содержащее элементы, присутствующие в обоих множествах, за исключением общих элементов. Симметричная разность между двумя множествами также называется дизъюнктивным объединением . Симметричная разность между двумя множествами — это множество элементов, которые находятся в обоих множествах, но не находятся на их пересечении. Симметричная разница между двумя наборами A и B представлена как A Δ B или A ? Б . Мы можем понять это на примерах. Example1 Предположим, что есть два набора с некоторыми элементами. Набор А = {1, 2, 3, 4, 5} Установить B = {3, 5} Итак, симметричная разность между заданными множествами A и B равна {1, 2, 4} Или мы можем сказать, что A Δ B = {1, 2, 4} . Example2 Предположим, что есть два набора с некоторыми элементами. Установить А = {а, б, с, к, м, п} Установить B = {c, n} Итак, симметричная разность между заданными множествами A и B равна {a, b, k, m} Или мы можем сказать, что A Δ B = {a, b, k, m} . На приведенной ниже диаграмме Венна вы можете увидеть симметричную разницу между двумя наборами. Часть, заштрихованная цветом кожи на приведенной выше диаграмме Венна, представляет собой симметричную разность между заданными множествами, т. е. A Δ B . Давайте посмотрим на некоторые свойства симметричной разности между двумя множествами. Свойства Ниже перечислены некоторые свойства симметричной разности;
‘Симметричная разность между двумя множествами’ v/s ‘Разность между двумя множествами’Разница между двумя наборами Разность между двумя множествами А и В есть множество всех тех элементов, которые принадлежат А, но не принадлежат В, и обозначается цифрой 9. Пример: Пусть A = {1, 2, 3, 4} и В = {3, 4, 5, 6} , тогда A — B = {3, 4} и B — A = {5, 6} Симметричная разность между двумя наборамиСимметричная разность между двумя множествами, A и B, — это множество, содержащее все элементы, которые есть в A или B, но не в обоих. Он представлен A Δ B или A ? Б . Пример: Пусть A = {1, 2, 3, 4} и В = {3, 4, 5, 6} , тогда A Δ B = {1, 2, 5, 6} Теперь давайте рассмотрим несколько примеров, чтобы лучше понять симметричную разницу между двумя множествами. Вопрос 1 — Предположим, у вас есть наборы A = {10, 15, 17, 19, 20} и B = {15, 16, 18}. Найдите разницу между обоими множествами A и B, а также найдите симметричную разницу между ними. Решение — Дано, А = {10, 15, 17, 19, 20} и В = {15, 16, 18} Разница между обоими комплектами — А — В = {10, 15, 17, 19, 20} — {15, 16, 18} = {10, 17, 19, 20} Симметричная разница между обоими наборами — А Δ В = {10, 15, 17, 19, 20} — {15, 16, 18} = {10, 16, 17, 18, 19, 20} Question2 — Предположим, у вас есть наборы A = {2, 4, 6, 8} и B = {2, 5, 7, 8}. Решение — Дано, A = {2, 4, 6, 8} и B = {2, 5, 7, 8} Мы знаем, что B ∆ A = (B ∪ A) — (B ∩ A) Попробуем решить вопрос поэтапно. Итак, первый шаг — найти объединение множества A и множества B. Следовательно, (B ∪ A) = {2, 5, 7, 8} ∪ {2, 4, 6, 8} = {2, 4, 5, 6, 7, 8} После этого нужно вычислить пересечение обоих множеств. (В ∩ А) = {2, 5, 7, 8} ∩ {2, 4, 6, 8} = {2, 8} Теперь нам нужно найти разницу между объединением и пересечением множеств A и B, как указано в формуле Итак, (В ∪ А) — (В ∩ А) = {2, 4, 5, 6, 7, 8} — {2, 8} = {4, 5, 6, 7} Следовательно, B ∆ A = {4, 5, 6, 7} Что будет равно A Δ B, как сказано выше, «Симметричная разность коммутативна». Теперь мы покажем симметричную разницу между обоими наборами с помощью диаграммы Венна. Сначала на диаграмме Венна мы нарисуем две окружности, представляющие множества A и B. Как подсчитано выше, пересечение между обоими множествами равно {2, 8}, поэтому мы перечислили эти элементы в области пересечения. Затем мы перечисляем оставшиеся элементы в их соответствующих кругах набора, т. Е. {4, 6} в наборе A и {5, 7} в наборе B. После размещения элементов диаграмма Венна будет — Когда мы смотрим на приведенную выше диаграмму Венна, мы видим универсальное множество U. Оба множества A и B являются подмножествами универсального множества U. Элементы {2, 8} являются пересекающимися элементами, поэтому они представлены в области пересечения. Область светло-оранжевого цвета является объединением множеств, за исключением пересекающейся области. Эта область представляет собой симметричную разность между наборами A и B и будет представлена как — .B Δ A = (B ∪ A) — (B ∩ A) = {4, 5, 6, 7} Вопросы 3 — Предположим, у вас есть наборы A = {5, 6, 8, 9, 10} и B = {2, 4, 7, 10, 19}. |