Касательная плоскость и нормаль к явно заданной поверхности.
Касательной плоскостью к поверхности в ее точке $M_0$ (точка касания) называется плоскость, содержащая в себе все касательные к кривым, проведенным на поверхности через эту точку.
Нормалью к поверхности называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.
Если уравнение поверхности имеет вид $$F(x,y,z)=0,$$ то уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ есть $$F_x'(x_0, y_0, z_0)(x-x_0)+F_y'(x_0, y_0, z_0)(y-y_0)+F_z'(x_0, y_0, z_0)(z-z_0)=0.$$
Уравнение нормали $$\frac{x-x_0}{F_x'(x_0, y_0, z_0)}=\frac{y-y_0}{F_y'(x_0, y_0, z_0)}=\frac{z-z_0}{F_z'(x_0, y_0, z_0)}.$$
В случае задания поверхности в явной форме $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$\frac{x-x_0}{f_x'(x_0, y_0)}=\frac{y-y_0}{f_y'(x_0, y_0)}=\frac{z-z_0}{-1}.
$$
Примеры:
7.229. а) Найти уравнения касательной плоскости и нормали к поверхности $z=\sin x\cos y$ в точке $(\pi/4, \pi/4, \pi/4).$
Решение.
Для поверхности $$z=f(x, y)$$ уравнение касательной плоскости в точке $M_0(x_0, y_0, z_0)$ имеет вид $$z-z_0=f_x'(x_0, y_0)(x-x_0)+f_y'(x_0, y_0)(y-y_0),$$ а уравнение нормали $$\frac{x-x_0}{f_x'(x_0, y_0)}=\frac{y-y_0}{f_y'(x_0, y_0)}=\frac{z-z_0}{-1}.$$
Находим частные производные:
$z’_x=(\sin x\cos y)’_x=\cos x\cos y;$
$z’_x(\pi/4, \pi/4)=\cos \frac{\pi}{4}\cos \frac{\pi}{4}=\frac{1}{\sqrt 2}\cdot\frac{1}{\sqrt 2}=\frac{1}{2};$
$z’_y=(\sin x\cos y)’_y=-\sin x\sin y;$
$z’_y(\pi/4, \pi/4)=-\sin \frac{\pi}{4}\sin \frac{\pi}{4}=-\frac{1}{\sqrt 2}\cdot\frac{1}{\sqrt 2}=-\frac{1}{2};$
Таким образом, уравнение касательной плоскости: $$z-\frac{\pi}{4}=\frac{1}{2}(x-\frac{\pi}{4})-\frac{1}{2}(y-\frac{\pi}{4})\Rightarrow$$ $$\frac{1}{2}x -\frac{1}{2}y-z+\frac{\pi}{4}=0.
2-2x+6y=4$ найти уравнение нормали, параллельной прямой $\frac{x+2}{1}=\frac{y}{3}=\frac{z+1}{4}.$
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  § 1. Действительные числа. § 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 22. Производные различных порядков § 23.  x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2.  Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19. 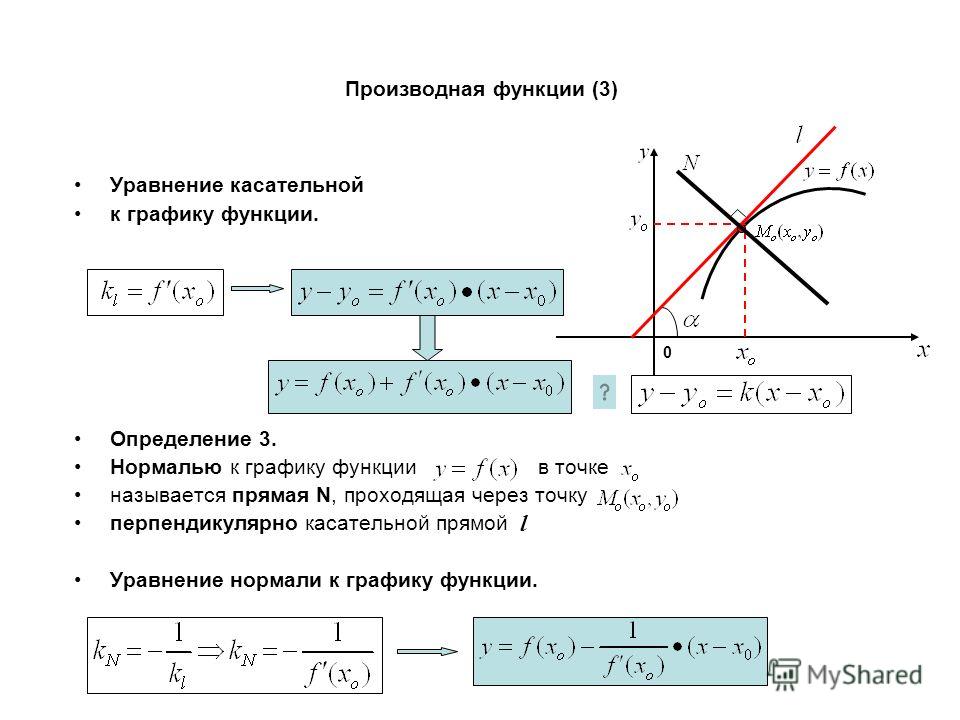 Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  Формула Чебышева§ 10. Интегралы, зависящие от параметра. Гамма-функция Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
многомерное исчисление — В каких точках поверхности касательная плоскость параллельна плоскости $xy$?
спросил
Изменено 6 лет, 5 месяцев назад
Просмотрено 13 тысяч раз
$\begingroup$
При каких очках.
{2}x + 3x$ касательная плоскость параллельна плоскости $xy$? 92=3.$$ Это уравнение гиперболы. В любой точке этой гиперболы касательная плоскость поверхности параллельна $OXY.$
$\endgroup$
$\begingroup$
Подсказка
Плоскость, параллельная плоскости $xy-$, будет иметь уравнение вида
$$z=z_0+0.x+0.y.$$
Ваша очередь решать систему
$$\frac{\partial F}{\partial x}(x_0,y_0)=0$$
$$\frac{\partial F}{\partial y}(x_0,y_0)=0$$
$\endgroup$
1.7: Касательные плоскости и нормальные линии
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 602
- Ларри Грин
- Общественный колледж озера Тахо
Касательные плоскости
Пусть \(z = f(x,y)\) — функция двух переменных.
Мы можем определить новую функцию \(F(x,y,z)\) трех переменных, вычитая \(z\). Это имеет условие
\[ F(x,y,z) = 0.\nonumber \]
Теперь рассмотрим любую кривую, заданную параметрически с помощью
\[x = x(t), \;\;\; у = у(t), \;\;\; z = z(t).\nonumber \]
Мы можем написать,
\[F(x(t), y(t), z(t)) = 0.\nonumber \]
Дифференцирование обеих частей по \(t\) и использование цепного правила дает
\[F_x(x, y, z) x’ + F_y(x, y, z) y’ + F_z(x , y, z) z’ = 0\nonumber \]
Обратите внимание, что это скалярное произведение функции градиента и вектора \(\langle x’,y’,z’\rangle \),
\[ \nabla F \cdot \langle x’, y’, z’\rangle = 0.\nonumber \]
В частности, вектор градиента ортогонален касательной к любой кривой на поверхности. Это приводит к:
Определение: Касательная плоскость
Пусть \(F(x,y,z)\) определяет поверхность, дифференцируемую в точке \((x_0,y_0,z_0)\), тогда касательная плоскость к \(F ( x, y , z )\) в точке \(( x_0, y_0, z_0)\) плоскость с вектором нормали
\[ \nabla \, F(x_0,y_0,z_0) \nonumber \]
, проходящая через точку \((x_0,y_0,z_0)\).
В частности, уравнение касательной плоскости имеет вид
\[ \nabla \, F(x_0,y_0,z_0) \cdot \langle x — x_0 , y — y_0 , z — z_0 \rangle = 0. \nonumber \]
Пример \(\PageIndex{1}\) 92 — xy — z\nonumber \]
затем
\[\nabla F = \langle 6x — y, -x, -1\rangle . \nonumber \]
В точке \((1,2,1)\) вектор нормали равен
\[\nabla F(1,2,1) = \langle 4, -1, -1\ ранг . \nonumber \]
Теперь используйте формулу нормали точки для плана
\[\langle 4, -1, -1\rangle \cdot \langle x — 1, y — 2, z — 1\rangle = 0\ nonumber \]
или
\[4(x — 1) — (y — 2) — (z — 1) = 0.\nonumber \]
Наконец, мы получаем
\[ 4x — y — z = 1.\nonumber \]
Нормальные линии
Для данных вектора и точки существует единственная линия, параллельная этому вектору, которая проходит через точку. В контексте поверхностей у нас есть вектор градиента поверхности в данной точке. Это приводит к следующему определению.
Определение: нормальная линия
Пусть \(F(x,y,z)\) определяет поверхность, которая дифференцируема в точке \((x_0,y_0,z_0)\), тогда нормальная линия к \(F(x,y,z)\) at \((x_0,y_0,z_0)\) — линия с вектором нормали
\[ \nabla \, F(x_0,y_0,z_0) .
\nonumber \]
, проходящая через точку \((x_0,y_0,z_0)\). В частности уравнение нормальной линии
\[ x(t) = x_0 + F_x(x_0,y_0,z_0) t, \nonumber \]
\[ y(t) = y_0 + F_y(x_0,y_0 ,z_0) t, \nonumber \]
\[ z(t) = z_0 + F_z(x_0,y_0,z_0) t. \nonumber \]
Пример \(\PageIndex{2}\)
Найдите параметрические уравнения для нормальной линии к 92y + 1\rangle = \langle 12, 2, 3\rangle .\nonumber \]
Теперь используйте формулу, чтобы найти
\[x(t) = 1 + 12t, \;\;\; у(t) = 2 + 2t, \;\;\; z(t) = 3 + 3t.\nonumber \]
На приведенной ниже диаграмме показаны поверхность и нормаль.
Угол наклона
Дана плоскость с вектором нормали n угол наклона , \(q\) определяется как
\[\cos q = \dfrac{|\textbf{n} \cdot k|}{ ||\textbf{n} ||}. \номер\] 92}{8} = 1\номер \]
в точке \((1,1,2)\).
Решение
Первое вычисление
\[ \nabla F = \langle \dfrac{x}{2}, \dfrac{y}{2}, \dfrac{z}{4}\rangle .
\nonumber \]
Теперь подключитесь, чтобы получить
\[\nabla F(1,1,2) = \langle \dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{ 2} \rangle .\nonumber \]
У нас есть
\[|\langle \dfrac{1}{2} , \dfrac{1}{2} , \dfrac{1}{2} \rangle \cdot \ шляпа {\ textbf {к}} | = \dfrac{1}{2} .\nonumber \] 92 — z) = \langle 2x, 2y, -1\rangle = \langle 2, 4, -1\rangle .\nonumber \]
Оба эти вектора будут перпендикулярны касательной к кривой в точке , следовательно, их векторное произведение будет параллельно этой касательной. Мы вычисляем
\[ \begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} & \hat{\textbf{k}} \\ 2 & 4 & 10 \\ 2 & 4 & -1 \end{vmatrix} = -44 \hat{\textbf{i}} + 22 \hat{\textbf{j}}. \nonumber \]
Следовательно, уравнение касательной равно
\[x(t) = 1 — 44t y(t) = 2 + 22t z(t) = 5.\nonumber \]
Авторы и авторство
Эта страница под заголовком 1.7: Касательные плоскости и нормальные линии распространяется по незаявленной лицензии, ее автором, ремиксом и/или куратором был Ларри Грин.