Обратная функция | Алгебра
Что такое обратная функция? Как найти функцию, обратную данной?
Определение.
Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.
Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.
Чтобы найти функцию, обратную данной функции y=f(x), надо:
1) В формулу функции вместо y подставить x, вместо x — y:
x=f(y).
2) Из полученного равенства выразить y через x:
y=g(x).
Пример.
Найти функцию, обратную функции y=2x-6.
1) x=2y-6
2) -2y=-x-6
y=0,5x+3.
Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.
Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).
y=2x-6 и y=0,5x+3 — линейные функции. Графиком линейной функции является прямая. Для построения прямой берём две точки.
Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой).
Теорема (необходимое и достаточное условие обратимости функции)
Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.
Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.
Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.
Классический пример — функция y=x². На промежутке [0;∞) функция возрастает. Условие обратимости выполнено, следовательно, можем искать обратную функцию.
Так как область определения функции y=x² — промежуток [0;∞), область значений на этом промежутке — также [0;∞), то область определения и область значений обратной функции — также [0;∞).
1) x=y².
2)
Так как y≥0, то
то есть на промежутке [0;∞) y=√x — функция, обратная к функции y=x². Их графики симметричны относительно биссектрисы I и III координатных четвертей:
В алгебре наиболее известными примерами взаимно обратных функций являются показательная и логарифмическая функция, а также тригонометрические и обратные тригонометрические функции.
Обратная функция – объяснение и примеры
Что такое обратная функция?
В математике обратная функция — это функция, которая отменяет действие другой функции.
Например, , сложение и умножение обратны вычитанию и делению соответственно.
Обратную функцию можно рассматривать как отражение исходной функции по линии y = x. Проще говоря, обратная функция получается заменой (x, y) исходной функции на (y, x).
Мы используем символ f − 1 для обозначения обратной функции. Например, если f (x) и g (x) обратны друг другу, то мы можем символически представить это утверждение как:
g(x) = f − 1 (x) или f(x) = g −1 (x)
Об обратной функции следует отметить, что обратная функция не совпадает с обратной, т. е. f – 1 (x) ≠ 1/f(x). В этой статье мы обсудим, как найти обратную функцию.
Поскольку не все функции имеют обратную функцию, важно проверить, есть ли у функции обратная функция, прежде чем приступать к определению ее обратной.
Мы проверяем, есть ли у функции обратная функция, чтобы не тратить время на поиск чего-то несуществующего.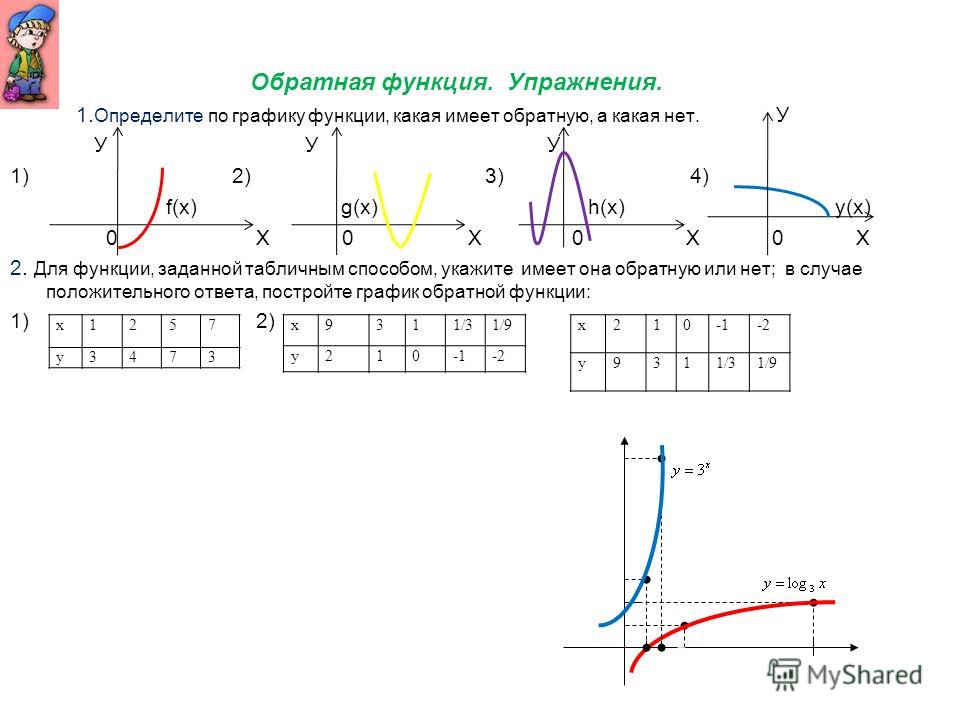
Взаимно-однозначные функции
Так как же доказать, что данная функция имеет обратную? Функции, имеющие обратную функцию, называются взаимно однозначными.
Функция называется взаимно однозначной, если для каждого числа y в диапазоне f существует ровно одно число x в области определения f такое, что f (x) = y.
Другими словами, область определения и область взаимно однозначной функции имеют следующие отношения:
- Область определения f −1 = Область определения f.
- Диапазон f −1 = Домен f.
Например, чтобы проверить, является ли f(x) = 3x + 5 заданной функцией один к одному, f(a) = 3a + 5 и f(b) = 3b + 5.
⟹ 3a + 5 = 3b + 5
⟹ 3а = 3б
⟹ а = б.
Следовательно, f (x) является взаимно однозначной функцией, поскольку a = b.
Рассмотрим другой случай, когда функция f задается выражением f = {(7, 3), (8, –5), (–2, 11), (–6, 4)}.
Эта функция является взаимно однозначной, поскольку ни одно из ее значений y не встречается более одного раза.
А как насчет этой другой функции h = {(–3, 8), (–11, –9), (5, 4), (6, –9)}? Функция h не является взаимно однозначной, поскольку значение y, равное –9, появляется более одного раза.
Вы также можете графически проверить функцию «один к одному», проведя вертикальную и горизонтальную линии через график функции. Функция является взаимно однозначной, если и горизонтальная, и вертикальная линии проходят через график один раз.
Как найти обратную функцию?
Поиск обратной функции — простой процесс, хотя нам действительно нужно быть осторожным с парой шагов. В этой статье мы предполагаем, что все функции, с которыми мы будем иметь дело, являются один к одному.
Вот процедура нахождения обратной функции f(x):
- Замените обозначение функции f(x) на y.
- Поменять местами x на y и наоборот.
- Начиная с шага 2, решите уравнение для y.
Будьте осторожны с этим шагом. - Наконец, измените y на f −1 (x). Это обратная функция.
- Вы можете проверить свой ответ, проверив, верны ли следующие два утверждения:
Будьте осторожны с этим шагом.⟹ (f ∘ f −1 ) (x) = x
⟹ (f −1 ∘ f) (x) = x
Давайте рассмотрим пару примеров.
Пример 1
Зная функцию f (x) = 3x − 2, найти ее обратную.
Решение
f(x) = 3x − 2
Заменить f(x) на y.
⟹ y = 3x − 2
Поменять x на y
⟹ x = 3y − 2
Найти y
x + 2 = 3y
Разделить на 3, чтобы получить;
1/3(x + 2) = y
x/3 + 2/3 = y
Наконец, замените y на f −1 (x). (x) = x f [f −1 (x)]
= f (x/3 + 2/3)
⟹ 3(x/3 + 2/3) – 2
⟹ x + 2 – 2
= x
Следовательно, f −1 (x) = x/3 + 2/3 является правильным отвечать.
Пример 2
Учитывая f(x) = 2x + 3, найдите f −1 (x).
Решение
F (x) = y = 2x + 3
2x + 3 = y
Swap x и y
⟹2y + 3 = x
Теперь решайте Y
⟹2y = x. – 3
⟹ y = x/2 – 3/2
Наконец, замените y на f −1 (x)
⟹ f −1 (x) = (x– 3)/2
Пример 3 ), найдите f −1 (x).
Решение
F (x) = log₁₀ (x)
заменен F (x) на Y
⟹ y = log 10 (x) ⟹ 10 y = x
Теперь SWAP x с x с y получить;
⟹ y = 10 x
Наконец, замените y на f −1 (х).
f -1 (x) = 10 x
Следовательно, обратное выражение f(x) = log 10 (x) равно f -1 (x) = 10 9 x 9004 Пример 4 2x -5) ⟹ y = (x + 4)/ (2x -5)
Поменять местами y с x и наоборот
y = (x + 4)/ (2x -5) ⟹ x = (y + 4) / (2г -5)
⟹ x(2y−5) = y + 4
⟹ 2xy − 5x = y + 4
⟹ 2xy – y = 4 + 5x
⟹ (2x − 1) y = 4 + 5x
7 Разделить оба часть уравнения на (2x — 1).
⟹ y = (4 + 5x)/ (2x − 1)
Заменить y на g – 1 (x)
= g – 1 (x) = (4 + 5x)/ (2x − 1)
Доказательство:
(g ∘ g −1 ) (x) = g [g −1 (x)]
= g [(4 + 5x)/ (2x − 1)]
= [(4 + 5x)/ (2x — 1) + 4]/ [2(4 + 5x)/ (2x — 1) — 5]
Умножьте числитель и знаменатель на (2x − 1).
⟹ (2x — 1) [(4 + 5x)/ (2x — 1) + 4]/ [2(4 + 5x)/ (2x — 1) — 5] (2x — 1).
⟹ [4 + 5x + 4(2x — 1)]/ [ 2(4 + 5x) — 5(2x — 1)]
⟹ [4 + 5x + 8x−4]/ [8 + 10x — 10x + 5]
⟹13x/13 = x
Следовательно, g – 1 (x) = (4 + 5x)/ (2x − 1)
Пример 5
Определите обратную формулу функция f(x) = 2x – 5
Решение
Замените f(x) на y.
f(x) = 2x – 5⟹ y = 2x – 5
Поменяйте местами x и y, чтобы получить;
⟹ x = 2y – 5
Изолировать переменную y.
2y = x + 5
⟹ y = x/2 + 5/2
Измените y обратно на f –1 (x).
⟹ f –1 (x) = (x + 5)/2
Пример 6.
Решение
Измените h (x) на y, чтобы получить;
h(x) = (x – 2) 3 ⟹ y = (x – 2) 3
Поменять местами x и y
⟹ x = (y – 2) 3
7 Изолировать
y 3 = x + 2 3
Найдите кубический корень из обеих частей уравнения.
3 √y 3 = 3 √x 3 + 3 √2 3
y = 3 √ (2 3 ) + 2
заменить Y на H — 1 (x)
H — 1 (x) = 3 √ (2 3 ) + 2
Пример 7
Найдите. (x) = (4x + 3)/(2x + 5)
Решение
Замените h (x) на y.
h (x) = (4x+3)/(2x+5) ⟹ y = (4x + 3)/(2x + 5)
Поменять местами x и y.
⟹ х = (4у + 3)/ (2у + 5).
Найдите y в приведенном выше уравнении следующим образом:
⟹ x = (4y + 3)/ (2y + 5)
Умножить обе части на (2y + 5)
⟹ x (2y + 5) = 4y + 3
Распределить x
⟹ 2xy + 5x = 4y + 3
Изолировать y.
⟹ 2xy – 4y = 3 – 5x
⟹ y (2x – 4) = 3 – 5x
Разделите на 2x – 4, чтобы получить;
⟹ y = (3 – 5x)/ (2x – 4)
Наконец, замените y на h – 1 (x).
⟹ h – 1 (x) = (3 – 5x)/ (2x – 4)
OpenAlgebra.com: обратные функции
Список воспроизведения YouTube для поиска обратных функций
Начнем с определения: Обратные функции – Функции f(x) и g(x) являются обратными, если обе
для всех x в домене g и f соответственно. Другими словами, если вы составите обратные функции, результат будет x .
При проверке того, что две функции обратны, необходимо получить исходное значение x при компоновке в обоих направлениях.
Определить, являются ли заданные функции обратными .
Если f и g являются обратными функциями, то g можно записать с использованием обозначения
который гласит: « г равно f, обратному ». Предупреждение: В этом контексте -1 указывает на обратную функцию, а не на отрицательный показатель степени.
Потратьте время на изучение функций один-к-одному (1-1), потому что оказывается, что если функция равна 1-1, то у нее есть обратная. Следовательно, мы можем думать о тесте горизонтальной линии как о тесте, который определяет, имеет ли функция обратную функцию или нет.
Далее мы описываем процедуру для фактического нахождения обратных функций .
Шаг 1 : Замените f(x) на y .
Шаг 2 : Поменяйте местами x и y .
Шаг 3 : Решите полученное уравнение для y .
Шаг 4 : Замените y на нотацию, обратную f .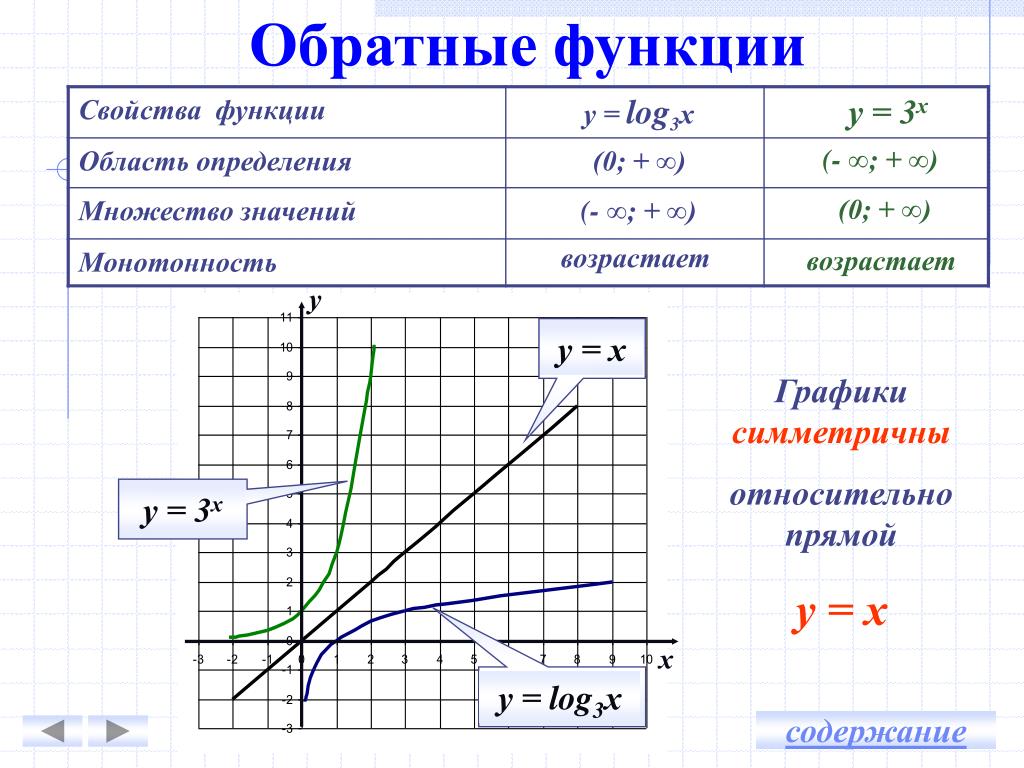
Шаг 5 : (Необязательно) Убедитесь, что функции являются обратными.
Найти обратную заданной функции .
Теперь, когда вы знаете определение обратной функции и как ее найти, мы теперь обратим внимание на их графики. Для любой однозначной функции
и имеем следующее свойство.
Симметрия обратных функций – Если ( a , b ) точка на графике функции f , то ( b , a ) — точка на обратном ему графике. Кроме того, два графика будут симметричны относительно линии y = x .
На следующем графике видно, что функции
имеют симметрию при построении графика на одном наборе осей.