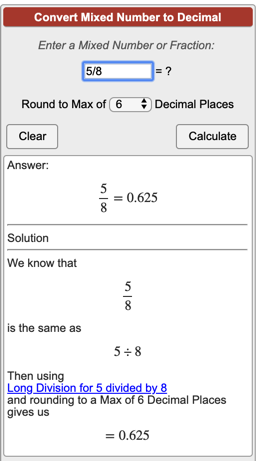
Дробь перевести в число калькулятор: Перевод дробей — онлайн конвертер

Содержание

Перевести бесконечную периодическую дробь в обыкновенную дробь. Онлайн калькулятор.

С помощью нашего калькулятора вы сможете перевести бесконечную периодическую десятичную дробь перевести в обыкновенную дробь или смешанное число с подробным пошаговым решением.

Определение периодической дроби

Периодическая дробь — это бесконечная десятичная дробь в записи которой с определённого места бесконечно повторяется определённая группа цифр. Например 2.2(3), 0.(7). Цифры в скобках называются периодом дроби.

Виды периодических дробей

Чистая периодическая десятичная дробь — это дробь в записи которой после точки сразу идёт периодическая часть. Например 1.(5), 0.(14), 12.(3).

Смешанная периодическая десятичная дробь — это дробь в записи которой между точкой и периодической частью присутствует одна или более цифр. Например 4.14(3), 0.51(34).

Как перевести периодическую дробь в обыкновенную

Алгоритм зависит от вида периодической дроби, чистая или смешанная дробь.

Алгоритм перевода чистой периодической дроби в обыкновенную

С алгоритмом перевода лучше разбираться на примере, переведём периодическую чистую дробь 0.(23) в обыкновенную.

1) Нужно обозначить дробь за x. x = 0.(23)
2) Затем равенство умножить на такое число, чтобы период стал целым числом. Т.е. в данном случае на 100. 100x = 23.(23)
3) Вычтем исходное равенство из полученного. 100x-x=23.(23)-0.(23), 99x=23
4) Вычислить x. x=23/99

Алгоритм перевода смешанной периодической дроби в обыкновенную

С алгоритмом перевода лучше разбираться на примере, переведём периодическую смешанную дробь 0.9(6) в обыкновенную.

1) Нужно обозначить дробь за x. x = 0.9(6)
2) Затем равенство умножить на такое число, чтобы период стал целым числом. Т.е. в данном случае на 100. 100x = 96.(6)
3) Затем равенство умножить на такое число, чтобы числа до периода оказались в целой части. Т.е. в данном случае на 10. 10x = 9.(6)
4) Вычтем равенства. 100x-10x=96.(6)-9.(6), 90x=87
5) Вычислить x. x=87/90=29/30

Пример перевода бесконечной периодической десятичной дроби в обыкновенную дробь

Переведём дробь 0.5(3)

1) Обозначим дробь за x. x = 0.5(3)
2) Затем равенство умножить на такое число, чтобы период стал целым числом. Т.е. в данном случае на 100. 100x = 53.(3)
3) Затем равенство умножить на такое число, чтобы числа до периода оказались в целой части. Т.е. в данном случае на 10. 10x = 5.(3)
4) Вычтем равенства. 100x-10x=53.(3)-5.(3), 90x=48
5) Вычислить x. x=48/90=8/15

Переведём дробь 0.(1)

1) Обозначим дробь за x. x = 0.(1)
2) Затем равенство умножить на такое число, чтобы период стал целым числом. Т.е. в данном случае на 10. 10x = 1.(1)
3) Вычтем равенства. 10x-x=1.(1)-0.(1), 9x=1
4) Вычислить x. x=1/9

Перевести бесконечную периодическую десятичную дробь 18.7(20) в обыкновенную дробь
Перевести бесконечную периодическую десятичную дробь 3. 3(20) в обыкновенную дробь
Перевести бесконечную периодическую десятичную дробь 16.(11) в обыкновенную дробь
Перевести бесконечную периодическую десятичную дробь 2.(01) в обыкновенную дробь
Перевести бесконечную периодическую десятичную дробь 15.(18) в обыкновенную дробь

Похожие калькуляторы

Перевести десятичную дробь в обыкновенную

Привести дробь к новому знаменателю

Деление дробей

Умножение дробей

Преобразовать смешанную дробь в неправильную дробь

Преобразовать неправильная дробь в смешанную дробь

Сравнение дробей

Сложение дробей

Вычитание дробей

Приведение дробей к наименьшему общему знаменателю

Сократить дробь

Калькулятор десятичной дроби в процентах

Решатели Алгебра

Инструкции: Используйте этот калькулятор, чтобы преобразовать предоставленную вами десятичную дробь в проценты, показывая все шаги. Введите одно десятичное число (например, число типа «3,4673» или число типа «.345279») в форму ниже:

Введите одно десятичное выражение (например, 5,3445 или 0,4562).

Этот десятичный преобразователь позволяет провести очень простую операцию, но это может оказаться очень полезным. Действительно, десятичные дроби и проценты тесно связаны между собой.

Если я спрошу вас «во сколько 0,40 перевести в проценты», вы, наверное, сможете мне прямо, не задумываясь, сказать «40%». Но если бы я спросил вас, «что такое 0,00000345, выраженное в процентах», вам, вероятно, пришлось бы подумать, как вы с этим справитесь.

Как перевести десятичную дробь в проценты

Стратегия проста. Базовая ассоциация состоит в том, что число 1 соответствует 100%. Затем по прямой пропорциональности, если задано десятичное число \(D\), все, что нам нужно сделать, чтобы преобразовать его в проценты, — это умножить его на 100.

Итак, формула преобразования десятичной дроби в проценты для десятичного числа D:

\[P = D \times 100 \%\]

Итак, в примере преобразования 0,00000345, выраженного в проценты, мы получаем \(P = 0.00000345 \cdot 100 \% = 0.000345 \%\).

Шаги для преобразования десятичной дроби в проценты

Определите десятичную дробь, которую вы хотите преобразовать, и назовите ее \(D\).
Убедитесь, что десятичная дробь \(D\) имеет соответствующее округление или вообще не округляется в соответствии с вашими потребностями.
Вычислите процент \(P\), используя формулу \(P = D \times 100 \%\)

Не забудьте добавить знак процента «%» в конце P

Примеры: Преобразование десятичных дробей в проценты

Что такое 0,050 в процентах?

Решение : Согласно нашим шагам, сначала мы идентифицируем данное десятичное число, в данном случае это \(D = 0. 050\). Формула для выражения этой десятичной дроби в процентах:

\[ P = D \times 100 \% = 0.050 \times 100 \% = 5 \%\]

Отсюда вывод, что 0,050 соответствует 5%.

Другие калькуляторы, которые связывают десятичные дроби, дроби и проценты

В зависимости от того, чего вы пытаетесь достичь, вполне вероятно, что вам потребуется какое-то преобразование между десятичными дробями, дробями и процентами, и у нас есть много калькуляторов для вас, чтобы сделать это.

Очень часто преобразовать десятичные дроби в проценты , особенно когда вы пытаетесь рассчитать что-то о финансах или процентных ставках.

Иногда процентные ставки приводятся в обычном процентном формате, а иногда — в виде десятичных дробей, и вам необходимо выполнить преобразование.

Дроби, особенно те, которые меньше единицы, обычно могут интерпретироваться как проценты в различных контекстах. Например, в контексте ипотеки вам может потребоваться заплатить «дополнительную 1/4 балла».

Итак, вы можете использовать это калькулятор доли в проценты , но также в зависимости от контекста вы можете лучше использовать дробь в десятичный калькулятор .

Десятичный калькулятор процентов десятичная дробь в процентах десятичная дробь Дробь в процент

Калькулятор неправильных дробей для смешанных чисел

Создано Ханной Памула, доктором философии

Отредактировано Домиником Черниа, доктором философии и Джеком Боуотером

Последнее обновление: 02 февраля 2023 г.

Содержание:

Что такое неправильная дробь? Определение неправильной дроби
Как из неправильной дроби сделать смешанное число?
Калькулятор неправильных дробей для смешанных чисел — пример

Добро пожаловать в калькулятор неправильных дробей для смешанных чисел — инструмент, который позволяет вам мгновенно преобразовать неправильную дробь в смешанное число . В короткой статье ниже вы узнаете основы, например, что такое неправильная дробь, и пошаговые инструкции о том, как превратить неправильную дробь в смешанное число. Чтобы выполнить обратную задачу, посетите наш калькулятор смешанных чисел и неправильных дробей.

Поскольку вы уже здесь и смотрите 👀 на этот калькулятор неправильных дробей для смешанных чисел, мы подозреваем, что вас могут заинтересовать другие темы дробей. По этой причине мы создали всеобъемлющий калькулятор дробей, который может выполнять семь основных операций с дробями. Если вы просто хотите выполнить задачу, противоположную этому инструменту

Что такое неправильная дробь? Неправильное определение дроби

Говоря об определении неправильной дроби, нам нужно начать с небольшого уточнения — что такое дробь вообще?

💡 Дробь говорит нам, сколько равных частей целого у нас есть . Мы записываем его как отношение целых чисел, разделенных чертой или косой чертой.

Мы называем верхнее число числителем , а нижнее число знаменателем .

Итак, в приведенном выше примере у нас есть 1 часть из 6 — 1/6 читается как одна шестая.

Теперь мы можем вернуться к нашему центральному вопросу: что такое неправильная дробь?

Согласно определению:

💡 Дробь неправильная, если числитель больше (или равен) знаменателю.

Поскольку числитель больше или равен нижнему числу, мы иногда называем неправильную дробь тяжелой дробью . Примеры неправильных дробей:

🍰 10 кусочков торта, когда каждый торт разрезали на 6 кусочков;
🍫 8 рядов шоколадки, когда вся шоколадка 5 рядов;
🍊 21 часть апельсина, если разрезать каждый апельсин на 8 равных частей.

Как из неправильной дроби сделать смешанное число?

Итак, что означает преобразование неправильных дробей в смешанные числа? В общем, смешанная дробь — это всего лишь еще один способ выражения неправильной дроби . Но как это работает?

Посмотрите еще раз на предыдущее изображение. В каждом из этих примеров у нас есть более одного целого, верно? Так, например, вместо того, чтобы говорить, что у нас есть 8 рядов шоколада (и в каждой плитке по 5 рядов), мы могли бы сказать: «Эй, у меня есть одна целая плитка шоколада и еще 3 части из 5». неправильные дроби в смешанные числа работает!

Давайте шаг за шагом рассмотрим наш пример, чтобы увидеть, как превратить неправильную дробь в смешанное число:

Разделите числитель на знаменатель (верхнее число на нижнее).
Если вы разделите 8 на 5, вы получите частное (целое число) и остаток:
⁸⁄₅ = 1 остаток 3 = 1 R 3
(узнайте, как это сделать с помощью калькулятора остатка)
Найти целую часть смешанного числа — взять целое число из деления:
1
Найдите дробную часть смешанного числа — остаток от деления будет новым числителем, а знаменатель останется прежним:

⅗
Чтобы получить смешанное число, сложите числа вместе :
1 ⅗

Вот и все, ⁸⁄₅ = 1 ⅗

Иногда нужно также упростить смешанную дробь, но здесь это не так.

Калькулятор неправильных дробей для смешанных чисел — пример

Итак, давайте быстро проверим, как этот инструмент преобразует неправильные дроби в смешанные числа. Допустим, у вас есть дробь 81/17, и вы хотите найти ее эквивалент в виде смешанного числа:

Введите числитель неправильной дроби . Это 81.
Введите знаменатель . 17 в нашем случае.
И все — калькулятор неправильной дроби в смешанные числа показывает результат:

Неправильная дробь

Смешанный номер

4 ¹³⁄₁₇

Что может быть проще? 🙂

Ханна Памула, доктор философии

Неправильная дробь

Числитель (n₁)

Знаменатель (d₁)

Пошаговое решение?

Посмотреть 18 похожих калькуляторов дробей 🍕

Сложение дробейСравнение дробейДесятичная дробь… 15 more

Сложение, вычитание, деление и умножение дробей

Инструкции по использованию

Введите дроби в приведенный выше калькулятор.
Выберите математическую операцию, которую вы хотите выполнить (сложение, вычитание, умножение, деление), используя серый раскрывающийся список между двумя дробями.
Результаты будут обновляться автоматически всякий раз, когда вы изменяете любое из значений в калькуляторе.
Флажок под калькулятором позволяет выбрать между сокращением дроби до эквивалента наименьшего общего знаменателя (если флажок установлен) или не уменьшением (если флажок не установлен).

Как вручную считать дроби

Как складывать дроби

Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
Умножьте каждый числитель на те же числа, на которые умножались знаменатели.
Сложите числители.
Уменьшить результат до максимально упрощенного числа.

Как вычитать дроби

Найдите наименьший общий знаменатель, умножив каждый знаменатель на другой.
Умножьте каждый числитель на те же числа, на которые умножались знаменатели.
Добавьте второй числитель к первому.
Уменьшить результат до максимально упрощенного числа.

Как умножать дроби

Перемножьте числа в верхней части вместе.
Перемножьте числа внизу вместе.
Уменьшить результат до максимально упрощенного числа.

Как делить дроби

Переверните вторую дробь вверх ногами, чтобы получить обратное число.
Умножьте дроби вместе (точно так же, как в разделе умножения выше).
Уменьшить результат до максимально упрощенного числа.

Дроби: история, актуальность и популярное использование

— Руководство Автор Corin B. Arenas , опубликовано 22 октября 2019 г.

Практически каждый день мы имеем дело с дробями. Думаю об этом. Получаете ли вы монеты за размен, покупаете одежду со скидкой 75 % или готовите на полстакана масла, вы используете дроби.

В этом разделе мы поговорим о происхождении дробей, их значении для передачи информации и золотом сечении.

Что такое дроби?

Дроби представляют собой части целого числа или любого количества равных частей. Он функционирует чтобы описать, как части соотносятся с целым числом.

Для иллюстрации представьте целое число как торт. Если вы разрежете торт на 4 равные части, один кусок будет частью этого торта. В данном случае это 1/4 часть всего торта.

1 представляет одну часть или часть целого числа, которое называется числителем .
4 представляет собой общее количество частей в целом числе, которое называется знаменателем .

Краткая история дробей

Происхождение слова: Термин дробь происходит от латинского слово дробь что означает «сломать». В раннем английском языке это означает «отломанный кусок или фрагмент». Английское слово «перелом» также имеет такое же происхождение слова.

Концепция дробей существует уже более 4000 лет.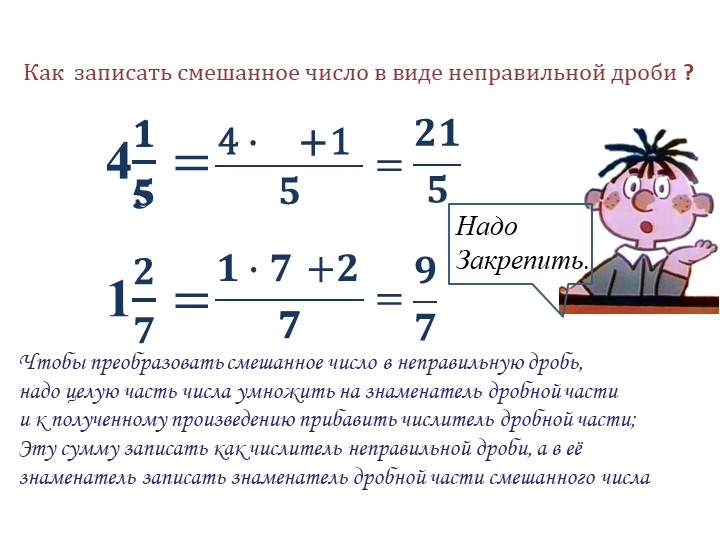 Но разные цивилизации по-своему стандартизируют дроби для универсального использования.

Египтяне

Согласно Математика сквозь века : Нежная история для учителей и других, египтяне были одними из первых, кто изобрел форму дроби еще в 1800 г. до н.э. Их концепция в основном ограничивалась частями, иначе известными как единичные дроби. Единичные дроби используют 1 в качестве числителя.

Египетские математики создали систему с основанием 10 идея, которая похожа на системы счисления, которые мы используем сегодня. Цифра иероглифы представляли их числа, а значит, символы соответствовали определенное значение.

Так как числитель всегда равен 1, нужно было указать только знаменатель. Египтяне отмечали знаменатель овалом или точкой над значением. Вот несколько примеров из Math Through the Ages :

Части были выражены в виде суммы единичных дробей. Однако система не позволяла повторять дробные единицы в этой последовательности, что затрудняло расчеты. Чтобы решить эту проблему, египтяне создали обширные списки таблиц, в которых были указаны двойные значения различных частей.

Вавилоняне

Еще одна цивилизация, создавшая сложную систему для Фракции были вавилонянами, по словам преподавателя математики и автора Лиз Памфри.

Вавилоняне организовали фракции в группы по 60 человек (базовое 60). Сегодня мы обычно объединяем числа в группы по 10. Но для вычислений, таких как углы и минуты для времени, мы также используем основание 60. Система группировала дроби по 10 и использовала два символа, один для единицы, а другой для 10.

Ниже приведены символы, представляющие вавилонскую систему счисления от 1 до 20:

Однако у них не было символа для нуля (который они позже добавили около 311 г. до н.э.) или знака, функционирующего как десятичная точка для указать доли целого числа. Это затрудняло интерпретацию чисел.

Например, приведенные ниже числа читаются как 12 и 15.

Согласно Памфри, символы также могут значения:

12 и 15 отдельными номерами
15/12
12 15/60
720 + 15

Как видите, отсутствие индикатора дроби делает его трудно отделить целые числа от дробей. Вероятно, они полагались на контекст, чтобы разобраться в числовых значениях.

И египетская, и вавилонская системы позже были переданы людям в Греции, а затем и средиземноморской цивилизации.

Греки

В Греции практика использования дробных значений в качестве сумм долей единицы была довольно распространена до средневековья. Например, Либер Abbaci итальянского математика Фибоначчи известный текст 13 века. Он широко использовал дроби, описывая различные способы преобразования других дробей в суммы единичных дробей.

Чтобы лучше понять, ниже приведена таблица греческих цифровые символы. Обратите внимание, что они такие же, как буквы в греческом языке. алфавит:

греческий запись дробей требует от читателей понимания контекста для правильного интерпретация. Чтобы выделить дробь, они ставят диакритический знак (‘) после знаменателя дроби.

Например, число β (2) становится ½ при записи через диакритический знак, β’ .

Аналогично, µβ (42) становится 1/42 при записи в виде µβ’ .

Однако здесь возникает путаница: µβ’ также может означать 40 ½. Вот почему понимание контекста имеет решающее значение при интерпретации греческих дробей.

Римлянам

Для римлян дроби выражались только словами, которые затрудняло какие-либо расчеты.

Их система была основана на единице веса, называемой «ас». При таком подходе 1 «ас» равнялся 12 унциям (римская основная единица измерения, положенная в основу современной унции). Таким образом, дроби имеют знаменатели со значениями, делящимися на 12.

В таблице ниже показаны римские дроби с соответствующими терминами:

Китайцы

Китайцы написали Девять Главы о математическом искусстве , датируемом примерно 100 г. до н.э. Он включает в себя текст о дробях, похожих на те, которые мы используем сегодня.

Согласно Math Through the Ages , он содержал большинство обычных правил вычисления с дробями, например, как складывать, делить и умножать дроби, а также приводить дробь к наименьшему значению.

Однако их система избегала использования неправильных дробей. Например, вместо неправильной дроби 9/4 они использовали эквивалентную ей смешанную дробь 2 1/4.

В отличие от западной математики, китайцы сосредоточились на практических приложениях, а не на теоретических рассуждениях и геометрии.

Индийцы

Индийцы разработали способ записи дробей, который намного ближе к тому, что мы используем сегодня.

Согласно ресурсному сайту The Story of Mathematics, до 1000 г. до н.э. индуистские мантры в ранний ведический период вызывали силы от десяти до сотен и даже до триллиона. Это свидетельствует о том, что ранняя индийская цивилизация использовала сложные математические операции, включая дроби, квадраты, кубы и корни.

Около 500 г. до н.э. они придумали систему письма под названием брахми, которая состояла из 9числовые символы и ноль. Учитель математики и писатель Лиз Памфри отмечает, что эти числа во многом повлияли на современные числа, которыми мы пользуемся сегодня. См. изображение ниже.

Индийская система записывала дроби, помещая одно значение поверх другого, точно так же, как сегодня числитель пишется над знаменателем. Тем не менее, они не провели черту между ними. Например, дробь 4/5 будет выглядеть так:

Позднее эту систему использовали арабы при торговле с индийцами. Именно арабы провели черту, чтобы отличить верхнее число от младшего в дроби. Это в конечном итоге привело к тому, как мы пишем дроби в современную эпоху.

Как дроби улучшают способ передачи информации

По словам доктора Петерсона из MathForum.org: «Дроби были изобретены, чтобы обеспечить способ работы с величинами меньше единицы».

Если бы люди использовали только целые числа, единственный способ обратиться к меньшее количество заключается в использовании меньших единиц. Так поступали римляне — они использовали целые числа для измерения футов и использовали дюймы, когда им нужно было учитывать более мелкие единицы.

Например, вместо 1/12 фута длина будет равна 1 дюйму, а 1/4 фута будет равна 3 дюймам. Но что, если вы имеете в виду 2 с половиной фута? Как насчет 1 и 3/4 футов?

Если вы основываете стандартную длину на футах, это сбивает с толку постоянное обращение к футам и дюймам одновременно. По сути, дроби позволяют проводить измерения, не обязательно создавая новые юниты. Было бы лучше учитывать измерения в последовательная мода.

В США чаще используют дроби (английское измерение), поскольку они используют чашки, а не весы для измерения при приготовлении пищи и выпечке.

Американцам еще предстоит перейти на метрическую систему, которая десятичная система, в которой используются единицы, связанные с коэффициентами 10. метрическая система обычно использует граммы и литры вместо американской системы измерения для унций, чашек, пинт и так далее.

В таблице ниже показано преобразование объема из английского измерения в его метрический эквивалент:

Преобразование объема в США в метрическую единицу

Кроме того, сохранение измерений в одной единице позволяет нам легко складывать, вычитать, умножать и делить дроби. Это устраняет проблему преобразования, которая невозможна, если измерение производится между двумя разными единицами измерения.

Для более простого расчета дробей используйте калькулятор в верхней части этой страницы.

Хотя десятичные дроби обеспечивают альтернативный способ указания дроби (и более простой способ расчета дробей с помощью калькулятора), это необходимо понимать традиционные дроби и то, как их значения влияют на целое число.

По данным Thoughtco.com, учащиеся, не усвоившие дроби в первые годы жизни, склонны запутаться и испытать математическую тревогу. Они также упомянули половину американской восьмерки оценщики не могут расположить дроби в порядке их значения.

Интуитивное изучение дробей помогает детям лучше понять теоретические математические концепции, позволяя им использовать их в реальной жизни. Это намного лучше, чем запоминать таблицы с единицами измерения или символами.

Золотое сечение и последовательность Фибоначчи

В математике отношение — это сравнение двух числа, которые зависят от вида сравниваемых чисел.

Вы можете встретить пример, написанный так: 1:3 или 1 из 3. Например, бутылка концентрата апельсинового сока состоит из 1 части апельсинового сока и 3 части воды. Это также может быть записано в виде дроби, 1/3.

Соотношения связаны с дробями, потому что они сравнивают разные значения, которые могут представлять собой целое. В этом примере вся часть — это бутылка. апельсинового сока.

Золотое сечение это специальное число, представленное греческим символом фи ( φ ) с приблизительным значением 1,618.

Получается путем деления линии на 2 части так, чтобы длинная часть (а) деленная на короткий участок (б) равна всей длине, деленной на длинный раздел.

Чтобы дать вам лучшее представление, вот иллюстрация со стандартным уравнением:

Исторически говорят, что это соотношение наблюдалось в древности. сооружения, такие как Парфенон и пирамиды Египта. В Великой пирамиде Гизы, отношение основания к высоте составляет примерно 1,5717, что составляет близко к золотому сечению. Он также встречается в повторяющихся закономерностях в природе, таких как как лепестки цветов, ракушки, ветки деревьев и спиральные галактики.

С другой стороны, Фибоначчи последовательность — еще одна известная формула в математике. Последовательность получена из сумма двух предшествующих ему чисел. Многие источники говорят, что Леонардо Фибоначчи (Леонардо Пизанский) популяризировал его в своей книге Либер Абакчи .

Но согласно Live Science, математик Кит Девлин, автор книги « В поисках Фибоначчи: поиски Откройте для себя заново забытого математического гения, изменившего мир что Леонардо Фибоначчи на самом деле не «открыл» эту последовательность.

Древние санскритские писания, в которых использовалось индийско-арабское числительное системы были первыми, кто обсудил ее за столетия до Леонардо Фибоначчи.

Последовательность Фибоначчи выглядит так:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811 и так далее…

Когда математики строят квадраты на основе этой последовательности, они могут нарисовать спираль.

Как золотое сечение связано с последовательностью Фибоначчи?

Исследователи заметили, что когда вы берете любые два последовательных числа Фибоначчи, их соотношение очень близко к золотому сечению. Таким образом, φ примерно равно 1,618. Чтобы дать вам представление, посмотрите таблицу ниже.

Итог

Концепция дробей была разработана различными древними цивилизациями. Одними из первых, кто разработал дробную систему с обширными таблицами, были египтяне. Другие древние общества, такие как вавилоняне, греки, римляне и китайцы, также внесли свой вклад в его улучшение. Но на современные цифры и то, как мы пишем дроби, больше всего повлияли индийцы, которые ввели индийско-арабскую систему счисления.

Использование дробей помогает нам легко передавать информацию об измерениях. Это удерживает людей от использования разных единиц измерения, облегчая их вычисление.

Наконец, дроби связаны со знаменитой золотой пропорцией и последовательностью Фибоначчи, которые в значительной степени повлияли на то, как мы проектируем всевозможные структуры.