Формула периметр трапеции: Периметр трапеции | Онлайн калькуляторы, расчеты и формулы на GELEOT.RU

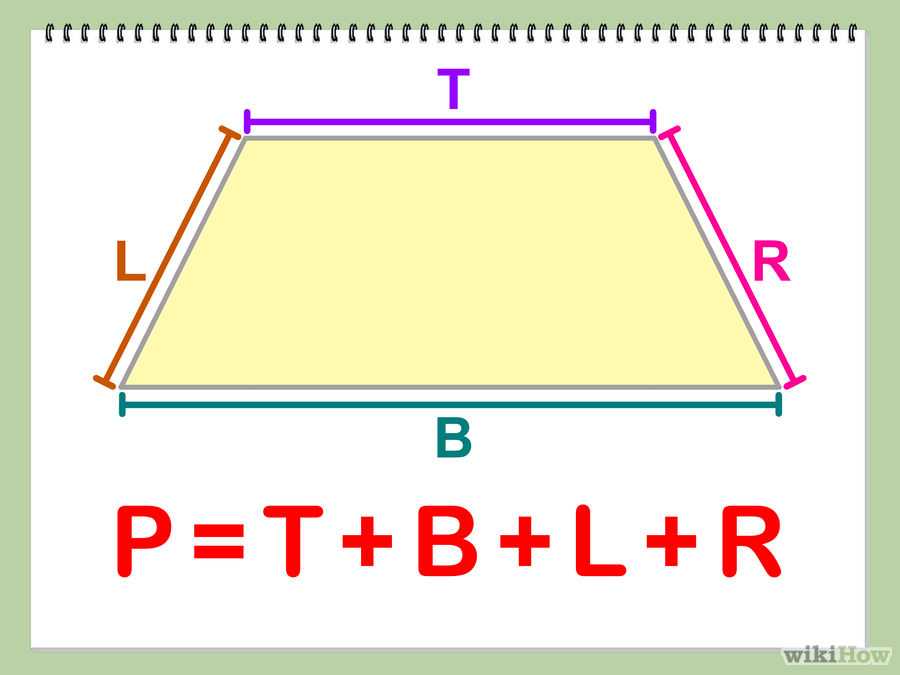
определение и формулы для его нахождения

Содержание:

• Трапеция. Основные понятия и определения
• Способы нахождения периметра
• Формулы для вычисления периметра к каждому из способов
• Примеры задач по теме и их решения

Содержание

• Трапеция. Основные понятия и определения
• Способы нахождения периметра
• Формулы для вычисления периметра к каждому из способов
• Примеры задач по теме и их решения

Трапеция.

Основные понятия и определения

Трапеция — четырехугольник, две противоположные стороны которого параллельны между собой.

Две параллельные стороны называют основаниями (верхним и нижним), а непараллельные — боковыми сторонами.

Выделяют особый вид трапеции — равнобедренную или равнобокую.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Равнобедренной называют трапецию, боковые ребра которой равны, и углы при нижнем основании равны между собой.

Примечание 1

Допускается применять как термин «равнобокая», так и «равнобедренная», так как эти понятия аналогичны друг другу.

В равнобедренную трапецию всегда можно вписать и описать около нее окружность.

Рассмотрим еще несколько основных понятий.

Диагональ трапеции — линия, соединяющая две ее несмежные вершины.

Средняя линия — отрезок, параллельный основаниям трапеции и равный их полу сумме.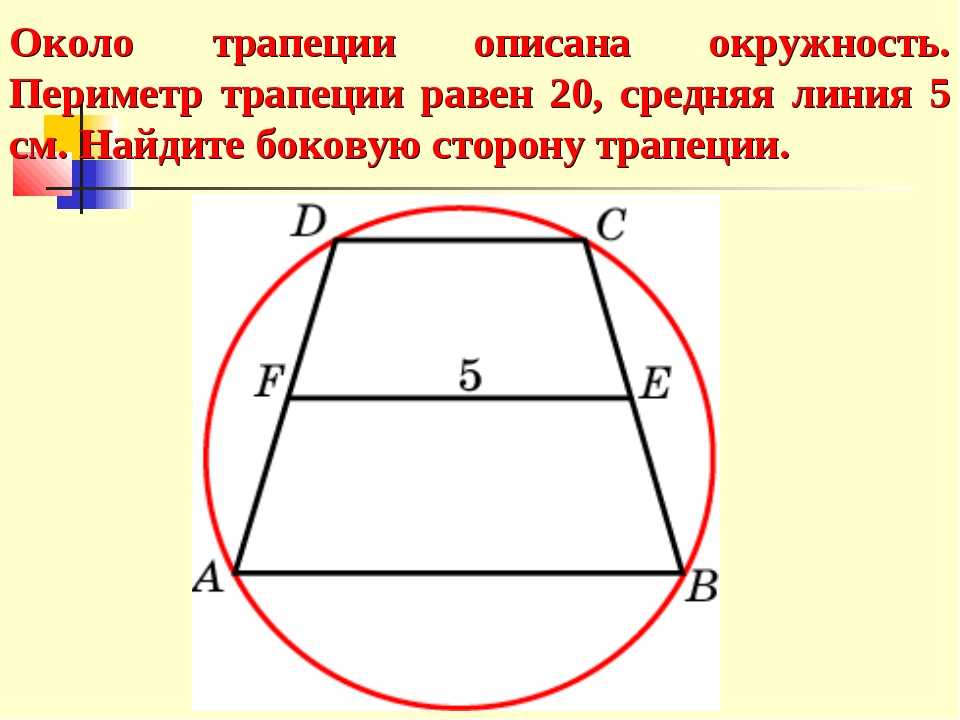

Высота — перпендикуляр, проведенный из любой точки одного из оснований трапеции ко второму ее основанию.

К количественным характеристикам трапеции относят:

• площадь;
• периметр.

В данной статье рассмотрим способы, с помощью которых можно найти периметр трапеции.

Периметр трапеции — величина, равная сумме длин всех четырех ребер фигуры.

Периметр обозначают в виде большой буквы P.

Способы нахождения периметра

Периметр фигуры можно найти, если:

1. В произвольной трапеции известны длины всех четырех ребер. Это самый простой способ, однако для его применения необходимо знать длину каждого из ребер, а это не всегда возможно.
2. В равнобедренной трапеции известны длина боковой стороны и длины оснований.
3. В равнобедренной трапеции известна длина высоты, проведенной из вершины меньшего из оснований, и длины оснований. Такая высота делит большее основание на два отрезка. Больший из получившихся отрезков при этом равен полу сумме оснований или средней линии. Затем используют теорему Пифагора для прямоугольного треугольника и вычисляют длину бокового ребра.
4. Известна длина средней линии произвольной трапеции и длины ее боковых ребер.

Формулы для вычисления периметра к каждому из способов

Приведем формулы вычисления периметра для каждого из указанных способов.

Вычисление периметра по четырем сторонам

Формула 1

\(P_{ABCD}=a+b+c+d\)

Вычисление периметра равнобокой трапеции по основаниям и боковой стороне

Формула 2

\(P_{ABCD}=2a+b+d\)

Вычисление периметра равнобокой трапеции по высоте и основаниям

Сначала определим длину отрезка AH и бокового ребра AB.

Формула 3

\(AH=AD-HD=d-\frac{b+d}2=\frac{d-b}2\)

Формула 4

\(AB=\sqrt{AH^2+BH^2}=\sqrt{\frac{\left(d-b\right)^2}4+h^2}\)

Периметр вычислим по формуле:

Формула 5

\(P_{ABCD}=2AB+AD+BC=2\cdot\sqrt{\frac{\left(d-b\right)^2}2+h^2}+d+b=\sqrt{\left(d-b\right)^2+4h^2}+d+b\)

Вычисление периметра трапеции по средней линии

Формула 4

\(P_{ABCD}=AB+CD+2\left(\frac{BC+AD}2\right)=a+c+2l\)

Примеры задач по теме и их решения

Пример 1

Периметр трапеции ABCD равен 40 см.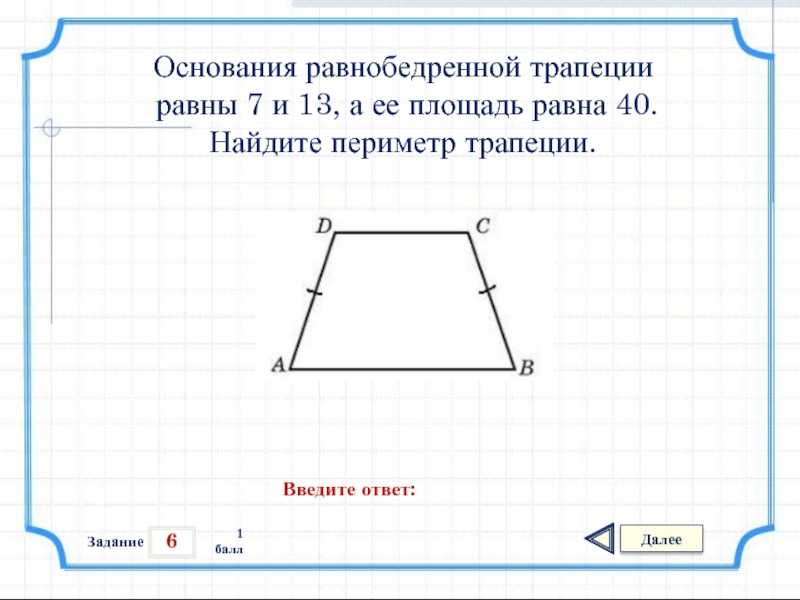 2}+42+30=92\;см\)

Ответ: 92 см.

Пример 4

Боковые ребра трапеции ABCD равны 12 см и 10 см. Известно, что одно основание больше другого в 2 раза, а периметр трапеции составляет 70 см. Найти длины оснований трапеции.

Решение

Решать задачу будем через среднюю линию – MN. Обозначим меньшее основание BC за x, тогда AD=2x.

Из условия задания известен периметр фигуры, а значит, можно определить длину отрезка MN:

\(P_{ABCD}=AB+CD+2MN=22+2MN=70\;см\)

\(MN=\frac{70-22}2=24\;см\)

Зная, что средняя линия равна полу сумме оснований, запишем и решим относительно переменной x следующее уравнение:

\(MN=\frac{BC+AD}2=\frac{x+2x}2=24\;см\)

\(\begin{array}{c}x+2x=48\;см\\3x=48\;см\\x=16\;см\end{array}\)

Получили, что меньшее основание BC равно 16 см, а большее AD – 32 см.

Ответ: 16 см и 32 см.

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Периметр трапеції — формули та приклади застосування

Навігація по сторінці.

1. Як знайти периметр трапеції?
2. Периметр трапеції – розв’язування задач.
3. Запитання для самоконтролю на тему периметр трапеції.
4. Блок-схема алгоритму знаходження периметра трапеції.

Як відомо, трапеція – це чотирикутник, у якого дві сторони паралельні, а дві інші сторони не паралельні.

Паралельні сторони називаються основами трапеції, а дві інші – боковими сторонами.

Так як у трапеції всі сторони можуть бути абсолютно різними по довжині, то знайти периметр трапеції можна за формулою периметра чотирикутника: .

Якщо трапеція рівнобічна, тобто її бічні сторони рівні, то формула периметра трапеції перепишеться в дещо іншому вигляду: , де  та  – основи трапеції і  – одна з її бічних сторін.

Зазначимо, що периметр трапеції, також, можна знайти не знаючи довжин основ, але знаючи довжину середньої лінії.

Середня лінія, по визначенню, дорівнює півсумі основ трапеції, тому, помноживши  на два, можна підставити її замість основ у формулі периметра: .

Зауваження: якщо позначити довжини сторін та середньої лінії буквами  та  відповідно, то формули периметра трапеції перепишуться у більш звичній буквенній формі:

Периметр трапеції – розв’язування задач.

Приклад 1: знайти периметр трапеції  зі сторонами .

Отже, для знаходження периметра трапеції скористаємося формулою . В результаті будемо мати:

Приклад 2: знайти периметр рівнобічної трапеції , сторони якої відповідно дорівнюють .

Для знаходження периметра заданої рівнобічної трапеції скористаємося формулою . Підставляючи в неї вихідні дані, отримаємо:

Приклад 3: периметр рівнобічної трапеції дорівнює .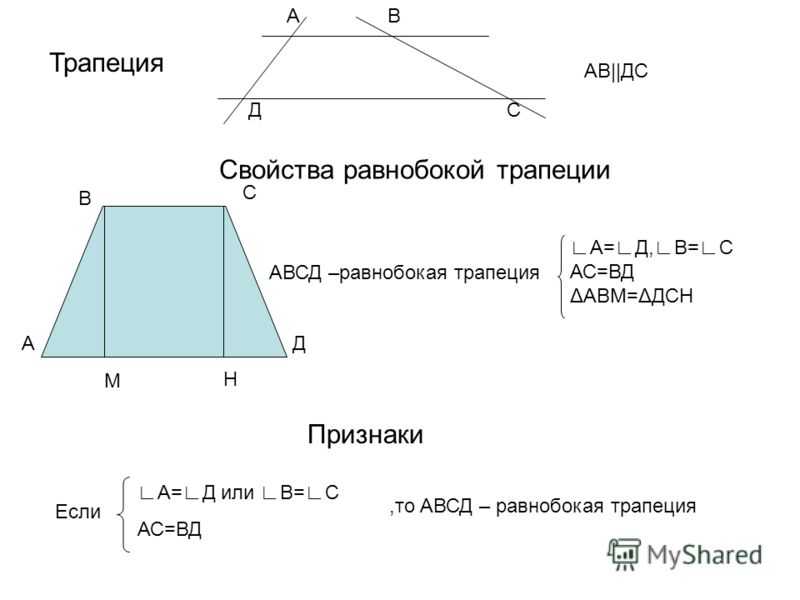 Знайти довжину бічної сторони, якщо основи трапеції рівні  і  відповідно.

Як відомо, периметр рівнобічної трапеції обчислюється за формулою: , де  – бічна сторона. Її довжина, помножена на два дорівнює:

Отже, довжина бокової сторони становить: .

Приклад 4: основи прямокутної трапеції дорівнюють  і  відповідно, а менша бічна сторона дорівнює . Знайти периметр трапеції.

Отже, опустимо висоту з вершини . Оскільки трапеція прямокутна, то  і . Тоді, .

Розглянемо далі трикутник . Зазначимо, що даний трикутник є прямокутним – сторона  є гіпотенузою. Знайдемо її довжину по теоремі Піфагора:

Після цього, периметр трапеції  знайдемо за формулою :

Запитання для самоконтролю на тему периметр трапеції.

1. Який чотирикутник називається трапецією?
2. Як називаються паралельні, не паралельні сторони трапеції?
3. Як знайти периметр трапеції?
4. Які дії необхідно виконати, щоб знайти периметр рівнобічної трапеції?
5. Запишіть формулу для знаходження периметра трапеції через її середню лінію.

Блок-схема алгоритму знаходження периметра трапеції

Ми в соціальних мережах

5.14: Площадь и периметр трапеций

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4998

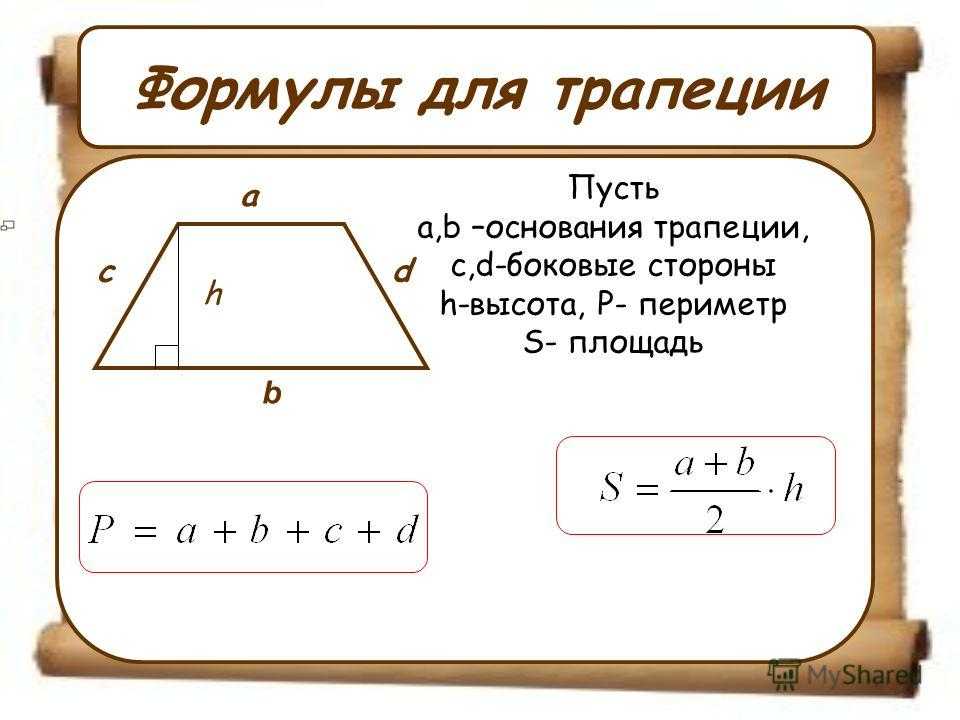
Площадь равна высоте, умноженной на среднее значение оснований; периметр это сумма сторон.

Трапеция представляет собой четырехугольник с одной парой параллельных сторон. Параллельные стороны называются основаниями, и мы будем называть длины оснований \(b_1\) и \(b_2\). Перпендикулярное расстояние между параллельными сторонами является высотой трапеции. Площадь трапеции равна \(A=\dfrac{1}{2}h(b_1+b_2)\), где \(h\) всегда перпендикулярна основаниям.

Рисунок \(\PageIndex{1}\)

Что, если бы вам были даны трапеция, размеры двух ее оснований и высота? Как можно найти полное расстояние вокруг трапеции и количество места, которое она занимает? 92 \конец{выровнено}\)

Пример \(\PageIndex{5}\)

Найдите периметр и площадь трапеции.

Рисунок \(\PageIndex{6}\)

Решение

Хотя длина второго основания нам не известна, мы можем найти его с помощью специальных прямоугольных треугольников. Оба треугольника на концах этой трапеции являются равнобедренными прямоугольными треугольниками, поэтому гипотенузы равны \(4\sqrt{2}\), а длина других катетов равна 4.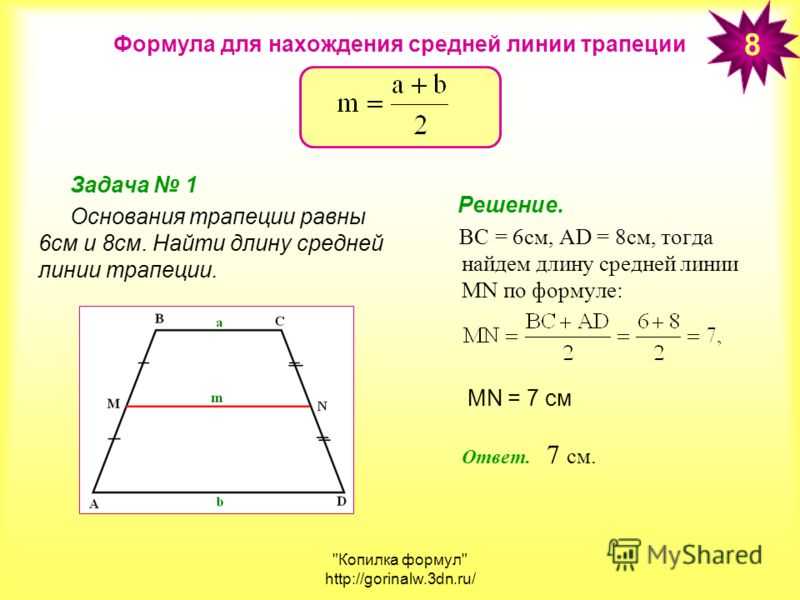 2 \end{выровнены}\)

Обзор

Найдите площадь и периметр следующих фигур. Округлите ответы до сотых.

1. Рисунок \(\PageIndex{7}\)
2. Рисунок \(\PageIndex{8}\)

Найдите площади следующих трапеций.

3. Трапеция с основаниями 3 и 7 дюймов и высотой 3 дюйма
4. Трапеция с основаниями 6 и 8 дюймов и высотой 5 дюймов
5. Трапеция с основаниями 10 дюймов и 26 дюймов и высотой 2 дюйма
6. Трапеция с основаниями 15 и 12 дюймов и высотой 10 дюймов
7. Трапеция с основаниями 4 и 23 дюйма и высотой 21 дюйм
8. Трапеция с основаниями 9 дюймов и 4 дюйма и высотой 1 дюйм
9. Трапеция с основаниями 12 и 8 дюймов и высотой 16 дюймов
10. Трапеция с основаниями 26 дюймов и 14 дюймов и высотой 19 дюймов

Используйте данные цифры, чтобы ответить на вопросы.

Рисунок \(\PageIndex{9}\)

11. Каков периметр трапеции?
12. Какова площадь трапеции?

Рисунок \(\PageIndex{10}\)

13. Каков периметр трапеции?
14. Какова площадь трапеции?

Рисунок \(\PageIndex{11}\)

15. Каков периметр трапеции?
16. Какова площадь трапеции?

Обзор (ответы)

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 10. 5.

Словарь

Срок	Определение
площадь	Количество места внутри фигуры. Площадь измеряется в квадратных единицах.
равнобедренная трапеция	Равнобедренная трапеция — это трапеция, у которой непараллельные стороны конгруэнтны.
средний сегмент (трапеции)	Отрезок, соединяющий середины непараллельных сторон.
периметр	Расстояние вокруг формы. К периметру любой фигуры должна быть привязана единица измерения. Если не указаны конкретные единицы измерения (футы, дюймы, сантиметры и т. д.), напишите единиц.
трапеция	Четырехугольник, у которого ровно одна пара параллельных сторон.

Дополнительные ресурсы

Интерактивный элемент

Видео: Примеры площади и периметра трапеций — основные положения

Упражнения: Площадь и периметр трапеций Вопросы для обсуждения

Учебные пособия: Треугольник s и четырехугольники Study Guide

Практика: Площадь и Периметр трапеций

Реальный мир: Периметр

---

Эта страница под названием 5.14: Площадь и периметр трапеций распространяется по лицензии CK-12 и была создана, изменена и/или курирована Фондом CK-12 с помощью исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

ПОД ЛИЦЕНЗИЕЙ

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   СК12

   Лицензия

   СК-12

   Программа OER или Publisher

   СК-12

   Показать оглавление

   нет

2. Теги

   1. источник@https://www. ck12.org/c/geometry

Как найти периметр трапеции?

Трапеция представляет собой плоскую замкнутую форму с четырьмя прямыми гранями и парой параллельных граней. Параллельные стороны трапеции называются основаниями, а непараллельные стороны – катетами. Трапеция также может иметь параллельные стороны. Параллельные плоскости могут быть горизонтальными, вертикальными или наклонными.

Трапеция

Трапеция — это многоугольник только с одной парой параллельных сторон. Эта параллельная сторона также называется параллельным основанием трапеции. Две другие стороны трапеции не параллельны и называются катетами трапеции. Одна школа математики утверждает, что у трапеции может быть пара параллельных сторон, а другая школа математики утверждает, что у трапеции может быть более одной пары параллельных сторон. Учитывая второе определение, параллелограмм также является трапецеидальным соответственно. Однако первое определение не считает параллелограмм трапецией.

Типы трапеций

Трапеции можно разделить на три категории:

• Прямоугольная трапеция: Прямоугольная трапеция — это трапеция, в которой пара прямых углов смежны друг с другом.

 

• Равнобедренная трапеция: Если непараллельные стороны или катеты трапеции имеют одинаковую длину, они называются равнобедренными трапециями.

 

• Несимметричная трапеция: Если стороны и углы трапеции не равны, мы называем ее разносторонней трапецией.

 

Периметр трапеции

Периметр трапеции равен сумме длин сторон трапеции. Формула периметра трапеции так же проста, как сумма длин ее четырех сторон. В приведенной ниже трапеции ABCD рассмотрим случай, когда стороны AB и CD (основание) параллельны друг другу, а стороны AD и BC (катетки) — нет. Периметр трапеции ABCD можно рассчитать по формуле периметр (P) = AB + BC + CD + DA. Его также можно выразить как сумму длин параллельных сторон и сумму длин непараллельных сторон. где стороны AB и CD параллельны, а стороны AD и BC непараллельны.

 

Как найти периметр трапеции?

Периметр трапеции можно рассчитать, выполнив следующие действия:

Шаг 1 : Запишите размеры всех сторон трапеции.

Шаг 2: Добавьте длины всех сторон.

Шаг 3: После получения значения периметра запишите единицы измерения с этим значением.

Пример: Чему равен периметр трапеции, если непараллельные стороны имеют длину 10 единиц, а параллельные стороны — 5 единиц?

Решение: 

Предположим, что сумма длин непараллельных сторон = 10 единицам, тогда сумма параллельных сторон = 5 единицам. Периметр трапеции = сумма длин параллельных сторон + сумма длин непараллельных сторон ⇒ P = 10 единиц + 5 единиц.

Итак, периметр (P) = 15 единиц.

Как найти периметр трапеции с отсутствующей стороной?

Периметр трапеции можно вычислить, даже если сторон недостаточно. В таких случаях вы можете использовать заданные стороны трапеции, применить теорему Пифагора и другие свойства, чтобы найти недостающие стороны, а затем вычислить периметр.

Пример: Найдите периметр трапеции PQRS с размерами  PQ = 110 м, SV = 40 м, VU = 110 м, UR = 70 м, QU = 80 м.

Решение : 

Используйте заданные размеры, чтобы найти отсутствующие поверхности PS и QR.

 

Шаг 1: Если мы возьмем △QUR, мы получим QU = 80 м и UR = 70 м. Мы видим, что △QUR — прямоугольный треугольник. Таким образом, мы можем использовать теорему Пифагора для вычисления значения QR.

Шаг 2: Согласно теореме Пифагора QR ² = QU ² + UR ² . Это означает QR ² = 80 ² + 70 ² . Таким образом, QR ² =  6400 + 4900 ⇒ QR = √11300 = 106,301 м.

Шаг 3: Поскольку QU = 80 м,  PQ параллельно SR, поэтому PV также равно 80 м, поэтому теперь мы можем вычислить недостающую сторону PS трапеции.

Шаг 4: Берем прямоугольный треугольник △PSV, PV = 80 м, SV = 40 м, поэтому, применяя теорему Пифагора, получаем PS ² = PV ² + SV ² . Это означает PS ² = 80 ² + 40 ² . Итак, PS ² = 6400 + 1600 ⇒ PS = √8000 = 89,44 м.

Шаг 5: Теперь, когда мы знаем все грани трапеции, мы можем сложить все четыре грани, чтобы найти периметр. Это означает, что периметр трапеции равен PQRS = PQ + QR + RS + SP ⇒ 110 + 106,301 + 220 + 89,44 = 525,741 м.

Примеры вопросов

Вопрос 1: Приведите две основные формулы трапеций.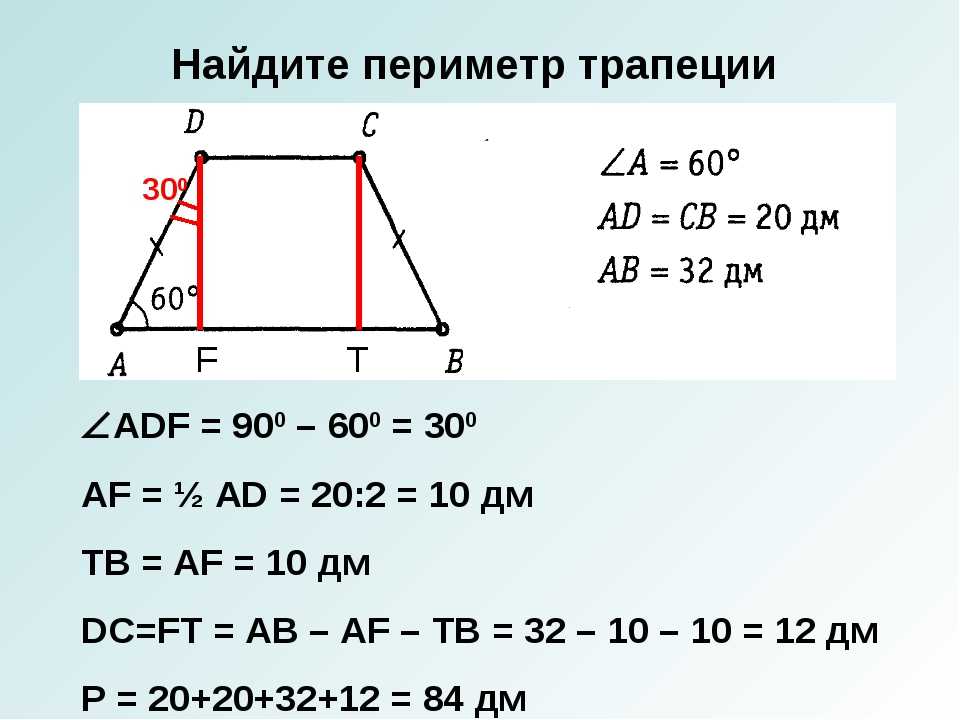

Ответ:

Периметр трапеции = сумма всех сторон трапеции = a + b + c +d

Площадь трапеции = A = [(a + b)/2] × h.

Где a , b , c , d длины четырех сторон трапеции.

Вопрос 2: Трапеция/трапеция считается четырехугольником?

Ответ: 

Четырехугольник — это замкнутая фигура, имеющая четыре стороны. В результате трапеции иногда называют четырехугольниками. Некоторые люди описывают трапецию как четырехугольник только с одним набором параллельных сторон и удаляют параллелограмм из определения. Другие определяют трапецию как четырехугольник по крайней мере с одной парой параллельных сторон, что делает параллелограмм особым типом трапеции. Трапеции бывают разных размеров углов.

Вопрос 3: В чем разница между трапецией и трапецией?

Ответ:  

Трапеция — это четырехугольник с парой параллельных сторон, обращенных друг к другу, трапеция — это также четырехугольник с одной из параллельных сторон, противоположных друг другу.

Итак, два термина трапеция и трапеция одинаковы, но имеют разное написание в разных странах. В американском английском это trapezium, а в британском английском — trapezium.

Вопрос 4: Назовите три свойства трапеции.

Ответ: 

• Если трапеция равнобедренная, то ее основание и диагональ равны.
• Пересечение диагоналей лежит на той же линии, что и середины двух противоположных сторон.
• Противоположные стороны равнобедренной трапеции равны.

Вопрос 5. Равны ли диагонали трапеции? Объяснять.

Ответ:  

Трапеции бывают трех типов: равнобедренные, многоцелевые и прямые. Для равнобедренной трапеции диагонали одинаковы, потому что непараллельные стороны или катеты трапеции имеют одинаковую длину. У разносторонней и прямой трапеции диагонали не равны.

Вопрос 6: Если периметр трапеции равен 60 единицам, а три стороны равны 10 единицам, 25 единицам и 12 единицам соответственно, используйте формулу трапеции, чтобы найти размер четвертой стороны.