Сравнение дробей с разными знаменателями. Видеоурок. Математика 6 Класс
Все мы знаем, как сравнивать натуральные числа. Ясно, что больше, чем , и неважно, о чем идет речь: об автомобилях, стульях или о конфетах. Главное, чтобы предметы, которые мы сравниваем, были одинаковыми. Как же сравнивать части целого? То есть как сравнивать обыкновенные дроби?
Пример 1. Сравнить дроби и .
Если объект разделен на равные части, сравнение дробей (количество частей) выполняется точно так же, как и сравнение количества целых объектов.
Правило: Если дроби имеют одинаковые знаменатели, то больше та дробь, у которой больше числитель.
Следовательно, (Рис. 1).
Рис. 1. Сравнение дробей
Пример 2. Сравнить дроби и .
Дробная черта заменяет знак деления. Представьте, что трёхкилограммовый торт разделили на четверых человек или же на семь. Понятно, что если пришло четверо гостей, каждому гостю достанется больший кусок торта (Рис. 2).
Следовательно, (Рис. 3).
Рис. 3.
Правило: если дроби имеют одинаковые числители, то больше та дробь, у которой меньше знаменатель.
Пример 3. Сравнить дроби и .
По иллюстрации видно, что меньше половины, а – больше половины (Рис. 4). Следовательно, .
Рис. 4. торта меньше его половины, а торта – больше половины
Если рассуждать логически и вспомнить, что дробная черта заменяет знак деления, то можно сравнить дроби следующим образом. Меньшее число делят на большее количество частей (на ). Большее число делят на меньшее количество частей (на ). Действительно, получится, что .
Пример 4. Сравнить дроби .
Логика и глазомер не смогут помочь при сравнении данных дробей (Рис. 5). Поэтому нужен универсальный способ, который позволит сравнивать любые дроби.
Рис. 5. Дроби
Сравнить дроби с одинаковыми знаменателями легче, чем с одинаковыми числителями (Рис. 6).
Вспомним, что если дроби имеют одинаковые знаменатели, то больше та дробь, у которой больше числитель.Если же дроби имеют одинаковые числители, то больше та дробь, у которой меньше знаменатель.
Рис. 6. Сравнение дробей с одинаковыми числителями и одинаковыми знаменателями
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на любое число, отличное от нуля, получится равная ей дробь.
Например, поделим числитель и знаменатель дроби на . Получится равная ей дробь . Если числитель и знаменатель дроби умножить на 2, то получим равную ей дробь . (Рис. 7).
Рис. 7. Основное свойство дроби
Пример 5. Привести дроби и к общему знаменателю.
Дополнительный множитель для дроби – это (знаменатель другой дроби). Дополнительный множитель для дроби – это (знаменатель первой дроби). Дополнительные множители записываются в правом верхнем углу над чертой.
Рис. 8. Дополнительные множители
Не забываем домножать на дополнительный множитель и числитель, и знаменатель.
Очевидно, что на . Возвращаясь к примеру 4, делаем вывод, что .
Мы рассмотрели все возможные способы сравнения обыкновенных дробей. Познакомились с универсальным способом сравнения дробей с разными знаменателями – приведением дробей к общему знаменателю. В качестве дополнительного множителя всегда подойдет знаменатель другой дроби. О том, как приводить дроби к общему знаменателю более удобными способами, вы узнаете на следующем уроке.
Список рекомендованной литературы
- Виленкин Н.Я. Математика. 6 класс: учеб. Для учащихся общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с.: илл.
- Зубарева И.И., Мордкович А.Г. Математика. 6 класс. – М.: Мнемозина.
- Истомина И.Б. Математика, 6 класс. – М.: Ассоциация ХХI век.
Рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «math-prosto.ru» (Источник)
- Интернет-портал «cleverstudents.ru» (Источник)
- Интернет-портал «yaklass.ru» (Источник)
Домашнее задание
1. Приведите к общему знаменателю дроби:
1) и ; 2) и ; 3) и ; 4) и .
2. Сравните дроби:
1) и ; 2) и ; 3) и ; 4) и .
3. Расположите в порядке убывания числа: .
interneturok.ru
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Сложение и вычитание дробей с разными знаменателями. Приведение дробей к наименьшему общему знаменателю. Примерно 6-класс (11-12 лет)
| ||||||
dpva.ru
«Сложение и вычитание дробей с разными знаменателями».
Урок математики в 6 классе
(разработано учителем математики
Сурковой Галиной Николаевной – ВКК)
Тема: Сложение и вычитание дробей с разными знаменателями.
Тип урока: Обобщение.
Цели:
систематизация знаний учащихся по данной теме;
закрепление знаний правил сложения и вычитания обыкновенных дробей с разными знаменателями;
развитие интереса учащихся к изучению математики.
Оборудование: учебник Зубарева И. И., Мордкович А. Г. 5 класс, жетоны пяти цветов, открытки с заданиями, табло результатов.
Ход урока
Класс разбивается на группы по 4-5 человек. Каждая группа-это команда, которому предстоит прогулка по весеннему лесу. Победить может та команда, которая знает законы сложения и вычитания дробей с разными знаменателями. Победит та команда, который наберет больше очков, пройдя по всей тропинке.
На столе у учащихся тетради, ручки для вычислений.
Каждый этап оценивается жетоном:
1 балл
2 балла
3 балла
4 балла
5 баллов
Цвет выданного жетона зависит от количества правильно решенных примеров.
Этапы урока:
1-й этап. Собираемся на прогулку.
2-й этап. Проложим тропинку.
3-й этап. Кто быстрей найдет подснежник.
4-й этап. Проверим все ли мы на месте.
5-й этап. Привал.
6-й этап. Дорога домой.
7-й этап. Подведение итогов.
1-й этап. Собираемся на прогулку.
Решить примеры и найти среди ответов, записанных на доске под определенным номером, свои ответы.

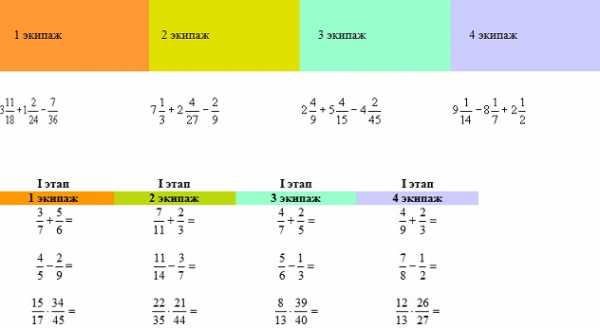
2-й этап. Составим карту тропинки.
Для этого необходимо собрать разрезанную открытку. На доске записаны 6 примеров и каждой команде дана разрезанная карточка с ответами.
Задание: решить примеры, найти среди разрезанных карточек с ответами свой ответ и сложить открытку.
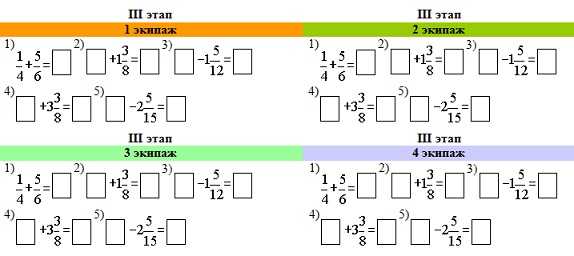
3-й этап. Кто быстрей найдет подснежник.
Всем командам выдаются одинаковые задания. Члены каждой команды выходят по очереди решая пример, записывают ответ в пустую клетку (правильно и быстро выполнить задание).
4-й этап. Проверим все ли мы на месте.
В примерах на карточках допущены ошибки. Найдите ошибки и объясните, почему они были допущены.

5-й этап. Привал.
Вы решили отдохнуть на поляне и нарвать цветов. Каждый лепесток цветка — это задание на сложение и вычитание дробей с разными знаменателями. На каждый стол дается «цветок» с заданиями. Задания одинаковые, вот только первоначальная дробь разная:
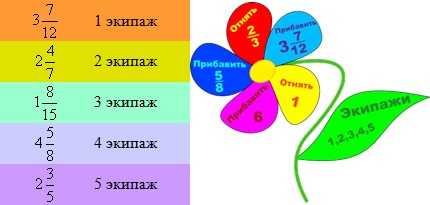
6-й этап. Дорога домой.
Чтобы успешно дойти до дома каждой команде нужно решить пример.
7-й этап. Подведение итогов.
Определение победителя по наибольшему количеству баллов.
Выставление оценок в журнал.
Приложение. Карточки для команд.

5.4.6. Сравнение обыкновенных дробей математика-повторение
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше. На самом деле, ведь знаменатель показывает, на сколько частей разделили одну целую величину, а числитель показывает, сколько таких частей взяли.
Получается, что делили каждый целый круг на одно и то же число 5, а брали разное количество частей: больше взяли — большая дробь и получилась.
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше. Ну и, в самом деле, если мы один круг разделим на 8 частей, а другой на 5 частей и возьмем по одной части от каждого из кругов. Какая часть будет больше?
Конечно, от круга, поделенного на 5 частей! А теперь представьте, что делили не круги, а торты. Вы бы какой кусочек предпочли, точнее, какую долю: пятую или восьмую?
Чтобы сравнить дроби с разными числителями и разными знаменателями, надо привести дроби к наименьшему общему знаменателю, а затем сравнивать дроби с одинаковыми знаменателями.
Примеры. Сравнить обыкновенные дроби:
Приведем эти дроби к наименьшему общему знаменателю. НОЗ(4; 6)=12. Находим дополнительные множители для каждой из дробей. Для 1-й дроби дополнительный множитель 3 (12:4=3). Для 2-й дроби дополнительный множитель 2 (12:6=2). Теперь сравниваем числители двух получившихся дробей с одинаковыми знаменателями. Так как числитель первой дроби меньше числителя второй дроби (9<10), то и сама первая дробь меньше второй дроби.
Аналогично рассуждаем и при решении остальных примеров.
Запись имеет метки: математика в 5 классе, сравнение обыкновенных дробей
www.mathematics-repetition.com
Дидактический материал по математике «Сложение и вычитание дробей с разными знаменателями» (6 класс)
Тема урока
«Сложение дробей
с разными знаменателями».
Работа в парах.
Сложите дроби:
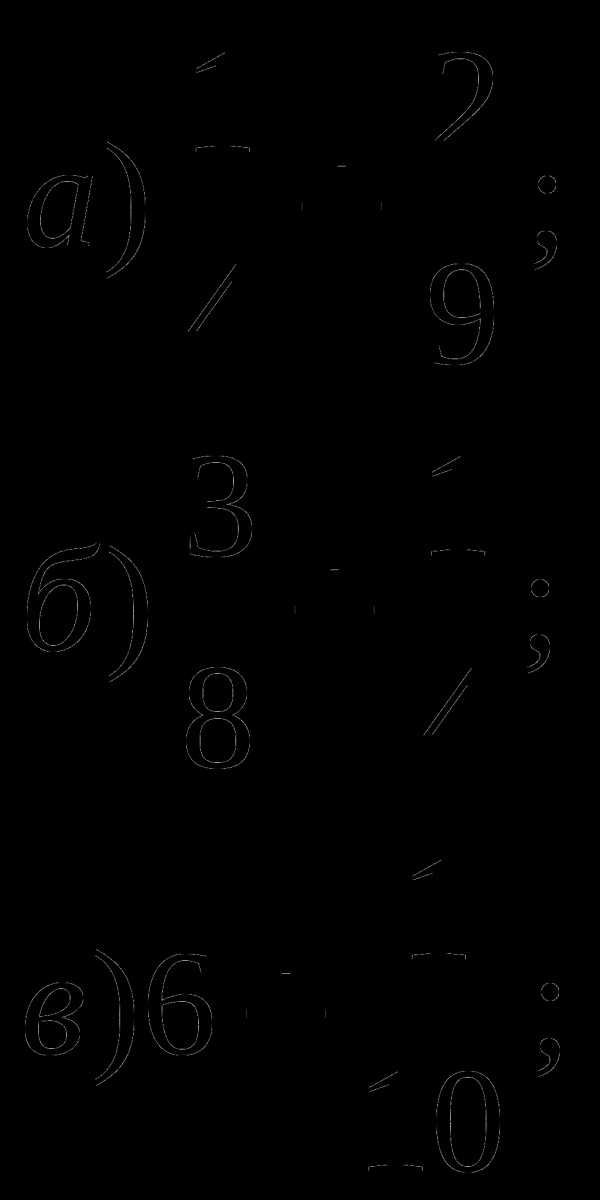
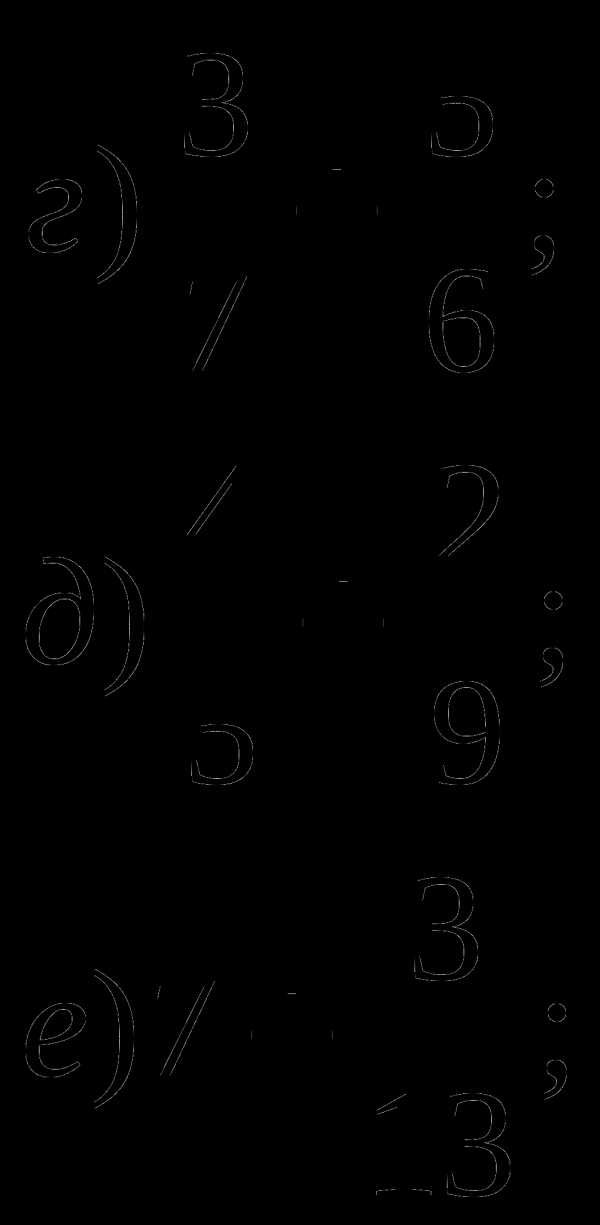
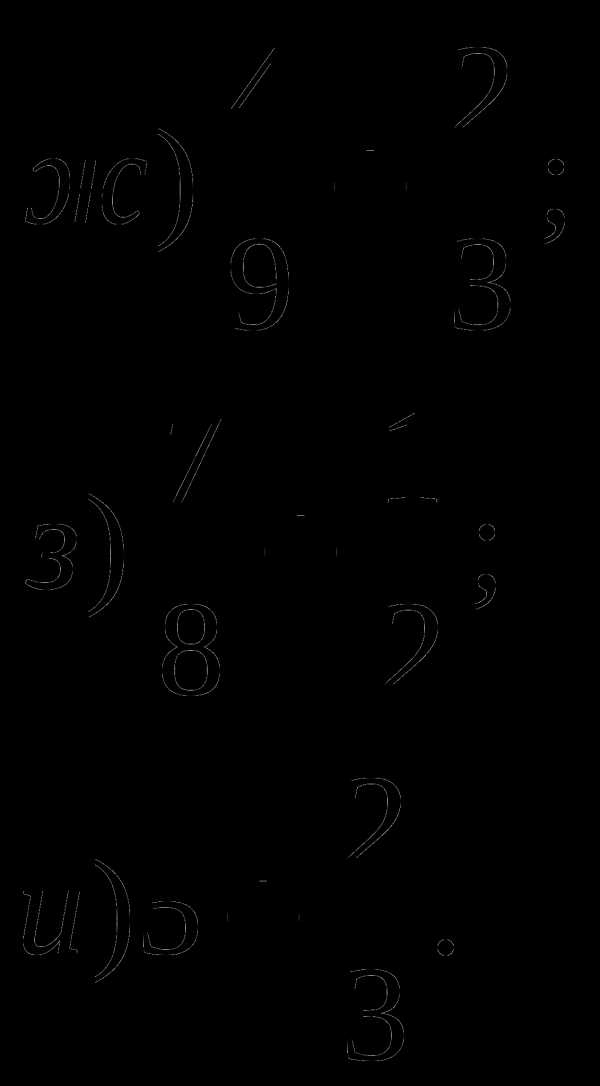
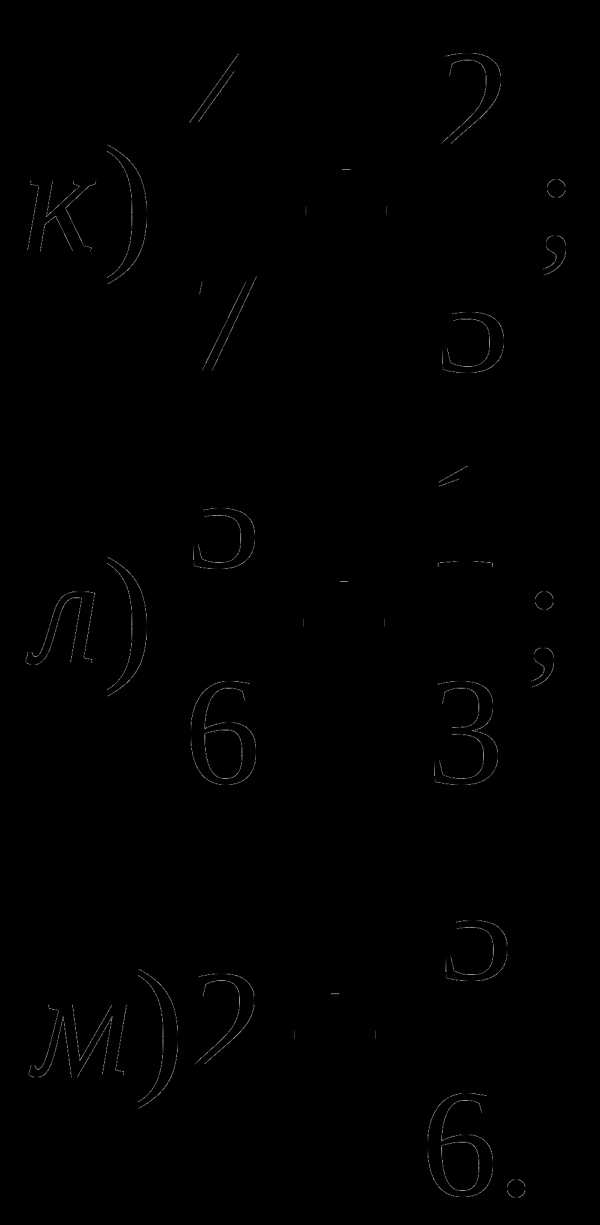
2. Приведите дроби к наименьшему общему знаменателю:
а) и
и 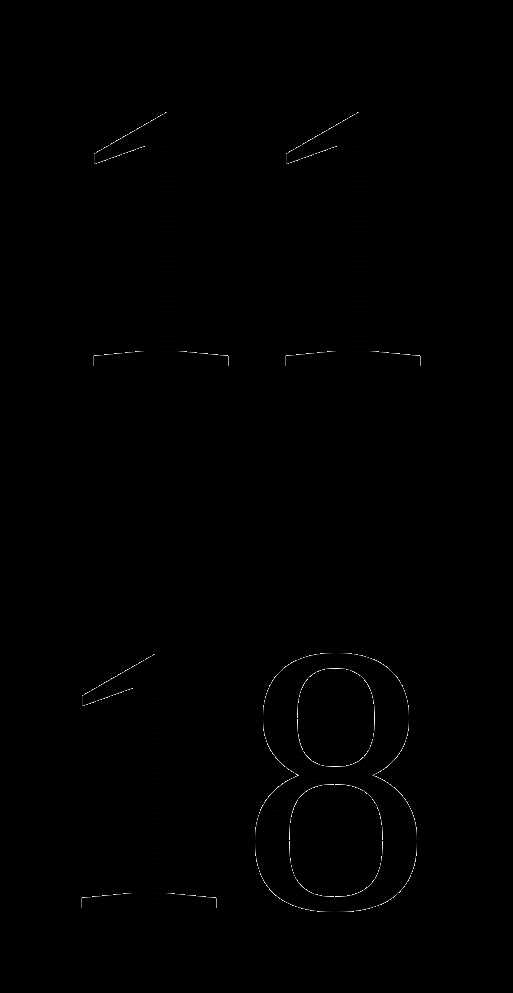 ; б)
; б) и
и 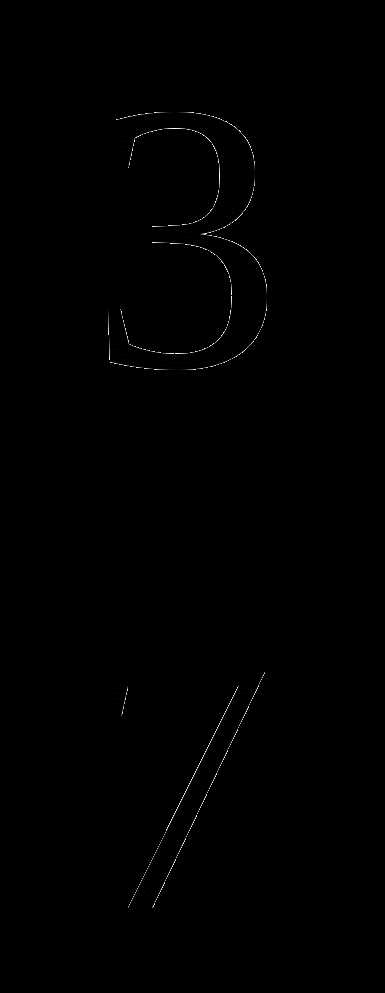 ; в)
; в) и
и  .
.
3. Сравните дроби:
а) 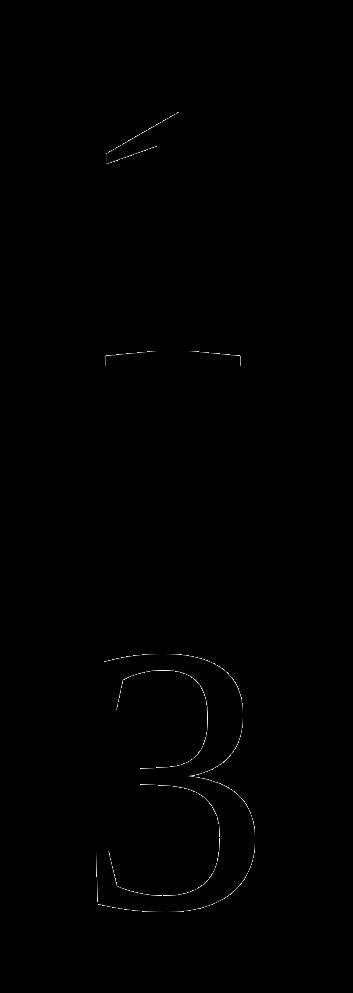 и
и  ; б)
; б)  и
и  ; в)
; в) и
и  .
.
4. Сложите дроби:
а)  +
+  ; б )
; б ) +
+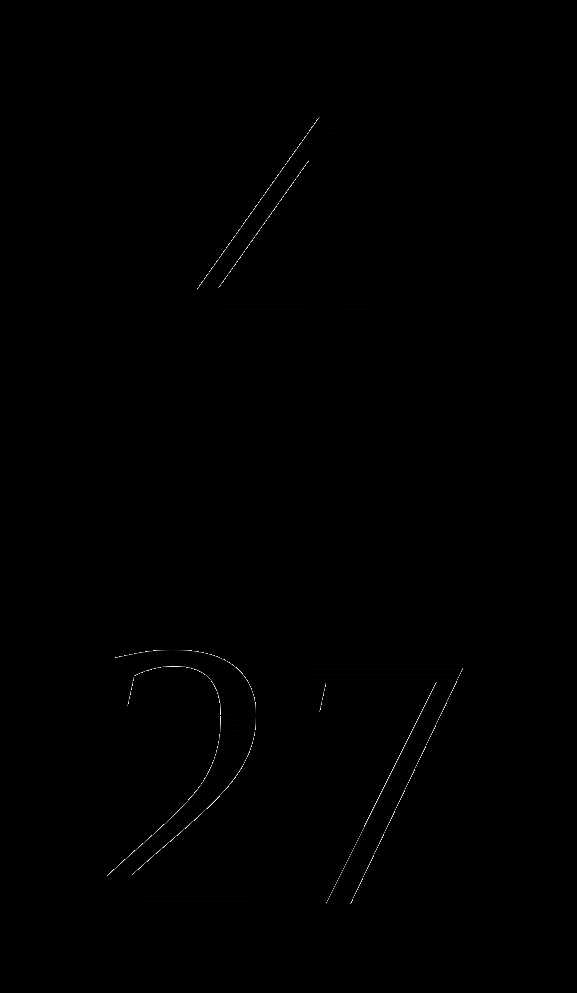 ; в)
; в)  +
+ 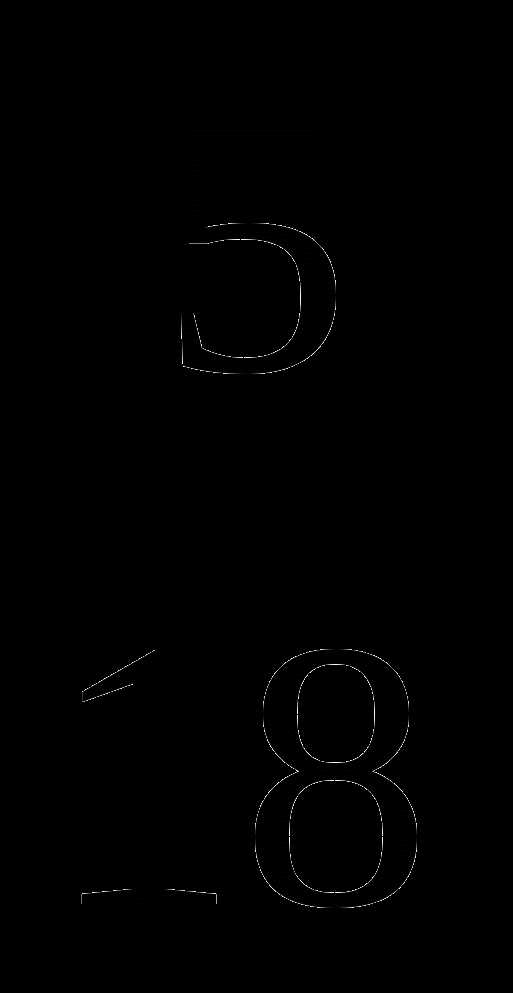 .
.
5. Чему равен х?
а)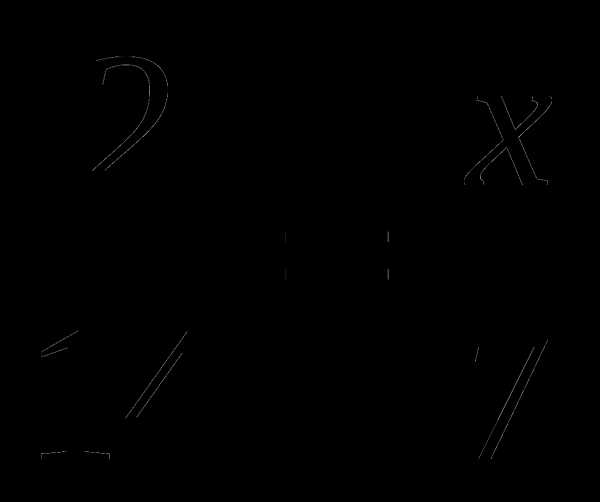 ; б)
; б) ; в)
; в)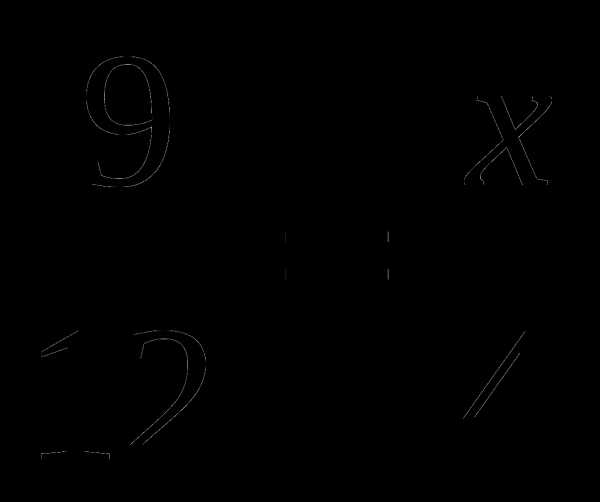 ; г)
; г)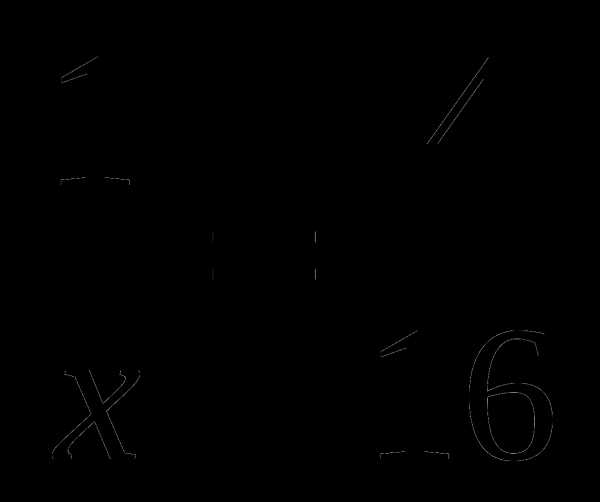 ;
;
д)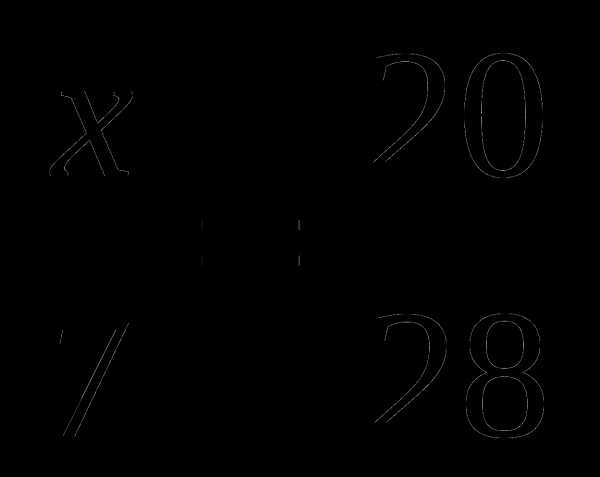 ; е)
; е)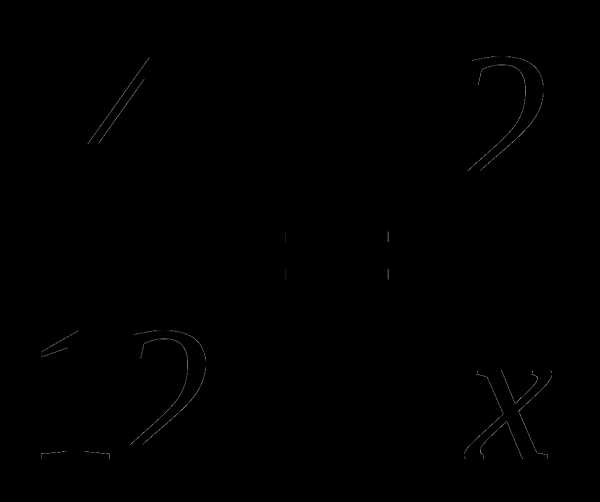 ; ж)
; ж)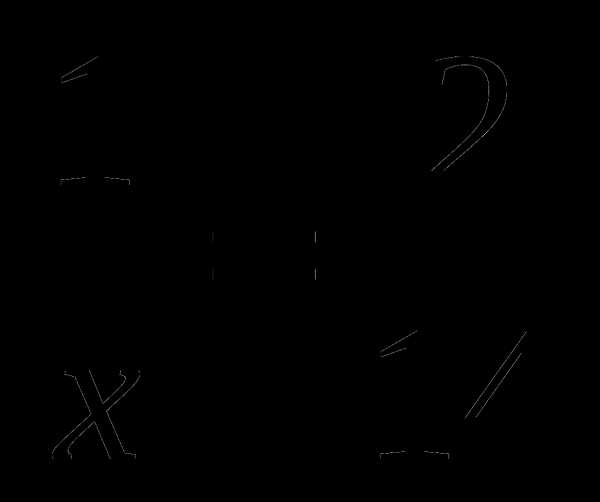 .
.
6. Верно ли утверждение?
а) 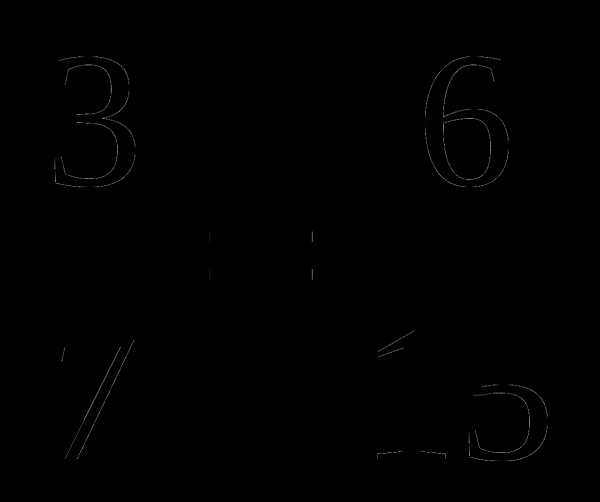 ; б)
; б) ; в)
; в)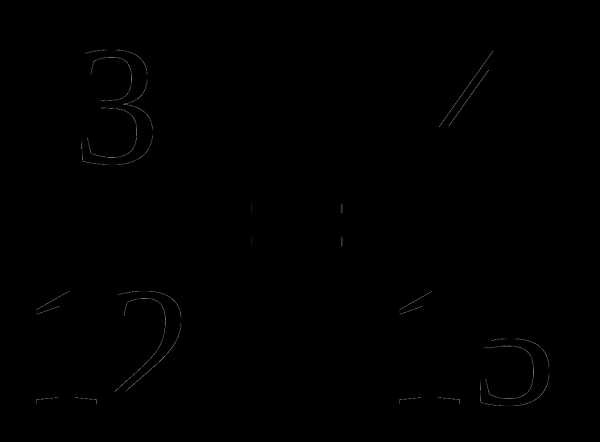 ; г)
; г)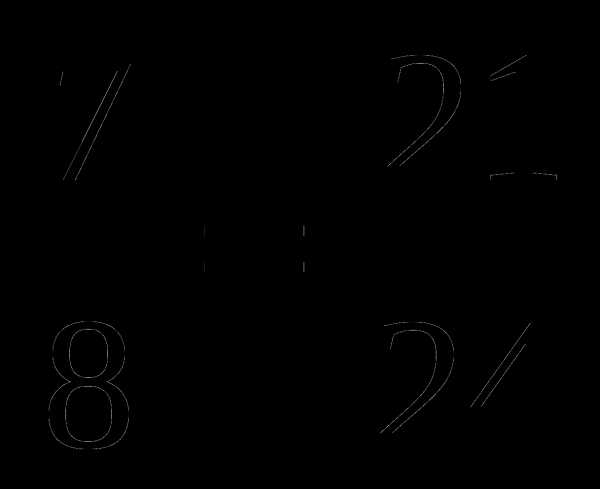 ;
;
д) ; е)
; е)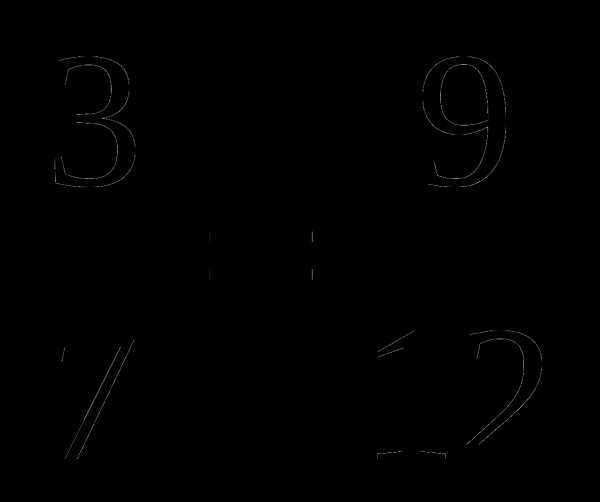 ; ж)
; ж)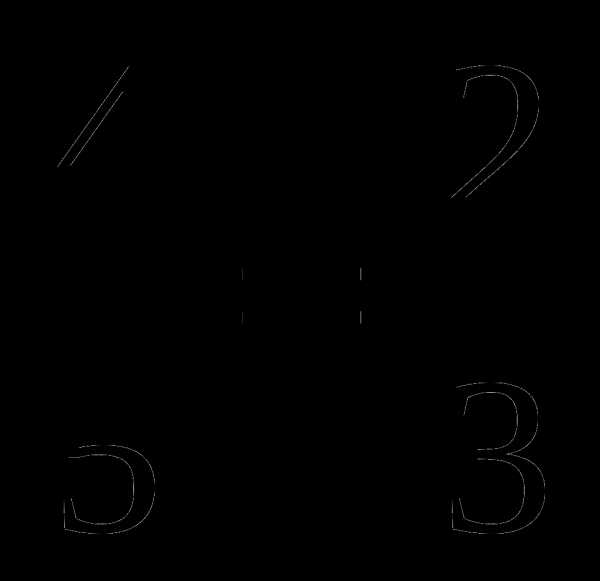 .
.
7. Определите, какая из дробей наибольшая, а какая наименьшая?
Домашнее задание:
прочитать с 79-80;
№9, №10, №11 с 77-78.
Тема урока
«Сложение дробей
с разными знаменателями».
Работа в парах.
Сложите дроби:
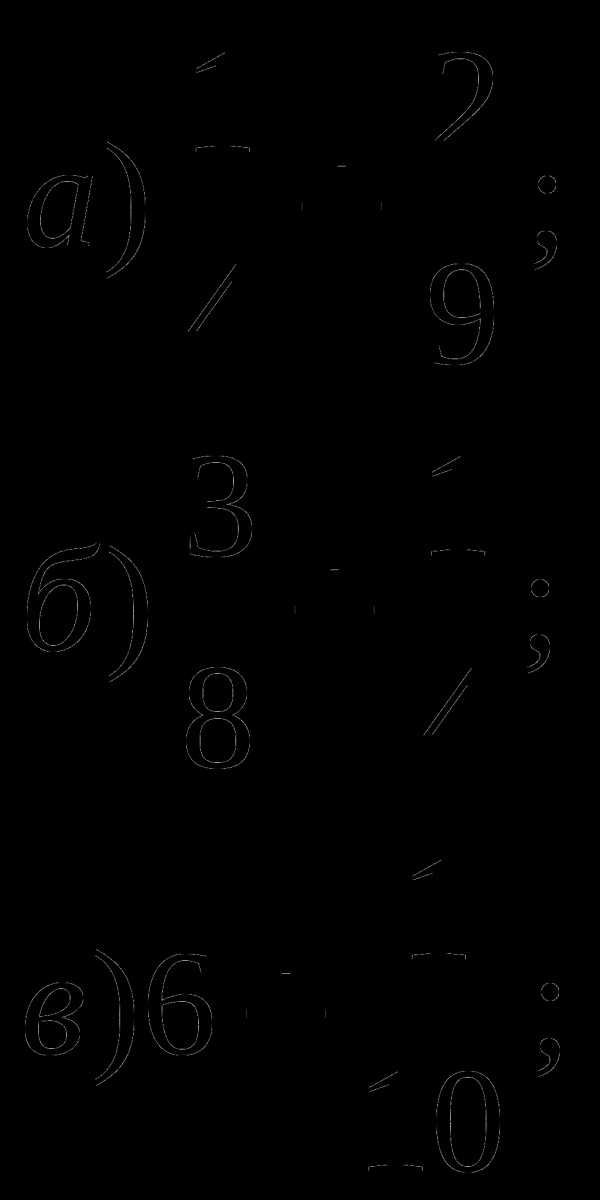
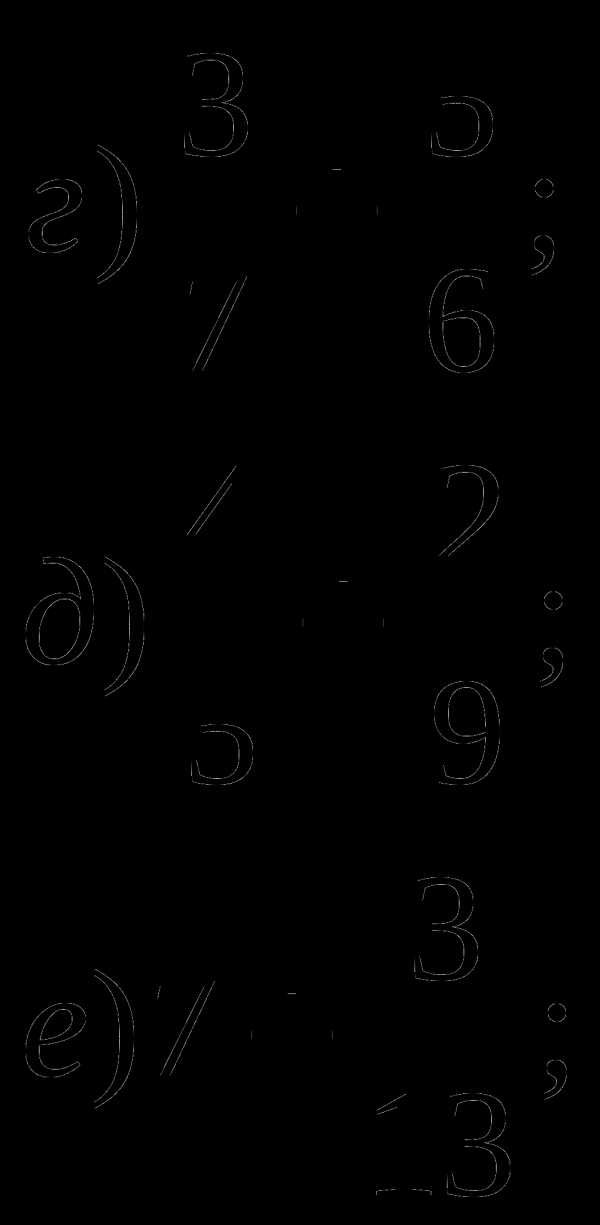
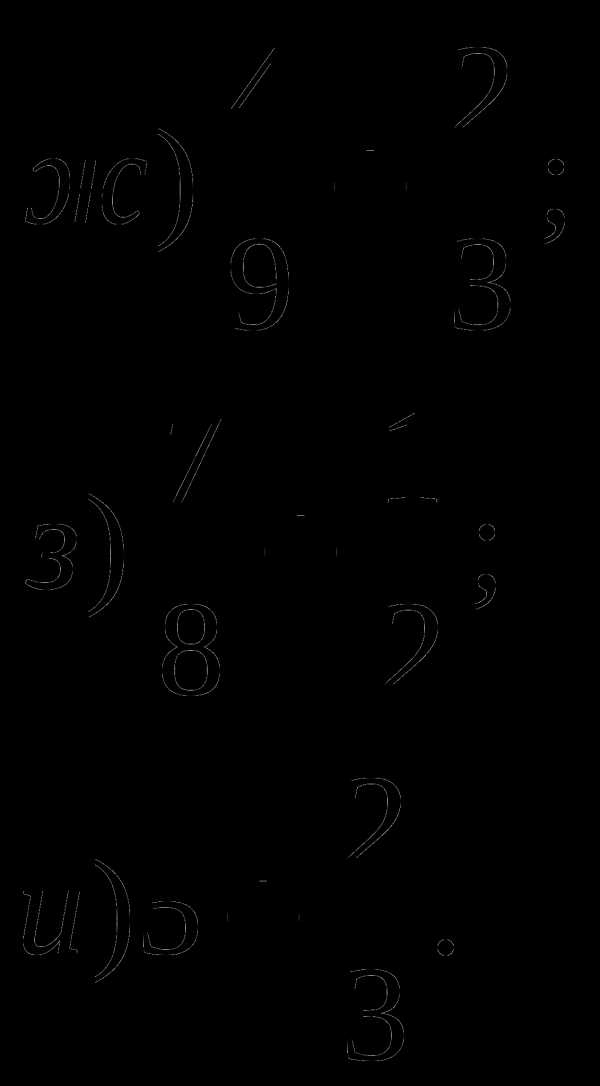
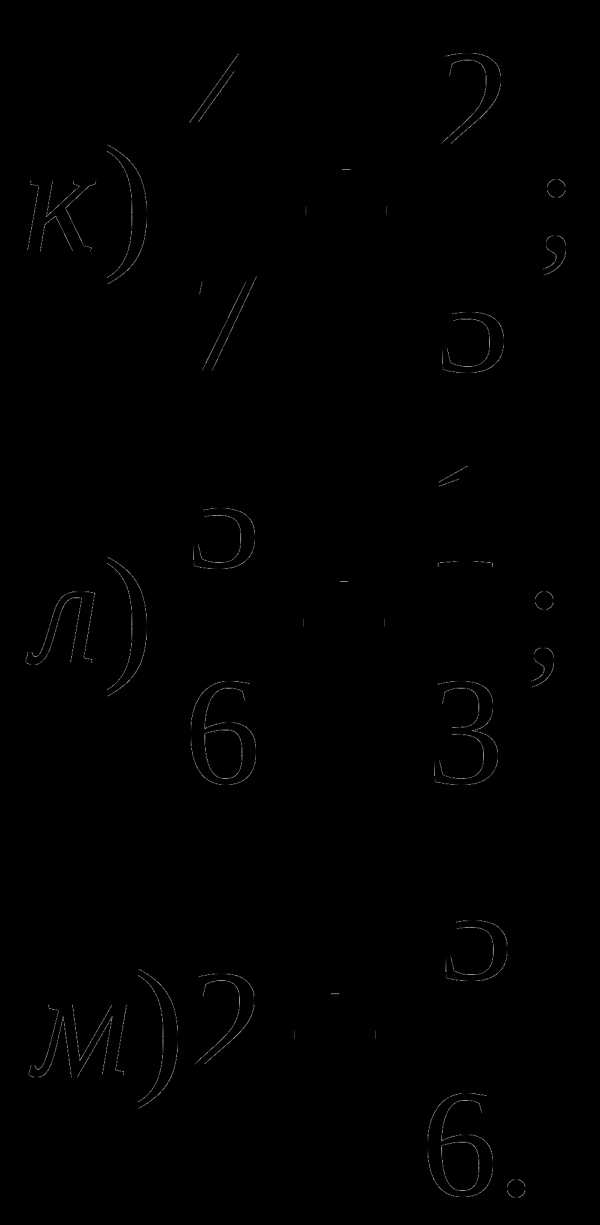
2. Приведите дроби к наименьшему общему знаменателю:
а) и
и  ; б)
; б) и
и 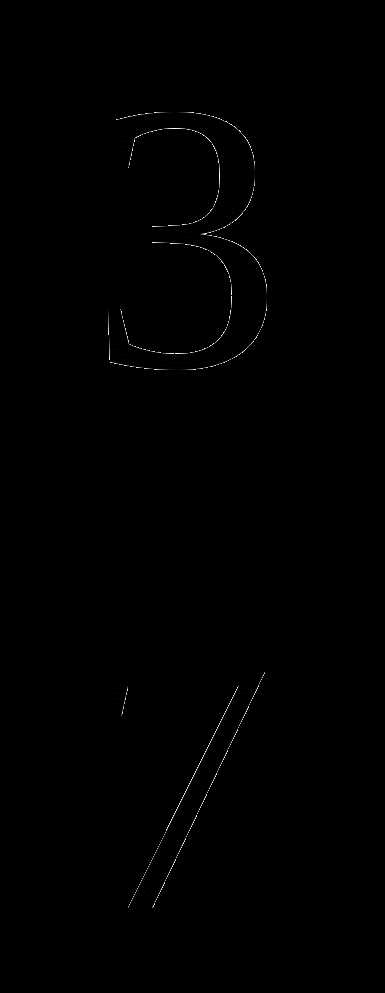 ; в)
; в) и
и  .
.
3. Сравните дроби:
а)  и
и  ; б)
; б)  и
и  ; в)
; в) и
и  .
.
4. Сложите дроби:
а)  +
+  ; б )
; б ) +
+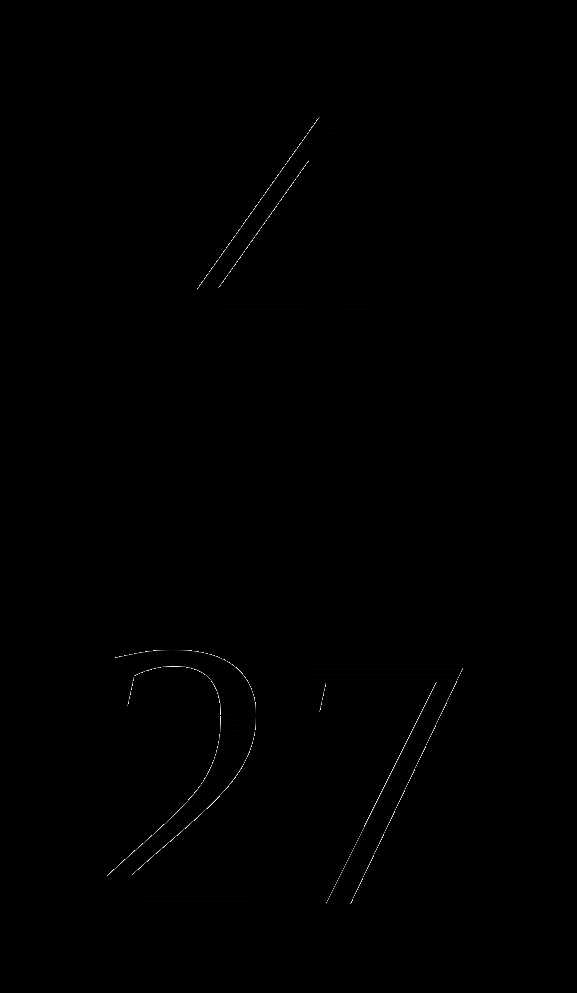 ; в)
; в)  +
+ 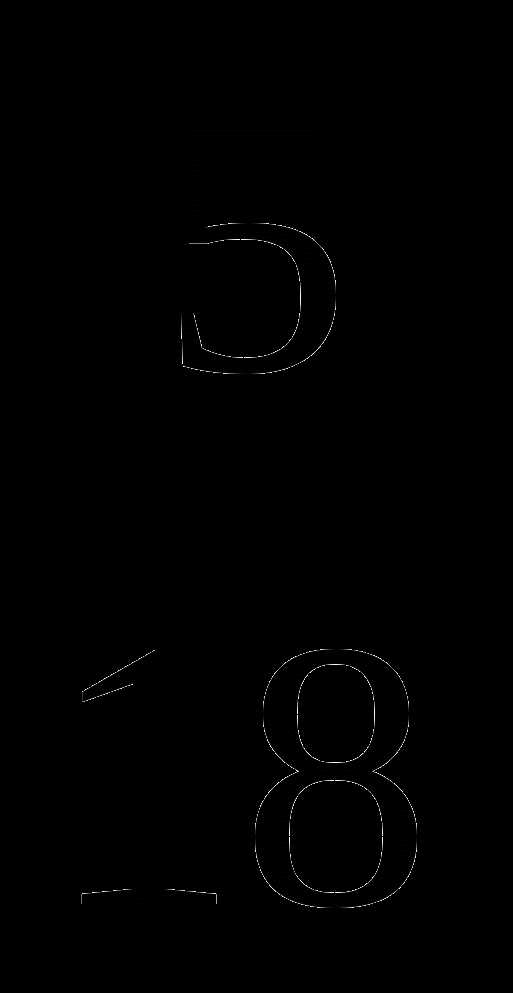 .
.
5. Чему равен х?
а)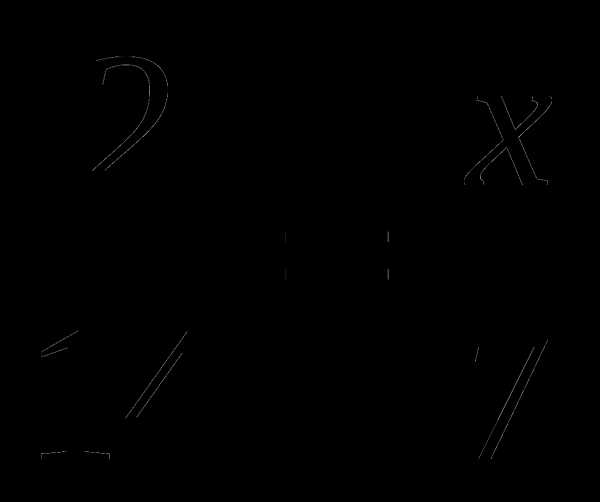 ; б)
; б) ; в)
; в)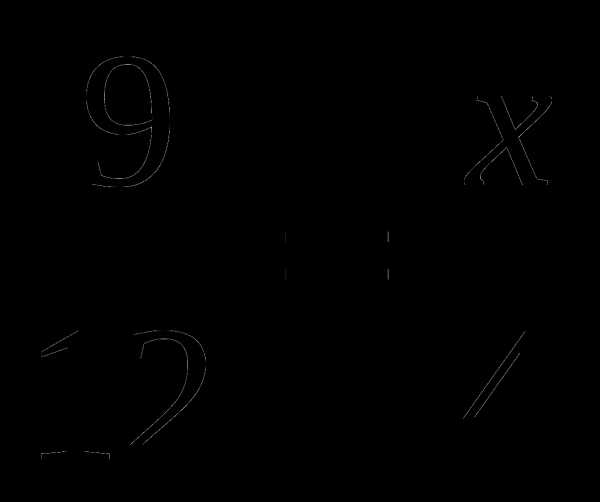 ; г)
; г)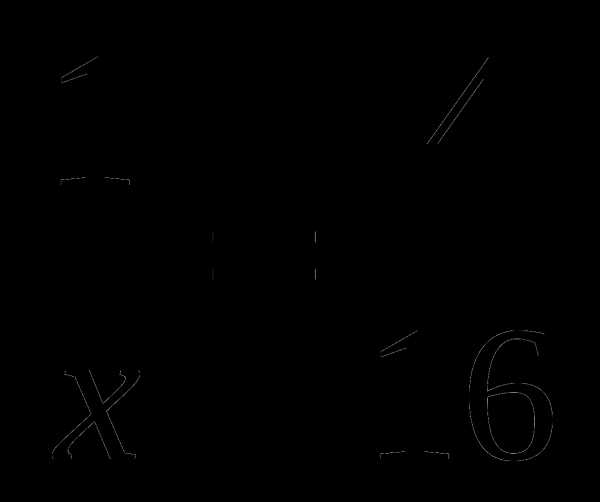 ;
;
д)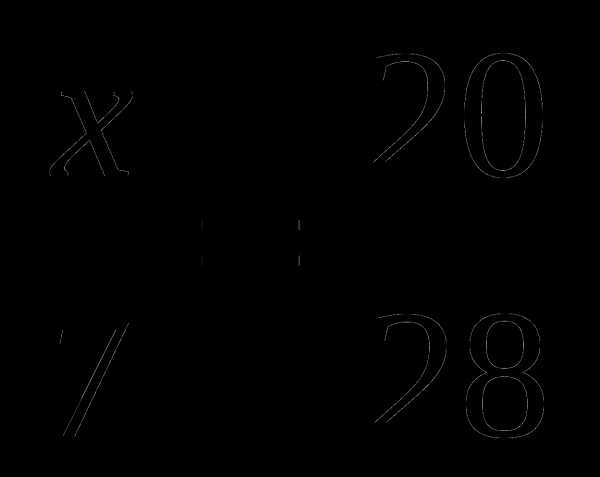 ; е)
; е)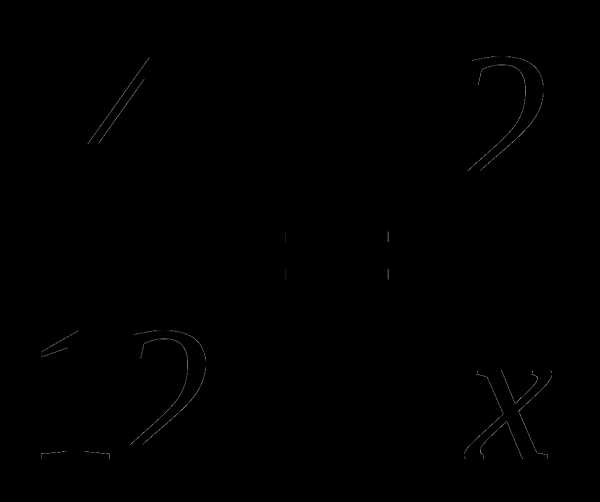 ; ж)
; ж)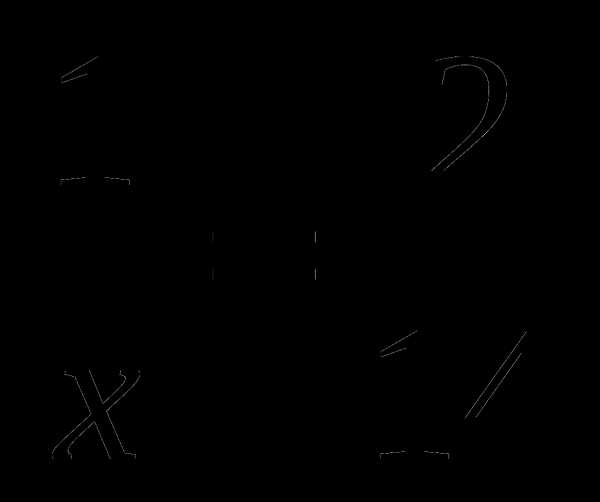 .
.
6. Верно ли утверждение?
а) 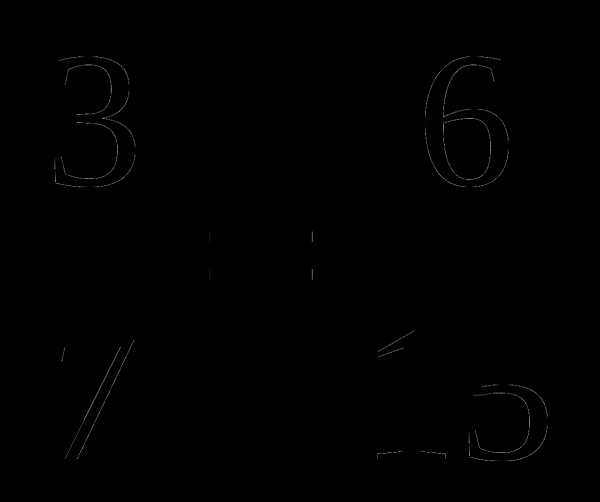 ; б)
; б) ; в)
; в)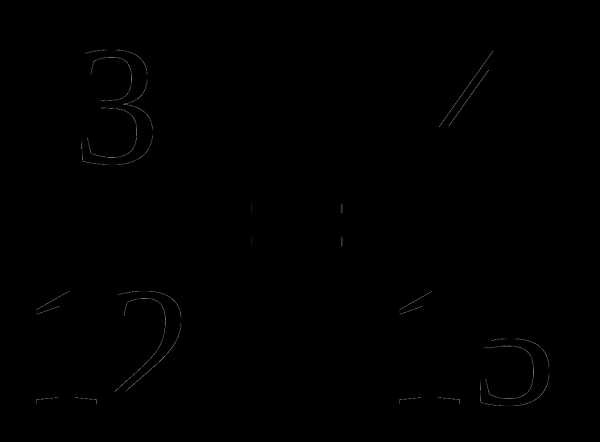 ; г)
; г)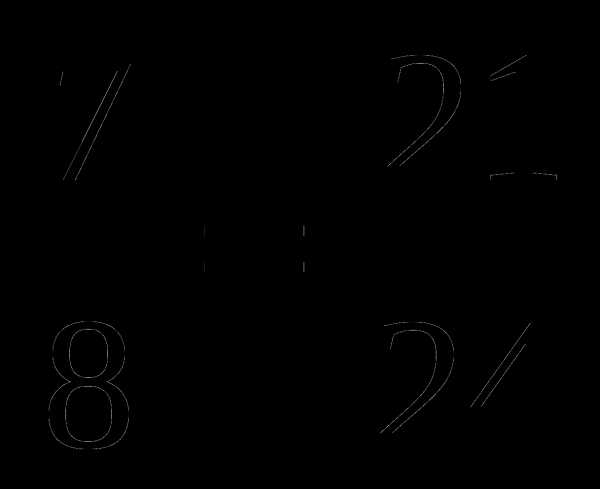 ;
;
д) ; е)
; е)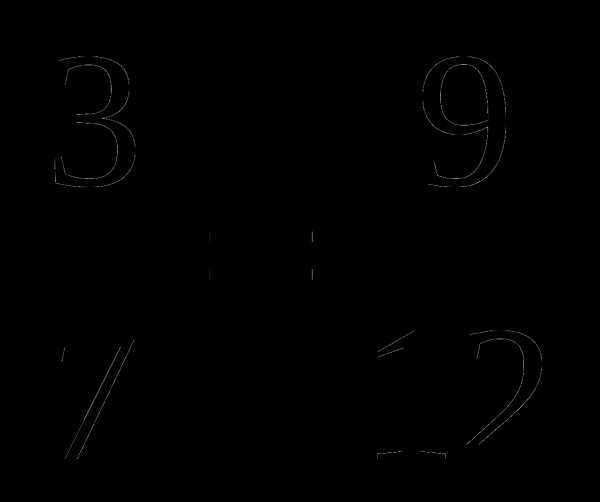 ; ж)
; ж) .
.
7. Определите, какая из дробей наибольшая, а какая наименьшая?
Домашнее задание:
прочитать с 79-80;
№9, №10, №11 с 77-78.
infourok.ru
6 класс. Математика. Сложение и вычитание дробей с разными знаменателями. Сравнение дробей — Сложение и вычитание дробей с разными знаменателями. Сравнение дробей
Комментарии преподавателя
Вспомним, что мы уже знаем об обыкновенных дробях.
1. Любая дробь представляет количество – часть от какого-то числа. Эту часть мы умеем вычислять. Например, от 100 – это .
2. Одну и ту же часть можно выразить эквивалентными дробями (см. рис. 1). Эквивалентные дроби имеют разную запись, однако выражают одно и то же количество, равны друг другу.
Рис. 1. Пример эквивалентных дробей
3. При сложении/вычитании дробей с одинаковыми знаменателями складываем/вычитаем числители.
4. При сравнении двух дробей с одинаковыми знаменателями большая та, у которой числитель больше (см. рис. 2).
Рис. 2. Пример сравнения дробей с одинаковым знаменателем
Теперь перейдем к вопросу: что делать, если у дробей будут разные знаменатели. Например, как нам сложить и (см. рис. 3)?
Рис. 3. Иллюстрация к примеру
Если мы заменим одну из дробей на эквивалентную, то их сумма, очевидно, не изменится.
Для дроби существует бесконечное множество дробей, которые ей эквивалентны. Давайте будем домножать числитель и знаменатель этой дроби на 2, 3, 4 и т.д. Тем самым мы получим цепочку эквивалентных дробей.
Аналогично поступим и со второй дробью:
Мы можем заменить дробь эквивалентной. Нам нужно найти такие две дроби, у которых знаменатель одинаковый, тогда мы сможем выполнить сложение. Одинаковый знаменатель у дробей и , заменим исходные дроби на них.
Рассмотрим еще несколько примеров.
Необходимо сложить дроби.
1)
Решение
1) Несложно заметить, что дробь легко превращается в эквивалентную дробь со знаменателем 4. Для этого нам нужно домножить ее числитель и знаменатель на 2.
Определите разность.
1) 2) 3)
Решение
1) Несложно увидеть, что мы вторую дробь может превратить в дробь со знаменателем 8, для этого умножим ее числитель и знаменатель на 2.
2) Обе дроби мы можем заменить эквивалентными дробями со знаменателем 6. Числитель и знаменатель первой дроби домножим на 3, а второй – на 2.
3) Общим знаменателем для этих дробей является число 30. По образцу решаем последний пример.
Таким образом, для сложения/вычитания двух дробей с разными знаменателями дроби необходимо свести к общему знаменателю.
Сравните дроби в примерах. Выполните действия.
1) 2)
Решение
1) Общий знаменатель слагаемых должен получаться из чисел 15 и 18 умножением на какие-то числа. Например, знаменатель 270 получается при умножении 15 и 18 друг на друга, а значит, может выступать в качестве общего знаменателя для исходных дробей. Теперь необходимо умножить первое слагаемое на 18, а второе – на 15. Полученные дроби после умножения можно сравнить:
Следовательно, пер­
www.kursoteka.ru
Приведение дробей к общему знаменателю (Москаленко М.В)
Тема: Сложение и вычитание дробей с разными знаменателями
Урок: Приведение дробей к общему знаменателю
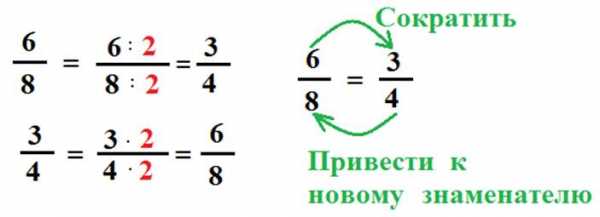
Повторение. Основное свойство дроби.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Например, числитель и знаменатель дроби можно разделить на 2. Получим дробь . Эту операцию называют сокращением дроби. Можно выполнить и обратное преобразование, умножив числитель и знаменатель дроби на 2. В этом случае говорят, что мы привели дробь к новому знаменателю. Число 2 называют дополнительным множителем.
Вывод. Дробь можно привести к любому знаменателю кратному знаменателю данной дроби. Для того чтобы привести дробь к новому знаменателю, ее числитель и знаменатель умножают на дополнительный множитель.
1. Приведите дробь к знаменателю 35.
Число 35 кратно 7, то есть 35 делится на 7 без остатка. Значит, это преобразование возможно. Найдем дополнительный множитель. Для этого разделим 35 на 7. Получим 5. Умножим на 5 числитель и знаменатель исходной дроби.
2. Приведите дробь к знаменателю 18.
Найдем дополнительный множитель. Для этого разделим новый знаменатель на исходный. Получим 3. Умножим на 3 числитель и знаменатель данной дроби.
3. Приведите дробь к знаменателю 60.
Разделив 60 на 15, получим дополнительный множитель. Он равен 4. Умножим числитель и знаменатель на 4.
4. Приведите дробь к знаменателю 24
В несложных случаях приведение к новому знаменателю выполняют в уме. Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби.
Дробь можно привести к знаменателю 15 и дробь можно привести к знаменателю 15. У дробей и общий знаменатель 15.
Общим знаменателем дробей может быть любое общее кратное их знаменателей. Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Пример. Привести к наименьшему общему знаменателю дроби и .

Сначала найдем наименьшее общее кратное знаменателей данных дробей. Это число 12. Найдем дополнительный множитель для первой и для второй дроби. Для этого 12 разделим на 4 и на 6. Три – это дополнительный множитель для первой дроби, а два – для второй. Приведем дроби к знаменателю 12.
Мы привели дроби и к общему знаменателю, то есть мы нашли равные им дроби, у которых один и тот же знаменатель.
Правило. Чтобы привести дроби к наименьшему общему знаменателю, надо
Во-первых, найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
Во-вторых, разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель.
В-третьих, умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
а) Привести к общему знаменателю дроби и .
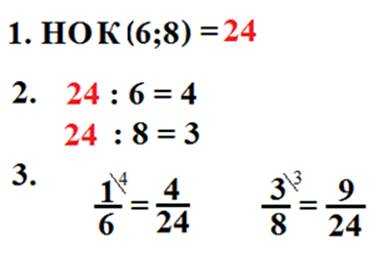
Наименьший общий знаменатель равен 12. Дополнительный множитель для первой дроби – 4, для второй – 3. Приводим дроби к знаменателю 24.
б) Привести к общему знаменателю дроби и .
Наименьший общий знаменатель равен 45. Разделив 45 на 9 на 15, получим, соответственно, 5 и 3. Приводим дроби к знаменателю 45.
в) Привести к общему знаменателю дроби и .
Общий знаменатель – 24. Дополнительные множители, соответственно, – 2 и 3.
Иногда бывает трудно подобрать устно наименьшее общее кратное для знаменателей данных дробей. Тогда общий знаменатель и дополнительные множители находят с помощью разложения на простые множители.
Привести к общему знаменателю дроби и .
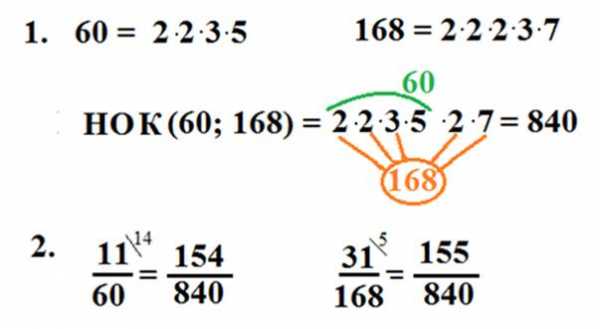
Разложим числа 60 и 168 на простые множители. Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби – это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия, 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – Просвещение, 1989.
4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс. – ЗШ МИФИ, 2011.
5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. – ЗШ МИФИ, 2011.
6. Шеврин Л.Н., Гейн А.Г., Коряков И.О. и др. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. – Просвещение, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Математика онлайн (Источник).
2. Math-portal.ru (Источник).
Можно скачать книги, указанные в п.1.2. данного урока.
Домашнее задание
Виленкин Н.Я., Жохов В.И., Чесноков А.С. и др. Математика 6. – М.: Мнемозина, 2012. (ссылка см. 1.2)
Домашнее задание: №297, №298, №300.
Другие задания: №270, №290
interneturok.ru

