Перпендикулярные векторы и условие перпендикулярности
Условие ортогональности векторов. Векторы и будут ортогональными тогда и только тогда, когда их скалярное произведение равно нулю:
Если векторы заданы своими координатами: и , то условие ортогональности запишется в виде:
Примеры решения задач
ПРИМЕР| Задание | Исследовать векторы и на ортогональность. |
| Решение |
Согласно условию ортогональности, два вектора перпендикулярны, если их скалярное произведение равно нулю. Вычислим скалярное произведение заданных векторов, оно равно сумме произведений соответствующих координат:
Поскольку в результате получили ненулевое значение, то делаем вывод, что векторы не являются ортогональными. |
| Ответ | Векторы и не ортогональны. |
| Задание | При каком значении параметра векторы и будут ортогональными? |
| Решение |
Два вектора ортогональны, если их скалярное произведение равно нулю:
Таким образом, заданные векторы ортогональны при . |
| Ответ |
Напомним определение перпендикулярных векторов на плоскости и в трехмерном пространстве.
Определение.
Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам ( 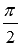 радиан).
радиан).
Теорема.
Для перпендикулярности двух ненулевых векторов 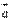 и
и 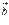 необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство
необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство  .
.
Доказательство.
Пусть векторы  и
и 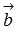 перпендикулярны. Докажем выполнение равенства
перпендикулярны. Докажем выполнение равенства 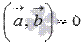
По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы  и
и 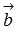 перпендикулярны, то угол между ними равен девяноста градусам, следовательно,
перпендикулярны, то угол между ними равен девяноста градусам, следовательно,  , что и требовалось доказать.
, что и требовалось доказать.
Переходим ко второй части доказательства.
Теперь считаем, что  . Докажем, что векторы
. Докажем, что векторы 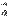 и
и 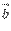 перпендикулярны.
перпендикулярны.
Так как векторы 
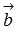 ненулевые, то из равенства
ненулевые, то из равенства  следует, что
следует, что  . Таким образом, косинус угла между векторами
. Таким образом, косинус угла между векторами  и
и 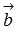 равен нулю, следовательно, угол
равен нулю, следовательно, угол  равен
равен 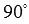 , что указывает на перпендикулярность векторов
, что указывает на перпендикулярность векторов  и
и 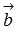
Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.
Как же выглядит условие перпендикулярности двух векторов в координатной форме?
В разделе скалярное произведение в координатах мы показали, что для двух векторов с заданными координатами  и
и  на плоскости справедливо равенство
на плоскости справедливо равенство  , а для двух векторов
, а для двух векторов  и
и  в пространстве
в пространстве 
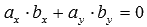 на плоскости, а в трехмерном пространстве
на плоскости, а в трехмерном пространстве 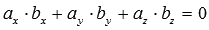 .
.Рассмотрим применение полученных условий на практике, для этого разберем решение нескольких примеров.
Пример.
Перпендикулярны ли векторы 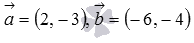 .
.
Решение.
Вычислим их скалярное произведение по координатам  . Следовательно, условие перпендикулярности двух векторов на плоскости выполнено, то есть, они перпендикулярны.
. Следовательно, условие перпендикулярности двух векторов на плоскости выполнено, то есть, они перпендикулярны.
Ответ:
да, векторы перпендикулярны.
Пример.
Перпендикулярны ли векторы 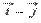 и
и  , где
, где  — координатные векторы прямоугольной системы координат в трехмерном пространстве.
— координатные векторы прямоугольной системы координат в трехмерном пространстве.
Решение.
Векторы 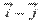 и
и  имеют соответственно координаты
имеют соответственно координаты 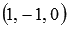 и
и 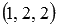 (при необходимости смотрите статью координаты вектора в прямоугольной системе координат). Проверим выполнение необходимого и достаточного условия перпендикулярности двух векторов:
(при необходимости смотрите статью координаты вектора в прямоугольной системе координат). Проверим выполнение необходимого и достаточного условия перпендикулярности двух векторов:
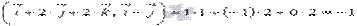
Так как  , то векторы
, то векторы 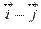 и
и  не перпендикулярны.
не перпендикулярны.
Ответ:
нет, не перпендикулярны.
Пример.
Найдите значение 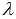 , при котором векторы
, при котором векторы 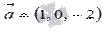 и
и  перпендикулярны.
перпендикулярны.
Решение.
Воспользуемся условием перпендикулярности двух векторов в пространстве в координатной форме
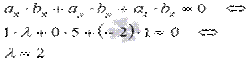
Ответ:
векторы перпендикулярны при 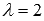 .
.
В некоторых случаях возможно ответить на вопрос о перпендикулярности двух векторов без использования необходимого и достаточного условия перпендикулярности. Например, когда известны длины всех сторон треугольника, построенного на двух векторах, то можно найти угол между векторами и посмотреть, равен ли он девяноста градусам.
Пример.
Стороны АВ, АС и ВС треугольника АВС равны соответственно 8, 6 и 10 см. Убедитесь, что векторы 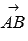 и
и 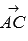 перпендикулярны.
перпендикулярны.
Решение.
Если векторы 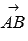 и
и 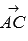 перпендикулярны, то треугольник АВС – прямоугольный и его гипотенузой является сторона ВС. Тогда по теореме Пифагора должно выполняться равенство
перпендикулярны, то треугольник АВС – прямоугольный и его гипотенузой является сторона ВС. Тогда по теореме Пифагора должно выполняться равенство 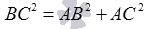 . Проверим его справедливость:
. Проверим его справедливость: 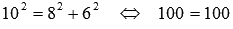 .
.
Следовательно, АВ и АС – катеты прямоугольного треугольника АВС, поэтому, векторы 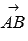 и
и 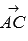 перпендикулярны.
перпендикулярны.
Ортогональность векторов.
Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = {a
a · b = ax · bx + ay · by = 0
Пример 1. Доказать что вектора a = {1; 2} и b = {2; -1} ортогональны.Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 — 2 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 2. Проверить являются ли вектора a = {3; -1} и b = {7; 5} ортогональными.Решение:
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 — 5 = 16Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Пример 3. Найти значение числа n при котором вектора a = {2; 4} и b = {n; 1} будут ортогональны.Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2n + 42n + 4 = 0
2n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = {ax; ay; az} и b = {bx; by; bz}, условие ортогональности запишется следующим образом:
a · b = ax · bx + ay · by + az · bz = 0
Пример 4. Доказать что вектора a = {1; 2; 0} и b = {2; -1; 10} ортогональны.Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 — 2 + 0 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 5. Проверить являются ли вектора a = {2; 3; 1} и b = {3; 1; -9} ортогональными.Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Пример 6. Найти значение числа n при котором вектора a = {2; 4; 1} и b = {n; 1; -8} будут ортогональны.Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 — 8 = 2n — 42n — 4 = 0
2n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.
Начнем с постановки задачи.
Пусть нам требуется найти координаты вектора в трехмерном пространстве, который одновременно перпендикулярен двум не коллинеарным векторам 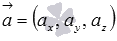 и
и 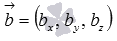 . Если векторы
. Если векторы  и
и 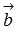 коллинеарные, то решением задачи будет вектор, перпендикулярный одному из векторов
коллинеарные, то решением задачи будет вектор, перпендикулярный одному из векторов  или
или 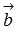 (о нахождении такого вектора мы говорили в предыдущем пункте).
(о нахождении такого вектора мы говорили в предыдущем пункте).
Одно из решений такой задачи основано на использовании понятия векторного произведения векторов.
Нам известно, что векторное произведение векторов  и
и 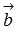 представляет собой вектор, перпендикулярный одновременно и вектору
представляет собой вектор, перпендикулярный одновременно и вектору  и
и 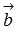 . Таким образом, векторное произведение
. Таким образом, векторное произведение  является решением нашей задачи. В координатной форме оно имеет вид
является решением нашей задачи. В координатной форме оно имеет вид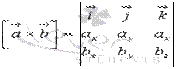
Разберем на примере.
Пример.
Найдите координаты какого-нибудь вектора, перпендикулярного одновременно двум векторам 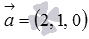 и
и 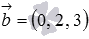 .
.
Решение.
Решением нашей задачи является векторное произведение заданных векторов. Найдем его (при необходимости смотрите статью вычисление определителя матрицы):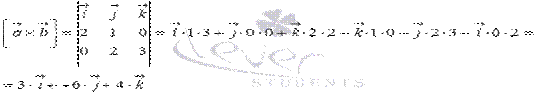
Ответ:
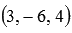 — один из векторов, одновременно перпендикулярный и вектору
— один из векторов, одновременно перпендикулярный и вектору 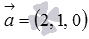 и
и 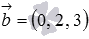 .
.
Умова перпендикулярності векторів a•b=0
Перевірку чи вектори перпендикулярні або колінеарні виконують при проходженні теми «Вектори».
Умова перпендикулярності
Якщо вектори перпендикулярні, то їх скалярний добуток a•b=0 рівний нулю:
ax•bx+ay•by+az•bz=0.
Інша умова, що також вимагає обчислення скалярного добутку полягає в тому, що косинус кута між перпендикулярними векторами рівний нулю
cos(phi)=0.
Розглянемо завдання на ознаку перпендикулярності.
Приклад 1. Чи перпендикулярні вектори?
1. a(-2;3;0), b(6;4;-11);
2. c(-8;5), d(1;7).
Розв’язання:Обчислюємо скалярний добуток векторів a,b:
a•b=-2•6+3•4+0•(-11)=0.
Вектори перпендикулярні a⊥b, оскільки їх скалярний добуток рівний нулю.
Перевіримо другу пару векторів, обчислимо скалярний добуток
c•d=-8•1+5•7=27.
Робимо висновок, що вектори c,d не перпендикулярні, оскільки ознака перпендикулярності не виконується
c•d=27≠0.
Далі розглянемо тести із ЗНО підготовки, де потрібно перевірити умову перпендикулярності.
Приклад 42.11 При якому значенні x вектори a(2;x) і b(-4;10) перпендикулярні?
Розв’язування: Вектори a(2;x) і b(-4;10) будуть перпендикулярними (a⊥b), якщо їх скалярний добуток дорівнюватиме нулю:
a•b=0.
З умови перпендикулярності a•b=2•(-4)+x•10=0 обчислюємо параметр x:
-8+10x=0,
10x=8,
x=8:10=0,8.
В декартовій площині вони мають вигляд
Відповідь: 0,8 – В.
Приклад 42.27 Установити відповідність між значеннями числа x (1–4), та парами векторів (А–Д), які за цих значень взаємно перпендикулярні.
Розв’язування: Умова перпендикулярності векторів an(a1;a2;a3) і bn(b1;b2;b3):
a⊥b, якщо a1b1+a2b2+a3b3=0.
Для кожної пари векторів обчислюємо скалярний добуток векторів і прирівнюємо його до нуля. Отримане рівняння розв’язуємо відносно «ікс»
Записуємо відповідь до тестів:
1 – Б, 2 – А, 3 – Г, 4 – В.
На ЗНО тестах такі завдання поширені, тому запам’ятайте алгоритм обчислень.
Приклад 42.20 a і b – ненульові вектори. |a+b|=|a-b|. Знайти кут між векторами a і b.
Розв’язування: В умові рисунку немає, його виконано на основі всіх розрахунків.
Нехай φ – кут між векторами a і b, виписуємо модуль суми та різниці векторів.
Далі прирівнявши довжини, складаємо рівняння для знаходження кута між векторами
Підносимо до квадрату та спрощуємо подібні доданки
Робимо висновок, що якщо |a+b|=|a-b|, то кут між векторами a і b дорівнює 90 градусів.
З рисунка добре видно, що при побудові суми (a+b) і різниці (a-b) векторів за правилом паралелограма отримали прямокутник, у якого (за властивістю) діагоналі є рівними (|a+b|=|a-b|).
Відповідь: 900 – Г.
Приклад 42.37 Знайти площу паралелограма, побудованого на векторах AB(3;0;-4) і AD(0;5;0).
Розв’язування: Знайдемо скалярний добуток векторів AB(3;0;-4) і AD(0;5;0):
він рівний нулю.
Це означає, що вектори перпендикулярні AB⊥AD і паралелограм ABCD є прямокутником.
Знайдемо модуль (довжину) вектора AB(3;0;-4):
Знайдемо модуль (довжину) вектора AD(0;5;0):
Оскільки у прямокутника дві сусідні сторони рівні, то він є квадратом. Знайдемо площу заданого паралелограма (квадрата) ABCD:
Відповідь: 25.
Скалярний добуток обчислюють через досить просту формулу, тому великого різноманіття прикладів на умову перпендикулярності Ви не знайдете. Спробуйте обчислити кілька завдань самостійно, Ви побачите, що тема не важка для вивчення. Набагато важчими в плані розрахунків є завдання на обчислення довжини суми чи різниці векторів, обчислення площ чи об’ємів тіл побудованих на векторах, але це вже інша тема.
- Вас може зацікавити:
- Колінеарні вектори. Перевірка умови колінеарності векторів
- Скалярний добуток (a,b)
- Розклад вектора за базисом
- Скалярний та векторний добутки. Проекція вектора на вектор
- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- физика
математический
- Алгебра
- Исчисление
- Геометрия
- Prealgebra
1.2 Результат перпендикулярных векторов (ESBK3)
В 10 классе вы узнали о результирующем векторе в одном измерении, мы собираемся расширить его до двух измерений. Напоминаем, что если у вас есть несколько векторов (пока что подумайте о силах), действующих одновременно, вы можете представить результат всех их вместе с одним вектором, известным как результирующий. Результирующий вектор будет иметь тот же эффект , что и все векторы, складывающиеся вместе.
Мы сосредоточимся на примерах, связанных с силами, но очень важно помнить, что это относится ко всем физическим величинам, которые могут быть описаны векторами, силами, смещениями, ускорениями, скоростями и многим другим.
Векторы на декартовой плоскости (ESBK4)
Первое, на что следует обратить внимание, это то, что в 10 классе мы работали с векторами, действующими по одной линии, по одной оси. Теперь мы пойдем дальше и начнем работать с двумя измерениями.Мы можем представить это, используя декартову плоскость, которая состоит из двух перпендикулярных (под прямым углом) осей. Оси являются осью \ (x \) и осью \ (y \). Обычно мы рисуем ось \ (x \) — слева направо (по горизонтали) и ось \ (y \) — вверх и вниз (по вертикали).
Мы можем рисовать векторы на декартовой плоскости. Например, если у нас есть сила \ (\ vec {F} \) величины \ (\ text {2} \) \ (\ text {N} \), действующая в положительном \ (x \) — направлении мы можем нарисовать его как вектор на декартовой плоскости.
Обратите внимание, что длина вектора, измеренная с использованием осей, равна \ (\ text {2} \), указанной величине. Вектор не обязательно должен начинаться с начала координат, но его можно разместить в любом месте на декартовой плоскости. То, где вектор начинается на плоскости, не влияет на физическую величину, пока величина и направление остаются неизменными. Это означает, что все векторы на диаграмме ниже могут представлять одну и ту же силу. Это свойство известно как равенство векторов .
На диаграмме векторы имеют одинаковую величину, потому что стрелки имеют одинаковую длину , и имеют одинаковое направление .Все они параллельны направлению \ (x \) — и параллельны друг другу.
Это в равной степени относится в направлении \ (y \). Например, если у нас есть сила \ (\ vec {F} \) величины \ (\ text {2,5} \) \ (\ text {N} \), действующая в положительном направлении \ (y \) -направление мы можем нарисовать как вектор на декартовой плоскости.
Так же, как и в случае направления \ (x \) -, вектор не обязательно должен начинаться с начала координат, но его можно разместить в любом месте на декартовой плоскости. Все векторы на диаграмме ниже могут представлять одну и ту же силу.
На следующем рисунке показан пример четырех векторов силы, двух векторов, параллельных друг другу и оси \ (y \), а также двух параллельных друг другу и оси \ (x \).
Чтобы подчеркнуть, что векторы перпендикулярны, вы можете видеть на рисунке ниже, что, когда они исходят из одной и той же точки, вектор находится под прямым углом.
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки в Интернете с помощью практики Siyavula.
Зарегистрируйтесь здесь Упражнение 1.1Нарисуйте следующие силы как векторы на декартовой плоскости, возникающие в начале координат:
- \ (\ vec {F} _ {1} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \). Теперь мы нарисуем векторы на декартовой плоскости (мы можем разместить векторы в любом месте на декартовой плоскости, мы разместим их, начиная с начала координат):
Нарисуйте следующие силы как векторы на декартовой плоскости:
- \ (\ vec {F} _ {1} = \ text {3} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \).Теперь мы нарисуем векторы на декартовой плоскости (мы можем разместить векторы в любом месте на декартовой плоскости):
Нарисуйте следующие силы как векторы на декартовой плоскости:
- \ (\ vec {F} _ {1} = \ text {3} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {2} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \).Теперь мы нарисуем векторы на декартовой плоскости (мы можем разместить векторы в любом месте на декартовой плоскости):
Нарисуйте следующие силы как векторы на декартовой плоскости:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в отрицательном направлении \ (y \) —
- \ (\ vec {F} _ {3} = \ text {2,5} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \).Теперь мы нарисуем векторы на декартовой плоскости (мы можем разместить векторы в любом месте на декартовой плоскости):
Векторы в двух измерениях не всегда параллельны оси. Мы можем знать, что сила действует под углом к оси, поэтому мы все еще знаем направление силы, и если мы знаем величину, мы можем нарисовать вектор силы. Например, мы можем нарисовать \ (\ vec {F} _ {1} = \ text {2} \ text {N} \), действующий в \ (\ text {45} \) \ (\ text {°} \) в положительное \ (x \) — направление:
Мы всегда указываем угол как против часовой стрелки от положительной оси \ (x \).Поэтому, если бы мы указали отрицательный угол, мы бы измерили его по часовой стрелке от оси \ (x \) -. Например, \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) действует на \ (- \ text {45} \) \ (\ text {°} \) положительное \ (x \) — направление:
Мы можем использовать множество других способов указания направления вектора. Направление просто должно быть однозначным. До сих пор мы использовали декартову систему координат и угол с осью \ (x \) -, но есть и другие распространенные способы указания направления, которые вам необходимо знать и с которыми удобно работать.
Указания компаса (ESBK5)
Мы можем использовать направления компаса, когда это уместно, чтобы указать направление вектора. Например, если бы мы описывали силы тектонических плит (движущихся участков земной коры), чтобы говорить о силах, связанных с землетрясениями, мы могли бы говорить о силе, которую движущие плиты оказывают друг на друга.
Рисунок 1.1: Карта 15 основных тектонических плит, составляющих земную кору.Четыре основных направления: север, юг, восток и запад при использовании компаса.Они показаны на этом рисунке:
Рисунок 1.2: Эскиз компаса.При указании направления вектора с помощью компаса направления задаются по имени, северу или югу. Если направление находится между двумя направлениями, мы можем объединить имена, например, Северо-Восток находится на полпути между Севером и Востоком. Это может произойти только для направлений под прямым углом друг к другу, вы не можете сказать север-юг, поскольку это неоднозначно.
Подшипники (ESBK6)
Другой способ использования компаса для указания направления числовым способом — использование подшипников.Подшипник — это угол, обычно измеряемый по часовой стрелке с севера. Обратите внимание, , что это отличается от декартовой плоскости, где углы против или против часовой стрелки от положительного направления \ (x \) -.
Результирующий вектор (ESBK7)
В 10 классе вы узнали о сложении векторов в одном измерении. Тот же принцип может быть применен к векторам в двух измерениях. Следующие примеры показывают добавление векторов. Векторы, которые параллельны, можно сместить так, чтобы они падали на линию.Векторы, попадающие на одну и ту же линию, называются совместно- векторов. Чтобы добавить коллинеарные векторы, мы используем метод хвоста к голове, который вы изучили в 10 классе. На рисунке ниже мы напоминаем вам о подходе добавления коллинеарных векторов для получения результирующего вектора.
Рисунок 1.3: Добавление коллинеарных векторов для получения результирующего вектора.
На рисунке выше синие векторы находятся в направлении \ (y \) -, а красные — в направлении \ (x \). Два черных вектора графически представляют результирующие значения коллинеарных векторов.
Что мы сделали, так это внедрили метод сложения векторов хвостом к голове для вертикального набора векторов и горизонтального набора векторов.
Рабочий пример 1. Пересмотр: сложение головы к хвосту в одном измерении
Используйте графический метод «голова к хвосту», чтобы определить результирующую силу для игрока в регби, если два игрока в его команде толкают его вперед с силами \ (\ stackrel {\ to} {{F} _ {1}} \ ) = \ (\ text {600} \) \ (\ text {N} \) и \ (\ stackrel {\ to} {{F} _ {2}} \) = \ (\ text {900} \) \ (\ text {N} \) соответственно, и два игрока из команды противника отталкивают его назад силами \ (\ stackrel {\ to} {{F} _ {3}} \) = \ (\ text {1 000} \) \ (\ text {N} \) и \ (\ stackrel {\ to} {{F} _ {4}} \) = \ (\ text {650} \) \ (\ text {N} \) соответственно.
Выберите масштаб и направление ссылки
Давайте выберем масштаб \ (\ text {100} \) \ (\ text {N} \): \ (\ text {0,5} \) \ (\ text {cm} \) и для нашей диаграммы мы определим положительное направление как направо.
Выберите один из векторов и нарисуйте его в виде стрелки правильной длины в правильном направлении.
Начнем с рисования вектора \ (\ stackrel {\ to} {{F} _ {1}} \) = \ (\ text {600} \) \ (\ text {N} \), указывающего на положительный направление.Используя нашу шкалу \ (\ text {0,5} \) \ (\ text {cm} \): \ (\ text {100} \) \ (\ text {N} \), длина стрелки должна быть \ (\ text {3} \) \ (\ text {cm} \) направо.
Возьмите следующий вектор и начертите его, начиная со стрелки предыдущего вектора.
Следующий вектор — это \ (\ stackrel {\ to} {{F} _ {2}} \) = \ (\ text {900} \) \ (\ text {N} \) в том же направлении, что и \ ( \ stackrel {\ to} {{F} _ {1}} \). Используя шкалу, стрелка должна быть длинной \ (\ text {4,5} \) \ (\ text {cm} \) и направлена вправо.
Возьмите следующий вектор и начертите его, начиная со стрелки предыдущего вектора.
Следующий вектор: \ (\ stackrel {\ to} {{F} _ {3}} \) = \ (\ text {1 000} \) \ (\ text {N} \) в направлении в направлении , Используя шкалу, эта стрелка должна быть \ (\ text {5} \) \ (\ text {cm} \) длинной и указывать на слева .
Примечание: Мы работаем в одном измерении, поэтому эта стрелка будет нарисована сверху первых векторов слева. Это будет сбивать с толку, поэтому мы нарисуем его рядом с реальной линией, чтобы показать вам, как это выглядит.
Возьмите следующий вектор и начертите его, начиная со стрелки предыдущего вектора.
Четвертый вектор — \ (\ stackrel {\ to} {{F} _ {4}} \) = \ (\ text {650} \) \ (\ text {N} \) в обратном направлении. Используя шкалу, эта стрелка должна быть \ (\ text {3,25} \) \ (\ text {cm} \) длинной и указывать налево.
Нарисуйте результат, измерьте его длину и найдите направление
Теперь мы нарисовали все векторы силы, которые применяются к игроку. Результирующий вектор — это стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора.
Результирующий вектор измеряет \ (\ text {0,75} \) \ (\ text {cm} \), который, используя наш масштаб, эквивалентен \ (\ text {150} \) \ (\ text {N} \ ) и указывает налево ( или — отрицательное направление, или — направление, в котором толкаются члены команды противника).
Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки в Интернете с помощью практики Siyavula.
Зарегистрируйтесь здесь Упражнение 1.2Найдите результирующий в направлении \ (x \) -, \ (R_x \) и \ (y \) — направлении \ (R_y \) для следующих сил:
- \ (\ vec {F} _ {1} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {2} \ text {N} \) в отрицательном \ (x \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \) и для нашей диаграммы мы определим положительное направление как направо.
Мы начнем с рисования вектора \ (\ stackrel {\ to} {{F} _ {1}} \) = \ (\ text {1,5} \) \ (\ text {N} \), указывающего на положительное направление. Используя наш масштаб \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \), длина стрелки должна быть \ (\ text {1,5} \) \ (\ text {cm} \), указывающий направо.
Следующий вектор \ (\ stackrel {\ to} {{F} _ {2}} \) = \ (\ text {1,5} \) \ (\ text {N} \) в том же направлении, что и \ (\ stackrel {\ to} {{F} _ {1}} \). Используя шкалу, стрелка должна быть длинной \ (\ text {1,5} \) \ (\ text {cm} \) и направлена вправо.
Следующий вектор — это \ (\ stackrel {\ to} {{F} _ {3}} \) = \ (\ text {2} \) \ (\ text {N} \) в направлении , противоположном направлению . Используя шкалу, эта стрелка должна быть \ (\ text {2} \) \ (\ text {cm} \) длинной и указывать на слева .
Примечание: Мы работаем в одном измерении, поэтому эта стрелка будет нарисована сверху первых векторов слева. Это будет сбивать с толку, поэтому мы нарисуем его рядом с реальной линией, чтобы показать вам, как это выглядит.
Теперь мы нарисовали все заданные векторы силы. Результирующий вектор — это стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора.
Результирующий вектор измеряет \ (\ text {1} \) \ (\ text {cm} \), который, используя наш масштаб, эквивалентен \ (\ text {1} \) \ (\ text {N} \) и направо ( или в положительном направлении). Это \ (\ vec {R} _ {x} \). Для этого набора векторов у нас нет векторов, указывающих в направлении \ (y \), и поэтому нам не нужно искать \ (\ vec {R} _ {y} \).
Найдите результат в направлении \ (x \) -, \ (\ vec {R} _x \) и \ (y \) — направлении \ (\ vec {R} _y \) для следующих сил:
- \ (\ vec {F} _ {1} = \ text {2,3} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в отрицательном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \) и для нашей диаграммы мы определим положительное направление как направо.
Прежде чем мы начнем рисовать векторы, отметим длину векторов, используя нашу шкалу:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {2,3} \ text {cm} \\ \ vec {F} _ {2} & = \ text {1} \ text {cm} \\ \ vec {F} _ {3} & = \ text {2} \ text {cm} \\ \ vec {F} _ {4} & = \ text {3} \ text {cm} \ Конец {*} выравниваниеТакже отметим направление, в котором находятся векторы:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {positive} x \ text {-direction} \\ \ vec {F} _ {2} & = \ text {отрицательный} x \ text {-direction} \\ \ vec {F} _ {3} & = \ text {positive} y \ text {-direction} \\ \ vec {F} _ {4} & = \ text {отрицательный} y \ text {-направление} \ Конец {*} выравниваниеТеперь рассмотрим два вектора в направлении \ (x \) -, чтобы найти \ (\ vec {R} _ {x} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (x \).Чтобы найти \ (\ vec {R} _ {x} \), отметим, что результирующим вектором является стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {x} \) есть \ (\ text {1,3} \) \ (\ text {cm} \) или \ (\ text {1,3} \) \ (\ text {N} \) в положительном \ (x \) — направлении.
Теперь рассмотрим два вектора в направлении \ (y \) -, чтобы найти \ (\ vec {R} _ {y} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (y \).Чтобы найти \ (\ vec {R} _ {y} \), отметим, что результирующим вектором является стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {y} \) — это \ (\ text {1} \) \ (\ text {cm} \) или \ (\ text {1} \) \ (\ text {N} \) в отрицательном направлении \ (y \).
\ (\ vec {R} _ {x} \) = \ (\ text {1,3} \) \ (\ text {N} \) и указывает в положительном \ (x \) — направлении. \ (\ vec {R} _ {y} \) = \ (\ text {1} \) \ (\ text {N} \) и указывает в отрицательном \ (y \) — направлении.
Найдите результат в направлении \ (x \) -, \ (\ vec {R} _x \) и \ (y \) — направлении \ (\ vec {R} _y \) для следующих сил:
- \ (\ vec {F} _ {1} = \ text {3} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {2} = \ text {1} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {2} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем шкалу \ (\ text {1} \) \ (\ text {N} \): \ (\ text {1} \) \ (\ text {cm} \) и для нашей диаграммы мы определим положительное направление как направо.
Прежде чем мы начнем рисовать векторы, отметим длину векторов, используя нашу шкалу:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {3} \ text {cm} \\ \ vec {F} _ {2} & = \ text {1} \ text {cm} \\ \ vec {F} _ {3} & = \ text {2} \ text {cm} \\ \ vec {F} _ {4} & = \ text {3} \ text {cm} \ Конец {*} выравниваниеТакже отметим направление, в котором находятся векторы:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {positive} x \ text {-direction} \\ \ vec {F} _ {2} & = \ text {positive} x \ text {-direction} \\ \ vec {F} _ {3} & = \ text {отрицательный} x \ text {-direction} \\ \ vec {F} _ {4} & = \ text {positive} y \ text {-direction} \ Конец {*} выравниваниеТеперь рассмотрим три вектора в направлении \ (x \) -, чтобы найти \ (\ vec {R} _ {x} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (x \).Чтобы найти \ (\ vec {R} _ {x} \), отметим, что результирующим вектором является стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {x} \) — это \ (\ text {2} \) \ (\ text {cm} \) или \ (\ text {2} \) \ (\ text {N} \) в положительном \ (x \) — направлении.
Теперь рассмотрим векторы в \ (y \) — направлении, чтобы найти \ (\ vec {R} _ {y} \). Мы замечаем, что у нас есть только один вектор в этом направлении, и поэтому вектор является результирующим.
Мы отмечаем, что \ (\ vec {R} _ {y} \) — это \ (\ text {3} \) \ (\ text {cm} \) или \ (\ text {3} \) \ (\ text {N} \) в положительном \ (y \) — направлении.
\ (\ vec {R} _ {x} \) = \ (\ text {2} \) \ (\ text {N} \) и указывает в положительном \ (x \) — направлении. \ (\ vec {R} _ {y} \) = \ (\ text {3} \) \ (\ text {N} \) и точки в положительном \ (y \) — направлении.
Найдите результат в направлении \ (x \) -, \ (\ vec {R} _x \) и \ (y \) — направлении \ (\ vec {R} _y \) для следующих сил:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в отрицательном направлении \ (y \) —
- \ (\ vec {F} _ {3} = \ text {2,5} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3} \ text {N} \) в положительном \ (y \) — направлении
Мы выбираем масштаб \ (\ text {1} \) \ (\ text {cm} \): \ (\ text {1} \) \ (\ text {N} \) и для нашей диаграммы мы определим положительное направление как направо.
Прежде чем мы начнем рисовать векторы, отметим длину векторов, используя нашу шкалу:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {2} \ text {cm} \\ \ vec {F} _ {2} & = \ text {1,5} \ text {cm} \\ \ vec {F} _ {3} & = \ text {2,5} \ text {cm} \\ \ vec {F} _ {4} & = \ text {3} \ text {cm} \ Конец {*} выравниваниеТакже отметим направление, в котором находятся векторы:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {positive} y \ text {-direction} \\ \ vec {F} _ {2} & = \ text {отрицательный} y \ text {-direction} \\ \ vec {F} _ {3} & = \ text {отрицательный} x \ text {-direction} \\ \ vec {F} _ {4} & = \ text {positive} y \ text {-direction} \ Конец {*} выравниваниеМы смотрим на векторы в \ (x \) — направлении, чтобы найти \ (\ vec {R} _ {x} \).Мы замечаем, что у нас есть только один вектор в этом направлении, и поэтому вектор является результирующим.
Мы отмечаем, что \ (\ vec {R} _ {x} \) — это \ (\ text {2,5} \) \ (\ text {cm} \) или \ (\ text {2,5} \) \ (\ text {N} \) в отрицательном \ (x \) — направлении.
Теперь рассмотрим три вектора в направлении \ (y \) -, чтобы найти \ (\ vec {R} _ {y} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (y \). Чтобы найти \ (\ vec {R} _ {y} \), отметим, что результирующим вектором является стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {y} \) это \ (\ text {3,5} \) \ (\ text {cm} \) или \ (\ text {3,5} \) \ (\ text {N} \) в положительном \ (y \) — направлении.
\ (\ vec {R} _ {x} \) = \ (\ text {2,5} \) \ (\ text {N} \) и указывает в отрицательном \ (x \) — направлении. \ (\ vec {R} _ {y} \) = \ (\ text {3,5} \) \ (\ text {N} \) и точки в положительном \ (y \) — направлении.
Найдите силу в направлении \ (x \) — \ (F_x \) и \ (y \) — \ (F_y \), которую можно добавить к следующим силам, чтобы сделать результирующим в \ (x \) — направление, \ (R_x \) и \ (y \) — направление, \ (R_y \) ноль:
- \ (\ vec {F} _ {1} = \ text {2,4} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {0,7} \ text {N} \) в отрицательном \ (y \) — направлении
- \ (\ vec {F} _ {3} = \ text {2,8} \ text {N} \) в отрицательном \ (x \) — направлении
- \ (\ vec {F} _ {4} = \ text {3,3} \ text {N} \) в положительном \ (y \) — направлении
Чтобы решить эту проблему, мы нарисуем векторы на декартовой плоскости, а затем посмотрим, что такое результирующий вектор.Затем мы определяем, какой вектор силы добавить, чтобы результирующий вектор был \ (\ text {0} \).
Мы выбираем масштаб \ (\ text {1} \) \ (\ text {cm} \): \ (\ text {1} \) \ (\ text {N} \) и для нашей диаграммы мы определим положительное направление как направо.
Прежде чем мы начнем рисовать векторы, отметим длину векторов, используя нашу шкалу:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {2,4} \ text {cm} \\ \ vec {F} _ {2} & = \ text {0,7} \ text {cm} \\ \ vec {F} _ {3} & = \ text {2,8} \ text {cm} \\ \ vec {F} _ {4} & = \ text {3,3} \ text {cm} \ Конец {*} выравниваниеТакже отметим направление, в котором находятся векторы:
\ Начать {*} Align \ vec {F} _ {1} & = \ text {positive} y \ text {-direction} \\ \ vec {F} _ {2} & = \ text {отрицательный} y \ text {-direction} \\ \ vec {F} _ {3} & = \ text {отрицательный} x \ text {-direction} \\ \ vec {F} _ {4} & = \ text {positive} y \ text {-direction} \ Конец {*} выравниваниеМы смотрим на векторы в \ (x \) — направлении, чтобы найти \ (\ vec {R} _ {x} \).Мы замечаем, что у нас есть только один вектор в этом направлении, и поэтому вектор является результирующим.
Мы отмечаем, что \ (\ vec {R} _ {x} \) есть \ (\ text {2,8} \) \ (\ text {cm} \) или \ (\ text {2,8} \) \ (\ text {N} \) в отрицательном \ (x \) — направлении.
Так что, если мы добавим силу \ (\ text {2,8} \) \ (\ text {N} \) в положительном \ (x \) — направлении, результирующим будет \ (\ text {0} \ ):
Теперь рассмотрим три вектора в направлении \ (y \) -, чтобы найти \ (\ vec {R} _ {y} \):
Теперь мы нарисовали все векторы силы, которые действуют в направлении \ (y \).Чтобы найти \ (\ vec {R} _ {y} \), отметим, что результирующим вектором является стрелка, которая начинается в хвосте первого вектора и заканчивается в начале последнего нарисованного вектора в этом направлении.
Мы отмечаем, что \ (\ vec {R} _ {y} \) — это \ (\ text {5} \) \ (\ text {cm} \) или \ (\ text {5} \) \ (\ text {N} \) в положительном \ (y \) — направлении.
Поэтому, если мы добавим силу \ (\ text {5} \) \ (\ text {N} \) в отрицательном направлении \ (y \) — результирующим будет \ (\ text {0} \):
Мы должны добавить силу \ (\ text {2,8} \) \ (\ text {N} \) в положительном \ (x \) — направлении и силу \ (\ text {5} \) \ (\ text {N} \) в отрицательном \ (y \) — направлении.
Величина результирующих векторов под прямым углом (ESBK8)
Мы применяем тот же принцип к векторам, которые находятся под прямым углом или перпендикулярно друг другу.
Эскизный метод «хвост к голове»
Хвост одного вектора помещается в головку другого, но в двух измерениях векторы могут быть не коллинеарными. Подход состоит в том, чтобы нарисовать все векторы, по одному за раз. Для первого вектора начинаются в начале декартовой плоскости, для второго вектора нарисуйте его из головы первого вектора.Третий вектор должен быть взят из головы второго и так далее. Каждый вектор взят из заголовка предшествующего ему вектора. Порядок не имеет значения, так как результат будет таким же, если порядок другой.
Давайте применим эту процедуру к двум векторам:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
Сначала мы нарисуем декартову плоскость с первым вектором в начале координат:
Следующий шаг — взять второй вектор и нарисовать его из головы первого вектора:
Результирующий, \ (\ vec {R} \), — это вектор, соединяющий хвост первого вектора, нарисованного с головой последнего нарисованного вектора:
Важно помнить, что порядок, в котором мы рисуем векторы, не имеет значения.Если бы мы нарисовали их в обратном порядке, мы получили бы тот же результат, \ (\ vec {R} \). Мы можем повторить процесс, чтобы продемонстрировать это:
Сначала мы нарисуем декартову плоскость со вторым вектором, начинающимся в начале координат:
Следующий шаг — взять другой вектор и нарисовать его из головы вектора, который мы уже нарисовали:
Результирующий, \ (\ vec {R} \), является вектором, соединяющим хвост первого вектора, нарисованного с головой последнего нарисованного вектора (вектор от начальной точки до конечной точки):
Рабочий пример 2: рисование векторов с использованием хвоста к голове
Нарисуйте результат следующих векторов силы методом хвоста к голове:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ text {1,5} \ text {N} \) в положительном \ (x \) — направлении
- \ (\ vec {F} _ {3} = \ text {1,3} \ text {N} \) в отрицательном направлении \ (y \) —
- \ (\ vec {F} _ {4} = \ text {1} \ text {N} \) в отрицательном \ (x \) — направлении
Рисуем декартову плоскость и первый вектор
Сначала нарисуйте декартову плоскость и силу, \ (\ vec {F} _ {1} \), начиная с начала координат:
Нарисуйте второй вектор
Начиная с заголовка первого вектора, рисуем хвост второго вектора:
Нарисуйте третий вектор
Начиная с заголовка второго вектора, рисуем хвост третьего вектора:
Нарисуйте четвертый вектор
Начиная с заголовка третьего вектора, рисуем хвост четвертого вектора:
Нарисуйте результирующий вектор
Начиная с начала координат, нарисуйте результирующий вектор в заголовке четвертого вектора:
Рабочий пример 3: рисование векторов с использованием хвоста к голове
Нарисуйте результирующий вектор следующих векторов силы, используя метод хвоста к голове, сначала определив результирующий в направлениях \ (x \) — и \ (y \) -:
- \ (\ vec {F} _ {1} = \ text {2} \ text {N} \) в положительном \ (y \) — направлении
- \ (\ vec {F} _ {2} = \ t
Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- физика
математический
- Алгебра
- Исчисление
- Геометрия
- Prealgebra
