Двойное неравенство Математика 5 класс Виленкин №152 – Рамблер/класс
Двойное неравенство Математика 5 класс Виленкин №152 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Трям , кто решал уже Задачку №152… есть ответ?!
152 Запишите с помощью двойного неравенства:
а) число 10 больше, чем 5, и меньше, чем 15;
в) число 21 меньше, чем 28, а число 28 меньше, чем 45.

ответы
а) 5<10<15; б) 8<11<18; в) 21<28<45.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
3 класс
Репетитор
Химия
Алгебра
похожие вопросы 5
Координатная прямая. Математика 5 класс.Зубарева И.И.Параграф 10, задание 191
Укажите начало отсчёта и координаты точек А, В, С, (Подробнее…)
ГДЗЗубарева И.И.Математика5 класс
Приветик! Кто решил? № 411 Математика 6 класс Виленкин.
Выполните вычисления с помощью микрокалькулятора и резуль-
3,281 ∙ 0,57 + 4,356 ∙ 0,278 — 13,758 (Подробнее…)
ГДЗМатематика6 классВиленкин Н.Я.
Помогите выбрать утверждения. Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Математика базовый уровень ЕГЭ — 2017. Вар.№1. Зад.№18. Под руководством Ященко И.В.
Здравствуйте! Перед волейбольным турниром измерили рост игроков волейбольной команды города N. Оказалось, что рост каждого из (Подробнее…)
ЕГЭЭкзаменыМатематикаЯщенко И.В.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Оценить число в неравенствах
☰
Для оценки чисел в неравенствах используются различные свойства числовых неравенств. Обычно в таких заданиях даются одно или несколько исходных неравенств, в которых присутствуют переменные. Требуется оценить результат арифметических действий над этими переменными (т. е. получаемые новые числа).
Например, даны два таких исходных двойных неравенства:
- –1 < p < 10;
- 2,5 < q < 3,2.
Требуется оценить числа, которые получаются в результате следующих действий над переменными:
- 0,1 × p,
- 1/q,
- p + q,
- q – p,
- p3.
При оценке числа 0,1p воспользуемся следующими свойством числовых неравенств:
- Если a < b и c > 0, то ac < bc. В данном случае c = 0,1.
- Если a < b и b < c, то a < c. В данном случае b = 0,1p, a = –1 × 0,1, c = 10 × 0,1.

На основе этих свойств мы можем умножить все части исходного двойного неравенства (не меняя знаки сравнения) на 0,1 и таким образом получить оценку для числа 0,1p:
–1 × 0,1 < 0,1p < 10 × 0,1
–0,1 < 0,1p < 1
То есть, число 0,1p лежит в пределах от –0,1 до 1.
При оценке числа 1/q следует воспользоваться свойством числовых неравенств, описывающим дроби:
- Если a < b и оба числа положительны, то 1/a > 1/b.
Отсюда можно заключить, что в исходном неравенстве следует поменять знаки сравнения на обратные:
1 / 2,5 > 1/q > 1/3,2
Запишем неравенство наоборот:
1/3,2 < 1/q < 1/2,5
Выполним действия:
0,3125 < 1/q < 0,4
Для оценки числа p + q используются такое свойство числовых неравенств:
- Если a < b, то a + c < b + c. Пусть в данном случае c = q.
Оба числовых неравенства складываются почленно:
–1 + 2,5 < p + q < 10 + 3,2
1,5 < p+q < 13,2
Число q – p можно представить в виде суммы: –p + q и решить также как выше. Однако по сравнению с предыдущим числом (p + q), здесь p сначала надо умножить на –1. Для выполнения этого действия воспользуемся таким свойством числовых неравенств:
Однако по сравнению с предыдущим числом (p + q), здесь p сначала надо умножить на –1. Для выполнения этого действия воспользуемся таким свойством числовых неравенств:
- Если a < b и c < 0, то ac > bc. В данном случае c = –1.
Таким образом, из исходного неравенства получается неравенство противоположного смысла, т. е. меняются знаки на обратные:
–1 × –1 > –1p > –1 × 10
Перевернем неравенство и выполним действия:
–10 < –p < 1
Теперь можно сложить q и –p:
–10 + 2,5 < q – p < 1 + 3,2
–7,5 < q – p < 4,2
Для оценки числа p3 воспользуемся таким свойством:
- Если n — нечетное число, то для любых чисел a и b если a < b, то и an < bn.
(–1)3 < p3 < 103
–1 < p3 < 1000
Если бы p возводился в квадрат или в любую другую четную степень, то таким свойством мы бы воспользоваться без оглядки на абсолютные значения не могли.
Как решить сложные неравенства за 3 простых шага — Mashup Math
Способность создавать, анализировать и решать сложное неравенство с помощью сложного неравенства график — чрезвычайно важный и полезный математический навык, который можно применять ко многим математическим понятиям, обычно встречающимся в начальной алгебре, алгебре I, алгебре II. , и даже предварительное исчисление и исчисление. В то время как многие студенты могут быть напуганы концепцией составного неравенства, когда они видят необычные графики, содержащие круги и стрелки, работа с составными неравенствами на самом деле проста и понятна.
Следующее бесплатное пошаговое руководство Как решить Составные неравенства научит вас создавать, анализировать и понимать сложные неравенства с помощью простого и эффективного трехэтапного метода, который можно применять к любой математике.
Вы готовы начать? Прежде чем вы узнаете о создании и чтении составных неравенств, давайте рассмотрим несколько важных словарных слов и определений, связанных с неравенствами.
Что такое неравенство?Прежде чем мы приступим к изучению составных неравенств, нам нужно повторить точное определение неравенства в сравнении с уравнениями.
Что такое уравнение?
Определение: В математике уравнение — это утверждение, которое показывает, что два математических выражения равны друг другу, используя знак «=».
Например, x=5 — это уравнение, в котором переменная и x равны значению 5 (и никакому другому значению).
Важно отметить, что уравнения ограничены только одним возможным решением, поэтому в этом случае 5 является единственным возможным значением, которому может быть равен x, и любое другое значение не применяется.
х=5
Единственное решение: 5
Что такое неравенство?
Определение: В математике неравенство — это отношение между двумя выражениями или значениями, которое делает сравнение неравным.
Например, x>5 — это неравенство, которое означает, что «x больше 5», где, в отличие от уравнения, имеющего только одно решение, x может иметь бесконечно много решений, а именно любое значение больше 5.
Мы можем визуализировать простое неравенство x>5 на числовой прямой ниже следующим образом:
По сравнению с уравнениями неравенства не ограничены только одним возможным решением. На самом деле неравенства имеют бесконечно много решений.
В этом случае решениями неравенства x>5 являются любые значения, превышающие пять (не включая пять).
x>5
Примеры решений: 6, 7, 10, 105, 2500 (все эти значения удовлетворяют неравенству, поскольку они больше 5)
Примеры нерешений: 5, 4, 0, -17, -1,001 (ни одно из этих значений не удовлетворяет неравенству, поскольку не больше 5)
В чем разница между уравнением и неравенство? Прежде чем мы перейдем к изучению неравенств и составных неравенств, важно понять основное различие между уравнением и неравенством.
По сути, ключевое различие между уравнением и неравенством заключается в следующем:
Графики неравенств на числовой прямойТеперь, когда вы понимаете разницу между уравнением и и неравенством, вы готовы научиться решать сложные неравенства и читать графики сложных неравенств.
Но сначала давайте быстро вспомним, как изображать простые неравенства на числовой прямой.
Существует четыре типа символов неравенства:
Важно понимать различия между этими символами, а именно значение линии под символом больше или меньше и как она связана с решением неравенства и его график на числовой прямой.
Например, рассмотрим следующие неравенства: x < 9 и x ≤ 9
Первое неравенство, x<9, имеет решение при любом значении меньше 9, но не включая 9 (поскольку 9 не равно меньше 9).
Второе неравенство x ≤ 9 имеет решение любого значения меньше 9 И самого значения 9 (поскольку 9 больше или равно 9).
На числовой прямой разница между этими двумя типами неравенств обозначается незамкнутым или закрытым (закрашенным кружком). Незакрашенный кружок означает, что соответствующее значение не входит в набор решений, а закрытый кружок означает, что соответствующее значение включено в набор решений.
Прежде чем двигаться дальше, убедитесь, что вы полностью понимаете разницу между графиками неравенства < или > и неравенства ≥ или ≤. Понимание разницы между решением и графиком имеет решающее значение для создания графиков сложных неравенств и решения сложных неравенств.
Для справки, вот еще несколько примеров простых графиков неравенства:
Опять же, незакрашенный кружок означает, что соответствующее значение числовой строки НЕ включено в набор решений. Закрашенный кружок означает, что оно входит в набор решений.
Что такое составное неравенство? Как решать сложные неравенства? В предыдущем разделе этого руководства мы рассмотрели, как отображать простые неравенства на числовой прямой и как эти графики представляют решение одного единственного неравенства.
Определение: A составное неравенство (иногда называемое комбинированным неравенством) представляет собой два соединенных вместе простых неравенства.
Неужели все так просто? Да! Составное неравенство — это всего лишь два простых неравенства, объединенных вместе, а график составного неравенства — это всего лишь два простых неравенства, построенных на одной и той же числовой прямой.
Составные неравенства бывают двух типов: или и и .
Определение: An или составное неравенство использует слово « или» для объединения двух неравенств.
Определение : В составном неравенстве и используется слово «и» для объединения двух неравенств.
Чтобы понять разницу между неравенствами или и и , давайте рассмотрим несколько примеров и примените следующий трехэтапный процесс:
решение задачи сложных неравенств или или и
Шаг № 2: Нарисуйте оба неравенства на числовой прямой.

Шаг 3. Проанализируйте и определите набор решений.
Пример № 1: График Составной неравенство x <6 или 444499928 x . Первый шаг прост, так как каждый пример будет включать слово 9.0128 или или и . В этом первом примере используется слово или , поэтому запишите это и двигайтесь дальше.
Затем отобразите два простых неравенства x<6 и x>10 на числовой прямой, чтобы создать следующий график сложного неравенства.
Теперь, когда у вас есть график, вы можете определить набор решений составного неравенства и привести примеры значений, которые будут работать как решения, а также примеры нерешений.
Например, значения 4 и 14 являются решениями этого составного неравенства, а число 8 не является решением.
Кроме того, значения 6 и 10 не являются решениями, поскольку они включены в набор решений, так как круги открыты.
Заштрихованная область на приведенном ниже графике представляет собой области решения графа сложного неравенства.
Как решать графы сложного неравенства Пример № 2: иПример № 2: График. Составное неравенство x > -2 и x <4
Обратите внимание, что этот пример использует слово и <4
, что в этом примере используется слово и , 9000, так и ,
, так что в этом примере. иметь в виду, так как это повлияет на то, как вы будете анализировать решение составного неравенства на шаге 3.
Затем нарисуйте оба простых неравенства x>-2 и x<4 на числовой прямой, чтобы создать следующий график сложного неравенства.
Это составное неравенство имеет решения для значений, которые равны и больше -2 и меньше 4.
Итак, например:
0 является решением, поскольку удовлетворяет условиям x>-2 и x<4.
-4 является , а не решением, потому что это решение только для x<4 (значение должно удовлетворять обоим неравенствам, чтобы быть решением этого составного неравенства)
8 также , а не решение, так как оно не удовлетворяет обоим неравенствам.
Обратите внимание, что это составное неравенство также может быть выражено как -2 < x < 4 , что означает, что x больше -2 и меньше 4 (или что x находится между -2 и положительным 4).
Как решать графики сложного неравенства: или против иОсновываясь на двух последних примерах, заметили ли вы разницу между или и и составные неравенства.
Снова сравним два графика:
Ключевое отличие здесь состоит в том, что:
Примерами решения или являются значения, удовлетворяющие первому неравенству или второму неравенству.
 Обратите внимание, что графики составных неравенств никогда не пересекаются (перекрываются).
Обратите внимание, что графики составных неравенств никогда не пересекаются (перекрываются).Решение 9Примеры 0003 и — это значения, которые удовлетворяют обоим первому неравенству, и второму неравенству. Обратите внимание, что графики составных неравенств действительно пересекаются (перекрываются).
Теперь давайте рассмотрим еще три примера, которые будут больше напоминать типы задач на сложные неравенства, которые вы увидите на тестах и экзаменах: : 2x+2 ≤ 14 или x-8 ≥ 0
Не паникуйте, если этот вопрос покажется вам сложным. Вы по-прежнему будете следовать тому же трехэтапному процессу, что и в примерах 1 и 2, но вам просто нужно сначала немного заняться алгеброй.
В этом случае, прежде чем использовать трехшаговый метод, решите каждое неравенство, чтобы изолировать x, следующим образом:
Теперь вы готовы применить трехэтапный метод для x≤6 или x ≥ 8
Вы уже знаете, что это сложное неравенство или , поэтому на графике не будет никакого перекрытия, и любые возможные решения должны удовлетворять только одному из двух неравенств (не обоим).
Обратите внимание, что в этом примере используются символы больше или равно и меньше или равно, поэтому ваши кружки будут заполнены следующим образом:
Опять же, решение составных неравенств, подобных этому, требует от вас определения набора решений, который, как мы уже выяснили, равен x≤6 или x ≥ 8.
Так, например, вот несколько примеров решений и нерешений:
10 является решением, поскольку удовлетворяет одному из неравенств (x ≥ 8)
6 является решением, поскольку удовлетворяет одно из неравенств (x≤6)
7 является , а не решением, поскольку оно не удовлетворяет ни одному из неравенств. Это также относится к нерешениям, таким как 6.1 и 7.75.
Найдите x: 3x+1 ≥ 10 и 2x+7 > 7
Как и в предыдущем примере, используйте свои навыки алгебры, чтобы решить каждое неравенство и выделить x следующим образом:
Становитесь ли вы более комфортно решать сложные неравенства? Обратите внимание, что решением этого составного неравенства являются все значения, которые удовлетворяют следующим условиям: x≥3 и x>0.
Теперь давайте продолжим наш трехэтапный метод:
Поскольку это сложное неравенство и , мы знаем, что все решения должны удовлетворять как x≥3, так и x>0
Обратите внимание на пересечение (или область перекрытия) вашего графика сложного неравенства:
Вы можете видеть, что все решения этого составного неравенства будут находиться в области, удовлетворяющей только x≥3, поэтому вы можете упростить свой окончательный ответ следующим образом:
Решение: x≥3
Кроме того, вот несколько примеров решений и нерешений:
5 является решением, поскольку удовлетворяет обоим неравенствам x x≥3 и x>0
7
является решением, поскольку удовлетворяет обоим неравенствам x x≥3 и x>02 является , а не решением, поскольку удовлетворяет только одному неравенству0007
-1 IS Не A Solution, потому что он не удовлетворяет неравенству
 -7
-7Как и прежде, решите каждое неравенство следующим образом:
После решения обоих неравенств остаются x<-2 и x≥-1
Обратите внимание, что его последний пример продемонстрирует, почему шаг №1 так важен. Помните, что для решения этого составного неравенства необходимо найти значения, которые удовлетворяют и x<-2, и x≥-1
Опять же, это задача и , что означает, что вы ищете пересечение или перекрытие двух линий на графике сложного неравенства.
Заметили что-нибудь странное в этом примере? На самом деле нет области, где неравенства пересекаются!
Так как мы ищем значения, которые удовлетворяют обоим неравенствам,
Мы можем заключить, что решений нет потому что нет значения для x равного оба меньше -2 и больше или равно -1 .
Вы можете решить любую задачу о сложных неравенствах, применяя следующий трехэтапный метод:
Шаг № 1. Определите, является ли решение задачи о сложных неравенствах или или и
Решения или задачи о сложных неравенствах должны удовлетворять только одному из неравенств, а не обоим.
Решения сложных задач неравенства должны удовлетворять обоим неравенствам.
Составные неравенства можно принимать к нулевым решениям.
Шаг № 2: Нанесите оба неравенства на числовую прямую.
Шаг 3. Проанализируйте и определите набор решений.
Комментарий
Составные неравенства и отличия от простых неравенств
A составное неравенство , иногда называемое комбинированным неравенством , представляет собой неравенство, которое объединяет два или более простых неравенства, объединенных вместе с или или и .
Чтобы быть решением или неравенства, значение должно делать только одну часть неравенства истинной. Это означает, что окончательным решением будет объединение решений отдельных неравенств. Чтобы быть решением неравенства и , оно должно выполнять обе части. Неравенства, условия которых ограничены и , не независимы друг от друга. Это означает, что окончательное решение будет пересечение решений отдельных неравенств.
Помните:
или $ \ rightarrow $ Union
и $ \ rightarrow $ recsection
Пример с или неравенством
В примере задан вопрос: какие числа можно подставить вместо $x$ так, чтобы одно из неравенств было верным?
$x<5 \стрелка вправо x \in \left<-\infty, 5\right>$
$x>9 \Rightarrow x \in \left<9, \infty\right>$
Ответом являются все числа меньше 5 и все числа больше 9, поэтому решение объединение двух интервалов $\left<-\infty, 5\right> \cup \left<9, \infty\right>$.
Пример с неравенством и
$x>4$ и $x<7$
Это утверждение эквивалентно $4 $x>4 \стрелка вправо x \in \left<4, \infty\right>$ $x<7 \Rightarrow x \in \left<-\infty, 7\right>$ Решение представляет собой пересечение двух интервалов $\left<-\infty, 7\right> \cap \ left<4, \infty\right>$, то есть интервал $\left<4, 7\right>$. Пример 1: Эту задачу можно решить двумя способами. I. Задача разбивается на два неравенства, которые затем решаются отдельно . Решением является пересечение индивидуальных решений. Из второго неравенства следует утверждение $0 < 5$, которое всегда верно, поэтому решением является все множество действительных чисел. Если бы случай был другим и утверждение было неверным, например $5 < 0$, то неравенство не имело бы решений. Например, неравенство $x Решением неравенства из примера 1 является множество $ \left<-\infty, – 2\right]$. II. При работе с уравнениями можно складывать, вычитать, умножать и делить выражение, но то, что изменено в одной части, должно быть изменено точно так же и в другой. Аналогично при работе с неравенствами. Если вы складываете, вычитаете, умножаете или делите, вы должны делать это для каждой части неравенства. В нашем примере мы можем вычесть $2x$. $ 2 + 2x \leqslant x < 5 + x$ $ – x < 5 – x$ всегда является истинным утверждением, поэтому единственная часть, которая ограничивает множество решений $ 2 \leqslant – x $. Следовательно, решением является множество $\left<-\infty, – 2\right]$. Пример 2: $57x$ вычитается из каждой части неравенства: $ 1 + x1 < – $9 < 2x0007 $ 1 + x < – 2x$ и $ – 2x < 10$ При делении выражения $ – 2x < 10$ на $-2$ знак неравенства меняется. $ 3x < – 1$ и $x > – 5$ Окончательное решение есть множество $ \left< - 5, -\frac{1}{3}\right>$. В случае, когда перекресток пустой, решений нет. Например, если $ x > 5$ и $ x < – 7$, то пересечение множеств $\left<5, \infty\right>$ и $\left<-\infty, -7\right >$ пусто. Следовательно, неравенство не имеет решений. Пример 3: $ 5 > x > 2$ $ 5 > x$ и $ x > 2 \Rightarrow x \in \left<2, 5\right> $ Пример 4: $ – 6 < x > 2$ $ x > – 6$ и $ x > 2 \Rightarrow x \in \left<2, +\infty\right>$ Пример 5: Решение первого неравенства задано $\left<2, \infty\right>$ а решение второго неравенства задано $\left<-\infty, – 7\right>$.

$ 2x > 4 \Rightarrow x > 2$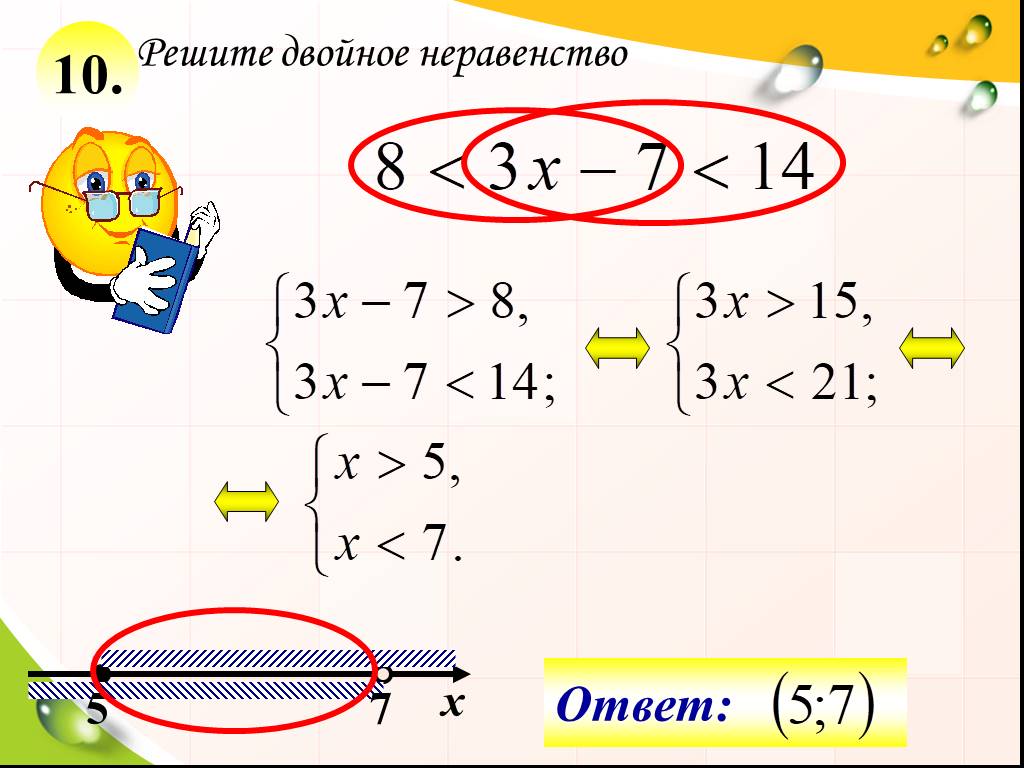



 Обратите внимание, что графики составных неравенств никогда не пересекаются (перекрываются).
Обратите внимание, что графики составных неравенств никогда не пересекаются (перекрываются).