Экспонента и число е: просто и понятно
Перевод большой статьи «An Intuitive Guide To Exponential Functions & e»
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
4=16 частей. Общая формула выглядит так:
рост = 2x
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
рост = (1+100%)x
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
рост = (1+прирост)x
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
Приглядимся поближе
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато.
Зеленые точки появляются внезапно.
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.
В следующий статье мы посмотрим на пример экспоненциального роста ваших денег.
Продолжение
Каково значение e power 0?
Каково значение e в степени 0? Значение e 0 равно 1 .
Запрос на удаление |
Посмотреть полный ответ на byjus.
com
Сколько будет e в степени O?
Мы также можем сказать, что все в степени 0 равно 1. Следовательно, значение e в степени 0 равно 1.
Запрос на удаление |
Посмотреть полный ответ на cuemath.com
Каково значение e power 1?
При этом e в степени 1. Согласно правилу экспоненты, любое число, возведенное в степень 1, равно самому числу. Итак, e в степени 1 можно записать как (e) 1 . Следовательно, значение e в степени 1 равно 2,718281828459045….
Запрос на удаление |
Посмотреть полный ответ на cuemath.com
Почему e в степени 0 1?
Итак, причина того, что любое число в нулевой степени равно единице, состоит в том, что любое число в нулевой степени является просто произведением отсутствия чисел вообще, что является мультипликативным тождеством, 1.
|
Посмотреть полный ответ на byjus.com
Каково значение 0 мощности?
Любое ненулевое число в нулевой степени равно единице. Ноль в любом положительном показателе равен нулю.
Запрос на удаление |
Посмотреть полный ответ на khanacademy.org
Почему ноль равен единице?
Чему равна 2 степень нуля?
Таким образом, 2 в нулевой степени будет равно 1. И, фактически, любое ненулевое число в нулевой степени равно 1 по той же причине.
Запрос на удаление | Посмотреть полный ответ на khanacademy.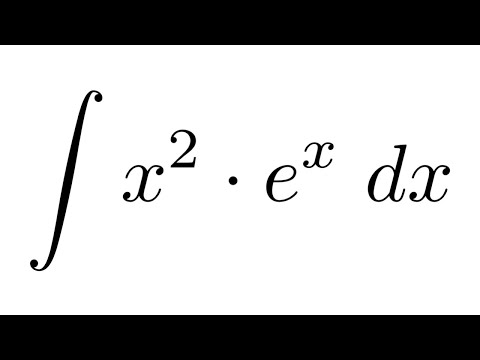
org Каково значение 0 Power 3?
Только один… ничего не ставь на стол, и это твой единственный вариант. Следовательно, правильно сказать, что 3 0 = 1. Есть и другие причины, по которым 0 должно равняться 1. Например, вы, возможно, слышали правило степени: ) = а б * а в . 9{-\infty}} = 0\]. Короче говоря, когда е возводится в бесконечную степень, это означает, что е увеличивается с очень высокой скоростью и, следовательно, стремится к очень большому числу, и поэтому мы говорим, что е, возведенное в бесконечную степень, стремится к бесконечности.
Запрос на удаление |
Посмотреть полный ответ на vedantu.com
Является ли e до бесконечности 0?
Число «е» известно как число Эйлера, которое является иррациональным числом. Это числовая константа, имеющая значение 2,718281828459.
|
Посмотреть полный ответ на byjusexamprep.com
Что такое значение e 2?
Его значение составляет примерно 2,718.
Запрос на удаление |
Посмотреть полный ответ на mathcentre.ac.uk
Что означает e 0?
Если вы помните свои показатели, ответ на этот вопрос прост. Для всех чисел возведение этого числа в 0-ю степень равно единице. Итак, мы знаем, что: e 0 =1.
Запрос на удаление |
Посмотреть полный ответ на sciencetrends.com
Что такое e power 3?
e 3 = (2,718281828) 3 = 2,718281828 х 2,718281828 х 2,718281828 = 20,08554.
e 4 = (2,718281828) 4 = 2,718281828 х 2,718281828 х 2,718281828 х 2,718281828 = 54,59815.
|
Посмотреть полный ответ на eguruchela.com
Сколько будет 4 в степени 0?
Ответ: 4 в степени 0 равно 1.
Давайте решим поставленный выше вопрос, используя нулевое свойство показателей. Согласно нулевому свойству показателей, любое число (кроме 0), возведенное в нулевую степень, всегда равно 1. Таким образом, 4 в степени 0 можно записать как 4 0 , что равно 1.
Запрос на удаление |
Посмотреть полный ответ на cuemath.com
Сколько будет 10 в степени O?
Ответ: 10 в степени 0 равно 10 9.0003 0 = 1.
Найдем значение числа 10, возведенного в степень 0. Объяснение: Показатель степени числа показывает, сколько раз число умножается само на себя.
|
Посмотреть полный ответ на cuemath.com
Что такое мощность минус 1?
Значение e в степени минус 1 равно 0,367.
Запрос на удаление |
Посмотреть полный ответ на brainly.in
Каков предел e?
Число e, также известное как число Эйлера, представляет собой математическую константу, примерно равную 2,71828, которую можно охарактеризовать разными способами. Это основание натуральных логарифмов. Это предел (1 + 1/n) n
, когда n приближается к бесконечности, выражение, которое возникает при изучении сложных процентов. Запрос на удаление |
Посмотреть полный ответ на en.wikipedia.org
Является ли e до бесконечности 1?
Ответ: e в степени бесконечности равно бесконечности (∞).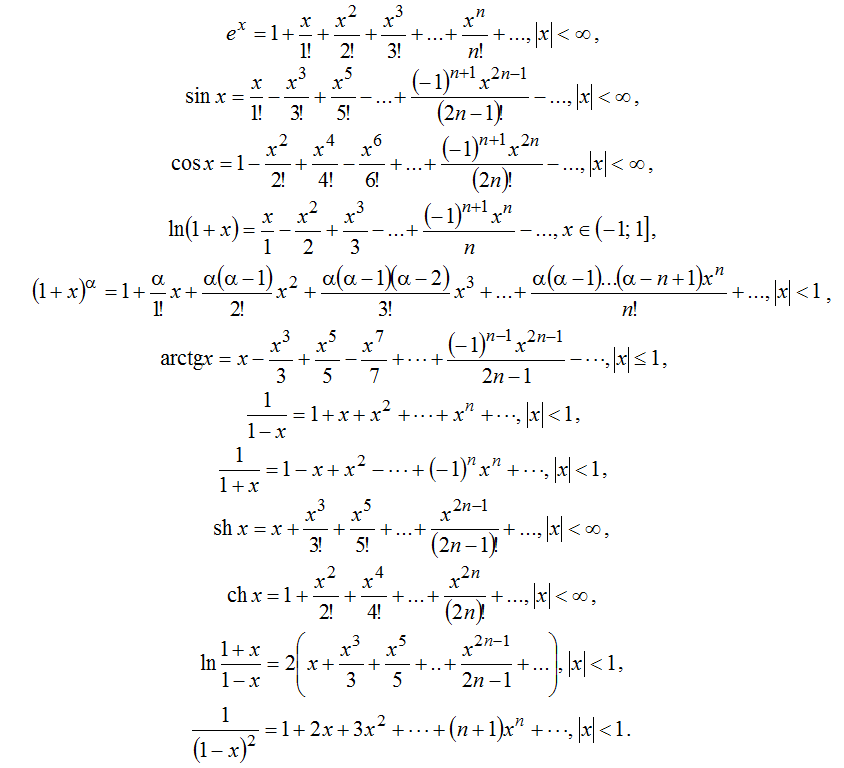
0 = 1.
|
Посмотреть полный ответ на сайте Study.com
Сколько будет 7 в степени 0?
Ответ: 7 в степени 0 равно 1.
Согласно нулевому свойству показателей, любое число (кроме 0), возведенное в нулевую степень, всегда равно 1.
Запрос на удаление |
Посмотреть полный ответ на cuemath.com
Как 8 в степени 0?
Мы знаем, что нулевое свойство показателей степени гласит, что любое число, кроме 0, возведенное в нулевую степень, всегда равно 1. Итак, 8 в степени 0 можно записать как 8
|
Посмотреть полный ответ на cuemath.com
Какова степень числа 1?
Таким образом, 1 в любой степени будет равно 1.
Запрос на удаление |
Посмотреть полный ответ на khanacademy.
org
Сколько будет 10 в степени 1?
Ответ: 10 в степени 1 равно 10 1 = 10.
Найдем значение 10 при возведении в степень 1. Объяснение: Всякий раз, когда число (x) умножается само на себя n раз, тогда полученный ответ записывается как х п . a 1 = a, что означает, что любое число, возведенное в степень 1, дает то же самое число.
Запрос на удаление | Просмотреть полный ответ на cuemath.comЛюбое число в степени 1 0?
Любое число в степени 1 — это само себя, а любое число в степени 0 — это 1. Помните, что единственным исключением из этого правила является 0, возведенный в степень 0.
Запрос на удаление |
Посмотреть полный ответ на content.byui.edu
← Предыдущий вопрос
Кто нравится Девам?
Следующий вопрос →
Плачут ли собаки, когда их усыпляют?
Откуда взялось e и что оно делает?
Поделитесь этой страницей
Январь 2001 г.
Предположим, вы положили 1 фунт стерлингов в банк. Банк выплачивает 4% годовых, и эта сумма зачисляется на ваш счет в конце года. Небольшое размышление показывает, что по истечении пяти лет сумма денег, равная фунту стерлингов, будет лежать в банке (этот банк не взимает комиссионных).
Однако, если бы проценты (все еще по годовой ставке 4%) «начислялись» каждый квартал, то сумма в конце пяти лет была бы £.
Если бы банк установил процентную ставку в размере 100% годовых, то через год баланс банка составил бы £, а если бы проценты начислялись ежеквартально, то это было бы £. Если вам повезет еще больше и вы найдете банк, который ежемесячно начисляет сложные проценты, 100% годовых процентной ставки дадут вам £ через год. Точно так же ежедневное начисление сложных процентов даст вам £.
Очевидно, что более частое начисление сложных процентов приводит к большему количеству денег в банке. Поэтому естественно задаться вопросом, приводит ли начисление сложных процентов в каждый момент времени (то есть непрерывно) к бесконечной сумме в банке.
Чтобы ответить на этот вопрос, нам нужно оценить
Эта величина снова оказывается — той же базовой величиной со свойством, что градиент графика равен единице при .
Теперь можно очень красиво расширить, используя проверенную старую биномиальную теорему. Находим, что
Этот ряд сходится, и вычисление суммы достаточно далеко, чтобы не дать изменения в четвертом десятичном знаке (это происходит после добавления седьмого члена), дает приближение для 2,718.
Великий математик Леонард Эйлер открыл число e 9.0264 и вычислил его значение до 23 знаков после запятой. Его часто называют числом Эйлера и, как и число пи, является трансцендентным числом (это означает, что оно не является корнем какого-либо алгебраического уравнения с целыми коэффициентами).
Существует замечательное свойство: если функция (известная как экспоненциальная функция а также обозначается как «») дифференцируется по , то в результате получается та же функция . Доказательство этого можно увидеть во многих учебниках по элементарному исчислению. Также верно, что для ,
На самом деле, верно, что данное уравнение:
тогда решение для где константа.
Также можно связать общую экспоненциальную функцию , с экспоненциальной функцией. Это потому, что некоторое число всегда можно выбрать так, чтобы .
Затем
Дифференциация по дает
, что говорит нам о том, что общее экспоненциальное соотношение , которое так часто встречается в приложениях, на самом деле является решением дифференциального уравнения
(На самом деле это единственный тип решения этого важного уравнения.)
Именно это уравнение возникает естественным образом при попытке моделирования различных процессов.
Назад к основной статье
Ян Гарбетт читает лекции по прикладной радиационной/радиологической физике в рамках курсов медицинской радиационной науки в Университете Чарльза Стерта, Вагга-Вагга, Новая Зеландия, Австралия.