Чему равна площадь четырехугольника: Площадь четырехугольника — формулы, примеры расчета

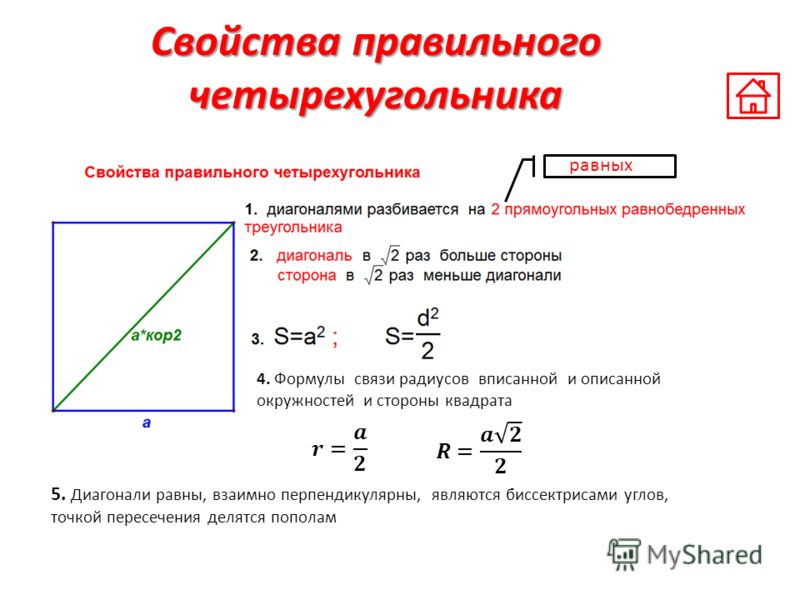
Как найти площадь выпуклого четырехугольника: формула

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади выпуклого четырехугольника: формула и пример

Выпуклый четырехугольник – это геометрическая фигура, полученная путем соединения на плоскости четырех точек, которые не должны лежать на одной прямой. При этом образованные таким образом стороны не должны пересекаться.

• Формула вычисления площади
  • По диагоналям и углу между ними
  • По четырем сторонам (формула Брахмагупты)
  • По радиусу вписанной окружности и сторонам
• Пример задачи

Формула вычисления площади

По диагоналям и углу между ними

Площадь (S) выпуклого четырехугольника равняется одной второй (половине) произведения его диагоналей и синуса угла между ними.

По четырем сторонам (формула Брахмагупты)

Чтобы воспользоваться формулой, необходимо знать длины всех сторон фигуры. Также вокруг четырехугольника должна быть возможность описать окружность.

p – полупериметр, вычисляется следующим образом:

По радиусу вписанной окружности и сторонам

Если в четырехугольник можно вписать окружность, вычислить его площадь можно, воспользовавшись формулой:

S = p ⋅ r

r – радиус окружности.

Пример задачи

Найдите площадь выпуклого четырехугольника, если его диагонали равны 5 и 9 см, а угол между ними составляет 30°.

Решение:
Подставляем в формулу известные нам значения и получаем: S = 1/2 * 5 см * 9 см * sin 30° = 11,25 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

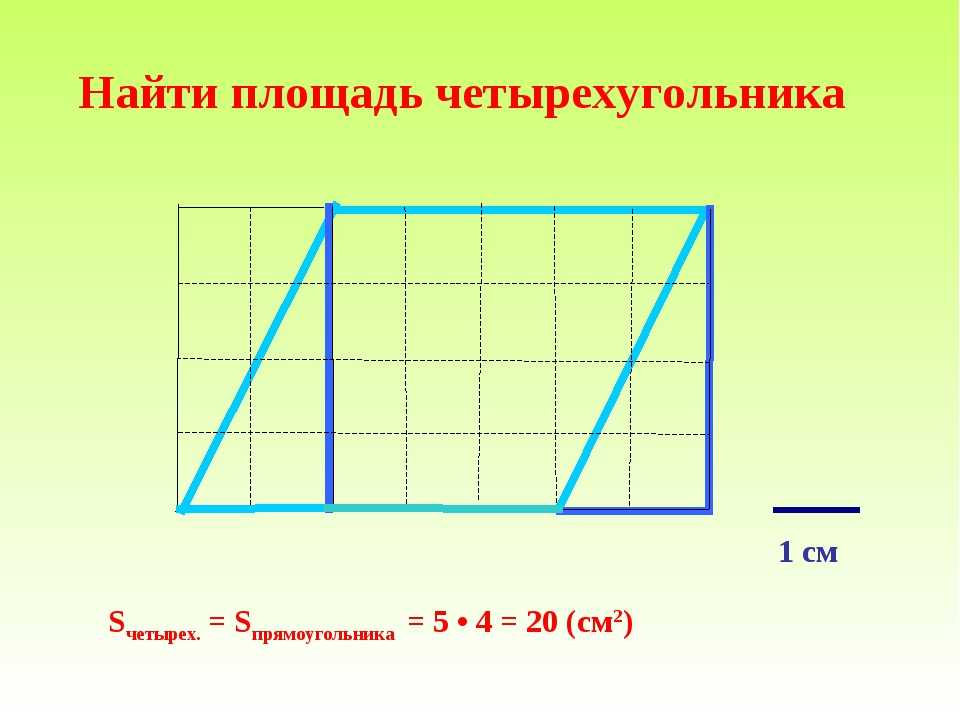
Урок геометрии в 9-м классе «Площади четырехугольников»

Цель урока: познакомить учащихся с 2 способами приближенного вычисления площадей плоских фигур: с помощью палетки и формулы Пика, продолжать развивать навыки нахождения площадей различных четырехугольников, развивать графическую культуру учащихся, воспитывать потребность расширения мировоззрения.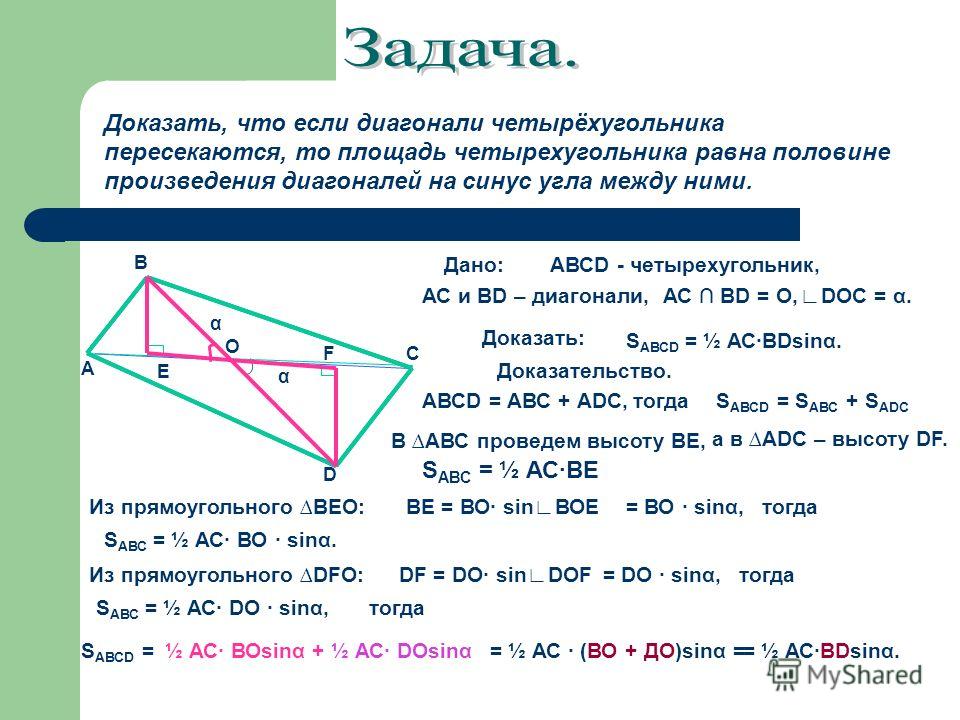

Оборудование: таблица “Формула Пика”, модели четырехугольников различных видов для лабораторной работы, палетки.

ХОД УРОКА

I. Повторение.

У доски работают два человека по карточкам.

Карточка № 1.

Задача.

Вычислить площадь выпуклого четырехугольника, диагонали которого перпендикулярны, а длины их равны 8 см и 12 см.

Карточка № 2.

Задача.

Доказать: если диагонали выпуклого четырехугольника пересекаются, то его площадь равна половине произведения диагоналей на синус угла между ними.

В это время 4 учащихся выполняют индивидуальные задания на местах по карточкам.

Карточка № 3.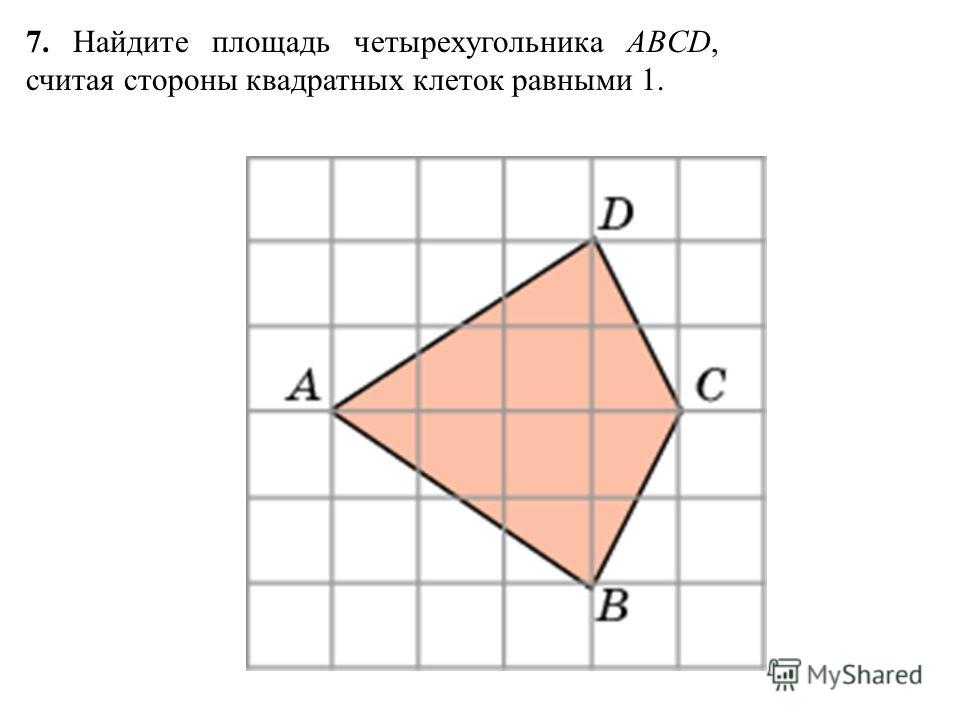

Найти площадь равнобокой трапеции, если меньшее основание 18 см, высота 9 см, а острый угол 45⁰.

Карточка № 4.

Два участка земли огорожены заборами одинаковой длины. Первый прямоугольный участок имеет стороны 220 м и 160 м, а второй имеет форму квадрата. Площадь какого участка больше и на сколько?

Карточка № 5.

Полкомнаты, имеющей форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета 30 см, а ширина 5 см. Сколько потребуется таких дощечек для покрытия пола?

Карточка № 6.

Вырезать из бумаги 2 равных прямоугольных треугольника и составить из них:

а) равнобедренный треугольник;

б) прямоугольник;

в) параллелограмм, отличный от прямоугольника.

Сравнить площадь полученных фигур.

Остальные учащиеся участвуют в проведении “Гимнастики ума”.

Гимнастика ума

1. Площадь каких четырехугольников мы можем находить к сегодняшнему уроку?
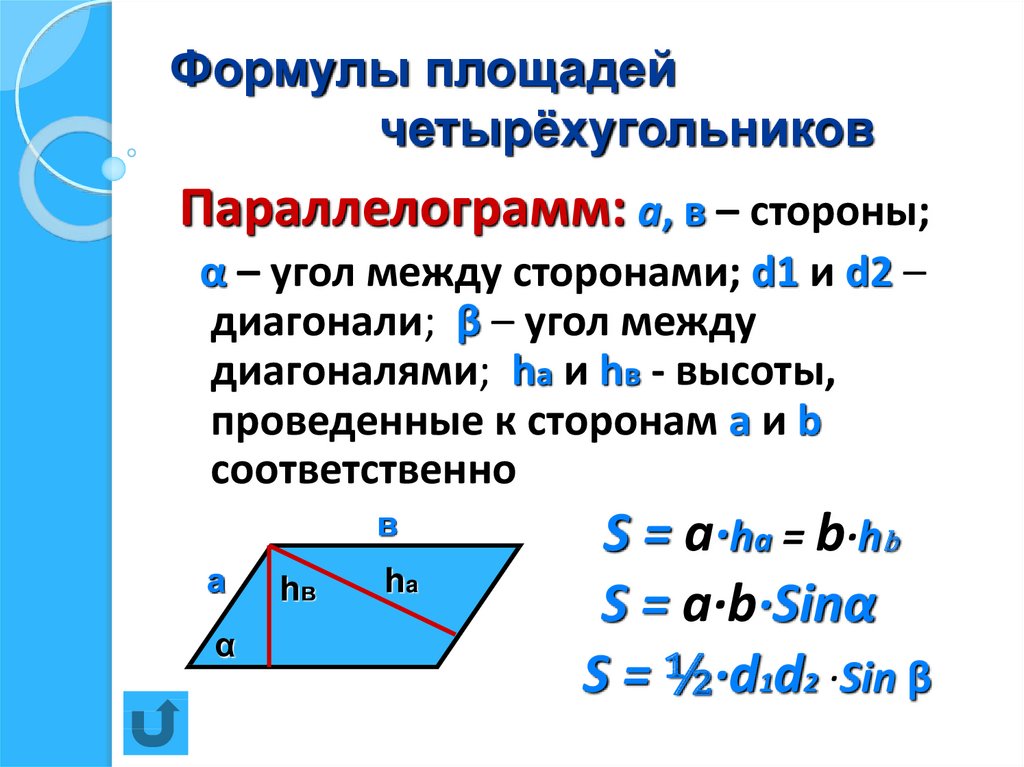
2. Как найти площадь параллелограмма, зная его сторону и высоту, проведенную к ней?
3. Какие формулы для площади параллелограмма вам еще известны (S = ab sin; S = 1/2d₁d₂ sin)?
4. Укажите формулу площади прямоугольника.
5. Какой из четырехугольников: прямоугольник или параллелограмм имеет большую площадь, если их стороны равны?
6. Как вычислить площадь ромба?
7. А как иначе найти площадь ромба?
8. Вычислить площадь ромба с диагоналями 10 см и 12 см.
9. Чему равна площадь трапеции?
10. А как практически найти площадь четырехугольника, не являющегося ни одним из перечисленных четырехугольников (разбить на 2 треугольника).
11. Можно ли для вычисления площади выпуклого четырехугольника применить другой подход?

Ответ на этот вопрос дает отвечающий у доски по карточке № 2, который комментирует решение задачи о нахождении площади выпуклого четырехугольника по его диагоналям и углу между ними.

Учитель: Кроме того, на прошлых уроках в ходе решения нестандартных задач мы познакомились с формулами для нахождения площади четырехугольника:

а) вписанного в окружность

S = (p-a)(p-b)(p-c)(p-d), p = (a+b+c+d)/2;

б) четырехугольника, который одновременно является и вписанным и описанным

S = abcd

Это формулы – аналоги формулы Герона.

I. За страницами учебника

Способы приближенного измерения площадей.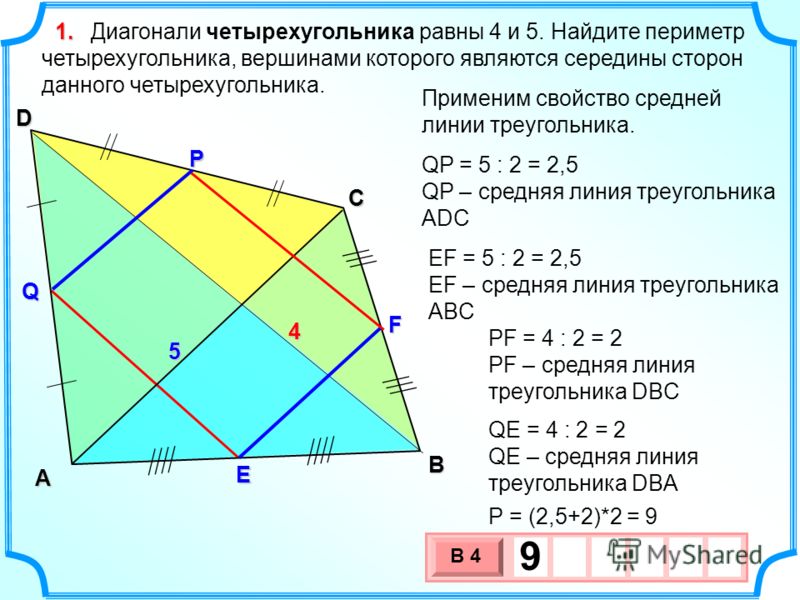

С помощью палетки.

Задача.

Можно ли очень точно определить площадь большого участка земли, имеющего форму четырехугольника?

Ответ.

Для этого используется метод приближенного нахождения площади. С помощью аэрофотосъемки получают карту этого участка с определенным масштабом. А затем с помощью палетки определяется площадь. Так, например, с помощью карты на уроке геометрии вы можете найти площадь государства, озера, какого-либо экономического района.

Этот способ определения площади применяется для любой фигуры, например, листа (в биологии это тоже приходиться иногда делать).

Считают количество полных квадратов (со стороной, например, 1 см), расположенных внутри фигуры, а затем считают число неполных квадратов.

Для нахождения площади к числу полных прибавляют половину числа неполных квадратов. Погрешность большая. Этой точности достаточно только в некоторых случаях.

А сейчас познакомимся с еще одним способом нахождения площади. Ученик рассказывает о формуле Пика.

II. Формула Пика

Пик Георг Александров (1859-1943 гг.) – австрийский математик открыл теоремы Пика, Пика – Жюлиа, Пика – Невалины, доказал неравенство Шварца – Пика.

Нарисуем на клетчатой бумаге какой-нибудь многоугольник. Например, такой, как вы видите на рисунке 1 (Приложение № 1). Попробуем теперь рассчитать его площадь. Как это сделать? Наверное, проще всего разбить его на прямоугольные треугольники и прямоугольники, площади которых уже нетрудно вычислить и сложить полученные результаты. Последовательно проводя вычисления получим, что площадь нашего многоугольника равна 20,5, если за единицу площади взять площадь одного квадрата клетчатой бумаги.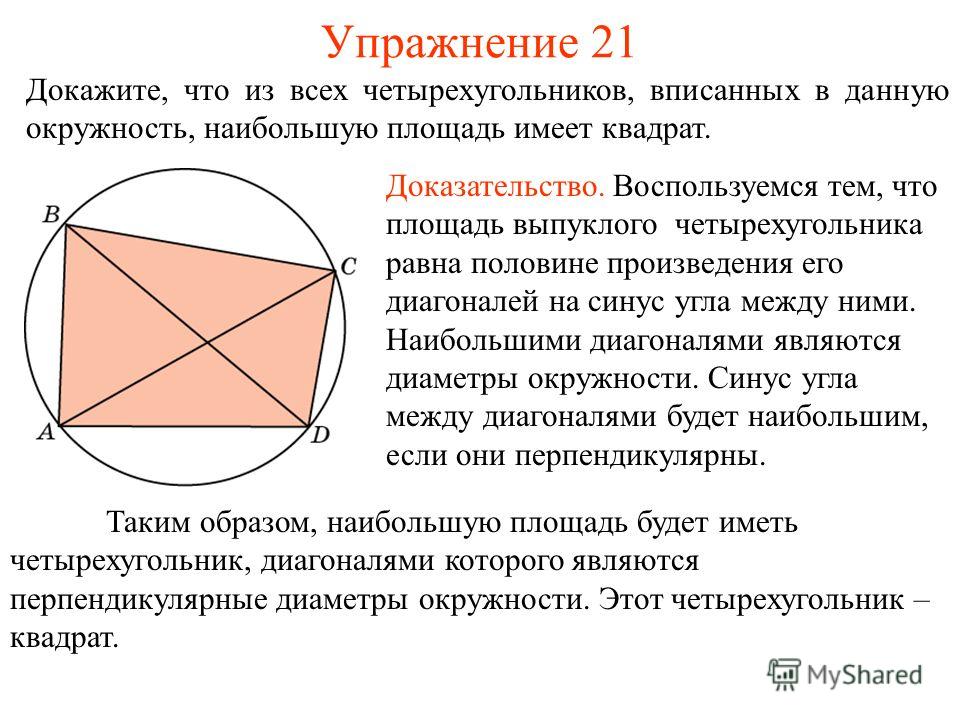

Но если вспомнить, что сторона такого квадрата равна 0,5 см, а значит его площадь равна четверти квадратного сантиметра, площадь нашего многоугольника в квадратных сантиметрах будет равна 20,5/4 = 5,125 см².

Использованный нами способ несложен, но очень громоздок, кроме того он годится не для всяких многоугольников. Так многоугольник на рисунке 2 (Приложение № 1) нельзя разбить на прямоугольные треугольники и прямоугольники, так как мы это проделали в предыдущем случае. Можно, например, попробовать дополнить наш многоугольник до “хорошего”, нужного нам, то есть до такого, площадь которого мы сможем вычислить описанным способом, потом из полученного числа вычесть площади добавленных частей. Однако оказывается, что есть очень простая формула, позволяющая вычислить площади таких многоугольников с вершинами в узлах квадратной сетки S = B + 0,5 Г – 1, где S – площадь многоугольника, выраженная в площадях единичных квадратиков сетки; Г – количество узлов сетки, лежащих на границах многоугольника, а В – количество узлов сетки, лежащих внутри многоугольника.

В нашем случае Г=7, В=18, S=18+3, 5-1 = 20,5.

Столь же просто сосчитать и площадь многоугольника на первоначальном рисунке: Г=12, В=11, S=11+6,1-1 = 16,0.

Формула, с которой мы познакомились, носит имя немецкого математика Пика, открывшего её.

S = В + Г/2 – 1

III. Лабораторная работа

(в группах по 5 человек).

I – II группа.

Каждому учащемуся учитель предлагает для выполнения задания произвольный четырехугольник.

1. Определить площадь фигуры с помощью палетки.
2. Выполнить на четырехугольнике необходимые построения и измерения и вычислить его площадь.

Сравнить полученные результаты.

III группа.

Площадь четырехугольника “по-вавилонски”.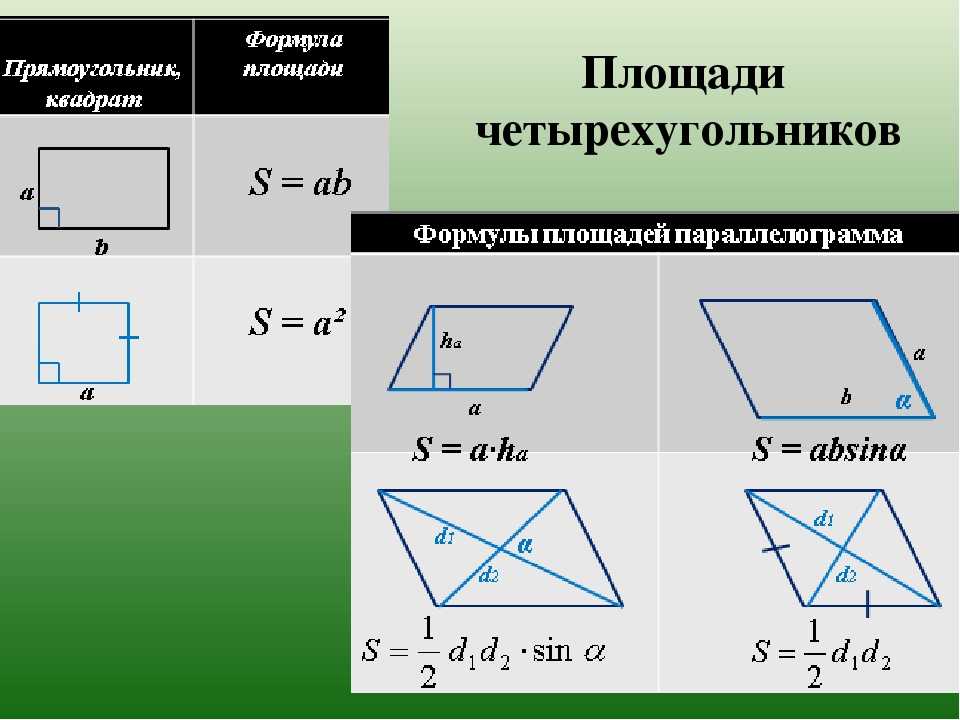

1. Древние вавилоняне вычислили площадь четырехугольника, перемножая полусуммы длин противоположных сторон. Можете ли вы установить, для каких четырехугольников такой способ вычисления дает правильное значение площади?
2. Определите площадь этой фигуры с помощью палетки и путем разбиения на 2 треугольника.
3. Каков в процентном отношении неточность измерения площади с помощью палетки по отношению к вычислению с помощью треугольников.

IV группа.

Площадь трапеции “по-египетски”.

Для вычисления площади равнобокой трапеции древние египтяне умножали полусумму длин оснований на длину боковой стороны. Какова в процентном отношении ошибка такого “египетского” способа для случая равнобокой трапеции с боковой стороной 20 см и основаниями 6 см и 4 см?

Найти относительную погрешность измерения с помощью палетки к точному определению площади.

IV. Итог урока.

Итак, на сегодняшнем уроке мы познакомились с некоторыми формулами нахождения площадей четырехугольников, методом приближенного нахождения площадей. Где используется измерение площадей?

V. Задание на дом.

1. Повторить тему “Площади фигур”.
2. Из предложенных 7 задач по-своему выбору решить 3 из них.

№ 1.

Сторона параллелограмма 8,1 см, а диагональ, равная 14 см, образует с ней угол 30⁰. Найти площадь параллелограмма.

№ 2.

Найти стороны прямоугольника, если его площадь равна 9 м², а его периметр равен 12 м.

№ 3.

Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими часть стены, имеющей форму прямоугольника со сторонами 3 м и 2,7 м.

№ 4.

Найти сторону квадрата, площадь которого равна площади прямоугольника со сторонами 8 м и 18 м.

№ 5.

Начертить квадрат, принять его за единицу измерения площадей.

Начертить:

а) квадрат, площадь которого выражена числом 4;
б) прямоугольник, площадь которого выражена числом 4;
в) треугольник, площадь которого выражена числом 2.

№ 6.

Найти стороны прямоугольника, если его площадь 250 см², а одна сторона в 2,5 раза больше другой.

№ 7.

Диагональ параллелограмма, равная 13 см, перпендикулярна стороне параллелограмма, равной 12 см. Найти площадь параллелограмма.

Приложение

Площадь четырехугольника — формулы, вывод и пример

Площадь четырехугольника обычно определяется как область, занимаемая внутри границ четырехугольника или плоского объекта или фигуры.

Площадь измеряется в квадратных единицах. Стандартной единицей измерения являются квадратные метры (м ² ).

О четырехугольнике

Четырехугольник – это четырехугольник, сумма внутренних углов которого равна 360 ^o .

Свойства четырехугольника:

• 4 вершины и 4 стороны.
• Сумма внутренних углов = 360 ^o
• Обычно могут иметь стороны разной длины и углы разной величины.

Примерами четырехугольника являются квадрат, прямоугольник, параллелограмм, трапеция, ромб и воздушный змей.

Примеры четырехугольников (источник)

Вычисление площади четырехугольника

В приведенном выше четырехугольнике h ₁ и h ₂ являются высотами треугольников ABC и ADC соответственно. BE и DF перпендикулярны диагонали AC.

Теперь, 

площадь (четверка ABCD) = площадь (△ABC) + площадь (△ADC)

площадь (△ABC) = \(\frac{(\mbox{основание * высота})}{2} = \frac{(AC*h_1)}{2}\)

площадь(△ADC) = \(\frac{(\mbox{основание * высота})}{2} = \frac{(AC*h_2)} {2}\)

⇒ площадь (четверка ABCD) = \(\frac{(AC*h_1)}{2} + \frac{(AC*h_2)}{2} = AC \left( \frac{h_1 + h_2}{2} \right) = \frac{1}{2}*AC*(h2+h3)\)

∴ Площадь четырехугольника = \(\frac{1}{2}\) * диагональ * Сумма высот двух треугольников

Areas of Different Quadrilaterals

Quadrilaterals	Areas
Area of ​​Square	(Side) 2
Area of ​​rectangle	Length * breadth
Площадь воздушного змея	\(\frac{1}{2}\) * Произведение диагоналей
Площадь параллелограмма	\(\mbox{основание} * \mbox{высота}\)
Площадь трапеции	\(\frac{\mbox{основание}_1 + \mbox{основание}_2}{2} * \mbox{высота}\)
Площадь ромба	\(\frac {1}{2} диагональ_1 \cdot диагональ_2\)

Решенный пример

Вопрос. В данном выше четырехугольнике ABCD, какова площадь ABCD, если диагональ AC = 24 см, а высоты равны 5 см и 10 см соответственно?

Раствор. Дано,
АС = 24см
ч 92\)

∴ Площадь четырехугольника ABCD = 180см ² .

Часто задаваемые вопросы

Какова площадь четырехугольника?

Площадь четырехугольника = \(\frac{1}{2}\) *Диагональ * Сумма высот двух треугольников

Какие существуют примеры четырехугольников?

Примерами четырехугольников являются квадраты, прямоугольники, параллелограммы и т. д.

Как найти площадь четырехугольника?

Площадь четырехугольника рассчитывается путем сложения площадей двух треугольников, которые по существу объединяются, чтобы получить четырехугольники.

Подробнее:
1. Площадь восьмиугольника
2. Площадь пятиугольника

Площадь четырехугольника — GED Math

Все ресурсы GED Math

4 Диагностические тесты 263 практических теста Вопрос дня Карточки Learn by Concept

← Предыдущий 1 2 3 4 5 6 Далее →

GED Math Help » Геометрия и графики » 2-мерная геометрия » Квадраты, прямоугольники и параллелограммы » Площадь четырехугольника

Найдите площадь трапеции:

Возможные ответы:

Правильный ответ:

Объяснение:

Площадь трапеции рассчитывается по следующей формуле:

Сообщить об ошибке

Длина каждой стороны квадрата увеличивается на 10%. На сколько процентов увеличилась его площадь?

Возможные ответы:

Правильный ответ:

Объяснение:

Пусть  – исходная длина стороны квадрата.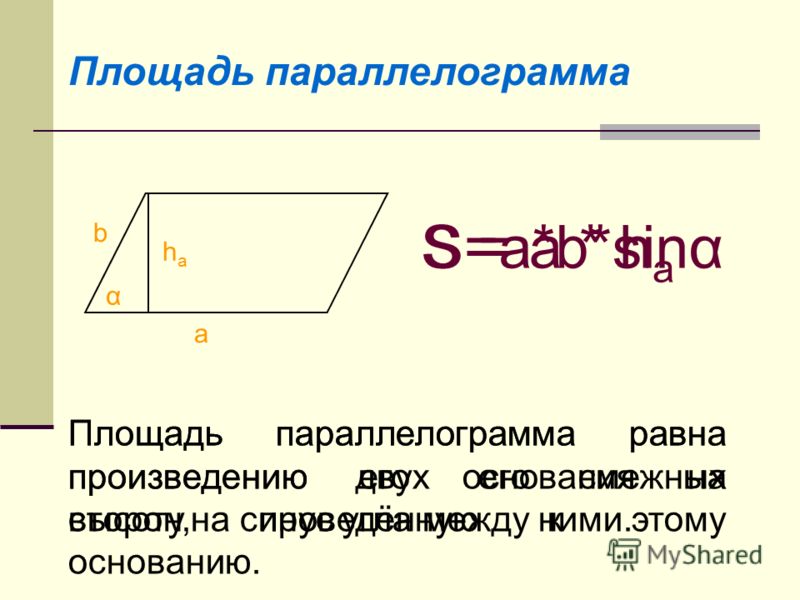 Увеличение этого значения на 10 % равносильно добавлению 0,1 кратной длины стороны к исходной длине стороны. Таким образом, новая длина стороны равна

. Площадь квадрата равна квадрату длины его стороны.

Площадь квадрата изначально ; сейчас

То есть площадь увеличилась на

.

Сообщить об ошибке

На приведенном выше рисунке показан прямоугольный бассейн в квартире. Управляющему квартирой необходимо приобрести брезент, который полностью покроет этот бассейн. Однако из-за режущего устройства, которое использует магазин бассейнов, длина и ширина брезента должны быть кратны четырем ярдам. Кроме того, брезент должен быть как минимум на один ярд длиннее и на один ярд шире, чем бассейн.

Какова минимальная площадь брезента, который купит менеджер?

Возможные ответы:

Правильный ответ:

Объяснение:

Три фута составляют ярд, поэтому длина и ширина бассейна равны ярдам и ярдам соответственно. Поскольку размеры брезента должны превышать размеры бассейна как минимум на один ярд, размер брезента должен быть не менее ярдов на ярды; но так как оба измерения должны быть кратны четырем ярдам, мы берем следующее кратное четырем для каждого.

Размер брезента должен быть 20 ярдов на 16 ярдов, поэтому площадь брезента равна произведению этих размеров или

квадратных ярдов.

Сообщить об ошибке

Примечание. Рисунок выполнен НЕ в масштабе

Какой процент прямоугольника  белый?

Возможные ответы:

Правильный ответ:

Объяснение:

Розовая область — это прямоугольник . Его длина и ширина равны

, поэтому его площадь равна произведению этих чисел, или

.

Длина и ширина прямоугольника равны

, поэтому его площадь равна произведению этих величин, или

.

Белая область – это Прямоугольник  , вырезанный из Прямоугольника , поэтому его площадь равна разнице двух:

.

Итак, мы хотим узнать, сколько процентов составляет 102 от 200, на что можно ответить следующим образом:

Сообщить об ошибке

Примечание: Рисунок выполнен НЕ в масштабе.

См. рисунок выше, на котором показан прямоугольный сад (зеленым цветом), окруженный грунтовой дорожкой (коричневым цветом). Грунтовая дорожка имеет ширину пять футов. Какой из следующих многочленов дает площадь 90 179 сада 90 180 в квадратных футах?

Возможные ответы:

Правильный ответ:

Объяснение:

Длина сада на фут меньше, чем длина всего участка, или

.

Ширина сада меньше ширины всего участка или

.

Площадь сада — это их продукт:

Сообщить об ошибке

Примечание: Рисунок НЕ выполнен в масштабе.

Вычислите площадь ромба на приведенной выше диаграмме, если:

Возможные ответы:

Правильный ответ:

Пояснение:

Площадь ромба равна половине произведения длин диагоналей  и . Это

.

Сообщить об ошибке

Примечание. Рисунок НЕ выполнен в масштабе

См. рисунок выше, на котором показан прямоугольный сад (зеленым цветом), окруженный грунтовой дорожкой (коричневым цветом). Грунтовая дорожка шириной в фут. Какой из следующих многочленов дает площадь 90 179 садов 90 180 ?

Возможные ответы:

Правильный ответ:

Объяснение:

Длина сада на фут меньше, чем длина всего участка, или

.

Ширина сада на фут меньше, чем ширина всего участка, или 

.

Площадь сада является их произведением:

Сообщить об ошибке

Примечание: Рисунок НЕ выполнен в масштабе

См. схему выше.

Половина прямоугольника  розовая. .

Оценить .

Возможные ответы:

Правильный ответ:

Объяснение:

Прямоугольник имеет длину и ширину, поэтому его площадь равна

.

Площадь прямоугольника в два раза больше площади прямоугольника, или 600. Его длина равна 

.

Ширина

.

Подставьте то, что мы знаем, и решите для:

 

Сообщить об ошибке

широкий на всем протяжении. Какова площадь этой грунтовой дорожки?

Возможные ответы:

Правильный ответ:

Объяснение:

Грунтовую дорожку можно рассматривать как область между двумя прямоугольниками.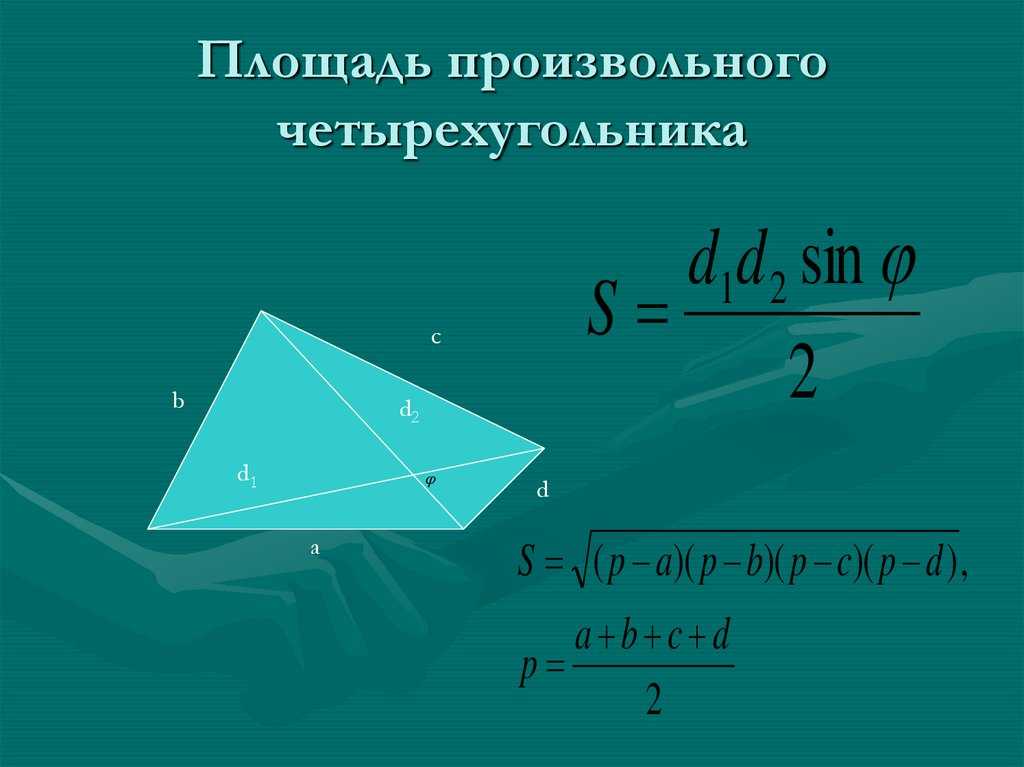 Внешний прямоугольник имеет длину и ширину 100 футов и 60 футов соответственно, поэтому его площадь равна

квадратных футов.

 

Внутренний прямоугольник имеет длину и ширину в футах и ​​футах соответственно, поэтому его площадь составляет

квадратных фута.

 

Площадь пути равна разности двух:

 квадратных футов.

Сообщить об ошибке

Примечание. Рисунок выполнен НЕ в масштабе

Какой процент прямоугольника  розовый?

Возможные ответы:

Правильный ответ:

Объяснение:

Розовая область — это прямоугольник . Его длина и ширина равны

, поэтому его площадь равна произведению этих величин, или

.

Длина и ширина прямоугольника равны

, поэтому его площадь равна произведению этих величин, или

.