Экстремумы функции (Лекция №9)
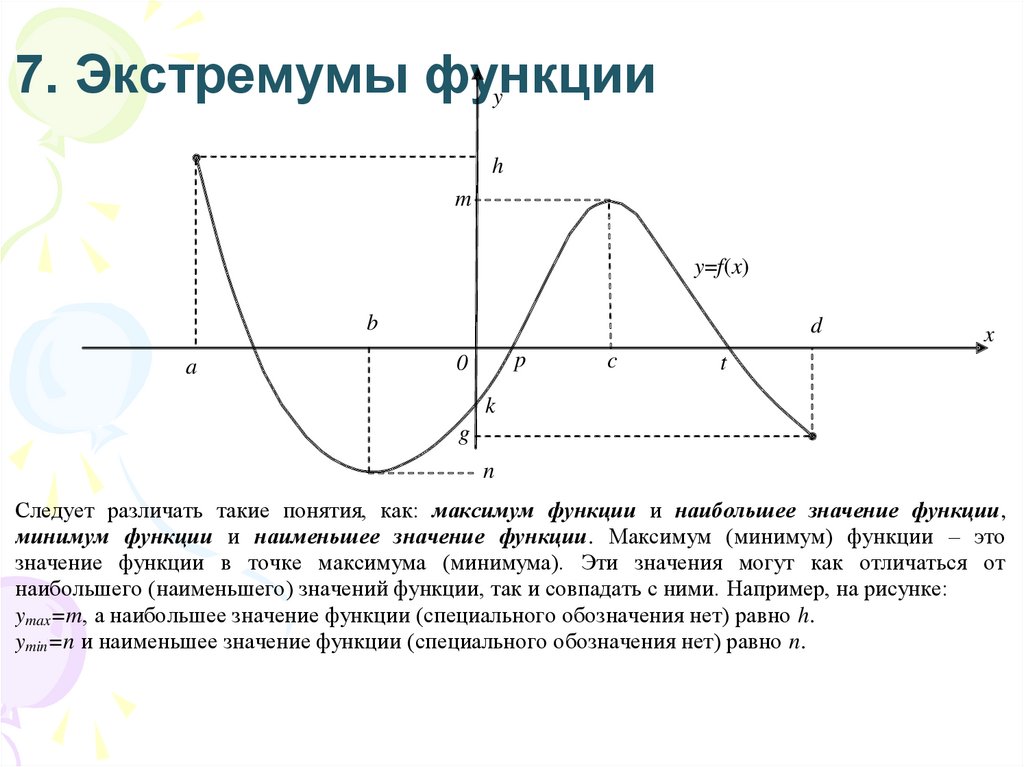
Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке.
Значение функции в точке x1 будет больше значений функции во всех соседних точках как слева, так и справа от x1. В этом случае говорят, что функция имеет в точке x1 максимум. В точке x3 функция, очевидно, также имеет максимум. Если рассмотреть точку x2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x2 минимум. Аналогично для точки x4.
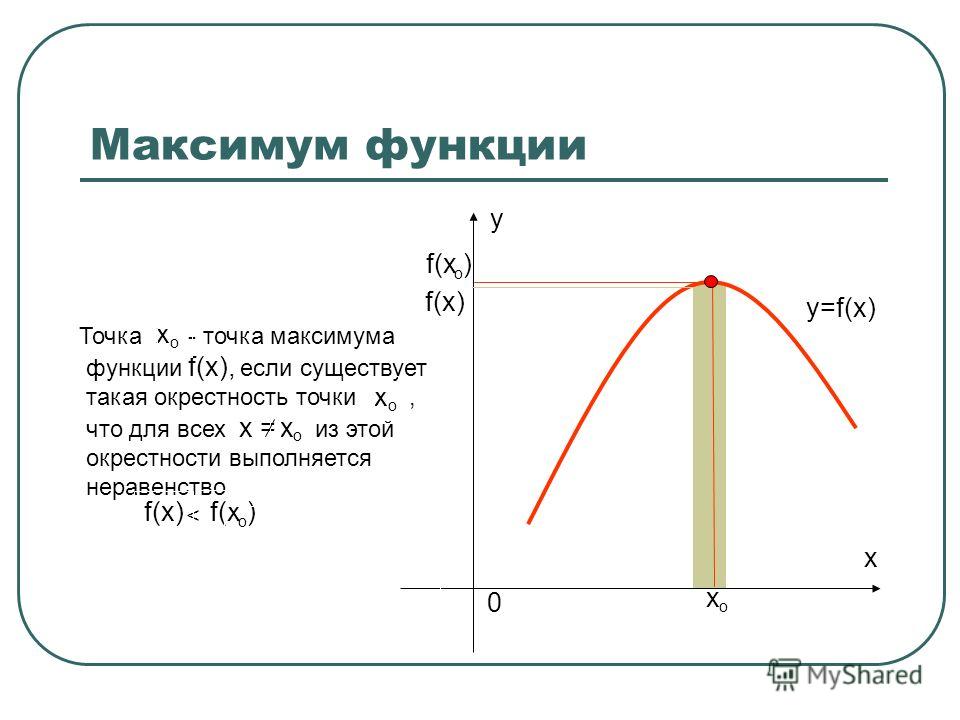
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее
значения во всех точках некоторого интервала, содержащего точку x0, т.е. если существует такая
окрестность точки x0, что для всех x≠x
Функция y=f(x) имеет минимум в точке x0, если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)>f(x0.
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
Отмети, что если функция
имеет в точке максимум, то это не означает, что в этой точке функция имеет
наибольшее значение во всей области определения. На рисунке, рассмотренном выше,
функция в точке x1 имеет максимум, хотя
есть точки, в которых значения функции больше, чем в точке x1. В частности, f(x1) < f(x4)
т. е. минимум функции больше максимума. Из определения максимума следует только,
что это самое большое значение функции в точках, достаточно близкихк точке максимума.
е. минимум функции больше максимума. Из определения максимума следует только,
что это самое большое значение функции в точках, достаточно близкихк точке максимума.
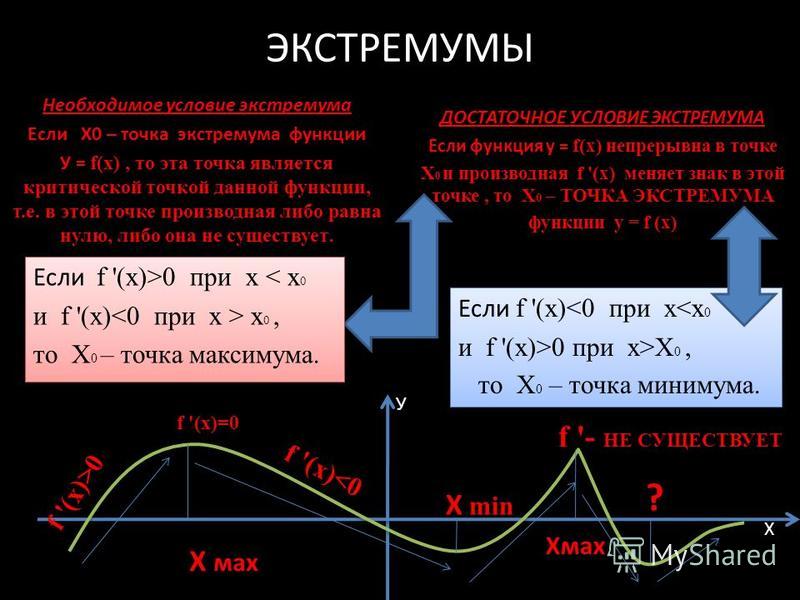
Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство. Пусть для определенности в точке x0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x0+ Δx)<f(x0), т.е. Но тогда
Переходя в этих неравенствах к пределу при Δ
 Так как f ‘(x0)
определяет число, то эти два неравенства совместны только в том случае, когда f ‘(x0) = 0.
Так как f ‘(x0)
определяет число, то эти два неравенства совместны только в том случае, когда f ‘(x0) = 0.Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.
Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.
Примеры.
- y=|x|.
Функция не имеет производной в точке x=0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как y(0)=0, а при всех x≠ 0y > 0.
-
Функция не имеет производной при x=0, так как обращается в бесконечность приx=0. Но в этой точке функция имеет максимум.

-
Функция не имеет производной при x=0, так как при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0.
Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует.
Однако, если в некоторой точке x0 мы знаем, что f ‘(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум.
Например. .
Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше.

Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками.
Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.
Теорема 2. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x0, и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x0). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x0 функция имеет максимум.
 Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.
Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.Таким образом, если
- f ‘(x)>0 при x<x0 и f ‘(x)<0 при x> x0, то x0 – точка максимума;
- при x<x0 и f ‘(x)>0 при x> x0, то x0 – точка минимума.
Доказательство. Предположим сначала, что при переходе через x0 производная меняет знак с плюса на минус, т.е. при всех x, близких к точке x0f ‘(x)>0 для x< x0, f ‘(x)<0 для x> x0. Применим теорему Лагранжа к разности f(x) — f(x0) = f ‘(c)(x- x0), где c лежит между x и x0.

- Пусть x < x0. Тогда c< x0 и f ‘(c)>0. Поэтомуf ‘(c)(x- x0)<0и, следовательно,
f(x) — f(x0)<0,т.е. f(x)< f(x0).
- Пусть x > x0. Тогда c> x0 и f ‘(c)<0. Значитf ‘(c)(x- x0)<0. Поэтому f(x) — f(x0)<0,т.е.f(x) < f(x0).
Таким образом, для всех значений x достаточно близких к x0f(x) < f(x0). А это значит, что в точке x0 функция имеет максимум.
Аналогично доказывается вторая часть теоремы о минимуме.
Проиллюстрируем смысл этой теоремы на рисунке. Пусть
f ‘(x)<0 при x< x1, f ‘(x)>0 при x> x1.

Тогда слева от точки x1 функция возрастает, а справа убывает, следовательно, при x = x1 функция переходит от возрастания к убыванию, то есть имеет максимум.
Аналогично можно рассматривать точки x2 и x3.
Схематически все вышесказанное можно изобразить на картинке:Правило исследования функции y=f(x) на экстремум
- Найти область определения функции f(x).
- Найти первую производную функции f ‘(x).
- Определить критические
точки, для этого:
- найти действительные корни уравнения f ‘(x)=0;
- найти все значения x при которых производная f ‘(x) не существует.
- Определить знак
производной слева и справа от критической точки. Так как знак производной
остается постоянным между двумя критическими точками, то достаточно определить
знак производной в какой-либо одной точке слева и в одной точке справа от
критической точки.

- Вычислить значение функции в точках экстремума.
Примеры. Исследовать функции на минимум и максимум.
- . Область определения функции D(y)=R.
Найдем производную заданной функции
Определим критические точки . Производная не существует при х
-
Критическая точка функции x =3. Точка x= –1 не входит в область определения функции.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ
Наибольшим значением функции на отрезке называется самое большое из всех ее значений на этом отрезке, а наименьшим – самое маленькое из всех ее значений.

Рассмотрим функцию y=f(x) непрерывную на отрезке [a, b]. Как известно, такая функция достигает своего наибольшего и наименьшего значений, либо на границе отрезка, либо внутри него. Если наибольшее или наименьшее значение функции достигается во внутренней точке отрезка, то это значение является максимумом или минимумом функции, то есть достигается в критических точках.
Таким образом, получаем следующее правило нахождения наибольшего и наименьшего значений функции на отрезке[a, b]:
- Найти все критические точки функции в интервале (a, b) и вычислить значения функции в этих точках.
- Вычислить значения функции на концах отрезка при x = a, x = b.
- Из всех полученных значений выбрать наибольшее и наименьшее.
Примеры.
- Найти наибольшее и наименьшее значения функции на отрезке [–2; –0,5].
Найдем критические точки функции.

Вычислим значения функции в найденной точке и на концах заданного отрезка.
Итак,
- Найти наибольшее и наименьшее значения функцииy=x-2·ln x на [1; e].
- Чему равна наименьшая площадь боковой поверхности
прямого кругового конуса объема 3π?
По теореме Пифагора
.
Следовательно, .
.
Найдем критические точки функции S: S‘ = 0, т.е.
Покажем, что при найденном значении h функция Sбок достигает минимума.
.
Найти радиус основания и высоту цилиндра наибольшего объема, который можно вписать в шар радиусом R.
Пусть r – радиус основания цилиндра, h – высота.
Нам нужно максимизировать объем цилиндра .

Используя условие задачи, найдем связь между r и h. По теореме Пифагора из треугольника ABC следует, что . Отсюда .
, по смыслу задачи 0≤h≤2R.
.
Покажем, что при найденном значении h функция V принимает наибольшее значение.
Максимумы, минимумы и экстремумы функций
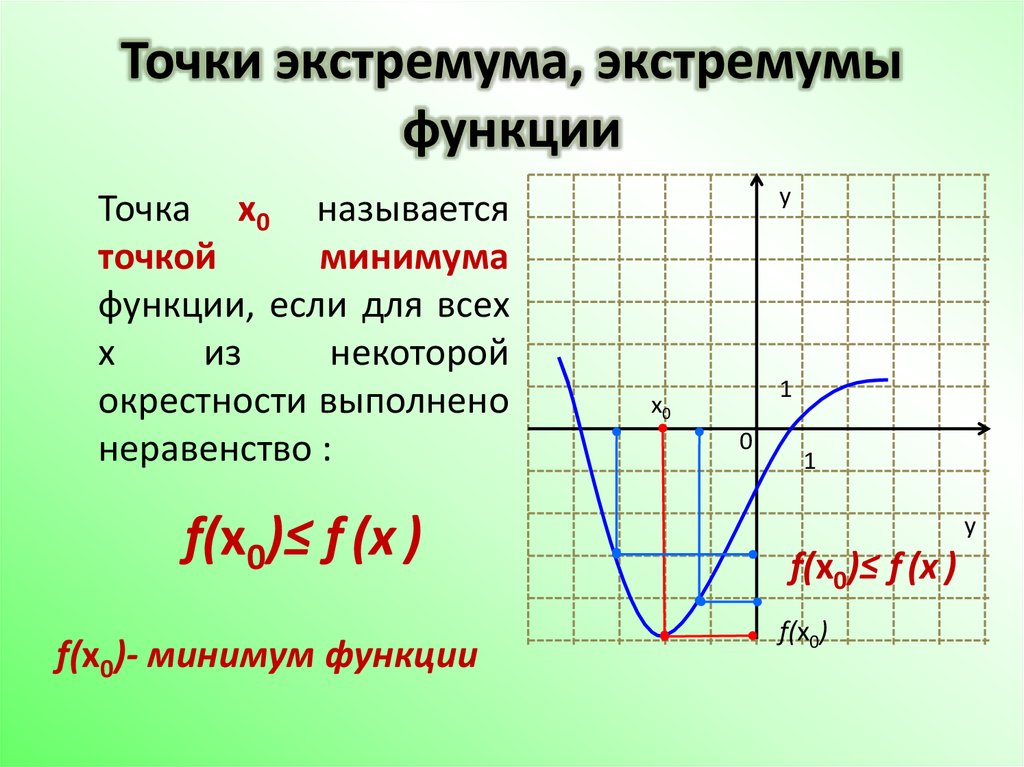
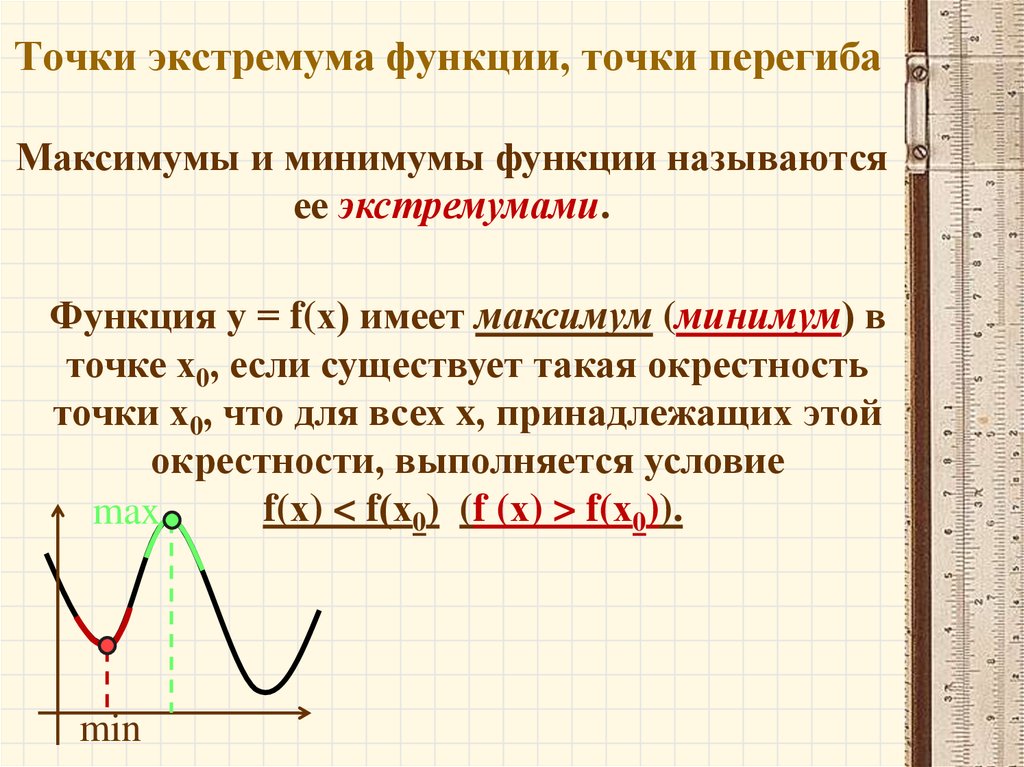
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.
Минимумы и максимумы вместе именуют
экстремумами функции.
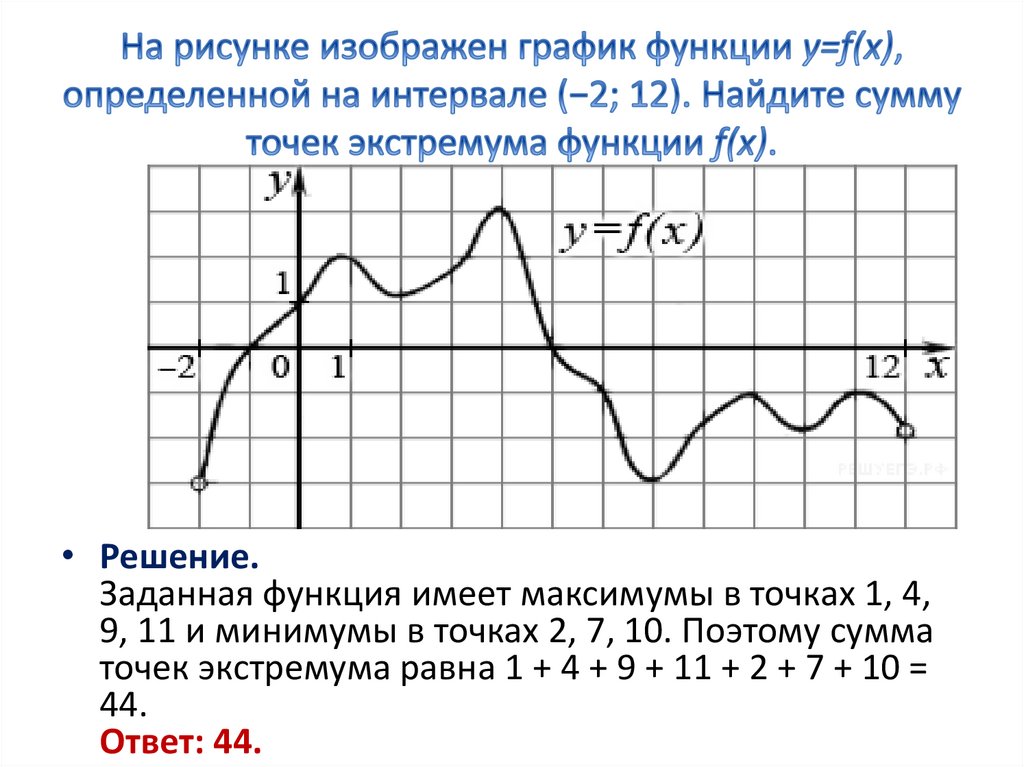
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. \(y\). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, \(-5\) точка минимума (или точка экстремума), а \(1\) – минимум (или экстремум).
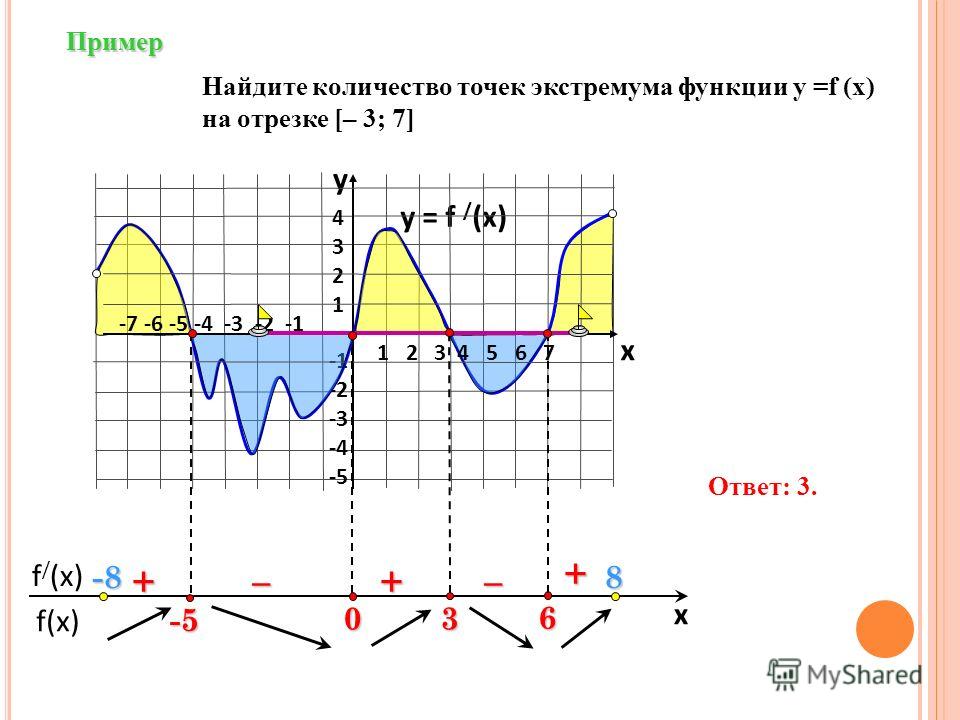
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
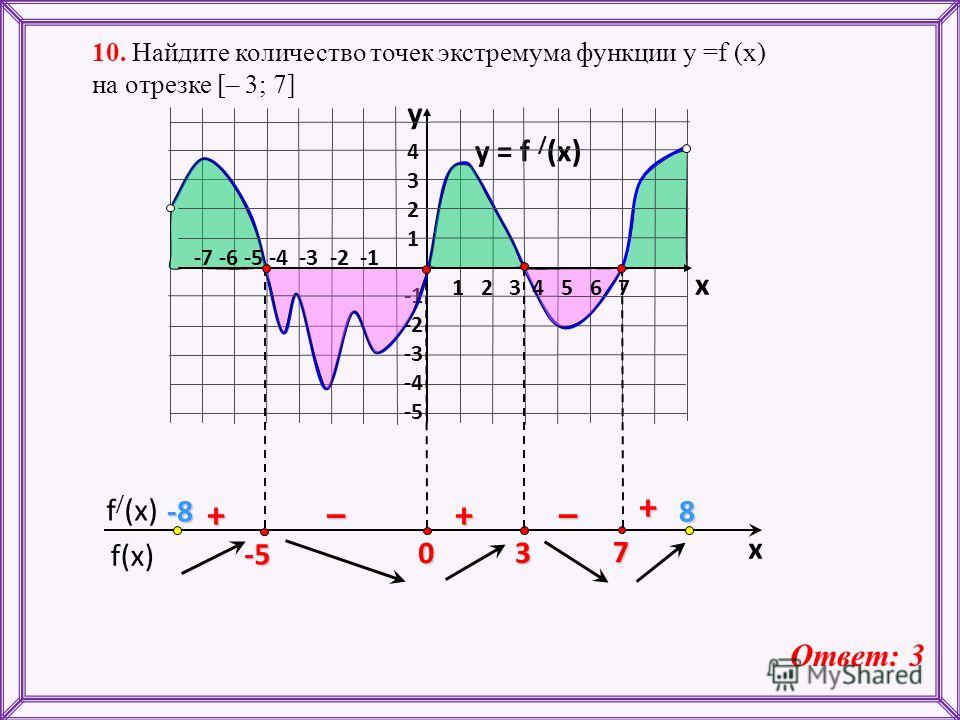
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:
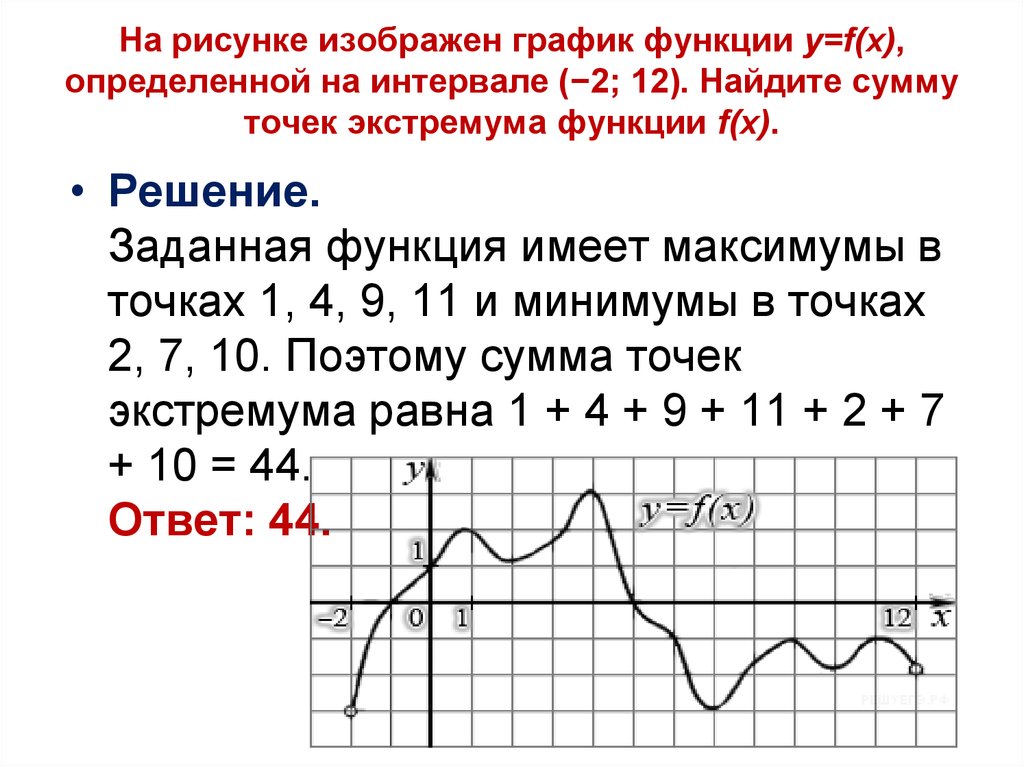
У нас дан график производная — значит ищем в каких точках на графике производная равна нулю.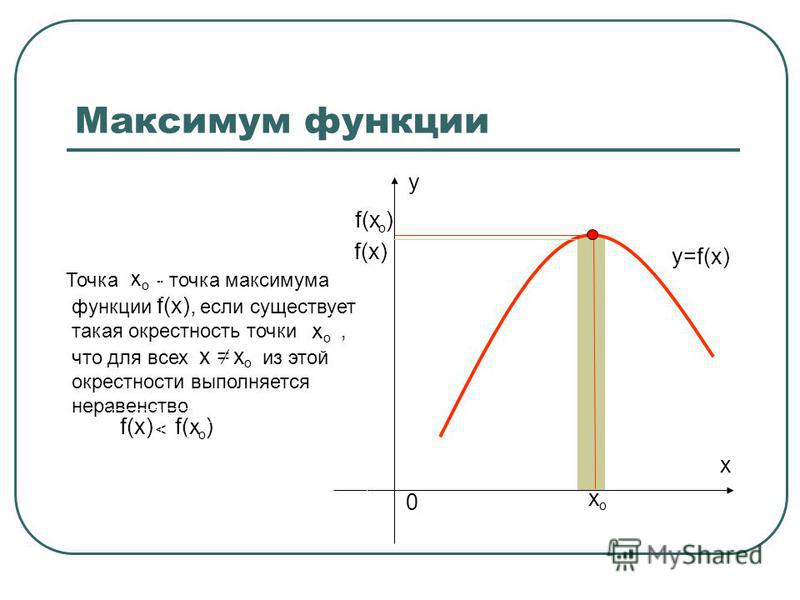 Очевидно, это точки \(-13\), \(-11\), \(-9\),\(-7\) и \(3\). Количество точек экстремума функции – \(5\).
Очевидно, это точки \(-13\), \(-11\), \(-9\),\(-7\) и \(3\). Количество точек экстремума функции – \(5\).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось \(x\)).
Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.
Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди \(-13\), \(-11\), \(-9\),\(-7\) и \(3\).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.
Начнем с \(-13\): до \(-13\) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что \(-13\) – точка максимума.
\(-11\): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что \(-11\) – это минимум.
\(- 9\): функция возрастает, а потом убывает – максимум.
\(-7\): минимум.
\(3\): максимум.
Все вышесказанное можно обобщить следующими выводами:
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
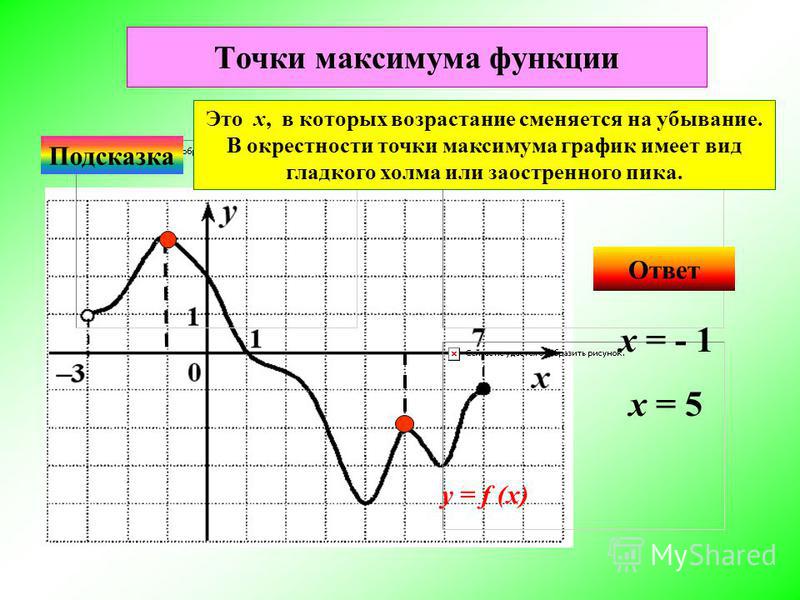
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции \(f'(x)\).
- Найдите корни уравнения \(f'(x)=0\).
- Нарисуйте ось \(x\) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью \(f'(x)\), а под осью \(f(x)\).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если \(f’(x)\) изменила знак с «\(+\)» на «\(-\)», то \(x_1\) – точка максимума;
— если \(f’(x)\) изменила знак с «\(-\)» на «\(+\)», то \(x_3\) – точка минимума;
— если \(f’(x)\) не изменила знак, то \(x_2\) – может быть точкой перегиба. 2-4=0\)
2-4=0\)
\(x=±2\)3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является \(-2\).
Ответ. \(-2\).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумовСкачать статью
Экстремум функции — определение и вычисление с примерами решения
Содержание:
Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при
Если дифференцируемая функция у = f(x) на отрезке возрастает (убывает), то ее производная на этом отрезке
Точка называется точкой локального максимума (минимума) функции если существует окрестность точки для всех точек которой верно неравенство
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках — ее экстремумами.

Необходимые условия экстремума. Если точка хо является точкой экстремума функции то либо не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть — критическая точка. Если f'(х) при переходе через точку меняет знак плюс на минус, то в точке функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке хо экстремума нет.
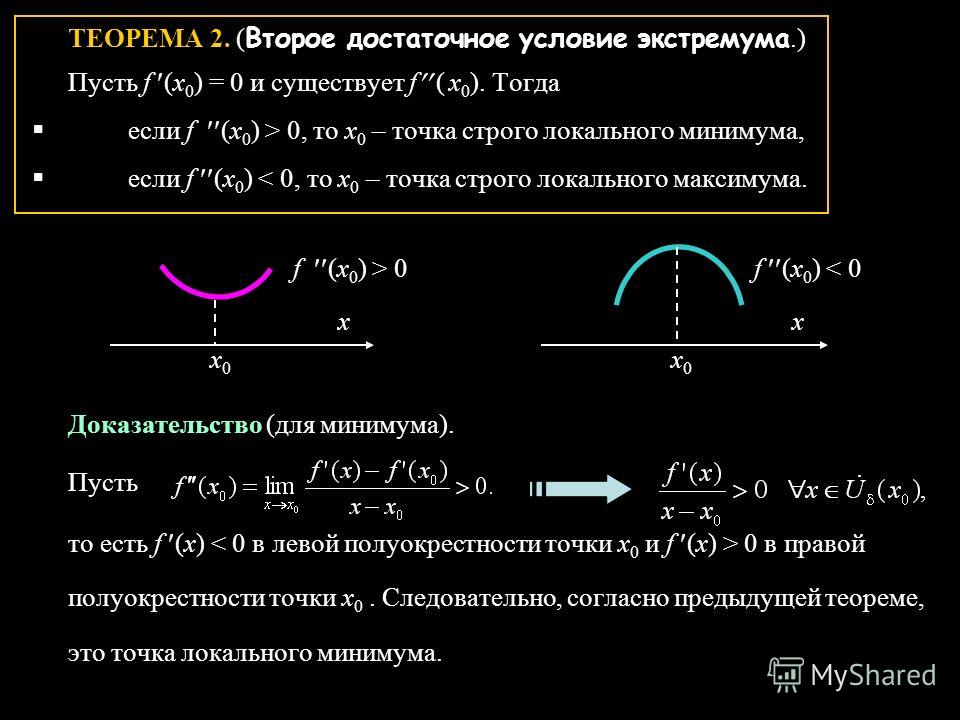
Второе достаточное условие. Пусть функция имеет производную f'(х) в окрестности точки и вторую производную в самой точке . Если то точка является точкой локального минимума (максимума) функции f(x). Если же то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке функция у = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка .
Пример:
Найти экстремумы функции
Решение:
Так как то критические точки функции и Экстремумы могут быть только в этих точках.
 Так как при переходе через точку производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку производная меняет знак минус на плюс, поэтому в точке у функции минимум. Вычислив значения функции в точках и найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.
Так как при переходе через точку производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку производная меняет знак минус на плюс, поэтому в точке у функции минимум. Вычислив значения функции в точках и найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.Пример:
Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется а погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение:
Обозначим стороны площадки через Площадь площадки равна Пусть у — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2х + у = а. Поэтому (длина и ширина площадки не могут быть отрицательными). откуда Поскольку — единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку.
 При значит, в точке функция S имеет максимум. Значение функции
При значит, в точке функция S имеет максимум. Значение функцииПоскольку S непрерывна на и ее значения на концах равны нулю, то найденное значение будет наибольшим значением функции.
Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является у = 2х.
Пример:
Требуется изготовить закрытый цилиндрический бак вместимостью Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Решение:
Площадь полной поверхности цилиндра равна Мы знаем объем цилиндра Значит, Находим производную этой функции:следовательно,
Экстремумы функции
Введём несколько новых понятий. Окрестностью точки называется любой промежуток, для которого является внутренней точкой.
Точка называется точкой минимума (максимума) функции если для всех из некоторой окрестности точки выполняется неравенство
Точки минимума и максимума обозначают соответственно.

Значение функции в точке минимума называется минимумом функции, а в точке максимума — максимумом функции. Обозначают их:
Точки минимума и максимума функции называют точками экстремума (лат. extremum — край, конец). Значения функции в точках её экстремума — её экстремальные значения, или экстремумы.
Например, для функции точка является точкой максимума (рис. 77). Её максимум:
Для функции точка является точкой минимума (рис. 78). Её минимум:
Функция, график которой изображён на рисунке 75, имеет четыре экстремальные точки: — точки максимума; и — точки минимума.
Точка экстремума функции не может принадлежать промежутку, на котором эта функция возрастает или убывает (почему?). Следовательно, те точки, в которых производная функции положительная или отрицательная, не могут быть точками её экстремума. Все остальные точки области определения функции являются её критическими точками. Поэтому точками экстремума функции могут быть только её критические точки.
 Это — необходимое условие существования экстремума.
Это — необходимое условие существования экстремума.Выбрать из критических точек функции точки экстремума позволяет достаточное условие существования экстремума.
Пусть функция непрерывна на промежутке и — её критическая точка, Тогда: точка при переходе через которую в направлении роста аргумента производная меняет знак с «плюса» на «минус», является точкой максимума, а точка, при переходе через которую производная меняет знак с «минуса» на «плюс» — точкой минимума.
Действительно, если производная функции отрицательная, то при переходе через точку возрастание функции изменяется на убывание (рис. 79). В этом случае — точка максимума. Если же при переходе через точку убывание функции изменяется на возрастание, то — точка минимума (рис. 80).
Если же производная функции в точке равна нулю, а слева и справа от производная функции положительная (рис.81) или слева и справа отрицательная, то не является точкой экстремума.
- Заказать решение задач по высшей математике
Пример №552
Найдите точки экстремума и экстремальные значения функции
Решение:
Критические точки функции: При переходе через точку производная меняет знаке поэтому —точка максимума.
 При переходе через точку производная меняет знак с поэтому — точка минимума (рис. 82).
При переходе через точку производная меняет знак с поэтому — точка минимума (рис. 82).Ответ.
Нахождение экстремумов функции можно оформлять в виде таблицы, как на с. 176. Особенно это удобно при общем исследовании функции, когда находят не только её экстремумы, но и другие свойства, строят её график.
Чтобы исследовать функцию, можно пользоваться следующей схемой:
- найти область определения функции;
- исследовать функцию на чётность, нечётность, периодичность;
- найти точки пересечения графика функции с осями координат;
- исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
- найти точки экстремума и экстремальные значения функции;
- найти асимптоты графика функции;
- построить график функции.
Пример №553
Исследуйте функцию и постройте её график.
Решение:
Область определения функции — все действительные числа, кроме Поскольку она не симметрична относительно нуля, то функция не может быть чётной или нечётной.
 Функция непериодическая.
Функция непериодическая.Уравнение не имеет решений, поэтому график функции не пересекает ось Ось он пересекает в точке с ординатой
Критические точки:
Составим и заполним таблицу.
На промежутках функция возрастает, на промежутках функция убывает. — точка максимума, —точка минимума,
Область значений функции:
График функции имеет вертикальную асимптоту так как
График этой функции изображён на рисунке 83.
Пример №554
Может ли нечётная функция иметь экстремум в точке А чётная функция?
Решение:
Нечётная функция не может. Если в окрестности точки функция имеет экстремум, то с одной стороны от нуля она возрастает, а с другой — убывает, или наоборот. А нечётная функция — или только возрастает, или только убывает в окрестности точки Чётная функция может. Например, функция
Пример №555
Существуют ли такие числа при которых имеет экстремум функция
Решение:
При любых действительных значениях В каждой точке производная данной функции неотрицательная.
 Функция возрастает на поэтому не может иметь экстремумов.
Функция возрастает на поэтому не может иметь экстремумов.Ответ. Не существуют.
Пример №556
Исследуйте функцию и постройте её график.
Решение.
2) Функция — нечётная, поскольку
Следовательно, её график симметричен относительно начала координат и достаточно исследовать функцию на промежутке
3) если — график пересекает оси координат только в точке
4) Найдём производную функции:
Очевидно, что для всех х из области определения. Следовательно, функция убывает на каждом из промежутков и не имеет максимумов и минимумов.
Для более точного построения вычислим значение функции в нескольких точках:
График функции имеет вертикальные асимптоты и (Убедитесь самостоятельно.)
График функции изображён на рисунке 84.
Исчисление I. Нахождение абсолютных экстремумов
Онлайн-заметки Пола
Главная / Исчисление I / Применение производных / Нахождение абсолютных экстремумовПоказать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Раздел 4-4: Нахождение абсолютных экстремумов
Пришло время рассмотреть наше первое крупное применение производных в этой главе. Учитывая непрерывную функцию \(f\left( x \right)\), на интервале \(\left[ {a,b} \right]\) мы хотим определить абсолютные экстремумы функции. Для этого нам понадобятся многие из идей, которые мы рассмотрели в предыдущем разделе.
Во-первых, поскольку у нас есть замкнутый интервал (, т.е. и интервал, включающий конечные точки), и мы предполагаем, что функция непрерывна, теорема об экстремальном значении говорит нам, что мы действительно можем это сделать.
 Это, конечно, хорошо. Мы не хотим пытаться найти то, чего может и не быть.
Это, конечно, хорошо. Мы не хотим пытаться найти то, чего может и не быть.Далее, в предыдущем разделе мы видели, что абсолютные экстремумы могут возникать в конечных точках или в относительных экстремумах. Кроме того, из предыдущего раздела мы знаем, что список критических точек также является списком всех возможных относительных экстремумов. Таким образом, конечные точки вместе со списком всех критических точек фактически будут списком всех возможных абсолютных экстремумов.
Теперь нам просто нужно вспомнить, что абсолютные экстремумы — это не что иное, как наибольшее и наименьшее значения, которые может принимать функция, поэтому все, что нам действительно нужно сделать, это получить список возможных абсолютных экстремумов, подставить эти точки в нашу функцию и затем определите наибольшее и наименьшее значения.
Вот процедура нахождения абсолютных экстремумов.
Нахождение абсолютных экстремумов \(f\left( x \right)\) на \(\left[ {a,b} \right]\)
- Проверка непрерывности функции на интервале \(\left [ {яркий]\).

- Найдите все критические точки \(f\left( x \right)\), которые находятся в интервале \(\left[ {a,b} \right]\). Это имеет смысл, если подумать. Поскольку нас интересует только то, что функция делает в этом интервале, нас не интересуют критические точки, выходящие за пределы интервала.
- Оцените функцию в критических точках, найденных на шаге 1, и в конечных точках.
- Определите абсолютные экстремумы.
В этой процедуре нет ничего особенного. Мы назвали первый шаг в процессе шагом 0, в основном потому, что все функции, которые мы собираемся здесь рассмотреть, будут непрерывными, но с этим нужно быть осторожным. Этот процесс будет работать только в том случае, если у нас есть функция, непрерывная на заданном интервале. Наиболее трудоемким этапом этого процесса является второй этап (шаг 1), на котором мы находим критические точки. Также важно отметить, что все, что нам нужно, это критические точки, находящиеся в интервале.
 2} + 6t — 12 = 6\left( {t + 2} \right)\left( {t — 1} \right)\]
2} + 6t — 12 = 6\left( {t + 2} \right)\left( {t — 1} \right)\]Похоже, у нас будет две критические точки, \(t = — 2\) и \(t = 1\). Обратите внимание, что на самом деле нам нужно нечто большее, чем просто критические точки. Нам нужны только критические точки функции, лежащие в рассматриваемом интервале. Оба они попадают в интервал, поэтому мы будем использовать их оба. Это может показаться глупым упоминать сейчас, но об этом часто забывают, обычно когда это становится важным, и поэтому мы будем упоминать об этом при каждой возможности, чтобы убедиться, что об этом не забыли.
Теперь мы оцениваем функцию в критических точках и конечных точках интервала.
\[\begin{align*}g\left( { — 2} \right) & = 24\hspace{1.0in} & g\left( 1 \right) & = — 3\\ g\left( { — 4 } \right) &= — 28\hspace{1.0in} & g\left( 2 \right) & = 8\end{align*}\]
Абсолютные экстремумы — это наибольшая и наименьшая функция, которые когда-либо будут, и эти четыре точки представляют единственные места в интервале, где могут возникать абсолютные экстремумы.
 Итак, из этого списка мы видим, что абсолютный максимум \(g\left( t \right)\) равен 24, и он приходится на \(t = — 2\) (критическая точка) и абсолютный минимум \( g\left( t \right)\) равно -28, что происходит в \(t = — 4\) (конечная точка). 92} — 12t + 4\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ {0,2} \right]\]
Итак, из этого списка мы видим, что абсолютный максимум \(g\left( t \right)\) равен 24, и он приходится на \(t = — 2\) (критическая точка) и абсолютный минимум \( g\left( t \right)\) равно -28, что происходит в \(t = — 4\) (конечная точка). 92} — 12t + 4\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ {0,2} \right]\]Показать решение
Обратите внимание, что эта проблема практически идентична первой. Разница лишь в интервале, на котором мы работаем. Однако это небольшое изменение полностью изменит наш ответ. С этим изменением мы исключили оба ответа из первого примера.
Первый шаг — снова найти критические точки. Из первого примера мы знаем, что это \(t = — 2\) и \(t = 1\).. Здесь важно напомнить, что нам нужны только критические точки, которые действительно попадают в рассматриваемый интервал. Это означает, что нам нужно только \(t = 1\), так как \(t = — 2\) выходит за пределы интервала.
Теперь оцените функцию в одной критической точке интервала и в двух конечных точках.

\[g\left( 1 \right) = — 3\hspace{0.5in}g\left( 0 \right) = 4\hspace{0.5in}g\left( 2 \right) = 8\]
Из этого списка значений мы видим, что абсолютный максимум равен 8 и произойдет при \(t = 2\), а абсолютный минимум равен -3, что произойдет при \(t = 1\).
Как мы видели в этом примере, простое изменение интервала может полностью изменить ответ. Это также показало нам, что нам нужно быть осторожными, чтобы исключить критические точки, которые не находятся в интервале. Если бы мы забыли об этом и включили \(t = — 2\), мы бы получили неправильный абсолютный максимум!
Это еще одна большая ошибка, которую ученики допускают в этих задачах. Слишком часто они забывают исключить критические точки, которые не входят в интервал. Если ваш инструктор похож на меня, это будет означать, что вы получите неправильный ответ. Несложно убедиться, что критическая точка вне интервала больше или меньше любой из точек в интервале.

Пример 3 Предположим, что популяция (в тысячах) определенного вида насекомых через \(t\) месяцев определяется следующей формулой. \[P\left( t \right) = 3\,t + \sin \left( {4t} \right) + 100\]
Определить минимальную и максимальную популяцию за первые 4 месяца.
Показать решение
Вопрос, который мы действительно задаем, состоит в том, чтобы найти абсолютные экстремумы \(P\left( t \right)\) на интервале \(\left[ {0,4} \right]\). Поскольку эта функция непрерывна везде, мы знаем, что можем это сделать.
Начнем с производной.
\[P’\влево( t \вправо) = 3 + 4\cos \влево({4t} \вправо)\]
Нам нужны критические точки функции. Производная существует везде, поэтому критических точек от нее нет. Итак, все, что нам нужно сделать, это определить, где производная равна нулю.

\[\begin{align*}3 + 4\cos \left( {4t} \right) & = 0\\ \cos \left( {4t} \right) & = — \frac{3}{4}\ конец {выравнивание *} \]
Решения для этого,
\[\begin{массив}{*{20}{c}}{4t = 2,4189+ 2\pi n,\,\,\,\,n = 0, \pm 1, \pm 2, \ldots }\\{4t = 3,8643 + 2\pi n,\,\,\,\,n = 0, \pm 1, \pm 2, \ldots }\end{array}\hspace{0,25in} \Rightarrow \hspace{0,25in}\begin{array}{*{20}{c}}{t = 0,6047 + \displaystyle \frac{{\pi n}}{2},\,\,\,\,n = 0, \pm 1, \pm 2, \ldots}\\{t = 0,9661 + \displaystyle \ frac{{\pi n}}{2},\,\,\,\,n = 0, \pm 1, \pm 2, \ldots}\end{массив}\]
Итак, это все критические точки. Нам нужно определить те, которые попадают в интервал \(\left[ {0,4} \right]\). Нам нечего делать, кроме как подставлять некоторые \(n\) в формулы, пока мы не получим их все.
\(n = 0\) :
\[t = 0,6047\hspace{1,0 дюйма} t = 0,9661\]
Нам понадобятся обе эти критические точки.

\(n = 1\)
\[t = 0,6047 + \ frac {\ pi} {2} = 2,1755 \ hspace {1,0 дюйм} t = 0,9661 + \ frac {\ pi} {2} = 2,5369 \]
Нам это понадобится.
\(n = 2\)
\[t = 0,6047 + \pi = 3,7463\hspace{1,0 дюйма} t = 0,9661 + \пи = 4,1077\]
В данном случае нам нужен только первый, так как второй находится вне интервала.
В интервале есть пять критических точек. Они есть,
\[0,6047,\,\,\,0,9661,\,\,\,2,1755,\,\,\,2,5369,\,\,\,3,7463\]
Наконец, чтобы определить абсолютный минимум и максимум населения, нам нужно только подставить эти значения в функцию, а также две конечные точки. Вот оценки функций.
\[\begin{align*}P\left( 0 \right) & = 100.
 0\hspace{1.0in} & P\left( 4 \right) & = 111.7121\\
P\left( {0,6047} \right) & = 102,4756\hspace{1,0in} & P\left( {0,9661} \right) & = 102,2368\\
P\left( {2,1755} \right) & = 107,1880\hspace{1.0in} & P\left( {2,5369} \right) & = 106,9492\\
P\влево({3,7463}\вправо) & = 111,9004 & & \end{выравнивание*}\]
0\hspace{1.0in} & P\left( 4 \right) & = 111.7121\\
P\left( {0,6047} \right) & = 102,4756\hspace{1,0in} & P\left( {0,9661} \right) & = 102,2368\\
P\left( {2,1755} \right) & = 107,1880\hspace{1.0in} & P\left( {2,5369} \right) & = 106,9492\\
P\влево({3,7463}\вправо) & = 111,9004 & & \end{выравнивание*}\]Из этих оценок видно, что минимальная численность населения составляет 100 000 (помните, что \(P\) выражается в тысячах…), что происходит при \(t = 0\), а максимальная численность населения составляет 111 900, что происходит при \(t = 3,7463). \).
Убедитесь, что вы можете правильно решать триггерные уравнения. Если бы мы забыли \(2\pi n\), мы бы пропустили три последние критические точки в интервале и, следовательно, получили бы неправильный ответ, поскольку максимальная популяция была в последней критической точке. 92}}}{8}}}\]
Определить минимальную и максимальную сумму денег на счете в течение первых 10 лет его открытия.

Показать решение
Здесь мы действительно запрашиваем абсолютные экстремумы \(A\left( t \right)\) на интервале \(\left[ {0,10} \right]\). Как и в предыдущих примерах, эта функция везде непрерывна, и мы знаем, что это можно сделать.
Сначала нам понадобится производная, чтобы мы могли найти критические точки. 92} = 4\hspace{0,5 дюйма} \Стрелка вправо \hspace{0,25 дюйма}\,\,\,\,t = \pm 2\]
У нас есть две критические точки, однако только \(t = 2\) на самом деле находится в интервале, поэтому мы будем использовать только эту критическую точку.
Теперь оценим функцию в единственной критической точке и в конечных точках интервала. Вот эти оценки функций.
\[A\влево( 0 \вправо) = 2000\hspace{0,5 дюйма}A\влево( 2 \вправо) = 1990,66\hspace{0,5 дюйма}A\влево({10}\вправо) = 1999,94\]
Таким образом, максимальная сумма на счете будет равна 2000 долларов США, что произойдет в \(t = 0\), а минимальная сумма на счете будет равна 199,66 долларов США, что произойдет на отметке 2 года.
 {\frac{2}{3}}}\hspace{0,5in}{\mbox{on}}\ hspace{0.5in}\left[ { — 5,\, — 1} \right]\]
9{\ гидроразрыва {1} {3}}}}} \ конец {выравнивание *} \]
{\frac{2}{3}}}\hspace{0,5in}{\mbox{on}}\ hspace{0.5in}\left[ { — 5,\, — 1} \right]\]
9{\ гидроразрыва {1} {3}}}}} \ конец {выравнивание *} \]Итак, похоже, у нас есть две критические точки.
\[\begin{align*}y & = — 4\hspace{0.5in} & & {\mbox{Поскольку производная здесь не существует.}}\\ y & = — \frac{{12}}{ 5} \hspace{0.5in} & & {\mbox{Потому что здесь производная равна нулю.}}\end{align*}\]
Оба они находятся в интервале, поэтому давайте оценим функцию в этих точках и в конечных точках интервала.
\[\begin{align*}Q\left( { — 4} \right) & = 0 & \hspace{0.5in} & & Q\left( { — \frac{{12}}{5}} \right ) & = — 9.849\\ Q\left( { — 5} \right) & = — 15 & \hspace{0.5in} & & Q\left( { — 1} \right) & = — 6.241\end{align *}\]
Функция имеет абсолютный нулевой максимум в точке \(y = — 4\), а абсолютный минимум функции будет равен -15 в точке \(y = — 5\).

Итак, если бы мы проигнорировали или забыли о критической точке, в которой производная не существует (\(y = — 4\)) мы бы не получили правильного ответа.
В этом разделе мы увидели, как можно использовать производную для определения абсолютных экстремумов функции. Это важное применение деривативов, которое время от времени будет возникать, поэтому не забывайте об этом.
Обзор исчисления AP: поиск абсолютных экстремумов — Блог Magoosh
Шон Олт, , 3 марта 2017 г., , AP
Абсолютные экстремумы функции — это наибольшее и наименьшее значения функции. Какова наибольшая прибыль, которую может получить компания? Какое минимальное количество забора необходимо для ограждения сада? Как только вы узнаете, как найти абсолютные экстремумы функции, вы сможете ответить на эти и многие другие вопросы!
Обзор: что такое абсолютные экстремумы?
абсолютных экстремумов функции f в заданном наборе доменов D являются абсолютным максимумом и абсолютным минимумом значений f ( x ), поскольку x находится в пределах D .

Другими словами, мы говорим, что M является абсолютным максимумом, если M = f ( c ) для некоторых c в D и f ( x ) ≤ M для всех остальных x в D .
Мы определяем абсолютный минимум м почти таким же образом, за исключением того, что f ( x ) ≥ м для всех x в D .
Функции с разрывом
Иногда функция может не иметь абсолютного минимума или максимума в заданном наборе доменов. Это часто происходит, когда функция имеет разрыв.
Эта функция не работает на указанном интервале. Он имеет абсолютное минимальное значение, 0, но не имеет абсолютного максимума.
Наборы доменов и экстремумы
Даже если функция непрерывна на множестве областей D , экстремумов может не быть, если D не является замкнутым или ограниченным .

Например, функция параболы f ( x ) = x 2 не имеет абсолютного максимума на множестве доменов (-∞, ∞). Это связано с тем, что значения x 2 продолжают увеличиваться и увеличиваться без ограничений, поскольку x → ∞. Кстати, у этой функции есть абсолютное минимальное значение на интервале: 0,
.Однако проблемы могут возникать даже в ограниченном наборе доменов. Приведенная ниже функция не имеет ни абсолютного минимума, ни максимума, потому что конечные точки интервала не находятся в ее области определения. Обратите внимание, что незакрашенные кружки на графике означают, что эти точки отсутствуют, поэтому экстремумов в этих точках быть не может.
Этот график определяется на открытом интервале (-4, 4). Абсолютных экстремумов нет.
Теорема об экстремальных значениях
На практике мы обычно требуем, чтобы D был замкнутым интервалом формы [ a , b ] для некоторых констант a < b .
 В этом случае теорема об экстремальных значениях гарантирует, что оба абсолютных экстремума должны существовать.
В этом случае теорема об экстремальных значениях гарантирует, что оба абсолютных экстремума должны существовать.- Теорема об экстремальном значении (EVT) Если функция f непрерывна на замкнутом ограниченном интервале [ a , b ], то f достигает обоих абсолютных экстремумов на этом интервале.
Будьте осторожны: EVT работает только в одном направлении. Если функция непрерывна на замкнутом ограниченном интервале, то она должна иметь абсолютные экстремумы на этом интервале. Однако функция может не соответствовать условиям EVT и по-прежнему иметь абсолютный максимум и/или минимум.
. Нахождение абсолютных экстремумов 90 198
В случае, если f непрерывно на [ a , b ], тогда следующая процедура найдет абсолютные экстремумы.
Метод закрытого интервала
Метод требует вычисления производной. Если вам нужно освежить свои знания, ознакомьтесь с этим обзором Calculus Review: Derivative Rules.

- Найдите все критические числа f в интервале [ a , b ]. То есть поставить f ‘(x) = 0, найдите x и рассмотрите только те решения x , которые удовлетворяют a ≤ x ≤ b .
- Подставьте каждое критическое число из шага 1 в функцию f ( x ).
- Вставьте конечные точки a и b в функцию f ( x ).
- Наибольшее значение является абсолютным максимумом, а наименьшее значение — абсолютным минимумом.
Пример
Найдем абсолютные экстремумы f ( x ) = x 3 – 12 x + 23 на интервале [-5, 3].
Поскольку f непрерывно на [-5, 3], что является закрытым и ограниченным интервалом, EVT гарантирует, что на данном интервале должны существовать как абсолютный максимум, так и минимум. Кроме того, мы можем использовать метод закрытого интервала, чтобы найти их.

Шаг 1: Сначала найдите критические числа.
f ‘(х) = 3 х 2 – 12 = 3( х 2 – 4) = 3( х – 2)( 90 10 х 04)
Установив 3( x – 2)( x + 2) = 0, мы находим два критических числа: -2 и 2, оба из которых находятся в заданном интервале.
Этапы 2 и 3: Я обычно комбинирую эти этапы в своей работе. Создайте таблицу значений x слева, включая критические числа и конечные точки интервала. Затем в правой колонке вставьте каждый в ф ( х ).
х f ( х ) = х 3 — 12 х
974 + 333 233-5 -42 Мин. -2 39 Макс. 2 7 3 14 Абсолютное максимальное значение 39(при х = -2), а абсолютный минимум -42 (при х = -5).

Глядя на график f , вы можете проверить максимальное и минимальное значения.
Резюме
- Абсолютные экстремумы функции на заданном наборе доменов D — это наибольшее и наименьшее значения функции на D .
- Теорема об экстремальных значениях гарантирует, что непрерывная функция должна иметь абсолютные экстремумы на ограниченном замкнутом интервале.
- Вы можете использовать метод закрытого интервала для обнаружения абсолютных экстремумов.
Теперь, когда вы знаете больше об абсолютных экстремумах, вы можете максимизировать свой результат на экзаменах AP по математическому анализу!
Гарантированно улучшите свой результат SAT или ACT. Начните свою 1-недельную бесплатную пробную версию Magoosh SAT Prep или 1-недельную бесплатную пробную версию Magoosh ACT Prep сегодня!
Автор
Кстати, Magoosh может помочь вам подготовиться к экзаменам SAT и ACT.
 Нажмите сюда, чтобы узнать больше!
Нажмите сюда, чтобы узнать больше!Расчет AP
← Предыдущий
Следующий →
Мы настоятельно рекомендуем учащимся помогать друг другу и отвечать на комментарии других учащихся, если это возможно!
Если вы являетесь студентом Premium Magoosh и хотели бы более персонализированного обслуживания от наших инструкторов, вы можете использовать вкладку «Справка» на панели управления Magoosh. Спасибо!
Относительный экстремум — Расчет 1
Все ресурсы расчета 1
10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Учитесь по концепции
Исчисление 1 Помощь » Функции » Графические функции » Интервалы » Относительный экстремум
Дано
Найдите -координату относительного максимума на интервале.
Возможные ответы:
Невозможно определить
Правильный ответ:
44 Объяснение:
Чтобы найти относительные максимумы, нам нужно найти, где наша первая производная меняет знак.
 Для этого найдите свою первую производную, а затем найдите, где она равна нулю.
Для этого найдите свою первую производную, а затем найдите, где она равна нулю.Начните с:
в
Это означает, что у нас есть экстремумы при x=0 и x=-8/3
Поскольку нас интересует только интервал от -5 до 0, мы необходимо проверить точки на этом интервале. Попробуйте точки между двумя нашими экстремумами, а также одну между -8/3 и -5.
Итак, наша первая производная переходит от отрицательной к положительной при -8/3, таким образом, это координата x нашего относительного максимума на этом интервале.
Сообщить об ошибке
Где находится максимальное значение функции
на интервале ?
Возможные ответы:
Правильный ответ:
Объяснение:
Несмотря на то, что существуют относительные максимумы в точках и (находятся путем приравнивания первой производной функции к нулю и решения для x.
 ), максимальное значение на всем интервале фактически находится в верхней конечной точке, когда . При поиске экстремумов вдоль интервала поиск нулей первой производной не учитывает экстремумы конечных точек.
), максимальное значение на всем интервале фактически находится в верхней конечной точке, когда . При поиске экстремумов вдоль интервала поиск нулей первой производной не учитывает экстремумы конечных точек.Сообщить об ошибке
Определить относительные максимумы функции:
Возможные ответы:
Правильный ответ:
4 Пояснение:
Чтобы определить относительные максимумы функции, мы должны определить, где первая производная функции меняется с положительной на отрицательную.
Первая производная функции
была найдена по следующему правилу:
Далее мы должны найти критические точки, значения, при которых первая производная равна нулю: первая производная:
Чтобы проверить знак первой производной, подставьте любое значение на каждом интервале в функцию первой производной.
 На первом интервале первая производная положительна, на втором – отрицательна, на третьем – положительна. Первая производная изменяется с положительной на отрицательную при , поэтому здесь существует относительный максимум.
На первом интервале первая производная положительна, на втором – отрицательна, на третьем – положительна. Первая производная изменяется с положительной на отрицательную при , поэтому здесь существует относительный максимум.Сообщить об ошибке
Найдите локальный максимум
, используя уравнение и/или следующий график.
Возможные ответы:
Правильный ответ:
Объяснение:
Заметим, что эта функция имеет 2 экстремума, которые расположены в и . Мы могли бы также найти это, взглянув на саму функцию:
.
Мы знаем, что экстремумы существуют, когда наклон функции равен нулю, поэтому мы берем производную, приравниваем ее к нулю, а затем находим x.
Производная следующая:
.
Поэтому приравнивая обе части к нулю, мы видим следующее:
и .

Чтобы выяснить, дает ли одно из этих значений x локальное минимальное или максимальное значение, требуется либо проверка первой производной, либо проверка второй производной, либо анализ графика. Мы видим, что для небольшой окрестности вокруг является наибольшим членом, следовательно, это локальный максимум. Точно так же для небольшой окрестности вокруг наименьший член, следовательно, это локальный минимум.
Следовательно, когда является единственным местом, в котором возникает локальный максимум. Помните, что не значение x должно быть самым большим, а соответствующее значение y.
Сообщить об ошибке
Ниже приведен список значений в определенных точках для непрерывной . По теореме о среднем значении сколько нулей должно быть у этой функции?
Возможные ответы:
Точно 1
Максимум 2
Минимум 2
Не менее 1
Ровно 2
Правильный ответ:
Не менее 2
Объяснение:
Теорема о среднем значении утверждает, что если непрерывное имеет , то для всех должно быть , которое отображается в , поэтому, поскольку указанное выше значение переходит от отрицательного к положительному дважды, ноль должен быть отображен как минимум дважды.

Сообщить об ошибке
Относительный минимум функции — это все точки x в области определения функции, такие, что это наименьшее значение для некоторой окрестности. Это точки, в которых первая производная равна 0 или не существует.
Найдите относительный минимум функции
, используя следующий график и функцию.
Возможные ответы:
Правильный ответ:
Объяснение:
Заметим, что эта функция имеет 2 экстремума, расположенных в точках x=-1 и x=0. Мы могли бы также найти это, взглянув на саму функцию:
.
Мы знаем, что экстремумы существуют, когда наклон функции равен нулю, поэтому мы берем производную, приравниваем ее к нулю, а затем находим x.
Производная следующая:
.
Поэтому приравнивая обе части к нулю, мы видим следующее:
и .


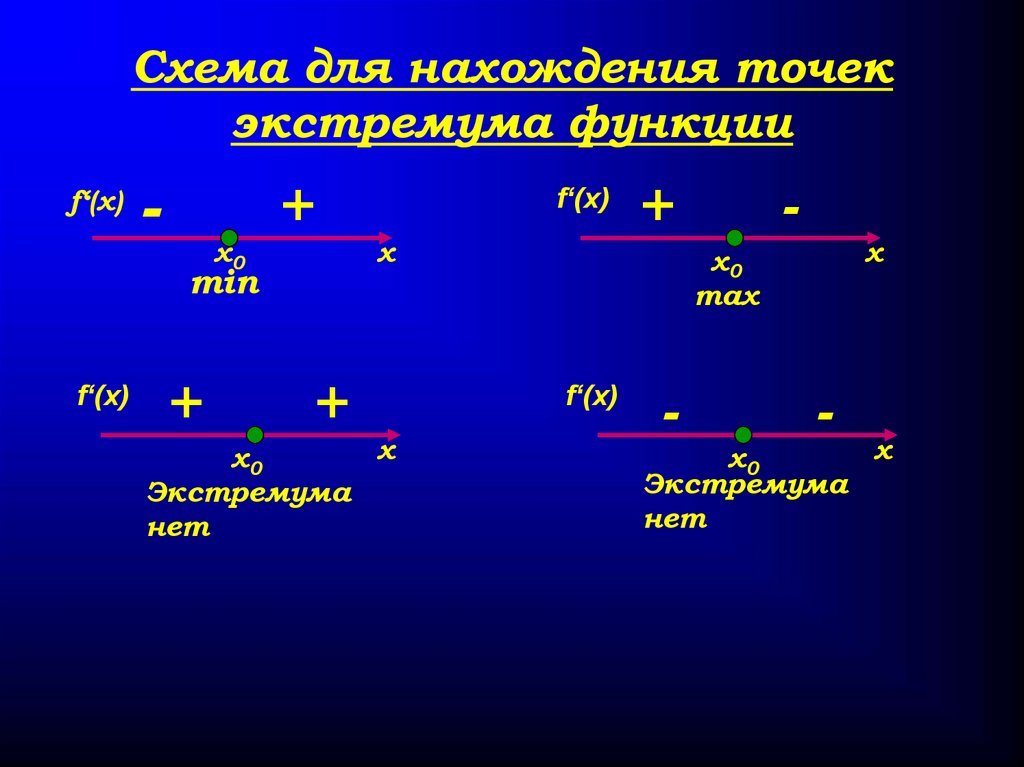
 Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.
Если же при переходе через x0
слева направо производная меняет знак с минуса на плюс, то функция имеет в этой
точке минимум.




 2-4=0\)
2-4=0\)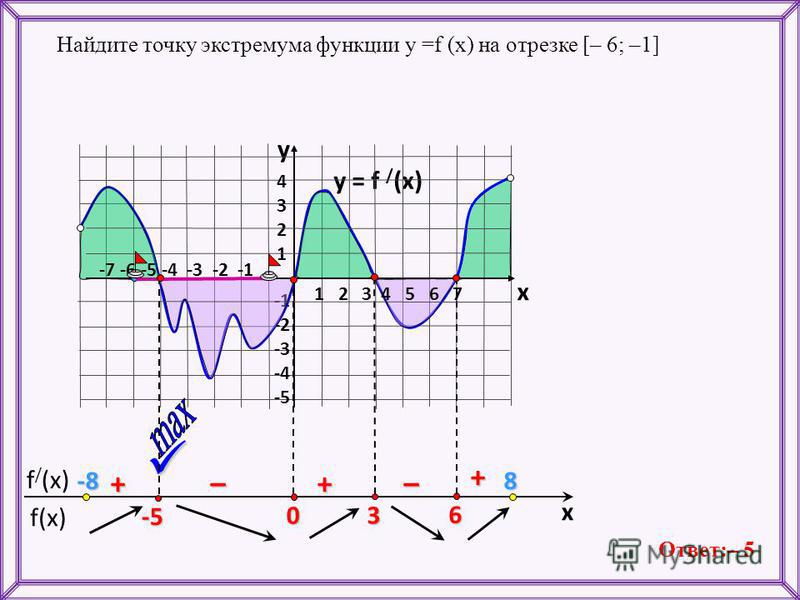
 Так как при переходе через точку производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку производная меняет знак минус на плюс, поэтому в точке у функции минимум. Вычислив значения функции в точках и найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.
Так как при переходе через точку производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку производная меняет знак минус на плюс, поэтому в точке у функции минимум. Вычислив значения функции в точках и найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13. При значит, в точке функция S имеет максимум. Значение функции
При значит, в точке функция S имеет максимум. Значение функции
 Это — необходимое условие существования экстремума.
Это — необходимое условие существования экстремума. При переходе через точку производная меняет знак с поэтому — точка минимума (рис. 82).
При переходе через точку производная меняет знак с поэтому — точка минимума (рис. 82). Функция непериодическая.
Функция непериодическая. Функция возрастает на поэтому не может иметь экстремумов.
Функция возрастает на поэтому не может иметь экстремумов. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Это, конечно, хорошо. Мы не хотим пытаться найти то, чего может и не быть.
Это, конечно, хорошо. Мы не хотим пытаться найти то, чего может и не быть.
 2} + 6t — 12 = 6\left( {t + 2} \right)\left( {t — 1} \right)\]
2} + 6t — 12 = 6\left( {t + 2} \right)\left( {t — 1} \right)\]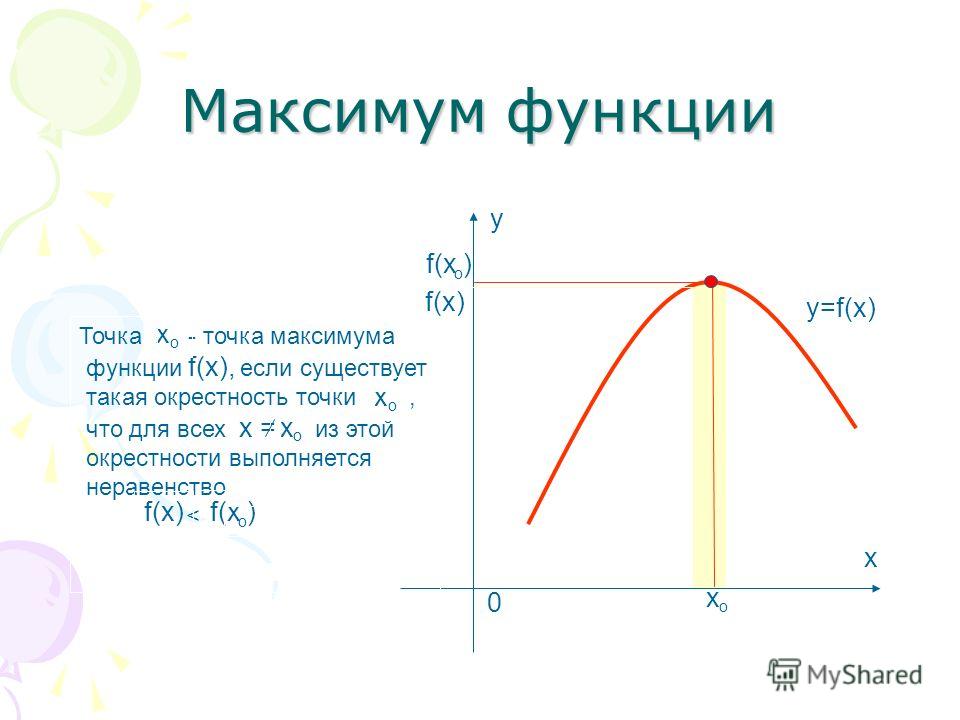 Итак, из этого списка мы видим, что абсолютный максимум \(g\left( t \right)\) равен 24, и он приходится на \(t = — 2\) (критическая точка) и абсолютный минимум \( g\left( t \right)\) равно -28, что происходит в \(t = — 4\) (конечная точка). 92} — 12t + 4\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ {0,2} \right]\]
Итак, из этого списка мы видим, что абсолютный максимум \(g\left( t \right)\) равен 24, и он приходится на \(t = — 2\) (критическая точка) и абсолютный минимум \( g\left( t \right)\) равно -28, что происходит в \(t = — 4\) (конечная точка). 92} — 12t + 4\hspace{0.25in}{\mbox{on}}\hspace{0.25in}\left[ {0,2} \right]\]

 0\hspace{1.0in} & P\left( 4 \right) & = 111.7121\\
P\left( {0,6047} \right) & = 102,4756\hspace{1,0in} & P\left( {0,9661} \right) & = 102,2368\\
P\left( {2,1755} \right) & = 107,1880\hspace{1.0in} & P\left( {2,5369} \right) & = 106,9492\\
P\влево({3,7463}\вправо) & = 111,9004 & & \end{выравнивание*}\]
0\hspace{1.0in} & P\left( 4 \right) & = 111.7121\\
P\left( {0,6047} \right) & = 102,4756\hspace{1,0in} & P\left( {0,9661} \right) & = 102,2368\\
P\left( {2,1755} \right) & = 107,1880\hspace{1.0in} & P\left( {2,5369} \right) & = 106,9492\\
P\влево({3,7463}\вправо) & = 111,9004 & & \end{выравнивание*}\]
 {\frac{2}{3}}}\hspace{0,5in}{\mbox{on}}\ hspace{0.5in}\left[ { — 5,\, — 1} \right]\]
9{\ гидроразрыва {1} {3}}}}} \ конец {выравнивание *} \]
{\frac{2}{3}}}\hspace{0,5in}{\mbox{on}}\ hspace{0.5in}\left[ { — 5,\, — 1} \right]\]
9{\ гидроразрыва {1} {3}}}}} \ конец {выравнивание *} \]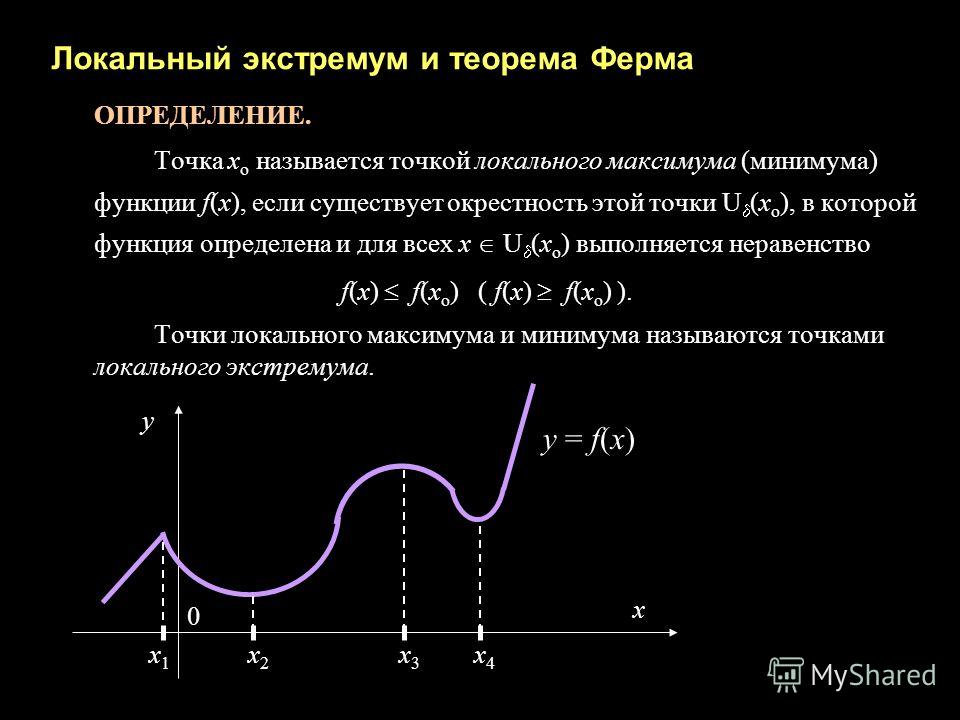
 В этом случае теорема об экстремальных значениях гарантирует, что оба абсолютных экстремума должны существовать.
В этом случае теорема об экстремальных значениях гарантирует, что оба абсолютных экстремума должны существовать.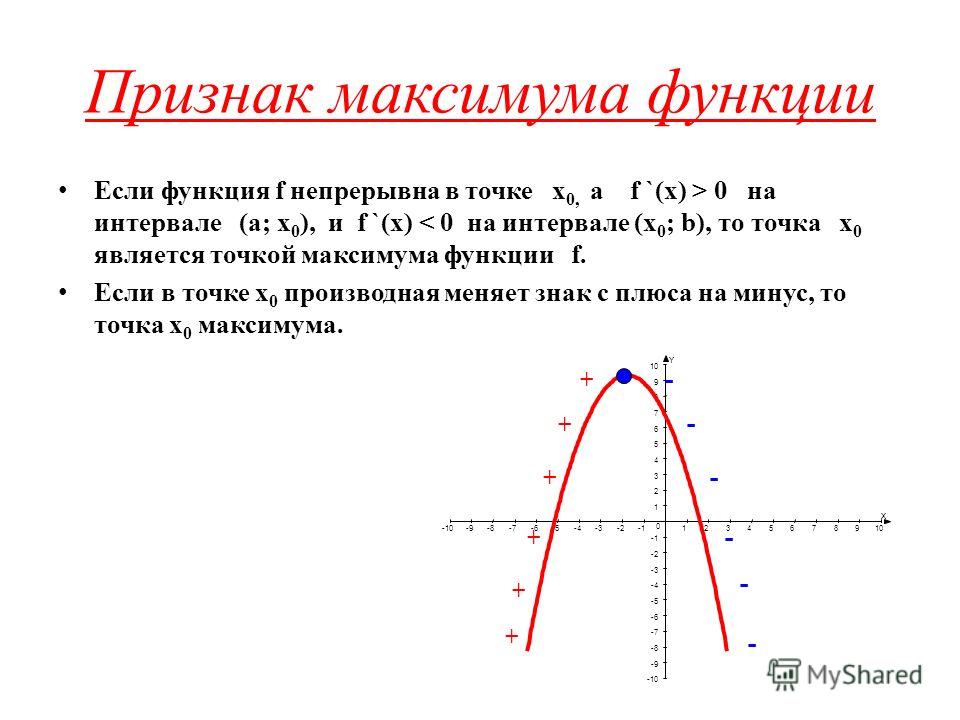


 Нажмите сюда, чтобы узнать больше!
Нажмите сюда, чтобы узнать больше!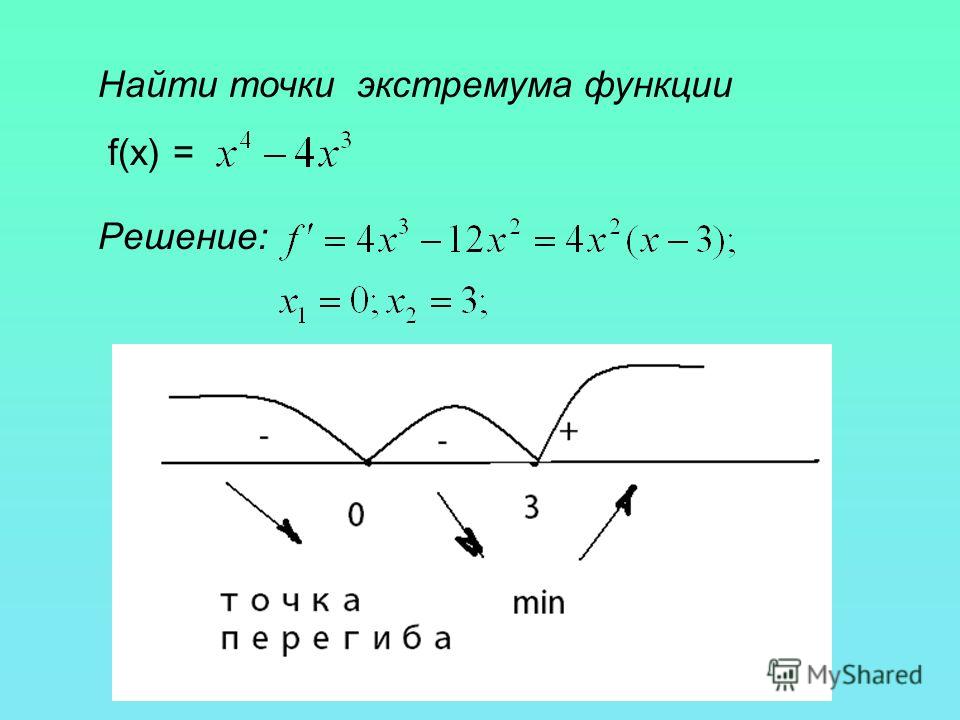 Для этого найдите свою первую производную, а затем найдите, где она равна нулю.
Для этого найдите свою первую производную, а затем найдите, где она равна нулю. ), максимальное значение на всем интервале фактически находится в верхней конечной точке, когда . При поиске экстремумов вдоль интервала поиск нулей первой производной не учитывает экстремумы конечных точек.
), максимальное значение на всем интервале фактически находится в верхней конечной точке, когда . При поиске экстремумов вдоль интервала поиск нулей первой производной не учитывает экстремумы конечных точек. На первом интервале первая производная положительна, на втором – отрицательна, на третьем – положительна. Первая производная изменяется с положительной на отрицательную при , поэтому здесь существует относительный максимум.
На первом интервале первая производная положительна, на втором – отрицательна, на третьем – положительна. Первая производная изменяется с положительной на отрицательную при , поэтому здесь существует относительный максимум.