Рациональные числа: определение, сравнение, арифметические действия
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Что такое рациональные числа
В данной публикации мы рассмотрим, что такое рациональные числа, как их сравнивать между собой, а также какие арифметические действия с ними можно выполнить (сложение, вычитание, умножение, деление и возведение в степень). Теоретические материал сопроводим практическими примерами для лучшего понимания.
- Определение рационального числа
- Арифметические действия с рациональными числами
- Сложение
- Вычитание
- Умножение
- Деление
- Возведение в степень
Определение рационального числа
Рациональным называется число, которой можно представить в виде обыкновенной (простой) дроби. Множество рациональных чисел имеет специальное обозначение – Q.
Правила сравнения рациональных чисел:
- Любое положительное рациональное число больше нуля. Обозначается “больше” специальным знаком “>“.
Например: 5>0, 12>0, 144>0, 2098>0 и т.д. - Любое отрицательное рациональное число меньше нуля. Обозначается “меньше” символом “<“.
Например: -3<0, -22<0, -164<0, -3042<0 и т.д. - Из двух положительных рациональных чисел больше то, у которого больше абсолютная величина.
Например: 10>4, 132>26, 1216<1516 и т.д. - Из двух отрицательных рациональных чисел большим является то, у которого меньше абсолютная величина.
Например: -3>-20, -14>-202, -54<-10 и т.д.
Арифметические действия с рациональными числами
Сложение
1. Чтобы найти сумму рациональных чисел с одинаковыми знаками, просто складываем их модули, затем перед получившимся результатом ставим их знак.
Например:
- 5 + 2 = + (5 + 2) = +7 = 7
- 13 + 8 + 4 = + (13 + 8 + 4) = +25 = 25
- -9 + (-11) = – (9 + 11) = -20
- -14 + (-53) + (-3) = – (14 + 53 + 3) = -70
Примечание: Если перед числом не стоит знак, то подразумевается “+“, т.е. оно является положительным. Также в полученном результате “плюс” можно опускать.
2. Для того, чтобы найти сумму рациональных чисел с разными знаками, мы к числу с большим модулем прибавляем те, у которых знак совпадает с ним, и отнимаем числа с противоположными знаками (величины берем абсолютные). Затем перед результатом ставим знак числа, из которого мы всё вычитали.
Например:
- -6 + 4 = – (6 – 4) = -2
- 15 + (-11) = + (15 – 11) = +4 = 4
- -21 + 15 + 2 + (-4) = – (21 + 4 – 15 – 2) = -8
- 17 + (-6) + 10 + (-2) = + (17 + 10 – 6 – 2) = 19
Вычитание
Для нахождения разности двух рациональных чисел к уменьшаемому прибавляем противоположное вычитаемому число.
Например:
- 9 – 4 = 9 + (-4) = 5
- 3 – 7 = 3 + (-7) = – (7 – 3) = -4
Если вычитаемых несколько, то сначала складываем все положительные числа, затем – все отрицательные (в т.ч. уменьшаемое). Таким образом мы получим два рациональных числа, разность которых находим по алгоритму выше.
Например:
- 12 – 5 – 3 = 12 – (5 + 3) = 4
- 22 – 16 – 9 = 22 – (16 + 9) = 22 – 25 = – (25 – 22) = -3
Умножение
Для нахождения произведения двух рациональных чисел просто перемножаем их модули, затем перед получившимся результатом ставим:
- знак “+“, если у обоих сомножителей один и тот же знак;
- знак “–“, если сомножители имеют разные знаки.
Например:
- 3 · 7 = 21
- -15 · 4 = -60
Когда сомножителей больше двух, то:
- Если все числа положительные – то результат будет со знаком “плюс”.
- Если есть как положительные, так и отрицательные числа, то считаем количество последних:
- четное количество – результат с “плюсом”;
- нечетное количество – результат с “минусом”.

Например:
- 5 · (-4) · 3 · (-8) = 480
- 15 · (-1) · (-3) · (-10) · 12 = -5400
Деление
Как и в случае с умножением, выполняем действие с модулями чисел, затем ставим соответствующий знак с учетом правил, описанных в пункте выше.
Например:
- 12 : 4 = 3
- 48 : (-6) = -8
- 50 : (-2) : (-5) = 5
- 128 : (-4) : (-8) : (-1) = -4
Возведение в степень
Возведение рационального числа a в степень n – это то же самое, что и умножить это число само на себя n-ое количество раз. Пишется как a n.
При этом:
- Любая степень положительного числа в результате дает положительное число.
- Четная степень отрицательного числа положительна, нечетная – отрицательна.
Например:
- 26 = 2 · 2 · 2 · 2 · 2 · 2 = 64
- -34 = (-3) · (-3) · (-3) · (-3) = 81
- -63 = (-6) · (-6) · (-6) = -216
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Рациональные числа.
 8-й класс
8-й класс
Цели урока:
Создать условия, при которых ученик:
- расширит представления учащихся о числе, сформирует понятие «рациональное число»;
- систематизирует знания о числовых множествах;
- познакомится с историей возникновения числовых множеств;
- приобретет навыки перевода рациональных чисел вида, а/n, где а — целое число, а n — натуральное в десятичную (конечную или бесконечную) дробь;
- приобретет навыки перевода бесконечных десятичных периодических дробей в рациональные числа вида а/n, где а — целое число, а n — натуральное;
- выявит различные способы перевода бесконечной десятичной периодической дроби в обыкновенную дробь;
- приобретет умения работать в парах,
- разовьет навыки самостоятельной работы, умения
анализировать, сравнивать.

В результате ученик:
- знает, как определить вид числа;
- умеет представлять десятичную дробь в виде дроби a/n, где а — целое число, а n — натуральное;
- умеет представлять рациональное число в виде конечной или бесконечной периодической дроби;
- умеет представлять бесконечную периодическую дробь в виде обыкновенной дроби;
- умеет правильно пользоваться математической символикой в процессе выполнения заданий.
Оборудование к уроку: проектор, компьютер, тетрадь с печатной основой (приложение1), презентация.
Ход урока
I. Мотивационно — ориентировочный этап.
-Проверим домашнее задание (слайд 2),которое поможет нам определить тему урока.
Домашнее задание после
предыдущего урока. Выполните вычисления: |
|
| Naturalis: ( 2) | Quotient: = () |
| Ratio: = () | Zahl: (-1)7+(-1)8= (0) |
Заполните пропуски в тетради с печатной основой (приложение, слайд 3)
Для счета предметов используются числа, которые называются натуральными. Для обозначения множества натуральных чисел употребляется буква : — первая буква латинского слова
 ) Название этого
множества происходит также от латинского слова : , что также
переводится как «отношение»
) Название этого
множества происходит также от латинского слова : , что также
переводится как «отношение»-Спрогнозируйте тему урока. (Числовые множества)
— Известны ли вам те числовые множества, о которых идет речь в тексте. (Известны, их мы начали изучать в начальной школе, затем продолжили в 5,6 и 7 классах).
-Приведите примеры натуральных, целых и рациональных чисел.
-Вспомните отношения между множествами, назовите самое большое из них. (Множество рациональных чисел)
Уточним тему урока «Рациональные числа« (слайд 4) и запишем ее в тетрадь.
Спрогнозируйте цель урока: систематизировать знания о рациональных числах.
Краткая информация из истории развития числа сопровождается записями в тетради
:N — множество всех натуральных чисел, « n — натуральное число» ,
Z — множество всех целых чисел , » m — целое число» ,
Q — множество всех рациональных чисел, » r
— рациональное число».
Историческая справка (слайды 5-18).
Натуральные числа возникли в силу необходимости вести счет любых предметов.
Натуральные числа несут ещё другую функцию: характеристику порядка предметов, расположенных в ряд.
О натуральном в смысле естественном ряде чисел говорится во «Введении в арифметику» греческого математика (неопифагорийца) Никомаха из Геразы.
В современном смысле понятие и термин «Натуральное число» встречается у французского философа и математика Ж.Даламбера(1717-1783)
Сумма и произведение натуральных чисел есть число натуральное.
Дроби естественно возникли при решении задач о разделе имущества, измерении земельных участков, исчислении времени.
Сумма, произведение и частное дробных чисел есть число дробное.
Доли или единичные дроби, у которых числитель единица, знаменателем же может быть любое целое число;
Дроби систематические, у которых числителями могут быть любые числа, знаменателями же - только числа некоторого частного вида, например, степени десяти или шестидесяти;
Дроби общего вида, у которых числители и
знаменатели могут быть любыми числами.
Десятичные дроби в XV веке ввел самаркандский ученый ал — Каши. Ничего, не зная об открытии ал - Коши, десятичные дроби открыл второй раз, приблизительно через 150 лет, после него, фламандский ученый математик и инженер Симон Стевин в труде «Децималь» (1585 г).
Понятие отрицательных чисел возникло в практике решения алгебраических уравнений.
Отрицательные числа трактовались так же как долг при финансовых и бартерных расчетах.
Отрицательные числа ввели в математический обиход Михаэль Штифель (1487-1567) в книге «Полная арифметика» (1544), и Никола Шюке (1445-1500)- его работа была обнаружена в 1848 году.
Сумма, произведение и разность целых чисел есть число целое.
Отношения между множествами натуральных, целых и рациональных чисел наглядно демонстрирует геометрическая иллюстрация — круги Эйлера.
Леонард Эйлер жил в России в середине XVIII века и
внес большой вклад в развитие математики.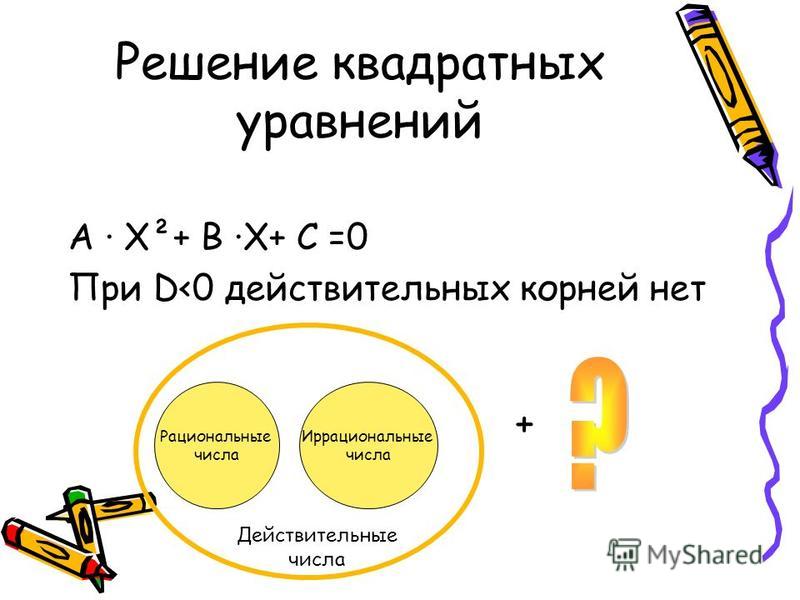
Операционно-исполнительский этап.
Задание 1. (выполняется самостоятельно с последующей проверкой) (слайд 19 — проверка по щелчку)
Вычислите значения числовых выражений и изобразите их на кругах Эйлера числа а, в, с, d, m , если
| а в с d m |
1 : 5+0,8 =_________________________________ (1) 0,6: 0,2- 22 =________________________________ (-1) 17:3 -5 = __________________________________(1/3) (-1) 3 +( -1)2 =_______________________________ (0) 13 :2 +0,5 = _________________________________ (7) Оставшуюся на диаграмме точку обозначьте буквой «к«. |
Задание 2 — интерактивный тест (слайд 20 -
триггер) устная работа.
Используя диаграмму, определите, какие из высказываний истинные, а какие ложные.
Нам уже известно, что любое рациональное число можно записать в виде отношения , где .
Выполните следующее задание:
Задание3 (работа в парах » сильный - слабый»)
Представьте в виде , где числа:
— 3; 2; 0; ; ; 0,23; -3,14
(; ; ; ; ; )
Вы также умеете записывать рациональные числа в виде десятичных дробей.
Задание 4 — интерактивный тест (слайд 21- триггер) устная работа.
Замените данные рациональные числа десятичными дробями.
| = (0,5) | = (0,2) | =(0,125) | = (0,(3)) |
| = (0,25) | = (0,4) | = (0,375) | =(0,6)) |
| =(0,75) | = (0,6) | =(0,625) | =(0,1(6)) |
Что замечаем? (Получились конечные и
бесконечные десятичные дроби. В записи дробной
части каждой бесконечной дроби повторяется одна
и та же группа цифр).
В записи дробной
части каждой бесконечной дроби повторяется одна
и та же группа цифр).
Как называем мы такие бесконечные десятичные дроби? (Бесконечные десятичные периодические дроби).
Вспомните, как коротко мы записывали такие дроби. (Мы выделяли повторяющуюся группу цифр и записывали ее в круглые скобки).
Как называют повторяющуюся группу цифр? (Периодом).
Итак, различные рациональные числа представили их в виде десятичных дробей (конечных или бесконечных). Какой можно сделать вывод? (Любое рациональное число можно представить в виде десятичной дроби (конечной или бесконечной).
Вспомните, как записываются и читаются бесконечные десятичные дроби, выполнив следующее задание.
Задание 5 (работа в парах) (слайд 22)
Прочитайте дроби.
1) 0,(2) 2) 2,(21) 3) 1,(1) 4) -3,0(3) 5) -0,0(6) 6) 12,45(7)
Иногда периодические дроби разделяют на
«чисто периодические», например.
Задание 6. Докажите, что равенства верны:
а) 0,222:= б) 0,8181:= в) 0,4666 :=
Каким способом мы это можем сделать?
Обыкновенную дробь представить в виде бесконечной десятичной периодической дроби, произведя деление числителя на знаменатель.
Сегодня мы рассмотрим два способа перевода десятичной периодической дроби в обыкновенную дробь (слайд 23, каждый шаг — по щелчку).
| Пусть х = 0,222:. 10 х = 2,222: 10х-х = 2,222:-0,222 9 х = 2 х = Значит, 0,222:= |
Сначала рассмотрим алгоритм перевода
чисто периодической дроби. Нужно умножить х
на такое число, чтобы запятая передвинулась
вправо ровно на один период. ( В периоде одна цифра, значит, надо умножить на 10). Вычтите из второго уравнение первое и найдите число х. |
По этому алгоритму проверьте второе равенство.
(Учащиеся записывают решение в тетради, один ученик выполняет задание у доски с комментариями)
Наводящий вопрос: на какое число нужно умножить бесконечную периодическую дробь, чтобы запятая передвинулась ровно на одну цифру.
В периоде две цифры, значит, надо умножить на 2.
х = 0,8181:
100 х = 81,8181:
100х—х = 81, 8181:-0,8181:
99 х = 81
х =
х = .
Значит, 0,8181:=
Запишем в виде обыкновенной дроби смешанную периодическую дробь 0,4666:
| х = 0,4666: 10х = 4,666: 100 х = 46,666: 100х -10 х = 46,666:-4,666. 90 х = 42 х = , значит, 0,4666:= |
Мы с вами изучили правило перевода
чистой периодической дроби в обыкновенную. Как
из смешанной периодической дроби получить
чистую периодическую дробь? Умножить на 10 k ,гдек — число цифр до периода. В нашем случае на 10. Далее ваши действия аналогичны примеру 1. (Выполняются самостоятельно с последующей проверкой) |
Существует еще одно правило перевода чисто периодических и смешанных дробей в обыкновенную дробь. Примем их без доказательства (слайд 25,26, каждый шаг — по щелчку).
Чтобы обратить чисто периодическую десятичную
дробь в обыкновенную, нужно в числителе
обыкновенной дроби поставить число,
образованное из цифр, стоящих в периоде, а в
знаменатель — написать цифру 9 столько раз,
сколько цифр в периоде.
Запишем дроби 0,222:и 0,8181: вторым способом
1) 0,222:= 2) 0,8181=
Чтобы обратить смешанную периодическую десятичную дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованное из цифр, стоящих после запятой до начала первого периода. Полученную разность взять в качестве числителя дроби; а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
1) 0,4(6) =
Какой способ позволяет быстрее достигнуть результата?
(Второй, но сформулировать правило достаточно сложно).
Задание 7 (взаимопроверка в парах) (слайд 27)
Представьте в виде обыкновенной дроби:
1) 1,(72) 2) 2,9(12) 3) 1,12(8)
Как представить данные десятичные дроби в виде обыкновенной дроби?
(Дробь нужно представить в виде суммы целого
числа и бесконечной периодической дроби,
бесконечную периодическую дробь перевести в
обыкновенную дробь по правилу, затем смешанную
дробь представить в виде , где.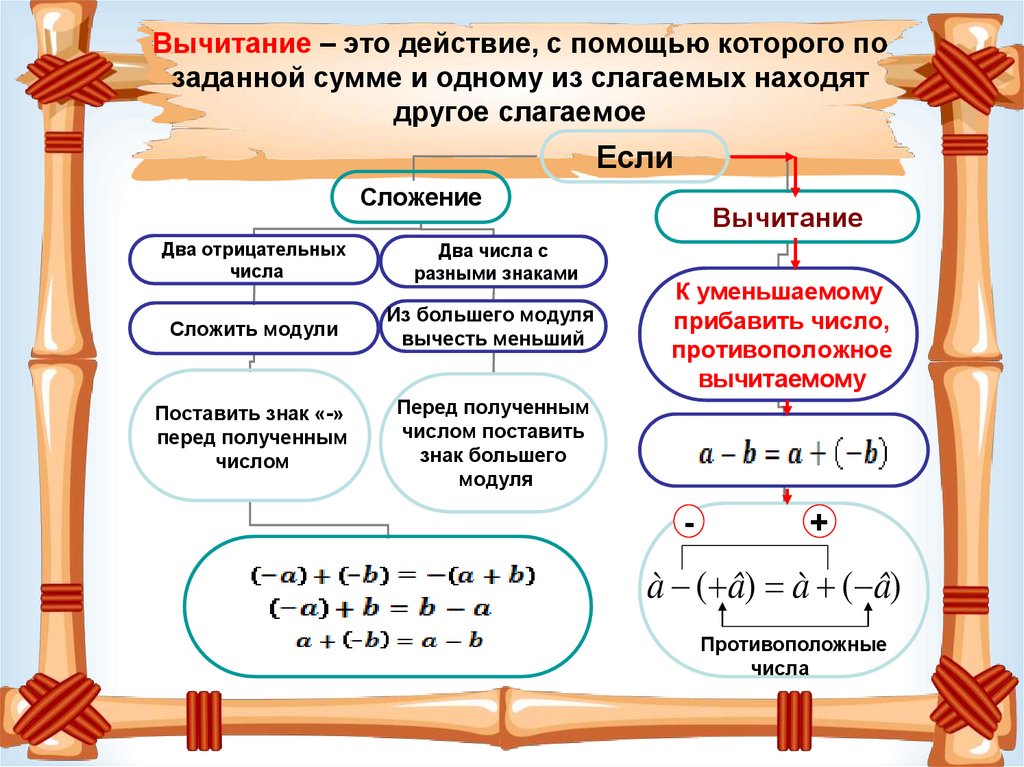 )
)
Рефлексивно-оценочный этап.
Итак, подведем итог нашего урока. Какова цель стояла перед нами в начале урока?
(Систематизировать знания о числовых множествах. Научиться переводить бесконечные периодические десятичные дроби в обыкновенные.)
Достигли ли мы этой цели?
(Цель наша достигнута. Мы знаем, что все числа объединены во множество рациональных чисел. На этом множестве выполняются все известные нам действия, кроме деления на ноль. Мы выделили свойства рациональных чисел: любое число может быть представлено в виде в виде дроби , где или в виде бесконечной периодической дроби. Научились переводить бесконечные периодические дроби в обыкновенные двумя способами, заметили, что второй способ трудно формулировать, но его применение ускорит получение результата).
Домашнее задание: по усмотрению учителя.
Графический диктант (проверка — слайд28).
1) 2011
2)
3) любое целое является рациональным.
4)
5)
6) любое целое число является натуральным.
7) любое рациональное число можно записать в виде конечной или бесконечной периодической дроби.
8) сумма, разность, произведение и частное (если делитель не ноль) рациональных чисел есть число рациональное.
9) (- 37,4 — 26,6) : (0,1) — натуральное.
10) Q -обозначение множества рациональных чисел.
Оценка настроения (слайд 29).
Рациональные числа — Справочник — 2022
Рациональные числа математика
Рациональные числа — это целые и дробные числа (обыкновенные дроби, конечные десятичные дроби и бесконечные периодические дроби).
Есть версия, что название рациональных чисел связано с латинским словом
«ratio» — разум.
Запомните!
Бесконечные непериодические дроби НЕ входят в множество рациональных чисел.
Поэтому число «Пи» (π = 3,14. ) , основание натурального логарифма
E (e = 2,718..) или √ 2 НЕ являются рациональными числами.
Примеры рациональных чисел:
Множество рациональных чисел обозначается заглавной английской буквой « Q » (кью).
Множество « Q » включает в себя множество целых чисел « Z » и натуральных чисел « N ».
Бесконечные непериодические дроби НЕ входят в множество рациональных чисел.
Math-prosto. ru
06.08.2018 10:40:42
2018-08-06 10:40:42
Источники:
Https://math-prosto. ru/ru/pages/rational/rational/
Какие числа называются Рациональными? Примеры и Определение » /> » /> .keyword { color: red; }
Рациональные числа математика
В переводе с латыни слово «рациональный» значит число, расчёт, нумерация, рассуждение, разум. Давайте узнаем, что значит рациональное число и перечислим его свойства.
О чем эта статья:
6 класс, 8 класс
Определение рациональных чисел
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.
Если число можно получить делением двух целых чисел, то это число рациональное.
Рациональные числа — это те, которые можно представить в виде
Где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
- десятичная дробь 1,15 — это 115/100; десятичная дробь 0,5 — это 1/2; целое число 0 — это 0/1; целое число 6 — это 6/1; целое число 1 — это 1/1; бесконечная периодическая дробь 0,33333. — это 1/3; смешанное число — это 25/10; отрицательная десятичная дробь -3,16 — это -316/100.
Свойства рациональных чисел
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
- Переместительное свойство сложения: a + b = b + a.
 Сочетательное свойство сложения: (a + b) +c = a + (b + c). Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a. У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0. Переместительное свойство умножения: ab = ba. Сочетательное свойство умножения: (a * b) * c = a * (b * c). Произведение рационального числа и едины не изменяет это число: a * 1 = a. У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1. Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.
Сочетательное свойство сложения: (a + b) +c = a + (b + c). Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a. У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0. Переместительное свойство умножения: ab = ba. Сочетательное свойство умножения: (a * b) * c = a * (b * c). Произведение рационального числа и едины не изменяет это число: a * 1 = a. У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1. Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.Кроме основных перечисленных есть еще ряд свойств:
Правило умножения рациональных чисел с разными знаками: (-a) * b = — ab. Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».
Правило умножения отрицательных рациональных чисел: (−a) * (−b) = ab. Запомнить поможет фраза: «минус на минус есть плюс».
Правило умножении произвольного рационального числа на нуль: a * 0 = 0 или 0 * a = 0. Докажем это свойство.
Докажем это свойство.
Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).
Распределительный закон позволяет переписать выражение:
A * d + a * (−d), а так как a * (−d) = — ad, то a * d + a * (-d) = a * d + (-ad).
Мы перечислили только свойства сложения и умножения. На множестве рациональных чисел вычитание и деление можно записать, как обратные к сложению и умножению. То есть, разность (a — b) можно записать, как сумму a + (-b), а частное a/b равно произведению a * b−1, при b ≠ 0.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Определение иррационального числа
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
- π = 3,1415926. √2 = 1,41421356. e = 2,71828182… √8 = 2.828427. -√11= -3.31662…
Обозначение множества иррациональных чисел: латинская буква I.
Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел:
- результат суммы иррационального числа и рационального равен иррациональному числу; результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу; результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному; результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).
Различие между целыми, натуральными и рациональными числами
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.
А вот, что точно не является натуральным числом:
- Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль. Отрицательные числа: -1, -2, -3, -4. Дроби: 1/2, 3/4, 5/6.
Целые числа — это натуральные числа, противоположные им и нуль.
Если два числа отличаются друг от друга знаком — их называют противоположными: +2 и -2, +7 и -7. Знак «плюс» обычно не пишут, и если перед числом нет никакого знака, значит оно положительное. Числа, перед которыми стоит знак «минус», называют отрицательными.
Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.
Рациональные числа — это конечные дроби и бесконечные периодические дроби.
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.
Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.
- десятичная дробь 1,15 — это 115/100; десятичная дробь 0,5 — это 1/2; целое число 0 — это 0/1; целое число 6 — это 6/1; целое число 1 — это 1/1; бесконечная периодическая дробь 0,33333. — это 1/3; смешанное число — это 25/10; отрицательная десятичная дробь -3,16 — это -316/100.
Правило умножения рациональных чисел с разными знаками: (-a) * b = — ab. Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».
Правило умножения отрицательных рациональных чисел: (−a) * (−b) = ab. Запомнить поможет фраза: «минус на минус есть плюс».
Правило умножении произвольного рационального числа на нуль: a * 0 = 0 или 0 * a = 0. Докажем это свойство.
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель натуральным.
Skysmart. ru
13.10.2020 7:09:23
2020-10-13 07:09:23
Источники:
Https://skysmart. ru/articles/mathematic/chto-takoe-racionalnye-chisla
Урок 36. рациональные числа — Математика — 6 класс — Российская электронная школа » /> » /> .keyword { color: red; }
Рациональные числа математика
Натуральные числа – числа, которые используются при счёте.
Целые числа – натуральные числа, число нуль, а также числа, противоположные натуральным.
Обязательная литература:
Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл.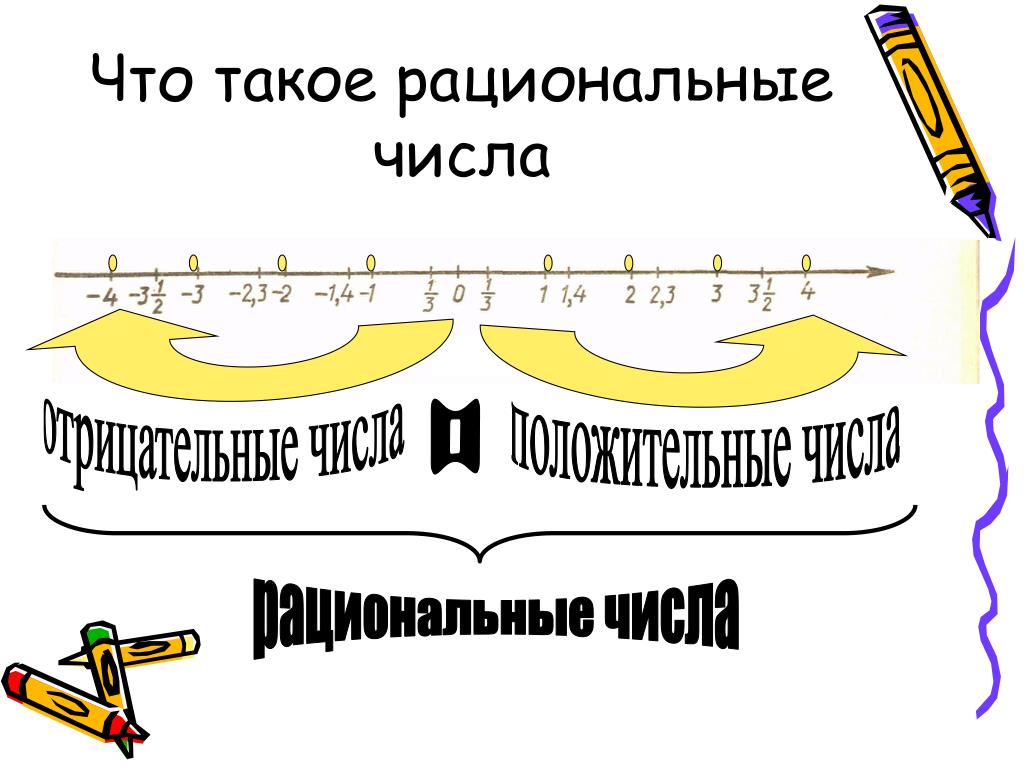 // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
// И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Рассмотрим на координатной оси
Натуральные, целые и дробные числа.
Натуральные (целые положительные): 1, 2, 3
Целые отрицательные: 1, 2, 3
Все эти числа можно записать в виде обыкновенных дробей. Поэтому они имеют общее название — рациональные числа.
Некоторые дроби считают равными. Равенство дробей устанавливают при помощи основного свойства дроби.
Если числитель и знаменатель дроби умножить на одно и то же целое, не равное нулю число, то получится равная ей дробь.
Равенство (2) означает, что если числитель и знаменатель дроби имеют общий множитель n (целое, не равное нулю число), то дробь можно сократить на n. При этом получается дробь, равная данной.
Итак, две дроби равны, когда одна из них может быть получена из другой сокращением на общий множитель её числителя и знаменателя.
Либо, сформулируем так:
Две дроби равны, когда одна из них может быть получена из другой умножением её числителя и знаменателя на одно и тоже число, не равное нулю.
Таким образом, любое целое число является рациональным числом.
Чтобы привести дроби к наименьшему общему знаменателю, надо:
1. найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2. разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на её дополнительный множитель.
Приведём дроби к положительному знаменателю
Название «рациональные числа» происходит от слова «рацио», что означает «отношение».
Мы выяснили, что рациональное число представляется виде дроби.
Уже в V веке до нашей эры люди понимали, что с помощью деления «единицы измерения» можно гораздо точнее приблизить любую величину.
Бывают случаи, когда без дробных чисел нам нельзя обойтись.
Например, кусок проволоки, длиной 4 метра, необходимо разрезать на три равные части. Сколько метров приходится на каждую часть?
Можем составить равенство:
Где х – и есть то количество метров, которое приходится на каждую часть.
Для решения подобных задач в далёком прошлом и появились дробные числа.
Интерес к ним не ослабевает и в наше время. Стремительное развитие вычислительной техники – главная причина этого интереса, так как компьютер может иметь дело только с рациональными числами.
Разбор заданий тренировочного модуля
Тип 1. Разместите нужные подписи под изображениями.
Целое положительное число
Для выполнения задания вспомним определения известных нам числовых множеств.
положительная дробь целое положительное число отрицательная дробь
Тип 2. Вставьте в текст нужные слова.
Если … и знаменатель дроби умножить на одно и то же целое, … нулю число, то получится … ей дробь.
Варианты слов для вставки:
Для выполнения задания обратимся к теоретическому материалу урока.
Если числитель и знаменатель дроби умножить на одно и то же целое, не равное нулю число, то получится равная ей дробь.
Для выполнения задания вспомним определения известных нам числовых множеств.
Resh. edu. ru
09.06.2020 13:09:31
2020-06-09 13:09:31
Источники:
Https://resh. edu. ru/subject/lesson/6886/conspect/
Определения, символы, списки, свойства, часто задаваемые вопросы
Рациональные числа — это все числа, существующие в природе. Рациональные числа — это все действительные числа, которые не являются иррациональными числами. То есть Рациональные числа могут быть выражены как отношение двух целых чисел.
В этой статье мы изучим, что такое рациональное число, его определение и типы, включая положительные и отрицательные рациональные числа, стандартную форму их записи. Мы также узнаем об операциях с этими числами, мультипликативной идентичности и их свойствах, а также поймем разницу между рациональными и иррациональными числами. Давайте посмотрим, как найти рациональное число между двумя иррациональными числами, Решенные примеры по рациональным числам и часто задаваемые вопросы
Мы также узнаем об операциях с этими числами, мультипликативной идентичности и их свойствах, а также поймем разницу между рациональными и иррациональными числами. Давайте посмотрим, как найти рациональное число между двумя иррациональными числами, Решенные примеры по рациональным числам и часто задаваемые вопросы
Что такое рациональное число?
Рациональные числа являются частью системы счисления. Понимание рациональных чисел является базовой математикой и важной темой алгебры. Все целые числа, а также все дроби, конечные десятичные дроби и повторяющиеся десятичные дроби входят в число рациональных чисел. Каждое рациональное число можно представить в виде дроби a/b, где a и b — целые числа. 3 можно выразить, например, как 3/1, -0. 175 представлено -7/40, а 1 1/6 представлено 7/6. Хотя все рациональные числа являются натуральными числами, целыми числами и целыми числами, не все рациональные числа являются натуральными числами, целыми числами или целыми числами.
Определение рациональных чисел
Число получается путем деления двух целых чисел (целое число — это число без дробной части).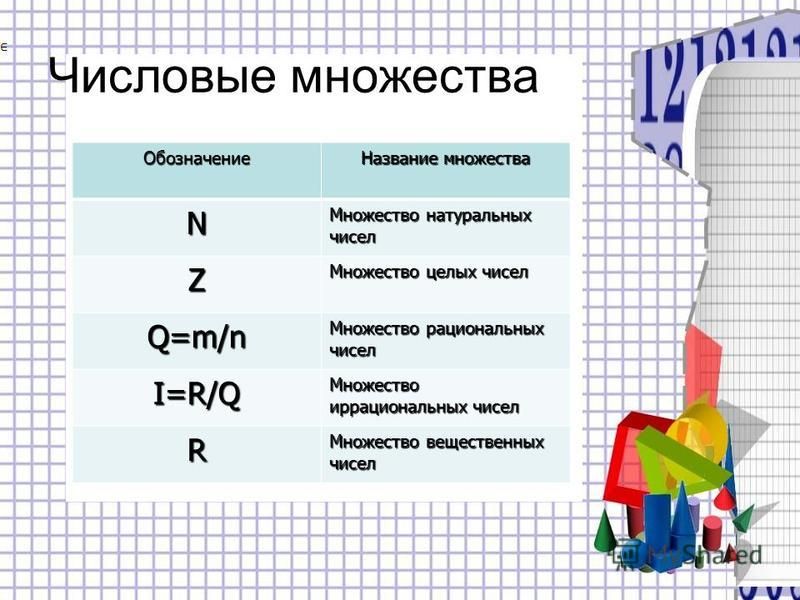 «Отношение» — это корень слова. В арифметике рациональное число — это число, которое можно выразить как частное p/q двух чисел с q ≠ 0. Множество рациональных чисел также включает все целые числа, которые можно выразить как частное с целым числом в качестве числителя. и 1 в знаменателе. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно.
«Отношение» — это корень слова. В арифметике рациональное число — это число, которое можно выразить как частное p/q двух чисел с q ≠ 0. Множество рациональных чисел также включает все целые числа, которые можно выразить как частное с целым числом в качестве числителя. и 1 в знаменателе. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно.
Пример:
- 1/2 — рациональное число (1 делится на 2 или отношение 1 к 2).
- Рациональное число (3/4) равно 0,75.
- 1 или (1/1) — рациональное число.
- Число два является рациональным числом (2/1).
- 2,12 или (212/100) — рациональное число.
- 6,6 или (66/10) — рациональное число.
Типы рациональных чисел
Существует два типа рациональных чисел: положительные рациональные числа и отрицательные рациональные числа.
Положительное рациональное число
Когда числитель и знаменатель рационального числа являются как положительными, так и отрицательными целыми числами, число считается положительным. Другими словами, если числитель и знаменатель рационального числа имеют один и тот же знак, то число положительное. n/1 можно записать как любое натуральное число n, где n и 1 — положительные целые числа. В результате каждое натуральное число является рациональным положительным числом. Имейте в виду, что рациональное число ноль не является ни положительным, ни отрицательным. 1/4, 2/9, -7/-11, -3/-13 и 5/12 являются положительными рациональными числами, тогда как 2/-5, -3/10, -4/7 и 11/-23 таковыми не являются.
Другими словами, если числитель и знаменатель рационального числа имеют один и тот же знак, то число положительное. n/1 можно записать как любое натуральное число n, где n и 1 — положительные целые числа. В результате каждое натуральное число является рациональным положительным числом. Имейте в виду, что рациональное число ноль не является ни положительным, ни отрицательным. 1/4, 2/9, -7/-11, -3/-13 и 5/12 являются положительными рациональными числами, тогда как 2/-5, -3/10, -4/7 и 11/-23 таковыми не являются.
Кроме того, здесь можно узнать о векторной алгебре.
Отрицательное рациональное число
Если числитель и знаменатель рационального числа имеют противоположные знаки, один из которых является положительным целым числом, а другой — отрицательным целым числом, то число называется отрицательным.
Другими словами, если числитель и знаменатель рационального числа имеют один и тот же знак, число отрицательное.
Отрицательное целое число n можно записать как n/1, где n — отрицательное число, а 1 — положительное число. В результате отрицательное рациональное число равно отрицательному целому числу. С другой стороны, рациональное число 0 не является ни положительным, ни отрицательным.
В результате отрицательное рациональное число равно отрицательному целому числу. С другой стороны, рациональное число 0 не является ни положительным, ни отрицательным.
Рациональные числа -1/6, 2/-7, -30/11, 13/-19, -15/23 являются отрицательными рациональными числами, однако рациональные числа -11/-18, 2/5, — 3/-5, а 1/3 нет.
Целые числа
Целое число — это целое, а не дробное число, которое может быть положительным, отрицательным или нулевым. Любое число, содержащееся в наборе комбинаций всех вышеперечисленных числовых категорий, называется целым числом.
- Целочисленный набор содержит все натуральные числа, целые числа и отрицательные числа. В результате каждое натуральное число, каждое целое число и каждое отрицательное число являются целыми числами.
- Дроби (в форме p/q) и десятичные числа не входят в набор целых чисел.
- Множество целых чисел бесконечно, то есть у него нет ни начала, ни конца ни с одной стороны.
 Это потому, что всегда есть другое число с увеличением или уменьшением на 1 для каждого числа как с положительной, так и с отрицательной стороны. Следовательно, множество целых чисел не может быть ограничено и поэтому неисчерпаемо.
Это потому, что всегда есть другое число с увеличением или уменьшением на 1 для каждого числа как с положительной, так и с отрицательной стороны. Следовательно, множество целых чисел не может быть ограничено и поэтому неисчерпаемо. - Целые числа представляют собой набор положительных и отрицательных счетных целых чисел, а также ноль, которые могут быть представлены без дробной части.
- Целое число может быть положительным, отрицательным или нулевым, как указано выше.
- Все натуральные числа являются целыми числами с начальной точкой 1 и пределом бесконечности. Все целые числа, начиная с 0 и заканчивая бесконечностью, также являются целыми числами.
Дроби
Дробь – это часть целого или, в более широком смысле, набор равных частей. В арифметике число выражается как частное, в котором числитель делится на знаменатель. Оба являются целыми числами в простой дроби. В числителе или знаменателе сложной дроби стоит дробь. Числитель правильной дроби меньше знаменателя. Неправильная дробь – это та, у которой числитель больше знаменателя. Смешанная дробь – это дробь, у которой есть и частное, и остаток.
Числитель правильной дроби меньше знаменателя. Неправильная дробь – это та, у которой числитель больше знаменателя. Смешанная дробь – это дробь, у которой есть и частное, и остаток.
Примеры: ⅔, 4 ½, 17/3 и т. д.
Конечные и неконечные десятичные дроби
Десятичное число, имеющее конечное число цифр после запятой, называется конечным десятичным числом. Десятичное число, имеющее бесконечное количество цифр после запятой, называется неконечным десятичным числом.
Символ рациональных чисел
Символ «Q» используется для обозначения набора рациональных чисел. Символ P используется для обозначения иррациональных чисел. Общепринятого символа для Рационалов не существует. Скорее всего, это связано с тем, что рациональные числа определены отрицательно: набор действительных чисел, которые не являются рациональными. Действительные числа обозначаются буквой R, а рациональные числа обозначаются буквой P.
- N – натуральные числа
- W – целые числа
- Z – целые числа
- Q – рациональные числа
Стандартная форма рационального числа числитель и знаменатель равны единице, а знаменатель всегда положительный.
 Кроме того, числитель может быть положительным. В стандартной форме такие числа называются рациональными числами. Ознакомьтесь с несколькими примерами, которые показывают, как выразить рациональное число в стандартной форме, чтобы лучше понять тему.
Кроме того, числитель может быть положительным. В стандартной форме такие числа называются рациональными числами. Ознакомьтесь с несколькими примерами, которые показывают, как выразить рациональное число в стандартной форме, чтобы лучше понять тему.Что такое стандартная форма рационального числа?
Говорят, что рациональное число a/b имеет стандартную форму, если между числителем и знаменателем нет общих множителей, кроме 1, а знаменатель b положителен.
Как преобразовать рациональное число в стандартную форму?
Чтобы выразить рациональное число в стандартной форме, выполните шаги, описанные ниже. Для лучшего понимания Подробная процедура подробно описана и соответствует рекомендациям.
Шаг 1: Проверьте представленное рациональное число.
Шаг 2: Определите, является ли знаменатель положительным. Если знаменатель отрицательный, умножайте или делите числитель и знаменатель на -1 до тех пор, пока знаменатель не перестанет быть отрицательным.
Шаг 3: Вычислите НОД абсолютных значений числителя и знаменателя.
Шаг 4: Используя НОД, полученный на предыдущем шаге, разделите числитель и знаменатель. После этого полученное рациональное число является стандартной формой данного рационального числа.
Операции с рациональными числами
Арифметические операции — это дисциплина математики, которая занимается изучением чисел и их операций, полезных во всех других разделах математики. Сложение, вычитание, умножение и деление являются наиболее распространенными операциями.
Арифметические выражения должны оцениваться в том порядке, в котором они были предназначены. Существует множество способов определить это, наиболее частым из которых является явное использование круглых скобок и использование правил приоритета или использование префиксной или постфиксной нотации, которые сами по себе фиксируют порядок выполнения. Поле — это совокупность объектов, над которыми могут быть выполнены все четыре арифметические операции (кроме деления на ноль) и которые подчиняются нормальным законам (включая дистрибутивность).
Узнайте больше о логарифмических функциях здесь.
Существуют четыре основные арифметические операции. Вот они:
Сложение рациональных чисел
Наиболее фундаментальной математической операцией является сложение. Сложение объединяет две величины в одну величину или сумму в ее самой основной форме. Давайте представим, что у вас есть группа из двух ящиков и группа из трех ящиков. Когда вы объедините две группы, вы получите группу из пяти блоков.
Пример: 2 + 3 = 5 является математическим представлением этого понятия.
Вычитание рационального числа
Противоположностью сложения является вычитание. Чтобы найти разницу между двумя величинами, мы вычитаем одну из другой, а не складываем их вместе. Предположим, вы начинаете с группы из пяти ящиков, как в предыдущем примере. После удаления трех ящиков из этой группы у вас останется два. Выражаясь математически:
Пример: 5 − 3 = 2 является математическим выражением этого понятия
Умножение рационального числа
Умножение также объединяет несколько величин в одну величину, которая называется продуктом. Умножение, по сути, можно представить как сумму многочисленных сложений. Произведение x и y является результатом сложения x и y вместе y раз. Произведение двух дробей равно произведению числителей, деленному на произведение знаменателей.
Умножение, по сути, можно представить как сумму многочисленных сложений. Произведение x и y является результатом сложения x и y вместе y раз. Произведение двух дробей равно произведению числителей, деленному на произведение знаменателей.
\({a\over{b}}\times{c\over{d}} = {ac\over{bd}}\)
Пример: \({2\over{3}}\times{ 4\over{5}} = {2\times4\over{3\times5}} = {8\over{15}}\)
Деление рационального числа
Деление противоположно умножению. Вы разделяете количество на меньшее значение, называемое частным, вместо того, чтобы умножать два или более числа вместе, чтобы получить большее значение. Умножение на обратную дробь идентично делению на нее. 1 деленное на число равно обратной величине. Мультипликативное обратное число есть величина, обратная этому числу. Обратное число и его произведение равно единице. Существует обратное значение для всех чисел, кроме 0,9.0003
\({a\over{b}}\div{c\over{d}}= {a\over{b}}\times{d\over{c}} = {ad\over{bc}} \)
Пример: \({2\over{3}}div{4\over{5}} = {2\times5\over{3\times4}} = {10\over{12}}\)
Прочтите эту статью о среднем арифметическом.
Сумма двух рациональных чисел
Рациональное число можно представить в виде дроби, в которой числитель и знаменатель являются целыми числами (знаменатель не равен нулю). Поскольку целые числа закрыты при сложении и умножении, сложение двух рациональных чисел равносильно сложению двух таких дробей, в результате чего получается еще одна дробь того же типа. В результате объединение двух рациональных чисел дает третье рациональное число.
Рациональное число + Рациональное число = Рациональное число.
Доказательство:
\(\begin{equation}
\text{Дано: }\\
{a\over{b}} \text{and} {c\over{d}}\\
\text{ рациональные числа с целыми числами a, b, c, d, где}\\
{b, d \neq 0}\\
\text{ Докажите: }\\
{a\over{b}} + {c\over{d}} \text{ являются рациональными числами }\\
\text{ Если знаменатели одинаковы: }\\
{a\over{b}} + {c\over{b}} = { a + c \over{b}}\\
\text{ Если знаменатели разные: }\\
{a\over{b}} + {c\over{d}} = {ad + bc \over{bd}}\\
\text{ Так как целые числа замкнуты при сложении и умножении,}\\
\text { a + c, ad, cb, bd и ad + cb — целые числа. }\\
}\\
\text{ Таким образом, } { a + c\over{b}} \text{ and } {ad + bc \over{bd}}
\end{equation}\)
Дроби с целыми значениями в числителе и знаменателе, что делает их рациональными числами.
Аналогично,
Рациональное число — Рациональное число = Рациональное число.
Произведение двух рациональных чисел
Рациональное число можно представить в виде дроби, в которой числитель и знаменатель являются целыми числами (знаменатель не равен нулю). Поскольку целые числа закрыты при сложении и умножении, сложение двух рациональных чисел равносильно сложению двух таких дробей, в результате чего получается еще одна дробь того же типа. В результате объединение двух рациональных чисел дает третье рациональное число.
Рациональное число × Рациональное число = Рациональное число.
\(\begin{equation}
\text{Дано: }\\
{a\over{b}} \text{and} {c\over{d}}\\
\text{ — рациональные числа с целыми числами a, b, c, d, где}\\
{b, d \neq 0}\\
\text{ Докажите: }\\
{a\over{b}} \times {c\over{ d}} \text{ рациональные числа }\\
{a\over{b}}\times{c\over{d}} = {ac\over{bd}}
\end{equation}\)
Поскольку целые числа замкнуты относительно умножения, ac и bd — целые числа. Таким образом, \({ac\over{bd}}\) — дробь с целыми числами в числителе и знаменателе, что делает его рациональным числом. 9{-1}\) или 1/а. Другими словами, если произведение двух чисел равно 1, они мультипликативно обратны друг другу. Обратное число — это мультипликативное обратное число.
Таким образом, \({ac\over{bd}}\) — дробь с целыми числами в числителе и знаменателе, что делает его рациональным числом. 9{-1}\) или 1/а. Другими словами, если произведение двух чисел равно 1, они мультипликативно обратны друг другу. Обратное число — это мультипликативное обратное число.
Мультипликативная идентичность рационального числа равна 1 как произведению двух чисел, а его обратное мультипликативное число равно 1. Произведение 1, умноженное на любое целое число, является самим числом. В результате для рациональных чисел, целых чисел и целых чисел 1 является мультипликативной единицей. Существует рациональное целое число b/a такое, что a/b x b/a = 1, где b/a известно как обратное или мультипликативное обратное число a/b для каждого ненулевого рационального числа a/b.
Также узнайте о среднем отклонении.
Свойства рациональных чисел
Рациональные числа обладают различными свойствами. Давайте посмотрим, какими свойствами обладают рациональные числа:
Свойство замыкания
Произведение двух натуральных чисел всегда является натуральным числом.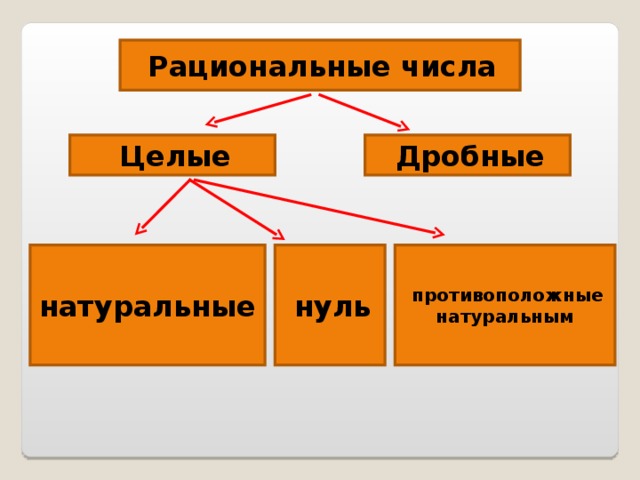 Следовательно, N замкнуто относительно умножения. Если a и b — любые два натуральных числа, то
Следовательно, N замкнуто относительно умножения. Если a и b — любые два натуральных числа, то
a x b = ab также является натуральным числом
Пример:
5 x 7 = 35 — натуральное число
Коммутативное свойство
Умножение натуральных чисел является коммутативным. Если a и b — любые два натуральных числа, то
a x b = b x a
Пример:
2 x 8 = 16
8 x 2 = 16
Следовательно, 2 x 8 = 8 x 2. 9000 2.
. Следовательно, свойство коммутативности верно для умножения.
Ассоциативное свойство
Умножение натуральных чисел ассоциативно. Если a, b и c — любые три натуральных числа, то
тогда a x (b x c) = (a x b) x c
Пример:
3 x (5 x 6) = 3 x 30 = 90
(3 x 5) x 6 = 15 x 6 = 90
3 Следовательно, 3 х (5 х 6) = (3 х 5) х 6.
Следовательно, для умножения верно ассоциативное свойство.
Мультипликативное тождество
Произведение любого натурального числа на 1 есть само целое число.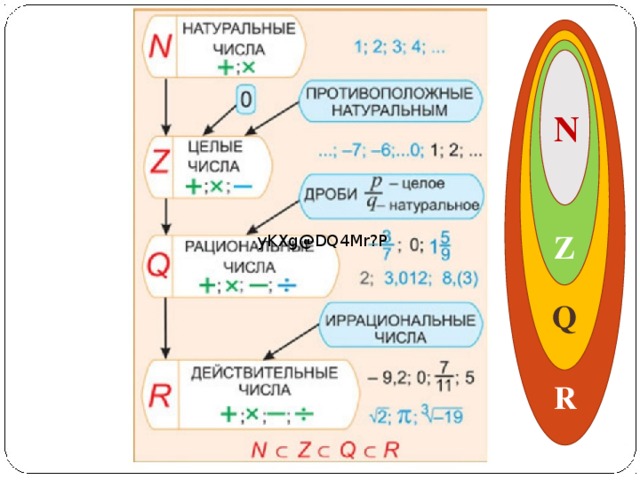 «Единица» — это мультипликативное тождество для натуральных чисел. Если a — любое натуральное число, то
«Единица» — это мультипликативное тождество для натуральных чисел. Если a — любое натуральное число, то
a x 1 = 1 x a = a
Пример:
8 x 1 = 1 x 8 = 8
Распределительное свойство умножения над сложением
Умножение натуральных чисел является дистрибутивным над сложением. Если a, b и c — любые три натуральных числа, то
a x (b + c) = ab + ac
Пример:
3 x (4 + 5) = (3 x 4) + (3 x 5) = 12 + 15 = 27
2 х (3 + 4) = 2 х (7) = 14
Следовательно, 2 х (3 + 4) = (2 х 3) + (2 х 4).
Следовательно, умножение дистрибутивно над сложением
Прочтите эту статью о среднем арифметическом.
рациональные числа по сравнению с иррациональными числами
Разница между рациональными и иррациональными числами заключается в следующем:
| Рациональные номера | IRUTARATION NUMPLANTIAL. в отношении двух целых чисел. | Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. |
| Рациональные числа выражаются дробью, где знаменатель ≠ 0 | Иррациональные числа не могут быть выражены дробью. | |
| Рациональные числа — это полные квадраты | Иррациональные числа — это сурды | |
| Рациональные числа — это конечные или повторяющиеся десятичные дроби | Иррациональные числа — это неконечные или неповторяющиеся десятичные дроби. | |
| Пример: 2, 3, 4, 5, 6… | Пример: \(\sqrt{2}, \sqrt{3}, \sqrt{4}, \sqrt{5}, \sqrt{6 }…\) |
Решенные примеры рациональных чисел
Que: Определите, находятся ли следующие рациональные числа в стандартной форме или нет? (i) -8/23 (ii) -13/-39
Ответ: Поскольку числитель и знаменатель не имеют общих элементов, кроме 1, -8/23 считается стандартной формой. На самом деле и числитель, и знаменатель положительны. В результате говорят, что рациональное число -8/23 находится в стандартной форме.
На самом деле и числитель, и знаменатель положительны. В результате говорят, что рациональное число -8/23 находится в стандартной форме.
-13/-39 не имеет стандартной формы, поскольку включает общий делитель 13, а также 1. Кроме того, знаменатель отрицательный. В результате мы можем заключить, что рассматриваемое рациональное число не имеет стандартной формы.
Que: Определите, является ли смешанная дробь \(1 {3\over{2}}\) рациональным числом.
Ответ: Простейшая форма \(1 {3\over{2}}\) равна 5/2
Числитель = 5, что является целым числом
Знаменатель = 2, является целым числом и не равен нуль.
Итак, да, 5/2 — рациональное число.
Надеюсь, эта статья о рациональных числах была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о рациональных числах
В.1 Что такое пример рационального числа?
Ответ 1 Число получается путем деления двух целых чисел (целое число — это число без дробной части). «Отношение» — это корень слова. В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q = 0. Множество рациональных чисел также включает все целые числа, которые могут быть выражены как частное с целым числом в качестве числителя и 1 в качестве знаменателя. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно. Каждое рациональное число можно представить в виде дроби a/b, где a и b — целые числа. 3 можно выразить, например, как 3/1, -0. 175 представлено -7/40, а 1 1/6 представлено 7/6. Хотя все рациональные числа являются натуральными числами, целыми числами и целыми числами, не все рациональные числа являются натуральными числами, целыми числами или целыми числами.
«Отношение» — это корень слова. В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q = 0. Множество рациональных чисел также включает все целые числа, которые могут быть выражены как частное с целым числом в качестве числителя и 1 в качестве знаменателя. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно. Каждое рациональное число можно представить в виде дроби a/b, где a и b — целые числа. 3 можно выразить, например, как 3/1, -0. 175 представлено -7/40, а 1 1/6 представлено 7/6. Хотя все рациональные числа являются натуральными числами, целыми числами и целыми числами, не все рациональные числа являются натуральными числами, целыми числами или целыми числами.
Q.2 Что означает иррациональное в математике?
Ответ 2 Иррациональные числа являются частным случаем чисел во всей системе счисления. Иррациональные числа в некотором роде противоположны рациональным. Это действительные числа, которые мы не можем записать в виде отношения \({p\over{q}}\), где p и q — целые числа, где q не может быть равно нулю. Например, \(\sqrt{2} = 1,414213….\) иррационально, потому что мы не можем записать это как часть целых чисел. Следовательно, иррациональные числа являются повторяющимися числами. Давайте теперь посмотрим, как мы можем определить иррациональные числа.
Иррациональные числа в некотором роде противоположны рациональным. Это действительные числа, которые мы не можем записать в виде отношения \({p\over{q}}\), где p и q — целые числа, где q не может быть равно нулю. Например, \(\sqrt{2} = 1,414213….\) иррационально, потому что мы не можем записать это как часть целых чисел. Следовательно, иррациональные числа являются повторяющимися числами. Давайте теперь посмотрим, как мы можем определить иррациональные числа.
Q.3 Как узнать, является ли число рациональным?
Ответ 3 Число получается путем деления двух целых чисел (целое число — это число без дробной части). «Отношение» — это корень слова. В арифметике рациональное число — это число, которое может быть выражено как частное p/q двух чисел с q = 0. Множество рациональных чисел также включает все целые числа, которые могут быть выражены как частное с целым числом в качестве числителя и 1 в качестве знаменателя. Рациональные числа — это либо завершающие, либо повторяющиеся десятичные дроби в десятичной форме. 1/7 = 0,142857, например, где 142857 не повторяется бесконечно.
1/7 = 0,142857, например, где 142857 не повторяется бесконечно.
Q.4 Является ли 5,676677666777 иррациональным числом?
Ответ 4 Нет, несмотря на наличие десятичной точки, это не иррациональное число, поскольку числа после десятичной точки не продолжаются вечно. Следовательно, 5,676677666777 — рациональное число.
В.5 Иррациональное число повторяется?
Ответ 5 Иррациональное число — это действительное число, которое не может быть выражено как отношение двух целых чисел. Точно так же иррациональное число, выраженное в десятичной системе счисления, никогда не оканчивается и не повторяется. Это действительные числа, которые мы не можем записать в виде отношения \({p\over{q}}\), где p и q — целые числа, где q не может быть равно нулю. Например, \(\sqrt{2} = 1,414213….\) иррационально, потому что мы не можем записать это как часть целых чисел.
Q.6 Является ли 3,14 рациональным числом?
Ответ 6 3. 14 можно представить в виде дроби двух целых чисел: 314100 и, следовательно, рационально. π нельзя записать в виде дроби от двух целых чисел.
14 можно представить в виде дроби двух целых чисел: 314100 и, следовательно, рационально. π нельзя записать в виде дроби от двух целых чисел.
Другие материалы на testbook.com
| Натуральные числа с определением, свойством, суммой, нечетными и четными натуральными числами |
| Декартово произведение множеств: изучите определение, свойства и способы нахождения с помощью решенных примеров |
| Свойства арифметической прогрессии: определение и формулы |
| Latus Rectum: определение, уравнение, важные свойства, с подробными изображениями |
| Иррациональные числа: выучите определения, символы, списки, свойства на примерах! |
Сравнение рациональных чисел в системе счисления: дроби, десятичные дроби и целые числа
. 2016 фев; 42 (2): 281-93.
дои: 10.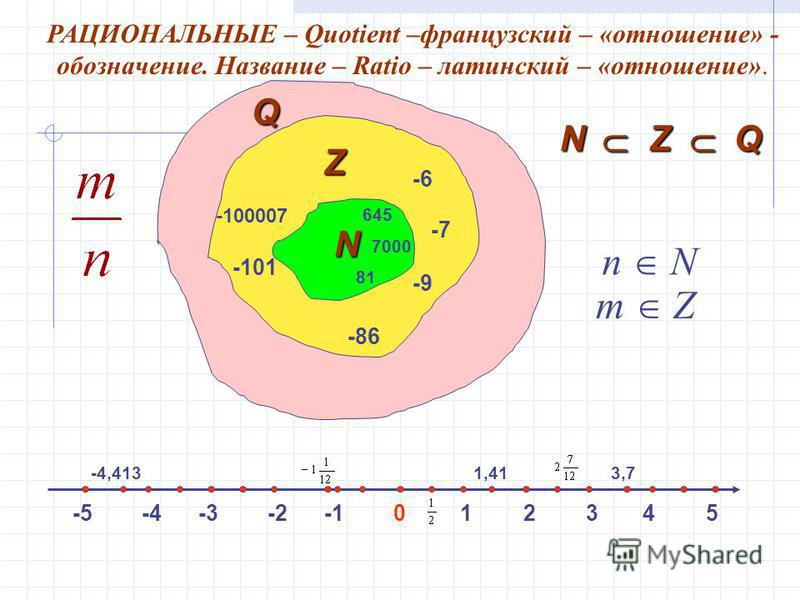 1037/xhp0000140.
Epub 2015 21 сентября.
1037/xhp0000140.
Epub 2015 21 сентября.
Мишель Херст 1 , Сара Кордес 1
принадлежность
- 1 Факультет психологии Бостонского колледжа.
- PMID: 26389612
- DOI: 10.1037/xhp0000140
Мишель Херст и др. J Exp Psychol Hum Percept Perform. 2016 фев.
. 2016 фев; 42 (2): 281-93.
дои: 10. 1037/xhp0000140.
Epub 2015 21 сентября.
1037/xhp0000140.
Epub 2015 21 сентября.
Авторы
Мишель Херст 1 , Сара Кордес 1
принадлежность
- 1 Факультет психологии Бостонского колледжа.
- PMID: 26389612
- DOI: 10.1037/xhp0000140
Абстрактный
Хотя дроби, десятичные числа и целые числа могут использоваться для представления одних и тех же значений рациональных чисел, неясно, воспринимают ли взрослые эти величины рациональных чисел как лежащие в одном и том же упорядоченном ментальном континууме. В текущем исследовании мы исследовали, демонстрирует ли обработка взрослыми величин рациональных чисел в виде дробей, десятичных и целых чисел систематическую зависящую от отношения характеристику интегрированного мыслительного континуума. Как время реакции (ВР), так и данные отслеживания взгляда в задаче на сравнение числа и величины выявили зависящую от отношения производительность, когда взрослые сравнивали относительные величины рациональных чисел как в рамках одного и того же обозначения (например, дроби против дробей), так и в разных обозначениях. (например, дроби против десятичных), указывая на интегрированный мыслительный континуум для рациональных чисел в различных типах обозначений. Кроме того, анализ слежения за движением глаз предоставил доказательства неявной погрешности в отношении целых чисел, когда мы сравнивали значения в представлении дробей, и индивидуальные различия в этой погрешности в отношении целых чисел были связаны с выполнением человеком арифметической задачи на дроби.
В текущем исследовании мы исследовали, демонстрирует ли обработка взрослыми величин рациональных чисел в виде дробей, десятичных и целых чисел систематическую зависящую от отношения характеристику интегрированного мыслительного континуума. Как время реакции (ВР), так и данные отслеживания взгляда в задаче на сравнение числа и величины выявили зависящую от отношения производительность, когда взрослые сравнивали относительные величины рациональных чисел как в рамках одного и того же обозначения (например, дроби против дробей), так и в разных обозначениях. (например, дроби против десятичных), указывая на интегрированный мыслительный континуум для рациональных чисел в различных типах обозначений. Кроме того, анализ слежения за движением глаз предоставил доказательства неявной погрешности в отношении целых чисел, когда мы сравнивали значения в представлении дробей, и индивидуальные различия в этой погрешности в отношении целых чисел были связаны с выполнением человеком арифметической задачи на дроби. Обсуждаются последствия наших результатов как для исследований когнитивного развития, так и для математического образования. (Запись базы данных PsycINFO
Обсуждаются последствия наших результатов как для исследований когнитивного развития, так и для математического образования. (Запись базы данных PsycINFO
(c) APA 2016 г., все права защищены).
Похожие статьи
Понимание детьми дробей и десятичных знаков, а также специфическое отношение нотации к предалгебраическим способностям.
Херст М.А., Кордес С. Херст М.А. и соавт. J Exp Детская психология. 2018 Апр; 168:32-48. doi: 10.1016/j.jecp.2017.12.003. Epub 2018 3 января. J Exp Детская психология. 2018. PMID: 29306108
Сравнение величин с различными типами рациональных чисел.
ДеВольф М., Граундс М.А., Бассок М., Холиок К.Дж. ДеВольф М. и соавт. J Exp Psychol Hum Percept Perform.
 2014 фев; 40 (1): 71-82. doi: 10.1037/a0032916. Epub 2013 10 июня.
J Exp Psychol Hum Percept Perform. 2014.
PMID: 23750968
Клиническое испытание.
2014 фев; 40 (1): 71-82. doi: 10.1037/a0032916. Epub 2013 10 июня.
J Exp Psychol Hum Percept Perform. 2014.
PMID: 23750968
Клиническое испытание.Знание дробей и десятичных знаков.
Брейтуэйт Д.В., Макмаллен Дж., Херст М.А. Брейтуэйт Д.У. и соавт. J Exp Детская психология. 2022 Январь; 213:105210. doi: 10.1016/j.jecp.2021.105210. Epub 2021 24 августа. J Exp Детская психология. 2022. PMID: 34450462
Проблема с процентами.
Джейкобс Данан Дж. А., Гельман Р. Джейкобс Данан Дж. А. и соавт. Philos Trans R Soc Lond B Biol Sci. 2017 19 февраля;373(1740):20160519. doi: 10.1098/rstb.2016.0519. Philos Trans R Soc Lond B Biol Sci. 2017. PMID: 29292346 Бесплатная статья ЧВК. Обзор.
Дроби: новый рубеж для теории числового развития.

Зиглер Р.С., Фацио Л.К., Бейли Д.Х., Чжоу С. Зиглер Р.С. и др. Тенденции Cogn Sci. 2013 Январь; 17 (1): 13-9. doi: 10.1016/j.tics.2012.11.004. Epub 2012 7 декабря. Тенденции Cogn Sci. 2013. PMID: 23219805 Обзор.
Посмотреть все похожие статьи
Цитируется
Символические дроби вызывают представление аналоговой величины у детей школьного возраста.
Калра П.Б., Бинзак Дж.В., Мэтьюз П.Г., Хаббард Э.М. Калра П.Б. и др. J Exp Детская психология. 2020 июль; 195:104844. doi: 10.1016/j.jecp.2020.104844. Epub 2020 31 марта. J Exp Детская психология. 2020. PMID: 32244000 Бесплатная статья ЧВК.
Логлинейная функция отклика задачи с ограниченной числовой линией не связана с психологическим представлением количества.

Коэн Диджей, Куинлан П.Т. Коэн Д.Дж. и др. Psychon Bull Rev. 2018 Feb;25(1):447-454. doi: 10.3758/s13423-017-1290-z. Psychon Bull Rev. 2018. PMID: 28429176
Быть богатым стикерами: числовой контекст влияет на поведение детей.
Посид Т., Фацио А., Кордес С. Посид Т. и др. ПЛОС Один. 4 ноября 2015 г .; 10 (11): e0138928. doi: 10.1371/journal.pone.0138928. Электронная коллекция 2015. ПЛОС Один. 2015. PMID: 26535900 Бесплатная статья ЧВК.
термины MeSH
ORCCA Набор обозначений и типов чисел
Когда мы говорим о сколько или сколько чего-то у нас есть, часто имеет смысл использовать разные типы чисел. Например, если мы подсчитываем собак в приюте, возможно только \(0,1,2,\ldots\text{. }\) (было бы трудно получить \(\frac{1}{2} \) собаки.) С другой стороны, если вы взвешиваете собаку в фунтах, нет смысла позволять себе работать только с целыми числами. Собака может весить что-то вроде \(28,35\) фунтов. Эти примеры показывают, как определенные типы чисел подходят для определенных ситуаций. В этом разделе мы классифицируем различные типы чисел.
}\) (было бы трудно получить \(\frac{1}{2} \) собаки.) С другой стороны, если вы взвешиваете собаку в фунтах, нет смысла позволять себе работать только с целыми числами. Собака может весить что-то вроде \(28,35\) фунтов. Эти примеры показывают, как определенные типы чисел подходят для определенных ситуаций. В этом разделе мы классифицируем различные типы чисел.
Подраздел 1.6.1 Установка обозначений
Какая математическая разница между этими тремя «списками»?
\begin{уравнение*} 28, 31, 30\qquad\{28, 31, 30\}\qquad(28, 31, 30) \end{уравнение*}
Для математика последняя единица \((28, 31, 30)\) — это упорядоченная тройка. Важны не только три числа, но и порядок их появления. Упорядоченная тройка \((28, 31, 30)\) не совпадает с \((30, 31, 28)\text{;}\) в них те же числа, но порядок изменился. В некотором контексте в феврале \(28\) дней; , затем В марте \(31\) дней; , затем В апреле \(30\) дней. Порядок трех чисел имеет значение в этом контексте.
Порядок трех чисел имеет значение в этом контексте.
С фигурными скобками и \(\{28, 31, 30\}\text{,}\) математик видит набор чисел и не особо заботится о том, в каком порядке они написаны. Такой набор называется набором . Все, что имеет значение, это то, что эти числа являются частью коллекции. Они были записаны в определенном порядке, потому что это необходимо для их записи. Но с тем же успехом вы могли бы положить три числа в мешок и встряхнуть мешок. Для некоторого контекста, возможно, три ваших любимых игрока НБА имеют номера на футболках \(30\text{,}\) \(31\text{,}\) и \(28\text{,}\), и все они вам нравятся одинаково Что ж. На самом деле не имеет значения, в каком порядке вы их перечисляете.
Итак, мы можем сказать:
\начать{выровнять*} \{28, 31, 30\}\amp=\{30, 31, 28\}\amp(28, 31, 30)\amp\neq(30, 31, 28) \конец{выравнивание*}
Как насчет того, чтобы просто написать \(28, 31, 30\text{?}\) Этот список из трех чисел неоднозначен. Без фигурных скобок или круглых скобок читателю неясно, важен ли порядок. Нотация набора — это использование фигурных скобок для заключения списка/набора чисел, и в этом разделе мы будем часто использовать нотацию набора.
Без фигурных скобок или круглых скобок читателю неясно, важен ли порядок. Нотация набора — это использование фигурных скобок для заключения списка/набора чисел, и в этом разделе мы будем часто использовать нотацию набора.
КПП 1.6.1. Установить обозначение.
Практика использования (и не использования) набора обозначений.
Подраздел 1.6.2 Различные наборы номеров
Во введении мы упомянули, что разные наборы чисел подходят для разных ситуаций. Вот основные наборы чисел, которые используются в базовой алгебре.
- Натуральные числа
Когда мы считаем, мы начинаем: \(1, 2, 3, \точки\) и продолжаем по этой схеме. Эти числа известны как натуральных числа .
\(\mathbb{N}=\{1,2,3,\dots \}\)
- Целые числа
Если мы включим ноль, то получим набор из целых чисел .
\(\{0,1,2,3,\dots \}\) не имеет стандартного символа, но есть некоторые варианты \(\mathbb{N}_0\text{,}\) \(\mathbb{N} \cup\{0\}\text{,}\) и \(\mathbb{Z}_{\geq0}\text{.
 }\)
}\)- Целые числа
Если мы включим отрицательные значения целых чисел, то получим набор из целых чисел .
\(\mathbb{Z}=\{\dots,-3,-2,-1,0,1,2,3,\dots \}\text{.}\)
A \(\mathbb{Z}\) используется, потому что одно слово в немецком языке для «числа» — «Zahlen».
- Рациональные числа
Рациональное число — это любое число, которое можно записать в виде дроби целых чисел, где знаменатель не равен нулю. Альтернативно, рациональное число — это любое число, которое можно записать с десятичной дробью, которая заканчивается или повторяется.
\(\mathbb{Q}=\left\{0,1,-1,2,\frac{1}{2},-\frac{1}{2},-2,3,\frac{1 {3},-\frac{1}{3},-3,\frac{3}{2},\frac{2}{3}\ldots\right\}\)
\(\mathbb{Q}=\left\{0,1,-1,2,0,5,-0,5,-2,3,0.\overline{3},-0.\overline{3},- 3,1.5,0.\overline{6}\ldots\right\}\)
A \(\mathbb{Q}\) используется, потому что дроби являются q делителями целых чисел.

- Иррациональные числа
Любое число, которое нельзя записать в виде дроби целых чисел, принадлежит множеству иррациональных чисел . Другой способ сказать это так: любое число, десятичные знаки которого идут бесконечно без повторения, является 9.0634 иррациональное число . Некоторые примеры включают \(\pi\приблизительно3.1415926\ldots\текст{,}\) \(\sqrt{15}\приблизительно3.87298\ldots\текст{,}\) \(e\приблизительно2.71828\ldots\ )
Для набора иррациональных чисел нет стандартного символа.
- Реальные числа
Любое число, которое можно отметить где-нибудь на числовой прямой, является действительным числом . Настоящие числа могут быть единственными числами, с которыми вы знакомы. Чтобы число , а не было реальным, вы должны начать рассматривать вещи, называемые 9.0612 комплексные номера , которые сейчас нас не интересуют.
Набор действительных чисел может быть обозначен с помощью \(\mathbb{R}\) для краткости.

Пример 1.6.4. Определите, относятся ли числа к тому или иному типу.
Определите, какие числа из набора \(\left\{-102, -7,25, 0, \frac{\pi}{4}, 2, \frac{10}{3}, \sqrt{19}, \sqrt {25}, 10.\overline{7} \right\}\) — натуральные числа, целые числа, целые числа, рациональные числа, иррациональные числа и действительные числа.
Объяснение
Все эти числа являются действительными числами, потому что все эти числа могут быть расположены на прямой с действительными числами.
Каждое действительное число либо рационально, либо иррационально, но не то и другое вместе. \(-102\text{,}\) \(-7.25\text{,}\) \(0\text{,}\) и \(2\) рациональны, потому что мы можем непосредственно видеть, что их десятичные выражения заканчиваются . \(10.\overline{7}\) также рационально, потому что его десятичное выражение повторяется. \(\frac{10}{3}\) рационально, потому что это отношение целых чисел. И последнее, но не менее важное: \(\sqrt{25}\) рационально, потому что это то же самое, что и \(5\text{. }\)
}\)
Остаются только \(\frac{\pi}{4}\) и \(\sqrt{19}\) в качестве иррациональных чисел. Их десятичные выражения продолжаются вечно, не входя в повторяющийся цикл.
Только \(-102\text{,}\) \(0\text{,}\) \(2\text{,}\) и \(\sqrt{25}\) (что на самом деле \( 5\)) — целые числа.
Из них только \(0\text{,}\) \(2\text{,}\) и \(\sqrt{25}\) являются целыми числами, поскольку целые числа исключают целые отрицательные числа.
Из них только \(2\) и \(\sqrt{25}\) являются натуральными числами, поскольку натуральные числа исключают \(0\text{.}\)
КПП 1.6.5.
КПП 1.6.6.
Во введении мы упомянули, что разные типы чисел подходят для разных ситуаций. Какой набор чисел вы считаете наиболее подходящим в каждой из следующих ситуаций?
Подраздел 1.6.3 Преобразование повторяющихся десятичных дробей в дроби
Мы узнали, что конечное десятичное число является рациональным числом. Конечное десятичное число легко преобразовать в дробь целых чисел: вам просто нужно умножить и разделить на одно из чисел в наборе \(\{10,100,1000,\ldots\}\text{. }\) Например , когда мы произносим число \(0,123\) вслух, мы говорим «сто двадцать три тысячных». Хотя это много, но становится очевидным, что это число может быть записано как отношение:
}\) Например , когда мы произносим число \(0,123\) вслух, мы говорим «сто двадцать три тысячных». Хотя это много, но становится очевидным, что это число может быть записано как отношение:
\begin{уравнение*} 0,123=\фракция{123}{1000}\текст{.} \end{уравнение*}
Аналогично,
\begin{уравнение*} 21.28=\frac{2128}{100}=\frac{532\cdot4}{25\cdot4}=\frac{532}{25}\text{,} \end{уравнение*}
, демонстрирующий, как любое завершающее десятичное число может быть записано в виде дроби.
Повторяющиеся десятичные дроби также можно записать в виде дроби. Чтобы понять, как это сделать, используйте калькулятор, чтобы найти десятичную дробь, скажем, для \(\frac{73}{99}\) и \(\frac{189}{999}\). Вы обнаружите, что
\begin{уравнение*} \frac{73}{99}=0,73737373\ldots=0.\overline{73}\qquad\frac{189}{999}=0,189189189\ldots=0.\overline{189}\text{.} \end{уравнение*}
Шаблон таков, что при делении числа на число из \(\{9,99,999,\ldots\}\) с тем же количеством цифр будет создана повторяющаяся десятичная дробь, начинающаяся с «\(0\text{. }\ )», а затем повторяет числитель. Мы можем использовать это наблюдение, чтобы реконструировать некоторые дроби из повторяющихся десятичных знаков.
}\ )», а затем повторяет числитель. Мы можем использовать это наблюдение, чтобы реконструировать некоторые дроби из повторяющихся десятичных знаков.
КПП 1.6.7.
Преобразование повторяющейся десятичной дроби в дробь не всегда так просто. Есть сложности, если число занимает несколько цифр, прежде чем оно начнет повторяться. Для вашего интереса, вот один пример того, как это сделать.
Пример 1.6.8.
Можем ли мы преобразовать повторяющуюся десятичную дробь \(9.134343434\ldots=9.1\overline{34}\) в дробь? Хитрость заключается в том, чтобы отделить завершающую часть от повторяющейся, например:
.\begin{уравнение*} 9.1+0.034343434\ldots\текст{.} \end{уравнение*}
Теперь обратите внимание, что завершающая часть — это \(\frac{91}{10}\text{,}\), а повторяющаяся часть почти такая же, как в наших предыдущих примерах, за исключением того, что она имеет дополнительный \(0\) сразу после десятичной дроби. . Итак имеем:
\begin{уравнение*}
\frac{91}{10}+\frac{1}{10}\cdot0. 34343434\ldots\text{.}
\end{уравнение*}
34343434\ldots\text{.}
\end{уравнение*}
С учетом того, что мы узнали из предыдущих примеров и базовой арифметики дробей, мы можем продолжить:
\начать{выровнять*} 9.134343434\ldots\amp=\frac{91}{10}+\frac{1}{10}\cdot0.34343434\ldots\\ \амп=\фракция{91}{10}+\frac{1}{10}\cdot\frac{34}{99}\\ \amp=\frac{91}{10}+\frac{34}{990}\\ \amp=\frac{91\multiplyright{99}}{10\multiplyright{99}}+\frac{34}{990}\\ \amp=\frac{9009}{990}+\frac{34}{990}=\frac{9043}{990} \конец{выравнивание*}
Убедитесь, что это правильно, введя \(\frac{9043}{990}\) в калькулятор и посмотрев, возвращает ли он десятичное число, с которого мы начали, \(9.134343434\ldots\text{.}\)
Упражнения 1.6.4 Упражнения
Обзор и прогрев
1.
Запишите десятичное число в виде дроби.
\(0,95\) =
2.
Запишите десятичное число в виде дроби.
\(0,15\) =
3.
Запишите десятичное число в виде дроби.
\(2,25\) =
4.
Запишите десятичное число в виде дроби.
\(3,85\) =
5.
Запишите десятичное число в виде дроби.
\(0,444\) =
6.
Запишите десятичное число в виде дроби.
\(0,508\) =
7.
Запишите дробь в виде десятичного числа.
\({{\frac{5}{16}}}\) =
\({{\frac{1}{20}}}\) =
8.
Запишите дробь в виде десятичного числа.
\({{\frac{19}{20}}}\) =
\({{\frac{3}{8}}}\) =
9.
Запишите смешанное число как десятичное число.
\({4 {\textstyle\frac{3}{25}}}\) =
\({2 {\textstyle\frac{3}{4}}}\) =
10.
Запишите смешанное число как десятичное число.
\({2 {\textstyle\frac{13}{25}}}\) =
\({9 {\textstyle\frac{19}{20}}}\) =
Набор обозначений
11.

Есть два числа, которые можно возвести в квадрат, чтобы получить \(1\text{.}\) Выразите этот набор из двух чисел, используя систему обозначений.
12.
Есть два числа, которые можно возвести в квадрат, чтобы получить \(4\text{.}\) Выразите этот набор из двух чисел, используя систему обозначений.
13.
Есть четыре положительных четных однозначных числа. Выразите этот набор из четырех чисел, используя систему обозначений.
14.
Существует шесть двузначных совершенных квадратных чисел. Выразите этот набор из шести чисел, используя систему обозначений.
15.
Существует набор из трех небольших положительных целых чисел, где вы можете возвести все три числа в квадрат, затем сложить результаты и получить \(61\text{.}\) Выразите этот набор из трех чисел, используя систему обозначений.
16.
Существует набор из трех небольших положительных целых чисел, где вы можете возвести все три числа в квадрат, затем сложить результаты и получить \(42\text{. }\) Выразите этот набор из трех чисел, используя систему обозначений.
}\) Выразите этот набор из трех чисел, используя систему обозначений.
Типы чисел
17.
Какие из следующих чисел являются целыми? Может быть более одного правильного ответа.
\(\displaystyle -{\frac{3}{62}}\)
\(\displaystyle -5.101001000100001\ldots\)
\(\displaystyle -28354\)
\(\displaystyle 44664\)
\(\displaystyle -0.189\)
\(\displaystyle \pi\)
\(\displaystyle 27\)
\(\displaystyle -8\)
18.
Какие из следующих чисел являются целыми? Может быть более одного правильного ответа.
\(\displaystyle 92\)
\(\displaystyle 86313\)
\(\displaystyle -2.101001000100001\ldots\)
\(\displaystyle -2392\)
\(\displaystyle 1.471\)
\(\displaystyle \sqrt{6}\)
\(\displaystyle -2\)
\(\displaystyle -1.
 4\overline{90}\)
4\overline{90}\)
19.
Какие из следующих чисел являются целыми числами? Может быть более одного правильного ответа.
\(\displaystyle 2.2\overline{35}\)
\(\displaystyle 0\)
\(\displaystyle -0.529\)
\(\displaystyle \sqrt{5}\)
\(\displaystyle 57\)
\(\displaystyle \pi\)
\(\displaystyle -8\)
\(\displaystyle -10568\)
20.
Какие из следующих чисел являются целыми числами? Может быть более одного правильного ответа.
\(\displaystyle \pi\)
\(\displaystyle 0\)
\(\displaystyle -3.9\overline{4}\)
\(\displaystyle \sqrt{6}\)
\(\displaystyle -4\)
\(\displaystyle -1674\)
\(\displaystyle \sqrt{4}\)
\(\displaystyle -4.
 985\)
985\)
21.
Какие из следующих чисел являются рациональными? Может быть более одного правильного ответа.
\(\displaystyle 11456\)
\(\displaystyle -{\frac{5}{87}}\)
\(\displaystyle -0.6\overline{18}\)
\(\displaystyle 0\)
\(\displaystyle \sqrt{7}\)
\(\displaystyle -8\)
\(\displaystyle -92781\)
\(\displaystyle \pi\)
22.
Какие из следующих чисел являются рациональными? Может быть более одного правильного ответа.
\(\displaystyle -7.9\overline{42}\)
\(\displaystyle \pi\)
\(\displaystyle -83888\)
\(\displaystyle 53\)
\(\displaystyle {\frac{4}{51}}\)
\(\displaystyle -4\)
\(\displaystyle 0\)
\(\displaystyle \sqrt{13}\)
23.

Какие из перечисленных чисел являются иррациональными? Может быть более одного правильного ответа.
\(\displaystyle 0\)
\(\displaystyle 9.101001000100001\ldots\)
\(\displaystyle \pi\)
\(\displaystyle {\frac{2}{73}}\)
\(\displaystyle -45028\)
\(\displaystyle -4.2\overline{54}\)
\(\displaystyle -9\)
\(\displaystyle 19\)
24.
Какие из перечисленных чисел являются иррациональными? Может быть более одного правильного ответа.
\(\displaystyle {\frac{2}{77}}\)
\(\displaystyle \sqrt{5}\)
\(\displaystyle -4\)
\(\displaystyle -66102\)
\(\displaystyle 3.093\)
\(\displaystyle 0\)
\(\displaystyle \pi\)
\(\displaystyle \sqrt{25}\)
25.

Какие из следующих чисел являются действительными? Может быть более одного правильного ответа.
\(\displaystyle -{\frac{9}{40}}\)
\(\displaystyle 78149\)
\(\displaystyle \sqrt{11}\)
\(\displaystyle 0\)
\(\displaystyle -8\)
\(\displaystyle -2.2\overline{72}\)
\(\displaystyle \pi\)
\(\displaystyle -57209\)
26.
Какие из следующих чисел являются действительными? Может быть более одного правильного ответа.
\(\displaystyle \sqrt{5}\)
\(\displaystyle -4\)
\(\displaystyle 6.597\)
\(\displaystyle 2.2\overline{74}\)
\(\displaystyle 14\)
\(\displaystyle \pi\)
\(\displaystyle 0\)
\(\displaystyle -48316\)
27.

Определите достоверность каждого утверждения, выбрав True или False. 92}\) иррационально
Число \(\frac{-\sqrt{5}}{37\sqrt{5}}\) иррационально
28.
Определите достоверность каждого утверждения, выбрав True или False.
Число \(\frac{2}{9}\) является рациональным, но не натуральным числом
Число \(\frac{0}{3}\) рационально, но не является целым числом
Число \(\sqrt{\frac{4}{81}}\) рационально, но не является целым числом
Число \(\sqrt{9}\) является действительным числом, но не рациональным числом
Число \(0,7070707070…\) рационально
29.
Какой набор чисел вы считаете наиболее подходящим в каждой ситуации?
Количество собак, которыми учащийся владел на протяжении всей своей жизни.
Это число лучше всего рассматривать как
натуральное число
целое число
целое число
рациональный номер
иррациональное число
реальный номер

Разница между прогнозируемыми годовыми расходами и фактическими годовыми расходами данной компании.
Это число лучше всего рассматривать как
натуральное число
целый номер
целое число
рациональный номер
иррациональное число
реальный номер
Длина вокруг бассейна в форме полукруга радиусом \(10\,\text{ft}\text{.}\)
Это число лучше всего рассматривать как
натуральное число
целый номер
целое число
рациональный номер
иррациональное число
реальный номер
Доля студентов колледжа, имеющих автомобиль.
Это число лучше всего рассматривать как
натуральное число
целый номер
целое число
рациональный номер
иррациональное число
реальный номер

Ширина листа бумаги в дюймах.
Это число лучше всего рассматривать как
натуральное число
целый номер
целое число
рациональный номер
иррациональное число
реальный номер
Количество людей, питающихся в непустом ресторане.
Это число лучше всего рассматривать как
натуральное число
целый номер
целое число
рациональный номер
иррациональное число
реальный номер
30.
Приведите пример целого числа, которое не является целым числом.
Приведите пример целого числа, которое не является целым числом.
Приведите пример рационального числа, не являющегося целым.
Приведите пример иррационального числа.




 Каково это число?
Каково это число? .
. Это потому, что всегда есть другое число с увеличением или уменьшением на 1 для каждого числа как с положительной, так и с отрицательной стороны. Следовательно, множество целых чисел не может быть ограничено и поэтому неисчерпаемо.
Это потому, что всегда есть другое число с увеличением или уменьшением на 1 для каждого числа как с положительной, так и с отрицательной стороны. Следовательно, множество целых чисел не может быть ограничено и поэтому неисчерпаемо. 2014 фев; 40 (1): 71-82. doi: 10.1037/a0032916. Epub 2013 10 июня.
J Exp Psychol Hum Percept Perform. 2014.
PMID: 23750968
Клиническое испытание.
2014 фев; 40 (1): 71-82. doi: 10.1037/a0032916. Epub 2013 10 июня.
J Exp Psychol Hum Percept Perform. 2014.
PMID: 23750968
Клиническое испытание.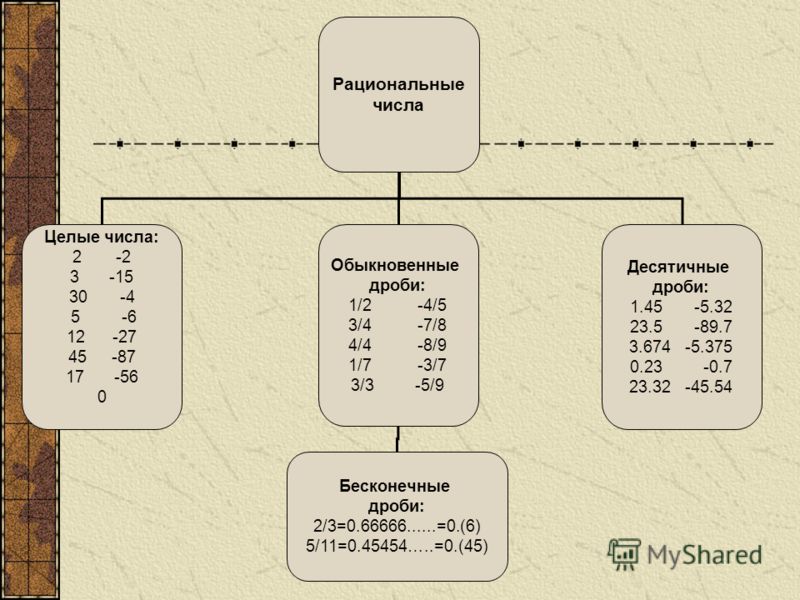

 }\)
}\)
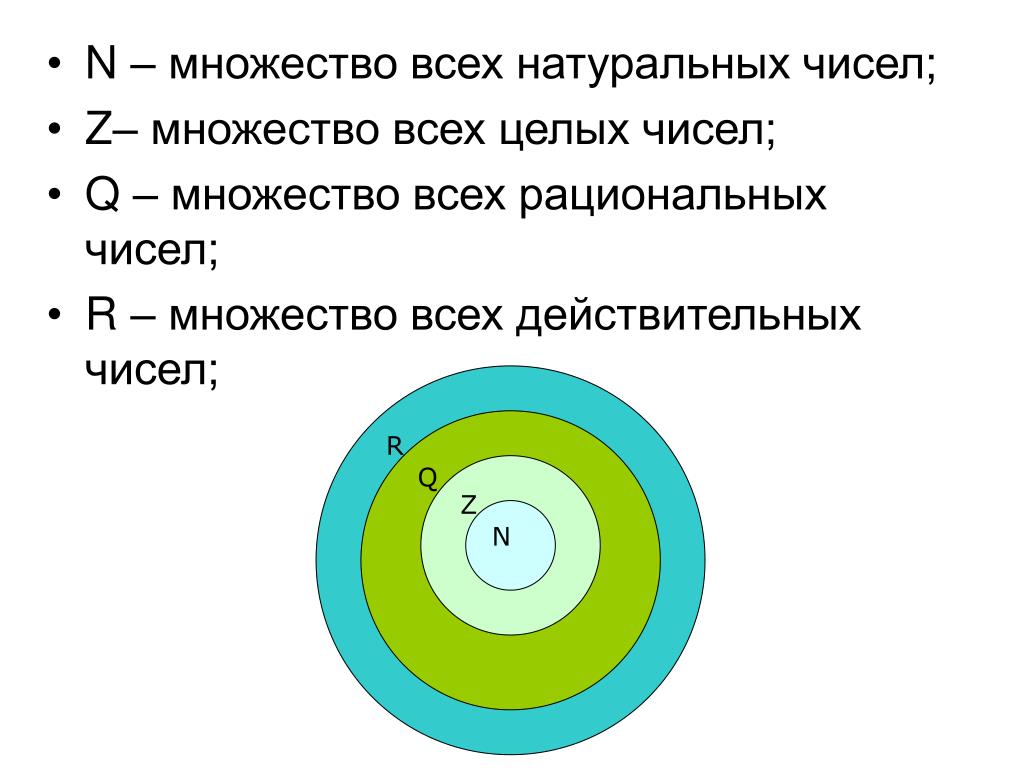
 4\overline{90}\)
4\overline{90}\) 985\)
985\)

