Элементарные преобразования матриц онлайн калькулятор: Приведение матрицы к ступенчатому виду онлайн

Калькулятор формы эшелона строк — MathCracker.com

Инструкции: Используйте этот калькулятор, чтобы показать все шаги процесса преобразования заданной матрицы в форму эшелона строк. Пожалуйста, введите любую матрицу, которую вы хотите уменьшить.

При необходимости измените размер матрицы, указав количество строк и количество столбцов. Когда у вас есть правильные размеры, которые вы хотите, вы вводите матрицу (вводя числа и перемещаясь по матрице с помощью «TAB»)

Эшелонированная форма строк — это тип структуры, которую может иметь матрица, которая выглядит как треугольная, но является более общей, и вы можете использовать идею эшелонированной формы строк для неквадратных матриц.

Этот калькулятор формы эшелона строк возьмет предоставленную вами матрицу и применит исключение Гаусса, показывая все шаги с указанием используемых элементарных матриц.

Что такое эшелонированная форма строки?

Эшелонная форма строк в матрице возникает, если первый ненулевой член в строке (иногда называемый ведущим членом) всегда находится слева от первого ненулевого члена, который находится ниже. Эта идея помогает нам изобразить соответствующие опережающие члены рядов в виде эшелонированной последовательности в случае перевернутой лестницы.

Что вы можете использовать в виде эшелонированной строки матричной формы?

• Это может упростить вычисление определителей
• Это может помочь вам решать системы линейных уравнений
• Это может облегчить некоторые матричные разложения

Как рассчитать форму эшелона строки?

Этот калькулятор формы эшелона может служить многим целям, и возможны разные подходы.

Но основная идея состоит в том, чтобы использовать ненулевые опорные точки для исключения всех значений в столбце, которые находятся ниже ненулевой опорной точки, процесс, иногда известный как исключение Гаусса. Необходимо выполнить следующие шаги:

Шаг 1 : проверьте, находится ли матрица уже в форме эшелона строк. Если это так, то остановитесь, мы закончили.

Шаг 2 : Посмотрите на первую колонку. Если значение в первой строке не равно нулю, используйте его как точку опоры. Если нет, проверьте столбец на наличие ненулевого элемента и, если необходимо, переставьте строки так, чтобы стержень находился в первой строке столбца. Если первый столбец равен нулю, переходите к следующему столбцу справа, пока не найдете ненулевой столбец.

Шаг 3 : Используйте опорную точку, чтобы исключить все ненулевые значения ниже опорной.

Шаг 4 : После этого, если матрица все еще не имеет форму строки-эшелона, переместите один столбец вправо и одну строку вниз, чтобы найти следующую опорную точку.

Шаг 5 : Повторите процесс, как описано выше. Ищите опору. Если ни один элемент не отличается от нуля в новой опорной позиции или ниже, найдите справа столбец с ненулевым элементом в опорной позиции или ниже и при необходимости переставьте строки. Затем удалите значения ниже опорной точки.

Шаг 6 : Продолжайте процесс поворота до тех пор, пока матрица не примет форму строки-эшелона.

Как рассчитать эшелон строки на калькуляторе?

Не все калькуляторы будут проводить исключение Гаусса-Жордана, но некоторые делают это. Как правило, все, что вам нужно сделать, это ввести соответствующую матрицу, для которой вы хотите ввести Форма RREF .

Этот калькулятор позволит вам определить матрицу (с любым выражением, например, с дробями и корнями, а не только с числами), а затем будут показаны все шаги процесса, как прийти к окончательной форме сокращенного эшелона строк.

Этот калькулятор работает как калькулятор элементарных операций со строками , и он покажет вам, какие именно элементарные матрицы используются на каждом шаге.

Пример: Расчет ступенчатой формы матрицы строк

Вопрос: Рассмотрим следующую матрицу:

\[A = \begin{bmatrix} \displaystyle 2&\displaystyle 1&\displaystyle 2\\[0. 6em]\displaystyle 3&\displaystyle 4&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{bmatrix} \]

Вычислите его строчно-эшелонную форму, показав ступени.

Отвечать: Предоставленная матрица представляет собой матрицу \(3 \times 3\).

Нам нужно найти ступенчатую форму строки этой матрицы.

Шаг 1 : Операции, используемые для уменьшения столбца \(1\):
\((1) -\frac{3}{2} R_{ 1} + R_{ 2} \rightarrow R_{ 2}, \quad (2) -\frac{1}{2} R_{ 1} + R_{ 3} \rightarrow R_{ 3}\)

\( \begin{bmatrix} \displaystyle 2&\displaystyle 1&\displaystyle 2\\[0.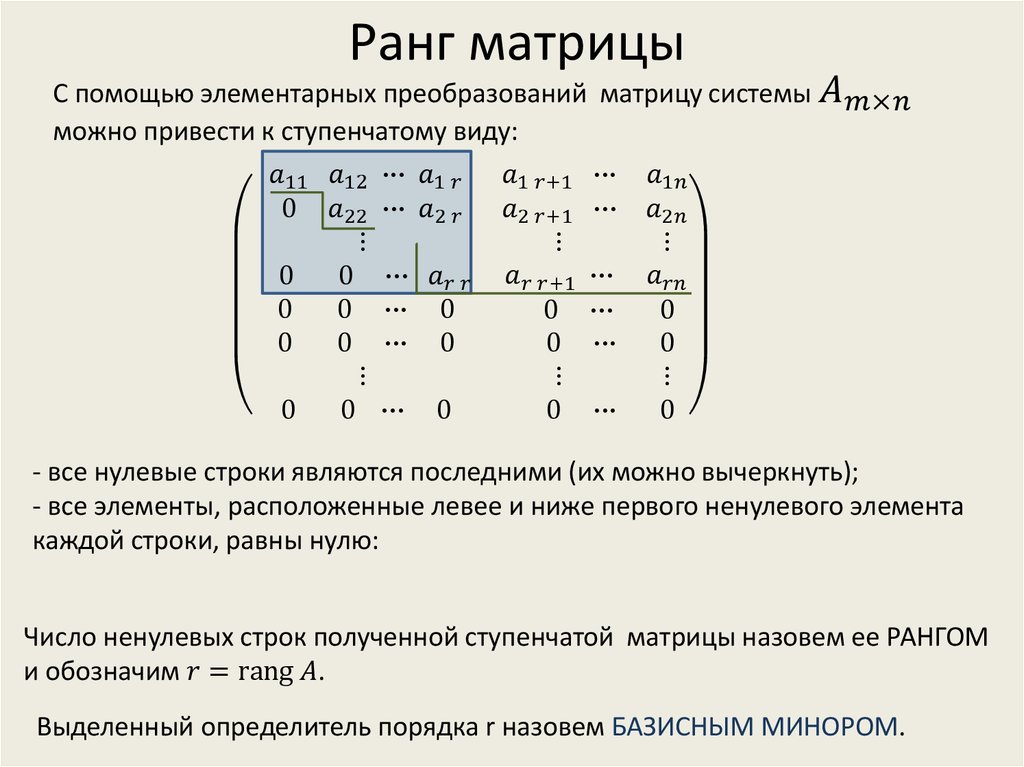

6em]\displaystyle 3&\displaystyle 4&\displaystyle 1\\[0.6em]\displaystyle 1&\displaystyle 1&\displaystyle 1 \end{bmatrix} \rightarrow \begin{bmatrix} \displaystyle 2&\displaystyle 1&\displaystyle 2\\[0.6em]\displaystyle 0&\displaystyle \frac{5}{2}&\displaystyle -2\\[0.6em]\displaystyle 0&\displaystyle \frac{1}{2}&\displaystyle 0 \end{bmatrix} \)

Шаг 2 : Операция, используемая для уменьшения столбца \(2\):
\((1) -\frac{1}{5} R_{ 2} + R_{ 3} \rightarrow R_{ 3}\)

\( \begin{bmatrix} \displaystyle 2&\displaystyle 1&\displaystyle 2\\[0. 6em]\displaystyle 0&\displaystyle \frac{5}{2}&\displaystyle -2\\[0.6em]\displaystyle 0&\displaystyle \frac{1}{2}&\displaystyle 0 \end{bmatrix} \rightarrow \begin{bmatrix} \displaystyle 2&\displaystyle 1&\displaystyle 2\\[0.6em]\displaystyle 0&\displaystyle \frac{5}{2}&\displaystyle -2\\[0.6em]\displaystyle 0&\displaystyle 0&\displaystyle \frac{2}{5} \end{bmatrix} \)

и мы пришли к ступенчатой форме строк данной матрицы.

Отсюда заключаем, что матрица в виде эшелона строк имеет вид:

\[ \begin{bmatrix} \displaystyle 2&\displaystyle 1&\displaystyle 2\\[0.6em]\displaystyle 0&\displaystyle \frac{5}{2}&\displaystyle -2\\[0.6em]\displaystyle 0&\displaystyle 0&\displaystyle \frac{2}{5} \end{bmatrix} \]

Ранг матрицы.

Навигация по странице:

• Ранг системы строк и столбцов матрицы
• Ранг матрицы
• Свойства матрицы связанные с рангом
• Методы вычисления ранга матрицы

Онлайн калькулятор. Ранг матрицы.

Определение.

Рангом системы строк (столбцов) называется максимальное количество линейно независимых строк (столбцов) этой системы.

Теорема.

Ранг системы строк матрицы равен её рангу системы столбцов.

Определение.

Рангом матрицы A называется ранг её системы строк или столбцов.

Обычно ранг матрицы A обозначается rank(A) или rang(A)

Свойства матрицы связанные с рангом

• Ранг матрицы не изменится, если к ее строкам (столбцам) применить элементарные преобразования.

• Ранг ступенчатой матрицы равен количеству её ненулевых строк.

Методы вычисления ранга матрицы

Метод элементарных преобразований

Используя свойства матрицы связанные с ее рангом, получен метод расчета ранга наиболее часто использующийся на практике.

Метод 1.

Ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду, используя элементарные преобразования над строками и столбцами матрицы.

Метод окаймления миноров

Теорема.

Ранг матрицы равен наибольшему порядку не равного нулю минора.

Метод 2.

Если в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. Если среди окаймляющих миноров найдется ненулевой, то вся процедура повторяется.

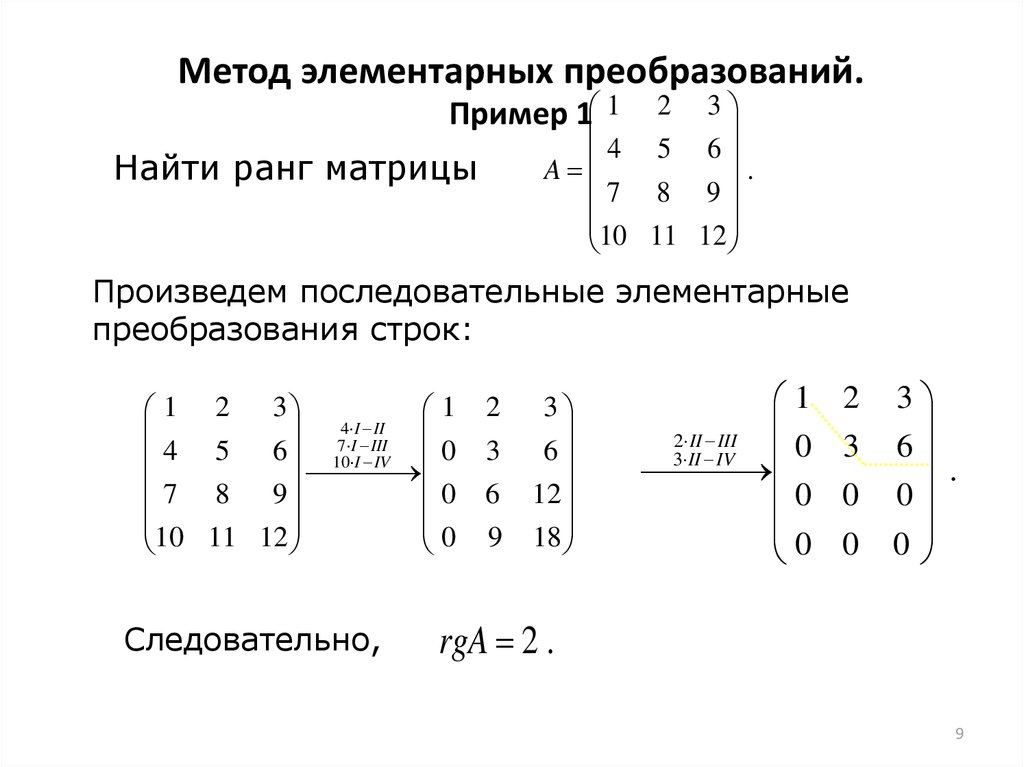
Пример.

Вычислить ранг матрицы A, где

A =		4	2	0	1
		2	1	2	3
		0	3	10	1
		4	2	4	6

Решение:

От 1-ой строки отнимем 2-ую умноженную на 2, от 4-той отнимем 2-ую умноженную на 2

	4	2	0	1		~		0	0	-4	-5		~
	2	1	2	3				2	1	2	3
	0	3	10	1				0	3	10	1
	4	2	4	6				0	0	0	0

Поменяем местами строки

~		2	1	2	3
		0	3	10	1
		0	0	-4	-5
		0	0	0	0

полученная матрица есть является ступенчатой, значит rank(A) = 3.

Ответ: rank(A) = 3.

Онлайн калькуляторы с матрицами.

Упражнения с матрицами.

Матрицы. вступление и оглавлениеМатрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матрицУмножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Matrix Elementary Transformation Online Calculator,Онлайн-вычисления, онлайн-калькулятор, онлайн-калькулятор расчета

1. Главная
2. Инструменты
3. Электронный
4. Текст

Категория: Электронный

Помогите изменить

Строка		умножить на		и добавлен в строку
Строка		умножить на
Обмен между линией		и строка
Колонна		умножить на		и добавлено в столбец
Колонна		умножить на
Колонна		заменяется столбцом

Исходная матрица:

После преобразования матрица:

---

Эта страница используется для элементарного преобразования матрицы.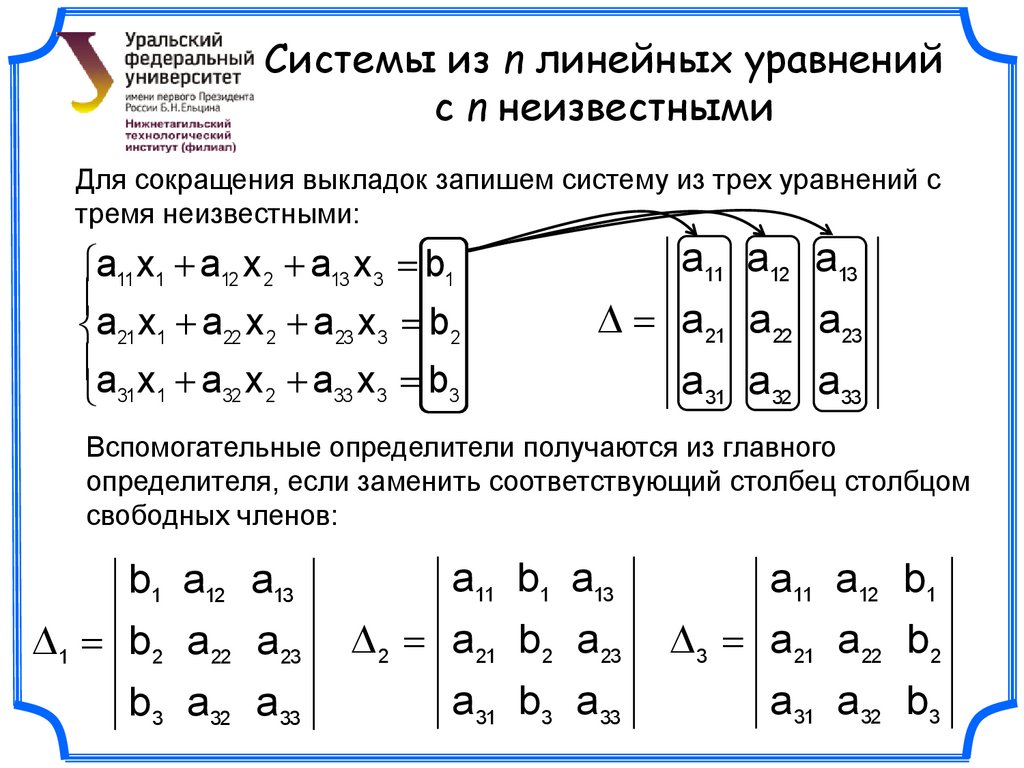 Введите данные матрицы в поле редактирования ниже, а затем нажмите кнопку «Начать загрузку», чтобы отправить данные в таблицу ниже, и затем выполнять различные элементарные операции преобразования. .

При вводе данных матрицы каждая строка отделяется символом «|» и каждое число отделяется запятая. Ввод каждого числа может иметь десятичное число, например 1,25 для одного-двух-пяти, или дробь, например, 2/3 для двух третей.

 

Список комментариев ( 0 )

 

Оценка

Связанное приложение

• Онлайн-калькулятор микрополосковой катушки индуктивности
• Онлайн-калькулятор цепи синхронизации 555
• 555 Онлайн-калькулятор — Расчет значения сопротивления на основе выходных условий Рабочий цикл ≤50%
• Интегральная схема 555 Таймер Онлайн Калькулятор
• Онлайн калькулятор частоты емкостного резистора
• Онлайн калькулятор значения индуктивности многослойной катушки
• Равнокомпонентный активный фильтр высоких частот Баттерворта Онлайн-калькулятор
• Калькулятор делителя динамика — L-образная схема затухания рупора динамика _ Онлайн-инструмент для расчета

Классификация приложений

Классическая физика алгебраический Геометрический Ежедневно Электронный Интернет Материал ОВОС Здоровье Тригонометрический

Недавно использованные

• Онлайн-калькулятор площади поверхности и объема эллиптического кольца
• Онлайн-инструмент для расчета бесплатной энергии Гиббса
• Онлайн-калькулятор индекса загрязнения воздуха
• Лоток выемки, без забоя, односторонняя планировка (поддерживающий уклон грунта) онлайн-калькулятор
• Размер женской одежды — конвертация размера онлайн

Чаще всего используется

• Калькулятор интерполяции кубических сплайнов_инструмент онлайн-расчетов
• Код BCD8421 и онлайн-инструмент конвертации десятичных чисел
• Длина волны, частота волны, скорость волны онлайн калькулятор
• Иррационально-рациональный онлайн-инструмент идентификации
• Онлайн-калькулятор стандартного соотношения роста мужчин и женщин

Преобразования и матрицы

Матрица может выполнять геометрические преобразования!

Попробуйте это приложение для 2D-преобразования:

 

Матрицы также могут преобразовываться из 3D в 2D (очень полезно для компьютерной графики), выполнять 3D-преобразования и многое другое.

Математика

Для каждой точки [x,y], из которой состоит фигура, мы делаем это матричное умножение:

=

ax + на

cx + dy ,d] — Матрица идентичности (матричный эквивалент «1»), значения [x,y] не изменяются:

=

1x + 0y

0x + 1y

=

Изменение «b» value приводит к преобразованию «сдвига» (попробуйте выше):

=

1x + 0,8y

0x + 1y

=

x+0,8y

y

А этот сделает диагональный «переворот» относительно линии x=y (попробуйте также):

=

0x + 1y

1x + 0y

=

Что еще вы можете открыть?

Много преобразований одновременно

Мы можем «цеплять» преобразования, перемножая матрицы.

Пример: диагональный флип с последующим горизонтальным сдвигом:

Будьте осторожны! Преобразования идут справа налево, так что это сдвиг × перевернуть = «перевернуть, затем сдвинуть»

И затем мы можем использовать этот результат в преобразовании:

=

0,8x+y

x

Эти два преобразования выполняются за один раз:

тогда

А что если мы изменим порядок этих двух преобразований?

Пример: горизонтальный сдвиг с последующим диагональным переворотом:

Помните порядок переворот × сдвиг = «сдвиг, затем переворот»

Это другой результат!

=

y

x+0,8y

Он выполняет эти два преобразования за один раз:

, затем

Этот материал является мощным, поскольку мы можем выполнять МНОГО преобразований одновременно и действительно ускорить вычисления. ОЧЕНЬ полезно для компьютерной графики.

Но мы должны быть осторожны, в каком порядке мы делаем преобразования!

Это также показывает нам, почему порядок умножения матриц важен (в отличие от обычных чисел, которые можно умножать в любом порядке, например 2×3=3×2).

Преобразование в код

Нужно кодировать самому? Вот как.

Буква F — это просто список координат:

 [3, 4], [3, 5], [0, 5], [0, 0], [1, 0], [1, 1.8], [2.5, 1.8], [2.5, 2.8], [1, 2.8], [1, 4] 

И мы перебираем эти точки, создавая новые точки, используя матрицу 2×2 «a,b,c,d» :

 for (пусть i = 0; i < shape.pts.length; i++) {
    пусть pt = shape.pts[i]
    пусть x = a * pt[0] + b * pt[1]
    пусть y = c * pt[0] + d * pt[1]
    newPts.push({х:х, у:у})
  }
 

Затем мы наносим исходные точки и преобразованные точки, чтобы мы могли видеть и то, и другое!

Вращение

Эта матрица выполняет поворот θ вокруг начала координат (0,0):

cos(θ)

−sin(θ)

sin(θ)

cos(0,043) Пример: Повернуть на 30°

Вычисление до 4 знаков после запятой:

cos(30°)

−sin(30°)

sin(30°)

cos(30°)

9016

=

=

−0,5

0,5

0,8660

Попробуйте в приложении сверху!

And let's try it on a point here:

0.