Решение некоторых задач по теории множеств
На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.
Введем определение множества, а так же некоторые обозначения.
Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.
Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.
Можно сделать такую запись определения множества:
, где
“” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.
Два множества будем называть равными, если они состоят из одних и тех же элементов
Например:
Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если , то , где “С” знак подмножества или включения.
Графически это выглядит так (рис.1):
(рис.1)
Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.
Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).
Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.
Это определение можно записать с помощью обозначений:
А υ В, где
где “ υ ” – знак объединения,
“ / ” – заменяет слова ”таких что“
(рис.2)
Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:
А ∩ В = С, где
“∩“ – знак пересечения. (рис.3)
(рис.3)
Обозначим буквой Е основное или универсальное множество, где A С Е (“”- любо число), т.е. А Е = Е; АЕ =А
Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается ĀЕ или Ā (рис.4)
Е
(рис.4)
Примерами для понимания этих понятий являются свойства:
_
А Ā=Е Ø = Е Е Ā=Ā
_
А ∩ Ā= Ø Ē = Ø (Ā)=А
Свойства дополнения имеют свойства двойственности:
________ _ _
АВ = А∩В
________ _ _
АВ = АUВ
Введем еще одно понятие – это мощность множества.
Для конечного множества А через m (A) обозначим число элементов в множестве А.
Из определение следуют свойства:
m (A) + m (Ā) = m (E)
А = В => m(A) = m(B)
Для любых конечных множеств справедливы так же утверждения:
m (AB) =m (A) + m (В) – m (А∩В)
m (A∩B) = m (A) + m (В) – m (АВ)
m (ABC) = m (A) + m (В) + m (С)– m (А∩В) — m (А∩С) – m (В∩С) – m (А∩В∩С).
А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.
Задача №1
В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.
По алгебре и геометрии решили 7 человек, по алгебре и тригонометрии – 9 человек. Ни одной задачи не решили 3 человека.
- Сколько учащихся решили все задачи?
- Сколько учащихся решили только две задачи?
- Сколько учащихся решили только одну задачу?
Задача № 2
Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.
Сколько студентов успешно решили только одну контрольную работу?
Задача № 3
В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.
Сколько учеников пользуются только одним видом транспорта?
Решение задачи № 1
Запишем коротко условие и покажем решение:
- m (Е) = 40
- m (А) = 20
- m (В) = 18
- m (С) = 18
- m (А∩В) = 7
- m (А∩С) = 8
- m (В∩С) = 9
___________
m (АВС) = 3 => m (АВС) = 40 – 3 = 37
Обозначим разбиение универсального множества Е множествами А, В, С (рис.5).
(рис.5)
К1 – множество учеников, решивших только одну задачу по алгебре;
К2 – множество учеников, решивших только две задачи по алгебре и геометрии;
К3 – множество учеников, решивших только задачу по геометрии;
К4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;
К5 – множество всех учеников, решивших все три задачи;
К6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;
К7 – множество всех учеников, решивших только задачу по тригонометрии;
К8 – множество всех учеников, не решивших ни одной задачи.
Используя свойство мощности множеств и рисунок можно выполнить вычисления:
- m (К5) = m (А∩В∩С)= m (АВС) — m (А) — m (В) — m (С) + m (А∩В) + m (А∩С) + m (В∩С)
- m (К5) = 37-20-18-18+7+8+9=5
- m (К2) = m (А∩В) — m (К5) = 7-5=2
- m (К4) = m (А∩С) — m (К5) = 8-5=3
- m (К6) = m (В∩С) — m (К5) = 9-5=4
- m (К1) = m (А) — m (К2) — m (К4) — m (К5) = 20-2-3-5=10
- m (К3) = m (В) — m (К2) — m (К6) — m (К5) = 18-2-4-5=7
- m (К7) = m (С) — m (К4) — m (К6) — m (К5) = 18-3-4-5 =6
- m (К2) + m (К4) + m (К6) = 2+3+4=9 – число учеников решивших только две задачи;
- m (К1) + m (К3) + m (К7) = 10+7+6=23 – число учеников решивших только одну задачу.
Ответ:
5 учеников решили три задачи;
9 учеников решили только по две задачи;
23 ученика решили только по одной задаче.
С помощью этого метода можно записать решения второй и третьей задачи так:
Решение задачи № 2
- m (АВ) = 33
- m (АС) = 31
- m (ВС) = 32
- m (К2) + m (К4) + m (К6) + m (К5) = 20
Найти m (К1) + m (К3) + m (К7)
- m (АUВ) = m (К1) + m (К2) + m (К3) + m (К4) + m (К5) + m (К6) = m (К1) + m (К3) + 20 = 33 =>
- m (К1) + m (К3) = 33 – 20 = 13
- m (АUС) = m (К1) + m (К4) + m (К2) + m (К5) + m (К6) + m (К7) = m (К1) + m (К7) + 20 = 31 =>
- m (ВUС) = m (К3) + m (К2) + m (К5) + m (К6) + m (К7) + m (К4) = m (К3) + m (К7) + 20 = 32 =>
- m (К3) + m (К7) = 32 – 20 = 12
- 2m (К1) + m (К3) + m (К7) = 13+11=24
- 2m (К1) + 12 = 24
- m (К3)= 13-6=7
- m (К7)=12-7=5
- m (К1) + m (К3) + m (К7) = 6+7+5=18
Ответ:
Только одну контрольную работу решили 18 учеников.
Решение задачи № 3
- m (Е) = 35
- m (А∩В∩С)= m (К5) = 6
- m (А∩В)= 15
- m (А∩С)= 13
- m (В∩С)= 9
Найти m (К1) + m (К3) + m (К7)
- m (К2) = m (А∩В) — m (К5) = 15-6=9
- m (К4) = m (А∩С) — m (К5) = 13-6=7
- m (К6) = m (В∩С) — m (К5) = 9-6=3
- m (К1) + m (К3) + m (К7) = m (Е) — m (К4) — m (К2) — m (К6) — m (К5) = 35-7-9-3-6=10
Ответ:
Только одним видом транспорта пользуется 10 учеников.
Литература: А.Х. Шахмейстер «Множества. Функции. Последовательности»
1. Записать множество Е, если  , причем А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
, причем А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Решение.
 есть не что иное, как объединение множеств А и В, т.е. множество Е будет состоять из элементов, принадлежащих как множеству А, так и множеству В: Е={2, 3, 4, 6, 8, 9, 10, 12}.
есть не что иное, как объединение множеств А и В, т.е. множество Е будет состоять из элементов, принадлежащих как множеству А, так и множеству В: Е={2, 3, 4, 6, 8, 9, 10, 12}.
2. Записать множество 
Требуется выполнить операцию пересечения т.е. множество Е будет состоять только из элементов, одновременно входящих как в множество А, так и в множество В: Е={6, 12}.
3. Записать множество  , если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
, если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Требуется выполнить операцию разности т.е. множество Е будет состоять из всех элементов множества А, не принадлежащих В: Е={2, 4, 8, 10}.
4. Записать множество  , если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
, если А={2, 4, 6, 8, 10, 12}, B={3, 6, 9, 12}.
Из предыдущего примера имеем  . Для получения окончательного ответа требуется выполнить операцию дополнения т.е. множество Е будет состоять из элементов множества В: Е={3, 6, 9, 12}.
. Для получения окончательного ответа требуется выполнить операцию дополнения т.е. множество Е будет состоять из элементов множества В: Е={3, 6, 9, 12}.
5. Проиллюстрировать с помощью кругов Эйлера следующую формулу: 
Выполняя действие в скобках  получим:
получим:

После этого получаем А\Е т.е. необходимо выделить участок множества А, не принадлежащий множеству Е. Ответ примет форму:

6. Проиллюстрировать с помощью Диаграмм Венна верность тождества:
 .
.
Проиллюстрируем левую часть тождества, обозначив сначала объединение множеств В и С,

затем пересечение множеств А и  . Окончательный вид левой части:
. Окончательный вид левой части:

Теперь проиллюстрируем правую часть:


окончательный вид правой части:

Как видим диаграммы совпадают, следовательно тождество верно.
7. По диаграмме Венна записать формулу:

Запишем сначала  ,
,

затем  , получим:
, получим:

8. Доказать 
Решение.
 ,
,
по закону да Моргана и закону дистрибутивности

Решение задач по теме «Множества и его элементы»
Множества и его элементы
УРОК 9 РЕШЕНИЕ ЗАДАЧ. Самостоятельная работа.
Цель: Систематизация знаний по теме «Множества и его элементы».
Повторение, проверка д/з:
Что обозначает слово «множество»?
Что мы называем элементом множества?
Что бывает элементами множества?
Как различают множества по числу элементов?
Какими способами можно задать множество? (перечисление элементов, характеристическое свойство)
Какое свойство называется характеристическим свойством?
Какие множества называются равными?
Какие математические «иероглифы» мы используем для сокращенной записи?
Что такое подмножество?
Что такое круги Эйлера? Зачем они? (Круги Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления)
Что такое объединение множеств? Знак объединения.
Что такое пересечение множеств? Знак пересечения. Решить упражнение 1.
Что такое разность множеств? Знак разности. Проверить упражнения 1, 2 из д/з.
Что такое дополнение множества?
Решить упражнение 2, 3, 4.
Проверить упражнения из домашнего задания:
Найти разность множеств: К = {1; 2; 3; 7; 8; 9} и М = {0; 2; 8}. Решение: К \ М = {1; 3; 7; 9}.
Даны множества: А = {a; b; c; d}, В = {c; d;} .
Найти: а) А \ В; б) В \ А; в) (А \ В) ∪ (В \ А). Решение: а) А \ В = {a; b}; б) В \ А = ; в) (А \ В) ∪ (В \ А) = {a; b} ∪ = {a; b}.
Каждая семья, живущая в нашем доме выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают и газету, и журнал. Сколько семей живет в нашем доме?
Решение:

Упражнение 1: Даны два множества А = {2; 4; 6; 8; 10} и В = {3; 6; 9; 12}. Найти объединение и пересечение этих множеств.
Решение: А ∪ В = {2; 4; 6; 8; 10; 3; 6; 9; 12}, А ∩ В = {6}.
Упражнение 2: Даны два множества Х = {0; 1; 3; 5} и У = {1; 2; 3; 4}. Найти разность множеств Х и У и разность множеств У и Х. Сделайте вывод.
Решение: Х \ Y = {0, 1, 3, 5} \ {1, 2, 3, 4} = {0, 5}. Y \ X = {2; 4}.
Упражнение 3: Объяснить рисунки:

Упражнение 4: Какое число является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Решение: Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Самостоятельная работа (с последующей взаимопроверкой и проверкой)
Вариант 1
№1 Записать множество А натуральных делителей числа 12.
№2 В данном множестве В = {лев, лисица, гиена, слон, рысь} все элементы, кроме одного, обладают некоторым свойством. Запишите это характеристическое свойство и найдите элемент, не обладающий им.
№3 Даны множества: А = {1, 2, 3, 4, 5, 6} и В = {3, 4, 5, 6, 7, 8}. Найти объединение, пересечение и разность этих множеств.
Вариант 2
№1 Записать множество А натуральных делителей числа 18.
№2 В данном множестве С = {яблоко, груша, огурец, слива, абрикос} все элементы, кроме одного, обладают некоторым свойством. Запишите это характеристическое свойство и найдите элемент, не обладающий им.
№3 Даны множества: А = {3, 4, 5, 6, 7, 8} и В = {4, 5, 6, 7, 8, 9, 10}. Найти объединение, пересечение и разность этих множеств.
Взаимопроверка, проверка.
РЕШЕНИЕ:
Вариант 1:
№1 А = {1, 2, 3, 4, 6, 12}
№2 В = {х│х — хищники}, слон – лишний элемент
№3 А ∪ В = {1, 2, 3, 4, 5, 6, 7, 8}; А ∩ В = {3, 4, 5, 6}; А \ В = {1, 2}.
Вариант 2:
№1 А = {1, 2, 3, 6, 9, 18}
№2 В = {х│х — фрукты}, огурец – лишний элемент
№3 А ∪ В = {3, 4, 5, 6, 7, 8, 9, 10}; А ∩ В = {4, 5, 6, 7, 8}; А \ В = {3}
РЕШЕНИЕ ЗАДАЧ
Проверить упражнение 3 из д/з (все предложенные детьми варианты решений).
Дома вы решаете задачи №3 разными способами. Сегодня на уроке мы разберем их решение, используя круги Эйлера.
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Напомню: круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Упражнение 4: Составьте рассказ по рисунку:
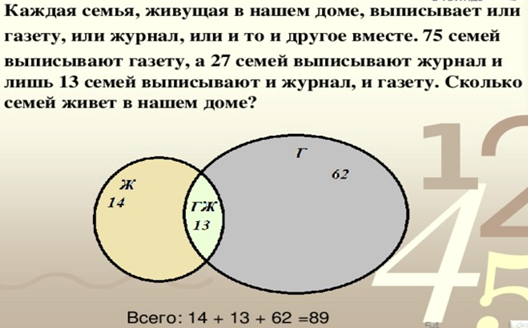
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.
Решим простую задачу, применив круги Эйлера:
Задача 1: В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит только мороженое?
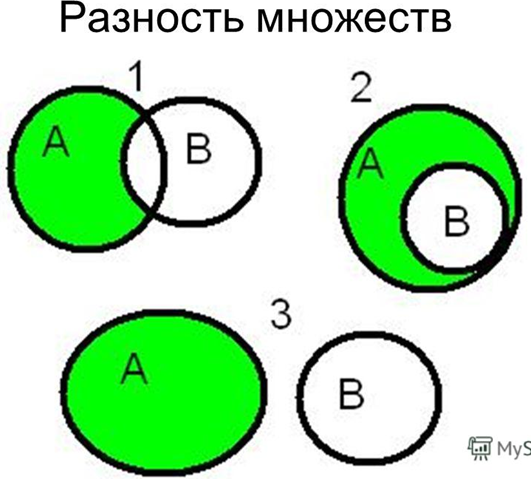
Аналогичным способом можно решить и домашнее упражнение 3. Давайте попытаемся это сделать!
Рассмотрим решение методом кругов Эйлера задач из прошлых д/з:
Задача: Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
Решение:

Задача: Из 220 школьников 16 играют в баскетбол, 175 в футбол, 24 не играют в эти игры. Сколько человек одновременно играют в баскетбол и в футбол?
Решение:

И новые задачи:
Задача 2: В классе 30 учащихся. Из них 18 человек занимаются в секции легкой атлетики, 10 – плаванием, 3 человека – и тем и другим. Сколько человек не занимается ничем?
Решение:

Задача 2: Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Решение:

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ: 20 человек не умеют кататься ни на одном спортивном снаряде.
Подведение итогов урока, рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке.
Домашнее задание: упражнения:
Найти объединение, пересечение и разность множеств А и В, если А = {1; 2; 3; 4; 5; 6} и В = {2; 4; 6; 8; 10; 12}.
Решение: А ∪ В = {1; 3; 4; 5; 6; 8; 10; 12}, А ∩ В = {2; 4; 6}, А \ В = {1; 3; 5}.
Даны множества: А – множество всех натуральных чисел, кратных 10 и В = {1; 2; 3; … 41}. Найти: А ∩ В.
Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекабтся коллекционированием?
Методическая разработка для спецкурса по математике в 9-м классе на тему: «Использование элементов теории множеств в решении задач»
Цели:
формировать у учащихся знания основ теории множеств;
познакомить учащихся с различными случаями применения теории множеств при решении задач;
формировать у учащихся умения применять элементы теории множеств в решении задач;
развивать общую математическую культуру, интерес к предмету;
воспитывать у учащихся ответственное отношение к учебному труду.
Оборудование: плакаты с изображением основных отношений и операций между множествами.
Содержание:
1. Основные понятия множества.
2. Отношения между множествами.
3. Операции над множествами.
4. Решение задач.
5. Контрольные вопросы
1. ОСНОВНЫЕ ПОНЯТИЯ МНОЖЕСТВА
Одно из основных понятий современной математики — множество. Это понятие обычно принимается за первичное и поэтому не определяется через другие.
Когда в математике говорят о множестве (чисел, точек, функций и т. д.), то объединяют эти объекты в одно целое — множество, состоящее из этих объектов (чисел, точек, функций и т. д.). Основатель теории множеств, немецкий математик Георг Кантор (1845–1918) выразил эту мысль следующим образом: “Множество есть многое, мыслимое как единое, целое”.
Множество — это совокупность объектов, объединённых между собой по какому-либо признаку.
Слово “множество” в обычном смысле всегда связывается с большим числом предметов. Например, мы говорим, что в лесу множество деревьев, но если перед домом два дерева, в обычной речи не говорят, что перед домом “множество деревьев”.
Математическое же понятие множества не связывается обязательно с большим числом предметов. В математике удобно рассматривать и “множества”, содержащие 3; 2 или 1 предмет и даже “множество”, не содержащее ни одного предмета (пустое множество). Например, мы говорим о множестве решений уравнения, до того как узнаем, сколько оно имеет решений (множество вещественных решений уравнения х2+1 = 0 — пустое множество).
Произвольные множества обозначают большими латинскими буквами А, В, С, … Пустое множество, т.е. множество, которое не имеет элементов, обозначается символом  .
.
О предметах, составляющих множество, говорят, что они принадлежат этому множеству, или являются его элементами. Элементы множества обозначают малыми латинскими буквами a, b, c, … или одной какой-нибудь буквой с индексом, например а1, а2, … ,аn.
Предложение “предмет а принадлежит множеству А”, или “предмет а — элемент множества А”, обозначают символом а  А.
А.
Способы задания множеств:
1) Множество может быть задано непосредственным перечислением всех его элементов (в произвольном порядке). В таком случае названия всех элементов множества записываются в строчку, отделяются между собой запятыми и заключаются в фигурные скобки.
Например: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}— множество цифр десятичной системы счисления,
Необходимо различать объекты, обозначаемые символами a и {a}. Символом a означается предмет, символом {a} — множество, состоящее из одного элемента а (единичное множество). Перечислением всех элементов можно задать лишь конечное множество. Такие множества, как, например, множество всех натуральных (N) или всех целых чисел (Z), нельзя задать таким способом, т.к. мы не можем перечислить все N и все Z — таких чисел бесконечное множество.
2) Имеется другой, универсальный, способ задания множества в том смысле, что этим способом может быть задано не только конечное, но и бесконечное множество. Множество может быть задано указанием характеристического свойства, т. е. такого свойства, которым обладают все элементы этого множества и не обладает ни один предмет, не являющийся его элементом.
Например: а) А = { х | sin x = 0}, б) А = {0, 1, 2, 3, 4}— множество всевозможных остатков от деления любого натурального числа на 5.
2. ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ
Множество В включается в множество А, если каждый элемент множества В является также элементом множества А. Множество В является подмножеством или частью множества А. Символическая запись:  .
.
Отношение включения обозначается символом  , т. е. предложение “множество В включается во множество А” записывается: В
, т. е. предложение “множество В включается во множество А” записывается: В А.
А.
Поскольку множество можно изобразить в виде геометрических фигур, логические рассуждения тоже изображаются геометрически.
Метод геометрической иллюстрации логических рассуждений был предложен великим математиком 18 века петербургским академиком Леонардом Эйлером (1707–1783) и широко применялся английским математиком Джоном Венном (1834–1923), т.е. для наглядности множества и логические рассуждения изображаются в виде кругов, которые называются кругами Эйлера или диаграммами Эйлера-Венна.

Например:
1) N Z
Z Q
Q R
R C.
C.
2) Множество прямоугольников  во множество параллелограммов
во множество параллелограммов  множество четырёхугольников.
множество четырёхугольников.
Частным случаем включения является равенство.
Два множества, состоящие из одних и тех же элементов называются равными (А = В).
Символическая запись: 

Как показывают приведённые выше примеры, если В А, то возможны два случая:
А, то возможны два случая:
1) Существует хотя бы один элемент множества А, не принадлежащий множеству В. В таком случае говорят, что В — собственная часть (или собственное подмножество) А, или что В строго включается в А. Отношение строгого включения обозначается : В  А.
А.
2) Не существует ни одного элемента множества А, не принадлежащего В. Этот случай равносилен отношению  , т. е. равенству А = В.
, т. е. равенству А = В.
3. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Объединением А В двух множеств А и В называется множество, состоящее из общих элементов этих множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А или множеству В.
В двух множеств А и В называется множество, состоящее из общих элементов этих множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А или множеству В.
Символическая запись:  .
.
Например:

Пересечением А В двух множеств называется множество, состоящее из всех элементов этих множеств, и не содержащее элементов других множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству А и множеству В.
В двух множеств называется множество, состоящее из всех элементов этих множеств, и не содержащее элементов других множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству А и множеству В.
Символическая запись: 

Разностью А \ В двух множеств А и В называется множество, состоящее из всех элементов множества А и не содержащее элементов множества В.
Символическая запись: 

Симметрической разностью А В двух множеств А и В называется множество
В двух множеств А и В называется множество 

Пусть даны два множества А и В, В  А, разность А \ В двух множеств А и В называется дополнением множества В до множества А (относительно множества А).
А, разность А \ В двух множеств А и В называется дополнением множества В до множества А (относительно множества А).

Сумма двух множеств является частным случаем объединения множеств.

Под парой будем всегда понимать упорядоченную пару элементов, т. е. два элемента, расположенных в определённом порядке. Элемент, занимающий первое место, называетсяпервой координатой пары, элемент, занимающий второе место, называется второй координатой пары.
Обозначают пару элементов круглыми скобками: (a,b).
Прямым произведением двух множеств называется множество всевозможных пар (a,b), таких, что: a А, b
А, b  В. Символическая запись:
В. Символическая запись:  .
.
4. РЕШЕНИЕ ЗАДАЧ
А. Задачи на прямое произведение множеств.
Задача №1


Задача №2
Изобразить на координатной плоскости множество М :
M = N  R, где N — множество натуральных чисел, R — множество действительных чисел.
R, где N — множество натуральных чисел, R — множество действительных чисел.
По определению прямого произведения: А В = {(a,b) : a
В = {(a,b) : a А, b
А, b В}
В}
М = {(1, х), (2, х), …| 1, 2, …  N и х
N и х  R}
R}
Изобразим это на графике:

B. Задачи на доказательство, решаемые с помощью диаграмм Эйлера-Венна.
Задача №1
Доказать: (А В)\А =
В)\А = 
Доказательство:
 ,
,
что и требовалось доказать.
Задача №2
Доказать: А\(В С) = (А\В)
С) = (А\В) (А\С)
(А\С)
Доказательство:
 ,
,
что и требовалось доказать.
Задача №3
Доказать: В (А\В) = А
(А\В) = А В
В
Доказательство:
 ,
,
что и требовалось доказать.
C. Логические задачи, решаемые с помощью диаграмм Эйлера-Венна.
Задача №1
В отделе научно-исследовательского института работают несколько человек, причём каждый из них знает хотя бы один иностранный язык: 6 человек — английский язык, 7 человек — немецкий язык, 4 человека — оба языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Только немецкий? Сколько человек знает только один язык?
Решение:
Пусть М1 — работники, знающие английский язык, М2 — работники, знающие немецкий язык.

1) | М1 М2| = |М1| + |М2| — |М1
М2| = |М1| + |М2| — |М1 М2| = 6 + 7 — 4 = 9 (человек) — работает в отделе.
М2| = 6 + 7 — 4 = 9 (человек) — работает в отделе.
2) |М1| — |М1 М2| = 6 – 4 = 2 (человека) — знают только английский язык.
М2| = 6 – 4 = 2 (человека) — знают только английский язык.
3) |М2| — |М1 М2| = 7 – 4 = 3 (человека) — знают только немецкий язык.
М2| = 7 – 4 = 3 (человека) — знают только немецкий язык.
4) 2 + 3 = 5 (человек) — знают только один язык.
Ответ: 9 человек, 2 человека, 3 человека, 5 человек.
Резервная задача
На пикник поехали 92 человека.
48 человек взяли бутерброды с колбасой,
38 человек взяли бутерброды с сыром,
42 человек взяли бутерброды с ветчиной,
28 человек взяли бутерброды с колбасой и с сыром,
21 человек взяли бутерброды с колбасой и с ветчиной,
26 человек взяли бутерброды с сыром и с ветчиной,
25 человек взяли бутерброды трёх видов.
А несколько человек взяли пирожки. Сколько человек взяли пирожки?
(Ответ: 14 человек взяли пирожки.)
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назовите основателя теории множеств.
2. С чем связывают в обычном смысле слово “множество”?
3. Из чего состоит множество?
4. Как обозначают множества, элементы множества?
5. Что называю пустым множеством?
6. Перечислите способы задания множества.
7. Расскажите об отношениях между множествами. Приведите примеры.
8. Расскажите об операциях, которые можно осуществлять между двумя множествами. Приведите примеры.
9. Как для наглядности изображаются множества и логические рассуждения?
10*(для желающих). Составьте несколько задач и решите их, используя элементы теории множеств.
Тема программы: Соответствия между множествами. Отображения.
Цели работы:
1) Обобщить теоретические знания по теме: «Соответствия между множествами. Отображения», решить задачи.
2) Рассмотреть алгоритмы решений заданий теме «Соответствия между множествами. Отображения».
3) Формировать умение самоконтроля, рассудительность, терпение, самостоятельность.
Время выполнения: 1 час.
Теоретические основы
Одно из основных понятий современной математики — множество. Это понятие обычно принимается за первичное и поэтому не определяется через другие.
Когда в математике говорят о множестве (чисел, точек, функций и т. д.), то объединяют эти объекты в одно целое — множество, состоящее из этих объектов (чисел, точек, функций и т. д.). Основатель теории множеств, немецкий математик Георг Кантор (1845–1918) выразил эту мысль следующим образом: “Множество есть многое, мыслимое как единое, целое”.
Множество — это совокупность объектов, объединённых между собой по какому-либо признаку.
Слово “множество” в обычном смысле всегда связывается с большим числом предметов. Например, мы говорим, что в лесу множество деревьев, но если перед домом два дерева, в обычной речи не говорят, что перед домом “множество деревьев”.
Математическое же понятие множества не связывается обязательно с большим числом предметов. В математике удобно рассматривать и “множества”, содержащие 3; 2 или 1 предмет и даже “множество”, не содержащее ни одного предмета (пустое множество). Например, мы говорим о множестве решений уравнения, до того как узнаем, сколько оно имеет решений (множество вещественных решений уравнения х2+1 = 0 — пустое множество).
Произвольные множества обозначают большими латинскими буквами А, В, С, … Пустое множество, т.е. множество, которое не имеет элементов, обозначается символом 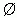 .
.
О предметах, составляющих множество, говорят, что они принадлежат этому множеству, или являются его элементами. Элементы множества обозначают малыми латинскими буквами a, b, c, … или одной какой-нибудь буквой с индексом, например а1, а2, … ,аn.
Предложение “предмет а принадлежит множеству А”, или “предмет а — элемент множества А”, обозначают символом а 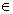 А.
А.
Способы задания множеств:
1) Множество может быть задано непосредственным перечислением всех его элементов (в произвольном порядке). В таком случае названия всех элементов множества записываются в строчку, отделяются между собой запятыми и заключаются в фигурные скобки.
Например: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}— множество цифр десятичной системы счисления,
Необходимо различать объекты, обозначаемые символами a и {a}. Символом a означается предмет, символом {a} — множество, состоящее из одного элемента а (единичное множество). Перечислением всех элементов можно задать лишь конечное множество. Такие множества, как, например, множество всех натуральных (N) или всех целых чисел (Z), нельзя задать таким способом, т.к. мы не можем перечислить все N и все Z — таких чисел бесконечное множество.
2) Имеется другой, универсальный, способ задания множества в том смысле, что этим способом может быть задано не только конечное, но и бесконечное множество. Множество может быть задано указанием характеристического свойства, т. е. такого свойства, которым обладают все элементы этого множества и не обладает ни один предмет, не являющийся его элементом.
Например: а) А = { х | sin x = 0}, б) А = {0, 1, 2, 3, 4}— множество всевозможных остатков от деления любого натурального числа на 5.
ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ
Множество В включается в множество А, если каждый элемент множества В является также элементом множества А. Множество В является подмножеством или частью множества А. Символическая запись: 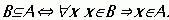 .
.
Отношение включения обозначается символом 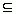 , т. е. предложение “множество В включается во множество А” записывается: В
, т. е. предложение “множество В включается во множество А” записывается: В 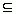 А.
А.
Поскольку множество можно изобразить в виде геометрических фигур, логические рассуждения тоже изображаются геометрически.
Метод геометрической иллюстрации логических рассуждений был предложен великим математиком 18 века петербургским академиком Леонардом Эйлером (1707–1783) и широко применялся английским математиком Джоном Венном (1834–1923), т.е. для наглядности множества и логические рассуждения изображаются в виде кругов, которые называются кругами Эйлера или диаграммами Эйлера-Венна.
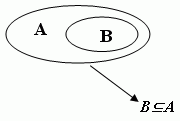
Например:
1) N 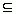 Z
Z 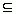 Q
Q 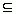 R
R 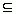 C.
C.
2) Множество прямоугольников 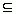 во множество параллелограммов
во множество параллелограммов 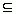 множество четырёхугольников.
множество четырёхугольников.
Частным случаем включения является равенство.
Два множества, состоящие из одних и тех же элементов называются равными (А = В).
Символическая запись: 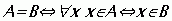
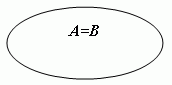
Как показывают приведённые выше примеры, если В 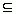 А, то возможны два случая:
А, то возможны два случая:
1) Существует хотя бы один элемент множества А, не принадлежащий множеству В. В таком случае говорят, что В — собственная часть (или собственное подмножество) А, или что В строго включается в А. Отношение строгого включения обозначается : В 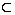 А.
А.
2) Не существует ни одного элемента множества А, не принадлежащего В. Этот случай равносилен отношению 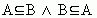 , т. е. равенству А = В.
, т. е. равенству А = В.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Объединением А 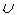 В двух множеств А и В называется множество, состоящее из общих элементов этих множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А или множеству В.
В двух множеств А и В называется множество, состоящее из общих элементов этих множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А или множеству В.
Символическая запись: 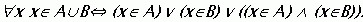 .
.
Например:
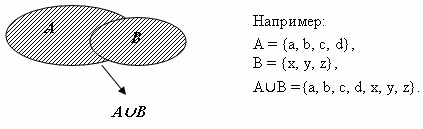
Пересечением А 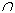 В двух множеств называется множество, состоящее из всех элементов этих множеств, и не содержащее элементов других множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству А и множеству В.
В двух множеств называется множество, состоящее из всех элементов этих множеств, и не содержащее элементов других множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству А и множеству В.
Символическая запись: 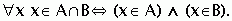
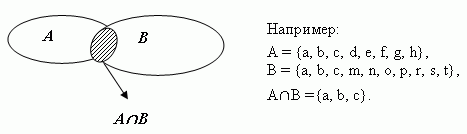
Разностью А \ В двух множеств А и В называется множество, состоящее из всех элементов множества А и не содержащее элементов множества В.
Символическая запись: 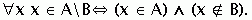
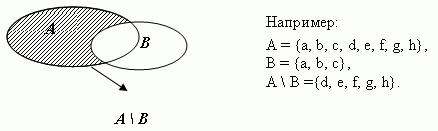
Симметрической разностью А 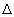 В двух множеств А и В называется множество
В двух множеств А и В называется множество 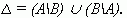

Пусть даны два множества А и В, В  А, разность А \ В двух множеств А и В называется дополнением множества В до множества А (относительно множества А).
А, разность А \ В двух множеств А и В называется дополнением множества В до множества А (относительно множества А).

Сумма двух множеств является частным случаем объединения множеств.
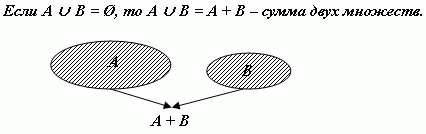
Под парой будем всегда понимать упорядоченную пару элементов, т. е. два элемента, расположенных в определённом порядке. Элемент, занимающий первое место, называется первой координатой пары, элемент, занимающий второе место, называется второй координатой пары.
Обозначают пару элементов круглыми скобками: (a,b).
Прямым произведением двух множеств называется множество всевозможных пар (a,b), таких, что: a 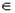 А, b
А, b 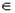 В. Символическая запись:
В. Символическая запись: 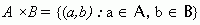 .
.
РЕШЕНИЕ ЗАДАЧ
|
МОУ Стародрожжановская средняя школа №2
Дрожжановского муниципального района Республики Татарстан
Утверждена 31 августа 2008 года.
«Элементы теории множеств»:
курс по выбору для учащихся 9 классов
(Авторская программа)
Ханзярова Гельфира Харисовна-
учитель математики
первой квалификационной категории
2008 год
Пояснительная записка
Во всякой школе есть ребята, которые хотят поступить в технические вузы, и поэтому готовы заниматься математикой значительно больше остальных учащихся. Таким ребятам тесны рамки обычной программы для общеобразовательных школ. Поэтому основной задачей обучения математике в школе является обеспечить прочное и сознательное овладение учащихся системой математических знаний и умений, необходимых в повседневной жизни трудовой деятельности каждому члену современного общества, достаточных для изучения сложных дисциплин и продолжения образования. А программа, составленная мною, предусматривает формирования у учащихся устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой. Интерес и склонность учащихся к математике всемирно подкрепляется, чтобы по окончании IX класса он смог сделать сознательный выбор в пользу дальнейшего углубленного, либо обычного изучения математики.
В научно-популярной математической литературе большое внимание уделено свойствам бесконечных множеств. Знакомство с понятием эквивалентности множеств, мощности множества и т.д. рекомендуется и программой факультативной занятий по математике в школе. У теории множеств есть, однако, более элементарная часть, в которой различие между конечными и бесконечными множествами не выступает явно. Это в первую очередь «алгебра множеств», в которой изучаются свойства операций над множествами. Как мы увидим, она ближе к проблематике школьной алгебры.
В настоящей работе вводятся основные определения, терминология и символика теории множеств и на хорошо известном школьном материале показано применения этих понятий. Язык теории множеств позволяет взглянуть с общих позиций на такие важные разделы школьного курса математики, как решить уравнений, неравенств и др., и способствует устранению устойчивых логических ошибок, встречающихся часто при изучении этих тем в средней школе.
Материал, изложенный в данной программе, рассчитан на 8 часов. Рекомендуемое распределение материала по урокам носит примерный характер. Может быть внесены коррективы в ход урока. Каждое занятие, а также все они в целом направлены на то, чтобы развить интерес школьников к предмету, познакомить их с новыми идеями и методами, расширить представление об изучаемом в основном курсе материале, а главное, порешить интересные задачи.
Понятия «множество» и «подмножество» употребляются не только в курсах алгебры и геометрии, а также при изучении других предметов, например, физики, химии, биологии, истории и др. Но ни в одном из них не дается определения этих понятий, не даются свойства множеств, операции над ними. В каждой из дисциплин понятие «множество» употребляется как термин при изучении отдельных тем данного предмета. Например, в курсе биологии учащиеся сталкиваются с таким понятием как «множество млекопитающих»; в курсе истории – с понятием «этническое множество» и т.д. У учащихся нет четкого представления о понятии «множество».
Предлагаемый курс дает учащимся необходимую базу для дальнейшего использования его составляющих при изучении, как математики, так и других предметов. Учащиеся осознанно и умело смогут употреблять понятия «множество», «подмножество» и др., использовать их свойства, совершать операции над ними для решения задач любых изучаемых школьных курсов.
Материал для занятий подобран таким образом, чтобы можно было проиллюстрировать применение математики на практике, показать связь математики с другими областями знаний, познакомить с некоторыми историческими сведениями, подчеркнуть эстетические аспекты изучаемых вопросов.
Как показывает опыт, эти вопросы интересны и доступны учащимся IXкласса и требует знаний только базового курса. Уровень сложности предлагаемых вопросов таков, что к их рассмотрению можно вовлечь значительное число школьников, а не только наиболее сильных. Для кого-то из школьников, которые пока не проявляют заметной склонности к математике, эти занятия могут стать толчком в развитии интереса к предмету и вызвать желание узнать больше.
Хотя при изучении курса по выбору не ставится цель, выработки каких либо специальных умений и навыков, при достаточно полном рассмотрении вопросов курса, несомненно, появится прогресс в подготовке учащихся.
Заметим, что проверка усвоения материала предполагается в форме зачета, но соответственные оценки не должны включаться на контрольные работы и выноситься на экзамены.
Цели курса по выбору:
– на популярном уровне познакомить учащихся с теоретико-множественной идеей в математике;
– познакомить учащихся с приложением элементов теории множеств при решении уравнений и неравенств, построении графиков уравнений и неравенств;
– помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшего обучения.
— формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики.
— развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе.
Задачи курса по выбору:
— ввести в математическую практику учащихся такие понятия, как множество, элемент множества, пустое множество, подмножество, конечные и бесконечные множества;
— научить учащихся выполнять основные действия с множествами; находить пересечение, объединение, дополнение и разность множеств;
— научить учащихся применять элементы теории множеств при решении уравнений и неравенств, построении графиков уравнений и неравенств;
— оказание обучающимся квалифицированной помощи в расширении, углублении, систематизации и обобщении их знаний по данному предмету.
— развитие у учащихся интуиции, формально-логического мышления, навыков использования математических методов для изучения смежных дисциплин.
— формирование в процессе обучения познавательной активности, умения приобретать и творчески распоряжаться полученными знаниями, потребностей к продолжению образования и самообразованию.
Данный курс рассчитан на 8 часов. На каждом уроке предполагается изложение теории с большим количеством примеров, решение типовых задач, самостоятельная работа. Основные формы организации уроков: лекция с применением информационно – коммуникационных технологий, практическая и самостоятельная работы, творческие задания. В курсе заложена возможность дифференцированного обучения, как путем использования задач различного уровня сложности, так и на основе различной степени самостоятельности освоения нового материала.
Программа курса способствует развитию познавательных интересов, мышления школьников, предоставляет возможность подготовиться к сознательному выбору профиля обучения и дальнейшей специализации.
В результате изучения курса учащиеся должны уметь:
— грамотно формулировать и обосновывать теоретические положения теории;
— применять изученные алгоритмы для решения соответствующих задач;
— применять теоретико-множественные подходы при решении уравнений и неравенств, построении графиков уравнений и неравенств.
Учебный тематический план курса по выбору
«Элементы теории множеств»
№п\п | Тема занятий | Количество часов |
1 | Множество, элемент множества. Характеристическое свойство множеств. | 1 |
2 | Числовые множества. Множество точек на прямой, задаваемые алгебраическими уравнениями и неравенствами с одной переменной. | 1 |
3 | Операции над множествами. Алгебра множеств | 1 |
4. | Разность двух множеств. | 1 |
5 | Дополнение множества. Универсальное множество | 1 |
6 | Конечные множества | 1 |
7 | Эквивалентность множеств. Счетные и несчетные множества | 1 |
8 | Зачетное занятие. | 1 |
ОБЯЗАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ ПО ОКОНЧАНИИ ИЗУЧЕНИЯ
КУРСА ВЫБОРУ «ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ»
В итоге изучения курса учащиеся должны:
— знать определения основных понятий курса;
— знать свойства множеств и уметь их применять при решении задач;
— знать основные операции над множествами и уметь их применять при решении задач;
— уметь дать характеристику множества;
— уметь применять составляющие курса при решении задач алгебры и геометрии.
Рецензия
на авторскую программу курса по выбору по теме:
«Элементы теории множеств»
Возраст детей, предусмотренный в программе для обучения 13-15 лет.
Реализуемая программа по математике состоит из пояснительной записки, цели курса по выбору, задачи курса по выбору, учебного тематического плана курса, содержательной части курса по выбору.
Анализ содержания программы позволяет, констатировать её соответствие программам по математике, рекомендованным МО РФ. Программа предполагает некоторое расширение и углубление содержания обучения, что позволяет учителю разнообразить задачный материал.
Данный курс способствует интеллектуальному и творческому развитию, формированию логического и теоретического мышления. Положительная особенность программы является то, что её реализация является хорошей основой для дальнейшего углубления изучения математики в 10-11 классах, а так же приобретенные знания способствуют сдаче итоговой аттестации на более высоком уровне. Основные темы и задачи, заявленные в программе, направлены на прочное и сознательное овладение учащимися системой математических знаний и умений. Таким образом, программа удовлетворяет всем основным требованиям к программе.
Программа рекомендуется к использованию в школе.
Рецензент: _______ /Абязова Зоя Васильевна/
Руководитель районного методического объединения учителей математики Дрожжановского муниципального района РТ, учитель высшей квалификационной категории.
31.08. 2008год.
Содержательная часть курса по выбору
Занятие №1.
Тема: Множество, элемент множества. Характеристическое свойство множеств.
Понятие “Множество ” является одним из основных понятий математики. Это понятие в явном виде не определяется, хотя на интуитивном уровне его можно описать, задать. Над множествами можно выполнять многие операции, которые будут рассмотрены при изучении этой темы.
Под множеством можно понимать — неупорядоченную совокупность элементов, набор объектов.
Примерами множеств может служить:
Множество людей. Группа детей одного класса – элементами служат учащиеся именно данного класса. Множество берез в лесу.
2. Совокупность всех классов некоторой школы – элементами являются именно группы детей, образующих каждый их этих классов.
3. N- Множество натуральных чисел. Натуральные числа – числа от 1 до бесконечности.
4.Z- множество целых чисел, Q -множество рациональных чисел, R — множество действительных чисел
5. Множество треугольников – любой треугольник является элементом этого класса.
6. Знаки препинания, буквы алфавита, цифры для записи чисел
7. D= {2, 4, 6, 8, 10, 12…} – множество четных чисел
8. V= {3, 6, 9, 12…} – множество чисел кратных трем
9. M={Иванов, Петров, Сидоров…} – множество спортсменов
10. Множество делителей числа 24.
11.Множество письменных принадлежностей
Если множество задано, каждый элемент (объект) его уникален, т. е. отличим от других; причем для любого объекта существует возможность установить, принадлежит ли он множеству или нет.
Множества обозначаются заглавными буквами, как правило, латинского алфавита. При этом элементы множества принято заключать в фигурные скобки.
Принадлежность элемента а множеству А обозначается символом €, например, а € А , не принадлежность символом.
Например: Х={1,2,3,4,5,6}.
3€Х – число 3 принадлежит множеству Х. 9X — число 9 не принадлежит множеству Х.
Совокупность {1,2,3,4,5,6} является множеством, последовательность (порядок) записи элементов не имеет значения, поэтому оно неотличимо от множества {1, 3, 5, 2, 4, 6}
Совокупность {1,2,3,1,3,3,5} множеством не является, здесь некоторые элементы записаны не единичным образом.
Множество считается заданным, если относительно любого объекта можно установить, является ли он элементом данного множества или нет. Рассмотрим способы, которыми может быть задано множество. Если множество состоит из конечного числа элементов, то оно может быть задано: а) перечислением; б) указанием отличительных свойств, которые выделяют элементы множества.
Может случиться, что ни один элемент не обладает отличительным свойством, определяющим А. Например, не существует ни одного натурального числа меньше ½. Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается Ø. Говорят, множество А натуральных чисел меньше ½, есть пустое множество; пишут А= Ø.
Если все элементы А являются и элементами множества В, то множество А называется подмножеством множества В или, говорят, что множество А содержится в множестве В и записывают так: АВ или ВА. Например, множество всех натуральных чисел N есть подмножество всех целых чисел Z: NZ.
Из определения следует, что само множество также является своим подмножеством, т.е. АА.
Полагают также, что пустое множество является подмножеством любого множества А: ØА для любого А. В самом деле, так как пустое множество не содержит ни одного элемента, то в нем нет и элементов, которые бы принадлежали множеству А.
Если А В и В А, то множества А и В называют равными и обозначают А=В. Например, множество А всех корней уравнения х2 – 2х +1 = 0 и множество В всех натуральных чисел, меньших чем 3/2, равны: и множество А, и множество В содержит один элемент- натуральное число 1.
Итак, свойство, с помощью которого задано множество, называется характеристическим свойством. Этим свойством должны обладать все элементы данного множества. А именно, все элементы заданного множества обладают характеристическим свойством и если некоторый из элементов не принадлежат этому множеству, то он не обладают заданным свойством.
Это условие является и основой методов проверки равенства двух множеств. Необходимость в проверке равенства множеств может возникнуть тогда, когда множество описано через различные свойства, и необходимо убедиться, что этим свойствам соответствует одно и то же множество. В общем случае задача проверки равенства множеств является достаточно сложной задачей, требующей больших вычислительных затрат.
Упражнения для самоподготовки.
1. Приведите примеры на множества, которые состоят из двух, трех элементов, одного элемента, пустого множества.
Занятие №2.
Тема: Числовые множества. Множество точек на прямой, задаваемые алгебраическими уравнениями и неравенствами с одной переменной.
При решении задач очень часто приходится иметь дело с множествами, элементами которых являются числа. Такие множества называют числовыми, все они являются подмножествами основного множества действительных чисел R. Множество натуральных чисел N, множество целых чисел Z, множество корней уравнения х2 – 5х +6 = 0 – все это числовые множества.
Пусть а и b – действительные числа, а
Задачи для самостоятельного решения:
1.Каково множество решений каждого из уравнений:
Х2 -1 = 0 х2 -2х + 1 =0; х2 + х +1 =0; IxI +x =0
Дайте в каждом случае геометрическую иллюстрацию.
Занятие №3
Тема: Операции над множествами. Алгебра множеств
Часто в курсе алгебры мы сталкиваемся с такой ситуацией, когда решение некоторого алгебраического уравнения или неравенства сводилось к решению других более простых уравнений или неравенств.
Например, пусть требуется решить уравнение (х2 –х)(х2 – 3х +2) =0. Чтобы произведение было равно нулю, необходимо и достаточно, чтобы обращался в нуль хотя бы один из множителей. Имеем, 1) х2 –х =0 ИЛИ 2)х2 -3х +2 =0. Связка ИЛИ здесь употреблена в неразделительном смысле, т.е. не исключается одновременное обращение в нуль обоих множителей.
Над множествами можно выполнять действия (операции), напоминающие сложение и умножение чисел. Но не тождественные им.
Объединением (суммой) множеств А и В называется множество, обозначаемое через АÈВ, содержащее те и только те элементы, которые принадлежат множеству А или В.
Краткая запись: АÈВ = {x | xÎ A или х Î В}.
Соответствующая диаграмма Эйлера – Венна:
АÈВ- заштрихованная область
Пример: А = {2, 5, 7, 9}, В = {3, 5, 8, 9, 12}.
АÈВ = {2, 5, 7, 9}È{3, 5, 8, 9, 12}= {2, 5, 7, 9, 3, 8, 12}.
Соответствующая диаграмма:
Пересечением (произведением) множеств А и В называется множество, состоящее из тех и только из тех элементов, которые принадлежат множеству А и множеству В.
Краткая запись: АÇВ = {x | xÎ A и хÎ В}.
Соответствующая диаграмма Эйлера- Венна:
АÇВ – заштрихованная область
Пример: АÇВ= {2, 5, 7, 9}Ç{3, 5, 8, 9, 12}= {5,9}.
Диаграмма:
Алгебра множеств. Свойства операций объединения и пересечения множеств.
Можно заметить, что объединение и пересечение множеств обладают свойствами, аналогичными свойствам суммы и произведения чисел( рассматриваются все свойства)
Упражнения для самопроверки:
1. Выполнить операции объединения и пересечения над множествами
a) А = {-1;0} B= {0;1} b) A={-1; 2; 3; 4}, B = {0;4}
2. Найти объединение и пересечение множества всех рациональных чисел и множества иррациональных чисел.
Занятие №4.
Тема: Разность двух множеств.
В теории множеств рассматривается также и разность двух множеств.
Разностью множеств А и В называется множество, обозначаемое через А\В и состоящее из тех и только из тех элементов, которые принадлежат А и не принадлежат В.
Краткая запись: А\В = {x| xÎ A и xÏ B}.
Соответствующая диаграмма Эйлера- Венна:
А\В- заштрихованная область
Пример: А\В = {2, 5, 7, 9}\{3, 5, 8, 9, 12}= {2, 7}.
Диаграмма:
Если АÇВ = Æ, то А\В= А и В\А = В.
А
В
Если А В, то А\В = Æ.
Примеры для самопроверки:
Проиллюстрировать на кругах Эйлера:
- Разностью множества четных чисел вида 2к и множества чисел 3к является множество четных чисел, не делящихся на 3 , т.е. чисел вида 6к ± 2.
- Разностью множества четных чисел и множества нечетных чисел является множество четных чисел.
- Разностью множества четных чисел и множества целых чисел является пустое множество.
Занятие №5
Тема: Дополнение множества. Универсальное множество.
Часто рассматриваются множества, элементами которых являются только некоторые действительные числа, т.е. по существу подмножества всех действительных чисел. Тогда имеет смысл ввести новое понятие – дополнение Ā к данному множеству А. Элементами его являются все действительные числа, не принадлежащие множеству А. Так, например, дополнением к множеству положительных чисел является множество всех неположительных чисел, состоящее из нуля и всех отрицательных чисел. Дополнением к отрезку [0;1] служит объединение двух открытых лучей (-∞; 0) и (0; +∞ ).
Для любых двух подмножеств А и В основного множества Е справедливы равенства, которые называются законам Моргана.
1.АВ = Ā В 2. АВ = Ā В,
Таким образом, определение дополнения существенно зависит от того, до чего мы данное множество дополняем. Это множество всех элементов, рассматриваемых в данном вопросе, называют универсальным, мы обозначим его буквой U. Именно относительно него и берутся дополнения, без его указания понятие дополнения остается неопределенным.
Из приведенных определений вытекает, что объединение множества и его дополнения есть универсальное множество ( АĀ = U), а пересечение множества и его дополнения пусто (АĀ = Ø)
Если U – универсальное множество и А U, то разность U\A называется дополнением множества А до множества U и обозначается .
Краткая запись: Ā= {x| xÎU и xÏ A}.
Соответствующая диаграмма Эйлера- Венна:
Очевидно, что для любого подмножества, можно указать его дополнение до данного множества.
Рассмотрим множество двузначных чисел:
А={10;11;12;…98;99}
В={10;20;30;40;50;50:70;80;90} – двузначные числа, оканчивающиеся нулем, являются подмножеством множества двузначных чисел.
C- {11; 12…} – двузначные числа, не оканчивающиеся нулем, которые и будут являться дополнением подмножества В до множества А
Если некоторое множество D дополняется до некоторого другого множества R, то такое множество R называется универсальным множеством. Предполагается, что дополнение происходит до некоторого универсального множества, определяемого предметной областью задачи. Универсальное множество часто обозначается символом U. Любое множество является подмножеством универсального множества. Например:
1. Для множества натуральных чисел универсальным множество можно считать множество действительных чисел.
2. Для множества детей человеческого общества, универсальным множеством является множество всех людей.
3. Для множества учащихся 9 класса, универсальным множеством является множество школьников района.
Задача по теме:
Доказать законы де Моргана с помощью кругов Эйлера.
Занятие №6.
Тема: Конечные множества.
Множество называется конечным, если оно содержит конечное число элементов. Пусть А – некоторое конечное множество. Обозначим m(A) количество элементов в множестве А. Если А={xR|x2 -1 = 0}, то m(A) =2. Число элементов пустого множества рано нулю: m(Ø)=0.
Если конечное множество Ф представлено в виде объединения непересекающихся множеств А1, А2, ….Аi, то А1А2….Аi и А1Аi = Ø, то
m(A) = m(A1)+m(A2) +….+ m(Ai)
Проиллюстрируем теперь применение операций над множест вами для решения задач о нахождении числа элементов мно жеств, заданных несколькими условиями. Ниже мы будем рас сматривать только конечные множества.
Пример: В классе 30 учащихся, 16 из них занимаются му зыкой, 17 увлекаются теннисом, а 10 занимаются и музыкой, и теннисом. Есть ли в классе ученики, равнодушные и к музыке, и к теннису, и если есть, то сколько их?
Решение: Если сложить число учащихся, интересующихся музыкой, с числом учащихся, занимающихся теннисом, т. е. 16+17=33, то учащиеся, интересующиеся и музыкой, и тенни сом, окажутся учтенными дважды. Поэтому, чтобы определить число учащихся, интересующихся музыкой или теннисом, нужно из суммы 16+17 вычесть число учащихся, учтенных дважды, т. е. тех, кто интересуется и музыкой, и теннисом. По условию их 10. Таким образом, число интересующихся теннисом или музы кой равно: 16+17—10=23 ученика. А так как в классе всего 30 учащихся, то 30—23 ==7 учащихся равнодушны и к музыке, и к теннису.
Задача решена по следующему алгоритму: пусть имеется два конечных множества А и В. Тогда:
m(АÈВ) = m(А) + m(В )- m(АÇВ) (1)
В нашем случае А — множество учащихся, интересующихся му зыкой, и m(A) = 16, В—множество учащихся, интересующихся теннисом, и m(B) = 17, m(AÇB) =10, и тогда по полученной формуле m(AUВ)=16+17-10=23.
Усложним задачу: пусть к тем, кто интересуется в классе му зыкой — множеству А, и к тем, кто увлекается теннисом — мно жеству В, добавляются еще и те, кто интересуется театром— множество С. Сколько учеников увлекается или музыкой, или теннисом, или театром, т. е. чему равно число m{AÈBÈC)?
Если множества А, В и С пересекаются лишь попарно, т. е. АÇВÇС=Æ, то подсчет можно вести, как и прежде: снача ла сложить m(А)+m(В)+m(С), а затем вычесть число тех эле ментов, которые подсчитаны дважды, т. е. вычесть число m{AÇB}+m(AÇC)+m(BÇC). Если же множество АÇВÇС¹Æ,, то его элементы оказались неучтенными: сначала их трижды учли, когда складывали m(А}+m (В)+m(С), а затем трижды отнимали их, вычитая m{AÇB}+m(AÇC)+m(BÇC). Таким об разом, число m(А)+m(В)+m(С )- (m{AÇB}+m(AÇC)+m(BÇC))
меньше истинного результата ровно на число элементов в пере сечении множеств АÇВÇС, которое и следует добавить для по лучения верного результата:
m(А)+m(В)+m(С )- (m{AÇB}+m(AÇC)+m(BÇC))+m(АÇВÇС) (2)
Аналогичная формула может быть получена для любого числа множеств.
В формулах (1) и (2) подсчитывается, сколько раз каждый элемент включается и исключается, поэтому их называют фор мулами включений и исключений.
Рассмотрим несколько примеров применения полученных формул.
Пример1: На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и стереометрии. Из 1000 абитуриентов задачу по алгебре решили 800, по планиметрии — 700, а по стереометрии — 600 абитуриентов. При этом задачи по алгебре и планиметрии решили 600 абитуриен тов, по алгебре и стереометрии — 500, по планиметрии и стерео метрии — 400. Все три задачи решили 300 абитуриентов. Суще ствуют ли абитуриенты, не решившие ни одной задачи, и если да, то сколько их?
Решение. Пусть U — множество всех абитуриентов, А —. множество абитуриентов, решивших задачу по алгебре, В — множество абитуриентов, решивших задачу по планиметрии, С — множество абитуриентов, решивших задачу по стереометрии. По условию n(U) =1000, n(A) = 800, n(В)=700, n(С)=600, n(AÇB)= 600, n(AÇC) = 500, n(BÇC) = 400, n(AÇBÇC) =300. В множество AÇBÇC включены все абитуриенты, решившие хо тя бы одну задачу. По формуле (2) имеем:
m(А U В U С) == 800 + 700 + 600 — 600 — 500 — 400 + 300 =900.
Отсюда следует, что не все поступающие решили хотя бы одну задачу. Ни одной задачи не решили
m(U) — m(AUBUC)=1000 — 900==100 (абитуриентов).
Пример2: Социологи опросили 45 учащихся девятых клас сов, среди которых 25 юношей. При этом выяснилось: 30 человек имеют за полугодие оценки 4 и 5, из них 16 юношей, спортом занимаются 28 учеников, среди них 18 юношей, и 17 учеников, успевающих только на хорошо и отлично, 15 юношей учатся на хорошо и отлично и занимаются спортом. Первый математик класса взглянул на результаты и заявил, что там есть ошибки. Как это ему удалось выяснить?
Решение: Обозначим через А множество юношей, В — множество успевающих на 4 и 5, С — множество спортсменов. По условию задачи m(A)=25,m(В)=30, m(С)=28, m(AÇB)=16, m(AÇC)=18, m(BÇC)=17, m(AÇBÇC)=15. Найдем общее чис ло учащихся, которые или являются юношами, или занимаются спортом, или успевают на 4 и 5. По формуле (2) получаем:
m (A UBUC)=25+30+28- 16- 18- 17+15=47. Этого быть не может, так как обследовалось всего 45 учеников! Следовательно, в данных сведениях есть ошибки.
На рисунке это решение проиллюстрировано с помощью диаграммы Эйлера — Венна. В пересечении множеств А, В и С за пишем число 15, так как по условию m(AÇBÇC)=15. В мно жестве AÇB\С запишем число 16—15=1, в множестве BÇC\А — число 18-15=3, в множестве BÇC\А—число 17-15=2, в множестве A\(BÈC)— число 25-(1+15+3)=6, в множестве В\(А ÈC) — число 30-(1 + 15+2)= 12, в множест ве С\(АÈВ)— число 28-(3+15+2)=8. Чтобы найти m(АÈВÈС), достаточно сложить записанные числа, поскольку они соответствуют множествам, не пересекающимся между со бой. Получим число 47 > 45, что невозможно по условию задания
Задачи для самостоятельного решения:
1. В классе 30 учеников. Известно, что 18 ребят имеют спртивный разряд по лыжам, а 16 –по плаванию. Десять учеников не имеют разряда ни по плаванию, ни по лыжам. Сколько ребят имеют спортивный разряд по плаванию, и по лыжам?
2. В группе туристов, посетивших нашу страну, 30 женщин, 25 человек из Польши, 15 мужчин из Канады, 43 человека из Европы. Треть женщин группы из Польши, а две женщины из Канады. Сколько туристов в этой группе, если каждый попал, хотя бы в одну из упомянутых групп?
Занятие №7
Тема: Эквивалентность множеств. Счетные и несчетные множества.
Основная характеристика множества есть его количество его элементов или его мощность.
Количество элементов в некотором множестве называется его численностью. Запись вида m(D)=12 обозначает, что число элементов в этом множестве D равно12.
Множества, имеющие одинаковую мощность, называются равномощными или эквивалентными множествами
Множества считаются равными, если они состоят из одних и тех же элементов.
Множество называется счетным, если оно равномощно множеству натуральных чисел. В противном случае множество называется несчетным.
Множество, содержащее конечное число элементов, называется конечным множеством, а множество, содержащее бесконечное число элементов – бесконечным множеством.
Множества называется конечным, если элементы их можно пересчитать.
Множество называется бесконечным, если число их элементов нельзя пересчитать или нельзя, по крайней мере, указать правило, которое позволяет теоретически установить число их элементов.
Проблема установления конечности или бесконечности множества, на первый взгляд кажется очевидной, но с точки теории множеств очень сложная.
Рассмотрим несколько примеров.
Число песчинок в стакане очень большое, но, тем не менее, их можно пересчитать, значит, их конечное число.
Множество N – натуральные числа бесконечно. В этом можно легко убедиться, если понять, что к любому, пусть даже самому большому натуральному числу всегда можно прибавить, по крайней мере, число 1.
Бесконечными являются и другие основные числовые множества:
Q -рациональные числа Z – целые числа R – действительные числа
Правомочен вопрос о сравнении числа элементов в этих множествах. А, именно, какое из основных числовых множеств “более бесконечное”, чем другие. Ответы на такие вопросы представляют чисто теоретический аспект и далеко выходят за рамки данного предмета разговора.
Рассмотрим способ сравнения множеств, который будет применим как к конечным, так и к бесконечным множествам. Допустим, к вам пришли гости, и вы должны накрыть стол. Для этого совсем не обязательно сначала пересчитать гостей, а потом отсчитать нужное количество тарелок и приборов. Можно просто рассадить гостей и перед каждым поставить тарелку и положить прибор. Такое попарное сочетание элементов разных множеств называется взаимно однозначным соответствием.
Теорема о количестве подмножеств конечного множества.
Рассмотрим множество А = {1, 2, 3 }, где |A| = 3, и множество В = {5, 6, 7, 8}, где |B| = 4.
Составим всевозможные подмножества множества А:
А, Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}.
Всего получили 8 подмножеств.
Составим всевозможные подмножества множества В:
В, Æ, {5}, {6}, {7}, {8}, {5,6}, {5,7}, {5,8}, {6,7}, {6,8}, {7,8}, {5,6,7}, {5,7,8}, {6,7,8}, {5,6,8}.
Получили 16 подмножеств.
Используя результаты рассмотренных примеров, можно предположить справедливость следующего равенства: n = 2m, где n – количество подмножеств данного конечного множества, m – мощность множества.
Справедливость предположения подтверждает теорема, которую мы примем без доказательства.
Теорема: Если для конечного множества А его мощность равна m, то количество всех подмножеств данного множества, обозначаемое Р(А), равно 2m.
Пример: Вычислить количество подмножеств множества М – делителей числа 20.
Составим множество М и найдем его мощность:
М = {1,2,4,5,10,20}. Мощность |M| = 6, тогда количество подмножеств равно Р(М) = 26 = 64.
Задачи для самостоятельного решения
1.Покажите, что множество рациональных чисел счетно.
2. Покажите, что множество чисел, кратных 4 счетно.
3.Покажите, что множество нечетных положительных чисел и множество положительных чисел, дающих при делении на 8 остаток 2, равномощны.
4. Покажите, что множества (1,4) и (-2,1) равномощны
Занятие №8
Зачетное занятие
Контрольные вопросы:
Объясните понятие множества. Приведите примеры множеств. Как обозначаются множества и их элементы?
Какие существуют способы задания множеств?
С помощью характеристического свойства задайте конечное, бесконечное несчетное, бесконечное счетное и пустое множества.
Как обозначается принадлежность элемента множеству и не принадлежность?
Какие существуют отношения между двумя множествами?
Перечислите операции над множествами с приведением соответствующих диаграмм Эйлера – Венна.
Перечислите тождества алгебры множеств.
Сформулируйте теорему о количестве подмножеств конечного множества.
Запишите формулы количества элементов в объединении двух и трех множеств.
Задачи
1.Задайте множества перечислением их элементов:
A={x €R$ (x4-1)(x4-9)=0}
B={x € Q$ (x3+1)(x4-4)=0}
Найдите АВ, А\В
2.Пусть А,В,С,Д – подмножества основного множества Е.
Найдите выражение для Д через А,В,С, если известно, что:
а) хД, и х принадлежит В, но не принадлежит А и С.
б) хД, и х принадлежит по крайней мере одному из множеств А,В,С.
в)хД, и х принадлежит ровно одному из множеств А,В,С.
г) хД, и х принадлежит ровно двум из множеств А,В,С.
3. Из 26 учеников класса 16 человек сдали норматив по лыжам, а 12 человек – по плаванию. Сколько учеников сдали оба норматива, если 4 ученика не смогли сдать ни одного.
4. Покажите, что множество рациональных чисел счетно.
Покажите, что множество чисел, кратных 4, счетно.
Покажите, что множество нечетных положительных чисел и множество положительных чисел, дающих при делении на 8 остаток 2 равномощны.
Покажите, что множества (1,3) и [4,8] равномощны.
Предлагаемая литература:
1. Элементы теории множеств и математической логики в школьном курсе математики. Создатель: Калужин Л. Издательство: Просвещение. 1978 год.
2. Дополнительные главы по курсу математики. Составитель: Стратилатов П.В. Москва. Просвещение. 1974 год.
3. Математическая логика. Автор: Колмогоров А.Н., Драгалин А.Г. Издательство: КомКнига. 2006 год.
4. Беседы о математике. Создатель: Болтянский В.Г., Савин А.П.. Издательство: МЦНМО. 2002 год.
Программу составила:
УЧИТЕЛЬ МАТЕМАТИКИ Ханзярова Гельфира Харисовна
МОУ СТАРОДРОЖЖАНОВСКАЯ СОШ № 2
Теория множеств имеет свои собственные обозначения и символы, которые могут показаться необычными для многих. В этом уроке мы рассмотрим несколько решенных примеров, чтобы понять, как работает теория множеств и какие проблемы можно использовать для ее решения.
Определение
Набор представляет собой набор объектов.
Это обычно представлено в цветочных скобках.
Например, :
Набор натуральных чисел = {1,2,3,…..}
Набор целых чисел = {0,1,2,3,… ..}
Каждый объект называется элементом множества.
Набор, содержащий все элементы данного набора, называется универсальным набором и представлен символом «µ», произносится как «mu».
Для двух комплектов A и B,
- n (AᴜB) — количество элементов, присутствующих в любом из наборов A или B.
- n (A∩B) — количество элементов, присутствующих в наборах A и B.
- n (AᴜB) = n (A) + (n (B) — n (A∩B)
Для трех комплектов A, B и C,
- n (AᴜBᴜC) = n (A) + n (B) + n (C) — n (A∩B) — n (B∩C) — n (C∩A) + n (A∩B∩C)
Рассмотрим следующий пример:
Вопрос: В классе из 100 учеников 35 — как наука, а 45 — как математика.10 как и то и другое. Кто из них любит кого-то, а кто нет?
Решение :
Общее количество студентов, n (µ) = 100
Число студентов естественных наук, n (S) = 35
Число студентов математики, n (M) = 45
Число студентов, которым нравятся оба, n (M∩S) = 10
Число студентов, которым нравится один из них,
n (MᴜS) = n (M) + n (S) — n (M∩S)
→ 45 + 35-10 = 70
Число студентов, которым не нравится ни = n (µ) — n (MᴜS) = 100 — 70 = 30
Самый простой способ решить проблемы на множествах — нарисовать диаграммы Венна, как показано ниже.
Как говорится, одна картинка стоит тысячи слов. Одна диаграмма Венна может помочь решить проблему быстрее и сэкономить время. Это особенно верно, когда в проблему вовлечено более двух категорий.
Давайте посмотрим еще несколько решенных примеров.
Задача 1: В классе 30 учеников. Среди них 8 студентов изучают английский и французский языки. Всего 18 студентов изучают английский язык. Если каждый студент изучает хотя бы один язык, сколько студентов изучают французский в целом?
Решение :
Диаграмма Венна для этой задачи выглядит следующим образом.
Каждый студент изучает хотя бы один язык. Следовательно, нет никого, кто попадет в категорию «ни».
Таким образом, в этом случае n (EᴜF) = n (µ).
В проблеме упоминается, что всего 18 учат английский. Это НЕ означает, что 18 учат только английский. Только тогда, когда слово «только» упоминается в проблеме, мы должны считать это так.
Сейчас 18 учат английский и 8 учат оба. Это означает, что 18 — 8 = 10 учат только английский.
n (µ) = 30, n (E) = 10
n (EᴜF) = n (E) + n (F) — n (E∩F)
30 = 18+ n (F) — 8
n (F) = 20
Таким образом, общее количество студентов, изучающих французский язык = 20.
Примечание : Вопрос был только об общем количестве студентов, изучающих французский язык, а не о тех, кто изучает ТОЛЬКО французский, что было бы другим ответом, 12.
Наконец, диаграмма Венна выглядит следующим образом.
Задача 2: Из группы студентов 50 играли в крикет, 50 играли в хоккей и 40 играли в волейбол.15 играли в крикет и хоккей, 20 играли в хоккей и волейбол, 15 играли в крикет и волейбол и 10 играли все три. Если каждый учащийся сыграл хотя бы в одну игру, найдите количество учеников и сколько из них сыграли только в крикет, только в хоккей и только в волейбол?
Решение :
n (C) = 50, n (H) = 50, n (V) = 40
n (C∩H) = 15
n (H∩V) = 20
n (C∩V) = 15
n (C∩H∩V) = 10
Число студентов, сыгравших хотя бы в одной игре
n (CᴜHᴜV) = n (C) + n (H) + n (V) — n (C∩H) — n (H∩V) — n (C∩V) + n (C∩H∩V)
= 50 + 50 + 40 — 15 — 20 — 15 + 10
Общее количество студентов = 100.
Позвольте обозначить количество людей, которые играли только в крикет и волейбол.
Пусть b обозначает количество людей, которые играли только в крикет и хоккей.
Пусть c обозначает число людей, которые играли только в хоккей и волейбол.
Пусть d обозначает количество людей, которые играли во все три игры.
Соответственно, d = n (CnHnV) = 10
Теперь n (CnV) = a + d = 15
n (CnH) = b + d = 15
n (HnV) = c + d = 20
Следовательно, a = 15 — 10 = 5 [только для игры в крикет и волейбол]
b = 15 — 10 = 5 [только для игры в крикет и хоккей)
с = 20 — 10 = 10 [только для хоккея и волейбола]
№студентов, которые играли только в крикет = n (C) — [a + b + d] = 50 — (5 + 5 + 10) = 30
Число учеников, которые играли только в хоккей = n (H) — [b + c + d] = 50 — (5 + 10 + 10) = 25
Число учеников, которые играли только в волейбол = n (V) — [a + c + d] = 40 — (10 + 5 + 10) = 15
В качестве альтернативы, мы можем решить это быстрее с помощью диаграммы Венна.
Диаграмма Венна для данной информации выглядит следующим образом.
Вычитание значений в пересечениях из отдельных значений дает нам количество студентов, которые играли только в одну игру.
Викторина по теории множеств: Решите эти проблемы на практике
Задача 1
В группе было 115 человек, чьи удостоверения личности были проверены. У некоторых был паспорт, у некоторых — удостоверение личности избирателя, а у некоторых — и то, и другое. Если у 65 был паспорт, а у 30 — оба, у скольких был только идентификатор избирателя, а не паспорт?
A. 30
B. 50
C. 80
D. Ничто из перечисленного
Ответ 1
B.
Объяснение
Давайте нарисуем диаграмму Венна для данной информации.
n (PᴜV) = n (P) + n (V) — n (P∩V)
115 = 65 + n (V) — 30
n (V) = 80
Люди только с идентификатором избирателя = 80-30 = 50
Задача 2
Среди группы людей 40% любят красный, 30% — синий и 30% — зеленый. 7% понравились как красный, так и зеленый, 5% — красный и синий, 10% — зеленый и синий. Если 86% из них понравился хотя бы один цвет, то какой процент людей понравились все три?
А.10
B. 6
C. 8
D. Нет
Ответ 2
C.
Объяснение :
n (RᴜBᴜG) = n (R) + n (B) + n (G) — n (R∩B) — n (B∩G) — n (R∩G) + n (R∩G∩B)
86 = 40 + 30 + 30-5-10-7 + n (R∩G∩B)
Решение этой проблемы дает 8.
,Основная Теория Множества
Наборы — это четко определенные коллекции, которые полностью характеризуется своими элементами. Таким образом, два набора равны, если и только если они имеют точно такие же элементы. Основное отношение в наборе теория — это элементность или членство. Мы пишем \ (a \ in A \) в указать, что объект \ (a \) является элементом , или член из набора \ (A \). Мы также говорим, что \ (a \) принадлежит до \ (А \).Таким образом, множество \ (A \) равно множеству \ (B \) тогда и только тогда, когда для каждый \ (a \), \ (a \ in A \) тогда и только тогда, когда \ (a \ in B \). В частности, есть только один набор без элементов вообще. Этот набор называется, естественно, пустой набор , и представлен символом \ ({\ Varnothing} \).
Мы говорим, что \ (A \) — это подмножество из \ (B \), написанное \ (A \ subseteq B \), если каждый элемент \ (A \) является элементом \ (B \). Таким образом, \ (A = B \), если и только если \ (A \ subseteq B \) и \ (B \ subseteq A \). Заметь \ ({\ varnothing} \ subseteq A \), для каждого множества \ (A \).
Для заданных множеств \ (A \) и \ (B \) можно выполнить несколько основных операций с они дают следующие наборы:
Набор \ (A \ cup B \), называемый объединением из \ (A \) и \ (B \), чей элементы — это элементы \ (A \) и элементы \ (B \).
Набор \ (A \ cap B \), называемый пересечением из \ (A \) и \ (B \), элементы которого являются элементами, общими для \ (A \) и \ (B \).
Набор \ (A-B \), называемый разницей из \ (A \) и \ (B \), чей элементы — это те элементы \ (A \), которые не являются членами \ (В \).
Обычно проверяется, удовлетворяют ли эти операции следующим Недвижимость:
Для данного объекта \ (a \) мы можем сформировать множество, в котором \ (a \) есть только его элемент. Этот набор обозначается \ (\ {a \} \). В целом, учитывая \ (a, b, c, \ ldots \), мы можем сформировать множество, имеющее \ (a, b, c, \ ldots \) в качестве его элементы, которые мы обозначим через \ (\ {a, b, c, \ ldots \} \). Конечно, мы можем на самом деле запишите все элементы набора, когда не слишком многие из них. В случае бесконечных множеств это явно не возможно.
Если \ (a = b \), то \ (\ {a, b \} = \ {a \} \). Кроме того, для любых \ (a \) и \ (b \) Пара \ (\ {a, b \} \) совпадает с парой \ (\ {b, a \} \). Итак, если мы хотим принять во внимание порядок, в котором два элемента пары учитывая, что нам нужно найти другой способ представления пары. Таким образом, мы определить упорядоченную пару \ ((a, b) \) как множество \ (\ {\ {a \}, \ { а, Ь \} \} \). Можно легко проверить, что две упорядоченные пары \ ((a, b) \) и \ ((c, d) \) равны тогда и только тогда, когда \ (a = c \) и \ (b = d \). Заказ сейчас важно, если \ (a \ ne b \), то \ ((a, b) \ ne (b, a) \).
Декартово произведение \ (A \ times B \) из двух множеств, \ (A \) и \ (B \), определяется как множество всех упорядоченных пар \ ((a, b) \) таких, что \ (a \ in A \) и \ (b \ in B \).
Определив упорядоченные пары, теперь можно определить упорядоченных утроить \ ((a, b, c) \) как \ ((a, (b, c)) \) или вообще упорядочить \ (n \) — кортежи \ ((a_1, \ ldots, a_n) \) as \ ((a_1, (a_2, \ ldots, a_n)) \).
декартово произведение \ (A_1 \ times \ ldots \ times A_n \) множеств \ (A_1, \ ldots, A_n \) — это множество всех \ (n \) — кортежей \ ((a_1, \ ldots, a_n) \) такой, что \ (a_i \ in A_i \), для каждого \ (1 \ leq i \ leq n \).п \).
Бинарное отношение \ (R \) на множестве \ (A \) называется рефлексивным , если \ ((a, a) \ in R \) для каждого \ (a \ in A \). Это называется симметричным, если \ ((b, a) \ in R \) всякий раз, когда \ ((a, b) \ in R \). И это называется переходным , если \ ((a, c) \ in R \) всякий раз, когда \ ((a, b) \ in R \) и \ ((b, c) \ in R \). Отношение, которое является рефлексивным, симметричным и переходным называется отношением эквивалентности . Отношение личности на любое множество \ (A \) является парадигматическим примером эквивалентности связь.Другим примером является отношение на множестве всех конечных множества натуральных чисел, состоящих из всех пар \ ((a, b) \) таких, что \ (a \) и \ (b \) имеют одинаковое количество элементов.
Если \ (R \) является отношением эквивалентности на множестве \ (A \) и \ ((a, b) \ in R \), тогда мы говорим, что \ (a \) и \ (b \) являются \ (R \) — эквивалентными . Для каждый \ (a \ in A \), класс эквивалентности из \ (a \), обычно обозначаемый \ ([a] _R \) — множество всех элементов \ (A \), эквивалентных \ (R \) к \ (а \).Множество всех \ (R \) — классов эквивалентности называется фактор-набор и обозначается \ (A / R \). Можно легко проверьте, что \ (A / R \) является разделом из \ (A \), то есть без элемента из \ (A / R \) пусто, любые два элемента \ (A / R \) не пересекаются, и каждый \ (a \ in A \) принадлежит (ровно) одному элементу \ (A / R \), а именно классу \ ([А] _R \).
Если \ (R \) — бинарное отношение, то вместо него обычно пишется \ (aRb \) из \ ((a, b) \ in R \).
Бинарное отношение \ (R \) на множестве \ (A \) называется антисимметричным если \ (a = b \) всякий раз, когда \ (aRb \) и \ (bRa \).Отношение \ (R \) на множестве \ (A \), которое рефлексивный, антисимметричный и транзитивный, называется (возвратный) частичный заказ . Если мы удалим из \ (R \) все пары \ ((a, a) \), для каждого \ (a \ in A \), тогда мы получим строгий частичный порядок. Отношение \ (\ subseteq \) на любом наборе множеств является примером частичный заказ. Частичный порядок на данном множестве \ (A \) обычно обозначается символом \ (\ leq \) и соответствующим строгим частичным упорядочение по \ (<\). Частичный порядок \ (\ leq \) на множестве \ (A \) с дополнительное свойство, которое \ (a \ leq b \) или \ (b \ leq a \), для всех элементы \ (a \) и \ (b \) of \ (A \), называется общим порядком , , или линейный порядок .2 \) также линейный порядок на \ (В \). Если \ (\ leq \) — линейный порядок на множестве \ (A \), то мы говорим, что \ (a \ in A \) является \ (\ leq \) — наименьшим элементом \ (A \), если нет \ (b \ in A \) отличного из \ (a \) такой, что \ (b \ leq a \). Число \ (0 \) является наименьшим элементом \ (\ mathbb {N} \), но \ (\ mathbb {Z} \) не имеет наименьшего элемента.
Линейный порядок \ (\ leq \) на множестве \ (A \) — это -порядковый номер , если
каждое непустое подмножество \ (A \) имеет \ (\ leq \) — минимум
элемент. Эквивалентно, если нет бесконечного строго по убыванию
последовательность \ [\ ldots A (\ (1 \) — ary) Функция на множестве \ (A \) является бинарным отношением \ (F \)
на \ (A \) такой, что для каждого \ (a \ in A \) существует ровно одна пара
\ ((a, b) \ in F \). Элемент \ (b \) называется значением из \ (F \) на
\ (a \) и обозначается через \ (F (a) \). И множество \ (A \) называется
домен из \ (F \).n \ to B \),
для некоторых \ (B \). Функция \ (F: A \ to B \) равна один к одному , если для всех элементов
\ (a \) и \ (b \) of \ (A \), если \ (a \ ne b \), то \ (F (a) \ ne F (b) \). И
с на , если для каждого \ (b \ in B \) найдется некоторое \ (a \ in A \) такое
что \ (F (a) = b \). Наконец, \ (F \) — это , биективное , если оно однозначно
и на. Таким образом, биекция \ (F: A \ to B \) устанавливает взаимно однозначное
соответствие между элементами \ (A \) и элементами \ (B \) и \ (A \) может быть выдано с \ (B \), если есть такая
биекция.Тождественная функция на множестве \ (A \), обозначаемая
\ (Id: A \ to A \) и состоит из всех пар \ ((a, a) \), причем \ (a \ in
А \), это тривиально биекция. Для заданных функций \ (F: A \ to B \) и \ (G: B \ to C \) композиция из
\ (F \) и \ (G \) , написанные \ (G \ circ F \), есть функция \ (G \ circ F: A \ to
C \), элементами которого являются все пары \ ((a, G (F (a))) \), где \ (a \ in A \). Если \ (F \)
и \ (G \) биекции, то \ (G \ circ F \). Формальный язык теории множеств — первый порядок
язык, единственным нелогичным символом которого является символ двоичного отношения
\(\в\). Для любой формулы \ (\ varphi (x, y_1, \ ldots, y_n) \) языка
теория множеств и множества \ (A, B_1, \ ldots, B_n \), можно составить множество всех
те элементы \ (A \), которые удовлетворяют формуле \ (\ varphi (x, B_1, \ ldots)
, B_n) \). Этот набор обозначается \ (\ {a \ in A: \ varphi (a, B_1, \ ldots)
, B_n) \} \). Ниже приведены некоторые примеры \ ({\ varnothing} = \ {a \ in A: a \ ne a \} \) \ (A = \ {a \ in A: a = a \} \) \ (A-B = \ {a \ in A: a \ not \ in B \} \). \ (A \ cap B = \ {a \ in A: a \ in B \} \). И если \ (B \) и \ (C \) являются подмножествами \ (A \), то Учитывая подмножество \ (C \ subseteq A \ times B \), проекция из
\ (C \) (по первой координате) — множество \ (\ {a \ in A: \ существует b \ in B ((a, b) \ in C) \} \). Это не тот случай, однако, учитывая любую формулу
\ (\ varphi (x, y_1, \ ldots, y_n) \) и множества \ (B_1, \ ldots, B_n \), можно сформировать
множество всех тех множеств, которые удовлетворяют формуле
\ (\ varphi (x, B_1, \ ldots, B_n) \).Ибо пусть \ (\ varphi (x) \) — формула
\ (х \ не \ в х \). Если \ (A \) было множество всех множеств, которые удовлетворяют
формула, то \ (A \ in A \) тогда и только тогда, когда \ (A \ not \ in A \). Противоречие!
Это противоречие известно как парадокс Рассела , после
Бертран Рассел, который открыл его в 1901 году (см. Запись на
Парадокс рассела). Первый порядковый номер — \ ({\ varnothing} \). Учитывая порядковый номер
\ (\ alpha \), следующий больший порядковый номер, называется
(немедленно) наследник из \ (\ alpha \), это набор \ (\ alpha \ cup \ {
\ alpha \} \).Таким образом, наследник \ (\ alpha \) — это просто множество \ (\ alpha \)
вместе с еще одним элементом, а именно, \ (\ alpha \)
сам. Конечные порядковые числа — это те, которые получены
начиная с \ ({\ varnothing} \) и повторно выбирая преемника. В теории множеств натуральные числа определяются как
конечные ординалы. Таким образом, \ (0 = {\ varnothing} \) \ (1 = {\ varnothing} \ cup \ {{\ varnothing} \} = \ {
{\ varnothing} \} \) \ (2 = \ {{\ varnothing} \} \ cup \ {\ {{\ varnothing} \} \} = \ {{\ varnothing},
\ {{\ varnothing} \} \} \) \ (3 = \ {{\ varnothing}, \ {{\ varnothing} \} \} \ cup \ {\ {{\ varnothing},
\ {{\ varnothing} \} \} \} = \ {{\ varnothing}, \ {{\ varnothing} \}, \ {
{\ varnothing}, \ {{\ varnothing} \} \} \} \) \ (\ vdots \) Обратите внимание, что \ (1 = \ {0 \} \), \ (2 = \ {0,1 \} \), \ (3 = \ {0,1,2 \} \) и в
В общем, мы имеем \ (n = \ {0,1,2, \ ldots, n-1 \} \).Итак, каждое натуральное число
\ (n \) — это просто набор его предшественников. Набор \ (A \) равен , конечный , если существует один-к-одному
соответствие между некоторым натуральным числом \ (n \) и элементами
\ (A \), т.е. биекция \ (F: n \ to A \), и в этом случае мы говорим, что \ (A \) имеет
\ (n \) элементов. Набор бесконечен , если он не конечен. Множество всех конечных ординалов обозначается греческой буквой омега
(\(\омега\)). Таким образом, \ (\ omega \) — это просто множество \ (\ mathbb {N} \) натурального
номера.\ (\ omega \) также ординал, первый бесконечный
порядковый. Обратите внимание, что \ (\ omega \) не является преемником какого-либо порядкового номера, и
поэтому он называется предельным порядковым номером . Как только у нас есть \ (\ omega \), мы можем
продолжайте генерировать больше порядковых чисел, взяв его преемника \ (\ omega \ cup
\ {\ omega \} \), затем его преемник \ ((\ omega \ cup \ {\ omega \}) \ cup
\ {\ omega \ cup \ {\ omega \} \} \) и так далее. Все порядковые номера больше
чем \ (0 \) производятся таким образом, а именно, беря
наследник последнего произведенного порядкового номера, или, если такого последнего нет
порядковый номер, взяв множество всех порядковых чисел, произведенных до
случай \ (\ omega \), который дает новый предельный ординал.Обратите внимание, однако,
что нельзя взять набор всех ординалов, для этого
set будет новым предельным порядковым числом, что невозможно, так как мы
уже были их все. Как и в случае конечных порядковых чисел, каждый бесконечный порядковый номер представляет собой просто набор
его предшественники. Одним из следствий этого является то, что отношение \ (\ in \)
строгий порядок на любом множестве ординалов. Таким образом, для любых ординалов
\ (\ alpha \) и \ (\ beta \) мы определяем \ (\ alpha <\ beta \) тогда и только тогда, когда
\ (\ alpha \ in \ beta \). Тогда связанный рефлексивный порядок
определяется как \ (\ alpha \ leq \ beta \) тогда и только тогда, когда \ (\ alpha <\ beta \) или
\ (\ alpha = \ beta \).Давайте теперь заметим, что \ (\ alpha \ subseteq \ beta \), если
и только если \ (\ alpha \ leq \ beta \). Если \ (A \) конечное множество, существует биекция \ (F: n \ to A \) между
натуральное число \ (n \) и \ (A \). Любая такая биекция дает , считая элементов \ (A \), а именно \ (F (0) \) является
первый элемент \ (A \), \ (F (1) \) — второй и т. д. Таким образом, все
конечные множества счетны. Бесконечное множество \ (A \) называется счетной , если есть биекция \ (F: \ omega \ to A \)
между множеством натуральных чисел и \ (A \).Множество \ (\ mathbb {N} \) из
натуральные числа (тривиально) счетны. Если \ (A \) бесконечное подмножество
из \ (\ omega \), то \ (A \) также счетно: так как пусть \ (F: \ omega \ to A \)
такой, что \ (F (n) \) — наименьший элемент из \ (A \), которого нет в множестве
\ (\ {F (m) \ in A: m Каждое бесконечное подмножество счетного множества также счетно: для
предположим, что \ (F: \ omega \ to A \) биекция, а \ (B \ subseteq A \)
бесконечный. Тогда множество \ (\ {n \ in \ omega: F (n) \ in B \} \) бесконечно
подмножество \ (\ omega \), следовательно, счетное, и поэтому существует биекция
\ (G: \ omega \ to \ {n \ in \ omega: F (n) \ in B \} \).Тогда композиция
Функция \ (F \ circ G: \ omega \ to B \) является биекцией. Объединение счетного множества и конечного множества также
счетно. Для заданных множеств \ (A \) и \ (B \), которые без потери
общности мы можем предположить, что они не пересекаются, и учитывая биекции
\ (F: \ omega \ to A \) и \ (G: n \ to B \), для некоторых \ (n <\ omega \) пусть \ (H: \ omega
\ to A \ cup B \) - биекция, определяемая как: \ (H (m) = G (m) \) для каждого
\ (m Кроме того, объединение двух счетных множеств также счетно:
мы уже показали, что объединение счетного множества и конечного
множество также исчисляемо, достаточно увидеть, что объединение двух
непересекающиеся счетные множества также счетны.Итак, предположим, что \ (A \) и \ (B \)
счетные множества и \ (F: \ omega \ to A \) и \ (G: \ omega \ to B \)
биекции, то функция \ (H: \ omega \ to A \ cup B \), состоящая из всех
пары \ ((2n, F (n)) \), плюс все пары \ ((2n + 1, G (n)) \) является биекцией. Таким образом, множество \ (\ mathbb {Z} \), являющееся объединением двух счетных множеств,
а именно \ [\ mathbb {N} \ cup \ {-1, -2, -3, -4, \ ldots \} \] также
счетно. Декартово произведение двух бесконечных счетных множеств также
счетно. Предположим, что \ (F: \ omega \ to A \) и \ (G: \ omega \ to B \)
биекциями.m (2n + 1) -1) = (F (m), G (n)) \) также является биекцией. Поскольку любое рациональное число задается парой целых чисел, то есть
частное \ (\ frac {m} {n} \), где \ (m, n \ in \ mathbb {Z} \) и \ (n \ ne 0 \),
множество \ (\ mathbb {Q} \) рациональных чисел также счетно. Однако Георг Кантор обнаружил, что множество \ (\ mathbb {R} \) вещественных
числа не исчисляются Предположим, стремясь к противоречию,
что \ (F: \ omega \ to \ mathbb {R} \) является биекцией. Пусть \ (a_0 = F (0) \). выберите
наименьшее \ (k \) такое, что \ (a_0 Существование несчетных множеств следует из гораздо более общего
факт, также обнаруженный Кантором.А именно, учитывая любой набор \ (A \), набор
все его подмножества, называемые мощностью от \ (A \), и обозначаются как
\ (\ mathcal {P} (A) \), не является биектабельным с \ (A \): поскольку предположим, что \ (F: A \ to
\ mathcal {P} (A) \) является биекцией. Тогда подмножество \ (\ {a \ in A: a \ not \ in
F (a) \} \) для \ (A \) является значением \ (F (a) \) некоторого \ (a \ in A \). Но тогда \ (а \ в
F (a) \) тогда и только тогда, когда \ (a \ not \ in F (a) \). Следовательно, если \ (A \) бесконечно
множество, то \ (\ mathcal {P} (A) \) несчетно. Есть также бесчисленные ординалы.Множество всех конечных и
исчисляемые порядковые числа также являются порядковыми числами, называемыми \ (\ omega_1 \), и являются
первый неисчислимый ординал Точно так же множество всех порядковых
bijectable с некоторым порядковым числом, меньшим или равным \ (\ omega_1 \), также
порядковый номер, называемый \ (\ omega_2 \) и не подлежащий биектированию с \ (\ omega_1 \),
и так далее. кардинальности, или размер, конечного множества \ (A \) является
уникальное натуральное число \ (n \) такое, что существует биекция \ (F: n \ to
А \). В случае бесконечных множеств их мощность задается, а не
натуральное число, но по бесконечному порядковому номеру. Однако в отличие от
конечные множества, бесконечное множество \ (A \) биектабельно с множеством различных
порядковые номера. Например, множество \ (\ mathbb {N} \) можно биэктивировать с
\ (\ omega \), но также и с его преемником \ (\ omega \ cup \ {\ omega \} \): by
присваивая \ (0 \) \ (\ omega \) и \ (n + 1 \) \ (n \), для всех \ (n \ in \ omega \) мы
получить биекцию между \ (\ omega \ cup \ {\ omega \} \) и \ (\ omega \).Но
поскольку порядковые порядки упорядочены, мы можем определить мощность
бесконечное множество как наименьший порядковый номер, который может быть с ним вычислен. В частности, мощность порядкового числа \ (\ alpha \)
наименьший порядковый номер \ (\ kappa \), который можно вычислить с ним. Заметь
\ (\ kappa \) не является биектабельным с меньшим порядковым числом, иначе
будет \ (\ альфа \). Порядковые числа, которые не могут быть с
любые меньшие порядковые номера называются кардинальными числами . Таким образом, все
натуральные числа являются кардиналами, как и \ (\ omega \), \ (\ omega_1 \),
\ (\ omega_2 \) и так далее.В общем, учитывая любого кардинала \ (\ каппа \), то
набор всех порядковых чисел, которые можно вычислить с помощью некоторого порядкового числа \ (\ leq
\ каппа \) тоже кардинал; это самый маленький кардинал больше, чем
\(\каппа\). Бесконечные кардиналы представлены буквой алеф
(\ (\ aleph \)) еврейского алфавита. Таким образом, наименьшее бесконечное
кардинал \ (\ omega = \ aleph_0 \), следующий — \ (\ omega_1 = \ aleph_1 \),
который является первым неисчислимым кардиналом, затем приходит
\ (\ omega_2 = \ aleph_2 \) и т. д. Мощность любого множества \ (A \), обозначаемого \ (| A | \), является единственным
кардинальное число, которое можно биэблокировать с \ (A \).Мы уже видели, что
\ (| \ mathbb {R} | \) неисчислимо, следовательно, больше \ (\ aleph_0 \), но оно
неизвестно, что это за кардинальное число. Предположение, что
\ (| \ mathbb {R} | = \ aleph_1 \), сформулированная Кантором в 1878 году, является
знаменитая гипотеза континуума . Объединение из двух наборов — это набор, содержащий все элементы в $ A $ или в
$ B $ (возможно, оба). Например, $ \ {1,2 \} \ cup \ {2,3 \} = \ {1,2,3 \} $. Таким образом, мы можем написать $ x \ in (A \ cup B) $
тогда и только тогда, когда $ (x \ in A) $ или $ (x \ in B) $.Обратите внимание, что $ A \ cup B = B \ cup A $. На рисунке 1.4
объединение множеств $ A $ и $ B $ показано заштрихованной областью на диаграмме Венна. Аналогичным образом мы можем определить объединение трех или более множеств. В частности, если $ A_1, A_2, A_3, \ cdots, A_n $ равны $ n $
множества, их объединение $ A_1 \ cup A_2 \ cup A_3 \ cdots \ cup A_n $ — это множество, содержащее все элементы, которые
по крайней мере, в одном из наборов.{n} A_i. $$
Например, если $ A_1 = \ {a, b, c \}, A_2 = \ {c, h \}, A_3 = \ {a, d \} $, то $ \ bigcup_ {i} A_i = A_1 \ cup А_2
\ cup A_3 = \ {a, b, c, h, d \} $. Мы можем аналогичным образом определить объединение бесконечно многих множеств
$ A_1 \ cup A_2 \ cup A_3 \ cup \ cdots $. Пересечение двух множеств $ A $ и $ B $, обозначаемое как $ A \ cap B $, состоит из всех элементов
которые оба находятся в $ A $ $ \ underline {\ textrm {and}} $ $ B $. Например, $ \ {1,2 \} \ cap \ {2,3 \} = \ {2 \} $.
На рисунке 1.5 пересечение множеств $ A $ и $ B $ показано заштрихованной областью с использованием диаграммы Венна. В более общем смысле для множеств $ A_1, A_2, A_3, \ cdots $ их пересечение $ \ bigcap_i A_i $ определяется как
множество, состоящее из элементов, которые находятся во всех $ A_i $. На рисунке 1.6 показано пересечение трех множеств. Дополнение набора $ A $, обозначаемое как $ A ^ c $ или $ \ bar {A} $, представляет собой множество всех элементов, которые
в универсальном множестве $ S $, но не в $ A $.с $. Два набора $ A $ и $ B $ являются взаимоисключающими или непересекающимися , если у них нет общих
элементы; то есть их пересечение — пустое множество, $ A \ cap B = \ emptyset $. В целом, несколько комплектов
называются непересекающимися, если они попарно не пересекаются, то есть ни один из них не имеет общих элементов.
На рисунке 1.9 показаны три непересекающихся множества. Если земная поверхность является нашим пробным пространством, мы можем разделить ее на разные континенты.
Аналогично, страну можно разделить на разные провинции. В общем, коллекция непустая
множеств $ A_1, A_2, \ cdots $ — это раздел множества $ A $, если они не пересекаются и их объединение равно $ A $.
На рисунке 1.10 наборы $ A_1, A_2, A_3 $ и $ A_4 $ образуют разбиение универсального набора $ S $. Для любых множеств $ A $, $ B $ и $ C $ мы имеем Если универсальный набор задан как $ S = \ {1,2,3,4,5,6 \} $ и $ A = \ {1,2 \} $, $ B = \ {2,4 , 5 \},
C = \ {1,5,6 \} $ — три набора, найдите следующие наборы: Декартово произведение из двух множеств $ A $ и $ B $, записанное как $ A \ times B $, является множеством, содержащим упорядоченных пары из $ A $ и $ B $.То есть, если $ C = A \ times B $, то каждый элемент в $ C $ имеет вид $ (x, y) $, где
$ x \ in A $ и $ y \ in B $:
$$ A \ times B = \ {(x, y) | x \ in A \ textrm {и} y \ in B \}. $$
Например, если $ A = \ {1,2,3 \} $ и $ B = \ {H, T \} $, то
$$ A \ times B = \ {(1, H), (1, T), (2, H), (2, T), (3, H), (3, T) \}. $$
Обратите внимание, что здесь пары упорядочены, например, $ (1, H) \ neq (H, 1) $. Таким образом, $ A \ times B $ составляет , а не так же, как $ B \ times A $. Если у вас есть два конечных набора $ A $ и $ B $, где $ A $ имеет $ M $ элементов, а $ B $ имеет $ N $ элементов, то $ A \ times B $
имеет $ M \ times N $ элементов.Это правило называется принципом умножения и очень полезно при подсчете
количество элементов в наборах. Количество элементов в наборе обозначается через $ | A | $, поэтому здесь мы пишем $ | A | = M,
| B | = N $ и $ | A \ times B | = MN $. В приведенном выше примере $ | A | = 3, | B | = 2 $, поэтому $ | A \ times B | = 3 \ times 2 = 6 $.
Аналогичным образом можно определить декартово произведение $ n $ множеств $ A_1, A_2, \ cdots, A_n $ как
$$ A_1 \ times A_2 \ times A_3 \ times \ cdots \ times A_n = \ {(x_1, x_2, \ cdots, x_n) | x_1 \ in A_1 \ textrm {and}
x_2 \ in A_2 \ textrm {and} \ cdots x_n \ in A_n \}.3 = \ mathbb {R} \ times \ mathbb {R} \ times \ mathbb {R} $ и так далее. Эта страница продолжается в разделе Введение в решение проблем, в котором вводится решение проблем как концепция и описываются этапы, используемые для успешного решения проблем. Эта страница охватывает первые два этапа процесса решения проблемы: Определение проблемы и Структурирование проблемы . Перед тем, как столкнуться с проблемой, необходимо определить ее существование.Это может показаться очевидным утверждением, но, довольно часто, проблемы будут оказывать влияние в течение некоторого времени, прежде чем они будут признаны или доведены до сведения того, кто может что-либо с ними сделать. Во многих организациях можно настроить формальные системы связи так, чтобы о проблемах сообщали рано, но неизбежно эти системы не всегда работают. После выявления проблемы необходимо определить ее точный характер: каковы цели и барьеры ? Некоторые из основных элементов проблемы могут быть изложены, и первая попытка определить проблему должна быть сделана.Это определение должно быть достаточно четким, чтобы вы могли легко объяснить природу проблемы другим. Рассмотрение проблемы с точки зрения целей и барьеров может предложить эффективный способ определения многих проблем и разделения больших проблем на более управляемые подзадачи. Иногда становится очевидным, что то, что кажется единственной проблемой, точнее является серией подзадач. Например, в задаче: «Мне предложили работу, которую я хочу, но у меня нет транспорта, чтобы добраться туда, и у меня нет достаточно денег, чтобы купить машину.” «Я хочу устроиться на работу» (основная проблема) Полезные способы описания более сложных проблем показаны в разделе « Структурирование проблемы» ниже. На этом первом этапе решения проблемы важно получить начальное рабочее определение проблемы. Хотя может потребоваться адаптация на более позднем этапе, хорошее рабочее определение позволяет описать проблему другим, кто может участвовать в процессе решения проблемы.Например: Второй этап процесса решения проблемы включает в себя более глубокое понимание проблемы.Во-первых, факты должны быть проверены. Необходимо задать вопросы. Является ли заявленная цель настоящей целью? Являются ли барьеры фактическими барьерами и какие еще существуют барьеры? В этом примере проблема на первый взгляд выглядит следующим образом: Это также хорошая возможность взглянуть на отношения между ключевыми элементами проблемы .Например, в проблеме «Job-Transport-Money» существуют сильные связи между всеми элементами. Рассматривая все взаимосвязи между ключевыми элементами, выясняется, что проблема заключается не столько в том, как достичь какой-либо одной из трех вещей, например в работе, транспорте или деньгах, потому что решение одной из этих подзадач, в свою очередь, решит другие. Этот пример показывает, насколько полезно иметь представление о проблеме. Визуальные и устные представления включают в себя: Цепные диаграммы — это мощный и простой способ представления задач с использованием комбинации диаграмм и слов. Элементы проблемы изложены в словах, обычно помещаются в коробки и размещаются в разных местах на листе бумаги, используя линии для представления отношений между ними. Цепные диаграммы — это самый простой тип, где все элементы представлены в упорядоченном списке, причем каждый элемент связан только с элементами непосредственно перед и после него. Цепные диаграммы обычно представляют последовательностей событий, необходимых для решения. Простой пример цепной диаграммы иллюстрирует пример задания-транспорта-денег следующим образом: Блок-схемы позволяют включать ответвления, сгибы, петли, точки принятия решений и многие другие взаимосвязи между элементами. На практике блок-схемы могут быть довольно сложными, и существует множество соглашений относительно того, как они нарисованы, но, как правило, простые диаграммы проще для понимания и помогают легче увидеть проблему. и их близкие родственники, дерево решений , представляют собой способы представления ситуаций, в которых необходимо рассмотреть ряд вариантов или различные возможные события. Эти типы диаграмм особенно полезны для рассмотрения всех возможных последствий решений. Помните, что цель визуализации — прояснить проблему. Слишком сложные диаграммы просто запутают и затруднят понимание проблемы. Перечисление элементов проблемы может также помочь представить приоритеты, порядок и последовательность в проблеме. Цели могут быть перечислены в порядке важности и барьеры в порядке сложности. Отдельные списки могут быть сделаны из связанных целей или барьеров.Барьеры могут быть перечислены в том порядке, в котором они должны быть решены, или элементы проблемы классифицированы различными способами. Возможностей много, но цель — дать более четкое представление о проблеме. 1.Получить деньги Визуальное представление и рабочее определение значительно упрощают описание проблемы для других. Многие проблемы будут намного сложнее, чем пример, используемый здесь. Функции
Наборы и формулы
Ординалы
Счетные и неисчисляемые множества
кардиналов
Дальнейшие чтения
, 1.2.2 Операции над множествами
 Рис.1.4 — Заштрихованная область показывает набор $ B \ cup A $.
Рис.1.4 — Заштрихованная область показывает набор $ B \ cup A $. Рис.1.5 — Заштрихованная область показывает набор $ B \ cap A $.
Рис.1.5 — Заштрихованная область показывает набор $ B \ cap A $. Рис.1.6 — Заштрихованная область показывает набор $ A \ cap B \ cap C $.
Рис.1.6 — Заштрихованная область показывает набор $ A \ cap B \ cap C $. Рис.1.8 — Заштрихованная область показывает набор $ A-B $.
Рис.1.8 — Заштрихованная область показывает набор $ A-B $. Инжир.1.9 — Множества $ A, B, $ и $ C $ не пересекаются.
Инжир.1.9 — Множества $ A, B, $ и $ C $ не пересекаются. Инжир.с $.
Инжир.с $.
Теорема : Дистрибутивный закон
Пример
, этап первый: выявление проблемы
ЦЕЛЬ (Я хочу …) БАРЬЕР (но…) Скажи другу, что мы находим что-то, что они делают раздражающим. Я не хочу обидеть их чувства. Куплю новый компьютер. Я не уверен, какую модель получить или сколько денег разумно потратить. Начать новый бизнес. Я не знаю с чего начать.
«Но у меня нет транспорта, чтобы туда добраться» (подзадача 1)
«И у меня нет достаточно денег, чтобы купить машину» (подпункт -проблема 2) Задача Рабочее определение «Я хочу устроиться на работу, но у меня нет
транспорта, чтобы добраться туда, и у меня нет
денег на покупку автомобиля». «Я хочу устроиться на эту работу». второй этап: структурирование проблемы
Задача Проверка фактов «Я хочу устроиться на работу, но у меня нет транспорта, чтобы добраться туда
, и у меня нет достаточно денег, чтобы купить машину». «Я действительно хочу работу?»
«У меня действительно нет доступа к транспорту?»
«Разве я не могу позволить себе купить машину?» Гол Барьер 1 Барьер 2 Принять работу Нет транспорта Нет денег Проблемы могут быть представлены следующими способами:
Цепные диаграммы
ПОЛУЧИТЬ ДЕНЬГИ 
ПОЛУЧИТЬ ТРАНСПОРТ 
ПРИНЯТЬ РАБОТУ
Блок-схемы Древовидные диаграммы
Древовидные диаграммы Объявление
Задача «Я хочу устроиться на работу, но у меня нет транспорта, чтобы добраться туда, и у меня нет достаточно денег, чтобы купить машину». Порядок, в котором барьеры должны быть решены
2. Получить машину
3. Получить работу
