Вычисление пределов примеры – Пределы. Примеры решений — matematika

Некоторые методы вычисления пределов

1. Случай отсутствия неопределённости

Если при подстановке предельного значения аргумента в функцию получается определённое число, то оно и является значением предела.

Пример 2. Вычислить предел:

Решение.

Ответ: 6.

Пример 3. Вычислить предел:

Решение.

Ответ: 1.

Пример 4. Вычислить предел:

Решение.

Ответ: .

Если в результате формальной подстановки в функцию предельного значения аргумента предел переходит в выражение типа:

то говорят, что под знаком предела неопределённость.

В этом случае нужно раскрыть неопределённость: тождественными преобразованиями «убирают» неопределённость, если это возможно, и вычисляют предел.

2. Случай неопределённости вида

Если в пределе приходим к неопределённости вида , то

необходимо в числителе и знаменателе дроби выделить сомножитель сократить на него и вычислить предел.

 

Пример 5.Вычислить предел:

Решение. Имеем неопределённость вида . Для её раскрытия разложим числитель и знаменатель дроби на множители и сократим на общий множитель (вспомним, что , где – корни уравнения ).

Ответ: 0,7.

Раскрытие неопределённости вида с иррациональностями

Рассмотрим на примере.

Пример 6. Вычислить предел:

Решение. Имеем неопределённость вида . Домножим числитель и знаменатель дроби, предел которой мы ищем, на выражение , сопряжённое числителю.

Ответ: .

Для пределов подобного вида способ домножения на сопряжённое выражение является типичным.

3. Случай неопределённости вида

Для раскрытия исходной неопределённости нужно разделить числитель и знаменатель дроби на переменную xв наибольшей степени, которая входит в данную дробь, учитывая, что величина обратная бесконечно большой есть бесконечно малая величина.

Пример 7. Вычислить предел:

Решение. Имеем неопределённость вида . Разделим числитель и знаменатель дроби на .

Ответ: .

В общем случае можно использовать правило:

4. Случай неопределённостей вида:

Эти неопределённости сводятся к неопределённостям вида одним из следующих способов:

а) приведение дробей к общему знаменателю,

б) преобразование функции к виду дроби,

в) избавление от иррациональности (домножение на сопряжённое выражение числителя и знаменателя дроби).

Пример 8. Вычислить предел:

Решение.

Ответ: 2.

Примеры для самостоятельного решения

Вычислить пределы:

Ответы

1.1. . 1.2. – 2. 1.3. 14. 1.4. 1. 1.5. . 1.6. –9. 1.7. 3. 1.8. . 1.9. . 1.10. 6.

1.11. . 1.12. 1.13. 1.14. . 1.15. . 1.16. . 1.17. . 1.18. . 1.19. ∞. 1.20. 0. 1.21. 1. 1.22. . 1.23. .

1.24. ∞. 1.25. . 1.26.2. 1.27. . 1.28. 0. 1.29. 0. 1.30. 2. 1.31. 0. 1.32. 1,5. 1.33. –∞. 1.34. +∞. 1.35. +∞. 1.36. +∞. 1.37. –∞. 1.38.–∞.

 

Вычисление предела функции с использованием замечательных пределов

Первым замечательным пределом называется предел вида:

.

Примеры с решениями

Пример 1. Вычислить предел:

Решение.

Ответ: a.

Пример 2. Вычислить предел:

Решение. Используем тригонометрические формулы:

Ответ: 4.

 

Вторым замечательным пределом называется предел вида:

Пример 3. Вычислить предел:

Ответ: .

Пример 4. Вычислить предел:

Решение.

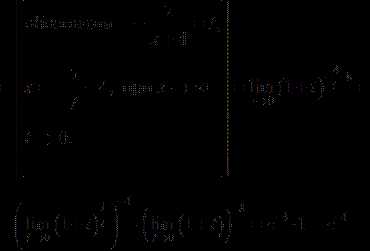
Ответ: .

Примеры для самостоятельного решения

Вычислить пределы:

Ответы

2.1. 5. 2.2. 3. 2.3. . 2.4. 2.5. – 4,5. 2.6. – . 2.7. 0,5. 2.8. 2. 2.9. – . 2.10.5. 2.11. 3. 2.12. 0. 2.13.cos 3. 2.14.

1. 2.15. 1,75. 2.16. . 2.17. – . 2.18. 14.

2.19. – 1. 2.20. – 0,5. 2.21. . 2.22. – . 2.23. .2.24. . 2.25. . 2.26. . 2.27. .2.28. . 2.29. . 2.30. . 2.31. 0. 2.32. . 2.33. 1. 2.34. –7.

 



infopedia.su

5.07.3 Примеры на вычисление пределов функций

Вычислить указанные пределы:

1. .

2.

.

3. . Так как числитель и знаменатель обратились в нуль при , то – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет . Получаем

.

4.

.

5.

.

6. – не существует, так как .

7. . Обозначим , причем заметим, что при . Получим

.

8. . (Ответ получается непосредственно подстановкой вместо .)

9. . Здесь следует рассмотреть односторонние пределы:

; .

Следовательно, – не существует (так как у функции разные односторонние пределы).

Для самостоятельного решения.

1) ; Ответ:.

2) ; Ответ: .

3) ; Ответ: .

4) ; Ответ: .

5) . Ответ: не существует.

6) ; Ответ: .

7) ; Ответ: .

8) Найти в точке односторонние пределы функции ; Ответ: .

9) ; Ответ: .

< Предыдущая		Следующая >

matica.org.ua

Правила вычисления пределов — Мегаобучалка

 

При вычислении пределов следует учитывать следующие основные правила:

 

1. Предел суммы (разности) функций равен сумме (разности) пределов слагаемых:

.

 

2. Предел произведения функций равен произведению пределов сомножителей:

.

 

3. Предел отношения двух функций равен отношению пределов этих функций:

.

 

4. Постоянный множитель можно выносить за знак предела:

.

 

5. Предел постоянной равен самой постоянной:

 

.

6. Для непрерывных функций символы предела и функции можно поменять местами:

 

.

 

Нахождение предела функции следует начинать с подстановки значения в выражение для функции. При этом если получается числовое значение 0 или ¥, то искомый предел найден.

Пример 2.1.Вычислить предел .

Решение.

.

Выражения вида , , , , , называются неопределённостями.

Если получается неопределенность вида , то для нахождения предела нужно преобразовать функцию так, чтобы раскрыть эту неопределенность.

Неопределенность вида обычно получается, когда задан предел отношения двух многочленов. В этом случае, для вычисления предела рекомендуется разложить многочлены на множители и сократить на общий множитель. Этот множитель равен нулю при предельном значении х.

Пример 2.2.Вычислить предел .

Решение.

Подставляя , получим неопределенность:

 

.

 

Разложим числитель и знаменатель на множители:

;

 

Сократим на общий множитель и получим

 

.

Неопределенность вида получается, когда задан предел отношения двух многочленов при . В этом случае для вычисления рекомендуется разделить оба многочлена на

х в старшей степени.

Пример 2.3. Вычислить предел .

Решение.При подстановке ∞ получается неопределенность вида , поэтому разделим все члены выражения на x³.

.

Здесь учитывается, что .

При вычислении пределов функции, содержащей корни, рекомендуется умножить и разделить функцию на сопряженное выражение.

Пример 2.4.Вычислить предел

Решение.

 

При вычислении пределов для раскрытия неопределенности вида или (1)^∞ часто используются первый и второй замечательные пределы:

и

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины.

Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа

e в задаче о сложных процентах. В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример.

Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед.

Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 × 1,5 = 150, а еще через полгода — в 150 × 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3)³ »237 (ден. ед.).

Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100 × (1 +1/10)¹⁰ » 259 (ден. ед.),

100 × (1+1/100)¹⁰⁰ » 270 (ден. ед.),

100 × (1+1/1000)¹⁰⁰⁰ » 271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что

Пример 2.5.Вычислить предел функции

Решение.

Пример 2.6.Вычислить предел функции .

Решение.Подставляя получим неопределенность:

 

.

Используя тригонометрическую формулу, преобразуем числитель в произведение:

 

В результате получаем

Здесь учитывается второй замечательный предел .

Пример 2.7.Вычислить предел функции

Решение.

.

Для раскрытия неопределенности вида или можно использовать правило Лопиталя, которое основано на следующей теореме.

Теорема.Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных

 

Заметим, что это правило можно применять несколько раз подряд.

Пример 2.8. Найти

Решение.При подстановке , имеем неопределенность вида . Применяя правило Лопиталя, получим

 

Непрерывность функции

 

Важным свойством функции является непрерывность.

Определение.Функция считается непрерывной, если малое изменение значения аргумента влечет за собой малое изменение значения функции.

Математически это записывается так: при

Под и понимается приращение переменных, то есть разность между последующим и предыдущим значениями: , (рисунок 2.3)

 

Рисунок 2.3 – Приращение переменных

Из определения функции , непрерывной в точке , следует, что . Это равенство означает выполнение трех условий:

1) функция определена в точке и ее окрестности функция ;

2) функция имеет предел при или, что равносильно, существуют и равны односторонние пределы и ;

3) предел функции при равен значению функции в точке .

Если нарушается хотя бы одно из этих условий, то точку называют точкой разрыва функции. Выделяют следующие типы точек разрыва.

1) Если в точке разрыва существуют односторонние конечные пределы функции, то называют точкой разрыва первого рода.

При этом если односторонние пределы совпадают, то называют точкой устранимого разрыва первого рода, если односторонние пределы не совпадают, то называют точкой конечного разрыва первого рода (или точкой скачка)

2) Если в точке хотя бы один из односторонних пределов функции не существует или бесконечен, то называют точкой разрыва второго рода.

Пример 2.9.Найти точки разрыва функции:

Решение.Для функции точка является подозрительной на разрыв, проверим это, найдем односторонние пределы

Следовательно, , значит — точка устранимого разрыва

Производная функции

 

megaobuchalka.ru

Замечательные пределы, примеры решений

Теория по замечательным пределам

Первый замечательный предел раскрывает неопределенность и имеет вид:

   

Следствия из первого замечательного предела:

   

Второй замечательный предел раскрывает неопределенность и имеет вид:

   

где . Он имеет следующие основные следствия:

   

Примеры

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Примеры на вычисление пределов функции

ПРИМЕРЫ НА ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ

ФУНКЦИИ

На основании изложенного выше рекомендуется следующий порядок нахождения предела функции:

1. Если заданная функция непрерывна в точке x₀, нахождение предела сводится к вычислению значения функции в точке x₀.

2. Если при подстановке значения x₀ в выражение функции оказалось, что имеет место одна из ситуаций, которые рассмотрены в п.4.3, 4.5 и 4.6, нужно воспользоваться соответствующими теоремами о пределах и свойствами бесконечно малых и бесконечно больших величин.

3. Если оказалось, что при x → x₀ имеет место неопределенное выражение (п. 4.4, 4.6, 4.7, 4.9), следует, установив вид неопределенности, найти специальный прием, позволяющий, как принято говорить, раскрыть данное неопределенное выражение. Специальные приемы раскрытия неопределенностей будут рассмотрены при решении задач.

1. Нахождение пределов в случае отсутствия

неопределенности

Пример 1. .

Использована непрерывность функции в точке x = 1

(п. 1.1).

Пример 2. .

Использована теорема о пределе частного.

Пример 3. .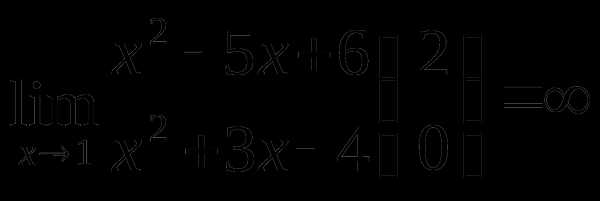

Использовали то, что величина обратная бесконечно малой, является бесконечно большой.

Пример 4. .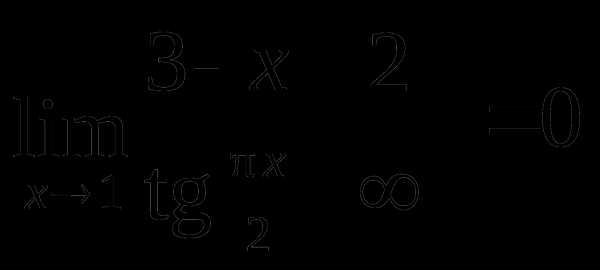

Использовали то, что величина, обратная бесконечно большой, является бесконечно малой.

2. Раскрытие неопределенностей вида

Способ нахождения 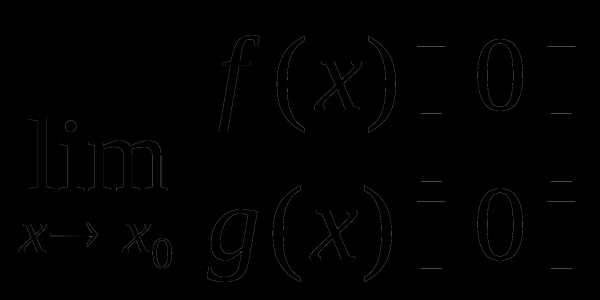зависит от того, каким классам функций принадлежат функции f(x) и g(x).

2.1. Нахождение 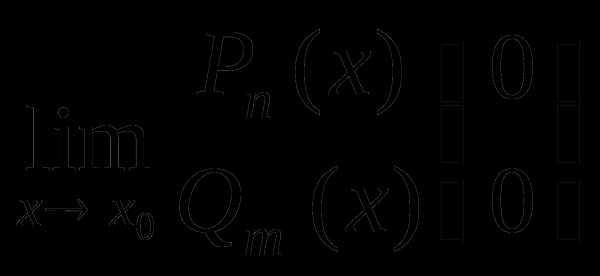, где P_n(x) и_{Qm(x) неко-}

торые многочлены, путем разложения числителя и

знаменателя на множители

Напомним, что если число x₁ является корнем многочлена P_n(x), то этот многочлен можно представить в виде

В частности, если x₁ и x₂ корни уравнения

, то

Пример 1. Найти .

Решение. Найдем корни трехчленов и разложим числитель и знаменатель на множители. Тогда

.

Пример 2. Найти .

Решение. Воспользуемся формулами

и .

Тогда

2.2. Раскрытия иррациональных неопределенностей вида

В этом случае проводятся преобразования, позволяющие далее использовать формулы:

;

Пример 1. Найти

Решение.

Пример 2. Найти

Решение.

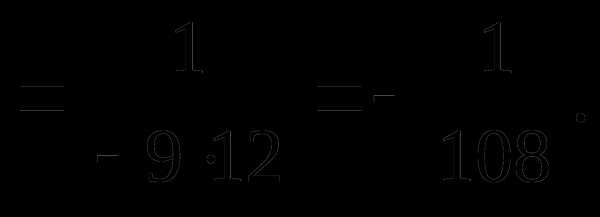
2.3. Раскрытие неопределенных выражений вида с помощью первого замечательного предела и его следствий

Первым замечательным пределом принято называть:

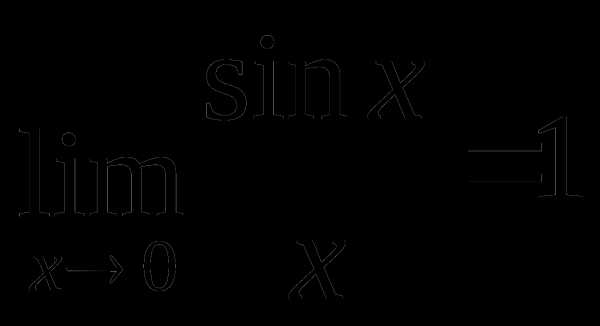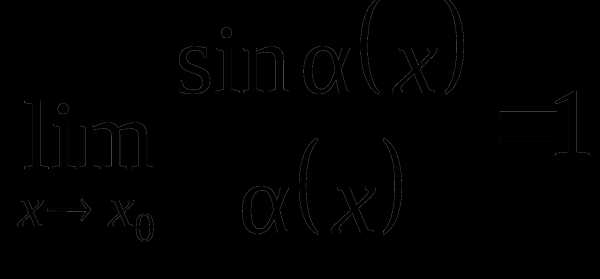(1) или , (2)

где при .

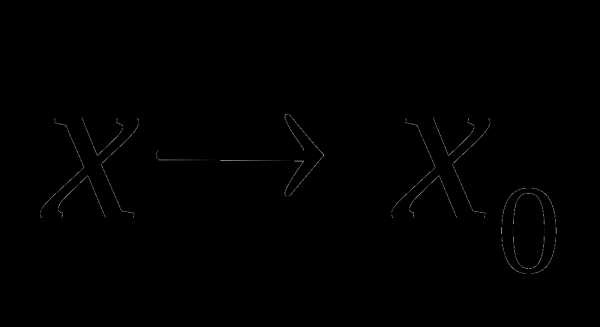Предел замечателен тем, что он позволяет сделать вывод: для значений аргумента, близких к 0, величина синуса практически не отличается от величины своего аргумента.

Подчеркнем (это важно!), что предел отношения синуса некоторого аргумента к своему аргументу равен 1, лишь когда аргумент синуса стремится к 0.

Например,

,

,

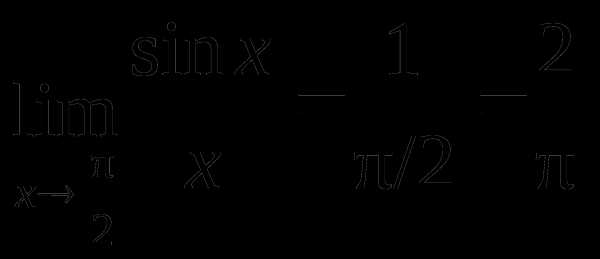и только .

На конкретных примерах покажем, как формально просто используется замечательный предел при раскрытии тригонометрических неопределенностей вида .

Пример 1. Найти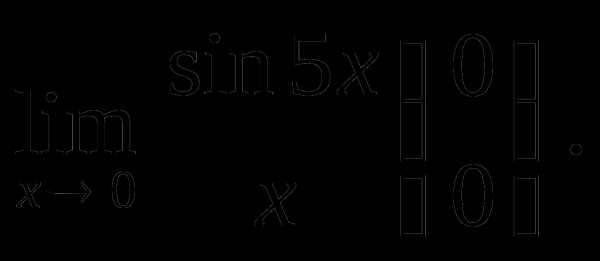

Решение.

Пример 2. Найти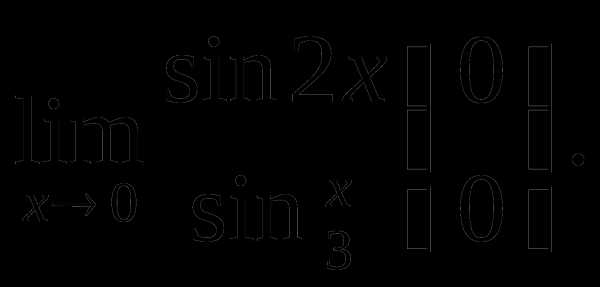

Решение. 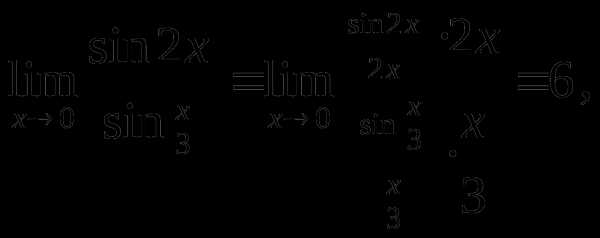так как

и .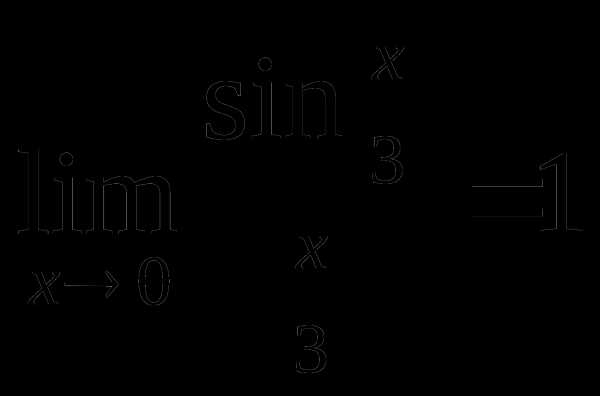

Пример 3. Найти

Решение.

Использованы формула и первый замечательный предел.

Пример 4. Найти

Решение.

так как

Пример 5. Найти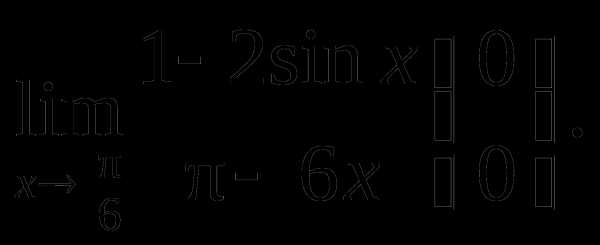

Решение.

так как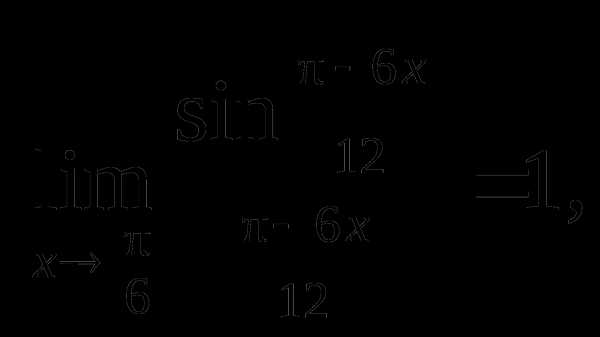а .

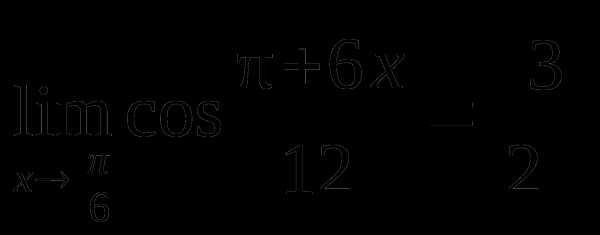Примеры 6–7 решены с использованием следствий первого замечательного предела:

Пример 6.

Пример 7. Найти

Решение.

2.4. Введение новой переменной

Во многих случаях, чтобы найти , имеет смысл сделать замену 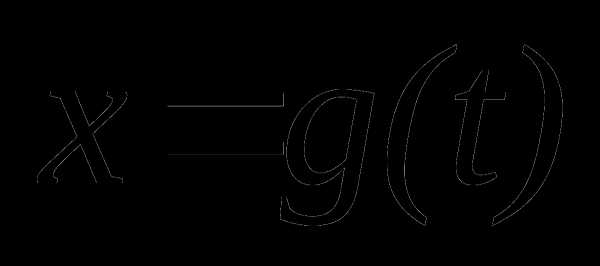, при этом если то .

Пример 1. Найти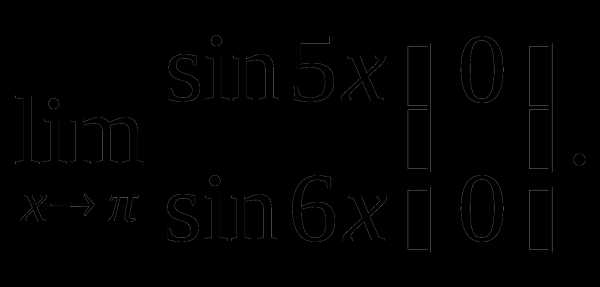

Решение. Введем новую переменную или Очевидно, при переменная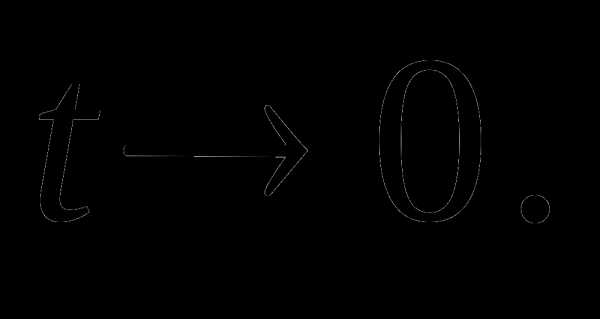

Тогда

Использованы формулы приведения и первый замечательный предел.

Пример 2. Найти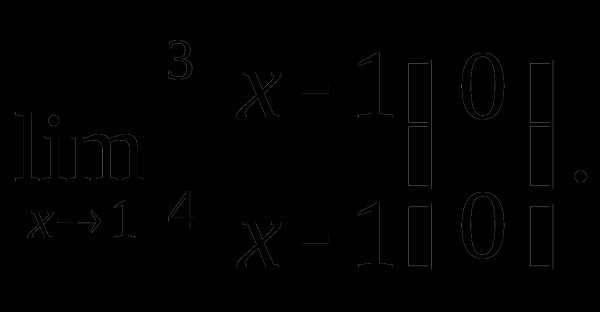

Решение. Введем новую переменную

При 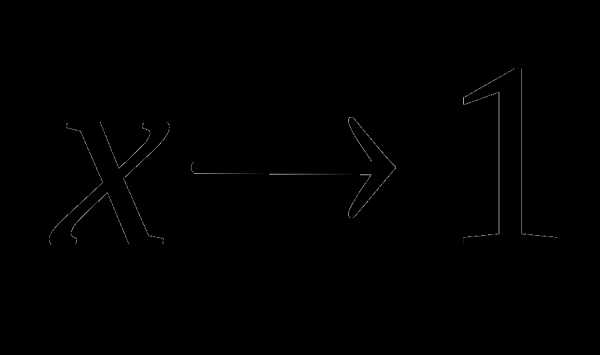переменная

Тогда

3. Раскрытие неопределенностей вида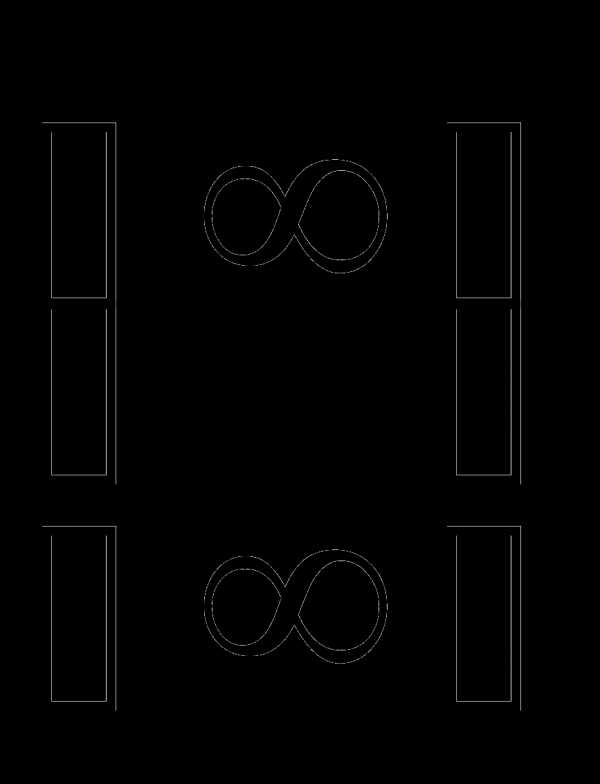

При нахождении 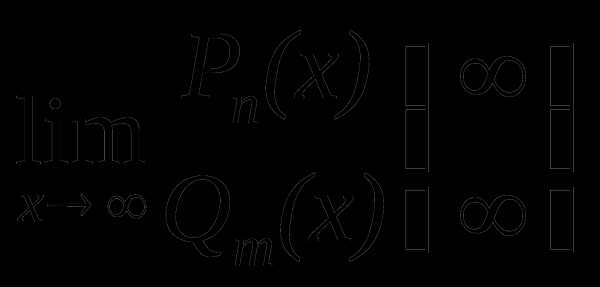, где P_n(x) и Q_m(x) – многочлены, используется метод деления числителя и знаменателя на x^k , где k – наибольшее из чисел m и n. Аналогичный прием используется и при нахождении пределов иррациональных неопределенностей вида .

Пример 1.

Решение. Разделим числитель и знаменатель дроби на x³. Тогда

так как – бесконечно малые величины при .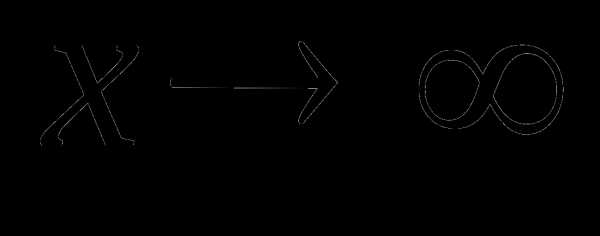

Пример 2.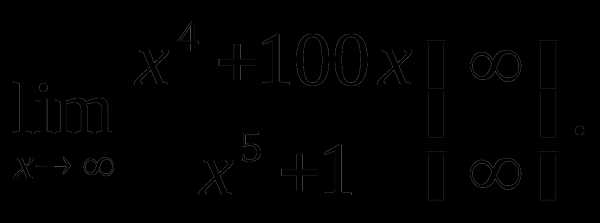

Решение. Разделим числитель и знаменатель дроби на x⁵. Тогда

Пример 3.

Решение. Разделим числитель и знаменатель дроби на x³. Тогда

Сравнивая полученные в примерах 1–3 результаты, можно сделать вывод:

(a_n и b_n – коэффициенты при xⁿ многочленов P_n(x) и Q_n(x) соответственно).

Этот вывод позволяет в простейших случаях находить без каких-либо преобразований.

Например,

Перейдем к решению более сложных примеров.

Пример 4.

Решение. Разделим числитель и знаменатель дроби на :

Заметим, что в этом примере наивысшие степени переменной в числителе и знаменателе равны (и там, и там это 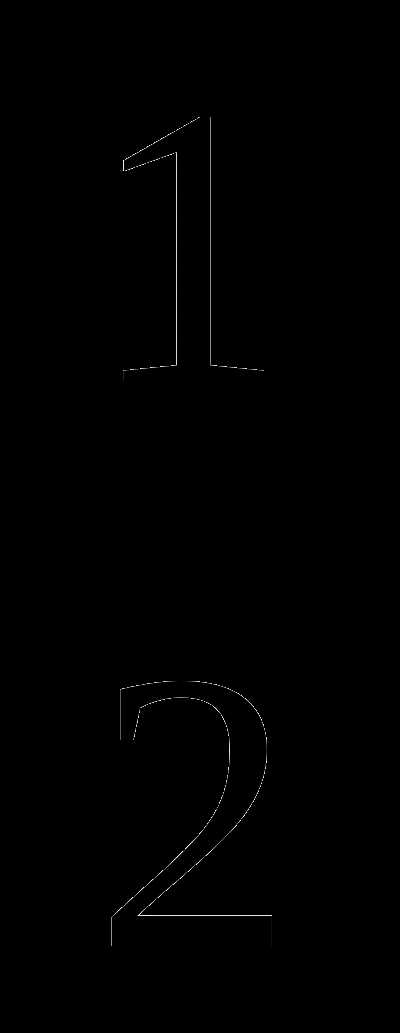), поэтому ответ оказался равным отношению коэффициентов при .

Пример 5.

Решение. Напомним, что Разделим почленно числитель на знаменатель:

4. Раскрытие неопределенностей вида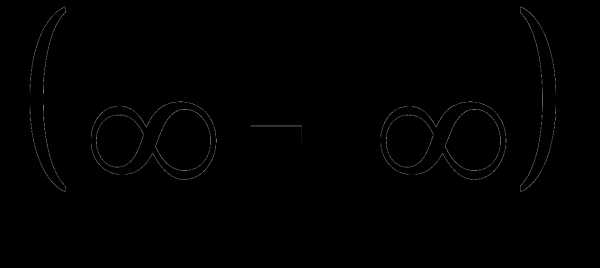

и

Каждую из неопределенностей 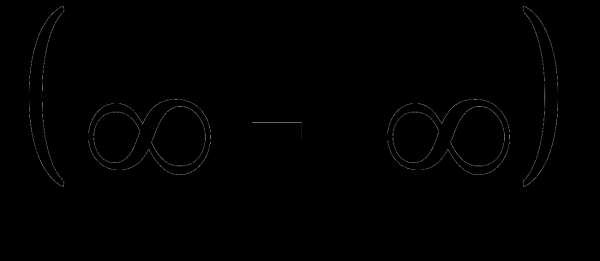и стараются свести к неопределенностям и 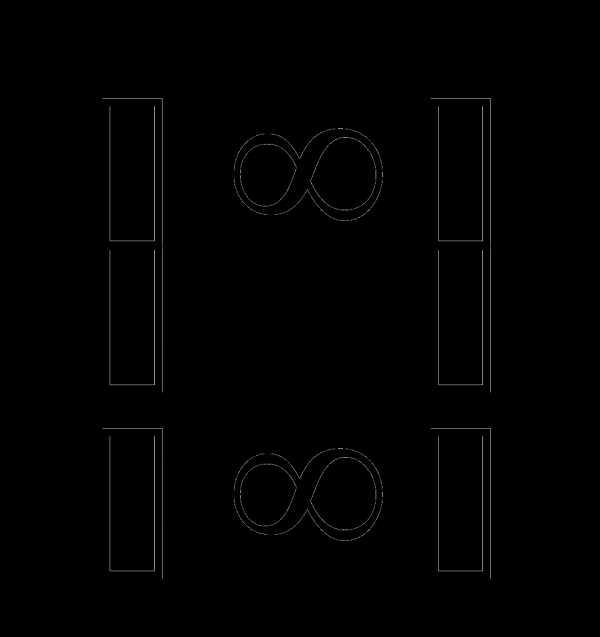. Далее используют соответствующий способ раскрытия неопределенного выражения полученного вида.

Пример 1. Найти

Решение. Вынесем знак минуса из знаменателей за общую скобку и приведем разность к общему знаменателю

Пример 2. Найти

Решение.

Осталось воспользоваться первым замечательным пределом

Пример 3. Найти

Решение. Умножим и поделим заданное выражение на сумму Тогда

Пример 4. Найти

Решение.

Использован первый замечательный предел:

( при ).

Пример 5. Найти

Решение. Воспользуемся тем, что

Тогда

Использованы непрерывность логарифмической функции и первый замечательный предел.

5. Раскрытие неопределенностей вида

Неопределенности вида раскрываются с помощью второго замечательного предела, который можно записывать двумя способами:

(3) 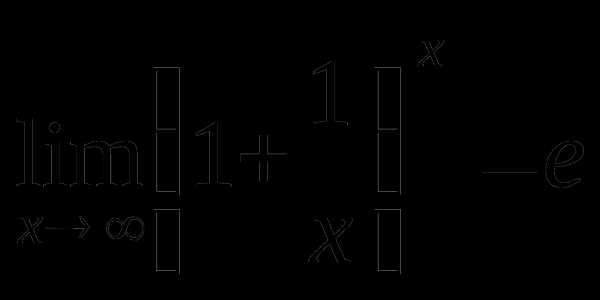или . (4)

Напомним, что второй замечательный предел получен на основании равенства

,

gigabaza.ru

Примеры нахождения пределов | Primer.by

Пример 1.

а)

б)

в)

г)

д)

 

Решение

 

а)

Имеем неопределенность вида  . Разделим числитель и знаменатель дроби на наибольшую степень х, то есть на х⁴

Ответ:

 

б)

Имеем неопределенность вида . Умножим числитель и знаменатель дроби на выражение, сопряженное числителю, то есть на :

 

Ответ:

 

в)

Имеем неопределенность вида . Преобразуем предел к виду второго замечательного предела:

Ответ:

г)

Имеем неопределенность вида . Преобразуем предел к виду первого замечательного предела:

 

Ответ:

 

д)  

(воспользуемся правилом Лопиталя)

Таким образом, .

Ответ:.

 

 

Пример 2.

Вычислить предел, пользуясь правилом Лопиталя.

 

Решение:

 

1) .

Искомый предел является неопределенностью типа . По правилу Лопиталя получаем:

.

2) .

Предел является неопределенностью вида . Преобразуем его к виду :

.

Применим правило Лопиталя:

.

3) .

Предел является неопределенностью вида . Проведем следующие преобразования:

.

 

Ответ: 1) ;     2) -1;     3) .

 

 

primer.by

Пределы функций. Примеры решений.

Пределы функций. Примеры решений.

Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.

Итак, что же такое предел?

Любой предел состоит из трех частей:

1) Всем известного значка предела . 
2) Записи под значком предела, в данном случае . Запись читается «икс стремится к единице». Чаще всего – именно , хотя вместо «икса» на практике встречаются и другие переменные. В практических заданиях на месте единицы может находиться совершенно любое число, а также бесконечность ().
3) Функции под знаком предела, в данном случае .

Сама запись  читается так: «предел функции  при икс стремящемся к единице».

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала , затем , , …, , …. 
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.

Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:

Готово.

Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!

Пример с бесконечностью:

Разбираемся, что такое ? Это тот случай, когда  неограниченно возрастает, то есть: сначала , потом , потом , затем  и так далее до бесконечности.

А что в это время происходит с функцией ? 
, , , …

Итак: если , то функция  стремится к минус бесконечности:

Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию   бесконечность и получаем ответ.

Еще один пример с бесконечностью:

Опять начинаем увеличивать  до бесконечности, и смотрим на поведение функции:

Вывод: при  функция   неограниченно возрастает:

И еще серия примеров:

Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:

, , , , , , , , , 
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если , попробуйте построить последовательность  , , . Если , то  , , .

Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.

Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: , то все равно , так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.

Что нужно запомнить и понять из вышесказанного?

1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

2) Вы должны понимать и сразу решать простейшие пределы, такие как , ,  и т.д.

Пределы с неопределенностью вида  и метод их решения

Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример:

Вычислить предел 

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что , и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим  в старшей степени:

Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим  в старшей степени:

Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность  необходимо разделить числитель и знаменатель на  в старшей степени.

Разделим числитель и знаменатель на 

Вот оно как, ответ , а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так:

Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Пример 2

Найти предел 
Снова в числителе и знаменателе находим  в старшей степени:

Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности  делим числитель и знаменатель на .
Полное оформление задания может выглядеть так:

Разделим числитель и знаменатель на 

Пример 3

Найти предел 
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( можно записать как )
Для раскрытия неопределенности  необходимо разделить числитель и знаменатель на . Чистовой вариант решения может выглядеть так:

Разделим числитель и знаменатель на 

Под записью  подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида  у нас может получиться конечное число, ноль или бесконечность.

Пределы с неопределенностью вида  и метод их решения

Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.

Пример 4

Решить предел 
Сначала попробуем подставить -1 в дробь:
 
В данном случае получена так называемая неопределенность .

Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.

Итак, решаем наш предел

Разложим числитель и знаменатель на множители

Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение:

Сначала находим дискриминант:

И квадратный корень из него: .

Далее находим корни: 

Таким образом:

Всё. Числитель на множители разложен.

Знаменатель. Знаменатель  уже является простейшим множителем, и упростить его никак нельзя.

Очевидно, что можно сократить на :

Теперь и подставляем -1 в выражение, которое осталось под знаком предела:

Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:

Разложим числитель на

infourok.ru