Раздел недели: Обезжиривающие водные растворы и органические растворители. Составы для очистки и обезжиривания поверхности. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Физический справочник / / Электрические и магнитные величины / / Электрическое сопротивление и проводимость проводников, растворов, почв. Поделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
| Специальный поиск | |||||||||||||||||
|
Физика Теория вероятностей и мат. статистика Гидравлика Теор. механика Прикладн. механика Химия Электроника Витамины для ума |
Главная Поиск по сайту Формулы Все задачи Помощь Контакты Билеты |
||||||||||||||||
цепь переменного тока частотой В цепь переменного тока частотой ν = 50 Гц включена катушка длиной l = 20 см и диаметром d = 5 см, содержащая N = 500 витков медного провода площадью поперечного сечения S = 0,6 мм2.
Задача 13729 В цепь переменного тока частотой ν = 50 Гц включена катушка длиной l = 30 см и площадью поперечного сечения S = 10 см2, содержащая N = 1000 витков. Определите активное сопротивление катушки, если известно, что сдвиг фаз φ между напряжением и током составляет 30°.
Задача 13734 В цепь переменного тока частотой ν = 50 Гц последовательно включены резистор сопротивлением R = 100 Ом и конденсате емкостью С = 22 мкФ. Определите, какая доля напряжения, приложенного к этой цепи, приходится на падение напряжения на конденсаторе.
Задача 13735 В цепь переменного тока с частотой ν = 50 Гц и действующим значением напряжения U = 300 В последовательно включены конденсатор, резистор сопротивлением R = 50 Ом и катушка индуктивностью L = 0,1 Гн.
Задача 13737 В цепи переменного тока с частотой ω = 314 рад/с вольтметр показывает нуль при L = 0,2 Гн. Определите емкость конденсатора.
Задача 13738 В цепи переменного тока с частотой ν = 50 Гц вольтметр показывает нуль при значении С = 20 мкФ. Определите индуктивность катушки.
Задача 60342 Катушка индуктивности, сопротивление которой R = 12 Ом, включена в цепь переменного тока с частотой 50 Гц. Сдвиг фазы между колебаниями тока и напряжения на катушке φ = 60. Определить индуктивность катушки.
Задача 60467 Определите индуктивность катушки, сопротивление которой в цепи переменного тока частотой 50 Гц равно 20 Ом.
Задача 60599 Емкостное сопротивление конденсатора в цепи переменного тока частотой 50 Гц равно ХС = 5 Ом. Какова его емкость?
Задача 60609 В цепь переменного тока с частотой 4 Гц включена катушка индуктивностью 0,001 Гн. Какой емкости конденсатор надо включить в эту цепь, чтобы осуществился резонанс?
Задача 15593 Конденсатор емкостью С = 20 мкФ и резистор, сопротивление которого R = 150 Ом, включены последовательно в цепь переменного тока частотой ν = 50 Гц. Какую часть напряжения U, приложенного к этой цепи, составляют падения напряжения на конденсаторе UC и на резисторе UR?
Задача 15597 Конденсатор емкостью С = 1 мкФ и резистор с сопротивлением R = 3 кОм включены в цепь переменного тока частотой ν = 50 Гц.
Задача 16466 В цепь переменного тока частотой ν = 50 Гц последовательно включены резистор сопротивлением R = 100 Ом и конденсатор емкостью С = 22 мкФ. Определить отношение амплитуды колебания напряжения на конденсаторе UCm к амплитуде колебания напряжения Um, приложенного к цепи.
Задача 16567 Конденсатор емкостью в C = 20 мкФ и реостат, активное сопротивление которого равно R = 80,0 Ом, включены последовательно в цепь переменного тока частотой ν = 50 Гц. Какую часть напряжения, приложенного к этой цепи, составляет падение напряжения: 1) на конденсаторе; 2) на реостате?
Задача 17202 Катушка длиной l = 25 см и радиусом r = 2 см имеет обмотку из N = 1000 витков медного провода площадью поперечного сечения S = 1 мм2.
Задача 17748 В цепь переменного тока с частотой 50 Гц последовательно включены резистор сопротивлением 100 Ом и конденсатор емкостью 22 мкФ. Определите, какая доля напряжения, приложенного к цепи, приходится на падение конденсатора и на резисторе.
Задача 20787 Реостат, активное сопротивление которого равно R = 90 Ом, и катушка индуктивностью L = 0,19 Гн включены последовательно в цепь переменного тока частотой ν = 50 Гц. Какую часть напряжения, приложенного к этой цепи, составляет падение напряжения: 1) на катушке. 2) на реостате? Oтвет: 1) 0,56; 2) 0,83.
| |||||||||||||||||
серии RLC Curry, резонансная частота, индуктивная реактивная реактивная и емкостная реактивность — Цепи переменного тока
Категории
Уроки экзаменов Физика
youtube.com/embed/2GvqQvohP2k?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Назначение чтения
. Почему воду не используют в качестве термометрического вещества.
ЗАДАНИЕ НА ВЫХОДНЫЕ
- Источник напряжения 12 В (среднеквадратичное значение) и частота 90 Гц подключен к резистору 4 Ом. Рассчитайте
пиковое значение тока. (a) 48,8 A (b) 30,0 A (c) 27,5 A (d) 4,2 A
- Конденсатор емкостью 2 мкФ соединен последовательно с резистором 5000 Ом. К ним подключено напряжение 5В действ. и частота I=100Гц. Что такое емкостное сопротивление?
- 795,5 Ом (b) 895,5 Ом (c) 1795 Ом (d) 2005,0 Ом
3. На какой частоте конденсатор 20 мкФ будет иметь реактивное сопротивление 500 Ом?
(a) 100 Гц (B) 50 Гц (C) 150 Гц (D) 100π Гц (E) 30 Гц
π π π π π
4. В серии RLC серия A, C Схема C рассеивается в (а) сопротивлении только (b) Только реактивное сопротивление (c) Сопротивление и реактивное сопротивление (d) Сопротивление, индуктивность и емкость
В серии RLC серия A, C Схема C рассеивается в (а) сопротивлении только (b) Только реактивное сопротивление (c) Сопротивление и реактивное сопротивление (d) Сопротивление, индуктивность и емкость
5. В последовательной LC-цепи индуктивность и емкость составляют 0,5 Гн и 20 мкФ соответственно. Рассчитайте резонансную частоту контура (а) 24,2 Гц (б) 36,7 Гц (в) 50,3 Гц (г) 60,5 Гц
ТЕОРИЯ
- Объясните, что означают термины импеданс, фазовый угол и реактивное сопротивление применительно к переменному току. схема. Рассчитайте импеданс и фазовый угол для переменного тока. цепь с сопротивлением 100 Ом, конденсатор 5 u f, включенный последовательно, если к цепи приложено переменное напряжение частотой 100 Гц.
- Нарисуйте векторную диаграмму отношения I и V для переменного тока. цепь, содержащая
(a) чистый индуктор (b) чистый конденсатор (c ) чистый резистор
Присоединяйтесь к дискуссионному форуму и выполняйте задание :
Найдите вопросы в конце каждого урока. Щелкните здесь, чтобы обсудить свои ответы на форуме
Щелкните здесь, чтобы обсудить свои ответы на форуме
Объявление: Получите БЕСПЛАТНУЮ Библию : Обрести истинный покой. Нажмите здесь, чтобы узнать, как получить БЕСПЛАТНУЮ Библию.
По вопросам размещения рекламы/партнерства пишите [email protected]
Загрузите наше бесплатное мобильное приложение для Android : Сохраняйте свои данные при использовании нашего бесплатного приложения. Нажмите на картинку, чтобы скачать. Нет подписки.
Мы заинтересованы в продвижении БЕСПЛАТНОГО обучения. Расскажите своим друзьям о Stoplearn.com. Нажмите кнопку «Поделиться» ниже!
Реактивное, индуктивное и емкостное сопротивление | Физика
Цели обучения
К концу этого раздела вы сможете:
- Зарисовывать зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
- Рассчитать индуктивное и емкостное сопротивление.
- Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.

Многие схемы также содержат конденсаторы и катушки индуктивности, помимо резисторов и источника переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.
Катушки индуктивности и индуктивное реактивное сопротивление
Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 1. Разумно предположить пренебрежимо малое сопротивление, поскольку на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что это оказывает незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.
Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.
График на рис. 1(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика после управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным. Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:
Напряжение переменного тока в катушке индуктивностиКогда к катушке индуктивности приложено синусоидальное напряжение, оно опережает ток на одну четвертую периода или на фазовый угол 90º.
Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС В = − л (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока I через дроссель L задается версией закона Ома:
Изменение тока индуцирует противо-ЭДС В = − л (Δ I / Δ t ). Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока I через дроссель L задается версией закона Ома:
[latex]I=\frac{V}{{X}_{L}}\\[/latex],
, где V — среднеквадратичное значение напряжения. через индуктор и X L определяется как
[латекс]{X}_{L}=2\pi{fL}\\[/латекс],
с f частотой источника переменного напряжения в герцах (анализ схемы с использованием правила контура Кирхгофа и исчисления фактически дает это выражение). Х Д называется индуктивным реактивным сопротивлением , потому что индуктор препятствует протеканию тока. X L измеряется в омах (1 Гн = 1 Ом ⋅ с, так что частота, умноженная на индуктивность, выражается в (циклах/с)(Ом ⋅ с)=Ом)), что соответствует его роли в качестве эффективное сопротивление. Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I / Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.
Имеет смысл, что X L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X L пропорционально частоте f , так как большая частота означает большее изменение тока. То есть Δ I / Δ t велико для больших частот (большие f , малые Δ t ). Чем больше изменение, тем больше сопротивление индуктора.
Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока
(a) Рассчитайте индуктивное реактивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия Индуктивное сопротивление находится непосредственно из выражения X L = 2πf L . После того, как X L найдено на каждой частоте, можно использовать закон Ома, как указано в уравнении I = V / X L , чтобы найти ток на каждой частоте.
После того, как X L найдено на каждой частоте, можно использовать закон Ома, как указано в уравнении I = V / X L , чтобы найти ток на каждой частоте.
Ввод частоты и индуктивности в уравнение x L = 2πf L Придает
x L = 2πf L = 6.28 (60,0/SE) (3,00 мх) = 1,136.
Аналогично, на частоте 10 кГц
X L = 2πf L = 6,28(1,00 × 10 4 кОм, 1 8,0 мГн при 10 90,0 мГн) (3 90 260 мГн)
Решение для (b)Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении I = В / X L , учитывая, что приложенное среднеквадратичное значение напряжения составляет 120 В. Для первой частоты это дает
[латекс]I=\frac{V}{{X}_{L }}=\frac{120\text{ V}}{1,13\text{ }\Omega}=106\text{ A при } 60\text{ Гц}\\[/latex].
Аналогично, на частоте 10 кГц
[латекс]I=\frac{V}{{X}_{L}}=\frac{120\text{ V}}{188\text{ }\Omega}= 0,637\text { A at } 10\text{ кГц}\\[/latex].
ОбсуждениеКатушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.
Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.
Конденсаторы и емкостное реактивное сопротивление
Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, и так что можно предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.
Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C, имеющим незначительное сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.
График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен ( 9на нем 0056 Q = 0 ) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:
Когда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четвертую периода или на угол сдвига фаз 90°.
Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I в цепи, содержащей только конденсатор C по другой версии закона Ома определяется как
[latex]I=\frac{V}{{X}_{C}}\\[/latex] ,
, где V является среднеквадратичным напряжением и x C определяется (как с x L , это выражение для x 9 . схема с использованием правил и исчисления Кирхгофа) должна быть
схема с использованием правил и исчисления Кирхгофа) должна быть
[латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex],
, где X C называется емкостным реактивным сопротивлением , потому что конденсатор реагирует на сопротивление току. X C измеряется в омах (проверка оставлена читателю в качестве упражнения). X C обратно пропорциональна емкости C ; чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Он также обратно пропорционален частоте ф ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.
Пример 2. Расчет емкостного реактивного сопротивления, а затем тока
(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?
Стратегия Емкостное реактивное сопротивление находится непосредственно из выражения в [latex]{X}_{C}=\frac{1}{2\pi fC}\\[/latex]. Однажды 9Для каждой частоты было найдено 0056 X C . Для определения тока на каждой частоте можно использовать закон Ома, сформулированный как I = В / X C .
Однажды 9Для каждой частоты было найдено 0056 X C . Для определения тока на каждой частоте можно использовать закон Ома, сформулированный как I = В / X C .
Ввод частоты и емкости в [латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex], дает
[ латекс]\begin{array}{lll}{X}_{C}& =& \frac{1}{2\pi fC}\\ & =& \frac{1}{6.28\left(60.0/\text {s}\right)\left(5.00\text{ }\mu\text{F}\right)}=531\text{ }\Omega\text{ at }60\text{ Гц}\end{массив}\ \[/латекс]. 9{4}/\text{s}\right)\left(5.00\mu\text{F}\right)}\\ & =& 3.18\text{ }\Omega\text{ при }10 \text{ кГц} \end{массив}\\[/латекс].
Решение для (b)Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I = В / X C при данном напряжении 1 . Для первой частоты это дает
[латекс]I=\frac{V}{{X}_{C}}=\frac{120 \text{V}}{531\text{ }\Omega}=0,226 \text{ A при }60\text{ Гц}\\[/latex].
Аналогично, на частоте 10 кГц
[латекс]I=\frac{V}{{X}_{C}}=\frac{120 \text{ V}}{3.18\text{ }\Omega}= 3,37 \text{ А при }10 \text{ Гц}\\[/latex].
ОбсуждениеКонденсатор очень по-разному реагирует на двух разных частотах, и совершенно противоположным образом реагирует индуктор. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.
Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X C стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .
Если частота стремится к нулю (постоянный ток), X C стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы действуют на цепи переменного тока противоположно действию катушек индуктивности .
Резисторы в цепи переменного тока
В качестве напоминания рассмотрим рис. 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:
Рис. 3. (a) Источник переменного напряжения, включенный последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.
Когда на резистор подается синусоидальное напряжение, оно точно совпадает по фазе с током — фазовый угол равен 0º.
Резюме раздела
- Для катушек индуктивности в цепях переменного тока мы обнаружили, что когда к катушке индуктивности прикладывается синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на фазовый угол 90º.
- Противодействие катушки индуктивности изменению тока выражается как вид сопротивления переменному току.
- Закон Ома для катушки индуктивности
[латекс]I=\frac{V}{{X}_{L}}\\[/латекс],
, где В — среднеквадратичное напряжение на катушке индуктивности.
- X L определяется как индуктивное реактивное сопротивление, определяемое формулой
[латекс]{X}_{L}=2\pi fL\\[/латекс],
с f частотой источника переменного напряжения в герцах.

- Индуктивное сопротивление X L выражается в омах и имеет наибольшее значение на высоких частотах.
- Для конденсаторов мы обнаружили, что когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90º.
- Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора
[латекс]I=\frac{V}{{X}_{C}}\\[/латекс],
, где В — среднеквадратичное напряжение на конденсаторе.
- Х С определяется как емкостное реактивное сопротивление, определяемое выражением
[латекс]{X}_{C}=\frac{1}{2\pi fC}\\[/latex].
- X C измеряется в омах и имеет наибольшее значение на низких частотах.
Концептуальные вопросы
1. Пресбиакузис — возрастная потеря слуха, которая постепенно влияет на более высокие частоты. Усилитель слухового аппарата предназначен для одинакового усиления всех частот. Чтобы настроить его выход на пресбиакузис, вы бы включили конденсатор последовательно или параллельно с динамиком слухового аппарата? Объяснять.
Усилитель слухового аппарата предназначен для одинакового усиления всех частот. Чтобы настроить его выход на пресбиакузис, вы бы включили конденсатор последовательно или параллельно с динамиком слухового аппарата? Объяснять.
2. Будете ли вы использовать большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул частотой 100 Гц в звуковой системе? Объяснять.
3. Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли сменный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.
4. Зависит ли индуктивность от тока, частоты или от того и другого? А индуктивное сопротивление?
5. Объясните, почему конденсатор на рис. 4(а) действует как фильтр низких частот между двумя цепями, а конденсатор на рис. 4(б) действует как фильтр высоких частот.
Рис. 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой частотой и низкой частотой.
4. Конденсаторы и катушки индуктивности. Конденсатор с высокой частотой и низкой частотой.
6. Если конденсаторы на рисунке 4 заменить катушками индуктивности, что будет работать как фильтр низких частот, а что как фильтр высоких частот?
Задачи и упражнения
1. При какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление 100 Ом?
2. Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм на частоте 500 Гц?
3. Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при частоте 60,0 Гц?
4. При какой частоте конденсатор емкостью 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом?
5. (a) Найдите ток через катушку индуктивности 0,500 Гн, подключенную к источнику переменного тока с частотой 60,0 Гц и напряжением 480 В. б) Какой будет сила тока на частоте 100 кГц?
6. (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ? б) Какой будет сила тока на частоте 25,0 кГц?
7. Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, производит ток силой 2,00 А. Индуктивность какая?
Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, производит ток силой 2,00 А. Индуктивность какая?
8. Источник 20,0 Гц, 16,0 В производит ток 2,00 мА при подключении к конденсатору. Какова емкость?
9. (a) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от источника питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц? б) Каково его реактивное сопротивление при частоте 60,0 Гц?
10. Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. (а) Какая емкость необходима для создания реактивного сопротивления 100 кОм на частоте 120 Гц? б) Каким будет его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
11. Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. (a) Какая емкость необходима для получения реактивного сопротивления [латекс]\текст{10,0 м\Омега}[/латекс] для сигнала частотой 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
(a) Какая емкость необходима для получения реактивного сопротивления [латекс]\текст{10,0 м\Омега}[/латекс] для сигнала частотой 5,00 кГц? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).
12. Необоснованные результаты При записи напряжений, вызванных мозговой активностью (ЭЭГ), на конденсатор подается сигнал 10,0 мВ с частотой 0,500 Гц, производящий ток 100 мА. Сопротивление незначительно. а) Чему равна емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
13. Создайте свою собственную задачу Рассмотрим использование катушки индуктивности последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц. Среди вещей, которые следует учитывать, — приемлемое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.

 … / / Таблица. Реактивное сопротивление емкости (конденсатора) в зависимости от частоты.(от 1 пф до 1000 мкФ ; от 50 Гц до 100 МГц)
… / / Таблица. Реактивное сопротивление емкости (конденсатора) в зависимости от частоты.(от 1 пф до 1000 мкФ ; от 50 Гц до 100 МГц) 6 МОм
6 МОм 6 кОм
6 кОм 6 кОм
6 кОм 6 Ом
6 Ом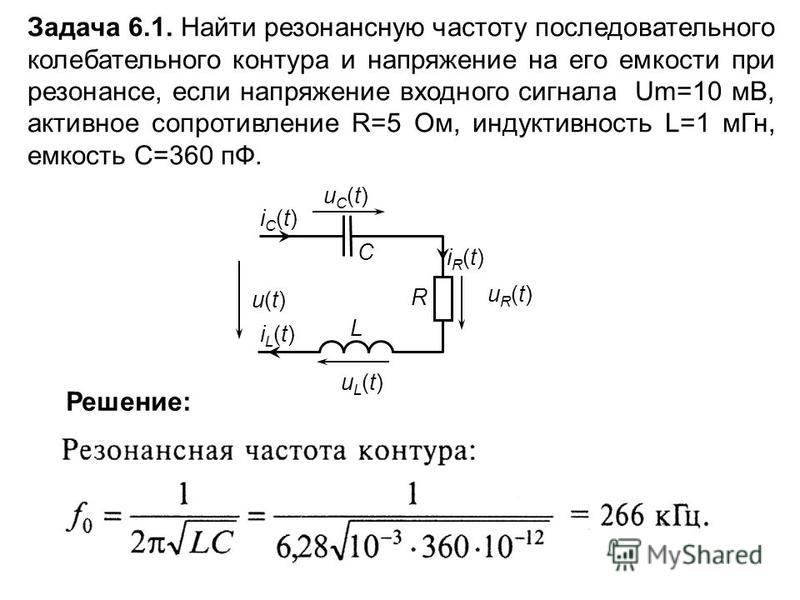
 Определите, какая доля полного сопротивления катушки приходится на реактивное сопротивление. Удельное сопротивление меди ρ = 17 нОм·м.
Определите, какая доля полного сопротивления катушки приходится на реактивное сопротивление. Удельное сопротивление меди ρ = 17 нОм·м. Падения напряжения U1:U2 = 1:2. Определите: 1) емкость конденсатора; 2) действующее значение силы тока.
Падения напряжения U1:U2 = 1:2. Определите: 1) емкость конденсатора; 2) действующее значение силы тока.
 Найти полное сопротивление Z цепи, если конденсатор и резистор включены: а) последовательно; б) параллельно.
Найти полное сопротивление Z цепи, если конденсатор и резистор включены: а) последовательно; б) параллельно. Катушка включена в цепь переменного тока частотой ν = 50 Гц. Какую часть полного сопротивления катушки составляет: 1) активное сопротивление, 2) индуктивное сопротивление?
Катушка включена в цепь переменного тока частотой ν = 50 Гц. Какую часть полного сопротивления катушки составляет: 1) активное сопротивление, 2) индуктивное сопротивление?
