Урок 11. Основные тригонометрические тождества
ВИДЕО УРОК
Формулы тригонометрии – это соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом.
Выражение, в котором переменная содержится под знаками тригонометрических функций, называют тригонометрическим.
Для преобразования тригонометрических выражений используют свойства тригонометрических функций и формулы тригонометрии.
Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла – аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.
Основные тригонометрические тождества.
Из пяти основных тождеств вытекают три дополнительные.
Соотношения между тригонометрическими функциями одного и того же угла.
Введём на плоскости прямоугольную систему координат хОу. Пусть α – произвольный угол, а ОМ – соответствующий этому углу радиус единичной окружности, так что угол, составленный с осью Ох этим радиусом ОМ, равен α.
1. Проведём через точку М прямую, перпендикулярную к оси Ох, и пуст Р – точка, в которой эта прямая пересечёт ось Ох. Длины отрезков ОР и РМ равны абсолютным величинам координат точки М:
ОР = |х|, РМ = |у|,
а длина отрезка ОМ равна единице:
ОМ = 1.
Из прямоугольного треугольника ОРМ
имеем:ОР2 + РМ2 = ОМ2,
или
|х|2 + |у|2 = 1,
или
х2 + у2 = 1.
Но
х = sin α,
у = cos α,
а поэтому
sin2α + cos2α = 1.
Если точка М совпадает с одной из точек
то одна из координат точки М равна +1 или –1, другая нулю, то есть формула
х2 + у2 = 1,
а следовательно, и формула
sin2α + cos2α = 1
верны и в этом случае.
2. Из формул
х = cos α, у = sin α,
tg α = у
находим
3. Так как
Разделив обе части тождества
sin2α + cos2α = 1
один раз на cos2α, другой раз на sin2α, получим:
или
sec2α = 1 + tg2α,
cosec2α = 1 + ctg2α.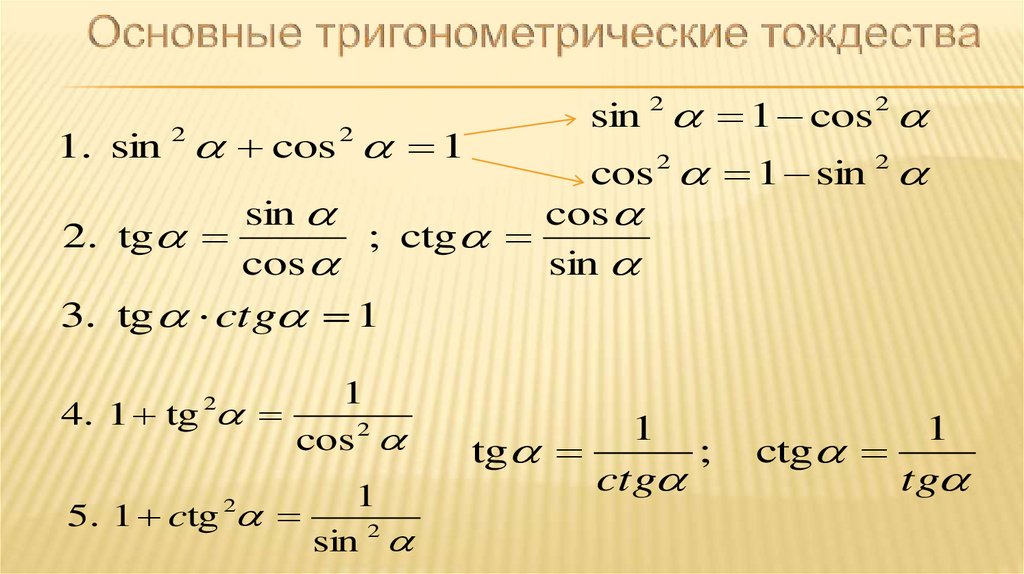
Формула
sin2α + cos2α = 1
верна при всех значениях α.
Формулы
верны при всех значениях α кроме тех, при которых не определены (не существуют) функции tg α и sec α, то есть значения
α = (2k + 1) π/2,
где k – любое целое число.
Формулы
верны при всех значениях α кроме α = kπ,
где k – любое целое число, так как, если α = kπ, то функция ctg α и cosec α не определены (не существуют).
Наконец, формула
tg α ∙ ctg α = 1
верна при всех значениях α кроме тех, при которых не определена хотя бы одна из функций tg α и ctg α, то есть при всех значениях α кроме
α = kπ/2,
где k – любое целое число.
Формулы
sec2α = 1 + tg2α
cosec2α = 1 + ctg2α
позволяют на чертеже
увидеть secα и cosec α.
secα – гипотенуза прямоугольного треугольника с катетами 1 и tg α, а соsecα – гипотенуза прямоугольного треугольника с катетами 1 и ctg α.
Все восемь формул
могут быть получены на чертеже.
Каждая из формул, связывающих квадраты двух функций
sin2α + cos2α = 1,
sec2α = 1 + tg2α,
cosec2α = 1 + ctg2α,
получается из
соответствующего прямоугольника на основании теоремы Пифагора.
ПРИМЕР:
Упростите выражение:
(1 – cos2 x)tg2 x.
РЕШЕНИЕ:
(1 – cos2 x)tg2 x = sin2 x tg2 x =
ОТВЕТ:
ПРИМЕР:
Упростите выражение:
(cos2α – 1)сtg2α.
РЕШЕНИЕ:
Воспользуемся формулами:
получим:
ОТВЕТ: –cos2α
ПРИМЕР:
Упростите выражение:
(1 + tg2 x)cos2 x.
РЕШЕНИЕ:
(1 + tg2 x)cos2 x =
cos2 x + tg2 x cos2 x
= cos2 x + sin2 x = 1.
ОТВЕТ: 1.
ПРИМЕР:
Вычислите:
cos x, если
sin x = 0,8,π/2 < х < π.
РЕШЕНИЕ:
sin x = 0,8,
sin2 x + cos2 x = 1,
cos2 x = 1 – sin2x =
1 – 0,64 = 0,36.
cos x = 0,6 або cos x = –0,6.
Так как аргумент принадлежит второй четверти
(π/2 < х < π), то
cos x < 0, cos x = –0,6.
ОТВЕТ:
ПРИМЕР:
Найдите значение выражения:
если ctg x = 1/3.
РЕШЕНИЕ:
Поделим числитель и знаменатель дроби на sin x. Так как ctg x = 1/3, то sin x не принимает значение нуль.ОТВЕТ: 11/13.
ПРИМЕР:
Упростить выражение:
РЕШЕНИЕ:
Имеем:
ОТВЕТ:Формулы, которые выражают зависимость между тригонометрическими функциями
одного и того же острого угла, представляют собой пример тригонометрических
тождеств. Они справедливы независимо
от величины угла.
Для доказательства
тригонометрического тождества можно или левую часть тождества преобразовать к
правой, или правую часть преобразовать к левой, или каждую из частей тождества
преобразовать к одному и тому же выражению.
ПРИМЕР:
Доказать тождество:
tg2 α – sin2 α = tg2 α sin2 α.
ДОКАЗАТЕЛЬСТВО:
Преобразуем левую часть этого равенства:
ПРИМЕР:
Доказать справедливость тождества:
ДОКАЗАТЕЛЬСТВО:
Первый
способ.
Преобразуем правую часть:
Второй
способ.
Преобразуем левую часть:
ПРИМЕР:
Доказать справедливость тождества:
cos4 α – sin4 α = cos2 α (1 – tg α)(1 + tg α).
ДОКАЗАТЕЛЬСТВО:
Первый способ.
Преобразуем правую часть:
cos2 α (1 – tg α)( 1 + tg α) =
cos2 α (1 – tg2α) =
cos2 α – sin2α.
Второй способ.
Преобразуем левую часть:
cos4 α – sin4 α =
(cos2 α – sin2 α)(cos2 α + sin2 α) =
cos2 α – sin2 α.
Правая и левая части данного равенства преобразованы в одно и то же выражение
cos2 α – sin2 α.
Отсюда заключаем, что данное тождество справедливо.
ПРИМЕР:
Доказать тождество
3(sin4 α + cos4 α) – 2(sin6 α + cos6 α) = 1.
ДОКАЗАТЕЛЬСТВО:
Преобразуем вначале левую часть равенства, а затем, используя формулу
находим
3(sin4 α + cos4α) – 2(sin6α + cos6α) =
3(sin4 α + cos4α) – 2(sin2α + cos2α) (sin4α – sin2α cos2α + cos4α)
= 3sin4 α + 3cos4α – 2sin4α + 2sin2α cos2α – 2cos4α =
sin4 α + 2sin2α cos2α
+ cos4α = (sin2α + cos2α)2 = 1.
ПРИМЕР:
Доказать тождество
sin3 α (1 + ctgα) + cos3α (1 + tgα) = sinα + cosα.
ДОКАЗАТЕЛЬСТВО:
sin3 α (1 + ctgα) + cos3α (1 + tgα) =
= sin2 α (sinα + cosα) + cos2 α (cosα + sinα)
= (sinα + cosα) (sin2 α + cos2 α) = (sinα + cosα).
Примеры применения тригонометрических тождеств
Класс 9 «Б»
Урок 63.
Дата: 10.02
Тема: примеры применение тригонометрических тождеств
Цели урока: Образовательные: повторить основные тригонометрические формулы и закрепить их в ходе выполнения упражнений; Развивающие: развивать вычислительные навыки, логическое мышление, навыки контроля и самоконтроля; Воспитательные: воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов.
Тип урока: урок повторения
Методы: поисковые, познавательные
Оборудование: карточки для учащихся, рабочие листы.
Ход урока
I. Организационныймомент.
Сообщение темы, цели урока и мотивации учебной деятельности учащихся.
II. Проверка знаний учащимися тригонометрических формул.
У доски 2 ученикапоочередно записывают тригонометрические формулы. Выигрывает тот, кто последним запишет формулу.
III. Устная работа (задания показываются с помощью презентации).
Какому выражению соответствует значение ?
а) sin30°;
б) cos;
в) tgВыбрать верное равенство
а) sinα =;
б) cosα = ;
в) sinα = -3,7.Какой из углов является углом II четверти?
а) ;
б) –145°;
в)В каких четвертях sinα и cosα имеют разные знаки?
а) II и IV;
б) I и III;
в) I и IV.Каким выражением можно заменить ?
а) cosα;
б) sinα;
в) — sinα.
Ответ: 1б; 2б; 3в; 4а; 1б.
IV. Математический диктант.
Вариант 1 | Вариант 2 |
1+tg2α = | 1+ctg2α= |
sin2α + cos2α= | tgα·ctgα= |
1- sin2α = | 1-cos2α= |
Все учащиеся работают в тетрадях. Два ученика выполняют работу на закрытых досках.
Учащиеся проверяют работы одноклассников, работающих на обратной стороне доски, и одновременно свои работы.
V. Применение тригонометрических формул к преобразованию выражений.
1. Вычислить.
Работа выполняется письменно в тетради с дальнейшей проверкой
№/№ | Задание | Ответ |
I. | | |
II. Самостоятельно с устной проверкой |
2. Найти значение выражения.
Учащиеся выполняют работу по вариантам, самостоятельно, для проверки меняются тетрадями с соседом.
Ответы : 1вар-134; 2вар-324.
3. Найти по заданному значению тригонометрической функции остальные функции.
Учащиеся выполняют заданиясамостоятельно письменно в тетрадях, проверяют их устно на доске.
I | II | III |
Дано: | Дано: | Дано: |
Ответ: | Ответ: | Ответ: |
4. Упростить тригонометрические выражения:
Упростить тригонометрические выражения:
а) задания для I и II групп:
I группа | Ответ | IIгруппа | Ответ |
б) третья группа выполняет задания покарточкам
Задание | Ответ |
Доказать тождество: |
|
Упростить: | |
Упростить выражение: |
VI. Резерв.
Резерв.
Учащиеся, выполнившиезадания, сдают в конце урока тетради на проверку.
1. Упростите выражения:
2) cos2α – (ctg2α +1) sin2α.=
3)
4)
2. Докажите тождество:
1) (tg α+ctg α)2– (tg α–ctg α)2= 4
Тождество доказано.
2) (1+tg α)2+(1-tg α)2=;
Тождество доказано.
3) (2+ sin β)(2- sin β)+(2+ cos β)(2– cos β)=7
Тождество доказано.
VII. Домашнее задание.
Доказать тождество:
VIII. Рефлексия. Подведение итогов урока.
Выставление оценок за работу на уроке.
Тригонометрия. Рабочие примеры
Рабочие примеры
Тригонометрические уравнения и тождества
Часть 1: пифагорейские тождества Напомним, что в разделе об единичной окружности мы установили, что для любого угла $\theta$, $\left(\cos\left(\theta\right),\sin\left(\theta\right)\right)$ координаты точки на единичной окружности. 2\влево(\тета\вправо) = 1$$
92\влево(х\вправо)} \\
&= \frac{1-\cos\left(x\right)}{\sin\left(x\right)}
\конец{выравнивание*}
2\влево(\тета\вправо) = 1$$
92\влево(х\вправо)} \\
&= \frac{1-\cos\left(x\right)}{\sin\left(x\right)}
\конец{выравнивание*} Часть 2: четно-нечетные тождества У нас также есть следующие тождества: $$\sin\left(-\theta\right)=-\sin\left(\theta\right) \hspace{10 mm} \cos\left(-\theta\right)=\cos\left(\theta \right) \hspace{10 мм} \tan\left(-\theta\right)=-\tan\left(\theta\right)$$ Они говорят нам, что $\sin$ и $\tan$ нечетны. Нечетной функцией $f$ является любая функция, удовлетворяющая условию $f(-x) = -f(x)$ для всех $x$ в своей области определения. функции, в то время как $\cos$ — четнаяЧетная функция $f$ — это любая функция, которая удовлетворяет условию $f(-x) = f(x)$ для всех $x$ в своей области определения. функция.
Пример. Вычислить $\sin\left(-\frac{\pi}{2}\right)$
$$\sin\left(-\frac{\pi}{2}\right)=-\sin\left(\frac{\pi}{2}\right)=-1$$Часть 3: Формулы сложения Мы можем свести $\sin$ и $\cos$ суммы двух углов к выражению, включающему $\sin$ и $\cos$ каждого из углов: \начать{выравнивать*} \sin\left(A+B\right) &= \sin\left(A\right)\cos\left(B\right) + \cos\left(A\right)\sin\left(B\right) \\ \cos\left(A+B\right) &= \cos\left(A\right)\cos\left(B\right) — \sin\left(A\right)\sin\left(B\right) \конец{выравнивание*} 9{\ круг} \ справа) \\ &= \frac{1}{\sqrt{2}}\left(\frac{\sqrt{3}}{2}\right) + \frac{1}{\sqrt{2}}\left(\frac {1}{2}\справа) \\ &= \ гидроразрыва {\ sqrt {3} + 1} {2 \ sqrt {2}} \конец{выравнивание*}
Часть 4.
 Тригонометрические уравнения Методы решения тригонометрических уравнений включают те же стратегии, что и решение полиномиальных уравнений (см. раздел «Полиномы и факторинг»), а также использование тригонометрических тождеств.
Тригонометрические уравнения Методы решения тригонометрических уравнений включают те же стратегии, что и решение полиномиальных уравнений (см. раздел «Полиномы и факторинг»), а также использование тригонометрических тождеств.Пример. Найдите решения уравнения 92\влево(\тета\вправо)+5\sin\влево(\тета\вправо)+4 = 0$$ Обратите внимание, что это квадратное уравнение, и после факторизации мы получаем: $$(\sin\left(\theta\right)+1)(\sin\left(\theta\right)+4) = 0$$ Опять же, нам нужно проверить, когда любой из множителей равен нулю. Для второго множителя получаем $\sin\left(\theta\right)+4 = 0$, т.е. $\sin\left(\theta\right)=-4$, не имеющее решения (поскольку левая часть не менее $-1$). Решая первый множитель, получаем $\sin\left(\theta\right)+1=0$, т.е. $\sin\left(\theta\right)=-1$. Единственный $\theta \in \left[0,2\pi \right]$, для которого это верно, — это $\theta= \frac{3\pi}{2}$.
Trig Identities — все, что вам нужно знать для подтверждения личности
Семь видеороликов, предназначенных для подробного объяснения того, как использовать, упрощать и проверять все тригонометрические тождества, встречающиеся в любом классе предварительного исчисления или тригонометрии.
54 мин. 12 примеров
- Введение в видео: основные тождества
- Обзор основных идентичностей и введение пифагорейских идентичностей
- Примеры №1–12: Упрощение с использованием фундаментальных тождеств
60 мин 10 примеров
- Введение в видео: Шаги для доказательства/проверки идентичности триггеров
- Шаги и приемы для доказательства/проверки личности триггера
- Примеры №1–5: упрощение с помощью умножения и/или факторизации
- Примеры № 6–8: упростите, получив общие знаменатели
- Примеры № 9-10: Упрощение с помощью Conjugate
1 час 32 минуты 15 примеров
- Введение в видео: Доказательство/проверка тригонометрических тождеств
- Обзор шагов и приемов для доказательства/проверки тригонометрических тождеств
- Примеры № 1–15: доказательство/проверка тригонометрического тождества
1 час 08 минут 10 примеров
- Введение в видео: сумма и разность тождеств
- Обзор тождеств суммы и разности и важных понятий
- Пример.



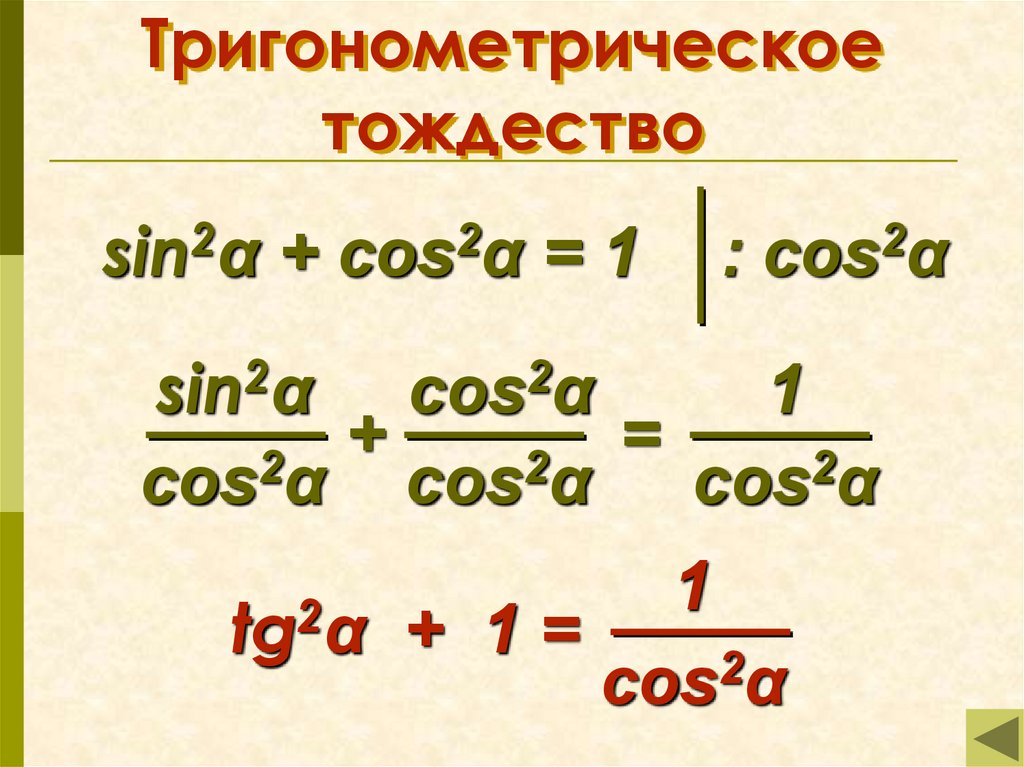 У доски с объяснением
У доски с объяснением