ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4.  Скользящие и приложенные векторные величины.6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 2. Основные теоремы о скалярных проекциях § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме.  4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 7. Скалярные произведения координатных ортов. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения.  § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b § 2. Произведения пяти и шести векторов 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов.  4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 4. Основные задачи, связанные с произведениями трех и более векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII.  ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ§ 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3.  Круг кривизны§ 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности.  5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2.  Криволинейный интеграл от линейной формы по произвольной кривой.4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV.  ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ§ 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. § 3. Потенциальное несжимаемое поле Глава XVIII.  ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ§ 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах.  § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты |
Векторное произведение | это… Что такое Векторное произведение?
Векторное произведение в трёхмерном пространстве.
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность.
Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
Содержание
|
Определение и история
Векторным произведением вектора на вектор в пространстве называется вектор , удовлетворяющий следующим требованиям:
- длина вектора равна произведению длин векторов и на синус угла между ними: ;
- вектор ортогонален каждому из векторов и ;
- вектор направлен так, что тройка векторов является правой;
- в случае пространства требуется ассоциативность тройки векторов .
Обозначение:
В литературе[1] определение векторного произведения может даваться по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах в правой и левой прямоугольной системе координат. А далее выводится данное выше определение, а также определение правой и левой тройки векторов.
Также для исходного определения может быть взят набор алгебраических свойств векторного произведения, а из них выводиться остальное.
Векторное произведение было введено У. Гамильтоном в 1846 году[2] одновременно со скалярным произведением в связи с кватернионами — соответственно, как векторная и скалярная часть произведения двух кватернионов, скалярная часть которых равна нулю[3].
Правые и левые тройки векторов в трёхмерном пространстве
Нахождение направления векторного произведения с помощью правила правой руки
Рассмотрим упорядоченную тройку некомпланарных векторов в трёхмерном пространстве.
Совместим начала этих векторов в точке (то есть выберем произвольно в пространстве точку и параллельно перенесём каждый вектор так, чтобы его начало совпало с точкой ). Концы векторов, совмещённых началами в точке , не лежат на одной прямой, так как векторы некомпланарны. Рассмотрим плоскость — единственную плоскость, проходящую через концы векторов, совмещённых началами в точке . Тогда можно в плоскости провести через концы векторов , совмещённых началами в точке , единственную окружность и выяснить направление обхода трёх точек на окружности, смотря на неё с одной из сторон от плоскости.
Упорядоченная тройка некомпланарных векторов в трёхмерном пространстве называется правой, если наблюдателю, находящемуся по одну сторону с точкой от плоскости , обход концов приведённых в общее начало векторов в указанном порядке кажется совершающимся в плоскости по часовой стрелке.
B противном случае — левая тройка. В этом случае наблюдателю, находящемуся с другой стороны от плоскости , обход концов таких векторов будет казаться совершающимся против часовой стрелки.
Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.
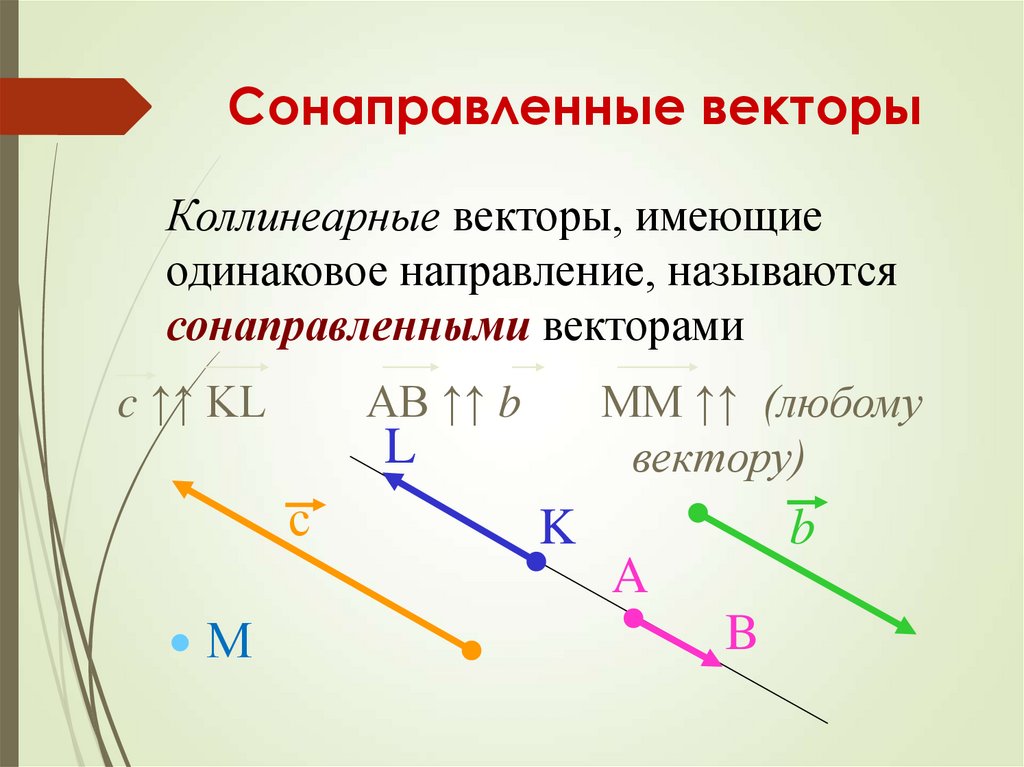
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
Заметим, что определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.
Свойства
Геометрические свойства векторного произведения
Рисунок 1: Площадь параллелограмма равна модулю векторного произведения.
Рисунок 2: Объём параллелепипеда при использовании векторного и скалярного произведения векторов; пунктирные линии показывают проекции вектора c на a × b и вектора a на b × c, первым шагом является нахождение скалярных произведений.
- Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.
- Модуль векторного произведения равняется площади параллелограмма, построенного на приведённых к общему началу векторах и (см. Рисунок 1)
- Если — единичный вектор, ортогональный векторам и и выбранный так, что тройка — правая, а — площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
- Если — какой-нибудь вектор, — любая плоскость, содержащая этот вектор, — единичный вектор, лежащий в плоскости и ортогональный к , — единичный вектор, ортогональный к плоскости и направленный так, что тройка векторов является правой, то для любого лежащего в плоскости вектора справедлива формула
- При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c (см. Рисунок 2). Такое произведение трех векторов называется смешанным.
На рисунке показано, что этот объём может быть найден двумя способами: геометрический результат сохраняется даже при замене «скалярного» и «векторного» произведений местами:
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения
| Представление | Описание |
|---|---|
| свойство антикоммутативности | |
| свойство ассоциативности относительно умножения на скаляр | |
| свойство дистрибутивности по сложению | |
| тождество Якоби, выполняется в и нарушается в | |
| формула «БАЦ минус ЦАБ», тождество Лагранжа | |
| Это частный случай мультипликативности нормы кватернионов | |
| значение этого выражения называют смешанным произведением векторов , , и обозначают либо |
Выражение для векторного произведения в декартовых координатах
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
а система координат правая, то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Если система координат левая, то их векторное произведение имеет вид
Для запоминания, аналогично:
или
Формулы для левой системы координат можно легко получить из формул правой системы координат, записав те же векторы и во вспомогательной правой системе координат ():
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов , и . Если представить вектор как кватернион , то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т.
п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь независимых компонент в -мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В трёхмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить как строку векторов.
Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например ( — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
— единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы вычисляется как векторное произведение матрицы на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерностей 3 и 7.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в -мерном пространстве на операцию с сомножителями. Используя символ Леви-Чивиты с индексами, можно явно записать такое -валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности .
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители.
Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .
Эта конструкция называется внешним произведением.
Для двумерного случая операция
- .
называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат есть псевдоскаляр. (Двухиндексное внешнее произведение, описанное выше, можно ввести и для двумерного пространства, однако оно, очевидно, достаточно тривиально связано с псевдоскалярным произведением, а именно внешнее произведение в этом случае представляется матрицей, на диагонали которой нули, а оставшиеся два недиагональных элемента равны псевдоскалярному произведению и минус псевдоскалярному произведению).
Алгебра Ли векторов
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли к группе Ли ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
- Псевдоскалярное произведение (только на плоскости!)
- Скалярное произведение векторов
- Смешанное (скалярно-векторное) произведение векторов (только в )
- Двойное (векторно-векторное) произведение векторов (только в )
Другое
- Ротор
- Дивергенция
Примечания
- ↑ И в различных учебных заведениях.
- ↑ Crowe M. J. A History of Vector Analysis – The Evolution of the Idea of a Vectorial System. — Courier Dover Publications, 1994. — С. 32. — 270 с. — ISBN 0486679101
- ↑ Hamilton W. R. On Quaternions; or on a New System of Imaginaries in Algebra // Philosophical Magazine. 3rd Series. — London, 1846. — Т. 29. — С. 30.
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Ссылки
- Многомерное векторное произведение
- Векторное произведение и его свойства. Примеры решения задач
- В. И. Гервидс Правое и левое вращение (flash). НИЯУ МИФИ (10.03.2011). — Физические демонстрации. Проверено 3 мая 2011.
Примеры решения задачВведение в векторное умножение
Векторное умножение можно разделить на две категории. Вектор имеет как величину, так и направление, и в результате скалярное произведение двух векторов и перекрестное произведение двух векторов являются двумя методами умножения векторов. Поскольку результирующее значение является скалярной величиной, скалярное произведение двух векторов часто называют скалярным произведением двух векторов. Перекрестное произведение называется векторным произведением, потому что на выходе получается вектор, перпендикулярный двум векторам, которые использовались для его вычисления.
Давайте изучим двустороннее умножение векторов, включая рабочее правило, свойства, приложения и примеры этого типа умножения.
Лучший способ умножения векторов
С вектором связаны как величина, так и направление.
Скалярное произведение и перекрестное произведение — это два метода умножения двух или более векторов. Пожалуйста, позвольте нам узнать больше о каждой из операций векторного умножения.
Скалярный продукт
Скалярное произведение векторов, широко известное как скалярное произведение векторов, представляет собой математическую операцию над векторами. Скалярное значение, полученное скалярным произведением векторов, является произведением векторов. Когда два вектора перемножаются, они образуют скалярное произведение, равное произведению их модулей плюс синус угла между двумя векторами. Консеквент скалярного произведения двух векторов расположен в той же плоскости, что и два вектора, которые использовались для его вычисления. Скалярный продукт может быть либо положительным действительным числом, либо отрицательным действительным числом в области действительных чисел.
Пусть a и b представляют два ненулевых вектора и пусть представляют собой угол между векторами.
Скалярное произведение, часто известное как скалярное произведение, обозначается символом a.b, который определяется как:
Отношение между переменными a и b равно | а | | б | cosθ.
,где |а| является величиной a, |b| является величиной b, а угол между ними представлен | а |, | b |, а θ — угол между ними.
Перекрестное произведение
В некоторых кругах векторное произведение иногда называют векторным произведением. Этот тип векторного умножения проводится между двумя векторами различной природы или сорта и известен как векторное произведение. Всякий раз, когда два вектора перемножаются друг с другом, а умножение также является векторной величиной, результирующий вектор называется перекрестным произведением двух векторов или векторным произведением соответственно. Когда два предоставленных вектора объединяются, результирующий вектор перпендикулярен плоскости, содержащей два вектора.
Мы можем лучше понять это, рассмотрев следующий пример: если у нас есть два вектора, лежащие в плоскости X-Y, их векторное произведение даст результирующий вектор, указывающий в направлении оси Z, которая перпендикулярна оси Z.
плоскость Х-У. Символ стрелки используется для соединения двух исходных векторов вместе. Следующая диаграмма иллюстрирует умножение векторов или векторное произведение двух векторов.
a x b=c
В этом уравнении есть два вектора, и результирующий вектор представлен буквой c. Предположим, что a и b образуют угол в 90 градусов, а n — единичный вектор, перпендикулярный плоскости, содержащей a и b. Перекрестное произведение двух векторов можно вычислить с помощью следующего уравнения:
a x b=|a | |b|sinθ
Заключение
Умножение векторов можно разделить на две категории. Вектор имеет как величину, так и направление, и в результате скалярное произведение двух векторов и перекрестное произведение двух векторов являются двумя методами умножения векторов. Поскольку результирующее значение является скалярной величиной, скалярное произведение двух векторов часто называют скалярным произведением двух векторов.
Перекрестное произведение называется векторным произведением, потому что на выходе получается вектор, перпендикулярный двум векторам, которые использовались для его вычисления. Вектор имеет как величину, так и связанное с ним направление. Скалярное произведение и перекрестное произведение — это два метода умножения двух или более векторов. Скалярное произведение векторов, широко известное как скалярное произведение векторов, представляет собой математическую операцию над векторами. Скалярное значение, полученное скалярным произведением векторов, является произведением векторов.
Векторное умножение: скалярное произведение
С технической точки зрения скалярное произведение является своего рода скалярным произведением.
Это означает, что это операция, которая берет два вектора и «умножает» их.
вместе, и производит скаляр. Однако нам не нужен скалярный продукт двух
векторы для получения любого скаляра. Было бы хорошо, если бы продукт мог
предоставить значимую информацию о векторах в терминах скаляров.
Что мы подразумеваем под «значимым»? Рад, что вы спросили. Для начала поищем скалярные величины, которые могут характеризовать вектор. Одним из простых примеров этого является длина, или величина вектора v , обычно обозначаемая | против |. Каждый из 2- и 3-мерных векторов, которые мы обсуждали, имеет длина, а длина является скалярной величиной. Например, чтобы найти длину вектор ( a , b , c ), нам просто нужно вычислить расстояние между началом и точка ( a , b , c ). (Идея та же самая в двух измерениях). Наше измерение даст скалярное значение величины без направления— вместо другой вектор! Этот тип скаляры звучит как вид значимой информации, точечный продукт может предоставить нам.
Компонентный метод
Теорема Пифагора говорит нам, что длина вектора ( a , b , c ) равна
данный . Это дает нам представление о том, как мы можем определить
скалярное произведение.
Например, если нам нужно скалярное произведение вектора v = ( v 1 , v 2 , v 3 ) с самим собой ( v · v ), чтобы дать нам информацию о длине v , имеет смысл потребовать, чтобы это выглядело так:
| v · v = v 1 v 1 + v 2 v 2 + v 3 v 3 |
Следовательно, скалярное произведение вектора на самого себя дает величину вектора в квадрате.
Хорошо, это то, что мы хотели, но теперь царит новый вопрос: что такое точка
произведение между двумя разными векторами? Важно помнить, что
как бы мы ни определяли общее правило, оно должно сводиться к тому, когда мы подключаем
два одинаковых вектора.
На самом деле, @@Equation @@ уже написано
наводя на размышления, чтобы указать, что общее правило для скалярного произведения между двумя
векторов U = ( U 1 , U 2 , U 3 ) и V = ( V 1 , 4 V 9999009.9.. 09. . . 09 9. . . . . . . . . . . 9. . . . 19 99. 19. 199. 19. 19. 9. . 3 ) может быть:
| u · v = u 1 v 1 + u 2 v 2 + u 3 v 3 |
Это уравнение точно соответствует формуле скалярного произведения двух
Трехмерные векторы.
(Обратите внимание, что количество, полученное справа, является скаляр, , хотя мы больше не можем сказать, что это представляет собой длину
либо вектор.) Для 2-мерных векторов, U = ( U 1 , U 2 ) и V = ( V 1 , V 919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919191919919191). мы
есть:
| u · v = u 1 v 1 + u 2 v 2 |
Опять же, подставляя u = v , мы восстанавливаем квадрат длины вектора в двух измерениях.
Геометрический метод
Так что же дает скаляр, полученный при скалярном произведении u .
v представляет?
Мы можем получить представление о том, что происходит, взглянув на скалярное произведение вектора.
с единичными векторами. В Unit Vectors мы определили единицу
векторы i , j и k для трехмерного случая. В двух измерениях мы имеем только i = (1, 0) и j = (0, 1). (Пока мы будем работать в двух измерениях, так как такие векторы легче представить графически.) Скалярные произведения вектора v = ( v 1 , v 2 ) с единичными векторами i и j определяются по формуле:
| v · i | = | v 1 1 + v 2 0 = v 1 | |
| v · j | = | v 1 0 + v 5 0 3 v 2 19091 2 |
Другими словами, скалярное произведение v на i выделяет компонент v в направлении x , и
точно так же скалярное произведение v с j выделяет компонент v , который лежит в направлении y .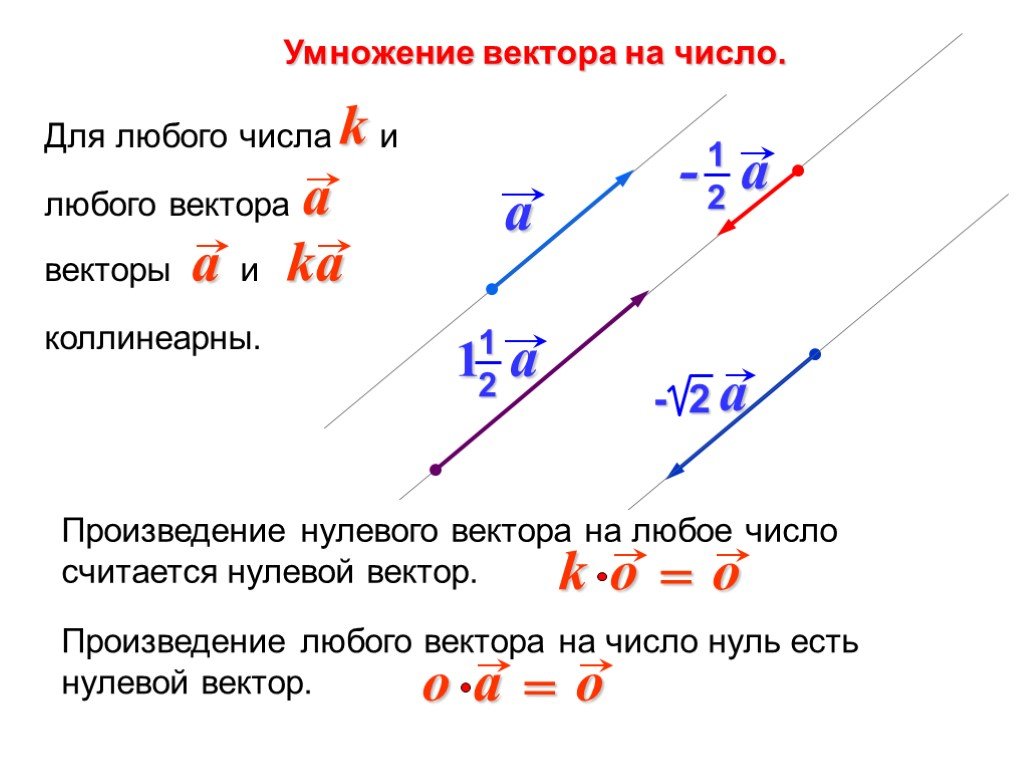
Это
то же самое, что вычисление величины проекции v на оси x и y соответственно.
Это может показаться не слишком захватывающим, поскольку в некотором смысле мы уже знали об этом, как только как мы записали наш вектор с точки зрения компонентов. Но что было бы, если бы вместо компонентов нам были даны только направление и величина вектора v , как на следующем рисунке?
Рисунок %: Вектор v с длиной l и направлением, заданным углом θ .В этом случае, заметив образовавшиеся два прямоугольных треугольника и вспомнив правила из тригонометрии находим, что v · i и v · j можно вычислить по-другому. А именно:
| v · i | = | | против | cos θ | |
| v · j | = | | против | sin θ = l cos(90 — θ ) |
Что произойдет, если мы возьмем скалярное произведение v с общим вектором, лежащим
чисто в направлении x (т.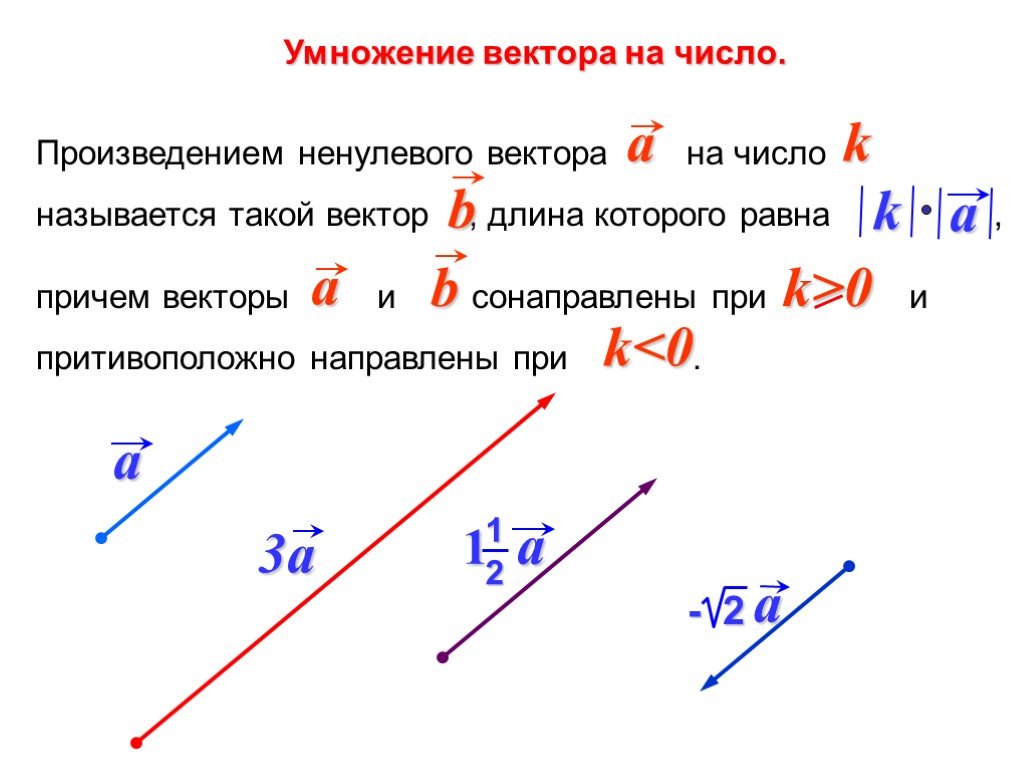
е. не обязательно единичный вектор)? Мы можем написать
такой вектор, как w = ( w 1 , 0) = w 1 (1, 0) = w 1 i , и ясно, что
величина w | с | = ш 1 . Следовательно, w = | с | и . Используя приведенное выше правило
для скалярного произведения между v и i находим, что:
| v · w = | против || с | cos θ |
На самом деле, это уравнение выполняется в общем случае: если мы возьмем v и w произвольными
векторы в двух или трех измерениях, и пусть θ будет углом между
их, мы находим, что эта версия формулы скалярного произведения точно согласуется с
формула компонента, которую мы нашли ранее.