Факториал формула стирлинга: Модификация формулы Стирлинга / Хабр

Двойной факториал | это… Что такое Двойной факториал?

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

.

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

Эта функция часто используется в комбинаторике, теории чисел и функциональном анализе.

Иногда словом «факториал» неформально называют восклицательный знак.

Содержание 1 Свойства 1.1 Комбинаторное определение 1.2 Связь с гамма-функцией 1.3 Формула Стирлинга 1.4 Разложение на простые числа 1.5 Другие свойства 2 Обобщения 2.1 Двойной факториал 2.2 Убывающий факториал 2.3 Возрастающий факториал 2.4 Праймориал или примориал 2.5 Суперфакториалы 2.6 Субфакториал 3 Ссылки 4 См. также

Свойства

Комбинаторное определение

В комбинаторике факториал определяется как количество перестановок множества из n элементов. Например, элементы множества {A,B,C,D} можно линейно упорядочить 4!=24 способами:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Связь с гамма-функцией

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

n! = Γ(n + 1)

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).

Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые в степени

Таким образом,

,

где произведение берется по всем простым числам.

Другие свойства

• x!² > x^x > x! > = x, при x>1

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,

По определению полагают 0!! = 1.

Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал дает число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

Праймориал или примориал

Примориал (англ. Primorial) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,

Последовательность праймориалов начинается так:

2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)

Суперфакториалы

Основная статья: Большие числа

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)

В общем

Последовательность суперфакториалов начинается (с n = 0) с

1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)

Идея была обобщена в 2000 Генри Боттомли (англ. ), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Первые члены (с n = 0) равны:

1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал n — произведение первых n (m − 1)-уровневых факториалов, то есть

где для n > 0 и .

Субфакториал

Основная статья: Субфакториал

Субфакториал определяется как количество беспорядков порядка , то есть перестановок -элементного множества без неподвижных точек.

Ссылки

• Онлайн Калькулятор Факториалов

См. также

• Факторион

Операция факториалов и история появления его в положительных рядах Выполнил: Павлов В. А. Проверила: Хлынова Т.

В.

Вы можете ознакомиться и скачать Операция факториалов и история появления его в положительных рядах Выполнил: Павлов В. А. Проверила: Хлынова Т. В.. Презентация содержит 9 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.

Слайды и текст этой презентации

---

Слайд 1

Описание слайда:

Операция факториалов и история появления его в положительных рядах Выполнил: Павлов В. n.

---

Слайд 5

Описание слайда:

Джеймс Стирлинг Джеймс Стирлинг (англ. James Stirling, май 1692—5 декабря 1770) — шотландский математик. Джеймс Стирлинг родился в неспокойное время. Четырьмя годами раньше был свергнут король Яков II, он же Яков VII Шотландский. В 1707 году Шотландия была присоединена к Англии. Когда Джеймсу было около 17 лет, его отец был арестован как якобит (сторонник свергнутого монарха) и обвинён в государственной измене. Суд его оправдал. Мятежи якобитов продолжались ещё долгое время. Образование Стирлинг получил в Оксфорде, затем, вероятно, в Глазго. Получить диплом ему мешало то, что при этом надо было непременно принести присягу английской королеве; Стирлинг категорически отказался делать это. Теперь уже угроза ареста нависла над ним самим. Стирлинг уезжает в Италию, где живёт до 1722 года. В Италии начинается научная деятельность Стирлинга.

Он публикует работу «Ньютоновские кривые третьего порядка», где изучает алгебраические кривые 3-й степени, уже исследованные Ньютоном. Стирлинг обнаружил 4 новых типа этих кривых, не замеченных великим аналитиком. В этой же работе доказан ряд теорем, высказанных Ньютоном без доказательства, изучаются кривая скорейшего спуска и цепная линия, решается лейбницевская задача об ортогональных траекториях. Стирлинг выяснил, что алгебраическая кривая n-го порядка определяется своими n(n+3)/2 точками.

---

Слайд 6

Описание слайда:

Научная деятельность 1724: Стирлинг приезжает в Лондон, работает преподавателем. Ведёт активные математические исследования. 1726: по рекомендации Ньютона, данной им незадолго до смерти, Стирлинг избран членом Королевского общества. 1730: опубликован главный труд Стирлинга, «Дифференциальные методы» (Methodus Differentialis). Это один из первых содержательных учебников по математическому анализу, излагающий помимо основ анализа немало личных открытий Стирлинга. Среди тем книги: бесконечные ряды, их суммирование и ускорение сходимости, теория интегрирования (квадратуры), интерполирование, свойства гамма-функции, асимптотические представления. Одно из таких представлений, несколько преобразованное де Муавром, известно сейчас как формула Стирлинга. Некоторые детали исследований Стирлинга можно почерпнуть из его переписки с де Муавром, Эйлером и Крамером. 1733: ещё один важный труд Стирлинга: «Двенадцать предложений о фигуре Земли». 1735: Стирлинг возвращается в Шотландию, куда приглашён управлять горной компанией. Административная работа хорошо ему даётся и хорошо оплачивается, но свободного времени практически нет. Единственная опубликованная его работа за этот период касается проблем шахтной вентиляции. На этой должности он оставался до конца жизни.

---

Слайд 7

Описание слайда:

Абрахам де Муавр Родился во Франции, в недворянской семье врача-гугенота; частицу де перед своей фамилией он добавил по собственной инициативе.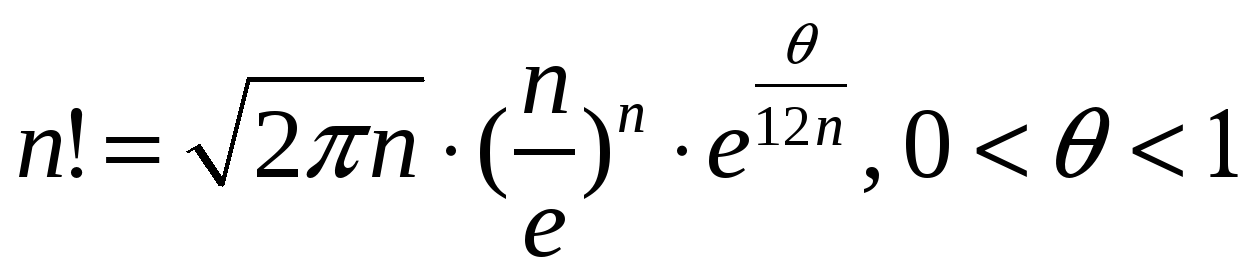

В 11 лет поступил в Протестантскую академию в Седане, где успел проучиться 4 года, после чего академия была запрещена властями (1682). Муавр продолжил образование в Сомюре (2 года). Вероятно, в это время он познакомился с теорией вероятностей по трудам Гюйгенса. Далее около года Муавр слушал лекции по физике и математике в Париже (в том числе у Озанама), но в 1685 году Людовик XIV официально отменил Нантский эдикт, возобновились притеснения протестантов, а сам Муавр попал в тюрьму. Подробности его заключения неизвестны, но так или иначе, он вынужден был покинуть родину.

---

Слайд 8

Описание слайда:

Научная деятельность Открыл (1707) формулу Муавра для возведения в степень (и извлечения корней) комплексных чисел, заданных в тригонометрической форме. Он первый стал использовать возведение в степень бесконечных рядов. Муавр также установил связь между рекуррентными последовательностями и разностными уравнениями.

Внёс вклад в теорию решения однородных линейных разностных уравнений с постоянными коэффициентами. Ему и Дж. Стирлингу принадлежит асимптотическое представление факториала, носящее название формулы Стирлинга. Помимо анализа, Муавр внёс большой вклад в теорию вероятностей. Доказал частный случаи теоремы Лапласа. Провёл вероятностное исследование азартных игр и ряда статистических данных по народонаселению. Кроме нормального, он использовал равномерное распределение. Большинство результатов де Муавра были вскоре перекрыты трудами Лапласа; степень возможного влияния де Муавра на Лапласа неясна.

---

Слайд 9

Описание слайда:

Спасибо за внимание

---

Вероятность

— Формула Стирлинга для n!

спросил 4 года, 1 месяц назад

Изменено 4 года, 1 месяц назад

Просмотрено 697 раз

$\begingroup$

Группа из $2N$ мальчиков и $2N$ девочек делится на две равные группы. 4 }$$ 9п $$ или, после отбрасывания тривиальных множителей, $2/\sqrt{\pi n}$, как вы ищете.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Приближение Стирлинга для факториалов

Приближение Стирлинга для факториалов

Существует довольно много известных формул для аппроксимации факториалов и логарифмы факториалов. По крайней мере, два из них названы в честь Джеймс Стирлинг: так называемое приближение Стирлинга к должно вероятно, можно назвать «первым» приближением Стирлинга, поскольку оно может можно рассматривать как первый термин в ряду Stirling .

Начнем с вывода основной формулы Стирлинга.

Мы всегда можем увеличить логарифм N! в качестве:

LN (N!) = LN (1)+LN (2)+LN (3)+⋯+LN (N) = = = = . пер.(и)

            (1)

На рисунке 1 и рисунке 2 мы рассматриваем пример, где N=8.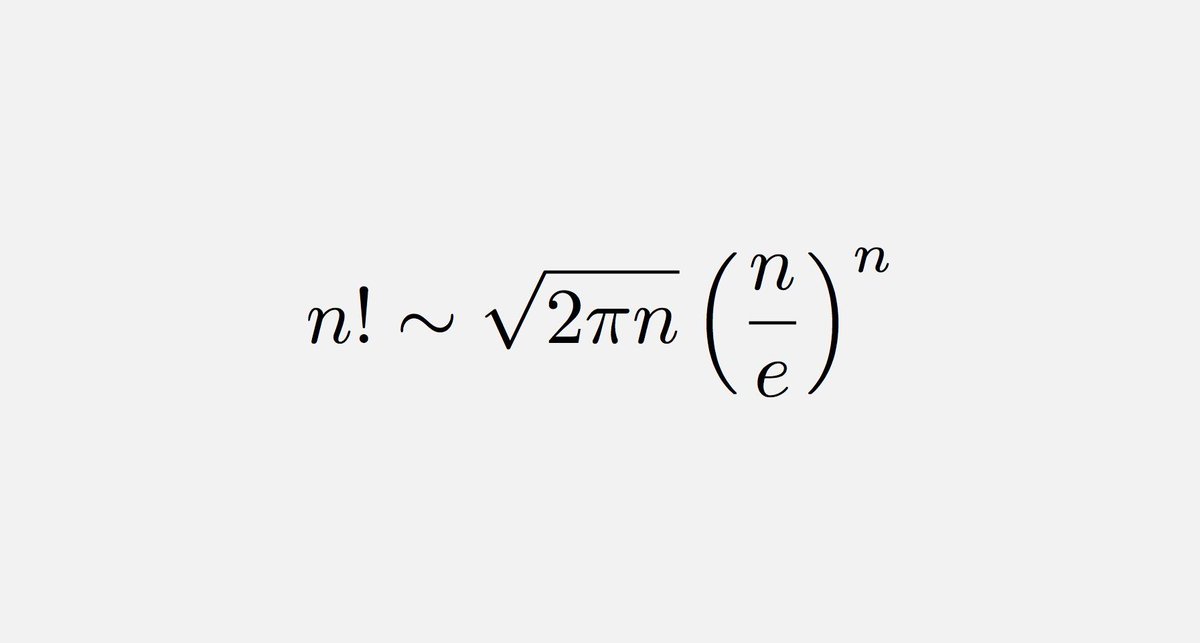 На каждом рисунке синяя область представляет ln[(N−1)!]. Желтая область представляет ln(N) так, чтобы синяя и желтая области вместе представляют ln(N!).

Рис. 1. Приближение Стирлинга: верхняя граница

 

Рис. 2. Приближение Стирлинга: нижняя граница

Мы можем использовать рисунок 1, чтобы получить верхнюю границу пер(Н!):

ln[(N−1)!]   =   ln(N!) − ln(N)      <   ∫  ln( х) дх    ln(N!)   <   ∫  ln(x) dx + ln(N)

(2)

Аналогично, мы можем использовать рисунок 2, чтобы получить нижнюю границу пер(Н!):

ln(N!)   >   ∫  ln(x) dx

(3)

Это полезно, потому что мы можем легко вычислить интеграл:

∫  ln(x) dx   =     x ln(x) − x   ⎪ ⎪ ⎪ ⎪ = NLN (N) — N+10091 (N).

(4)

Мы всегда можем вычесть 1 из нижней границы, чтобы получить более свободное нижнее значение. граница. Суммируя результаты, мы имеем:

N ln(N) − N + 1 <   ln(N!) <   (N+1) ln(N) − N + 1

(5)

Перейдем теперь от получения оценок к получению оценок и приближения. Некоторые интересные приближения включают:

LN (N!) ≈ N LN (N)-N Low-Low, AKA Lame Stirling LN (N N ln(N) − N + 1       low  ln(N!)   ≈   (N+½) ln(N) − N + 1       middle  ln(N!)   ≈   (N+½) ln(N) − N + ½ ln(2π)       first Stirling  ln(N!)   ≈   (N+1) ln(N) − N + 1       высокий

(6)

Нижний-нижний приближение можно получить, вычитая 1 из нижнего для получения более слабой нижней границы.