Производная функции, заданной неявно
Рассмотрим уравнение
.
Очевидно, есть пары значений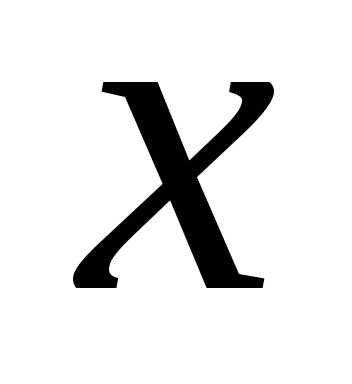 и
и ,
обращающих его в верное числовое
равенство, например:и т.д. Однако не всякая пара
,
обращающих его в верное числовое
равенство, например:и т.д. Однако не всякая пара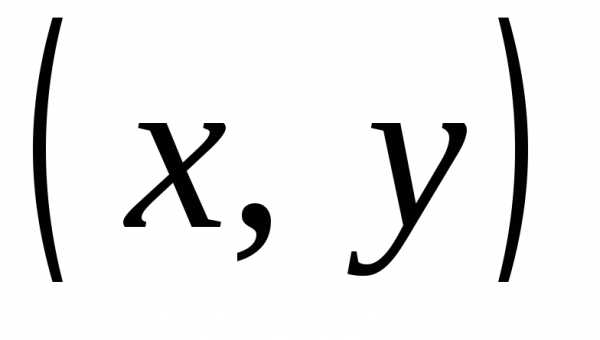 удовлетворяет этому уравнению. Значит,
можно утверждать, что этим уравнением
задана некоторая функция
удовлетворяет этому уравнению. Значит,
можно утверждать, что этим уравнением
задана некоторая функция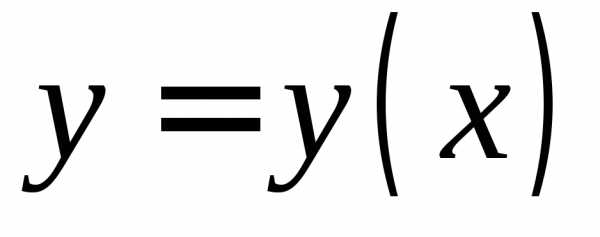 (или
(или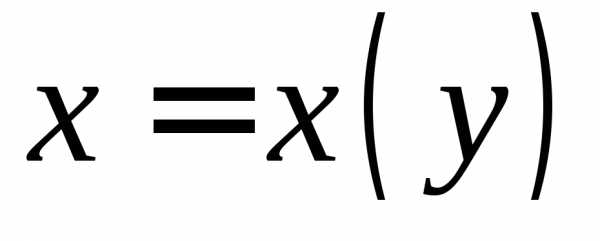 ),
хотя явно вид этой зависимости в данном
случае получить довольно сложно.
),
хотя явно вид этой зависимости в данном
случае получить довольно сложно.
Функция, определенная из неразрешенного уравнения, связывающего независимые и зависимую переменные, называется неявной функцией.
В приведенном
примере равенство
задает неявную функцию одной переменной.
Уравнениемтакже задается неявная функция, которая
легко может быть представлена в явном
виде:или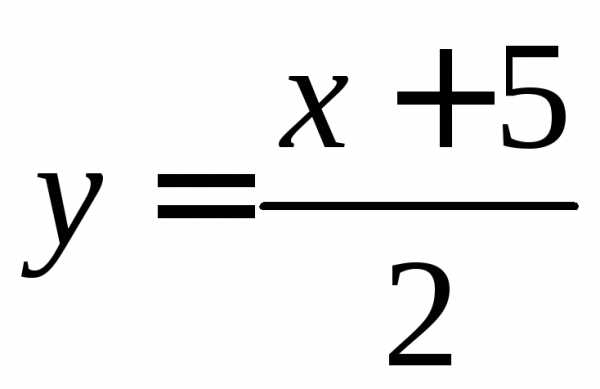
Однако не всякое уравнение, не разрешенное относительно одной из переменных, определяет неявную функцию. Например, уравнение не задает функцию, так как, очевидно, нет ни одной пары действительных чисел, которая ему удовлетворяет.
Кроме неявных функций одной переменной, существуют неявные функции нескольких переменных. Так, например, тройки чисел обращают выражениев верное числовое равенство, поэтому– функция двух переменных, заданная неявно. Здесь ни одну из трех переменных невозможно явно выразить через две другие.
–также неявная функция двух переменных, но – та же функция, заданная явно.
Пусть в общем случае дано уравнение .
ОПРЕДЕЛЕНИЕ
. Если каждому значению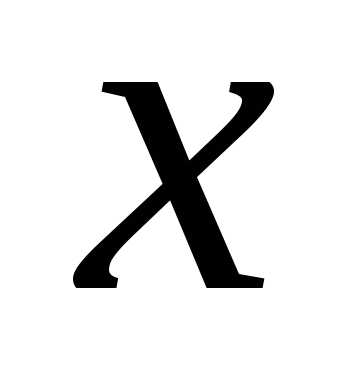 из некоторого множества
из некоторого множества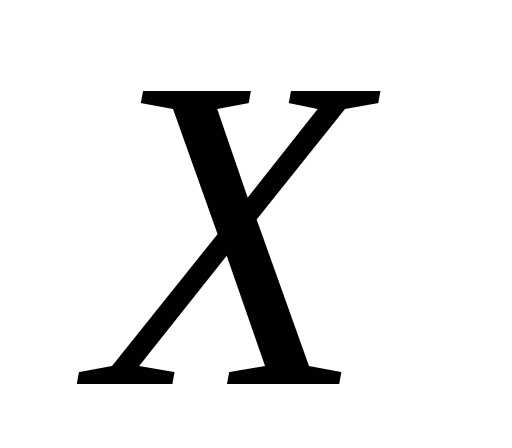 соответствует единственное значение
соответствует единственное значение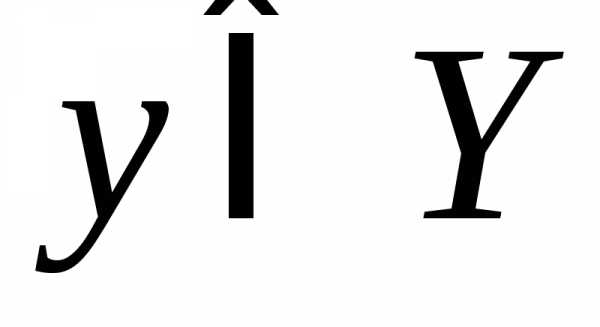 ,
которое вместе с
,
которое вместе с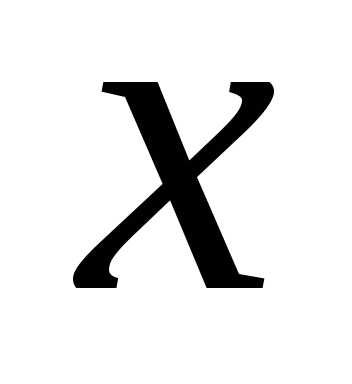 удовлетворяет уравнению,
то говорят, что это уравнение определяет
на множестве
удовлетворяет уравнению,
то говорят, что это уравнение определяет
на множестве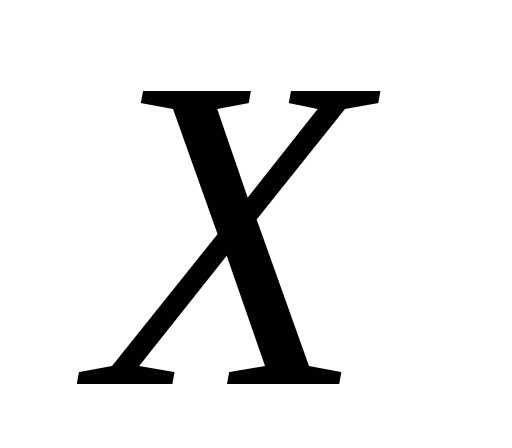 неявную
функцию одной переменной
неявную
функцию одной переменной 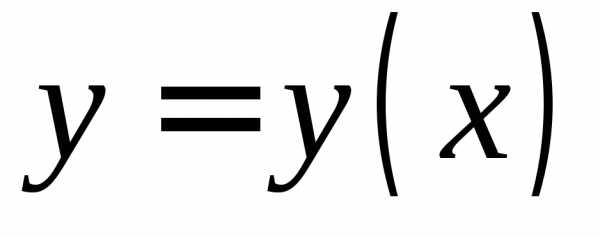 .
.Таким образом, для неявной функции имеет место тождество .
В некоторых случаях
каждому  соответствует несколько значений
соответствует несколько значений .
Тогда равенствоопределяет не одну, а несколько неявных
функций. Например, уравнениезадает две неявные функции, которые
можно записать в явном виде, разрешив
его относительно
.
Тогда равенствоопределяет не одну, а несколько неявных
функций. Например, уравнениезадает две неявные функции, которые
можно записать в явном виде, разрешив
его относительно
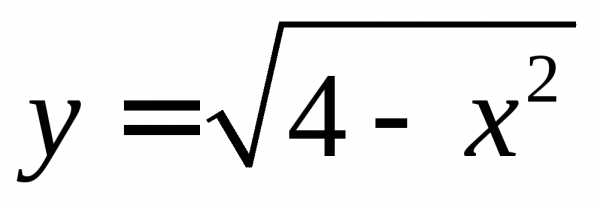 или.
или. Ответ на вопрос,
каким условиям должна удовлетворять
функция
,
чтобы уравнениеопределяло единственную функцию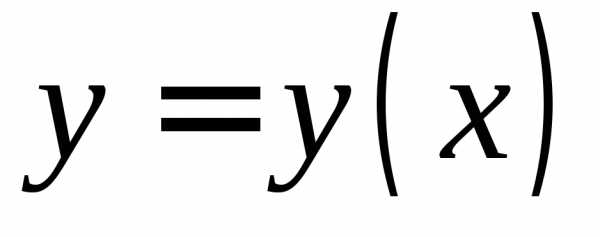 ,
дает теорема о существовании неявной
функции.
,
дает теорема о существовании неявной
функции.
ТЕОРЕМА.
Пусть функция 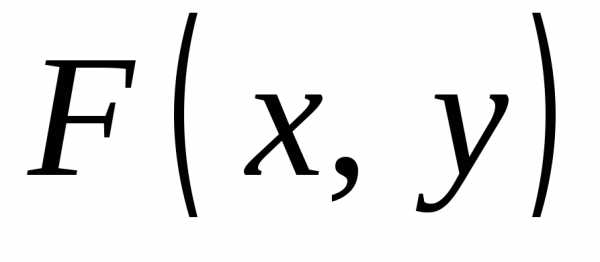 и ее частные производныенепрерывны в некоторой окрестности
точки
и ее частные производныенепрерывны в некоторой окрестности
точки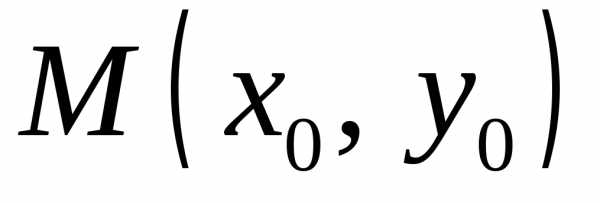 и при этом,
а.
Тогда уравнениеопределяет в этой окрестности точки
и при этом,
а.
Тогда уравнениеопределяет в этой окрестности точки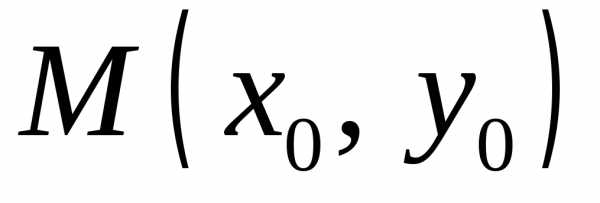 единственную неявную функцию,
непрерывную и дифференцируемую в
некотором интервале, содержащем точку
единственную неявную функцию,
непрерывную и дифференцируемую в
некотором интервале, содержащем точку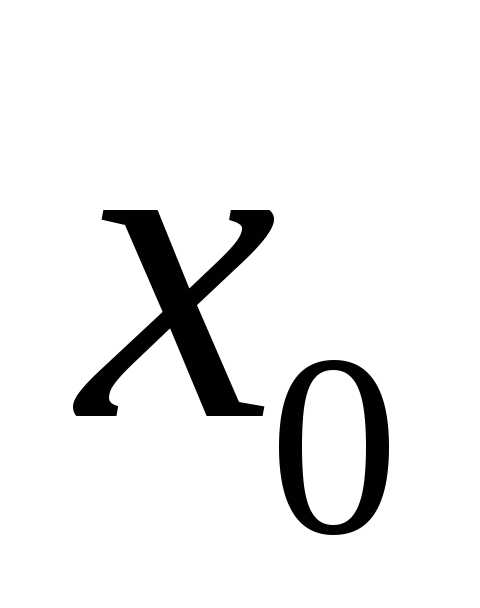
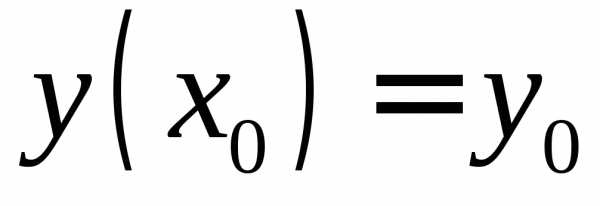 .
.(Без доказательства).
Рассмотрим функцию 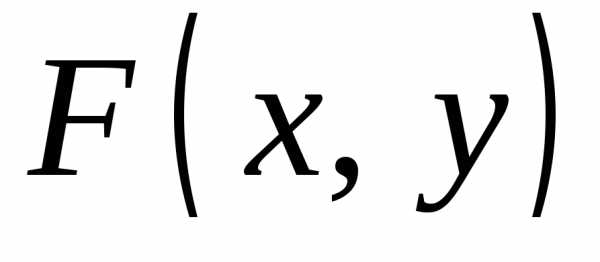 ,
удовлетворяющую всем условиям теоремы
о существовании неявной функции. Тогда
равенствоопределяет неявную функцию
,
удовлетворяющую всем условиям теоремы
о существовании неявной функции. Тогда
равенствоопределяет неявную функцию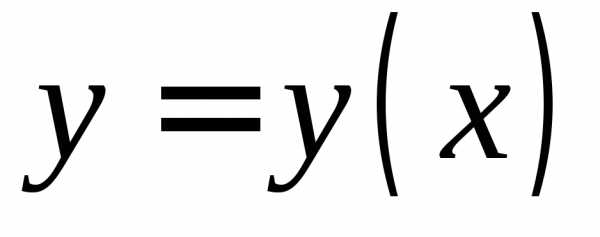 ,
для которой в окрестности точки
,
для которой в окрестности точки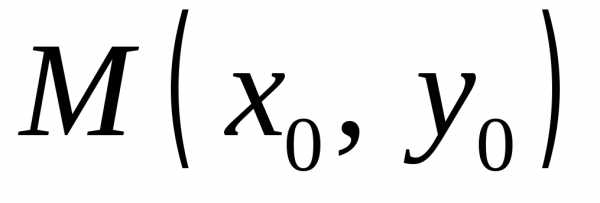 имеет место тождество.
Так как производная функции, тождественно
равной нулю, также равна нулю, то полная
производная
имеет место тождество.
Так как производная функции, тождественно
равной нулю, также равна нулю, то полная
производная
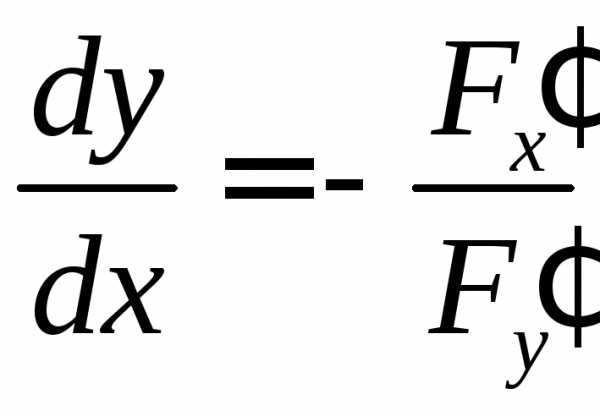
– формула для вычисления производной неявной функции одной переменной.
ПРИМЕР. Найти производную неявной функции .
.
Если
считать, что это равенство задает функцию 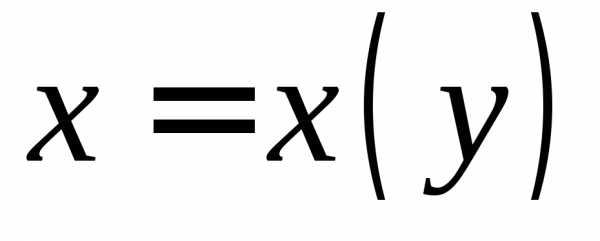 ,
то
,
то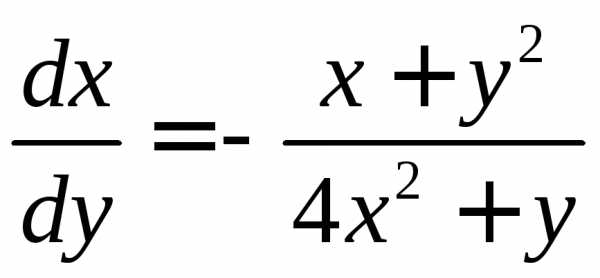 .
.
Рассмотрим теперь
уравнение
.
При условиях, аналогичных сформулированным
в теореме о существовании неявной
функции, это уравнение определяеткак функцию двух переменных.
Поэтому– тождество. Продифференцировав его
по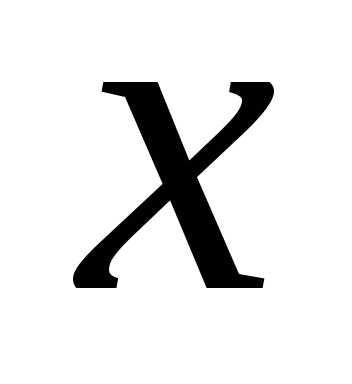 и по
и по ,
получим:
,
получим:
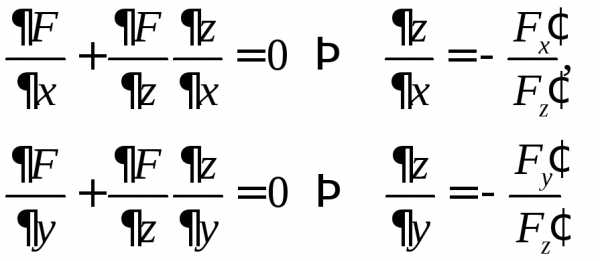 при условии, что
при условии, что 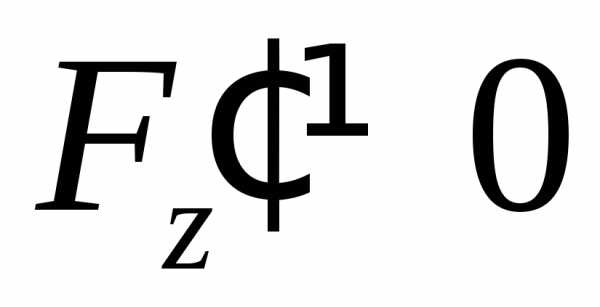 .
.
ПРИМЕР.
Найти частные производные  и
и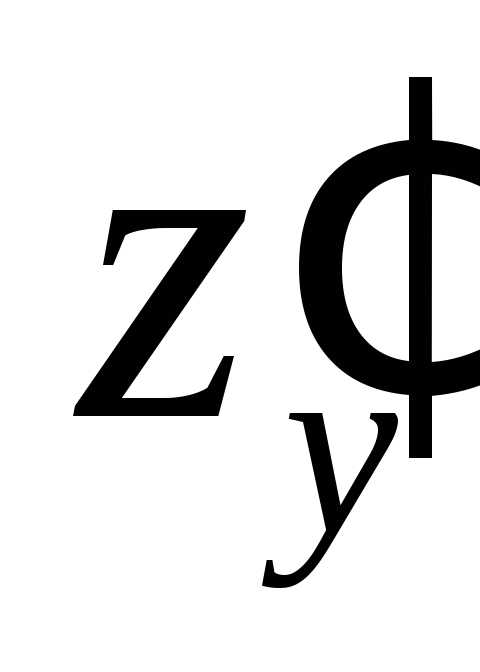
при условии, что .
studfiles.net
Производные высших порядков неявно заданной функции.
Пусть
функция 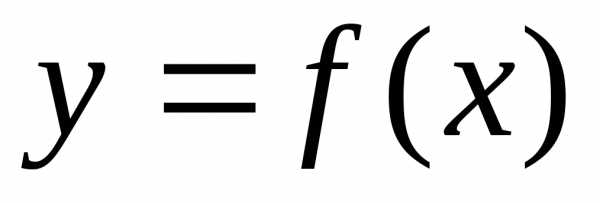 задана неявно в виде уравнения
.
Продифференцировав это уравнение по х и разрешив полученное уравнение
относительно производной
задана неявно в виде уравнения
.
Продифференцировав это уравнение по х и разрешив полученное уравнение
относительно производной  ,
найдем производную первого порядка
(первую производную). Продифференцировав
по х первую производную получим вторую
производную от неявной функции. Подставляя
уже найденное значение
,
найдем производную первого порядка
(первую производную). Продифференцировав
по х первую производную получим вторую
производную от неявной функции. Подставляя
уже найденное значение  в выражение второй производной, выразим
в выражение второй производной, выразим 
Пример. Найти  ,
если
.
,
если
.
Решение:
дифференцируем уравнение по х: 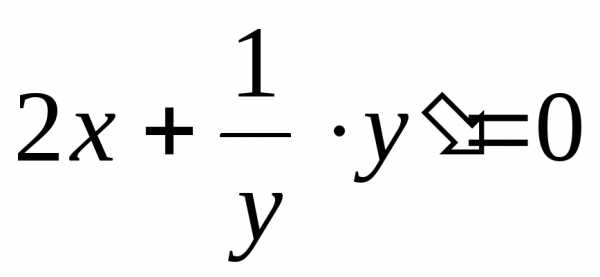 .
Отсюда находим
.
Далее
.
.
Отсюда находим
.
Далее
.
Производные высших порядков от функций заданных параметрически.
Пусть
функция 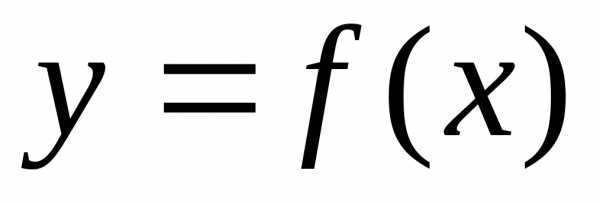 задана параметрическими уравнениями .
задана параметрическими уравнениями .
Как
известно первая производная 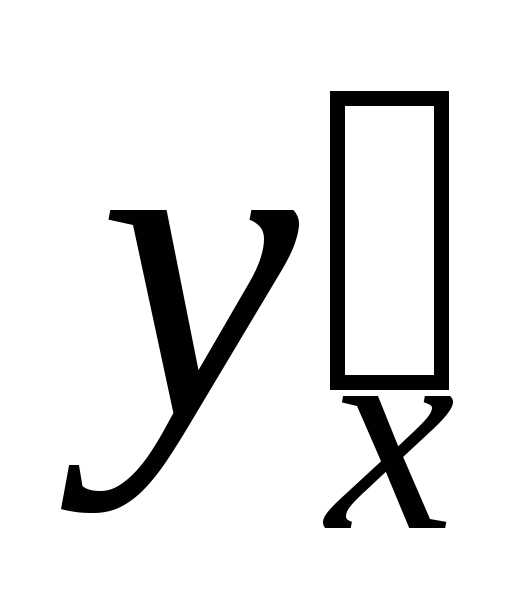 находится
по формуле
находится
по формуле 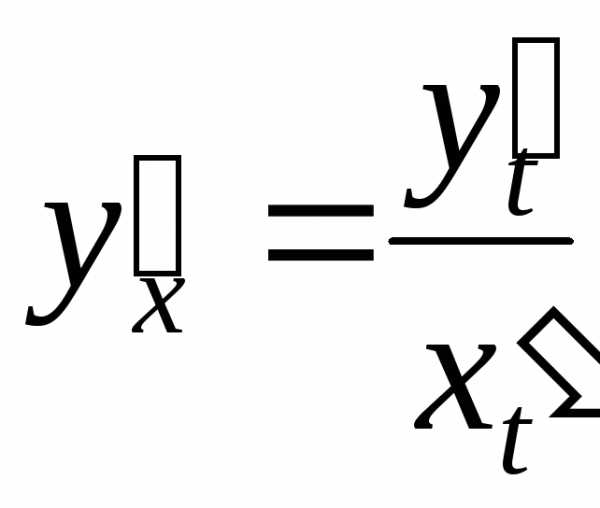 .
Найдем вторую производную
,
т.е.
.
Найдем вторую производную
,
т.е.  .
Аналогично
.
Аналогично 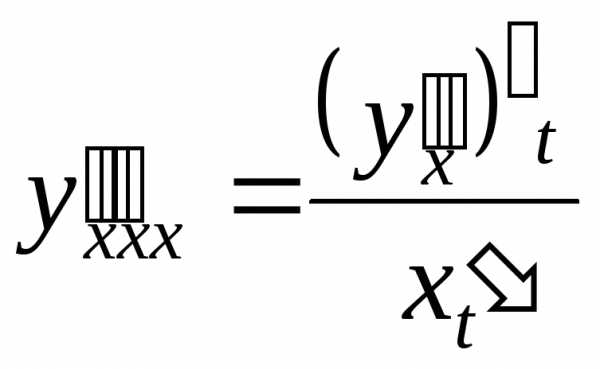
Пример.
Найти вторую производную 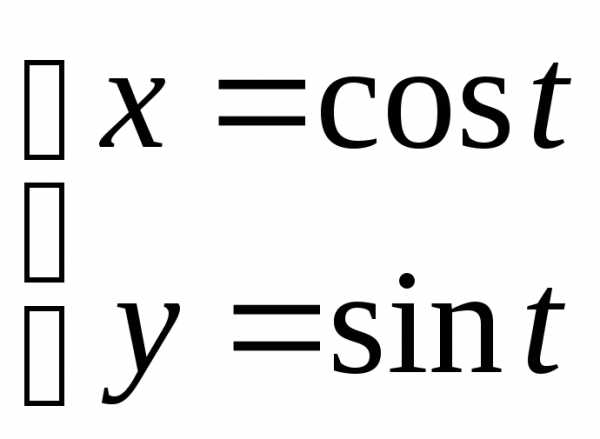 .
.
Решение: находим первую производную . Находим вторую производную .
Дифференциал функции.
Пусть
функция 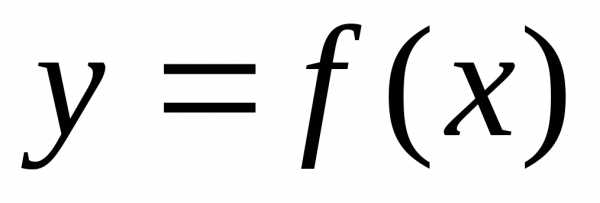 дифференцируема на
дифференцируема на  .
Производная этой функции в некоторой
точке
.
Производная этой функции в некоторой
точке  определяется равенством
определяется равенством  .
Отношение
.
Отношение 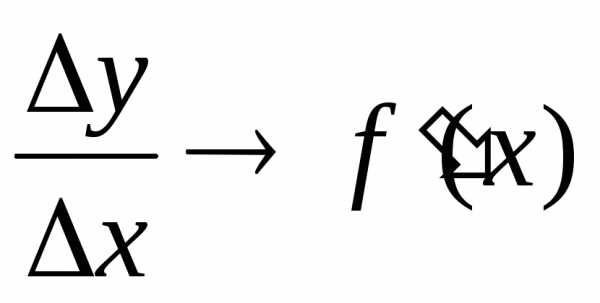 при
,
следовательно отличается от производной
при
,
следовательно отличается от производной 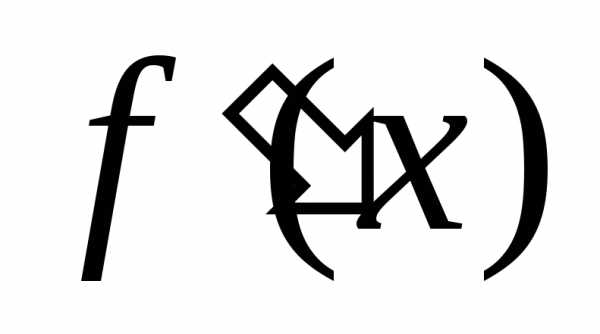 на
величину б.м., т.е. можно записать
на
величину б.м., т.е. можно записать  ().
Умножим все на
().
Умножим все на 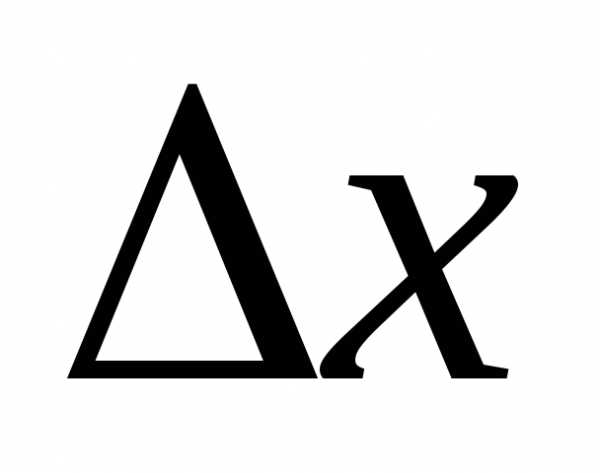
 состоит
из двух слагаемых . первое слагаемое
состоит
из двух слагаемых . первое слагаемое 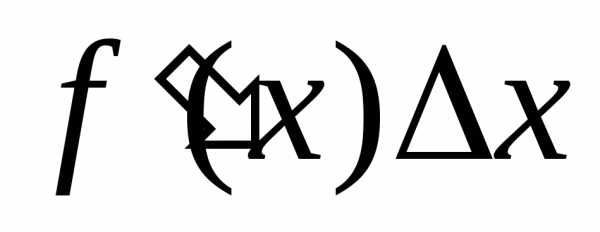 — главная часть приращения, есть
дифференциал функции.
— главная часть приращения, есть
дифференциал функции.Опр.
Дифференциалом функции 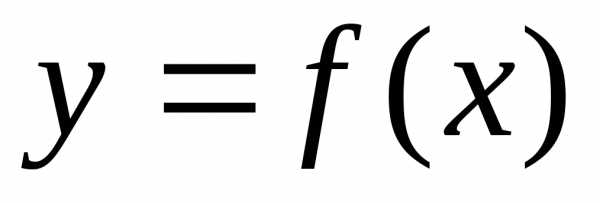 называется произведение производной
на приращение аргумента. Обозначается
.
называется произведение производной
на приращение аргумента. Обозначается
.
Дифференциал независимого переменного совпадает с его приращением .
().
Таким образом, формулу для дифференциала
можно записать
.
Дифференциал функции равен произведению
производной на дифференциал независимой
переменной. Из этого соотношения следует,
что производную можно рассматривать
как отношение дифференциалов 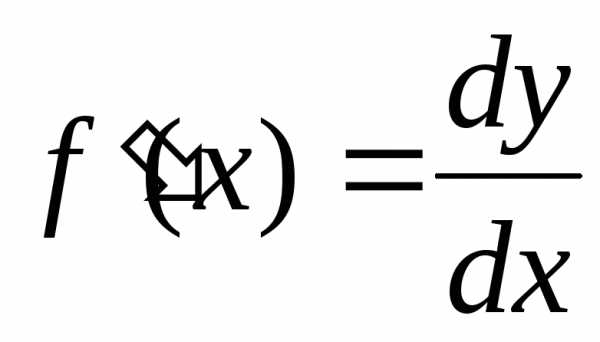 .
.
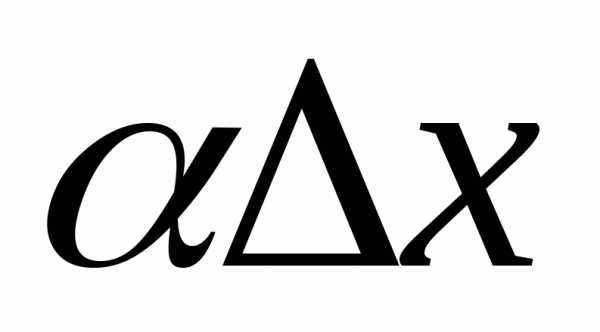 бесконечно малая величина пользуются
приближенным равенством
бесконечно малая величина пользуются
приближенным равенством 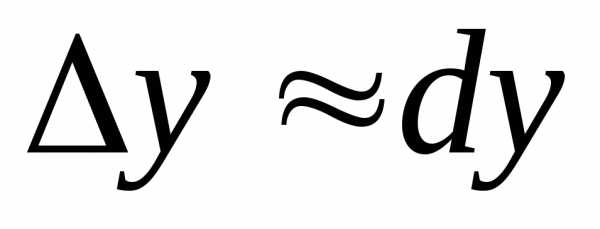 или в развернутом виде
или в развернутом виде(*)
Пример:
вычислить приближенное значение  .
.
Функция 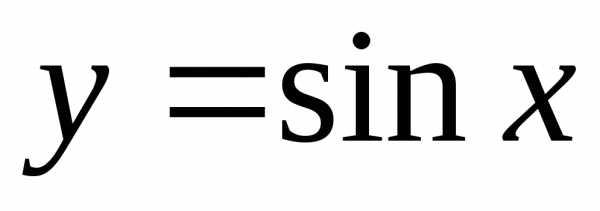 имеет производную
имеет производную 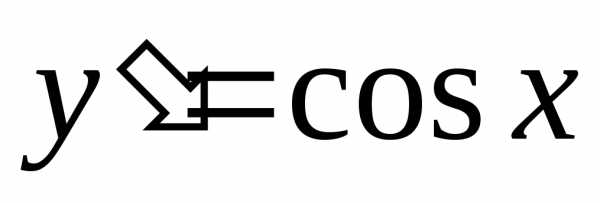 .
.
По формуле (*) : .
Пример: найти дифференциал функции
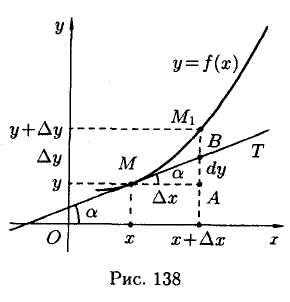
Геометрический смысл дифференциала.
К
графику функции  в точке М(x;y)
проведем касательную и рассмотрим
ординату этой касательной для точки x+∆x.
На рисунке АМ=∆х АМ1=∆у из
∆МАВ
в точке М(x;y)
проведем касательную и рассмотрим
ординату этой касательной для точки x+∆x.
На рисунке АМ=∆х АМ1=∆у из
∆МАВ 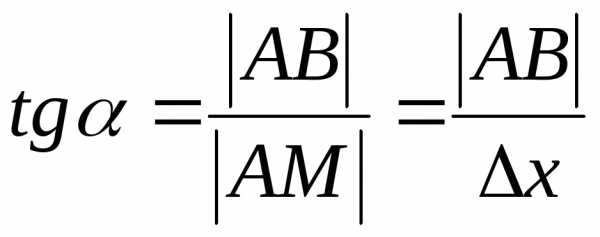 ,
отсюда
,
но согласно геометрическому смыслу
касательной
.
Поэтому
.
Сравнивая эту формулу с формулой
дифференциала получаем, что
,
отсюда
,
но согласно геометрическому смыслу
касательной
.
Поэтому
.
Сравнивая эту формулу с формулой
дифференциала получаем, что 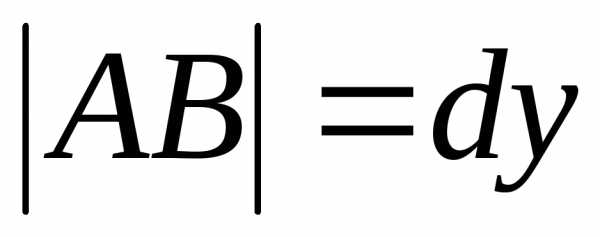 ,
т.е. дифференциал функции
,
т.е. дифференциал функции 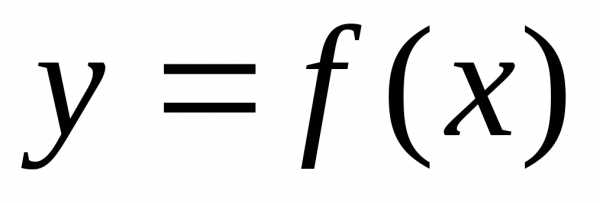 в
точке х равен
приращению ординаты касательной к
графику функции в этой точке, когда х получает приращение ∆х.
в
точке х равен
приращению ординаты касательной к
графику функции в этой точке, когда х получает приращение ∆х.
Правила вычисления дифференциала.
Поскольку
дифференциал функции 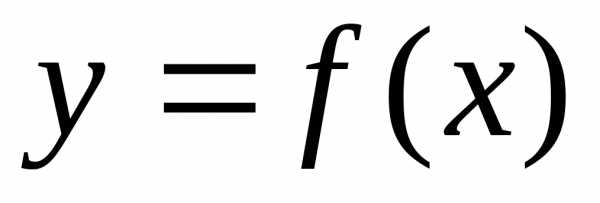 отличается
от производной множителем
отличается
от производной множителем 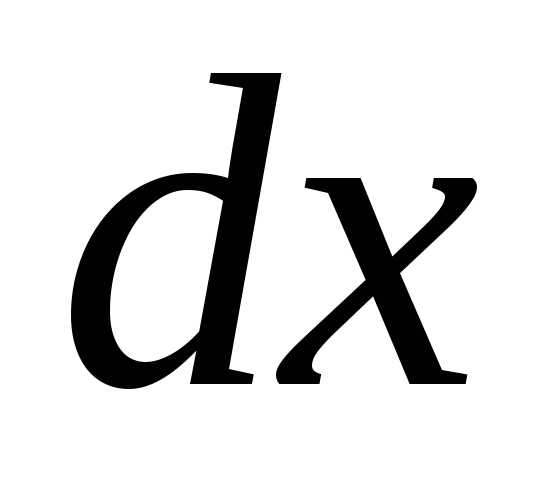 ,
то все правила вычисления производной
используются и для вычисления дифференциала
(отсюда и термин «дифференцирование»).
,
то все правила вычисления производной
используются и для вычисления дифференциала
(отсюда и термин «дифференцирование»).
Пусть
даны две дифференцируемые функции 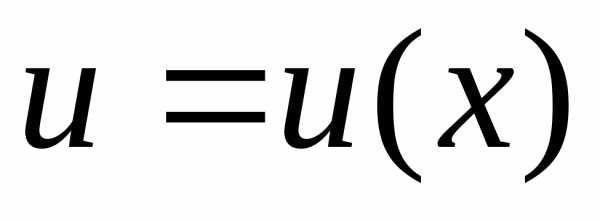 и
и 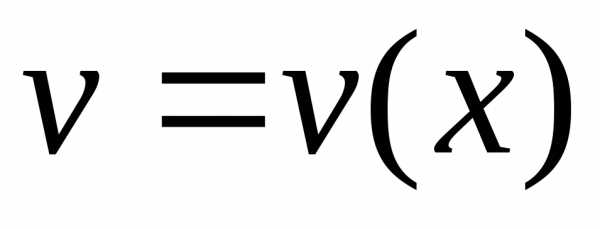 ,
тогда дифференциал находится по следующим
правилам:
,
тогда дифференциал находится по следующим
правилам:
1)
2) с –const
3)
4) 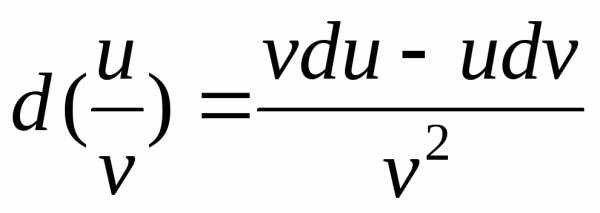 (
(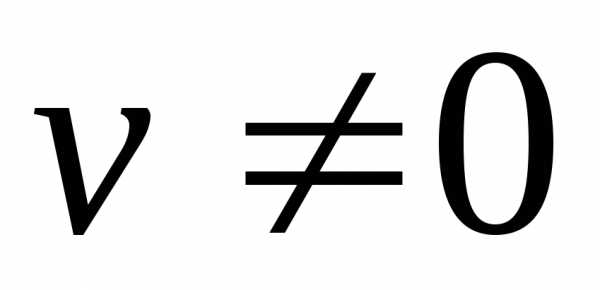 )
)
5)
для сложной функции  ,
где
,
где 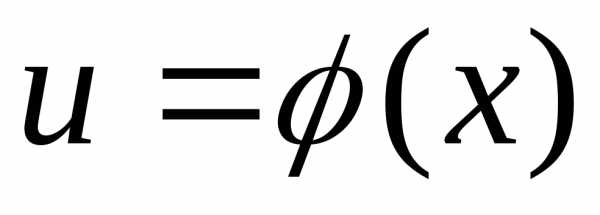
(т.к. ).
Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Приложения производной.
Теоремы о среднем значении.
Теорема
Ролля.
Если функция  непрерывна
на отрезке
непрерывна
на отрезке  и дифференцируема в открытом промежутке
и дифференцируема в открытом промежутке  и если принимает на концах отрезка
равные значения
,
то в интервале
и если принимает на концах отрезка
равные значения
,
то в интервале 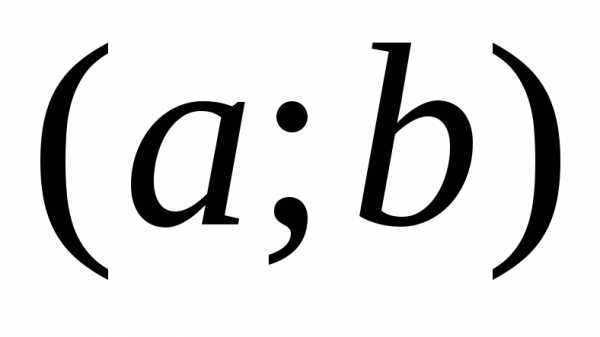 найдется,
хотя бы одна такая точка с,
в которой производная обращается в
ноль, т.е.
найдется,
хотя бы одна такая точка с,
в которой производная обращается в
ноль, т.е. 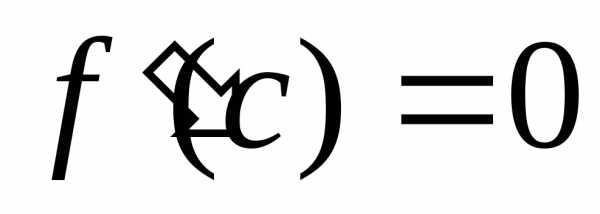 , a<c<b.
, a<c<b.
Геометрически
теорема Ролля означает, что на графике
функции 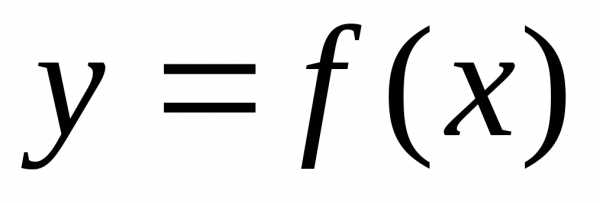 найдется точка, в которой касательная
к графику параллельна оси Ох.
найдется точка, в которой касательная
к графику параллельна оси Ох.

Теорема
Лагранжа.
Если функция 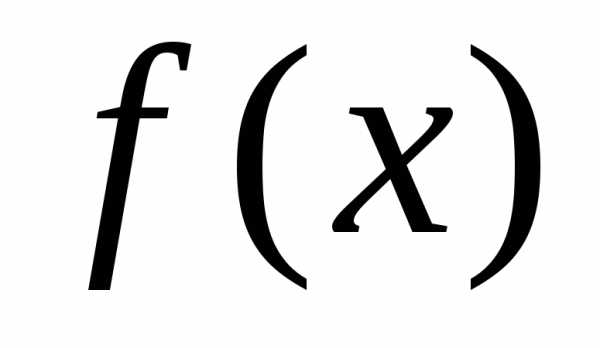 непрерывна
на отрезке
непрерывна
на отрезке 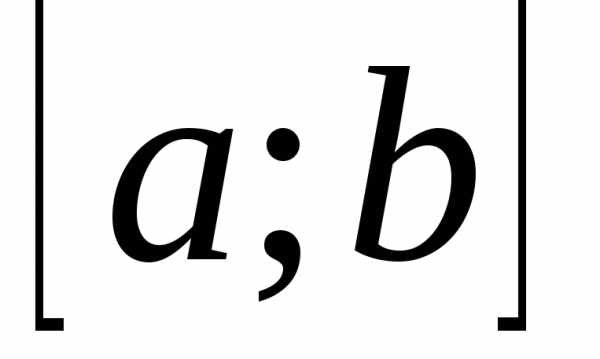 и дифференцируема на интервале
и дифференцируема на интервале 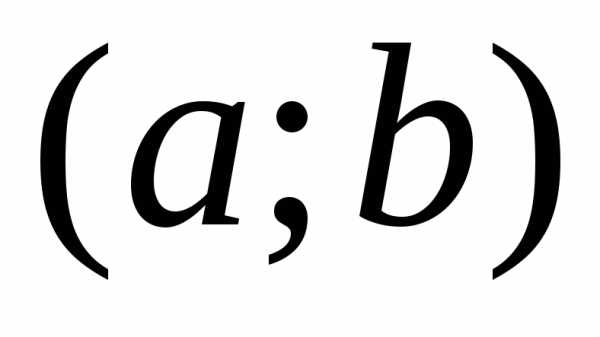 ,
то найдется, хотя бы одна точка
,
то найдется, хотя бы одна точка 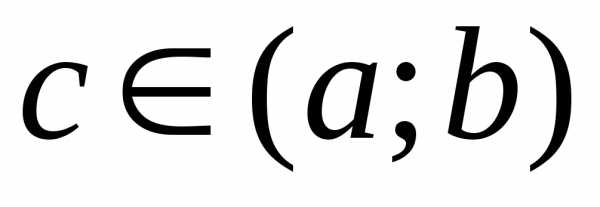 такая, что выполняется равенство
.
такая, что выполняется равенство
.
Формулу
называют формулой Лагранжа или формулой
о конечном приращении: приращение
дифференцируемой функции на отрезке 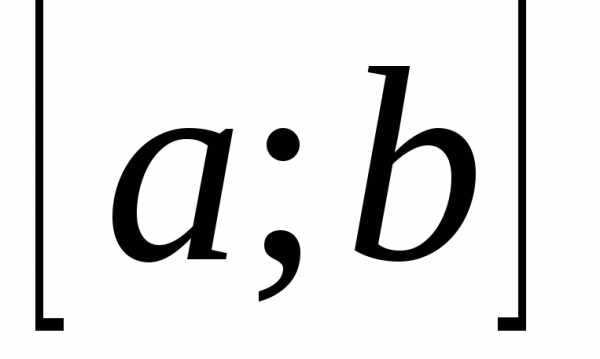 равно приращению аргумента, умноженному
на значение производной в некоторой
внутренней точке этого отрезка.
равно приращению аргумента, умноженному
на значение производной в некоторой
внутренней точке этого отрезка.
Геометрический
смысл теоремы Лагранжа: на графике
функции  найдется
точка С(с;f(c)),
в которой касательная к графику функции
параллельна секущей АВ.
найдется
точка С(с;f(c)),
в которой касательная к графику функции
параллельна секущей АВ.

Теорема
Коши.
Если функции 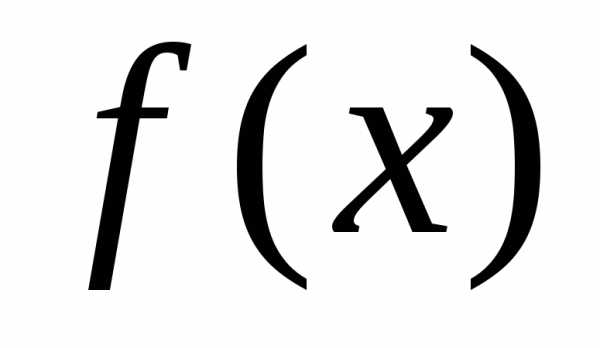 и
и  непрерывны на отрезке
непрерывны на отрезке 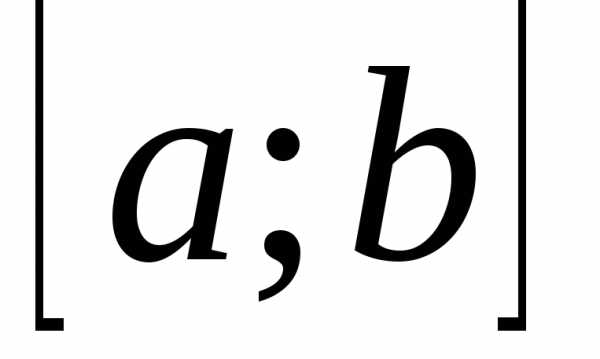 ,
дифференцируемы на интервале
,
дифференцируемы на интервале 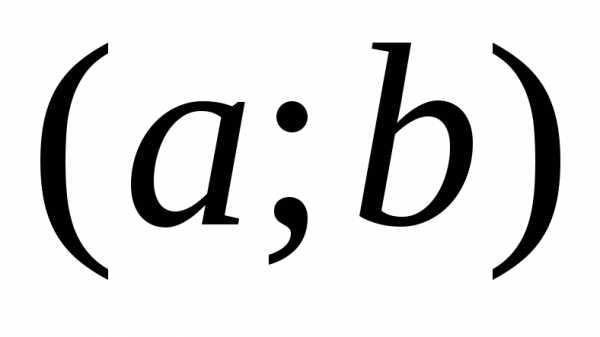 ,
причем
,
причем 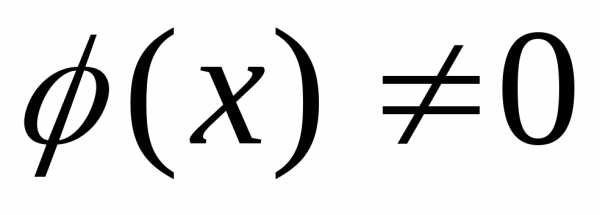 для
для 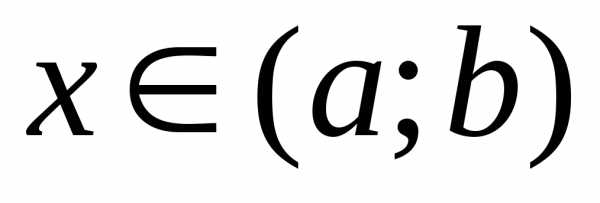 ,
то найдется хотя бы одна точка
,
то найдется хотя бы одна точка 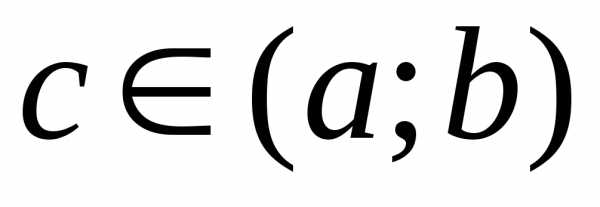 такая,
что выполняется равенство
.
такая,
что выполняется равенство
.
Теорема Коши служит основанием для нового правила вычисления пределов.
Правило Лопиталя.
Теорема: (Правило Лопиталя раскрытие неопределенностей
вида 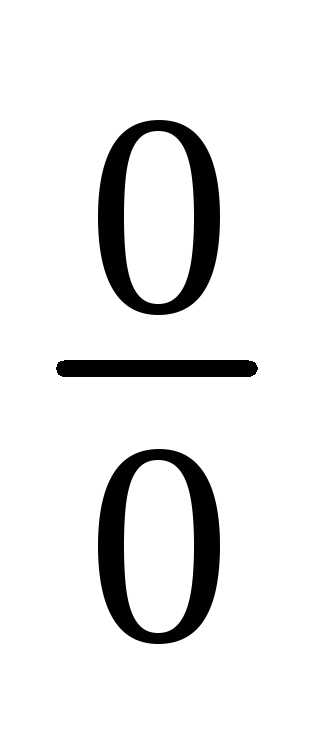 ).
Пусть функции
).
Пусть функции 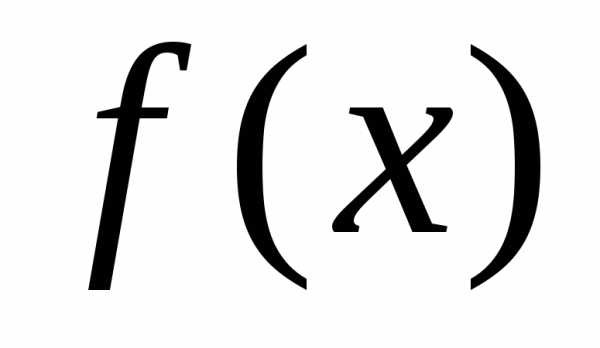 и
и 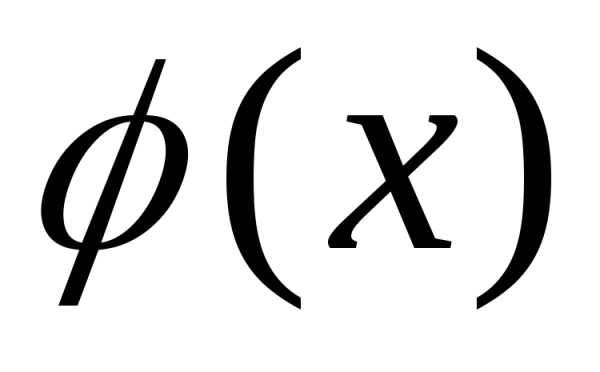 непрерывны и дифференцируемы в
окрестности точки х0 и обращаются в нуль в этой точки
.
И пусть
непрерывны и дифференцируемы в
окрестности точки х0 и обращаются в нуль в этой точки
.
И пусть 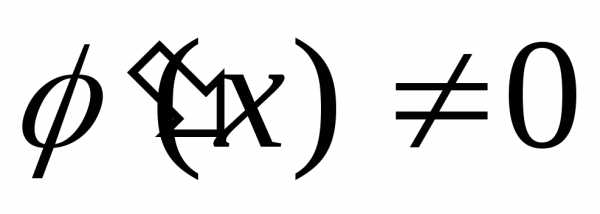 в окрестности точки х0 . если существует предел
в окрестности точки х0 . если существует предел 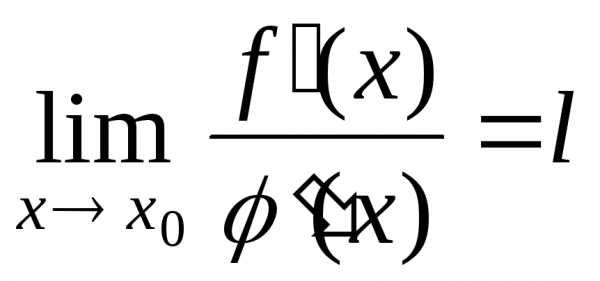 ,
то
.
,
то
.
Доказательство:
применим к функциям 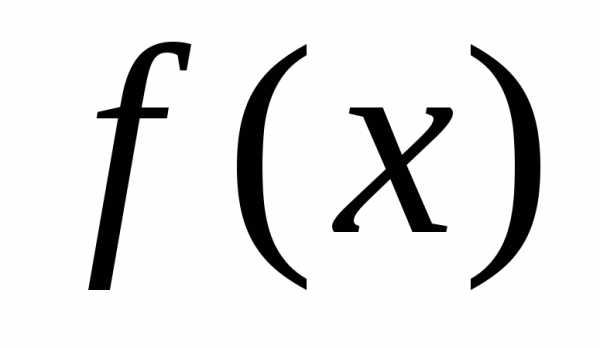 и
и 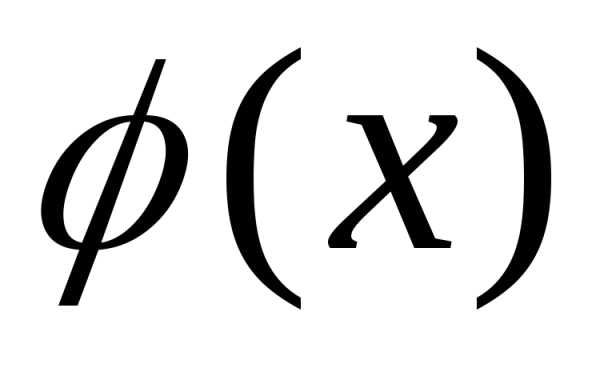 теорему Коши для отрезка
теорему Коши для отрезка 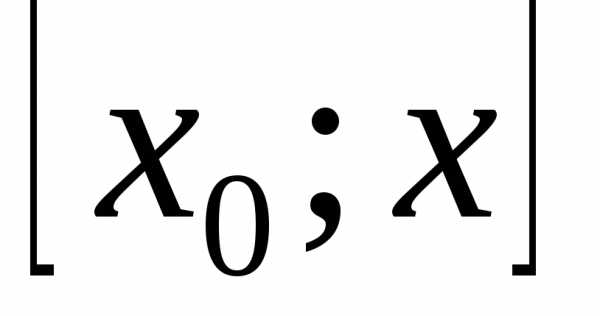
,
лежащего в окрестности точки х0.
Тогда
,
где x0<c<x.
Так как получаем 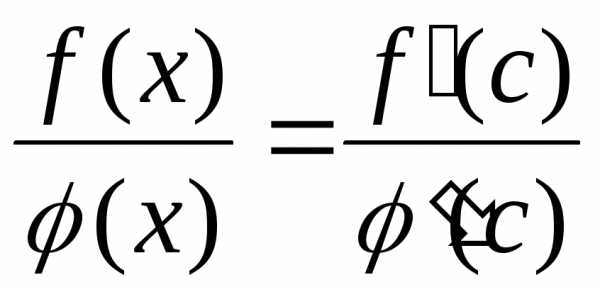 .
Перейдем к пределу при
.
Т.к.
.
Перейдем к пределу при
.
Т.к. 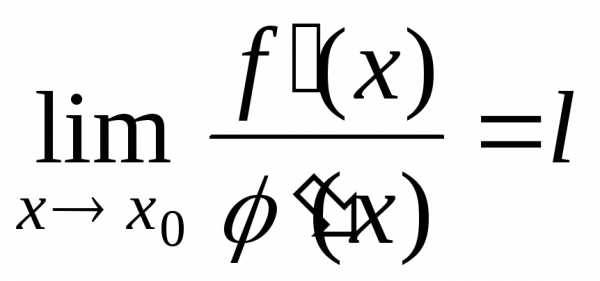 ,
то
,
то  ,
поэтому
,
поэтому 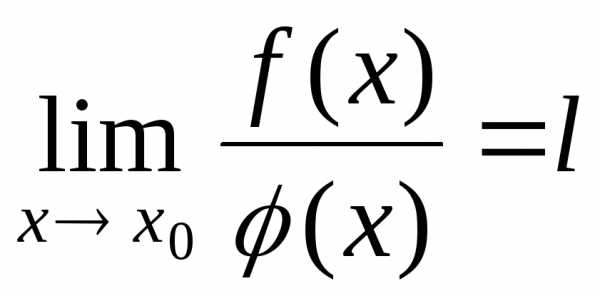 .
.
Итак предел отношения двух б.м. равен пределу отношения их производных, если последний существует .
Пример:
Теорема.(правило
Лопиталя раскрытия неопределенностей
вида 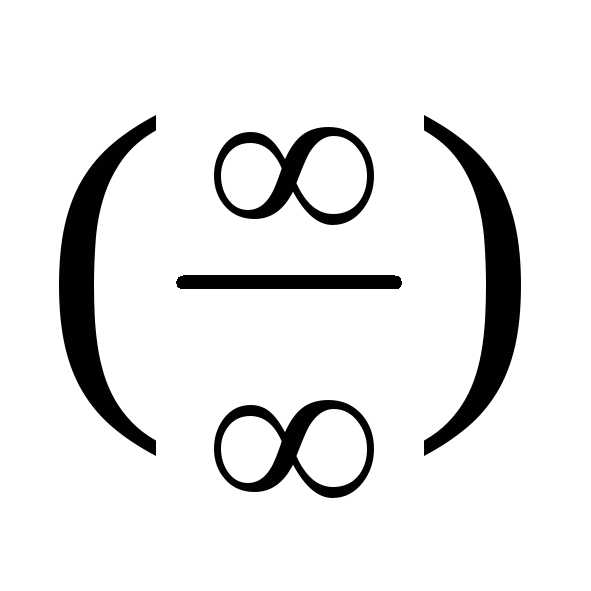 )
Пусть функции
)
Пусть функции 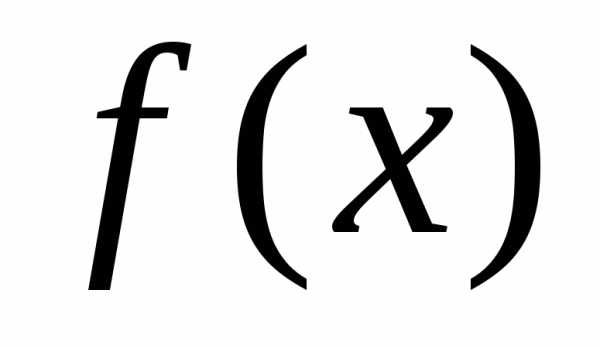 и
и 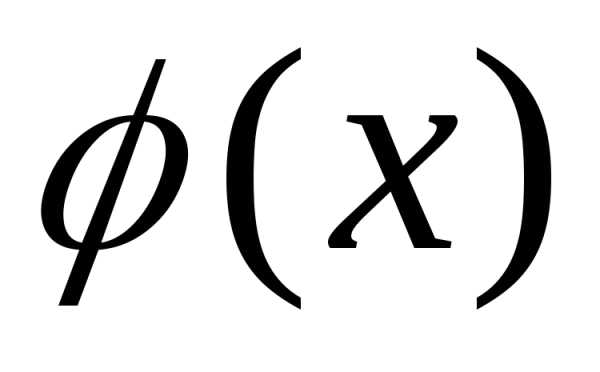 непрерывны и дифференцируемы в окрестности
точки х0 (кроме, может быть, точки х0),
в этой окрестности
,
непрерывны и дифференцируемы в окрестности
точки х0 (кроме, может быть, точки х0),
в этой окрестности
, 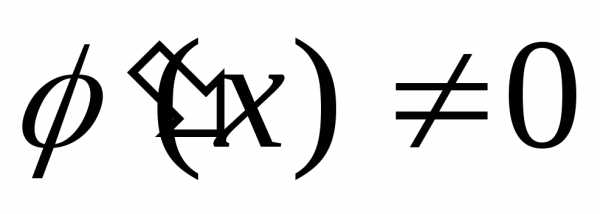 .
Если существует предел
.
Если существует предел
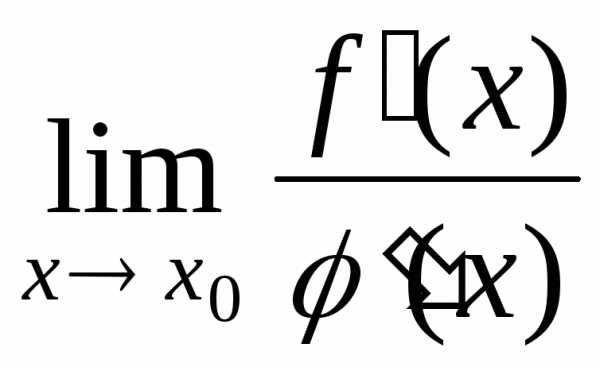 ,
то
.
,
то
.
Пример:
Неопределенности
вида ()
сводятся к двум основным ( ),
),  путем тождественных преобразований.
путем тождественных преобразований.
Пример:
studfiles.net
10.Производная сложной и неявной функции двух переменных
Как известно, неявно заданная функция одной переменной определяется так: функция у независимой переменной x называется неявной, если она задана уравнением, не разрешенным относительно y :
Пример 1.11.
Уравнение
неявно задаёт две функции:
А уравнение
не задаёт никакой функции.
Теорема 1.2 (существования неявной функции).
Пусть функция z =f(х,у) и ее частные производные f’x и f’y определены и непрерывны в некоторой окрестности UM0 точки M0(x0y0). Кроме того, f(x0,y0)=0 и f'(x0,y0)≠0, тогда уравнение (1.33) определяет в окрестности UM0 неявную функцию y= y(x), непрерывную и дифференцируемую в некотором интервале D с центром в точке x0, причем y( x0)=y0.
Без доказательства.
Из теоремы 1.2 следует, что на этом интервале D:
то- есть имеет место тождество по
Поэтому
где «полная» производная находится согласно (1.31)
То есть (1.35) дает формулу нахождения производной неявно заданной функции одной переменной x .
Аналогично определяется и неявная функция двух и более переменных.
Например, если в некоторой области V пространства Oxyz выполняется уравнение:
то при некоторых условиях на функцию F оно неявно задаёт функцию
При этом по аналогии с (1.35) ее частные производные находятся так:
Пример 1.12. Считая, что уравнение
неявно задаёт функцию
найти z’x, z’y.
Решение
Имеем:
поэтому согласно (1.37) получаем ответ.
Ответ.
11.Использование частных производных в геометрии.
12.Экстремумы функции двух переменных.
Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной (см. п. 25.4).
Пусть функция z = ƒ(х;у) определена в некоторой области D, точка N(x0;y0) Î D.
Точка (х0;у0) называется точкой максимума функции z=ƒ(х;у), если существует такая d-окрестность точки (х0;у0), что для каждой точки (х;у), отличной от (хо;уо), из этой окрестности выполняется неравенство ƒ(х;у)<ƒ(хо;уо).
А налогично
определяется точка минимума функции:
для всех точек (х; у), отличных от (х0;у0),
из d-окрестности точки (хо;уо) выполняется
неравенство: ƒ(х;у)>ƒ(х0;у0).
налогично
определяется точка минимума функции:
для всех точек (х; у), отличных от (х0;у0),
из d-окрестности точки (хо;уо) выполняется
неравенство: ƒ(х;у)>ƒ(х0;у0).
На рисунке 210: N1 — точка максимума, а N2 — точка минимума функции z=ƒ(x;у).
Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум и минимум функции называют ее экстремумами.
Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке (х0;у0) сравнивается с ее значениями в точках, достаточно близких к (х0; у0). В области D функция может иметь несколько экстремумов или не иметь ни одного.
46.2. Необходимые и достаточные условия экстремума
Рассмотрим условия существования экстремума функции.
Теорема 46.1 (необходимые условия экстремума). Если в точке N(x0;y0) дифференцируемая функция z=ƒ(х;у) имеет экстремум, то ее частные производные в этой точке равны нулю: ƒ’x(х0;у0)=0, ƒ’y(х0;у0)=0.
Зафиксируем одну из переменных. Положим, например, у=у0. Тогда получим функцию ƒ(х;у0)=φ(х) одной переменной, которая имеет экстремум при х = х0. Следовательно, согласно необходимому условию экстремума функции одной переменной (см. п. 25.4), φ'(х0) = 0, т. е. ƒ’x(х0;y0)=0.
Аналогично можно показать, что ƒ’y(х0;у0) = 0.
Геометрически равенства ƒ’x(х0;у0)=0 и ƒ’y(х0;у0)=0 означают, что в точке экстремума функции z=ƒ(х;у) касательная плоскость к поверхности, изображающей функцию ƒ(х;у), параллельна плоскости Оху, т. к. уравнение касательной плоскости есть z=z0 (см. формулу (45.2)).
Замечание. Функция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Например, функцияимеет максимум в точке О(0;0) (см. рис. 211), но не имеет в этой точке частных производных.
Точка, в которой частные производные первого порядка функции z ≈ ƒ(х; у) равны нулю, т. е. f’x=0, f’y=0, называется стационарной точкой функ ции z.
Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Рассмотрим, например, функцию z = ху. Для нее точка О(0; 0) является критической (в ней z’x=у и z’y — х обращаются в ноль). Однако экстремума в ней функция z=ху не имеет, т. к. в достаточно малой окрестности точки О(0; 0) найдутся точки для которых z>0 (точки I и III четвертей) и z < 0 (точки II и IV четвертей).
Таким образом, для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.
Теорема 46.2 (достаточное условие экстремума). Пусть в стационарной точке (хо;уо) и некоторой ее окрестности функция ƒ(х;у) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке (х0;у0) значения A=f»xx(x0;y0), В=ƒ»xy(х0;у0), С=ƒ»уy(х0;у0). Обозначим
Тогда:
1. если Δ > 0, то функция ƒ(х;у) в точке (х0;у0) имеет экстремум: максимум, если А < 0; минимум, если А > 0;
2. если Δ < 0, то функция ƒ(х;у) в точке (х0;у0) экстремума не имеет.
В случае Δ = 0 экстремум в точке (х0;у0) может быть, может не быть. Необходимы дополнительные исследования.
ЗАДАЧИ
1.
Пример. Найти
промежутки возрастания и убывания
функции . Решение. Первым
шагом является нахождение
обрасти определения функции.
В нашем примере выражение в знаменателе
не должно обращаться в ноль,
следовательно, . Переходим
к производной функции: Для
определения промежутков возрастания
и убывания функции по достаточному
признаку решаем неравенства и на
области определения. Воспользуемся
обобщением метода интервалов. Единственным
действительным корнем числителя
является x
= 2,
а знаменатель обращается в ноль при x
= 0.
Эти точки разбивают область определения
на интервалы, в которых производная
функции сохраняет знак. Отметим эти
точки на числовой прямой. Плюсами и
минусами условно обозначим интервалы,
на которых производная положительна
или отрицательна. Стрелочки снизу
схематично показывают возрастание или
убывание функции на соответствующем
интервале. Таким
образом, и . В
точке x
= 2 функция
определена и непрерывна, поэтому ее
следует добавить и к промежутку
возрастания и к промежутку убывания. В
точке x
= 0 функция
не определена, поэтому эту точку не
включаем в искомые интервалы. Приводим
график функции для сопоставления с ним
полученных результатов. 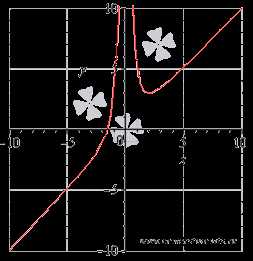 Ответ: функция
возрастает при ,
убывает на интервале (0;
2].
Ответ: функция
возрастает при ,
убывает на интервале (0;
2].
2.
Примеры.
Установить интервалы выпуклости и вогнутости кривой y = 2 – x2.
Найдем y » и определим, где вторая производная положительна и где отрицательна. y‘ = –2x, y» = –2 < 0 на (–∞; +∞), следовательно, функция всюду выпукла.
y = ex. Так как y» = ex > 0 при любых x, то кривая всюду вогнута.
y = x3. Так как y» = 6x, то y» < 0 при x < 0 и y» > 0 при x > 0. Следовательно, при x < 0 кривая выпукла, а при x > 0 вогнута.
3.


4. Дана функция z=x^2-y^2+5x+4y, вектор l=3i-4j и точка А(3,2). Найти dz/dl (я так понял производная функции по направлению вектора), gradz(A), |gradz(A)|. Найдем частные производные: z(по х)=2x+5 z(по y)=-2y+4 Найдем значения производных в точке А(3,2): z(по х)(3,2)=2*3+5=11 z(по y)(3,2)=-2*2+4=0 Откуда, gradz(A)=(11,0)=11i |gradz(A)|=sqrt(11^2+0^2)=11 Производная функции z по направлению вектора l: dz/dl=z(по х)*cosa+z(по у)*cosb, a,b-углы вектора l с осями координат. cosa=lх/|l|, cosb=ly/|l|, |l|=sqrt(lx^2+ly^2) lx=3, ly=-4, |l|=5. cosa=3/5, cosb=(-4)/5. dz/dl=11*3/5+0*(-4)/5=6,6.
studfiles.net
Производная неявной функции нескольких переменных.
Пусть непрерывная функция у от х задаётся неявно F(x, y) = 0, где F(x, y), F ‘ x(x, y), F ‘ y(x, y) есть непрерывные функции в некоторой области D, содержащей точку (х, у), координаты которой удовлетворяют соотношениям F (x, y) = 0, F ‘ y(x, y) ≠ 0. Тогда функция у от х имеет производную
.
Доказательство (смотри рисунок.). Пусть F ‘ y(x, y) > 0. Так как производная F ‘ y(x, y) непрерывна, то можно построить квадрат [х0 — δ’ , х0 + δ’ , у0 — δ’ , у0 + δ’ ], чтобы для всех его точек было F ‘y (x, y) > 0, то есть F(x, y) является монотонной по у при фиксированном х. Таким образом, выполнены все условия теоремы существования неявной функции у = f (x), такой, что F(x, f (x)) º 0.
Зададим приращение Δ х. Новому значению х + Δ х будет соответствовать у + Δ у = f (x + Δ x), такое, что эти значения удовлетворяют уравнению F (x + Δ x, y + Δ y) = 0. Очевидно, что
Δ F = F(x + Δ x, y + Δ y) − F(x, y) = 0
и в этом случае
, (7)
где
.
Из (7) имеем
.
Так как неявная функция у = f (x) будет непрерывна, то Δ у → 0 при Δ х → 0, значит α → 0 и β → 0. Откуда окончательно имеем
.
Что и требовалось доказать.
Частные производные и дифференциалы высших порядков.
Пусть частные производные функции z = f (x, y ), определенной в окрестности точки М, существуют в каждой точке этой окрестности. В этом случае частные производные представляют собой функции двух переменных х и у, определенные в указанной окрестности точки М. Назовем их частными производными первого порядка. В свою очередь, частные производные по переменным х и у от функций в точке М, если они существуют, называются частными производными второго порядка от функции f (М) в этой точке и обозначаются следующими символами
Частные производные второго порядка вида , , называются смешенными частными производными.
Дифференциалы высших порядков
Будем рассматривать dx в выражении для dy как постоянный множитель.Тогда функция dy представляет собой функцию только аргумента x и ее дифференциал в точке x имеет вид (при рассмотрении дифференциала от dy будем использовать новые обозначения для дифференциалов):
δ (d y) = δ [f ‘ (x) d x] = [f ‘ (x) d x] ‘ δ x = f » (x) d(x) δx .
Дифференциал δ (d y) от дифференциала dy в точке x, взятый при δx = dx, называется дифференциалом второго порядка функции f (x) в точке x и обозначается d2y, т.е.
d2y = f »(x)·(dx)2.
В свою очередь, дифференциал δ(d2y) от дифференциала d2y, взятый при δx = dx, называется дифференциалом третьего порядка функции f(x) и обозначается d3y и т.д. Дифференциал δ(dn-1y) от дифференциала dn-1f, взятый при δx = dx, называется дифференциалом n — го порядка (или n — м дифференциалом) функции f(x) и обозначается dny.
Докажем, что для n — го дифференциала функции справедлива формула
dny = y(n)·(dx)n, n = 1, 2, … (3.1)
При доказательстве воспользуемся методом математической индукции. Для n = 1 и n = 2 формула (3.1) доказана. Пусть она верна для дифференциалов порядка n — 1
dn−1y = y(n−1)·(dx)n−1,
и функция y(n-1)(x) дифференцируема в некоторой точке x. Тогда
Полагая δx = dx, получаем
что и требовалось доказать.
Для любого n справедливо равенство
или
т.е. n — я производная функции y = f ( x ) в точке x равна отношению n — го дифференциала этой функции в точке x к n — й степени дифференциала аргумента.
Производная по направлению функций нескольких переменных.
Рассматривается функция и единичный вектор . Проводится прямая l через т.М0 с направляющим вектором
Определение 1. Производная функции u = u(x, y, z) по переменной t называется производной по направлению l
Так как на этой прямой u – сложная функция одной переменной, то производная по t равна полной производной по t (§ 12).
Она обозначается и равна
Градиент функции. Связь между производной по направлению и градиентом функции.
Градиентом функции u(х1,х2,…,хn) называется вектор, координаты которого равны частным производным функции u :
В нашем случае Таким образом, производная по направлению равна:
, где φ − угол между направляющим вектором прямой и градиентом функции в данной точке. Отсюда следует геометрический и физический смысл градиента функции (необходимо помнить, что скорость изменения функции вдоль прямой l ):
1. Градиент ортогонален касательной плоскости к поверхности уровня в данной точке.
2. Градиент направлен в сторону максимального роста (изменения) функции в т.М0 .
{Этот максимум достигается при φ = 0, т.е. при }
3. Величина наибольшей скорости роста функции равна .
infopedia.su
Дифференциал неявной функции, теория и примеры
ОПРЕДЕЛЕНИЕ Если независимая переменная и функция связаны уравнением которое нельзя разрешить относительно то говорят, что функция задана неявно.По определению дифференциал функции равен
То есть вначале надо найти производную заданной неявно функции а затем подставить ее в последнее соотношение.
Чтобы найти указанную производную, необходимо продифференцировать обе части уравнения и из полученного равенства выразить производную
Отметим, что при дифференцировании надо не забывать, что не является независимой переменной, а есть функция от поэтому производную от нее надо находить как от сложной функции.
Примеры вычисления дифференциалов неявных функций
ПРИМЕР 1| Задание | Найти дифференциал функции заданной неявно уравнением |
| Решение | Дифференцируем левую и правую части заданного равенства:
Согласно свойствам производной, производная суммы равна сумме производных. Тогда имеем:
Применяем правило дифференцирования произведения:
Из последнего равенства находим производную :
Итак, искомый дифференциал
|
| Ответ |
| Задание | Найти дифференциал функции заданной неявно: |
| Решение | Вначале по свойствам логарифмов упростим выражение. Известно, что логарифм произведения равен сумме логарифмов от каждого из сомножителей, то есть имеем:
Дифференцируем левую и правую части последнего равенства:
Производная суммы равна сумме производных, а также производная константы равна нулю. Тогда получаем:
Находим записанные производные и производную от находим как производную сложной функции:
А тогда искомый дифференциал
|
| Ответ |
ru.solverbook.com
Производная неявно заданной функции. Примеры
Часто на практике встречаются функции в которых независимая переменная и функция связаны между собой зависимостью
из которой нельзя отделить саму функцию. В этом случае функция называется неявной функцией от.
Однако саму производную функции по переменной можно вычислить. Для этого дифференцируют функцию по , при этом учитывают, что сама функция зависит от переменной . Из полученного уравнения группируют слагаемые, содержащиеся при производной и выражают ее.
Для закрепления материала рассмотрим следующие примеры.
Пример 1.
Найти производные функций, заданных неявно (Дубовик В.П., Юрик И.И. «Высшая математика. Сборник задач»)
1) (5.219)
2) (5.223)
3) (5.227)
4) (5.236)
Решение.
1) Продифференцируем правую и левую части
Полученное выражение разделим на общий множитель и сгруппируем слагаемые, содержащие производную и перенесем их в одну сторону за знак равенства. В результате получим
Поделив на множитель при производной получим ее значение
Для упрощения, вынесем из числителя и знаменателя общие множители исоответственно. В результате будем иметь
Как видите ничего сложного мы не делали но быстро нашли производную неявно заданной функции. Рассмотрим следующую задачу.
2) Проведем дифференцировки
Выделяем слагаемые, содержащие производную
Разделим на множитель при производной и найдем ее значение
Задача полностью решена.
3) Вычислим производную правой и левой части
Найдем производную частки функций
Первых два множителя равны синусу двойного угла. Поэтому производные можем записать в виде
Умножим правую и левую части на чтобы избавиться знаменателей и сгруппируем слагаемые при производной
Из последней зависимости находим значение искомой производной
В такого рода примерах главное не ошибиться при отыскании производных.
4) Проведем дифференцирования функций
Выделим слагаемые, содержащие и сгруппируем их
Сведем выражения к общему знаменателю
и подставим их на свои места
Отсюда выразим производную
На этом решения примера завершено.
При вычислении производной неявно заданной функции типичными ошибками на практике являются неправильное взятие производной и неразбериха со знаками при группировке подобных слагаемых. Будьте внимательны в таких ситуациях и не допускайте ошибок.
yukhym.com
ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ
Количество просмотров публикации ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ — 407
Пусть значения двух переменных x и y связаны между собой некоторым уравнением, ĸᴏᴛᴏᴩᴏᴇ символически запишем так:
В случае если на некотором множестве D каждому значению переменной x соответствует единственное значение y, ĸᴏᴛᴏᴩᴏᴇ вместе с x удовлетворяет уравнению (1), то будем говорить, что это уравнение задает неявную функцию y=f(x).
Из определения следует, что для любой неявной функции y=f(x), заданной уравнением (1), имеет место тождество F(x, f(x)) ≡ 0, справедливое при всех x Î D.
К примеру, уравнение x2 + y2 – a2 = 0 неявно определяет две элементарные функции . Действительно, после подстановки в исходное уравнение этих значений получим равенство x2+(a2–x2) – a2 = 0.
При этом, не всякую неявно заданную функцию можно представить явно, ᴛ.ᴇ. в виде y=f(x).
К примеру, функции, заданные уравнениями y2– y – x2=0 или , не выражаются через элементарные функции, ᴛ.ᴇ. эти уравнения нельзя разрешить относительно y.
Заметим, что каждая явная функция y=f(x) должна быть представлена и как неявная y–f(x) = 0.
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, неявная функция — ϶ᴛᴏ определенный способ задания зависимости между переменными x и y.
Рассмотрим правило нахождения производной неявной функции, не преобразовывая ее в явную, ᴛ.ᴇ. не представляя в виде y=f(x).
Чтобы найти производную у‘ неявной функции F(x, y)=0, нужно обе части этого уравнения продифференцировать по x, рассматривая у как функцию от x, и из этого полученного уравнения найти искомую производную y‘. Чтобы найти y», нужно уравнение F(x, y)=0 дважды продифференцировать по x и выразить y» и т.д.
Примеры. Найти производные функций заданных неявно.
1.
2.
Итак, производная неявной функции выражается, как правило, не только через аргумент, но и через функцию.
referatwork.ru
