Формулы сокращённого умножения многочленов — Википедия
Формулы сокращённого умножения многочленов — часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем бинома Ньютона. Изучаются в средней школе в курсе алгебры.
Содержание
- 1 Формулы для квадратов
- 2 Формулы для кубов
- 3 Формулы для четвёртой степени
- 4 Формулы для n-ой степени
- 5 Некоторые свойства формул
- 6 См. также
- 7 Литература
Формулы для квадратов
- (a±b)2=a2±2ab+b2{\displaystyle (a\pm b)^{2}=a^{2}\pm 2ab+b^{2}}
- a2−b2=(a+b)(a−b){\displaystyle a^{2}-b^{2}=(a+b)(a-b)}
- (a+b+c)2=a2+b2+c2+2ab+2ac+2bc{\displaystyle \left(a+b+c\right)^{2}=a^{2}+b^{2}+c^{2}+2ab+2ac+2bc}
Формулы для кубов
- (a±b)3=a3±3a2b+3ab2±b3{\displaystyle (a\pm b)^{3}=a^{3}\pm 3a^{2}b+3ab^{2}\pm b^{3}}
- a3±b3=(a±b)(a2∓ab+b2){\displaystyle a^{3}\pm b^{3}=(a\pm b)(a^{2}\mp ab+b^{2})}
- (a+b+c)3=a3+b3+c3+3a2b+3a2c+3ab2+3ac2+3b2c+3bc2+6abc{\displaystyle \left(a+b+c\right)^{3}=a^{3}+b^{3}+c^{3}+3a^{2}b+3a^{2}c+3ab^{2}+3ac^{2}+3b^{2}c+3bc^{2}+6abc}
Формулы для четвёртой степени
- (a±b)4=a4±4a3b+6a2b2±4ab3+b4{\displaystyle (a\pm b)^{4}=a^{4}\pm 4a^{3}b+6a^{2}b^{2}\pm 4ab^{3}+b^{4}}
- a4−b4=(a−b)(a+b)(a2+b2){\displaystyle a^{4}-b^{4}=(a-b)(a+b)(a^{2}+b^{2})} (выводится из a2−b2{\displaystyle a^{2}-b^{2}})
Формулы для n-ой степени
- an−bn=(a−b)(an−1+an−2b+an−3b2+…+a2bn−3+abn−2+bn−1){\displaystyle a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+a^{n-3}b^{2}+…+a^{2}b^{n-3}+ab^{n-2}+b^{n-1})}
- a2n−b2n=(a+b)(a2n−1−a2n−2b+a2n−3b2−…−a2b2n−3+ab2n−2−b2n−1){\displaystyle a^{2n}-b^{2n}=(a+b)(a^{2n-1}-a^{2n-2}b+a^{2n-3}b^{2}-…-a^{2}b^{2n-3}+ab^{2n-2}-b^{2n-1})}, где n∈N{\displaystyle n\in N}
- a2n−b2n=(an+bn)(an−bn){\displaystyle a^{2n}-b^{2n}=(a^{n}+b^{n})(a^{n}-b^{n})}
- a2n+1+b2n+1=(a+b)(a2n−a2n−1b+a2n−2b2−…+a2b2n−2−ab2n−1+b2n){\displaystyle a^{2n+1}+b^{2n+1}=(a+b)(a^{2n}-a^{2n-1}b+a^{2n-2}b^{2}-…+a^{2}b^{2n-2}-ab^{2n-1}+b^{2n})}, где n∈N{\displaystyle n\in N}
Некоторые свойства формул
- (a−b)2n=(b−a)2n{\displaystyle (a-b)^{2n}=(b-a)^{2n}}, где n∈N{\displaystyle n\in N}
- (a−b)2n+1=−(b−a)2n+1{\displaystyle (a-b)^{2n+1}=-(b-a)^{2n+1}}, где n∈N{\displaystyle n\in N}
См. также
- Многочлен
- Бином Ньютона
- Факторизация многочленов
Литература
- М. Я. Выгодский. Справочник по элементарной математике. — Москва, 1958.
Формулы сокращенного умножения: таблица, примеры использования
Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.
В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.
Формулы сокращенного умножения. Таблица
Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.
Формулы сокращенного умножения- формула квадрата суммы: a+b2=a2+2ab+b2
- формула квадрата разности: a-b2=a2-2ab+b2
- формула куба суммы: a+b3=a3+3a2b+3ab2+b3
- формула куба разности: a-b3=a3-3a2b+3ab2-b3
- формула разности квадратов: a2-b2=a-ba+b
- формула суммы кубов: a3+b3=a+ba2-ab+b2
- формула разности кубов: a3-b3=a-ba2+ab+b2
Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.
Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.
Шестая и седьмая формулы — соответственно умножение суммы и разности выражений на неполный квадрат разности и неполный квадрат суммы.
Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.
При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Формулы сокращенного умножения
Формулы сокращенного умножения.
Цели:
— Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.
— Применение формул сокращенного умножения при решении примеров.
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения.
Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b)2 = a2 + 2ab + b2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b)2 = a2 — 2ab + b2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.a2 — b2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b)3 = a3 — 3a2b + 3ab2 — b3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
a3 + b3 = (a + b) (a2 — ab + b2)
7. Разность кубов
a3 — b3 = (a — b) (a2 + ab + b2)
Применение формул сокращенного умножения при решении примеров.
Пример 1.
Вычислить
а) (40+1)2
б) 982
Решение:
а) Используя формулу квадрата суммы двух выражений, имеем
(40+1)2 = 402 + 2 · 40 · 1 + 12 = 1600 + 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получим
982 = (100 – 2)2 = 1002 — 2 · 100 · 2 + 22 = 10000 – 400 + 4 = 9604
Пример 2.
Вычислить
Решение
Используя формулу разности квадратов двух выражений, получим
Пример 3.
Упростить выражение
(х — у)2 + (х + у)2
Решение
Воспользуемся формулами квадрата суммы и квадрата разности двух выражений
(х — у)2 + (х + у)2 = х2 — 2ху + у2 + х2 + 2ху + у2 = 2х2 + 2у2
Формулы сокращенного умножения в одной таблице:
(a + b)2 = a2 + 2ab + b2
(a — b)2 = a2 — 2ab + b2
a2 — b2 = (a — b) (a+b)
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a — b)3 = a3 — 3a2b + 3ab2 — b3
a3 + b3 = (a + b) (a2 — ab + b2)
a3
Формулы сокращённого умножения | Алгебра
При выполнении преобразований разных выражений часто встречаются некоторые частные случаи умножения. Равенства, выражающие эти случаи, называются формулами сокращённого умножения.
Формулы сокращённого умножения – это выражения, в которых пропущены промежуточные вычисления, поэтому их и называют сокращёнными.
a2 + b2 = (a + b)2 — 2ab – сумма квадратов
a2 — b2 = (a + b)(a — b) – разность квадратов
(a + b)2 = a2 + 2ab + b2 – квадрат суммы
(a — b)2 = a2 — 2 ab + b2 – квадрат разности
a3 + b3 = (a + b)(a2 — ab + b2) – сумма кубов
a3 — b3 = (a — b)(a2 + ab + b2) – разность кубов
(a + b)3 = a3 + 3a2b + 3ab2 + b3 – куб суммы
(a — b)3 = a3 — 3a2b + 3ab2 — b3 – куб разности
Обратите внимание, что a
и b
в формулах сокращённого умножения могут быть как числами, так и выражениями.
Рассмотрим каждую формулу подробнее и приведём доказательство верности формул сокращённого умножения:
- Сумма квадратов двух чисел равна разности квадрата суммы этих чисел и их удвоенного произведения:
a2 + b2 = (a + b)2 — 2ab
Доказательство: выполним преобразование правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)2 — 2ab = (a + b)(a + b) — 2ab =
= a2 + ab + ab + b2 — 2ab = a2 + b2
- Разность квадратов двух чисел равна произведению суммы этих чисел на их разность:
a2 — b2 = (a + b)(a — b
)Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a — b) = a2 — ab + ab — b2 = a2 — b2
- Квадрат суммы двух чисел равен сумме квадрата первого числа, удвоенного произведения первого числа на второе и квадрата второго числа:
(a + b)2 = a2 + 2ab + b2
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab +
- Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого числа на второе, плюс квадрат второго числа:
(a — b)2 = a2 — 2ab + b2
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)2 = (a — b)(a — b) = a2 — ab — ab + b2 = a2 — 2ab + b2
- Сумма кубов двух чисел равна произведению суммы первого и второго числа на неполных квадрат разности этих чисел:
a3 + b3 = (a + b)(a2 — ab + b2)
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a + b)(a2 — ab + b2) = a3 — a2b + ab2 + a2b — ab2 + b3 = a3 + b3
- Разность кубов двух чисел равна произведению разности первого и второго числа на неполный квадрат суммы этих чисел:
a3 — b3 = (a — b)(a2 + ab + b2)
Доказательство: выполним умножение многочленов из правой части формулы, приведём подобные члены и получим левую часть формулы:
(a — b)(a2 + ab + b2) = a3 + a2b + ab2 — a2b — ab2 — b3 = a3 — b3
- Куб суммы двух чисел равен сумме четырёх слагаемых: куб первого числа, утроенное произведение квадрата первого числа на второе число, утроенное произведение первого числа на квадрат второго и куб второго числа:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a + b)3 = (a + b)(a + b)2 = (a + b)(a2 + 2ab + b2) =
= a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
- Куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе число, плюс утроенное произведение первого числа на квадрат второго, минус куб второго числа:
(a — b)3 = a3 — 3a2b + 3ab2 — b3
Доказательство: представим степень в виде произведения, выполним умножение и приведение подобных членов:
(a — b)3 = (a — b)(a — b)2 = (a — b)(a2 — 2ab + b2) =
= a3 — 2a2b + ab2 — a2b + 2ab2 — b3 = a3 — 3a2b + 3ab2 — b3
Неполный квадрат суммы
Выражение:
a2 + 2ab + b2
это квадрат суммы, которое также называется полным квадратом суммы, относительно выражения:
a2 + ab + b2,
которое называется неполным квадратом суммы. Неполный квадрат суммы – это сумма квадратов двух чисел и их произведения. Неполный квадрат суммы отличается от полного только произведением чисел, которое не удваивается.
Неполный квадрат разности
Выражение:
a2 — 2ab + b2
Это квадрат разности, который также называется полным квадратом разности относительно выражения:
a2 — ab + b2,
которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.
Формулы сокращенного умножения с примерами
Формулами сокращенного умножения (ФСУ) называют несколько наиболее часто встречающихся в практике случаев умножения многочленов.
ФСУ используются при упрощении алгебраических выражений (в том числе в работе с алгебраическими дробями), решении уравнений и неравенств, при разложении на множители и т.д. Ниже мы рассмотрим наиболее популярные формулы и разберем как они получаются.
Квадрат суммы
Пусть у нас возводиться в квадрат сумма двух одночленов, вот так: \((a+b)^2\). Возведение в квадрат – это умножение числа или выражения само на себя, то есть, \((a+b)^2=(a+b)(a+b)\). Теперь мы можем просто раскрыть скобки, перемножив их как делали это здесь, и привести подобные слагаемые. Получаем:
А если мы опустим промежуточные вычисления и запишем только начальное и конечное выражения, получим окончательную формулу:
Квадрат суммы: \((a+b)^2=a^2+2ab+b^2\)
Большинство учеников учат ее наизусть. А вы теперь знаете, как эту формулу вывести, и если вдруг забудете – всегда можете это сделать.
Хорошо, но как ей пользоваться и зачем эта формула нужна? Квадрат суммы позволяет быстро писать результат возведения суммы двух слагаемых в квадрат. Давайте посмотрим на примере.
Пример. Раскрыть скобки: \((x+5)^2\)
Решение:
Обратите внимание, насколько быстрее и меньшими усилиями получен результат во втором случае. А когда вы эту и другие формулы освоите до автоматизма – будет еще быстрее: вы сможете просто сразу же писать ответ. Поэтому они и называются формулы СОКРАЩЕННОГО умножения. Так что, знать их и научиться применять – точно стоит.
На всякий случай отметим, что в качестве \(a\) и \(b\) могут быть любые выражения – принцип остается тем же. Например:
Если вы вдруг не поняли какие-то преобразования в двух последних примерах – повторите свойства степеней и тему приведения одночлена к стандартному виду.
Пример. Преобразуйте выражение \((1+5x)^2-12x-1 \) в многочлен стандартного вида.
Решение:
|
\((1+5x)^2-12x-1= \) |
Раскроем скобки, воспользовавшись формулой квадрата суммы… |
|
|
\(=1+10x+25x^2-12x-1=\) |
…и приведем подобные слагаемые. |
|
|
\(=25x^2-2x\) |
Готово. |
Ответ: \(25x^2-2x\).
Важно! Необходимо научиться пользоваться формулами не только в «прямом», но и в «обратном» направлении.
Пример. Вычислите значение выражения \((368)^2+2·368·132+(132)^2\) без калькулятора.
Решение:
|
\((368)^2+2·368·132+(132)^2=\) |
Мда… возводить в квадрат трехзначные числа, перемножить их же, а потом все это складывать – удовольствие ниже среднего. Давайте искать другой путь: обратите внимание, что данное нам числовое выражение очень похоже на правую часть формулы. Применим ее в обратную сторону: \(a^2+2ab+b^2=(a+b)^2\) |
|
|
\(=(368+132)^2=\) |
Вот теперь вычислять гораздо приятнее! |
|
|
\(=(500)^2=250 000.\) |
Готово. |
Ответ: \(250 000\).
Квадрат разности
Выше мы нашли формулу для суммы одночленов. Давайте теперь найдем формулу для разности, то есть, для \((a-b)^2\):
В более краткой записи имеем:
Квадрат разности: \((a-b)^2=a^2-2ab+b^2\)
Применяется она также, как и предыдущая.
Пример. Упростите выражение \((2a-3)^2-4(a^2-a)\) и найдите его значение при \(a=\frac{17}{8}\).
Решение:
|
\((2a-3)^2-4(a^2-a)=\) |
Если сразу подставить дробь в выражение – придется возводить ее в квадрат и вообще делать объемные вычисления. Попробуем сначала упростить выражение, воспользовавшись формулой выше и раскрыв скобки. |
|
|
\(=4a^2-12a+9-4a^2+4a=\) |
Теперь приведем подобные слагаемые. |
|
|
\(=-8a+9=\) |
Вот теперь подставляем и наслаждаемся простотой вычислений. |
|
|
\(=-8·\frac{17}{8}+9=-17+9=8\) |
Пишем ответ. |
Ответ: \(8\).
Разность квадратов
Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:
Получили формулу:
Разность квадратов \(a^2-b^2=(a+b)(a-b)\)
Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями.
Пример. Сократите дробь \(\frac{x^2-9}{x-3}\).
Решение:
|
\(\frac{x^2-9}{x-3}\)\(=\) |
Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус! |
|
|
\(=\) \(\frac{x^2-3^2}{x-3}\)\(=\)\(\frac{(x+3)(x-3)}{x-3}\)\(=\) |
Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки. |
|
|
\(=x+3\) |
Готов ответ. |
Ответ: \(x+3\).
Пример.Разложите на множители \(25x^4-m^{10} t^6\).
Решение:
|
\(25x^4-m^{10} t^6\) |
Воспользуемся формулами степеней: \((a^n )^m=a^{nm}\) и \(a^n b^n=(ab)^n\). |
|
|
\(=(5x^2 )^2-(m^5 t^3 )^2=\) |
Ну, а теперь пользуемся формулой \(a^2-b^2=(a+b)(a-b)\), где \(a=5x^2\) и \(b=m^5 t^3\). |
|
|
\(=(5x^2-m^5 t^3 )(5x^2+m^5 t^3 )\) |
Готов ответ. |
Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.
Пример (повышенной сложности!).Сократите дробь \(\frac{x^2-4xy-9+4y^2}{x-2y+3}\) .
Решение:
|
\(\frac{x^2-4xy-9+4y^2}{x-2y+3}\)\(=\) |
На первый взгляд тут тихий ужас и сделать с ним ничего нельзя (вариант «лечь и помереть» всерьез не рассматриваем). |
|
|
\(\frac{(x^2-4xy+4y^2)-9}{x-2y+3}\)\(=\) |
Теперь немного преобразуем слагаемые в скобке: |
|
|
\(\frac{(x^2-4xy+(2y)^2)-9}{x-2y+3}\)\(=\) |
Теперь приглядимся – и заметим, что в скобке у нас получилась формула квадрата разности, у которой \(a=x\), \(b=2y\). Сворачиваем по ней к виду скобки в квадрате. И одновременно представляем девятку как \(3\) в квадрате. |
|
|
\(\frac{(x-2y)^2-3^2}{x-2y+3}\)\(=\) |
Еще раз внимательно смотрим на числитель… думаем… думаем… и замечаем формулу разности квадратов, у которой \(a=(x-2y)\), \(b=3\). Раскладываем по ней к произведению двух скобок. |
|
|
\(\frac{(x-2y-3)(x-2y+3)}{x-2y+3}\)\(=\) |
И вот теперь сокращаем вторую скобку числителя и весь знаменатель. |
|
|
\(x-2y-3\) |
Готов ответ. |
Формулы сокращенного умножения
Для того что бы упростить алгебраические многочлены, существуют формулы сокращенного умножения. Их не так уж и много и они легко запоминаются, а запомнить их нужно. Обозначения которые используются в формулах, могут принимать любой вид (число или многочлен).
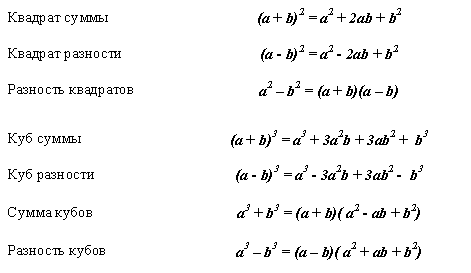
Первая формула сокращенного умножения называется разность квадратов. Она заключается в том что из квадрата одного числа отнимается квадрат второго числа равен величине разности данных чисел, а также их произведению.
а2 — b2 = (а — b)(a + b)
Разберем для наглядности:
222 — 42 = (22-4)(22+4)=18 * 26 = 468
9а2 — 4b2c2 = (3a — 2bc)(3a + 2bc)
Вторая формула о сумме квадратов. Звучит она как, сумма двух величин в квадрате равняется квадрату первой величины к ней прибавляется двойное произведение первой величины умноженное на вторую, к ним прибавляется квадрат второй величины.
(а + b)2 = a2 +2ab + b2Благодаря данной формуле, становится намного проще вычислять квадрат от большого числа, без использования вычислительной техники.
Так к примеру: квадрат от 112 будет равен
1) В начале разберем 112 на числа квадраты которых нам знакомы
112 = 100 + 12
2) Вписываем полученное в скобки возведенные в квадрат
1122 = (100+12)2
3) Применяя формулу, получаем:
1122 = (100+12)2 = 1002 + 2 * 100 * 12 + 122 = 10000 + 2400+ 144 = 12544
Третья формула это квадрат разности. Которая гласит о том, что две вычитаемые друг друга величины в квадрате равняются, тому что, от первой величины в квадрате отнимаем двойное произведение первой величины умноженное на вторую, прибавляя к ним квадрат второй величины.
(а +b)2 = а2 — 2аb + b2
где (а — b)2 равняется (b — а)2. В доказательство чему, (а-b)2 = а2-2аb+b2 = b2-2аb + а2 = (b-а)2
Четвертая формула сокращенного умножения называется куб суммы. Которая звучит как: две слагаемые величины в кубе равны кубу 1 величины прибавляется тройное произведение 1 величины в квадрате умноженное на 2-ую величину, к ним прибавляется тройное произведение 1 величины умноженной на квадрат 2 величины, плюс вторая величина в кубе.
(а+b)3 = а3 + 3а2b + 3аb2 + b3
Пятая, как вы уже поняли называется куб разности. Которая находит разности между величинами, как от первого обозначения в кубе отнимаем тройное произведение первого обозначения в квадрате умноженное на второе, к ним прибавляется тройное произведение первого обозначения умноженной на квадрат второго обозначения, минус второе обозначение в кубе.
(а-b)3 = а3 — 3а2b + 3аb2 — b3
Шестая называется — сумма кубов. Сумма кубов равняется произведению двух слагаемых величин, умноженных на неполный квадрат разности, так как в середине нет удвоенного значения.
а3 + b3 = (а+b)(а2-аb+b2)
По другому можно сказать сумму кубов можно назвать произведение в двух скобках.
Седьмая и заключительная, называется разность кубов (ее легко перепутать с формулой куба разности, но это разные вещи). Разность кубов равняется произведению от разности двух величин, умноженных на неполный квадрат суммы, так как в середине нет удвоенного значения.
а3 — b3 = (а-b)(а2+аb+b2)
И так формул сокращенного умножения всего 7, они похожи друг на друга и легко запоминаются, единственно важно не путаться в знаках. Они так же рассчитаны на то, что их можно использовать в обратном порядке и в учебниках собрано довольно много таких заданий. Будьте внимательны и все у вас получится.
Если у вас появились вопросы по формулам, обязательно пишите их в комментариях. Будем рады ответить вам!
Если Вы находитесь в декретном отпуске, но хотите зарабатывать деньги. Просто перейдите по ссылке Интернет бизнес с Орифлейм. Там все очень подробно написано и показано. Будет интересно!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Формула-2 — Википедия
Материал из Википедии — свободной энциклопедии
Эта статья — о классе автомобильных гонок. О ныне существующей гоночной серии см. ФИА Формула-2.
Формула-2 — это класс автомобилей с открытыми колёсами, существующий с 1948 года. В иерархии FIA серия занимает место между Формулой-1 и Формулой-3.
- История
Между мировыми войнами параллельно с гонками Гран-при существовали соревнования малолитражек, позволявшие малообеспеченным и неопытным пилотам-частникам проявить себя в мире автогонок. Также эти соревнования давали возможность участвовать в спорте на межнациональном уровне маленьким фирмам-автопроизводителям, не имеющим ресурсов для построения автомобилей для гонок Гран-при. К началу II мировой войны правила для малолитражек ограничивали объём двигателя полутора литрами (без нагнетателя), а автомобили Гран-при должны были иметь атмосферный двигатель объёмом не более 4,5 литров или двигатель с нагнетателем объёмом не более трех литров.
Формула-1 (первоначально под именем Formula-A) была создана сразу после войны: в 1946 году на основе требований к старым автомобилям Гран-при. Требования к атмосферным двигателям были оставлены прежними (4,5 литра), а вот объём двигателей с нагнетателем был уменьшен с трех литров до полутора для выравнивания шансов с техникой старого малолитражного класса. Подобные изменения не предполагали существования соревнований классом ниже Формулы-1, коими до этого служили малолитражки при соревнованиях автомобилей Гран-при. Количество потенциальных желающих выйти на старт гонок, впрочем, вскоре оказалось таковым, что к идее младшего класса вернулись и в 1948 году был введён регламент Формулы-2 (первоначально — Формула-B), допускавший в свои соревнования атмосферные двигатели объёмом два литра или силовые установки с нагнетателем объёмом 750 куб. см, максимально приблизив гоночные моторы к наиболее популярным серийным собратьям. Новые технические требования заинтересовали и большое число небольших частных фирм, быстро предложивших потенциальным участникам серии различные варианты автомобилей нового класса. Чемпионат быстро набрал популярность, дав мировому первенству многих сильных пилотов, а в 1952 году, когда прежний регламент Формулы-1 доказал свою нежизнеспособность, и стал на два года базовым для чемпионата мира.
Введение в 1954 году нового регламента Формулы-1 заметно снизила популярность гонок младшего класса, превратив его в испытательный полигон не только для молодых пилотов, но и для революционных технических решений. Так в эти годы в серии прошёл обкатку проект британской фирмы Cooper с революционным, по тем временам, задним расположением двигателя и независимой подвеской колёс, вскоре модернизированный под требования чемпионата мира и быстро доказавший свои явные преимущества и на том уровне. Сближение Регламентов Ф1 и Ф2 вскоре привело к ликвидации Формулы-2 как самостоятельного первенства — отдельные машины были доработаны до требований Формулы-1, а новые проекты с 1961 года строились уже под требования новой категории — Формулы-Юниор, предполагавшуюся в виде единого регламента для младших первенств и в 1959 году уже сменившей Формулу-3.
К 1964 году к идее Формулы-2 вновь вернулись, когда стало понятно, что концепция Формулы-Юниор нуждается в разбиении на более мелкие ступени, предложив всем желающим регламент старшего первенства, где силовая установка предполагалась в виде однолитрового четырёхцилиндрового двигателя без наддува. Новую концепцию поддержали производители и постепенно под новым регламентом стали возникать различные чемпионаты — сначала национальные, а к 1967 году была занята и наиболее престижная ниша: было организовано общеевропейское первенство. Под это событие в FIA согласились увеличить рабочий объём двигателей класса до 1,6 литров, а чтобы поднять престиж гонок дали возможность стартовать в них и пилотам чемпионата мира, правда не дав им возможности бороться за позиции в личном зачёте, оставив их результаты лишь в протоколах гонок. Регламент новой серии также допускал частную доработку купленных заводских двигателей, впоследствии повлияв на рост небольших компаний из бюро по доработки до статуса самостоятельных производителей. К 1972 году, впрочем назрела новая техническая революция: двигатели Ford вытеснили с рынка всех своих конкурентов по спортивным соображениям и федерации пришлось пересмотреть регламент на силовые установки, увеличив их рабочий объём до двух литров, а число цилиндров — до шести. Новый регламент дал увеличение числа производителей, но не слишком сказался в лучшую сторону на посещаемости. Гонки серии всё больше превращались в молодёжное первенство, а борьба за титул зачастую все менее зависела от чистой скорости пилота, завися от его опыта в таких гонках и уровня техники, предоставляемой ему командой. К началу 1980-х годов ситуация усугубилась, когда в серию пришла компания Honda, сама занимавшаяся постройкой и доработкой своих силовых агрегатов, а также помогая своей партнёрской компании Ralt в улучшении их шасси. Как итог их альянс, даже выставляя на гонки серии лишь по две машины, год за годом оказывался сильнее многих конкурентов, выиграв к 1985 году три из четырёх последних личных титулов в серии. Борьба с ними других команд привела к удорожанию участия в серии и к 1985 году назрела очередная смена регламента, упразднившая Формулу-2 как класс и введшее вместо неё Формулу-3000, куда японский автоконцерн уже решил не идти. Национальные чемпионаты Формулы-2 прожили дольше — некоторые были постепенно закрыты из-за дороговизны участия, а некоторые переняли регламент Ф-3000. Самым успешным из них стала японское первенство, до сих пор существующее, но уже под вывеской Суперформула.

В 2008 к идее Формулы-2 вернулись, когда в очередном эпизоде борьбы с всё возрастающими затратами FIA вновь решила удешевить старший класс своей «формульной» иерархии перед Формулой-1. При поддержке MotorSport Vision было создано монокомандное европейское первенство FIA Формула-2, в качестве конкурента тогда существовавшим в этой роли GP2 (ранее сменившим главное европейское первенство Формулы-3000) и Формулу-Рено 3.5. Серия просуществовала четыре сезона, но так и не вывела ни одного из своих призёров в Формулу-1 и накануне сезона-2013, из-за малости заявок, была закрыта.
В 2017 году на основе ликвидировавшегося GP2 была создана очередная версия Формулы-2.
- Серии
Наиболее известные серии, существовавшие по данному регламенту или использовавшие его технику:
