Что такое формула a2 b2 c2? – Обзоры Вики
Теорема Пифагора описывает соотношение между тремя сторонами прямоугольного треугольника. В любом прямоугольном треугольнике сумма площадей квадратов, образованных катетами треугольника, равна площади квадрата, образованного гипотенузой: а2 + Ь2 = с2.
Теорема Пифагора только для прямоугольных треугольников? Теорема Пифагора работает только для прямоугольных треугольников, так что вы можете использовать его, чтобы проверить, имеет ли треугольник прямой угол или нет.
Кроме того, является ли алгебра теоремы Пифагора? Теорема Пифагора очень важно для математики. Вы, вероятно, впервые узнаете об этом в алгебре, но вы будете буквально использовать это в алгебре, геометрии, тригонометрии, предварительном исчислении, исчислении и не только!
Является ли теорема Пифагора тригонометрией? Тригонометрическое тождество Пифагора, также называемое просто тождеством Пифагора, представляет собой тождество, выражающее теорему Пифагора в терминах тригонометрических функций. Наряду с формулой суммы углов это одно из основных соотношений между функциями синуса и косинуса.
Наряду с формулой суммы углов это одно из основных соотношений между функциями синуса и косинуса.
Как найти теорему Пифагора, используя только гипотенузу?
Как найти b2 в теореме Пифагора? Длина стороны b равна квадратный корень из квадрата гипотенузы минус квадрат стороны а.
Каков вывод теоремы Пифагора?
Теорема Пифагора утверждает, что «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон».. Стороны этого треугольника называются перпендикуляром, основанием и гипотенузой. Здесь гипотенуза является самой длинной стороной, так как она противоположна углу 90°.
Также когда нельзя использовать теорему Пифагора? Это прямоугольный треугольник; при суммировании квадратов длин сторон, вы получите квадрат длины гипотенузы. Неправильно. Это не прямоугольный треугольник, поэтому вы не можете использовать теорему Пифагора, чтобы найти r.
Неправильно. Это не прямоугольный треугольник, поэтому вы не можете использовать теорему Пифагора, чтобы найти r.
Является ли теорема Пифагора предалгеброй?
Теорема Пифагора (предалгебра, прямоугольные треугольники и алгебра) – Mathplanet.
Пришел ли Пифагор в Индию? Что еще менее известно, так это то, что Пифагор посетил Индию. … Находясь в Индии, кажется, что Пифагор находился под сильным влиянием джайнской философии и стал вегетарианцем. К сожалению, эти факты вообще не упоминаются в большинстве школ при преподавании предмета.
Почему теорема Пифагора не является законом?
Почему теорема Пифагора не является законом? Потому что его нарушение не должно быть уголовным преступлением. Если бы теорема Пифагора была законом, вы не смогли бы его нарушить, но это верно не для всех геометрий, поэтому вы можете. На самом деле это верно только в евклидовой геометрии (в двух или более измерениях).
Каковы 3 пифагорейских тождества?
Тождества Пифагора выводятся из теоремы Пифагора и описывают взаимосвязь между синусом и косинусом на единичной окружности. Три личности cos2t+sin2t=1 t + sin 2 , 1+tan2t=sec2t 1 + tan 2 t = sec 2 и 1+cot2t=csc2t 1 + кроватка 2 t = csc 2 .
Три личности cos2t+sin2t=1 t + sin 2 , 1+tan2t=sec2t 1 + tan 2 t = sec 2 и 1+cot2t=csc2t 1 + кроватка 2 t = csc 2 .
Как написать косеканс? Косеканс (косеканс) — функция тригонометрии
В прямоугольном треугольнике косеканс угла — это длина гипотенузы, деленная на длину противоположной стороны. В формуле он сокращается до «csc».
Как найти a и b прямоугольного треугольника?
Учитывая две стороны
- если сторона a — недостающая сторона, преобразовать уравнение к форме, когда a находится на одной стороне, и извлечь квадратный корень: a = √ (c² — b²)
- если нога b неизвестна, то. b = √ (c² — a²)
- если гипотенуза c отсутствует, формула имеет вид. c = √ (a² + b²)
Как найти A и B, если у вас есть C?
com/embed/yl4D02A9Kic» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Кто является отцом теоремы Пифагора? Пифагор Самосский был известным греческим математиком и философом (ок. 570 – ок. 495 до н.э.). Он наиболее известен доказательством важной теоремы Пифагора о прямоугольных треугольниках.
С какими двумя типами ситуаций вы можете столкнуться при решении с помощью теоремы Пифагора?
Упражнение 3: Использование формулы
При использовании теоремы Пифагора для нахождения третьей стороны прямоугольного треугольника вы столкнетесь с двумя ситуациями: решение для гипотенузы и решение для катета.
Как использовать теорему Пифагора для решения задачи? Используя теорему Пифагора, найдите длину гипотенузы.
…
пример.
| Шаг 1. Прочитайте задачу. | |
|---|---|
| Шаг 5. Решите уравнение. | 9+16=c2 25=c2 √25=c2 5=c |
Шаг 6. Проверьте: Проверьте: | 32+42=52 9+16?=25 25 25+25✓ |
| Шаг 7. Ответьте на вопрос. | Длина гипотенузы равна 5. |
Как найти Пифагора с помощью гипотенузы?
Формула гипотенузы просто берет теорему Пифагора и решает для гипотенузы, c . Находя гипотенузу, мы просто берем квадратный корень из обеих частей уравнения a² + b² = c² и находим c . При этом мы получаем с = √(а² + b²) .
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 15 из 15
У некоторых людей существует трудности с использованием формул сокращённого умножения. Все эти степени и скобки, внезапно превращающиеся в произведения ― да как это вообще работает? На самом деле, основная причина непонимания как раз и кроется в этом вопросе: «Как это вообще работает?» Простая зубрёжка не всегда даёт свои результаты, в то время как осознание того, откуда появляются эти выражения (что, кстати, совсем несложно, в чём мы сейчас и убедимся) позволяет раз и навсегда расправиться с проблемами в этой теме.
Сейчас мы увидим три основных формулы сокращённого умножения, поймём, почему они называются именно так, докажем их, а затем для каждого случая рассмотрим конкретные примеры.
Возьмём самую распространённую формулу:
a2 – b2 = (a – b)∙(a + b).
Для начала отвлечёмся от математики и попытаемся прочитать левую часть этой формулы.
Теперь давайте взглянем на правую часть. У нас есть произведение двух скобок ― так почему бы не попробовать просто перемножить эти скобки, элемент за элементом?
(a – b)∙(a + b) = a2 + ab – ba – b2 = a2 + ab – ab – b2 = a2 – b2.
Так, постойте. Но это же…как раз и есть левая часть нашего равенства! Неужели, просто раскрыв скобки и приведя подобные слагаемые, мы получили нашу загадочную формулу?
Правильный ответ ― да, так оно и есть! Более того, математически эта формула доказывается именно таким образом. Конечно, это не единственное существующее доказательство* ― но определённо самое простое.
Посмотрим на конкретном примере. Разложим на простые множители x2 – 4:
x2 – 4 = (x – 2)∙(x + 2).
Теперь давайте взглянем на другую формулу, которую можно назвать паронимом нашей первой (пароним ― это похожие по звучанию, но различные по смыслу слова):
(a – b)2 = a2 – 2ab + b2.
Я уже вижу возмущение на ваших лицах ― как же так, они же выглядят совсем по-разному! Тем не менее, давайте попробуем прочитать левую часть. Мы вычитаем одно число из другого, а затем возводим получившееся в квадрат. Ещё раз ― вычитание, а затем возведение в степень. Это определённо квадрат разницы (и снова слово «чисел» опускается). Вот теперь и правда похоже, даже несколько пугающе похоже. Как же их различить? Да очень просто ― по смыслу, так же, как мы только что делали с вами вместе. Главное правильно читать математическую (или русскую запись) и понимать, что идёт за чем ― вначале возведение в квадрат и затем вычитание, или наоборот ― вначале вычитание, а затем возведение в квадрат.
Но вернёмся к нашей формуле. Что такое число в квадрате? Это его произведением на самого себя, то есть:
(a – b)2 = (a – b)∙(a – b).
Как и в первом случае, у нас снова есть произведением двух скобок. Так давайте поступим точно так же и почленно перемножим их:
(a – b)∙(a – b) = a2 – ab – ba + b2 = a2 – ab – ab + b2 = a2 – 2ab + b2.
Вуаля! Снова, как и в предыдущем примере, мы пришли к нужному результату, просто перемножив скобки и приведя подобные слагаемые.
Давайте закрепим успех, использовав эту формулу на конкретном примере. Раскроем скобки (1 – 2xy)2:
(1 – 2xy)2 = 1 – 4xy + 4x2y2.
И ещё одна формула ― на этот раз внешне очень похожая на вторую, но имеющая другой смысл (в русском языке нет подходящего определения для таких слов.
(a + b)2 = a2 + 2ab + b2.
Вспоминаем, что такое число в квадрате, и опять перемножаем скобки:
(a + b)∙(a + b) = a2 + ab + ba + b2 = a2 +
Отлично, вот мы доказали и это выражение! Но как же оно называется? Посмотрим, что у нас есть. Два числа вначале складываются, а потом возводятся в квадрат. Это явно квадрат суммы.
Раскроем скобки и успростим (5 + 3х)2 – 9х2:
(5 + 3х)2 – 9х2 = 25 + 30х + 9х2 – 9х2 = 30х + 25.
Итак, мы с вами успешно разобрались с тремя основными формулами сокращённого умножения, а главное ― поняли, как именно они выводятся. Ещё две формулы (куб разницы и куб суммы, соответственно) ждут вас в домашнем задании, так же как и около десяти примеров для закрепления полученных знаний.
Успехов!
_____________________________________________________________________________ * Некоторые правила сокращённого умножения были известны ещё около 4 тысяч лет тому назад. Их знали вавилоняне, греки и другие народы древности. Правда, доказывались эти формулы не алгебраически, а геометрически (вообще, практически вся математика в то время сводилась к геометрии). Например, для доказательства разницы квадратов рисовались два квадрата (один в другом), один со стороной a, другой ― со стороной b. Тогда a2 – b2 ― это разница площадей квадратов, то есть закрашенная оранжевым часть. (Любопытствующие могут посчитать эту площадь и убедиться, что она равна (a – b)∙(a +b)).
Целые числа Числовые множества Натуральные числа — это числа 1, 2, 3,… Натуральные числа мы используем для счёта, а счёт начинается с единицы. Поэтому ноль не является натуральным числом! Множество натуральных чисел обозначается N. Целые числа — это числа 0, ±1, ±2, ±3,… Натуральные числа являются целыми положительными числами. Множество целых чисел обозначается Z (именно это обозначение мы использовали в тригонометрических уравнениях для записи ответов). Рациональные числа — это всевозможные дроби , где m ϵ Z, n ϵ N. Множество рациональных чисел обозначается Q. Все натуральные числа являются целыми, все целые — рациональными. То есть N Z Q. Делимость Понятие делимости относится к целым числам. Определение. Число a делится на число b ≠ 0, если найдётся число c такое, что a = bc. Иногда вместо слова делится говорят делится нацело. Обозначение a b. Если a делится на b, то число b называется делителем числаa. Например, число 16 имеет пять делителей: это 1, 2, 4, 8 и 16. Признаки делимости: · a делится на 2 ⇔ последняя цифра a есть 0, 2, 4, 6 или 8; · a делится на 5 ⇔ последняя цифра a есть 0 или 5; · a делится на 10 ⇔ последняя цифра a равна 0; · a делится на 3 ⇔ сумма цифр a делится на 3; · a делится на 9 ⇔ сумма цифр a делится на 9. Чётность Определение. Число называется чётным, если оно делится на 2. Число называется нечётным, если оно не делится на 2. Все чётные числа: 0, ±2, ±4, ±6,… Если aчётно, то оно имеет вид a = 2n. Все нечётные числа: ±1, ±3, ±5,… Если aнечётно, то оно имеет вид a = 2n + 1. Деление с остатком Любое число a можно разделить с остатком на любое число b ≠ 0. А именно, найдутся два числа q и r такие, что a = b·q + r, причем 0 ≤ r ≤ │b│. Число q называется частным (иногда, неполным частным), а число r — остатком от деленияaна b. Простые числа Всякое число делится на 1 и на само себя. Если натуральное число a не равно 1 и не имеет других натуральных делителей, кроме 1 иa, то такое число a называетсяпростым. Вот первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19. Число 2 — единственное чётное простое число. Число, не равное 1 и не являющееся простым, называетсясоставным. Всякое число можно разложить на простые множители. Такое разложение единственно с точностью до порядка множителей и называетсяканоническим разложением. Например, 600 = 8 · 25 · 3 = 23 · 52 · 3. Взаимно простые числа Числа называются взаимно простыми, если они не имеют общих делителей кроме 1. Иными словами, числа a и b взаимно просты, если НОД (a, b) = 1, или по-другому дробь несократима. ⇐ Предыдущая6789101112131415 Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Формулы сокращенного умножения » Kupuk.net
Формулы сокращенного умножения (ФСУ) — раздел алгебры, который используется с целью упрощения решения выражений. В этой статье мы поговорим об основных особенностях применения ФСУ, а также дадим вывод этих формул. Довольно часто, причем не самые слабые ученики, при знакомстве с этой темой выносят для себя впечатление о ФСУ, как о чем-то сложном. Однако это не так, и в нашей статье мы это докажем. Ведь по самому названию — формулы сокращенного умножения, можно понять, что математики пытаются облегчить жизнь, сократить усилия и уменьшить время, которое потребуется на ту или иную операцию.
Формулы
Первые упоминания о ФСУ мы встречаем во времена древнегреческих математиков. Так, тождества встречаются в работах Евклида, известного автора работ, посвященных геометрии. В его “Началах» есть практическое обоснование и доказательство одного из тождеств ФСУ. Вот так выглядят все ФСУ:
Так, тождества встречаются в работах Евклида, известного автора работ, посвященных геометрии. В его “Началах» есть практическое обоснование и доказательство одного из тождеств ФСУ. Вот так выглядят все ФСУ:
Рассмотрим несколько примеров:
(a + b)2 = a2 + 2ab + b2
(a — b)2 = a2 — 2ab + b2
Важно! Будьте внимательны при запоминании формул. Рекомендуется выучить всю таблицу наизусть.
Первая формула Возьмем сначала первую формулу. Что такое (a + b)2 ? Это выражение (а+b), умноженное само на себя:
(а+b)(а+b)
Дальше весь вывод состоит, фактически, в простом раскрытии скобок:
(а + b)(а + b)= a2 + аb + аb + b2
Важно! Надо обратить внимание на то, что при раскрытии скобок мы перемножаем b на а (два раза), но записываем и в первом, и во втором случае как аb, так как от перемены мест множителей произведение не меняется.

Приглядевшись к тому , что у нас получилось, мы заметим, что аb встречается два раза. Теперь осуществим задачу, которая называется приведением подобных членов. Напомним, что подобные члены — это переменные, которые встречаются в одном и том же выражении несколько раз:
a2 + ab + ab + b2 = a2 + 2ab + b2
Первая формула выведена. Теперь вторая:
(a — b)2=(a — b)(a — b)
Также, как и в первый раз, мы раскрываем скобки:
(a — b)(a — b)=a2 — ab — ab + b2=a2 — 2ab + b2
Запомнить очень просто, как оказывается на практике. При раскрытии скобок видно, что отличие первой от второй формулы в одном знаке, перед 2аb:
(a + b)(a — b)=a2 + ab — ab — b2=a2 — b2
Выражения ab и -ab сокращаются и остается тождество, которое у нас получилось. По такому же принципу решаются и формулы для кубов.
Использование ФСУ
А сейчас, используя ФСУ (простейшие из них), мы выведем несколько широко известных и довольно часто применяемых неравенств:
a2 + b2 ≥ 2ab
Это неравенство получается из формулы (a — b)2 = a2 — 2ab + b2 Так как квадрат любого выражения НЕ может быть меньше нуля, то это выражение должно быть больше или равно 0:
(a — b)2 = a2 — 2ab + b2 ≥ 0
В неравенствах, как и в уравнениях мы можем прибавить к их обеим частям одно и то же число, и неравенство от этого не потеряет свой смысл. Например, если к верному неравенству 5 больше 3 прибавить число 10, то 5 больше или равно 3 превратится в 15 больше или равно 13, то есть останется верным. Так и в случае нашего доказательства можно прибавить к обеим частям 2аb, другими словами, перенести 2аb из левой части в правую с переменой знака. В левой части 2аb исчезнет, останется a2 + b2, в правой — к нулю прибавится 2аb и останется неравенство a2 + b2 ≥ 2ab При кажущейся простоте и очевидности вывода это неравенство широко известно и очень часто используется. А сейчас выведем еще одно неравенство, которое является прямым следствием предыдущего:
Например, если к верному неравенству 5 больше 3 прибавить число 10, то 5 больше или равно 3 превратится в 15 больше или равно 13, то есть останется верным. Так и в случае нашего доказательства можно прибавить к обеим частям 2аb, другими словами, перенести 2аb из левой части в правую с переменой знака. В левой части 2аb исчезнет, останется a2 + b2, в правой — к нулю прибавится 2аb и останется неравенство a2 + b2 ≥ 2ab При кажущейся простоте и очевидности вывода это неравенство широко известно и очень часто используется. А сейчас выведем еще одно неравенство, которое является прямым следствием предыдущего:
a2 + b2 + c2 ≥ ab + ac + bc
Это можно доказать следующим способом:
a2 + b2 ≥ 2ab
a2 + c2 ≥ 2ac
b2 + c2 ≥ 2bc
Сложение
Эти три неравенства мы можем сложить. Если сложить между собой левую и правую часть неравенства, то знак между ними останется прежним:
a2 + b2 ≥ 2ab
a2 + c2 ≥ 2ac
b2 + c2 ≥ 2bc
2a2 + 2b2 + 2c2 ≥ 2ab + 2ac + 2bc
Сокращение
Также мы имеем право сокращать неравенства, то есть делить обе его части на одно и то же положительное число, от этого оно не перестает быть справедливым:
a2 + b2 + c2 ≥ ab + ac + bc
В нашем неравенстве сокращается число 2, и остается неравенство, которое требовалось доказать.
Вывод новых алгебраических соотношений
Есть также еще одно, менее известное. Его нам кажется уместным здесь упомянуть как образец применения ФСУ для вывода новых алгебраических соотношений, а именно
a + b ≥ 1 ⇒ a4 + b4 ≥ 1/8
Довольно неочевидное следствие, особенно для неподготовленного человека. Возведем в квадрат обе части неравенства (при положительных значениях обеих частей мы имеем право это делать):
a2 + 2ab + b2 ≥ 1
a2 — 2ab + b2 ≥ 0
Складываем эти два неравенства почленно:
2a2 + 2b2 ≥ 1
И разделим обе части на 2:
a2+b2 ≥ 1/2
Возведем обе части в квадрат:
a4 + 2a2b2 + b4 ≥ 1/4
a4 — 2a2b2 + b4 ≥ 0
2a4 + 2b4 ≥ 1/4
Разделим обе части на 2 и получаем искомое неравенство:
a4 + b4 ≥ 1/8
ФСУ и бином Ньютона
Формула квадрата разности является частным случаем формулы бинома Ньютона. Исходная ситуация, в которой нам приходится применять бином Ньютона, и собственно формула, которая позволяет нам раскрывать n-ное количество скобок. То есть, в общем случае:
То есть, в общем случае:
(а+b)n
Эта формула дает нам ответ на вопрос, чему равно произведение n-ного количества скобок (n — натуральная степень). Владея этим аппаратом, вы можете расписать выражение в виде некоторого количества слагаемых, которое получается в результате перемножения скобок такого типа n раз на себя.
Примеры решения
Теперь приведем несколько примеров на использование формул сокращенного умножения:
Итак, в этой статье мы ознакомились с историей формул сокращенного умножения, их применением, вывели основные тождества ФСУ. Этот важный аспект алгебры играет важную роль в преобразовании выражений, да и попросту экономит ваше время. Как запомнить все формулы и правильно применять другие варианты ФСУ на практике, смотрите в этом видео.
Формулы сокращённого умножения — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Формулы сокращённого умножения.
Проект подготовили ученики 8 “Б” класса:Францкевич Михаил и Иващенко Егор.
Преподаватель:Ильина Наталья
Виниаминовна.
2. Цель:
2Цель:
Рассмотреть формулы сокращённого умножения
для их применения при решении сложных задач.
3. Задачи:
31.
Описать принципы умножения многочленов при помощи
формул сокращённого умножения.
2.
Изучить формулы сокращённого умножения при
увеличении количества слагаемых.
3.
Рассмотреть построение треугольника Паскаля и его
применение для определения коэффицентов многочлена.

4.
Проанализировать формулу бинома Ньютона.
5.
Провести исследования скорости вычислений без
применения и с применением формул.
6.
Познакомить с формулами одноклассников.
4. Введение:
4В современной жизни каждому человеку часто приходится выполнять
огромное количество расчётов и вычислений. Поэтому цель нашей работы – показать
лёгкие, быстрые и точные методы вычислений. Основополагающим элементом
вычислительной культуры являются сознательные и прочные вычислительные
навыки.
Владение вычислительными умениями и навыками имеет большое значение
для усвоения изучаемого материала. Однако, в последнее время уровень
вычислительных навыков, преобразований выражений имеет тенденцию к
снижению, все часто используют калькулятор и компьютер, что отрицательно
сказывается на уровне математических знаний.
Поэтому данный материал полезен для изучения.
5. Принципы умножения многочленов при помощи формул сокращённого умножения:
5Принципы умножения многочленов при
помощи формул сокращённого умножения:
Для упрощения выражений, разложения многочленов на множители, приведения
многочленов к стандартному виду используются формулы сокращенного умножения.

Формулы сокращенного умножения нужно знать наизусть.
1. Квадрат суммы двух выражений
(a + b)2 = a2 + 2ab + b2
2. Квадрат разности двух выражений
(a — b)2 = a2 — 2ab + b2
3. Разность квадратов двух выражений a2 — b2 = (a — b) (a + b)
4. Куб суммы двух выражений
(a + b)3 = a3 + 3a2b + 3ab2 + b3
5. Куб разности двух выражений
(a — b)3 = a3 — 3a2b + 3ab2 — b3
6. Сумма кубов двух выражений
a3 + b3 = (a + b) (a2 — ab + b2)
7. Разность кубов двух выражений
a3 — b3 = (a — b) (a2 + ab + b2)
Название «Формулы сокращенного умножения» совсем не случайно.
6
Возьмем самую простую первую формулу квадрат суммы (a + b)2 и попробуем
последовательно возвести сумму в скобках в квадрат, то есть, умножить (a + b) само на
себя:
(a + b) * (a + b) = a2 +аb +bа +b2
приводим подобные слагаемые:
a2 +аb +bа +b2 = a2 + 2аb + b2
Таким образом выводятся все формулы сокращенного умножения. Можно выводить их
каждый раз самостоятельно, а можно не тратить на это время и быстро посчитать
необходимый пример, зная конечное значение формул.

Конечно, квадрат суммы посчитать вручную не так сложно, но что насчет куба суммы
или куба разности?
7
Куб суммы означает, что необходимо (a+b) само умножить на себя три раза: (a+b) *
(a+b) * (a+b) = a3 +аb2 +bа2 +b3……. И т.д.
И это мы расписали перемножение только первой скобки, а тоже самое необходимо
сделать со второй и с третьей… Согласись, запутаться очень легко, а, как правило, от
того, как ты посчитаешь это простое действие, зависит ответ всего примера.
Таким образом, формулы сокращенного умножения позволяют сократить трудоемкое
перемножение членов друг на друга и получить быстрый результат.
Как они могут пригодится просто так, в жизни?
Это очень просто! Сколько будет 103 2 ? Не нужно кидаться перемножать 103 на 103 в
столбик, и уж тем более не стоит набирать цифры на калькуляторе. Просто представь
103, как сумму 100 и 3 и возведи ее в квадрат:
1032=(100+3)2=1002+2⋅100⋅3+32=10000+600+9=10609
С помощью формул квадрат суммы и квадрат разности мы можем легко находить
квадраты больших чисел, не используя калькулятор и не считая в столбик.
 Необходимо
Необходимопросто представить число в виде суммы (или разности) чисел, квадрат которых мы
хорошо знаем.
8. Формулы сокращённого умножения при увеличении количества слагаемых:
8Формулы сокращённого умножения при
увеличении количества слагаемых:
Полезной бывает формула возведения в квадрат суммы трех, четырех и большего количества
слагаемых вида: (a1+a2+…+an)2= a12+a22+…+an−12+an2+2·a1·a2+2·a1·a3+2·a1·a4+…+2·a1·an−1+2·a1·an+
+2·a2·a3+2·a2·a4+…+2·a2·an−1 +2·a2·an+…+ 2·a n−1·an.
Она читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых
и удвоенных произведений всех возможных пар этих слагаемых (с учетом правила знаков).
Для примера возведем в квадрат с использованием этой формулы сумму трех слагаемых a, b и c,
имеем (a+b+c)2=a2+b2+c2+2·a·b+2·a·c+2·b·c.
Выведем еще несколько формул:
1. Квадрат разности трёх слагаемых (a — b + c)2 = a2+b2+c2 -2ab+2ac-2bc.
2. Квадрат разности трёх слагаемых (a + b — c)2 = a2+b2+c2+2ab-2ac-2bc.

3. Квадрат разности трёх слагаемых (a — b — c)2 = a2+b2+c2 -2ab-2ac+2bc.
4. Квадрат суммы четырёх слагаемых (a + b + c + d)2 = a2 + b2 + c2 + d2 + 2ab + 2ac + 2ad + 2bc + 2bd
+ 2cd.
9. Бином Ньютона:
9Бином Ньютона — формула разложения произвольной натуральной степени двучлена (а+b)n в
многочлен. Бином (лат. bis — дважды, nomen — имя) или двучлен — частный случай полинома
(многочлена), состоящего из двух слагаемых мономов (одночленов).
Где m – порядковый номер слагаемого в многочлене.
Факториал – произведение натуральных чисел от 1 до n, то есть 1*2*3*…*n – обозначается n!, например,
4!=1*2*3*4=24
10. Свойства Бинома Ньютона
1011
12. Треугольник Паскаля:
12Каждый из нас знает наизусть формулы «квадрата суммы» (а+b)2 и «куба суммы»
(а+b)3, но при увеличении показателя степени с определением коэффициентов при
членах многочлена начинаются трудности.
Видимо, для того чтобы облегчить этот труд, великий французский математик и физик
Блез Паскаль триста пятьдесят лет назад придумал специальный инструмент—
«треугольник Паскаля».
 В верхней строчке треугольника располагается одинокая
В верхней строчке треугольника располагается одинокаяединица. В остальных строках каждое число является суммой двух своих соседей
этажом выше — слева и справа. Если какой-то из соседей отсутствует, он считается
равным нулю. Треугольник бесконечно простирается вниз; здесь приведено лишь
одиннадцать верхних строчек:
13
Единица соответствует выражению (a + b)0, поскольку любое число, возведённое в
нулевую степень, даёт единицу. Достраивая треугольник, ниже пишем ещё по единице.
Это коэффициенты разложения того же двучлена, возведённого в первую степень:
(a+b)1=a+b.
Идём дальше. Стороны треугольника образуют единицы, а между ними — сумма двух
единичек, находящихся сверху, то есть 2. Это и есть коэффициенты трёхчлена «квадрат
суммы»: a2+2ab+b2.
Следующий ряд, как и предыдущий, начинается и заканчивается единицами, а между
ними — суммы цифр, находящихся сверху: 1, 3, 3, 1. Мы получили коэффициенты
разложения «куба суммы». Ряд коэффициентов двучлена четвёртой степени составят 1, 4,
6, 4, 1 и так далее.

Для примера с помощью треугольника Паскаля разложим в многочлен сумму двучленов в
шестой степени: (a + b)6=a6+6a5b + 15a4b2+20a3b3 + 15a2b4+6ab5+b6.
Числа в n-ой строке треугольника являются биномиальными коэффициентами, то есть
коэффициентами в разложении n-ой степени бинома Ньютона. Некоторые историки науки
приписывают Блезу Паскалю авторство не только треугольника, позволяющего находить
биномиальные коэффициенты, но и самой формулы бинома. Они считают, что Паскаль
вывел её несколько раньше Ньютона, а тот лишь обобщил формулу для разных
показателей степеней.
14. Исследования скорости вычислений без применения и с применением формул.
14Исследования скорости вычислений без
применения и с применением формул.
Мы провели исследование в нашем классе. Целью нашего исследования было узнать насколько
увеличивает скорость вычислений применение формул сокращённого умножения
Класс был поделен на две группы. Первая группа решала задание без применения формул
сокращённого умножения, а вторая группа решала с помощью формул.

Для эксперимента двум группам были предложены следующие примеры.
(y+2+3+x)2
(2+6+3+5)2
(x+5) 3
1032
(9+3+2)2
(1+1)7
(2+3) 4
972
С заданием первая группа справилась за 10 минут, а вторая группа благодаря формулам
сокращенного умножения справилась всего за 5 минут.
15. Заключение
15В итоге разработки нашего проекта мы научились, применяя формулы
сокращённого умножения, вычислять достаточно сложные и громоздкие выражения
без применения вычислительных средств.
Изучили как можно, зная формулы, возводить в квадрат полиномы с любым
количеством слагаемых.
Научились, применяя формулу бинома Ньютона и, находя по треугольнику
Паскаля биномиальные коэффициенты, вычислять биномы любой степени.
Проверили и установили значительное различие во времени вычислений без
применения и с применением формул сокращенного умножения (особенно очевидна
разница при увеличении показателя степени, в которую возводиться выражение).

И сделали вывод, что формулы сокращённого умножения – неисчерпаемый
источник различных математических радостей!
16
Спасибо за внимание!
English Русский Правила
Навигация по странице: |
|
Презентация по математике на тему Формулы сокращенного умножения доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по математике на тему Формулы сокращенного умножения, предмет презентации: Алгебра. Этот материал в формате pptx (PowerPoint) содержит 18 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 18 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Формулы сокращенного умножения
(разность квадратов, квадрат суммы и квадрат разности )
УЧИТЕЛЬ МАТЕМАТИКИ
МОУ
« ПАРТЕНИТСКАЯ ШКОЛА»
Г. АЛУШТЫ
ГЛАДЖИКУРКА ВИТА
ПАРФИРЬЕВНА
(7-b)(7+b)
(k-t)(k+t)
4m2-25
16-x2
(4-a)(4-a) (5+a)(5+a)
(3x+y)(3x+y)
(c-6)(c-6) (k-t)(k-t)
(c+z)(c+z)
Вспомните формулу разности квадратов
Можно применить формулу разности
квадратов
Нельзя применить формулу разности
квадратов
Устный счет
(a-b)(a+b)=a2-b2
или
a2-b2= (a-b)(a+b)
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы
Формула разности квадратов
Устный счет
Нова я
тема
(c+9)(c-9) 9) (2-3d3) (2+3d3)
(7-b)(7+b) 10) ( 12z2-7a4)(12z2-7a4)
(3+2x)(2x-3)
(4y2-1)(4y2-1)
(10a3+3)(10a3-3)
(1-3k)(1+3k)
(8b+5)(8b-5)
(11c+7m)(7m-11c)
Выполни умножение ,применяя формулу разности квадратов
C2-81
49-b2
4×2-9
16y4-1
100a6-9
1-9k2
64b2-25
49c2-121m2
4-9d6
144z4-49a8
Проверь себя
Оцени себя
«0» ошибок –
«1-2» ошибок –
«3-4» ошибок –
больше 5 ошибок —
(7-b)(7+b)
(k-t)(k+t)
4m2-25
16-x2
(4-a)(4-a) (5+a)(5+a)
(3x+y)(3x+y)
(c-6)(c-6) (k-t)(k-t)
(c+z)(c+z)
Можно применить формулу разности
квадратов
Нельзя применить формулу разности
квадратов
На какие две группы можно разделить данные выражения?
Рассмотрим выражения второй группы
(c-6)(c-6)
(k-t)(k-t)
(4-a)(4-a)
(a+5)(a+5)
(3x+y)(3x+y)
(c+z)(c+z)
Можно ли в этих выражениях выполнить умножение быстрым способом?
Существует ли формула ?
На эти вопросы мы попробуем сегодня ответить в конце урока?
Проблема:
«Существует ли формула?
Если да, то какая?»
(a+5)2=
(3x+y)2=
(c+z)2=
Как можно записать эти же выражения по-другому (более компактно)?
Возведем сумму в квадрат, перемножая скобку на скобку старым способом.
= a2+5a+5a+25=
= 9×2+3xy+3xy+y2=
= c2+cz+cz+z2=
a2+10a+25
9×2+6xy+y2
c2+2cz+z2
(a+5)(a+5)
(3x+y)(3x+y)
(c+z)(c+z)
2×5a
2×3xy
2×cz
Правило умножения
многочлена нa многочлен
(a+b)(x+y)=ax+ay+bx+by
Формула квадрата
суммы
( a + b ) 2 = a 2 + 2 a b + b 2
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
Проблема:
«Существует ли формула? Если да, то какая?
Формула квадрата суммы
(a+b)2=a2+2ab+b2
Как быстро выполнить умножение второй группы выражений?
Можно ли использовать формулу квадрата суммы?
(с-6)(с-6)
(4-a)(4-a)
(k-t)(k-t)
(с-6)2=
(k-t)2=
(4-a)2=
Как можно записать эти же выражения по-другому (более компактно)?
Возведем разность в квадрат, перемножая скобку на скобку старым способом.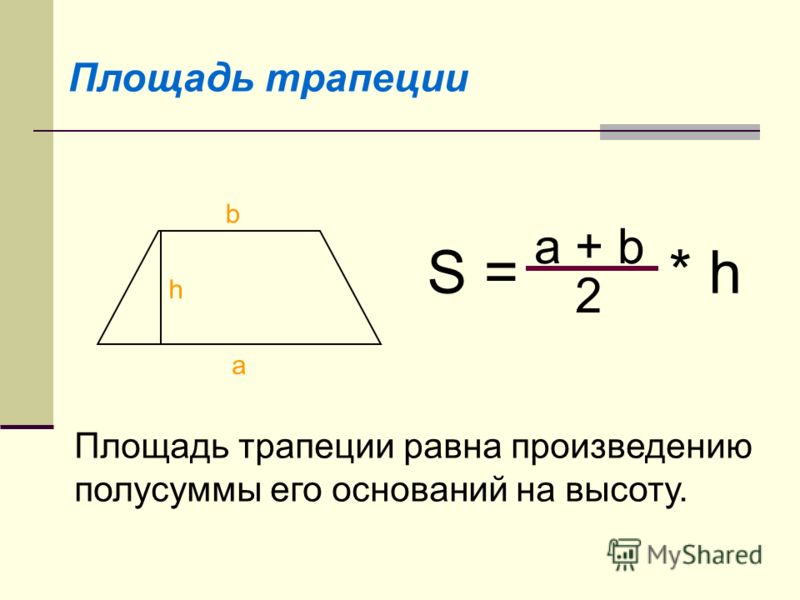
= c2-6c-6c+36=
= k2-kt-kt+t2=
= 16-4a-4a+a2=
C2-12c+36
K2-2kt+t2
16-8a+a2
(c-6)(c-6)
(k-t)(k-t)
(4-a)(4-a)
2×6c
2×kt
2×4a
Формула квадрата разности
(a-b)2=a2-2ab+b2
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное
произведение первого числа на второе плюс квадрат второго числа.
Проблема:
«Существует ли формула? Если да, то какая?
Формула квадрата суммы формула квадрата разности
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
Сравни
Формула квадрата суммы формула квадрата разности
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
Формула разности квадратов
(a-b)(a+b)=a2-b2
Выполни умножение ,применяя формулы:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
(3a+1)2
(8a-3)2
(a+2b)2
(1+3a)2
(4a-3)2
( c-4 )2
( m +d )2
(5a-6b)2
(4t+3a)2
(a-1)2
(4z-8n)2
(3a+2d)2
(3s-8n)2
(1-4f)2
(6-5c)2
(1-3ab)2
(5xy+1)2
(3ab-3t)2
(xy-4m)2
(2cd-7z)2
(1+5xyz)2
(2a+3bc)2
(4a-3kn)2
(3a-4t)2
(4a-7c)2
(9x+5z)2
(1-3a)2
(4xy+1)2
(5s+2p)2
(1-9a)2
4a2 +4ab+b2
4a2- 4ab+b2
9a2 — 60ab+100b2
4×2 -20xb+25b2
1- 6b+9b2
16a2 +8a+1
b2 -2a b +a2
a2b 2 +2ab+1
1- 16c +64c2
1+10a +25a2
(3a4 +2b 8 )2
(4×2 -3z 4 )2
(1- 5×2 y 4 z6 )2
(2a 4 +3k2 )2
(9a -2d 2 )2
(4a4 b +1)2
(2m2 n -3)4
(6a 2 b +c 2 )4
(2x 2 +5y6 z3 )4
(a 3 b5 – c2 d )3
25 x2 -30x +9
81b2 -36b +4
9 y 2+24y +16
49 z2 – 28mz+4m2
100a2 +80az +16z2
1 – 6d +9 d2
121p4 + 44p 2t+4t2
169 – 78a2 +9a4
4b9 -12b3 c2 +9c4
1+ 20ab2 +100a2b4
Выполни умножение ,применяя формулы:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
Скачать презентацию
 ru?
ru?Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Что такое формула a2 b2 c2? – Reviews Wiki
Теорема Пифагора описывает отношения между тремя сторонами прямоугольного треугольника. В любом прямоугольном треугольнике сумма площадей квадратов, образованных катетами треугольника, равна площади квадрата, образованного гипотенузой: a2 + b2 = c2 .
Теорема Пифагора только для прямоугольных треугольников? Теорема Пифагора работает только для прямоугольных треугольников , поэтому вы можете использовать ее, чтобы проверить, есть ли у треугольника прямой угол или нет.
Дополнительно Является ли алгебра теоремой Пифагора? Теорема Пифагора очень важна для математики . Вы, вероятно, впервые узнаете об этом в алгебре, но вы будете буквально использовать это в алгебре, геометрии, тригонометрии, предварительном исчислении, исчислении и не только!
Является ли теорема Пифагора тригонометрией? Тригонометрическое тождество Пифагора, также называемое просто тождеством Пифагора, представляет собой тождество, выражающее теорему Пифагора в терминах тригонометрических функций. Наряду с формулой суммы углов это одно из основных соотношений между функциями синуса и косинуса.
Как найти теорему Пифагора, используя только гипотенузу?
Как найти b2 в теореме Пифагора? Длина стороны b равна квадратному корню из квадрата гипотенузы минус квадрат стороны a .
Каков вывод теоремы Пифагора?
Теорема Пифагора утверждает, что « В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон» . Стороны этого треугольника были названы перпендикуляром, основанием и гипотенузой. Здесь гипотенуза является самой длинной стороной, так как она противоположна углу 90°.
Также Когда нельзя использовать теорему Пифагора? Это прямоугольный треугольник; , когда вы суммируете квадраты длин сторон , вы получаете квадрат длины гипотенузы. Неправильно. Это не прямоугольный треугольник, поэтому вы не можете использовать теорему Пифагора, чтобы найти r.
Является ли теорема Пифагора предалгеброй?
Теорема Пифагора (предалгебра, прямоугольные треугольники и алгебра) – Mathplanet.
Пришел ли Пифагор в Индию? Что еще менее известно, так это то, что Пифагора посетили Индию . … Находясь в Индии, кажется, что Пифагор находился под сильным влиянием джайнской философии и стал вегетарианцем. К сожалению, эти факты вообще не упоминаются в большинстве школ при преподавании предмета.
К сожалению, эти факты вообще не упоминаются в большинстве школ при преподавании предмета.
Почему теорема Пифагора не является законом?
Почему теорема Пифагора не является законом? Потому что его взлом не должен быть уголовным преступлением . Если бы теорема Пифагора была законом, вы бы не смогли ее нарушить, но она верна не для всех геометрий, так что вы можете. На самом деле это верно только в евклидовой геометрии (в двух или более измерениях).
Какие 3 пифагорейские тождества?
Тождества Пифагора выводятся из теоремы Пифагора и описывают соотношение между синусом и косинусом на единичной окружности. Три тождества: cos2t+sin2t=1 t + sin 2 , 1+tan2t=sec2t 1 + tan 2 t = sec 2 и 1+cot2t=csc2t 1 + кроватка 2 t = csc 2 .
Как пишется косеканс? Косекан ( csc ) – Тригонометрическая функция
В прямоугольном треугольнике косеканс угла равен длине гипотенузы, деленной на длину противоположной стороны. В формуле это сокращается до просто «csc».
В формуле это сокращается до просто «csc».
Как найти a и b прямоугольного треугольника?
Даны две стороны
- если сторона a отсутствует, то преобразовать уравнение к виду, когда a находится на одной стороне, и извлечь квадратный корень: a = √(c² – b²)
- если ветвь b неизвестна, то. b = √(c² – a²)
- для гипотенузы c отсутствует формула. c = √(a² + b²)
Как найти A и B, если у вас есть C?
Кто является отцом теоремы Пифагора? Пифагор Самосский был известным греческим математиком и философом (ок. 570 – ок. 495 до н.э.). Он наиболее известен доказательством важной теоремы Пифагора о прямоугольных треугольниках.
С какими двумя типами ситуаций вы можете столкнуться при решении с помощью теоремы Пифагора?
Упражнение 3: Использование формулы
При использовании теоремы Пифагора для нахождения третьей стороны прямоугольного треугольника вы столкнетесь с двумя ситуациями: нахождение гипотенузы и нахождение катета.
Как вы используете теорему Пифагора для решения задачи? Используя теорему Пифагора, найдите длину гипотенузы.
…
пример.
| Шаг 1. Прочтите задачу. | |
|---|---|
| Шаг 5. Решить уравнение. | 9+16=c2 25=c2 √25=c2 5=c |
| Шаг 6.Проверить: | 32+42=52 9+16?=25 25 25+25✓ |
| . Ответить на вопрос. | Длина гипотенузы равна 5 . |
Как найти Пифагора с помощью гипотенузы?
Формула гипотенузы просто берет теорему Пифагора и вычисляет гипотенузу c . Находя гипотенузу, мы просто берем квадратный корень из обеих частей уравнения a² + b² = c² и находим c . При этом получаем с = √(а² + b²) .
При этом получаем с = √(а² + b²) .
КВАДРАТ A МИНУС B КВАДРАТ ( A2 – B2 ) – Уравнение исследования уравнение. Формулу (a+b)(a-b) можно использовать для быстрого получения формулы a
2 – b 2 . В следующих частях давайте изучим их с помощью нескольких случаев, которые были решены. Формула a 2 – b 2 также известна как «формула разности квадратов». Квадрат SUBTRACTED b используется для вычисления несоответствия квадратов, а не только для вычисления самих квадратов. Математическое алгебраическое уравнение (a+b) (a-b) было доказано с использованием двух различных методов.Formula:
a 2 – b 2 =(a – b) (a + b)
Table of Contents
Algebraic Approach
The algebraic expression a 2 – b 2 обозначает разницу между двумя квадратными целыми числами. Его можно рассматривать как объединение двух исключительных биномов, a+b и ab. Математическая факторизация позволяет определить дифференциал значения факторизации квадратов с помощью алгебраических уравнений.
Математическая факторизация позволяет определить дифференциал значения факторизации квадратов с помощью алгебраических уравнений.
Метод 1:
Давайте рассмотрим доказательство формулы a квадрат минус b квадрат. Чтобы продемонстрировать, что LHS = RHS, мы должны установить, что a 2 – b 2 = (a – b) (a + b). Попробуем разобраться в уравнении:
a квадрат – b квадрат равно (a – b) + (a + b)
Результат умножения (a – b) и (a + b) равен =a(a+ б).
Другими словами, -b(a + b) = a 2 + ab – ba – b2 = a 2 + 0 + b2 = a 2 – b 2
В результате Подтверждено a 2 – b 2 = (a – b) (a +b).
A SQUARE MINUS B SQUAREГеометрический подход:
Тождество a 2 -b 2 может быть выражено как масштабированное произведение биномов a+b и a-b, чтобы показать разницу между двумя справедливыми стоимостями. Площади геометрических фигур можно использовать для математического определения формы факторизации уравнения а 2 -b 2 .
вычитание площади квадрата:
1. Предположим, квадрат со сторонами, каждая из которых имеет длину в одну единицу. Следовательно, 2 — это площадь квадрата.
2. В каждом углу маленького квадрата сделайте маленький квадрат со стороной a из b единиц. Следовательно, b 2 — это площадь маленького квадрата.
3. Квадрат площадью b 2 следует вычесть из площади корта a 2 . Он устанавливает другую геометрическую форму, площадь которой равна 2 – б 2 .
Разделить площадь измененной фигуры
Начните делить только что уменьшенную геометрическую форму на два отдельных прямоугольника, длина одного из которых равна одной единице.
Относительно верхнего прямоугольника: Этот прямоугольник имеет ширину и длину в геометрических единицах.
Точно так же изучите нижний прямоугольник. Этот прямоугольник имеет ширину, равную единицам, и длину, равную единицам.
Квадратное отличие с помощью метода факторинга
Длина нижнего прямоугольника также равна a-b, как и ширина верхнего прямоугольника, которая равна a-b. Ширина обоих прямоугольников совпадает, если нижний прямоугольник повернут на 90 градусов, что позволяет объединить их в один прямоугольник.
Ширина обоих прямоугольников совпадает, если нижний прямоугольник повернут на 90 градусов, что позволяет объединить их в один прямоугольник.
Разделите два прямоугольника.
Объедините два прямоугольника, повернув нижний прямоугольник на 90 градусов. Был создан еще один прямоугольник.
Полученные длина и ширина прямоугольника умножаются на b и делятся на a. В результате (a+b)(a-b) площадь этого прямоугольника. 92 = (a+b)(a-b)
В геометрии установлено, что произведение двучленов (a+b) и (a-b) равно квадрату, вычтенному из квадрата b.
КВАДРАТ A МИНУС B КВАДРАТДоказательство уравнения a 2 –b 2 :
Аргумент, объясняющий, почему (a + b) равно значению a 2 – b 2 (a – b) . Давайте подумаем об изображении выше. Рассмотрим два квадрата со сторонами a и b соответственно. Это можно представить как произведение площадей двух прямоугольников. На одной стороне прямоугольника находится длина в одну единицу и ширина в (a – b) единиц. С другой стороны есть длина (a – b) и ширина b единиц. Чтобы получить последовательные значения, суммируйте площади двух прямоугольников. Соответствующие площади двух прямоугольников равны (a – b) a = a (a – b) и (a – b) b = b. (а – б). Фактическое полученное результирующее выражение, т. е. a(a + b) + b(a – b) = (a + b), представляет собой сумму площадей прямоугольников (a – b). Результат еще одной перестановки различных квадратов и прямоугольников: (a+b)(ab)=a 2 б 2 .
С другой стороны есть длина (a – b) и ширина b единиц. Чтобы получить последовательные значения, суммируйте площади двух прямоугольников. Соответствующие площади двух прямоугольников равны (a – b) a = a (a – b) и (a – b) b = b. (а – б). Фактическое полученное результирующее выражение, т. е. a(a + b) + b(a – b) = (a + b), представляет собой сумму площадей прямоугольников (a – b). Результат еще одной перестановки различных квадратов и прямоугольников: (a+b)(ab)=a 2 б 2 .
Объясните шаги по использованию формулы a 2 – b 2 .
При применении формулы a 2 – b 2 выполняются следующие шаги.
1. Во-первых, посмотрите на структуру цифр, чтобы увидеть, имеют ли они степень 2 или нет.
2. Уравнение для a 2 – b 2 записывается как a 2 – b 2 = (a – b) (a + b).
3. Упростить a 2 – b 2 путем замены значений a и b.
Примеры формулы A 2 -B 2
A квадрат минус B (A2 -B2). Вопрос и ответы с использованием A 2 -B 2 . Определение A 2 -B 2 . Определение A 2 -B 2 . результат 1062 – 62.Решение: Область поиска: 1002 – 62.
Предположим, что an равно 100, а b равно 6.
Мы подставим их в a 2 – b 2 расчет вместо.
(а – б) (а + б) = а 2 – б 2
1062 – 62 = (106 + 6) (106 – 6)
= (100) (112)
2 =
5 11200 Факторизация формулы 25×2 – 64. Решение: 25×2 – 64 должно быть учтено.
Приведенное выше выражение можно записать как
25×2 – 64 = (5x)2 – 82
В формулу для a 2 – b 2 вместо этого мы подставим a = 5x и b = 8.
(a – b) (a + b) = a 2 – b 2
(5x)2 – 82 = (5x + 8)(5x – 8)
КВАДРАТ A МИНУС КВАДРАТ B Применить a 2 – b 2 формула для уменьшения 102 – 52.
Ответ: найти 102 – 52.
Предположим, что a равно 10, а b равно 5.
Применяя уравнение (a – b ) = (а – б) (а + б)
102-52 = (10 – 5) (10 + 5) равно 10(10 +5) – 5(10 + 5) = 10(15) – 5(15) \s= 150-75 = 75
102 минус 52 равно 75.
КВАДРАТ A МИНУС КВАДРАТ B Решите 3a 2 – 2b 2 в качестве примера. Решение: оно продолжается как:
Предоставленное уравнение 3a 2 – 2b 2 (т.
Если a = 3a и b = 2b, то
Применение значений параметров a и b к тождеству, т. е. a 2 – b 2 = (a + b) (a – b), получаем:
3a 2 – 2b 2 = (3a + 2b) (3a – 2b)
Следовательно, 3a 2 – 2b 2 = 3a + 2b (3a – 2b)
Решите (6m + 9n) в примере 2. (6m – 9n) Решение: Это продолжается как:
6m + 9n) (6m – 9n) обозначает тождественную треть, или a 2 – b 2 .
a = 6 м, тогда как b = 9 n
Применяя значения переменных a и b к уравнению, т. е. a 2 – b 2 = (a + b) (a – b), получаем:
(6m + 9n) (6m – 9n) = (6m)2 – (9n) 2
Получаем = 36m2 – 81n2 путем расширения экспоненциальных выражений на LHS.
Получается, что (6м + 9н) (6м – 9н) = 36м2 – 81н2.
Что такое формула квадрата минус квадрат B Формула a 2 – b 2 есть (a+b)(a-b).
Подробнее: Как рассчитать SGPA на основе онлайн-оценки — уравнение исследования 92?
Как решить a2 b2 c2?
Формула A2 + B2 = C2 , это так же просто, как одна сторона треугольника в квадрате плюс другая сторона треугольника в квадрате равна гипотенузе в квадрате.
Как найти a2 и b2, имея только c2?
a2 + 2ab + b2 = c2 + 2ab Каждая сторона этого уравнения представляет собой площадь большого квадрата. a2 + b2 = c2 Вычесть 2ab с обеих сторон . Последнее уравнение, a2 + b2 = c2, называется теоремой Пифагора. Мы говорим: «Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы».
Последнее уравнение, a2 + b2 = c2, называется теоремой Пифагора. Мы говорим: «Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы».
Кроме того, какова формула a2 b2 c2?
a 2 + b 2 + c 2 формула читается как квадрат плюс b квадрат плюс c квадрат. Его расширение выражается как 2 + b 2 + c 2 = (a + b + c) 2 – 2(ab + bc + ca) .
Во-вторых, работает ли теорема Пифагора для всех треугольников? Теорема Пифагора работает только для прямоугольных треугольников , поэтому вы можете использовать ее, чтобы проверить, есть ли у треугольника прямой угол или нет.
Какова формула A² B²?
(A²-B²) = (A-B)² + 2AB .
16 Похожие вопросы Ответы Найдено
Содержание
Теорема Пифагора только для прямоугольных треугольников? Гипотенуза — самая длинная сторона, и она всегда лежит против прямого угла. Теорема Пифагора работает только для прямоугольных треугольников , поэтому вы можете использовать ее, чтобы проверить, есть ли у треугольника прямой угол или нет. В треугольнике выше, если.
Теорема Пифагора работает только для прямоугольных треугольников , поэтому вы можете использовать ее, чтобы проверить, есть ли у треугольника прямой угол или нет. В треугольнике выше, если.
Что означает буква С в формуле a2 b2 c2? Теорема Пифагора — это формула, определяющая отношение между сторонами прямоугольного треугольника. Теорема Пифагора применима только к ПРАВИЛЬНЫМ треугольникам. … Сторона «с» называется , гипотенуза . Стороны, примыкающие к прямому углу, называются «а» и «б».
Какова формула a³ B³? a³-b³= (a-b)(a²+ab+ b²) — это формула. Выражаясь словами, разность кубов двух величин есть произведение разности двух величин на «несовершенный квадрат суммы».
Что такое формула 3 b 3? Формула a 3 – b 3 также известна как одно из важных алгебраических тождеств. Читается как куб минус b куб. Его формула a 3 – b 3 выражается как
Как называется 2 B 2 C 2? а 2 + б 2 = в 2 . Это известно как уравнение Пифагора , названное в честь древнегреческого мыслителя Пифагора. Это соотношение полезно, потому что, если известны две стороны прямоугольного треугольника, можно использовать теорему Пифагора для определения длины третьей стороны.
Это известно как уравнение Пифагора , названное в честь древнегреческого мыслителя Пифагора. Это соотношение полезно, потому что, если известны две стороны прямоугольного треугольника, можно использовать теорему Пифагора для определения длины третьей стороны.
Применяется ли теорема Пифагора к непрямоугольным треугольникам? Итак, теорема Пифагора работает для любого треугольника. Когда мы начинаем с непрямоугольного треугольника , теорема работает, не давая равенства . Конечно, закон косинусов дает квадрат стороны любого треугольника, учитывая противолежащий угол и две другие стороны.
Сводится ли закон косинусов к теореме Пифагора для прямоугольных треугольников? Закон косинусов применим к любому треугольнику со сторонами a,b,c и углами A,B,C. Обратите внимание, что если угол C прямой, то cos(C) = 0 и закон косинусов сводится к теореме Пифагора: a2 + b2 = c2 .
Какое правило a2 b2? а + б)2 = а2 + 2аб + б2; a2 + b2 = (a + b)2 − 2ab .
Является ли a2 b2 таким же, как AB 2? a2 – b2 = (a+b) (a-b) действительно верно . Сначала давайте посмотрим на это численно. Хотя бы для начального уровня проверки. Возьмем, к примеру, a = 9 и b = 4.
Какова формула для A² B²? (A²-B²) = (A-B)² + 2AB .
Что такое теорема Пифагора простыми словами? Теорема Пифагора, хорошо известная геометрическая теорема о том, что сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы (стороне, противоположной прямому углу) — или, в привычных алгебраических обозначениях, 2 + б 2 = в 2 .
Как использовать теорему Пифагора для нахождения прямоугольных треугольников?
Прямоугольные треугольники и теорема Пифагора
- Теорема Пифагора, a2+b2=c2, a 2 + b 2 = c 2 , может быть использована для нахождения длины любой стороны прямоугольного треугольника.

- Сторона, противолежащая прямому углу, называется гипотенузой (сторона с на рисунке).
Какая теорема Пифагора используется для прямоугольных треугольников? Теорема Пифагора утверждает, что в любом прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов прямоугольного треугольника . Это же соотношение часто используется в строительной отрасли и называется правилом 3-4-5.
Как с помощью теоремы Пифагора решить прямоугольный треугольник?
Ключевые точки
- Теорема Пифагора, a2+b2=c2, a 2 + b 2 = c 2 , используется для нахождения длины любой стороны прямоугольного треугольника.
- В прямоугольном треугольнике один из углов имеет значение 90 градусов.
- Самая длинная сторона прямоугольного треугольника называется гипотенузой, и это сторона, лежащая против угла 90 градусов.
Является ли a2 b2 c2 только для прямоугольных треугольников? Теорема Пифагора применима к прямоугольным треугольникам. Напомним, что теорема Пифагора утверждает, что для прямоугольного треугольника с катетами длины a и b и гипотенузой длины c а2+b2=с2 .
Напомним, что теорема Пифагора утверждает, что для прямоугольного треугольника с катетами длины a и b и гипотенузой длины c а2+b2=с2 .
Что такое а³ В³? Разность двух квадратов: a² – b² = (a+ b)(a – b) Сумма двух кубов: a³ + b³ = ( a + b)(a² – ab + b²) Разность двух кубов: a³ – b³ = (a – b)(a² + ab + b²) Запоминание этих формул поможет вам быстро решать квадратные уравнения. …
Что такое a³ +B³? 0
Что такое B³? B³ ( Мозг — Тело — Баланс ) — это форма нейромышечной терапии (НМТ). … Философия B³ заключается в том, что МОЗГ действует как центральный центр управления, используя механизмы биологической обратной связи для обеспечения постоянной взаимной проверки и баланса с каждой клеткой тела.
Что такое формула 2 B 2? Формула a 2 – b 2 также известна как « формула разности квадратов» . Квадрат a минус квадрат b используется для нахождения разницы между двумя квадратами без фактического вычисления квадратов. Это одно из алгебраических тождеств. Он используется для факторизации биномов квадратов.
Квадрат a минус квадрат b используется для нахождения разницы между двумя квадратами без фактического вычисления квадратов. Это одно из алгебраических тождеств. Он используется для факторизации биномов квадратов.
Что такое 3 Б? (бейсбол) Triple , бейсбольная статистика, показывающая, что бегун благополучно продвинулся на третью базу. инициализм.
Mathway | Популярные проблемы
1 Найти том сфера (5) 2 Найдите площадь круг (5) 3 Найдите площадь поверхности сфера (5) 4 Найдите площадь круг (7) 5 Найдите площадь круг (2) 6 Найдите площадь круг (4) 7 Найдите площадь круг (6) 8 Найти том сфера (4) 9 Найдите площадь круг (3) 9(1/2) 11 Найти простую факторизацию 741 12 Найти том сфера (3) 13 Оценить 3 квадратный корень из 8*3 квадратный корень из 10 14 Найдите площадь круг (10) 15 Найдите площадь круг (8) 16 Найдите площадь поверхности сфера (6) 17 Найти простую факторизацию 1162 18 Найдите площадь круг (1) 19 Найдите окружность круг (5) 20 Найти том сфера (2) 21 Найти том сфера (6) 22 Найдите площадь поверхности сфера (4) 23 Найти том сфера (7) 24 Оценить квадратный корень из -121 25 Найти простую факторизацию 513 26 Оценка квадратный корень из 3/16* квадратный корень из 3/9 27 Найти том коробка (2)(2)(2) 28 Найдите окружность круг (6) 29 Найдите окружность круг (3) 30 Найдите площадь поверхности сфера (2) 31 Оценить 2 1/2÷22000000 32 Найди том коробка (5)(5)(5) 33 Найти том коробка (10)(10)(10) 34 Найдите окружность круг (4) 35 Преобразование в проценты 1,7 36 Оценить (5/6)÷(4/1) 37 Оценить 3/5+3/5 38 Оценить ф(-2) 40 Найдите площадь круг (12) 41 Найти том коробка (3)(3)(3) 42 Найти том коробка (4)(4)(4) 92-4*-1+2 45 Найти простую факторизацию 228 46 Оценить 0+0 47 Найдите площадь круг (9) 48 Найдите окружность круг (8) 49 Найдите окружность круг (7) 50 Найти том сфера (10) 51 Найдите площадь поверхности сфера (10) 52 Найдите площадь поверхности сфера (7) 53 Определить, является простым или составным 5 60 Преобразование в упрощенную дробь 2 1/4 61 Найдите площадь поверхности сфера (12) 62 Найти том сфера (1) 63 Найдите окружность круг (2) 64 Найти том коробка (12)(12)(12) 65 Добавить 2+2= 66 Найдите площадь поверхности коробка (3)(3)(3) 67 Оценить корень пятой степени из 6* корень шестой из 7 68 Оценить 7/40+17/50 69 Найти простую факторизацию 1617 70 Оценить 27-(квадратный корень из 89)/32 71 Оценить 9÷4 72 Оценка 92 74 Оценить 1-(1-15/16) 75 Преобразование в упрощенную дробь 8 76 Оценка 656-521 79 Оценить 4-(6)/-5 80 Оценить 3-3*6+2 81 Найдите площадь поверхности коробка (5)(5)(5) 82 Найдите площадь поверхности сфера (8) 83 Найдите площадь круг (14) 84 Преобразование в десятичное число 11/5 85 9-2 88 Оценить 1/2*3*9 89 Оценить 12/4-17/-4 90 Оценить 11. 02+17.19
02+17.19 91 Оценить 3/5+3/10 92 Оценить 4/5*3/8 93 Оценить 6/(2(2+1)) 94 Упростить квадратный корень из 144 95 Преобразование в упрощенную дробь 725% 96 Преобразование в упрощенную дробь 6 1/4 97 Оценить 7/10-2/5 98 Оценить 6÷3 99 Оценить 5+4 100 Оценить квадратный корень из 12- квадратный корень из 192
Что такое формула a2 b2?
Содержание
- 1 Что такое формула a2 b2?
- 2 Какова формула a2 +b2?
- 3 Что такое a2 b2 =?
- 4 Что означает a2 в математике?
- 5 Является ли A² B² таким же, как B ²?
- 6 Что означает b2 в математике?
- 7 Что получится, если из 5xy вычесть 3xy?
- 8 Что такое a2 b2 A B A B?
- 9 Что такое a2 2ab b2?
- 10 Что такое а² А?
- 11 Что такое расширенная форма B 2?
- 12 Как B ² A² 2ab B²?
- 13 Как найти гипотенузу?
- 14 Является ли a 2 B 2 C 2 только для прямоугольных треугольников?
- 15 Сколько членов в выражении 5xy 9yz 3zx +5x *?
- 16 Как называется сумма задачи на вычитание?
- 17 Сколько факторов в 7xy?
- 18 Что означает 1 2bh?
- 19 В чем ошибка Лашандры?
- 20 Какова формула 4ab?
- 21 Что называется двучленом?
- 22 Какое произведение равно a2 2ab b2?
- 23 Какова стандартная форма 12345?
- 24 Что такое A² ³?
- 25 Что такое целый квадрат B?
- 26 Что такое расширение AB?
- 27 Что такое расширение B ³?
- 28 Что такое ABC Square?
- 29 Какой из следующих терминов аналогичен 8xy?
- 30 Чему равна гипотенуза 3 и 4?
- 31 Что такое математика гипотенузы?
Что такое формула a2 b2? . В этой статье мы сообщим вам подробности вашего вопроса. Также мы поделимся с наиболее часто задаваемым вопросом людей в конце этой статьи. Давайте проверим это!
В этой статье мы сообщим вам подробности вашего вопроса. Также мы поделимся с наиболее часто задаваемым вопросом людей в конце этой статьи. Давайте проверим это!
Что такое формула a2 b2?
a2 – b2 = (a + b)(a – b) .
Вот несколько связанных вопросов, которые люди задают в различных поисковых системах.
Какова формула a2 +b2?
(A²-B²) = (A-B)² + 2AB .
Что такое a2 b2 =?
а2 + Ь2 = ( a+b )2 – 2ab nd a2 – b2 = (a + b)(a – b)
Что означает a2 в математике?
Все курсы по математике уровня A состоят из двух частей, по три отдельных модуля в каждой части. Студенты сначала изучают курс AS (Advanced Subsidiary). Некоторые затем продолжат изучение второй части курса A Level , которая называется A2.
Является ли A² B² таким же, как B ²?
Оба совершенно разные .
Что означает b2 в математике?
b1, b2 длины каждой базы . h это высота (высота) Напомним, что основаниями являются две параллельные стороны трапеции. Высота (или высота) трапеции — это перпендикулярное расстояние между двумя основаниями.
h это высота (высота) Напомним, что основаниями являются две параллельные стороны трапеции. Высота (или высота) трапеции — это перпендикулярное расстояние между двумя основаниями.
Что получится, если из 5xy вычесть 3xy?
Ответ: 8xy — правильный ответ.
Что такое a2 b2 A B A B?
Произведение суммы и разности тех же двух членов равно разнице. между квадратами этих терминов. Также показано как: Разность двух полей: a2 – b2 = (a+b) (a-b)
Что такое a2 2ab b2?
а2 + 2аб + Ь2 = (а + Ь)2 . а также. а2 – 2аб + Ь2 = (а – Ь)2. 2. Использование: если первый и последний члены трехчлена являются квадратами, попробуйте написать полный квадрат; затем используйте квадратную формулу, чтобы убедиться, что вы правы.
Что такое а² А?
A² ЗНАЧИТ В НИХ 2А ПОЭТОМУ ИХ ВЫЧИТАЕМ. 1jaiz4 и еще 14 пользователей считают этот ответ полезным. Спасибо 8.
Что такое расширенная форма B 2?
(а + b)2 = а 2 + 2ab + b2 . 2. (а – б)2 = а2 – 2аб + б2.
Как B ² A² 2ab B²?
пусть a =1 и b = 2 и теперь подставьте значения, которые вы взяли в тождестве. а теперь решите L.H.S и R.H.S. и видим, что L.H.S равно R.H.S. поэтому LHS не равно RHS, потому что формула неверна, на самом деле формула (a+b)²=a²+2ab+b² .
Как найти гипотенузу?
Гипотенуза называется наибольшей стороной прямоугольного треугольника. Чтобы найти самую длинную сторону, мы используем формулу гипотенузы, которую можно легко вывести из теоремы Пифагора: (Гипотенуза)2 = (Основание)2 + (Высота)2. Формула гипотенузы = √((основание)2 + (высота)2) (или) c = √(a2 + b2) .
Формула гипотенузы = √((основание)2 + (высота)2) (или) c = √(a2 + b2) .
Является ли 2 B 2 C 2 только для прямоугольных треугольников?
Теорема Пифагора применима к прямоугольным треугольникам. Напомним, что теорема Пифагора утверждает, что для прямоугольного треугольника с катетами длины a и b и гипотенузой длины c a2+b2=c2 . Гипотенуза — это сторона, лежащая напротив прямого угла, и это самая длинная сторона треугольника.
Сколько членов в выражении 5xy 9yz 3zx +5x *?
В этом выражении 5 терминов .
Как называется сумма задачи на вычитание?
Ответ задачи на вычитание называется разностью .
Сколько факторов в 7xy?
7 ,х,у. х, у.
х, у.
Что означает 1 2bh?
Треугольник — это многоугольник с тремя сторонами. Мы знаем, что площадь прямоугольника равна b×h, где b — основание, а h — высота прямоугольника. … Итак, площадь треугольника A определяется формулой A=12bh , где b — основание, а h — высота треугольника . Пример: Найдите площадь треугольника.
В чем ошибка Лашандры?
В чем ошибка Лашандры? А. Она должна была умножить на 2, а не делить на 2.
Какова формула 4ab?
Ответ: Формула для 4ab: ( 4ab) =( a+b )²- ( a-b )² .
Что называют биномиальным?
Полиномиальное уравнение с двумя членами, обычно соединенными знаком плюс или минус, называется биномиальным. Биномы используются в алгебре. … Многочлен с двумя членами называется биномом; это может выглядеть как 3x + 9. Биномы легко запомнить, так как бином означает 2, а бином будет иметь 2 члена.
Какой продукт равен a2 2ab b2?
Для любых двух чисел a и b произведение a−b на себя равно a2−2ab+b2.
Какая стандартная форма 12345?
Стандартная форма числа 12345 равна «1,2345 ×».
Что такое A² ³?
сила 6. Пошаговое объяснение: несколько сил.
Что такое целый квадрат B?
Формула (a + b)2 также известна как одно из важных алгебраических тождеств. Читается как плюс б целый квадрат. Его формула (a + b)2 выражается как (a + b)2 = a2 + 2ab + b2.
Что такое расширение AB?
Ответ: a²+b²-2ab.
Что такое расширение B ³?
(a + b) куб = a куб + b куб + 3 a квадрат b + 3 a b квадрат. Надеюсь, это поможет вам!
Что такое ABC Square?
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca.
Какой из следующих терминов похож на 8xy?
Ответ: -8xy — правильный ответ, потому что это почти то же самое, что термин 7 xy.
Чему равна гипотенуза 3 и 4?
Итак, гипотенуза равна 5 .
Что такое математика гипотенузы?
Определение гипотенузы 1: сторона прямоугольного треугольника, лежащая против прямого угла.
Алгебра A3-B3 Формула/बीजगणित किस सूत्र से संबंधित समस्याएं
बीजगणित के सूत्र (формула A3-B3)- गणित व व्यापक विभागों में से एक है, बीजगणित A2-B2 Формула जो गणित अन अन्य सभी Формула में एक एक a2-b2 Формула, формула A3-B3 हैं।।
अपने स सामान्य रूप में, बीजगणित के प प्रतीकों औान इन पшить में बीजगणित के प प्रतीकों और इन प्रतीकों में हेर-फेर क के नियमों का अध्ययन कराता है।।।।।।।। क नियमों
बीजगणित के (Алгебра Формулы, формула A2-B2, формула A3-B3) लगभग सम्पूा Формула है गणित
इसे अवश्य पढ़ें Формулы алгебры Пробный тест
गणित के सभी महत्वपूर्ण फार похоже
Алгебра A2+B2+C2 Формула
- 1.
 (A+B+C) ² = A²+B²+C²+2AB+2BC+2CA
(A+B+C) ² = A²+B²+C²+2AB+2BC+2CA 68 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918
918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 918 9187. a-b-c)²= a²+b²+c²-2ab+2bc+2ca- 3. (a-b+c)²= a²+b²+c²-2ab-2bc+2ca
- 4. (a+ b-c)²= a²+b²+c²+2ab-2bc-2ca
- 5. (a+b+c)² = a²+b²+c²+2(ab+bc+ca)
Алгебра a2+ формула b2, формула a2-b2
- 6. (a + b)²= a² + b² + 2ab
- 7. (a – b)²= a² + b² – 2ab
- 8. (a + b)²= (a + b)² + 4ab
- 9. (a – b) ²= (a + b)² – 4ab
Алгебра формула a2-b2, формула a2+b2
- 10. 2(a² + b²) = (a+ b)² + (a – b)²
- 11. a² + b²= (a + b)² – 2ab
- 12. a² + b²= (a – b)² + 2ab
- 13. a² – b² =(a + b)(a – б)
Алгебра формула a2+b2, формула a2-b2
- 14.
 4ab = (a + b)² – (a – b)²
4ab = (a + b)² – (a – b)²
- 15. (a + b)² = (a – b)² + 4ab
- 16. ab ={ (a+b )/2}²-{(a-b)/2}²
- 17. (a+ b)² – (a – b)² = 2ab
Алгебра формула a3-b3, a3+b3 формула
- 18. (a + b)³ = a³ + b³ + 3a²b + 3ab²
- 19. (a + b)³ = a³ + b³ + 3ab (a + b)
20,073 ( a – b)³ = a³ – b³ – 3a²b + 3ab²
- 21. (a – b)³ = a³ – b³ – 3ab (a + b)
Алгебра формула a3+b3, формула a3-b3
- 22. a³ + b³ = (a + b) (a² + b² -ab)
- 23. a³ + b³ = (a + b)³ – 3ab(a + b)
- 24. a³ – b³ = (a – b) (a² +b²+ ab)
- 25. a³ – b³ = (a – b)³ + 3ab(a – b)
इसे अवश्य पढ़ें Формула онлайн-теста
Алгебра A2-B2 Формула A3-B3 Пример
0140
प्रश्न-1. यदि (a – 2)²+ (b + 3)+ (c – 4) = 0 हो, तो a – b + c का होगा।
हल:
⇒ Короткие трюки, a = 2, b= -3,c = 4
⇒ a – b + c = 2 -(-3) + 4 = 9 Анс.
प्रश्न-2. यदि ˣ⁺¹/ₓ= -2 हो, तो x³² + ¹/x⁴⁷ का मान ज्ञात कीजिए।
हल:
⇒ दिया है, ˣ⁺¹/ₓ= -2 , x³² + ¹/x⁴⁷ = ?
⇒ Короткие трюки 9.0005
⇒ माना x का मान -1 000
⇒ ⁻⁻⁺/₋₁ = -2
⇒ -1 -1 = -2
⇒ -2 = -2
∵ X³² + ¹/x⁴⁷ में x का मान -1 रखने पर
⇒ -1³² + 1/-1⁴⁷
⇒ -1 -1 = 0 Анс.
प्रश्न-3. यदि ˣ⁺¹/ₓ= 5 हो, तो x² + 1 का मान ज्ञात कीजिए।
हल:⇒
दिया है, ˣ⁺¹/ₓ= 5 , x² + 1 = ?
⇒ Короткие трюки, ˣ⁺¹/ₓ = 5
⇒ x² + 1= 5x
= 5x Ответ.
प्रश्न-4. यदि ˣ ⁻ ¹/ₓ= 0 हो, तो x⁷⁴ + ¹/x⁷⁴ का मान ज्ञात कीजिए।
हल:
⇒ दिया है, ˣ ⁻ ¹/ₓ= 0 , x⁷⁴ + ¹/x⁷⁴ = ?
⇒ Короткие уловки
⇒ माना x कान 1 000
⇒ ¹ ⁻ ¹/₁ = 0
⇒ 1 — 1 = 0
⇒ 0 = 0
∵ x⁷⁴ + ¹/x⁷⁴ में x क ⇒ 0 = 0
∵ x⁷⁴ + ¹/x⁷⁴ में में क क क क क ⇒ ⇒ 0 = 0
∵ x⁷⁴ + ¹/x में में क क क. मान 1 रखने पर
मान 1 रखने पर
⇒ 1³² + 1/1⁴⁷
⇒ 1+1 = 2· Ответ.
प्रश्न-5. यदि ˣ⁺¹/ₓ= 1 हो, तो x³ + 1 का मान ज्ञात कीजिए।
हल:
⇒ दिया है, ˣ⁺¹/ₓ= 1 , x³ + 1= ?
⇒ Короткие уловки
∵ x के घातांक में 3 का अंतर है तो घ घ घ कातांक में 3 का अंतर है तो घ घ घ कातांक में 3 क000 है तो तो घ घ घ कातांक में 3 क000 है है तो घ घ घ कातांक में 3 क000 है है तो घ घ घ कातांक में 3 क अंत है है तो तो घ घ घ कातांक में होता है
⇒ x³ + 1 = 0 ANS.
प्रश्न-6. यदि ˣ⁺¹/ₓ= 1 हो, तो x²⁵ + x²² -x¹⁹ का मान ज्ञात कीजिए।
हल:
⇒ दिया है, ˣ⁺¹/ₓ= 1 , x²⁵ + x²² -x¹⁹ = ?
⇒ Короткие уловки
∵ x के घातांक में 3 का अंतर है तो घ घ घ कातांक में 3 का अंतर है तो घ घातांक काम माना 0 होता है
⇒ x²⁵ + x² -x⁹ = 0 + 0 + 0
⇒ = 0 .
प्रश्न-7. यदि (3x + 2y)/(3x – 2y)= 4/3 हो, तो (x² + y²)/(x² – y²) का मान ज्ञात कीजिए।
हल:
⇒ दिया है, (3x + 2y)/(3x – 2y)= 4/3 , (x² + y²)/(x² – y²) = ?
⇒ Короткие трюки
⇒ (3x + 2г)/(3x – 2г)= 4/3
⇒ 9x + 6y = 12x – 8y
⇒ 9x – 12x = -8y – 6y
⇒ – 3x = -14y
⇒ x/y = 14/3
+(x²/²) (x²) y²)
⇒ (14² + 3²)/(14² – 3²)
⇒ 205/187 Ответ.
प्रश्न-8. यदि ˣ⁺¹/ₓ= 1 हो, तो x² +1/x² का मान ज्ञात कीजिए।
Код:
⇒ दिया है, ˣ⁺¹/ₓ= 1 , x² + 1/x² = ?
⇒ Короткие уловки
⇒ ˣ⁺ˣ⁺/ₓ = 1 दोनों पक्ष को वर्ग करने प प выполнение
⇒ (x +1/x) ² = 1²
⇒ x² +1/x +2 = 1²
⇒ x² x² +1/x/x +2 = 1000
⇒ x². +1/x² = 1-2
= -1 Анс.
प्रश्न-9. यदि ˣ⁺¹/ₓ= 3 हो, तो x³ +1/x³ का मान ज्ञात कीजिए।
हल:
⇒ दिया है, ˣ⁺¹/ₓ= 3 , x³ + 1/x³ = ?
⇒ Короткие трюки 9.0005
⇒ ˣ⁺ˣ⁺/ₓ = 3 दोनों पक्ष को घन क क000
⇒ (x +1/x) ³ = 3³
⇒ x³ +1/x³ +3 (ˣ⁺/ₓ) = 3³
⇒ x³ +1/x³ +3 (3) = 27
⇒ x³ +1/x³ + 9 = 27
⇒ x³ +1/x³ = 27 – 9
= 19 Ответ.
प्रश्न-10. यदि x³ +1/x³= 16 और ˣ⁺¹/ₓ = 4 हो, तो x² +1/x² का मान ज्ञात कीजिए।
हल:
⇒ दिया है, x³ +1/x³= 16 और ˣ⁺¹/ₓ = 4 , x² +1/x² = ?
⇒ Короткие трюки
⇒ {∵ a³ + b³ = (a+b) (a² + b² – 2ab)}
⇒ x³ +1/x³= 16
⇒ (ˣ⁺¹/ₓ)(x² + 1/x² – 2)= 16
⇒ (4)(x² + 1/x² – 2)= 16
⇒ (x² + 1/x² – 2)= 4
⇒ (x² + 1/x²)= 4 + 2
= 6 Ответ .
प्रश्न-11. जब a + b= 12, b + c = 4, तथा c = 8 हैं तो (a+b+c)² इसका क्या मान होगा ?
⇒ हल:- दिया है
⇒ a + b = 12 …..(i)
⇒ b + c = 4 …..(ii)
⇒ c= 8 …..0 (02iii) 900 (02iii) ⇒ (а+б+с)²=? … .. (iv)
समीकरण (ii) में c का मान रखनेरखने परण
⇒ b + c = 4
⇒ b + 8 = 4
⇒ b = -4
मान रखनेरखने पर
⇒ a + b = 12
⇒ a+(-4) = 12
⇒ a = 16
अब समीकरण (iv) में a, b, c का मान रखने पर
⇒ (a+b+c) ² = 200
= 200 √ Ответ.
प्रश्न-12. जबकि दिया है, a = 5, b = 4 और c = 3 तो a²+b²+c² बीजगणितीय का माऍ२ कग।२ कग।२ कग।२
⇒ हल:-
⇒ दिया है a = 5, b = 4 और c = 3
⇒ a²+b²+c²= ? …..(i)
फॉर्मूला-
⇒ (a+b+c)²=a²+b²+c²+2(ab+bc+ca)
अब a, b, c का मान रखने पर
⇒ a²+b²+c² = 50
= 50 √ Анс.
प्रश्न-13 . यदि (a + b)² = 25 और ab = 6 तो a² + b² इसका मान ज्ञात कीजिए।
हल:- दिया है , (a + b)² = 25 और ab = 6
⇒ a² + b² = ? … . . (i)
. (i)
⇒ फॉर्मूला- (a + b) ² = a² + b² + 2ab
⇒ अब (a + b) ² और ab मान रखने पर
⇒ a² + b² = 13
= 13 √ Ответ.
प्रश्न-14. यदि (a – b)²= 100 और a= 20, b= 10 है तो (a + b/2)² इसका मान ज्ञात कीजिए।
हल:-
⇒ दिया है , (a – b)²= 100 और a= 20, b= 10
⇒ (a + b/2)² = ? …..(i)
⇒ फॉर्मूला- (a – b)²= (a + b)² – 4ab
⇒ (a + b/2)² = 475
= 475√ Ответ.
प्रश्न-15. यदि (a + b)² = 16, (a – b)²= 4 हैं,तो a² + b² मान ज्ञान किजिए।
हल:-
⇒ दिया है ,(a + b)² = 16, (a – b)²= 4
⇒ a² + b² = ? …..(i)
⇒ फॉर्मूला- 2(a² + b²) = (a+ b)² + (a – b)²
⇒ a² + b² = 10
= 10√ Ответ.
प्रश्न-16. यदि a² + b²= 10 है, तो ab का मान ज्ञान कीजिए।
हल:-
⇒ दिया है, a² + b²= 10, ab = ?
⇒ फॉर्मूला- a² + b²= (a + b)² – 2ab
⇒ ab = {(a + b)² – 10}/2
⇒ = {(a + b)² }/2 – 5 √ Ответ.
प्रश्न-17 . यदि (a – b)²= 100 और ab= 20 हैं, तो (a+ b)² का मान ज्ञान कीजिए।
हल:-
⇒ दिया है ,(a – b)²= 100 और ab= 20,(a+ b)² = ?
⇒ फॉर्मूला, (a + b)² – (a – b)² = 2ab
⇒ (a + b)² = 140
= 140√ Ответ.
प्रश्न-18. यदि (a + b)= 12 और ab= 32 हैं, तो a³ + b³ का मान ज्ञान कीजिए।
हल:-
⇒ दिया है , (a + b)= 12 और ab= 32 ,a³ + b³ = ?
⇒ फॉर्मूला, (a + b)³ = a³ + b³ + 3ab (a + b)
⇒ (12)³ = a³ + b³ + 3×32×12
+ 15 ³2 а 1728
⇒ a³ + b³= 1728-1152
⇒ = 576√ Ответ.
प्रश्न-19. दि a³ – b³ = 936,a² +b²=116और ab=40 हैं, तो (a – b) का मान ज्ञान कीजिए।
हल:-
⇒ दिया है , a³ – b³ = 936,a² +b²=116और ab=40
⇒ (а – б)= ?
⇒ फॉर्मूला, a³ – b³ = (a – b) (a² +b²+ ab)
⇒ (a – b) = 6
= 6√ Анс.
प्रश्न-20. यदि a + b= 24 और a – b=12 हैं, तो a³ – b³ का मान ज्ञान कीजिए।
उत्तर ??
इस प्रश्न का उत्तर क्या है कमेंट बॉक्स में जरूर दें।।।।।।।।।
इसे भी पढ़ें वृद्धा पेंशन योजना के लिए आवेदन क выполнение
Формулы алгебры
जैसा कि आपको पता होगा कि हम बीजगणित के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के के
алгебра формулаалгебра формулаалгебра формулаалгебра формулаबीजगणित सूत्रबीजगणित सूत्र
0
600 7 дней
बीजगणित सूत्रpdf
0a2 – формула b2
0
3,3 тыс. 4 дня
формула a2-b2 ответы
0
2,1 тыс. 3 дня
формула a2-b2
0
350 31 авг
примеры формул a2 – b2
0
300 1 сен
формула a2-b2 по математике
2
250 31 авг
формула a2 -b2
Н/Д
150
Вопросы по формуле a2-b2
Таблица формул 0алгебры
24
6,3 тыс. 2 дня
основная формула алгебры
28
2,1 тыс. 4 дня
вся формула алгебры
21
2.0K 4 дня
формула математической алгебры
18
1,3 тыс. 2 дня
формула математической алгебры
18
1,1 тыс. 4 дня
список формул алгебры
28
700 6 дней
вся формула алгебры pdf
16
700 в день
формула булевой алгебры
28
600 2 дня
формула алгебрыpdf
0
600 в день
формула алгебры ssc
Зарегистрируйтесь в Ahrefs
300 1 августа
алгебраическая формула для ssc cgl
300
10-я формула алгебры
200 1 августа
формула алгебры на хинди
200 25 июл
формула алгебры класс 10
200 24 июл
формула алгебры pdf скачать
200 23 июл
формула линейной алгебры
200 4 дня
формула алгебры класс 7
200 22 июл
формула элементарной алгебры
150 1 авг.
формула ab алгебры
150 26 июн
формула алгебры класс 8
150 22 июл
формула базовой алгебрыpdf
150
что такое алгебраическая формула
150 28 июл
важная формула алгебры
100 27 июл
формула алгебры класс 6
100
9Таблица формул алгебры th класса
100 22 июл
формула шпаргалки по алгебре
100 3 августа
лист формул алгебры
100 28 июл
вопросы по формулам алгебры
90 22 июл
формула кубической алгебры
90
формула алгебры все
80
лист формул алгебры pdf
70 в день
алгебраическая формула для ssc
70 1 авг.
4 дня
формула a2-b2 ответы
0
2,1 тыс. 3 дня
формула a2-b2
0
350 31 авг
примеры формул a2 – b2
0
300 1 сен
формула a2-b2 по математике
2
250 31 авг
формула a2 -b2
Н/Д
150
Вопросы по формуле a2-b2
Таблица формул 0алгебры
24
6,3 тыс. 2 дня
основная формула алгебры
28
2,1 тыс. 4 дня
вся формула алгебры
21
2.0K 4 дня
формула математической алгебры
18
1,3 тыс. 2 дня
формула математической алгебры
18
1,1 тыс. 4 дня
список формул алгебры
28
700 6 дней
вся формула алгебры pdf
16
700 в день
формула булевой алгебры
28
600 2 дня
формула алгебрыpdf
0
600 в день
формула алгебры ssc
Зарегистрируйтесь в Ahrefs
300 1 августа
алгебраическая формула для ssc cgl
300
10-я формула алгебры
200 1 августа
формула алгебры на хинди
200 25 июл
формула алгебры класс 10
200 24 июл
формула алгебры pdf скачать
200 23 июл
формула линейной алгебры
200 4 дня
формула алгебры класс 7
200 22 июл
формула элементарной алгебры
150 1 авг.
формула ab алгебры
150 26 июн
формула алгебры класс 8
150 22 июл
формула базовой алгебрыpdf
150
что такое алгебраическая формула
150 28 июл
важная формула алгебры
100 27 июл
формула алгебры класс 6
100
9Таблица формул алгебры th класса
100 22 июл
формула шпаргалки по алгебре
100 3 августа
лист формул алгебры
100 28 июл
вопросы по формулам алгебры
90 22 июл
формула кубической алгебры
90
формула алгебры все
80
лист формул алгебры pdf
70 в день
алгебраическая формула для ssc
70 1 авг. формула алгебры 8 класса
70
все формулы алгебры pdf скачать
60 1 формула авгмата
22
44К 19 часов
диаграмма математической формулы
21
3,8 тыс. 2 дня
математическая формула класс 10
13
2,9 тыс. 3 дня
математическая формулаpdf
10
1,9 тыс. 5 дней
математическая формула на хинди
0
1,6 тыс. 7 дней
Таблица математических формул на хинди в формате pdf
0
1,4 тыс. 7 дней
математическая формула класс 93
1,4 тыс. 5 дней
математическая формула класс 8
4
1.0K 4 дня
10-я математическая формула
14
700 2 дня
область математической формулы
38
700 2 дня
простая математическая формула
Зарегистрируйтесь в Ahrefs
600 3 часа
12-я математическая формула
600 6 дней
все математические формулы
600 в день
математическая формула на хиндиpdf
500 7 дней
математическая формула класс 7
500 29 июл
математическая формула 9 класс pdf
500 16 часов
продвинутая математическая формула
500 24 июл
математическая формула 10 класс
500 7 дней
математическая формула в формате pdf на хинди
500 7 дней
математическая формула объема
450 17 часов
расширенная математическая формула
400 26 июл
математическая формула круга
400
математическая формула ряда
400
ап математическая формула
400
9 классвсе математические формулы 9 класса
400 2 дня
6 класс математическая формула
350 31 июл
математическая формула 6 класс
350
9-я математическая формула
350 24 июл
10 класс все математические формулы
300 4 дня
буклет с математическими формулами
300 19 июл
Математическая формула для 9 класса.
формула алгебры 8 класса
70
все формулы алгебры pdf скачать
60 1 формула авгмата
22
44К 19 часов
диаграмма математической формулы
21
3,8 тыс. 2 дня
математическая формула класс 10
13
2,9 тыс. 3 дня
математическая формулаpdf
10
1,9 тыс. 5 дней
математическая формула на хинди
0
1,6 тыс. 7 дней
Таблица математических формул на хинди в формате pdf
0
1,4 тыс. 7 дней
математическая формула класс 93
1,4 тыс. 5 дней
математическая формула класс 8
4
1.0K 4 дня
10-я математическая формула
14
700 2 дня
область математической формулы
38
700 2 дня
простая математическая формула
Зарегистрируйтесь в Ahrefs
600 3 часа
12-я математическая формула
600 6 дней
все математические формулы
600 в день
математическая формула на хиндиpdf
500 7 дней
математическая формула класс 7
500 29 июл
математическая формула 9 класс pdf
500 16 часов
продвинутая математическая формула
500 24 июл
математическая формула 10 класс
500 7 дней
математическая формула в формате pdf на хинди
500 7 дней
математическая формула объема
450 17 часов
расширенная математическая формула
400 26 июл
математическая формула круга
400
математическая формула ряда
400
ап математическая формула
400
9 классвсе математические формулы 9 класса
400 2 дня
6 класс математическая формула
350 31 июл
математическая формула 6 класс
350
9-я математическая формула
350 24 июл
10 класс все математические формулы
300 4 дня
буклет с математическими формулами
300 19 июл
Математическая формула для 9 класса. 300 3 дня
математическая формула pdf скачать
300 19 июл
математическая формула 9 класс
300 7 дней
математическая формула класс 6
300 26 Июл5.1K 4 дня
Решение учебника по математике для 7 класса
5,0 тыс. 5 дней
математический проект
4,9 тыс. 2 дня
9 класс математика
4,6 тыс. в день
математический решатель майкрософт
4,6К 3 часа
математический клипарт
4,6 тыс. 3 дня
фото математика
4,6 тыс. 2 дня
10 класс математика
4,6 тыс. 2 дня
доска для математики 8 класс
4,5 тыс. в день
математическая магия
4,5 тыс. 5 дней
книга по математике
4,5 тыс. 4 дня
название математических символов
4,3 тыс. 4 дня
8 класс математика
4,2 тыс. 4 дня
значит по математике
4,2 тыс. в день
математические загадки
4,2К 21 час
6 класс математики
4,1 тыс. 21 час
модель задание задание 7 класс математика
4.0K 3 дня
модель задание задание 6 класс математика
4.0K 2 дня
решение по математике 10 класс
3,8 тыс. 2 дня
математические головоломки
3,8 тыс. 4 дня
диаграмма математической формулы
3,8 тыс. 2 дня
решение по математике 12 класс
3,8 тыс.
300 3 дня
математическая формула pdf скачать
300 19 июл
математическая формула 9 класс
300 7 дней
математическая формула класс 6
300 26 Июл5.1K 4 дня
Решение учебника по математике для 7 класса
5,0 тыс. 5 дней
математический проект
4,9 тыс. 2 дня
9 класс математика
4,6 тыс. в день
математический решатель майкрософт
4,6К 3 часа
математический клипарт
4,6 тыс. 3 дня
фото математика
4,6 тыс. 2 дня
10 класс математика
4,6 тыс. 2 дня
доска для математики 8 класс
4,5 тыс. в день
математическая магия
4,5 тыс. 5 дней
книга по математике
4,5 тыс. 4 дня
название математических символов
4,3 тыс. 4 дня
8 класс математика
4,2 тыс. 4 дня
значит по математике
4,2 тыс. в день
математические загадки
4,2К 21 час
6 класс математики
4,1 тыс. 21 час
модель задание задание 7 класс математика
4.0K 3 дня
модель задание задание 6 класс математика
4.0K 2 дня
решение по математике 10 класс
3,8 тыс. 2 дня
математические головоломки
3,8 тыс. 4 дня
диаграмма математической формулы
3,8 тыс. 2 дня
решение по математике 12 класс
3,8 тыс. 2 дня
брикс математика ком
3,7 тыс. 4 дня
Селина 10 класс математика
3,7 тыс. 3 дня
модель задание задание 5 класс математика
3,7 тыс. 3 дня
табби математика логин
3,6 тыс. 3 дня
Академия Тивари 9 классй математика
3,6 тыс. 3 дня
вопросы по математике
3,6 тыс. 5 дней
математическая площадка
3,6 тыс. 3 дня
бихар доска класс 8 математическое решение
3,5 тыс. 4 дня
математический решатель онлайн
3,5 тыс. 14 часов
математические обои
3,4 тыс. 4 дня
математический лист
3,3 тыс. 4 дня
математика
3,3 тыс. 4 дня
математические рабочие листы
3,3 тыс. 3 дня
значение символа в математике
3,3 тыс. 2 дня
идеи математических проектов
3,3 тыс. 3 дня
математика 9 класс
3,3 тыс. 2 дня
sd yadav математическая книга
3,3 тыс. 4 дня
белур математический тайминг
3,3 тыс. 4 дня
математика в шестом классе
3,2 тыс. 4 дня
9 класс математика глава 1 mcq
3,2 тыс. 3 дня
экзамен по математике 10 класс
3,2 тыс. 2 дня
10 класс математика
3,2 тыс. 2 дня
математический день
3,1 тыс. 3 дня
первый по математике
3,1 тыс. 2 дня
лист по математике для 3 класса
3,1 тыс.
2 дня
брикс математика ком
3,7 тыс. 4 дня
Селина 10 класс математика
3,7 тыс. 3 дня
модель задание задание 5 класс математика
3,7 тыс. 3 дня
табби математика логин
3,6 тыс. 3 дня
Академия Тивари 9 классй математика
3,6 тыс. 3 дня
вопросы по математике
3,6 тыс. 5 дней
математическая площадка
3,6 тыс. 3 дня
бихар доска класс 8 математическое решение
3,5 тыс. 4 дня
математический решатель онлайн
3,5 тыс. 14 часов
математические обои
3,4 тыс. 4 дня
математический лист
3,3 тыс. 4 дня
математика
3,3 тыс. 4 дня
математические рабочие листы
3,3 тыс. 3 дня
значение символа в математике
3,3 тыс. 2 дня
идеи математических проектов
3,3 тыс. 3 дня
математика 9 класс
3,3 тыс. 2 дня
sd yadav математическая книга
3,3 тыс. 4 дня
белур математический тайминг
3,3 тыс. 4 дня
математика в шестом классе
3,2 тыс. 4 дня
9 класс математика глава 1 mcq
3,2 тыс. 3 дня
экзамен по математике 10 класс
3,2 тыс. 2 дня
10 класс математика
3,2 тыс. 2 дня
математический день
3,1 тыс. 3 дня
первый по математике
3,1 тыс. 2 дня
лист по математике для 3 класса
3,1 тыс. 3 дня
решатель математических задач
3,1 тыс. 14 часов
9 классматематическое решение
3,1 тыс. 2 дня
решение математических задач 11K 3 дня формула a3-b3
0
35 тыс. 5 дней
формула а3 – b3
0
5,2 тыс. 3 дня
решение формулы a3-b3
0
1.4K 4 сен
формула a3 -b3
Н/Д
300
формула a3-b3
0
200 29 авг
формула a3-b3 по математике
Н/Д
70
формула а³-b³
0
70 6 сен
формула a3 -b3 математика
Н/Д
20
формула a3-b3 вики
Н/Д
10
Вопросы по формуле a3-b3
Н/Д
10
что такое формула a3-b3
Зарегистрируйтесь в Ahrefs
10
математические формулы a3-b3
10
формула а3-б3 формула
10
формула a3 – b3 по математике
10
Пример формулы a3-b3
10
3a2b 3ab2 a3-b3 формула 10K 4 дня
математический решатель
81
9.8K 4 дня
8 класс математики
Зарегистрируйтесь в Ahrefs
9,6 тыс. 3 дня
rs aggarwal книга по математике
9,4 тыс. 4 дня
математическое решение
9,3 тыс. 4 дня
крутые математические игры
9,3 тыс. 2 дня
9 класс математики
8,6 тыс. 3 дня
ncert 9 класс математическое решение
8,4К 19 часов
математические игры
8,3 тыс. 3 дня
8 класс математика
8,2 тыс.
3 дня
решатель математических задач
3,1 тыс. 14 часов
9 классматематическое решение
3,1 тыс. 2 дня
решение математических задач 11K 3 дня формула a3-b3
0
35 тыс. 5 дней
формула а3 – b3
0
5,2 тыс. 3 дня
решение формулы a3-b3
0
1.4K 4 сен
формула a3 -b3
Н/Д
300
формула a3-b3
0
200 29 авг
формула a3-b3 по математике
Н/Д
70
формула а³-b³
0
70 6 сен
формула a3 -b3 математика
Н/Д
20
формула a3-b3 вики
Н/Д
10
Вопросы по формуле a3-b3
Н/Д
10
что такое формула a3-b3
Зарегистрируйтесь в Ahrefs
10
математические формулы a3-b3
10
формула а3-б3 формула
10
формула a3 – b3 по математике
10
Пример формулы a3-b3
10
3a2b 3ab2 a3-b3 формула 10K 4 дня
математический решатель
81
9.8K 4 дня
8 класс математики
Зарегистрируйтесь в Ahrefs
9,6 тыс. 3 дня
rs aggarwal книга по математике
9,4 тыс. 4 дня
математическое решение
9,3 тыс. 4 дня
крутые математические игры
9,3 тыс. 2 дня
9 класс математики
8,6 тыс. 3 дня
ncert 9 класс математическое решение
8,4К 19 часов
математические игры
8,3 тыс. 3 дня
8 класс математика
8,2 тыс.

 Последнее уравнение, a2 + b2 = c2, называется теоремой Пифагора. Мы говорим: «Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы».
Последнее уравнение, a2 + b2 = c2, называется теоремой Пифагора. Мы говорим: «Сумма квадратов катетов прямоугольного треугольника равна квадрату его гипотенузы». Теорема Пифагора работает только для прямоугольных треугольников , поэтому вы можете использовать ее, чтобы проверить, есть ли у треугольника прямой угол или нет. В треугольнике выше, если.
Теорема Пифагора работает только для прямоугольных треугольников , поэтому вы можете использовать ее, чтобы проверить, есть ли у треугольника прямой угол или нет. В треугольнике выше, если. Это известно как уравнение Пифагора , названное в честь древнегреческого мыслителя Пифагора. Это соотношение полезно, потому что, если известны две стороны прямоугольного треугольника, можно использовать теорему Пифагора для определения длины третьей стороны.
Это известно как уравнение Пифагора , названное в честь древнегреческого мыслителя Пифагора. Это соотношение полезно, потому что, если известны две стороны прямоугольного треугольника, можно использовать теорему Пифагора для определения длины третьей стороны.
Прямоугольные треугольники и теорема Пифагора

Ключевые точки
 Напомним, что теорема Пифагора утверждает, что для прямоугольного треугольника с катетами длины a и b и гипотенузой длины c а2+b2=с2 .
Напомним, что теорема Пифагора утверждает, что для прямоугольного треугольника с катетами длины a и b и гипотенузой длины c а2+b2=с2 . Квадрат a минус квадрат b используется для нахождения разницы между двумя квадратами без фактического вычисления квадратов. Это одно из алгебраических тождеств. Он используется для факторизации биномов квадратов.
Квадрат a минус квадрат b используется для нахождения разницы между двумя квадратами без фактического вычисления квадратов. Это одно из алгебраических тождеств. Он используется для факторизации биномов квадратов.Mathway | Популярные проблемы
 02+17.19
02+17.19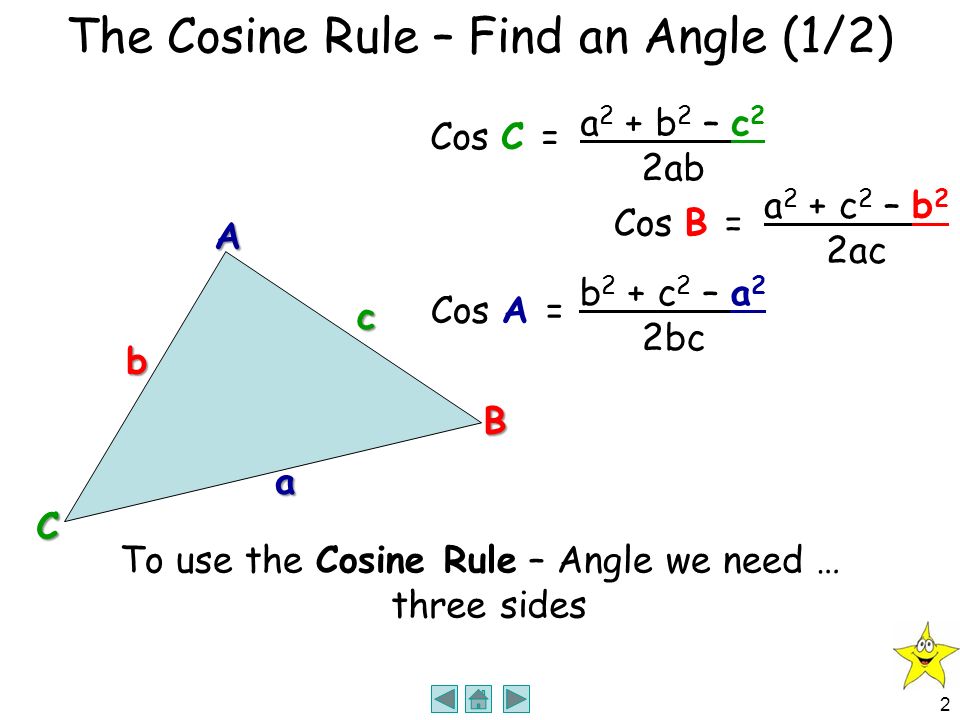 В этой статье мы сообщим вам подробности вашего вопроса. Также мы поделимся с наиболее часто задаваемым вопросом людей в конце этой статьи. Давайте проверим это!
В этой статье мы сообщим вам подробности вашего вопроса. Также мы поделимся с наиболее часто задаваемым вопросом людей в конце этой статьи. Давайте проверим это! h это высота (высота) Напомним, что основаниями являются две параллельные стороны трапеции. Высота (или высота) трапеции — это перпендикулярное расстояние между двумя основаниями.
h это высота (высота) Напомним, что основаниями являются две параллельные стороны трапеции. Высота (или высота) трапеции — это перпендикулярное расстояние между двумя основаниями.
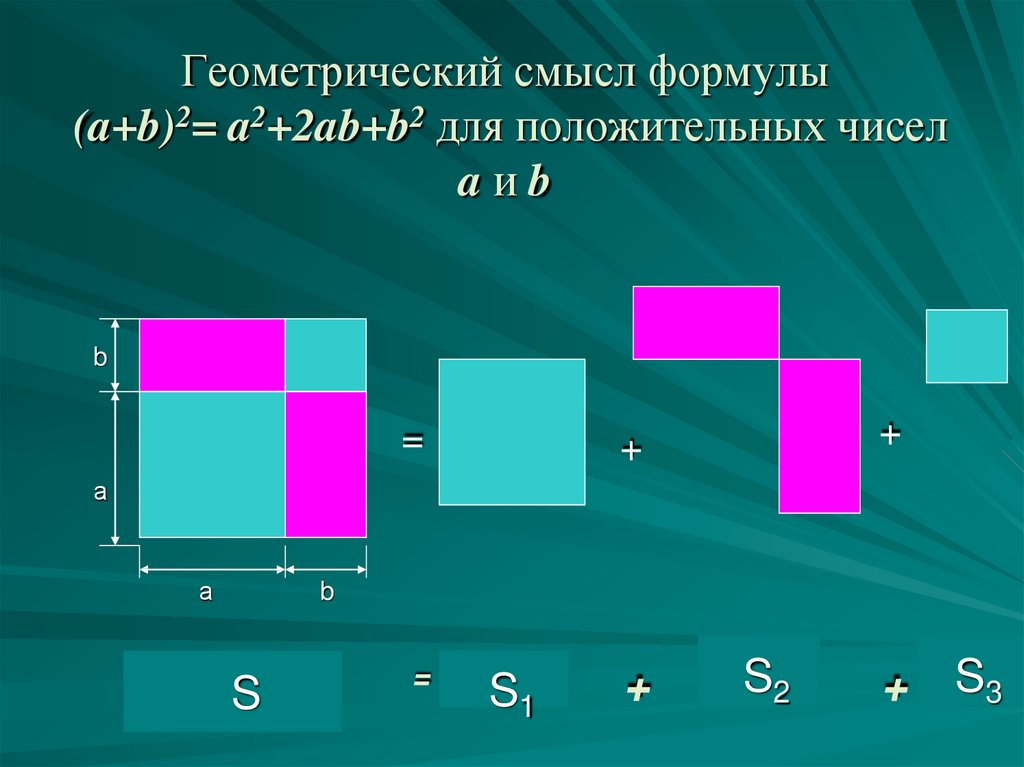 Формула гипотенузы = √((основание)2 + (высота)2) (или) c = √(a2 + b2) .
Формула гипотенузы = √((основание)2 + (высота)2) (или) c = √(a2 + b2) . х, у.
х, у.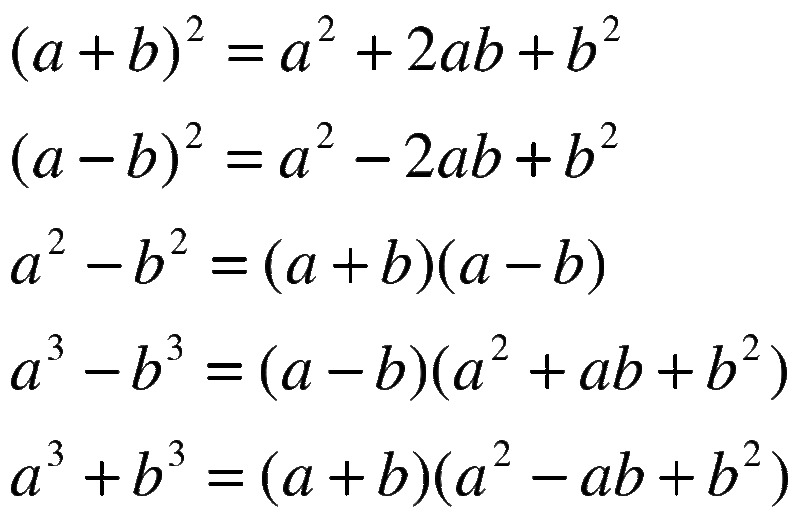
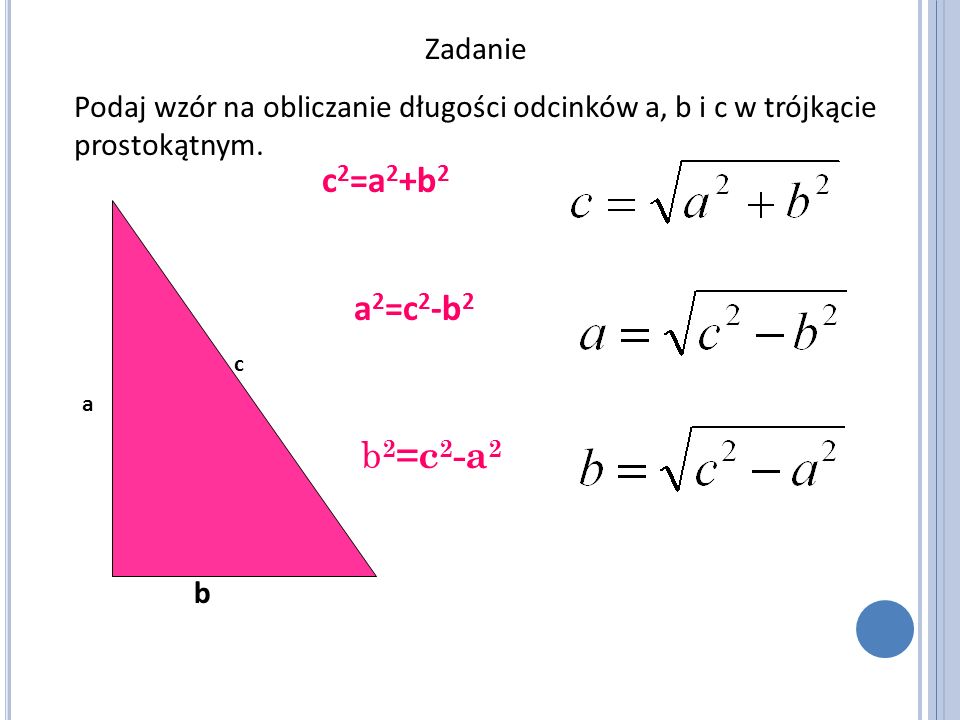
 (A+B+C) ² = A²+B²+C²+2AB+2BC+2CA
(A+B+C) ² = A²+B²+C²+2AB+2BC+2CA 4ab = (a + b)² – (a – b)²
4ab = (a + b)² – (a – b)²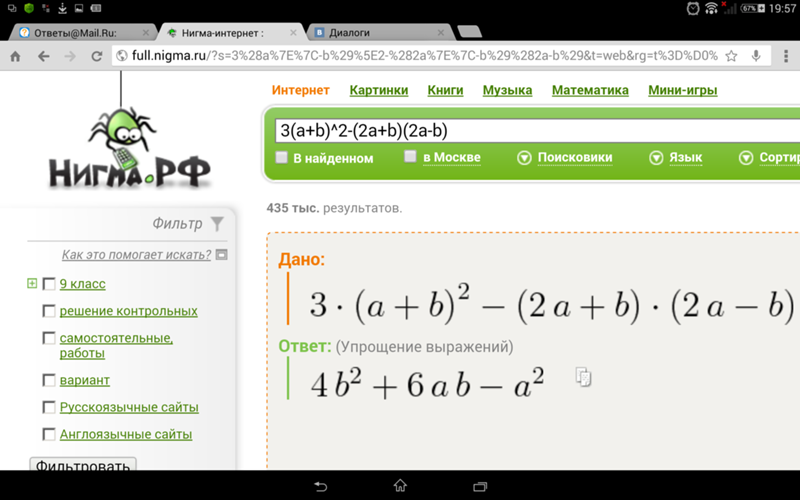
 मान 1 रखने पर
मान 1 रखने पर

 . (i)
. (i)


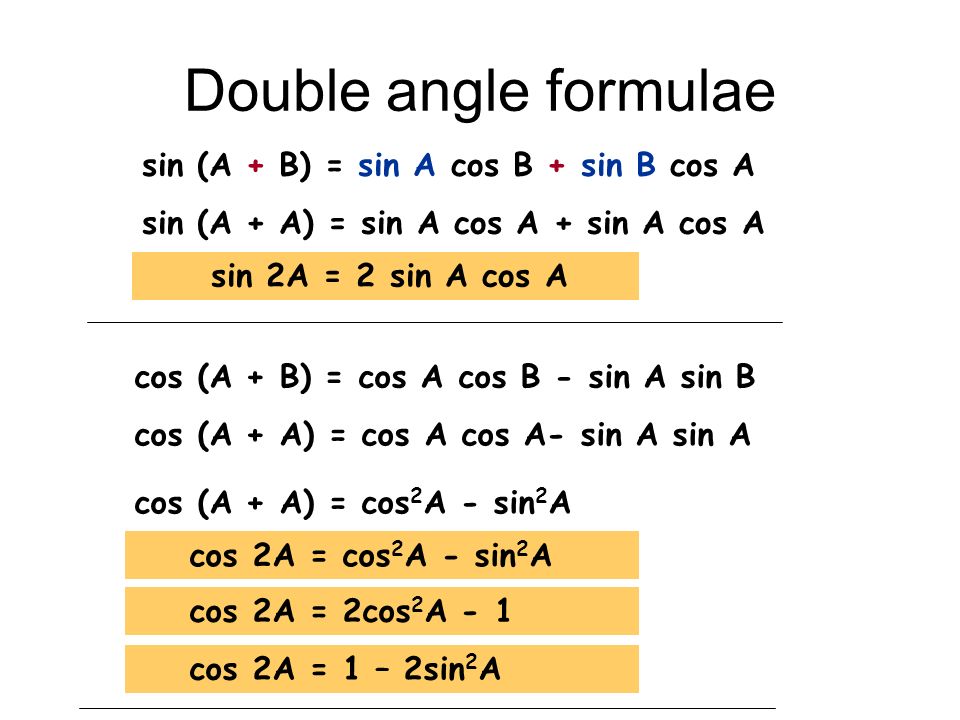
 Да-да, вы не ослышались ― именно прочитать, можно даже слегка нараспев и с выражением. У нас есть два числа в квадрате, и мы вычитаем одно из другого. Таким образом, у нас есть разница квадратов (слово «чисел» обычно опускается). Собственно, это и есть формальное название этой формулы.
Да-да, вы не ослышались ― именно прочитать, можно даже слегка нараспев и с выражением. У нас есть два числа в квадрате, и мы вычитаем одно из другого. Таким образом, у нас есть разница квадратов (слово «чисел» обычно опускается). Собственно, это и есть формальное название этой формулы.
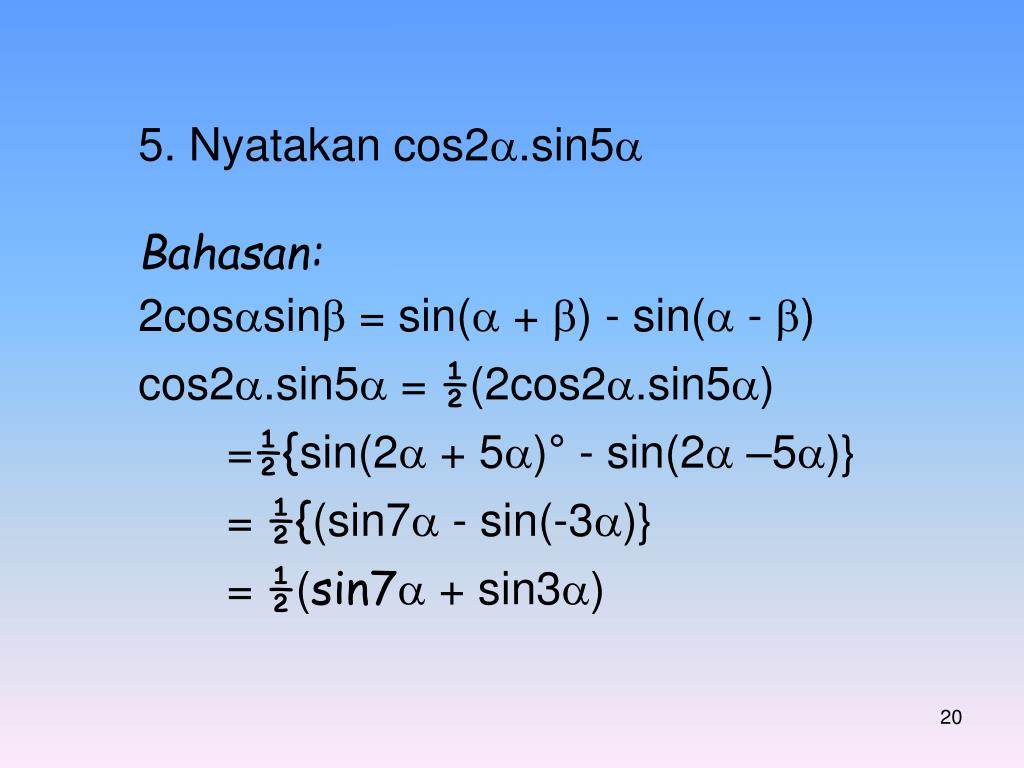
 Может, оно и к лучшему):
Может, оно и к лучшему): Сейчас же давайте ещё раз повторим, что мы узнали:
Сейчас же давайте ещё раз повторим, что мы узнали:

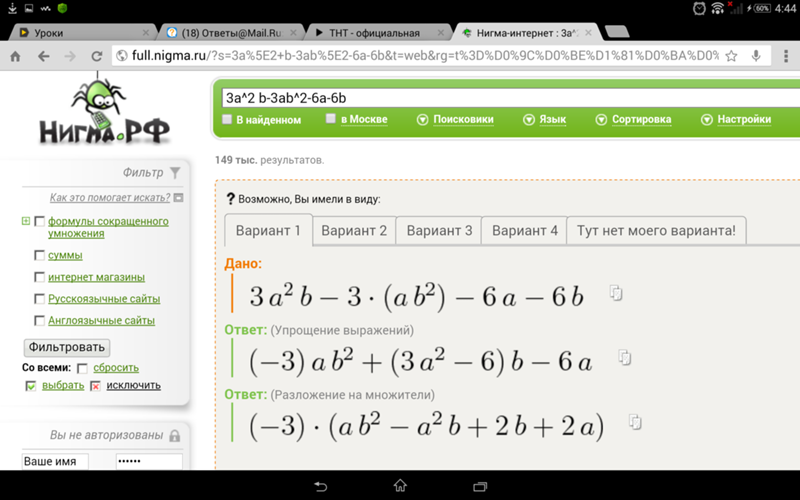
 Утверждение о существовании и единственности канонического разложения называется основной теоремой арифметики.
Утверждение о существовании и единственности канонического разложения называется основной теоремой арифметики. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.014 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.014 с.)
 79 Mb.
79 Mb.

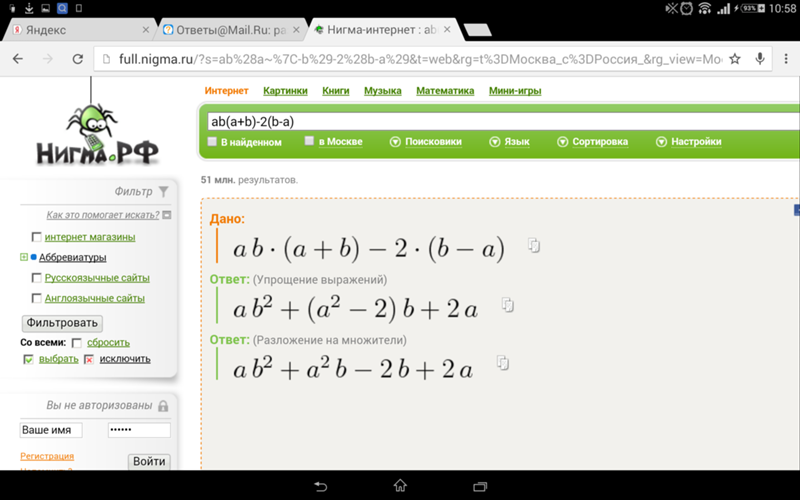

 4 дня
формула a2-b2 ответы
0
2,1 тыс. 3 дня
формула a2-b2
0
350 31 авг
примеры формул a2 – b2
0
300 1 сен
формула a2-b2 по математике
2
250 31 авг
формула a2 -b2
Н/Д
150
Вопросы по формуле a2-b2
Таблица формул 0алгебры
24
6,3 тыс. 2 дня
основная формула алгебры
28
2,1 тыс. 4 дня
вся формула алгебры
21
2.0K 4 дня
формула математической алгебры
18
1,3 тыс. 2 дня
формула математической алгебры
18
1,1 тыс. 4 дня
список формул алгебры
28
700 6 дней
вся формула алгебры pdf
16
700 в день
формула булевой алгебры
28
600 2 дня
формула алгебрыpdf
0
600 в день
формула алгебры ssc
Зарегистрируйтесь в Ahrefs
300 1 августа
алгебраическая формула для ssc cgl
300
10-я формула алгебры
200 1 августа
формула алгебры на хинди
200 25 июл
формула алгебры класс 10
200 24 июл
формула алгебры pdf скачать
200 23 июл
формула линейной алгебры
200 4 дня
формула алгебры класс 7
200 22 июл
формула элементарной алгебры
150 1 авг.
формула ab алгебры
150 26 июн
формула алгебры класс 8
150 22 июл
формула базовой алгебрыpdf
150
что такое алгебраическая формула
150 28 июл
важная формула алгебры
100 27 июл
формула алгебры класс 6
100
9Таблица формул алгебры th класса
100 22 июл
формула шпаргалки по алгебре
100 3 августа
лист формул алгебры
100 28 июл
вопросы по формулам алгебры
90 22 июл
формула кубической алгебры
90
формула алгебры все
80
лист формул алгебры pdf
70 в день
алгебраическая формула для ssc
70 1 авг.
4 дня
формула a2-b2 ответы
0
2,1 тыс. 3 дня
формула a2-b2
0
350 31 авг
примеры формул a2 – b2
0
300 1 сен
формула a2-b2 по математике
2
250 31 авг
формула a2 -b2
Н/Д
150
Вопросы по формуле a2-b2
Таблица формул 0алгебры
24
6,3 тыс. 2 дня
основная формула алгебры
28
2,1 тыс. 4 дня
вся формула алгебры
21
2.0K 4 дня
формула математической алгебры
18
1,3 тыс. 2 дня
формула математической алгебры
18
1,1 тыс. 4 дня
список формул алгебры
28
700 6 дней
вся формула алгебры pdf
16
700 в день
формула булевой алгебры
28
600 2 дня
формула алгебрыpdf
0
600 в день
формула алгебры ssc
Зарегистрируйтесь в Ahrefs
300 1 августа
алгебраическая формула для ssc cgl
300
10-я формула алгебры
200 1 августа
формула алгебры на хинди
200 25 июл
формула алгебры класс 10
200 24 июл
формула алгебры pdf скачать
200 23 июл
формула линейной алгебры
200 4 дня
формула алгебры класс 7
200 22 июл
формула элементарной алгебры
150 1 авг.
формула ab алгебры
150 26 июн
формула алгебры класс 8
150 22 июл
формула базовой алгебрыpdf
150
что такое алгебраическая формула
150 28 июл
важная формула алгебры
100 27 июл
формула алгебры класс 6
100
9Таблица формул алгебры th класса
100 22 июл
формула шпаргалки по алгебре
100 3 августа
лист формул алгебры
100 28 июл
вопросы по формулам алгебры
90 22 июл
формула кубической алгебры
90
формула алгебры все
80
лист формул алгебры pdf
70 в день
алгебраическая формула для ssc
70 1 авг. формула алгебры 8 класса
70
все формулы алгебры pdf скачать
60 1 формула авгмата
22
44К 19 часов
диаграмма математической формулы
21
3,8 тыс. 2 дня
математическая формула класс 10
13
2,9 тыс. 3 дня
математическая формулаpdf
10
1,9 тыс. 5 дней
математическая формула на хинди
0
1,6 тыс. 7 дней
Таблица математических формул на хинди в формате pdf
0
1,4 тыс. 7 дней
математическая формула класс 93
1,4 тыс. 5 дней
математическая формула класс 8
4
1.0K 4 дня
10-я математическая формула
14
700 2 дня
область математической формулы
38
700 2 дня
простая математическая формула
Зарегистрируйтесь в Ahrefs
600 3 часа
12-я математическая формула
600 6 дней
все математические формулы
600 в день
математическая формула на хиндиpdf
500 7 дней
математическая формула класс 7
500 29 июл
математическая формула 9 класс pdf
500 16 часов
продвинутая математическая формула
500 24 июл
математическая формула 10 класс
500 7 дней
математическая формула в формате pdf на хинди
500 7 дней
математическая формула объема
450 17 часов
расширенная математическая формула
400 26 июл
математическая формула круга
400
математическая формула ряда
400
ап математическая формула
400
9 классвсе математические формулы 9 класса
400 2 дня
6 класс математическая формула
350 31 июл
математическая формула 6 класс
350
9-я математическая формула
350 24 июл
10 класс все математические формулы
300 4 дня
буклет с математическими формулами
300 19 июл
Математическая формула для 9 класса.
формула алгебры 8 класса
70
все формулы алгебры pdf скачать
60 1 формула авгмата
22
44К 19 часов
диаграмма математической формулы
21
3,8 тыс. 2 дня
математическая формула класс 10
13
2,9 тыс. 3 дня
математическая формулаpdf
10
1,9 тыс. 5 дней
математическая формула на хинди
0
1,6 тыс. 7 дней
Таблица математических формул на хинди в формате pdf
0
1,4 тыс. 7 дней
математическая формула класс 93
1,4 тыс. 5 дней
математическая формула класс 8
4
1.0K 4 дня
10-я математическая формула
14
700 2 дня
область математической формулы
38
700 2 дня
простая математическая формула
Зарегистрируйтесь в Ahrefs
600 3 часа
12-я математическая формула
600 6 дней
все математические формулы
600 в день
математическая формула на хиндиpdf
500 7 дней
математическая формула класс 7
500 29 июл
математическая формула 9 класс pdf
500 16 часов
продвинутая математическая формула
500 24 июл
математическая формула 10 класс
500 7 дней
математическая формула в формате pdf на хинди
500 7 дней
математическая формула объема
450 17 часов
расширенная математическая формула
400 26 июл
математическая формула круга
400
математическая формула ряда
400
ап математическая формула
400
9 классвсе математические формулы 9 класса
400 2 дня
6 класс математическая формула
350 31 июл
математическая формула 6 класс
350
9-я математическая формула
350 24 июл
10 класс все математические формулы
300 4 дня
буклет с математическими формулами
300 19 июл
Математическая формула для 9 класса. 300 3 дня
математическая формула pdf скачать
300 19 июл
математическая формула 9 класс
300 7 дней
математическая формула класс 6
300 26 Июл5.1K 4 дня
Решение учебника по математике для 7 класса
5,0 тыс. 5 дней
математический проект
4,9 тыс. 2 дня
9 класс математика
4,6 тыс. в день
математический решатель майкрософт
4,6К 3 часа
математический клипарт
4,6 тыс. 3 дня
фото математика
4,6 тыс. 2 дня
10 класс математика
4,6 тыс. 2 дня
доска для математики 8 класс
4,5 тыс. в день
математическая магия
4,5 тыс. 5 дней
книга по математике
4,5 тыс. 4 дня
название математических символов
4,3 тыс. 4 дня
8 класс математика
4,2 тыс. 4 дня
значит по математике
4,2 тыс. в день
математические загадки
4,2К 21 час
6 класс математики
4,1 тыс. 21 час
модель задание задание 7 класс математика
4.0K 3 дня
модель задание задание 6 класс математика
4.0K 2 дня
решение по математике 10 класс
3,8 тыс. 2 дня
математические головоломки
3,8 тыс. 4 дня
диаграмма математической формулы
3,8 тыс. 2 дня
решение по математике 12 класс
3,8 тыс.
300 3 дня
математическая формула pdf скачать
300 19 июл
математическая формула 9 класс
300 7 дней
математическая формула класс 6
300 26 Июл5.1K 4 дня
Решение учебника по математике для 7 класса
5,0 тыс. 5 дней
математический проект
4,9 тыс. 2 дня
9 класс математика
4,6 тыс. в день
математический решатель майкрософт
4,6К 3 часа
математический клипарт
4,6 тыс. 3 дня
фото математика
4,6 тыс. 2 дня
10 класс математика
4,6 тыс. 2 дня
доска для математики 8 класс
4,5 тыс. в день
математическая магия
4,5 тыс. 5 дней
книга по математике
4,5 тыс. 4 дня
название математических символов
4,3 тыс. 4 дня
8 класс математика
4,2 тыс. 4 дня
значит по математике
4,2 тыс. в день
математические загадки
4,2К 21 час
6 класс математики
4,1 тыс. 21 час
модель задание задание 7 класс математика
4.0K 3 дня
модель задание задание 6 класс математика
4.0K 2 дня
решение по математике 10 класс
3,8 тыс. 2 дня
математические головоломки
3,8 тыс. 4 дня
диаграмма математической формулы
3,8 тыс. 2 дня
решение по математике 12 класс
3,8 тыс. 2 дня
брикс математика ком
3,7 тыс. 4 дня
Селина 10 класс математика
3,7 тыс. 3 дня
модель задание задание 5 класс математика
3,7 тыс. 3 дня
табби математика логин
3,6 тыс. 3 дня
Академия Тивари 9 классй математика
3,6 тыс. 3 дня
вопросы по математике
3,6 тыс. 5 дней
математическая площадка
3,6 тыс. 3 дня
бихар доска класс 8 математическое решение
3,5 тыс. 4 дня
математический решатель онлайн
3,5 тыс. 14 часов
математические обои
3,4 тыс. 4 дня
математический лист
3,3 тыс. 4 дня
математика
3,3 тыс. 4 дня
математические рабочие листы
3,3 тыс. 3 дня
значение символа в математике
3,3 тыс. 2 дня
идеи математических проектов
3,3 тыс. 3 дня
математика 9 класс
3,3 тыс. 2 дня
sd yadav математическая книга
3,3 тыс. 4 дня
белур математический тайминг
3,3 тыс. 4 дня
математика в шестом классе
3,2 тыс. 4 дня
9 класс математика глава 1 mcq
3,2 тыс. 3 дня
экзамен по математике 10 класс
3,2 тыс. 2 дня
10 класс математика
3,2 тыс. 2 дня
математический день
3,1 тыс. 3 дня
первый по математике
3,1 тыс. 2 дня
лист по математике для 3 класса
3,1 тыс.
2 дня
брикс математика ком
3,7 тыс. 4 дня
Селина 10 класс математика
3,7 тыс. 3 дня
модель задание задание 5 класс математика
3,7 тыс. 3 дня
табби математика логин
3,6 тыс. 3 дня
Академия Тивари 9 классй математика
3,6 тыс. 3 дня
вопросы по математике
3,6 тыс. 5 дней
математическая площадка
3,6 тыс. 3 дня
бихар доска класс 8 математическое решение
3,5 тыс. 4 дня
математический решатель онлайн
3,5 тыс. 14 часов
математические обои
3,4 тыс. 4 дня
математический лист
3,3 тыс. 4 дня
математика
3,3 тыс. 4 дня
математические рабочие листы
3,3 тыс. 3 дня
значение символа в математике
3,3 тыс. 2 дня
идеи математических проектов
3,3 тыс. 3 дня
математика 9 класс
3,3 тыс. 2 дня
sd yadav математическая книга
3,3 тыс. 4 дня
белур математический тайминг
3,3 тыс. 4 дня
математика в шестом классе
3,2 тыс. 4 дня
9 класс математика глава 1 mcq
3,2 тыс. 3 дня
экзамен по математике 10 класс
3,2 тыс. 2 дня
10 класс математика
3,2 тыс. 2 дня
математический день
3,1 тыс. 3 дня
первый по математике
3,1 тыс. 2 дня
лист по математике для 3 класса
3,1 тыс. 3 дня
решатель математических задач
3,1 тыс. 14 часов
9 классматематическое решение
3,1 тыс. 2 дня
решение математических задач 11K 3 дня формула a3-b3
0
35 тыс. 5 дней
формула а3 – b3
0
5,2 тыс. 3 дня
решение формулы a3-b3
0
1.4K 4 сен
формула a3 -b3
Н/Д
300
формула a3-b3
0
200 29 авг
формула a3-b3 по математике
Н/Д
70
формула а³-b³
0
70 6 сен
формула a3 -b3 математика
Н/Д
20
формула a3-b3 вики
Н/Д
10
Вопросы по формуле a3-b3
Н/Д
10
что такое формула a3-b3
Зарегистрируйтесь в Ahrefs
10
математические формулы a3-b3
10
формула а3-б3 формула
10
формула a3 – b3 по математике
10
Пример формулы a3-b3
10
3a2b 3ab2 a3-b3 формула 10K 4 дня
математический решатель
81
9.8K 4 дня
8 класс математики
Зарегистрируйтесь в Ahrefs
9,6 тыс. 3 дня
rs aggarwal книга по математике
9,4 тыс. 4 дня
математическое решение
9,3 тыс. 4 дня
крутые математические игры
9,3 тыс. 2 дня
9 класс математики
8,6 тыс. 3 дня
ncert 9 класс математическое решение
8,4К 19 часов
математические игры
8,3 тыс. 3 дня
8 класс математика
8,2 тыс.
3 дня
решатель математических задач
3,1 тыс. 14 часов
9 классматематическое решение
3,1 тыс. 2 дня
решение математических задач 11K 3 дня формула a3-b3
0
35 тыс. 5 дней
формула а3 – b3
0
5,2 тыс. 3 дня
решение формулы a3-b3
0
1.4K 4 сен
формула a3 -b3
Н/Д
300
формула a3-b3
0
200 29 авг
формула a3-b3 по математике
Н/Д
70
формула а³-b³
0
70 6 сен
формула a3 -b3 математика
Н/Д
20
формула a3-b3 вики
Н/Д
10
Вопросы по формуле a3-b3
Н/Д
10
что такое формула a3-b3
Зарегистрируйтесь в Ahrefs
10
математические формулы a3-b3
10
формула а3-б3 формула
10
формула a3 – b3 по математике
10
Пример формулы a3-b3
10
3a2b 3ab2 a3-b3 формула 10K 4 дня
математический решатель
81
9.8K 4 дня
8 класс математики
Зарегистрируйтесь в Ahrefs
9,6 тыс. 3 дня
rs aggarwal книга по математике
9,4 тыс. 4 дня
математическое решение
9,3 тыс. 4 дня
крутые математические игры
9,3 тыс. 2 дня
9 класс математики
8,6 тыс. 3 дня
ncert 9 класс математическое решение
8,4К 19 часов
математические игры
8,3 тыс. 3 дня
8 класс математика
8,2 тыс.