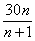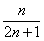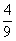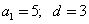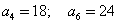Формула арифметической прогрессии суммы: Арифметическая прогрессия

Арифметическая прогрессия. Сумма арифметической погрессии

Первую часть статьи об арифметической прогрессии смотрим здесь.

Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100.

Юный Гаусс (10 лет) мгновенно получил результат: 5050.

1+2+3+4+5+5+…+97+98+99+100=?

А как бы считали вы?

+ показать

Первое и последнее слагаемые суммы дают 101, также как и второе и предпоследнее слагаемые и т.д. Всего таких пар будет 50. Вот и все!

Вот по такому же принципу мы и будем считать сумму n-первых членов арифметической прогрессии.

Пример.

Найдем сумму двадцати первых членов арифметической прогрессии

-9, -6, -3, 0, 3, …

Решение:

Мы пока не знакомы с формулой суммы n-первых членов арифметической прогрессии, давайте будем следовать тому же принципу, что и при вычислении суммы натуральных чисел от 1 до 100.

Найдем $a_{20}$ по формуле n-го члена арифметической прогрессии:

$a_{20}=a_1+19d$ , где – разность арифметической прогрессии.

$a_{20}=48;$

Сумма чисел из ряда -9, -6, -3, 0, 3, …48 состоит из 10 одинаковых слагаемых, равных 39.

Значит, сумма указанных чисел окажется равной 390.

Ответ: 390.

Содержание

Сумма n первых членов арифметической прогрессии
Сумма первых   членов арифметической прогрессии  может быть найдена по формулам
1) $S_n=\frac{a_1+a_n}{2}\cdot n$
2) $S_n=\frac{2a_1+(n-1)d}{2}\cdot n$
,
где   — первый член прогрессии,  — член с номером ,  — количество суммируемых членов.
(Вторая формула – результат подстановки формулы
в первую формулу).
Примеры
Пример 1.
Арифметическая прогрессия задана формулой
Найдите сумму первых десяти членов прогрессии.
Решение: + показать
Пример 2.
Найдите сумму натуральных четных чисел, не превосходящих 40.
Решение:  + показать
Перед нами арифметическая прогрессия: 2; 4; 6; … 38; 40.
$a_1=2,\;d=2,\;n=20$
Воспользуемся формулой $S_n=\frac{2a_1+(n-1)d}{2}\cdot n$
:
$S_{20}=\frac{2a_1+(20-1)d}{2}\cdot 20;$
$S_{20}=\frac{4+38}{2}\cdot 20=420;$
Ответ: 420.

Пример 3.
Сколько последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы их сумма была равна 153?
Решение:  + показать
Шаг (
) равен 1;
Обращаемся к формуле $S_n=\frac{2a_1+(n-1)d}{2}\cdot n$ :
$153=\frac{2\cdot 1+(n-1)\cdot 1}{2}\cdot n;$
$153=\frac{1+n}{2}\cdot n;$
$n=\frac{-1\pm\sqrt{1-4\cdot (-306)}}{2};$
Поскольку мы работаем с натуральными , то
Ответ: 17.

Пример 4.
Арифметическая прогрессия задана формулой
Найдите сумму членов данной прогрессии с 5-го по 16 включительно.
Решение:  + показать
Найдем первые два члена прогрессии и разность прогрессии:
$a_1=103-5\cdot 1=98;$
$a_2=103-5\cdot 2=93;$
Последовательность чисел арифметической прогрессии, начиная с 5-го (по 16), – также арифметическая прогрессия.
Поэтому обозначим $b_1=a_5,\;b_2=a_6$ и т.д., будем считать сумму двенадцати первых членов арифметической прогрессии {} по формуле $S_n=\frac{2a_1+(n-1)d}{2}\cdot n$ :
$S_{12}=\frac{2b_1+(12-1)d}{2}\cdot 12,$
где $b_1=a_5=103-5\cdot5=78;$
$S_{12}=\frac{156-55}{2}\cdot 12=606;$
Ответ: 606.

Пример 5.
Найдите сумму двузначных натуральных чисел, не кратных 4.
Решение: + показать
Двузначные числа: 10; 11; 12; 13; … 97; 98; 99.
Если вычеркнуть в ряду числа, кратные 4,
то оставшиеся числа не будут собою образовывать арифметическую прогрессию, а значит, их сумму мы не сможем посчитать по указанным выше формулам.
Мы поступим так:
1) вычислим сумму $S_{dvuznach}$ всех двузначных чисел;
2) вычислим сумму всех двузначных чисел $S_{:4}$ , кратных 4, то есть 12+16+…+96;
3) из суммы $S_{dvuznach}$ вычтем сумму $S_{:4}$ ;
Итак, $S_{dvusnach}=\frac{10+99}{2}\cdot 90=4905;$
Как узнать количество двузначных чисел, кратных 4?
Обозначим порядковый номер числа 96 в ряду 12, 16, … 96 за . Сам ряд, конечно же, образует арифметическую прогрессию ().
Найдем .
Тогда $S_{:4}=\frac{12+96}{2}\cdot 22=1188;$
Итак, $S=S_{dvuznach}-S_{:4}=4905-1188=3717;$
Ответ: 3717.

Вы можете пойти тест по теме «Сумма арифметической прогрессии».

Сумма арифметической прогрессии | Онлайн калькулятор

Когда речь идет о таком параметре, как сумма арифметической прогрессии, подразумевается всегда сумма первых членов арифметической прогрессии

или сумма членов прогрессии с k по n, то есть количество членов, которые берутся для суммы, строго ограничено в заданных условием пределах. В противном случае задание не будет иметь решения, так как вся числовая последовательность именно арифметической прогрессии начинается с конкретного числа — первого члена a₁, и продолжается бесконечно.

Бытует мнение, что формула суммы арифметической прогрессии была открыта еще Гауссом, как быстрый и точный способ расчета суммы чисел в определенной последовательности. Он заметил, что такая прогрессия является симметричной, то есть сумма симметрично расположенных с начала и конца членов прогрессии является постоянной для данного ряда.

a₁+a_n=a₂+a_(n-1)=a₃+a_(n-2)=⋯

Соответственно, он нашел данную сумму и умножил ее на половину от общего количества чисел в последовательности, участвующих в расчете суммы. Таким образом, была выведена

формула суммы арифметической прогрессии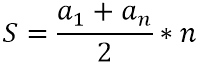

Пример. Предположим, задано условие: «Найдите сумму первых десяти (10) членов арифметической прогрессии». Для этого понадобится следующие данные: разность прогрессии и первый ее член. Если в задаче дан какой-либо n член арифметической прогрессии вместо первого, тогда сначала нужно воспользоваться разделом, где представлена формула нахождения первого члена прогрессии, и найти его. Затем исходные данные вбиваются в калькулятор и он производит расчеты, складывая первый и десятый члены, и умножая полученную сумму на половину от общего количества складываемых членов – на 5. Аналогично происходит, если нужно найти сумму первых шести членов или любого другого количества.

В случае, когда необходимо найти сумму членов арифметической прогрессии

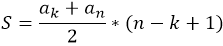
, начинающихся не с первого, а с пятого члена, к примеру, тогда среднее арифметическое остается тем же, а общее количество членов берется как увеличенная на единицу разность между порядковыми номерами взятых членов.

Смотрите также

Арифметическая прогрессия — методическая рекомендация. Алгебра, 9 класс.

1.	Разность арифметической прогрессии	2 вид — интерпретация	лёгкое	1 Б.	Вычисление разности арифметической прогрессии, если даны последовательные члены прогрессии.
2.	Нахождение члена и разности арифметической прогрессии	2 вид — интерпретация	лёгкое	1 Б.	Нахождение следующего члена арифметической прогрессии, если даны два предыдущих, разность прогрессии.
3.	Нахождение членов арифметической прогрессии	2 вид — интерпретация	лёгкое	5 Б.	Нахождение первых четырёх и десятого членов арифметической прогрессии, если дана общая формула.
4.	Сумма членов арифметической прогрессии	2 вид — интерпретация	среднее	1 Б.	Нахождение суммы первых n членов арифметической прогрессии, если известны первый член и разность.
5.	Нахождение члена арифметической прогрессии, даны разность и первый член	2 вид — интерпретация	среднее	3 Б.	Вычисление n-ого члена арифметической прогрессии, если даны разность и первый член прогрессии.
6.	Сумма первых членов арифметической прогрессии	2 вид — интерпретация	среднее	4 Б.	Вычислить сумму первых n членов арифметической прогрессии, если даны первые два члена.
7.	Разность арифметической прогрессии	2 вид — интерпретация	лёгкое	2 Б.	Вычисление разности и третьего члена арифметической прогрессии.
8.	Сумма членов арифметической прогрессии	2 вид — интерпретация	среднее	2 Б.	Вычисление суммы членов арифметической прогрессии, если даны два первых члена.
9.	Прогрессия в текстовой задаче, вычисление высоты	2 вид — интерпретация	среднее	4 Б.	Использование прогрессии при вычислении высоты.
10.	Сумма натуральных чисел	3 вид — анализ	сложное	4 Б.	В условии дан остаток деления. При решении используется неравенство.
11.	Вычисление разности при наименьшем значении членов прогрессии	3 вид — анализ	сложное	4,5 Б.	При вычислении используются свойства квадратичной функции.
12.	Арифметическая прогрессия и трапеция	2 вид — интерпретация	сложное	8 Б.	Трапеция и арифметическая прогрессия.

Арифметическая прогрессия, формула суммы элементов, разности, произведения, примеры с решением, чем отличается от геометрической

Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией.

Одна из главных отличительных особенностей такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций.

Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др.

Онлайн-калькулятор арифметической прогрессии

Определение и примеры арифметической прогрессии

Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.

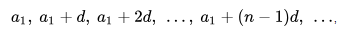
Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности.

Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.

Кроме этого, существуют виды таких рядов:

возрастающая – числа ряда увеличиваются по своему значению,
убывающая – каждое последующее число ряда уменьшается.

В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.

Виды арифметической (алгебраической) прогрессии

Разновидности строятся на основании характеристики разности (d), а именно на основании отличия последней от нуля.

Таким образом, можно встретить определенные вариации:

разность d&lt,0 – прогрессия будет считаться убывающей, а каждый последующий член будет меньше предыдущего,
разность d&gt,0 – это предполагает, что каждый член в ряду будет больше предыдущего, а прогрессию будут называть возрастающей,
при d=0 ряд тоже будет иметь свойства прогрессии, которую именуют стационарной, и все члены будут одинаковыми (не будут изменяться).

Если прогрессия не изменяется с каждым шагом на одну и ту же разность, то эта прогрессия непостоянная и арифметической не является.

Важно знать: арифметическая от геометрической отличается тем, что в последней производится увеличение каждого последующего на один и тот же множитель.

Формулы арифметической прогрессии

Одно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда.

Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (an-1), к которому прибавляют разность (d):

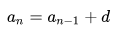
Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки.

Итак, нам понадобится значение первого числа в ряду (a1) и последнего (an), а также информация об общем количестве чисел в ряду. Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом:

Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы.

Произведение членов арифметической прогрессии можно находить по похожей формуле:

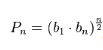
где, Pn – произведение, b1 и bn – соответственно первое и последнее числа, а n – количество членов.

Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента:

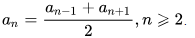
Примеры задач с решением

Рассмотрим как решать задачи на заданную тему.

Пример 1

Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…».

Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a1) и о разности (d). Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – и получаем d = 7. Теперь мы можем считать по формуле:

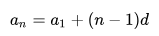
Подставляя полученные значения, получим выражение вида a574 = 8 + (574-1) * 7.

После вычисления получаем ответ: a574 = 4019.

Пример 2

Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8.

Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера:

Подставляя известные значения, получаем выражение – а544 = 17 + (544 1) * 8.

Вычисляя, получаем ответ а544 = 4361.

Пример 3

Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов.

Требуется выяснить, сколько времени у студента ушло на подготовку.

Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных:

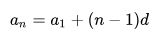
После подстановки получаем выражение: 730 = 17 + (n 1) * 27.

После вычислений определяем ответ – 27 дней.

Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется.

Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм.

Калькулятор арифметической прогрессии с формулами и примерами решений

Представим, что подряд выписаны все четные натуральные числа: 2, 4, 6, 8, 10, 12, 14, 18, 18, 20, 22… Это — последовательность четных натуральных чисел. Число 2 — ее первый член, 4 — второй, 6 — третий, 20 — десятый и т. д.

Приведем еще несколько примеров числовых прогрессий:

1, 2, 3, 4, 5… — последовательность натуральных чисел,
1, 3, 5, 7, 9… — последовательность нечетных натуральных чисел,
1, 1/2, 1/3, 1/4, 1/5… – последовательность чисел, обратных к натуральным.

Последовательности бывают конечные и бесконечные. Конечной, например, есть последовательность однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Последовательность всех натуральных чисел — бесконечная. Записывая бесконечную последовательность, после нескольких ее первых членов ставят многоточие. Первый, второй, третий члены последовательности четных натуральных чисел равны соответственно 2, 4, 6. Пишут: a1 = 2, а2 = 4, а3 = 6

А чему равен ее n-й член An? Поскольку каждый член последовательности парных натуральных чисел вдвое больше от своего порядкового номера, то ее n-й член равен 2n, т. е.

An = 2n.

Это формула n-го члена последовательности парных натуральных чисел.

An = 2n − 1

Формула n-го члена последовательности нечетных натуральных чисел.

Если известна формула n-го члена последовательности, то нетрудно вычислить любой ее член. Напишем несколько первых членов последовательности, n-й член которой:

An = n² + 2

Предоставляя переменной п значения 1, 2, 3, 4, 5… получим первые члены последовательности: 6, 11, 18, 27, 38, 51… Тысячный член этой последовательности а1000 = 1000² + 2 = 1000002.

Гораздо труднее решать обратную задачу — для данной последовательности найти ее n-й член. Например, формула n-го члена последовательности простых чисел: 2, 3, 5, 7, 11, 13… — неизвестна до сих пор, хотя математики искали ее более 2000 лет.

Несколько первых членов последовательности не задают ее однозначно.

Например, существует множество различных последовательностей, первые члены которых 2, 4, 6, 8. В частности, такие первые члены имеют последовательности, n-е члены которых:

An = 2n
Cn = 2 n + (n − 1) (n − 2) (n − 3) (n − 4)

Из двух соседних членов a1 и a2 последовательности член a2 называют следующим за а1, а а1 — предыдущим по отношению к а2. Последовательность называют растущей, если каждый ее член, начиная со второго, больше предыдущего. Последовательность называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего.

Замечания

Иногда рассматривают также прогрессивности, членами, которых являются различные выражения, функции, фигуры то что. Можно говорить и о последовательности месяцев в году, дней в неделе, букв в слове, фамилий в списке, вагонов в поезде, станций на железной дороге и т. д. Мы дальше будем говорить только о числовых последовательностях, хотя и зовем их коротко последовательностями.

Понятие арифметической прогрессии

Арифметической прогрессией называется прогрессивность, каждый член которой, начиная со второго, равен предыдущему члену, к которому добавляют одно и то же число. Это постоянное для данной последовательности число d называется разницей арифметической прогрессии.

Первый член и разность арифметической прогрессии могут быть какими угодно числами. Арифметическая прогрессия растущая, если ее разница положительная, или нисходящая, если ее разница отрицательная.

Пример нисходящей арифметической прогрессии: 11, 9, 7, 5, 3, 1, −1, −3…

Чтобы получить любой член арифметической прогрессии, начиная со второго, надо к предыдущему члена добавить разницу d. Поэтому если первый член и разность арифметической прогрессии равны соответственно а и d, то первые члены этой арифметической прогрессии:

a1, a1 + d, a1 + 2d, a1 + 3d, a1 + 4d…

Обратите внимание: коэффициент при d на 1 меньше порядкового номера члена прогрессии. Так же находим а6 = а1 + 5d, а7 = а1 + 6d и вообще:

An = a1 + (n − 1)d

Это формула n-го члена арифметической прогрессии. Сумма членов конечной арифметической прогрессии равна полусумме крайних ее членов, умноженной на число членов.

Sn = [(a1 + an) / 2] × n

Примеры задач

Пример 1

В арифметической прогрессии a1 = 4, d = 3. Найдите a20.

В калькуляторе задаем:

Первое число: 3
Последнее число: 20
Разница (шаг): 3

Получаем:

Арифметическая прогрессия: 61
Сумма членов прогрессии: 650
Последовательность: 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55, 58, 61

Проверяем самостоятельно по формулам с теории:

a20 = а1 + 19d = 4 + 19 × 3 = 61

Пример 2

Найдите сумму первых двадцати членов арифметической прогрессии 5, 7, 9…

В калькуляторе задаем:

Первое число: 5
Последнее число: 20
Разница (шаг): 2

Результаты рассчета:

Арифметическая прогрессия: 43
Сумма членов прогрессии: 480
Последовательность: 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43

Проверяем:

Здесь а1 = 5, d = 2. Поэтому а20 = 5 + 19 × 2 = 43
S = [(5 + 43) / 2] × 20 = 480

Онлайн-калькулятор делает вычисления намного проще: он экономит время, избавляя от необходимости делать вычисления вручную по формулам.

Урок по алгебре на тему «формула суммы n-членов арифметической прогрессии»

«Формула суммы n-членов арифметической прогрессии»

Цель урока: Вывести формулу суммы n-членов арифметической прогрессии, выработать навыки непосредственного применения данной формулы.

Задачи урока:

Учебная: познакомить учащихся с формулой суммы n-первых членов арифметической прогрессии. Выработать навыки применения формулы суммы п— первых членов арифметической прогрессии при решении заданий по данной теме.
Развивающая: развивать мыслительную деятельность учащихся, самостоятельность при решении заданий по теме. любознательность и вычислительные навыки.
Воспитательная: воспитывать интерес к предмету, внимательность.

Тип урока: Урок изучения новой темы и целевого применения изученного.

Оборудование: Электронный учебник, интерактивная доска, презентационные слайды с использованием мультимедий.

Эпиграф урока:

Давным-давно сказал один мудрец
Что прежде надо
Связать начало и конец
У численного ряда.

Ход урока

Математический диктант
Объяснение новой темы.
Закрепление темы.
Задание на дом.
Сообщения учащихся
Рефлексия

1. Математический диктант по вариантам. Двое учащихся работают на оборотной стороне доски. Взаимопроверка диктанта
  Вариант1
  Вариант2
  1
  Найти 5-й член числовой последовательности заданной формулой
  Ответ: 25.
  Найти 4-й член числовой последовательности заданной формулой
  Ответ:
  2
  Чему равна разность арифметической прогрессии: 1; 4; 7; …
  Ответ: 3
  Чему равна разность арифметической прогрессии: 3; 0; -3; -6; …
  Ответ: -3
  3
  Найдите пятый член арифметической прогрессии: 3; 7; 11; …
  Ответ: 19
  Найдите шестой член арифметической прогрессии; если
  Ответ: 20
  4
  Найти 10-й член арифметической прогрессии если
  Ответ: 43
  Найти 5-й член арифметической прогрессии если
  Ответ: 21
2. Объяснение новой темы.

Учитель: найдите сумму всех натуральных чисел от единицы до ста. Кто быстрее? Я предложила вам задачу, которую Гаусс решил в шестилетнем возрасте

Эпизод из жизни немецкого математика К. Ф. Гаусса (1777 – 1855). Когда ему было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу: «Сосчитать сумму натуральных чисел от 1 до 100 включительно: 1 + 2 + 3 + …98+99 +100. Каково же было удивление учителя, когда один из учеников (это был Гаусс) через минуту воскликнул: «Я уже решил…» Большинство учеников после долгих подсчетов получили неверный результат. В тетради Гаусса было написано одно число и притом верное: 5050

Учитель: Попытаемся найти ответ на данный вопрос. Кто увидел закономерность?

Ответ: Второе слагаемое на единицу больше первого, а предпоследнее на единицу меньше последнего, так что сумма должна быть такой же. То же будет происходить и с каждой новой парой чисел. Таких сумм 50, так как всего чисел 100 и все они разделены на пары. Значит, вся сумма равна числу 101 умноженному на 50.

Учитель: Что собой представляет последовательность чисел

1;2;3;…;98;99;100?

Ответ: арифметическую прогрессию, первый член которой 1, а разность арифметической прогрессии 1.

Учитель: Что собой представляет сумма: 1+2+3+4+…+99+100?

Ответ: Сумму арифметической прогрессии.

Учитель: тема урока : формулы суммы п— первых членов арифметической прогрессии.

Пусть сумма первых n членов арифметической прогрессии равна Sn тогда:

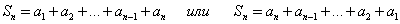
Складывая эти равенства почленно, получим:

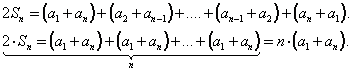
Отсюда имеем формулу:

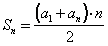Теорема

Сумма первых n членов арифметической прогрессии равна полусумме крайних членов, умноженной на число членов.

Тренировочные упражнения:

(an) – арифметическая прогрессия. a1 = 6, a5 = 26. Найти S5.
Решение: Sn = (а1+а5) : 2 × 5 Теперь вычислим сумму пяти первых членов арифметической прогрессии: S5 = (6+26) : 2 × 5=80. Ответ: 80.
(an) – арифметическая прогрессия. a1 = 12, d = — 3. Найти S16.

Решение: S16 = (а1+а16):2×16

Заметим, что в данной прогрессии не задан последний член этой суммы. Найдем 16 член прогрессии: а16 = 12+ 15×(-3) =12+(-45) =-33

Теперь вычислим сумму: S16 = (12+ (-33)) ×16: 2 = (-21) ×8 = -168. Ответ: -168.

Учитель: При решении таких задач можно воспользоваться второй формулой для нахождения Sn.

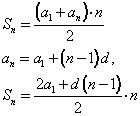
Если учесть, что

то получим формулу

Закрепление темы.

Если в арифметической прогрессии первый член равен 20, разность арифметической прогрессии равен (- 0,5) и сумма п-го члена равна 371, то найдём п и ап.

Дано:

Решение:

Ответ:

Работа по учебнику. Выполнить самостоятельно, с последующей проверкой с помощью интерактивной доски.

1 вариант — № 371(а), №372 (а).

2 вариант — № 371(б), №372 (б).

Домашнее задание.

Найдите сумму первых шестнадцати членов арифметической прогрессии, в которой а1 = 6, d = 4.
Найдите сумму первых n – членов арифметической прогрессии, 1,6; 1,4; …, если n = 6.
Найти сумму натуральных чисел начиная с 20 по 110 включительно.
Найдите сумму первых восьми членов арифметической прогрессии (аn), в которой а1 = 6, а7 = 26.
Сообщения учащихся.

Это интересно:

1 ученик: (презентация). Информация о задаче, которую решил шестилетний Колмогоров.

Когда шестилетний Колмогоров нашёл, что сумма первых нечётных чисел равна п², он вероятно рассуждал так: « Возьмем число 1, 1 = 12. Представим это геометрически, как один квадратик. Теперь прибавим к единице число 3. К нашему квадратику прибавим ещё тир квадратика. Затем прибавим число 5, добавим ещё 5 квадратиков – 2 сверху. 2 справа и один в углу. Получится квадратик 3 на 3. Девять. Каждый раз мы будем прибавлять к квадрату п на п новый уголок, состоящий из п квадратиков сверху, п квадратиков справа и одного в углу. Вот и будет получаться новый квадрат со стороной п + 1. Значит, прибавляя последовательные нечётные числа, мы всегда будем получать квадрат их количества».

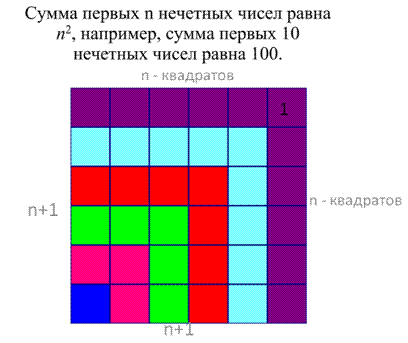
Рисунок 1

2 ученик (презентация): Информация о стихотворных слогах ямбе и хорее, связь их с арифметической прогрессией.

В романе А.С.Пушкина «Евгений Онегин» была такая фраза: «Не мог он ямба от хорея, как мы не бились отличить…» Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха. Ямб – стихотворный размер с ударением на чётных слогах, хорей с ударением на нечётных слогах.

Ямб – стихотворный метр с ударениями на четных слогах стиха

«Мой дя-дя са-мых чест-ных пра-вил…» то есть ударными являются 2-й, 4-й, 6-й, 8-й и т. д. Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и с разностью, равной двум: 2; 4; 6; 8 …

Хорей – стихотворный размер с ударением на нечетных слогах стиха.

«Бу-ря мгло-ю не-бо кро-ет» Номера ударных слогов также образуют арифметическую прогрессию, но ее первый член равен единице, а разность по-прежнему равна двум: 1; 3; 5; 7; …

Рефлексия.

Каждому учащемуся предлагается закончить одно из следующих предложений:

Я сегодня на уроке узнал о…

Мне понравились на уроке моменты…

Я чувствую себя…

Мне не понравилось…

У меня сейчас настроение…

Я узнал на уроке новое о…

По данной теме мне хотелось бы узнать еще о…

Мне было сегодня на уроке…

Мое состояние сейчас я оцениваю, как……

Я хотел бы изучить подробнее по данной теме следующие вопросы…

Данная тема была для меня…

Урок был…

Формула суммы арифметической последовательности с решенным примером вопроса

- Классы
  Класс 1 — 3
  Класс 4 — 5
  Класс 6 — 10
  Класс 11 — 12
- КОНКУРСЫ
  BBS
  000000000 Книги
  NCERT Книги для 5 класса
  NCERT Книги Класс 6
  NCERT Книги для 7 класса
  NCERT Книги для 8 класса
  NCERT Книги для 9 класса
  NCERT Книги для 10 класса
  NCERT Книги для 11 класса
  NCERT Книги для 12-го класса
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT Exemplar Class 12
  9000al Aggar Agaris Agard Agard Agard Agard Agard 2000 12000000
  Решения RS Aggarwal класса 10
  Решения RS Aggarwal класса 11
  Решения RS Aggarwal класса 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  Решения класса RD Sharma
  Решения класса 9 Шарма 7 Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  ФИЗИКА
  Механика
  000000 Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  МАТС
  Теорема Пифагора
  Отношения и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Делительные дроби
  000 ФОРМУЛЫ
  Математические формулы
  Алгебровые формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  S000
  S0003
  Pегипс Класс 6
  Образцы документов CBSE для класса 7
  Образцы документов CBSE для класса 8
  Образцы документов CBSE для класса 9
  Образцы документов CBSE для класса 10
  Образцы документов CBSE для класса 11
  Образец образца CBSE pers for Class 12
  CBSE Документ с вопросами о предыдущем году
  CBSE Документы за предыдущий год Class 10
  CBSE Вопросы за предыдущий год Class 12
  HC Verma Solutions
  HC Verma Solutions Класс 11 Физика
  Решения HC Verma Class 12 Physics
  Решения Lakhmir Singh
  Решения Lakhmir Singh Class 9
  Решения Lakhmir Singh Class 10
  Решения Lakhmir Singh Class 8
  Примечания
  CBSE
  Notes
  CBSE Класс 7 Примечания CBSE
  Класс 8 Примечания CBSE
  Класс 9 Примечания CBSE
  Класс 10 Примечания CBSE
  Класс 11 Примечания CBSE
  Класс 12 Примечания CBSE
  Примечания пересмотра
  CBSE Редакция
  CBSE
  CBSE Class 10 Примечания к пересмотру
  CBSE Class 11 Примечания к пересмотру 9000 4
  Замечания по пересмотру CBSE класса 12
  Дополнительные вопросы CBSE
  Дополнительные вопросы CBSE 8 класса
  Дополнительные вопросы CBSE 8 по естественным наукам
  CBSE 9 класса Дополнительные вопросы
  CBSE 9 дополнительных вопросов по науке CBSE
  9000 Класс 10 Дополнительные вопросы по математике
  CBSE Класс 10 Дополнительные вопросы по науке
  Класс CBSE
  Класс 3
  Класс 4
  Класс 5
  Класс 6
  Класс 7
  Класс 8
  Класс 9
  Класс 10
  Класс 11
  Класс 12
  Решения для учебников
- Решения NCERT
  Решения NCERT для класса 11
  Решения NCERT для физики класса 11
  Решения NCERT для класса 11 Химия
  Решения для класса 11 Биология
  NCERT Решения для класса 11 Математика
  9 0003 NCERT Solutions Class 11 Бухгалтерия
  NCERT Solutions Class 11 Бизнес исследования
  NCERT Solutions Class 11 Экономика
  NCERT Solutions Class 11 Статистика
  NCERT Solutions Class 11 Коммерция
  NCERT Solutions для класса 12
  NCERT Solutions для Класс 12 Физика
  Решения NCERT для 12 класса Химия
  Решения NCERT для 12 класса Биология
  Решения NCERT для 12 класса Математика
  Решения NCERT Класс 12 Бухгалтерский учет
  Решения NCERT Класс 12 Бизнес исследования
  Решения NCERT Класс 12 Экономика
  NCERT Solutions Class 12 Бухгалтерский учет Часть 1
  NCERT Solutions Class 12 Бухгалтерский учет Часть 2
  NCERT Solutions Class 12 Микроэкономика
  NCERT Solutions Class 12 Коммерция
  NCERT Solutions Class 12 Макроэкономика
  NCERT Solutions Для Класс 4
  Решения NCERT для математики класса 4
  Решения NCERT для класса 4 EVS
  Решения NCERT для класса 5
  Решения NCERT для математики класса 5
  Решения NCERT для класса 5 EVS
  Решения NCERT для класса 6
  Решения NCERT для класса 6 Maths
  Решения NCERT для класса 6 Science
  Решения NCERT для класса 6 Общественные науки
  Решения NCERT для класса 6 Английский
  Решения NCERT для класса 7
  Решения NCERT для класса 7 Математика
  Решения NCERT для 7 класса Science
  Решения NCERT для 7 класса Общественные науки
  Решения NCERT для 7 класса Английский
  Решения NCERT для 8 класса Математические решения
  для 8 класса Математика
  Решения NCERT для класса 8 Science
  Решения NCERT для класса 8 Общественные науки
  NCERT Solutio ns для класса 8 Английский
  Решения NCERT для класса 9
  Решения NCERT для класса 9 Общественные науки
  Решения NCERT для класса 9 Математика
  Решения NCERT для класса 9 Математика Глава 1
  Решения NCERT Для класса 9 Математика 9 класса Глава 2
  Решения NCERT для математики 9 класса Глава 3
  Решения NCERT для математики 9 класса Глава 4
  Решения NCERT для математики 9 класса Глава 5
  Решения NCERT для математики 9 класса Глава 6
  Решения NCERT для Математика 9 класса Глава 7
  Решения NCERT для математики 9 класса Глава 8
  Решения NCERT для математики 9 класса Глава 9
  Решения NCERT для математики 9 класса Глава 10
  Решения NCERT для математики 9 класса Глава 11
  Решения NCERT для Математика 9 класса Глава 12
  Решения NCERT для математики 9 класса Глава 13
  Решения NCERT для математики 9 класса Глава 14
  Решения NCERT для математики класса 9 Глава 15
  Решения NCERT для науки 9 класса
  Решения NCERT для науки 9 класса Глава 1
  Решения NCERT для науки 9 класса Глава 2
  Решения NCERT для класса 9 Наука Глава 3
  Решения NCERT для 9 класса Наука Глава 4
  Решения NCERT для 9 класса Наука Глава 5
  Решения NCERT для 9 класса Наука Глава 6
  Решения NCERT для 9 класса Наука Глава 7
  Решения NCERT для 9 класса Научная глава 8
  Решения NCERT для 9 класса Научная глава
  Научные решения NCERT для 9 класса Научная глава 10
  Научные решения NCERT для 9 класса Научная глава 12
  Научные решения NCERT для 9 класса Научная глава 11
  Решения NCERT для 9 класса Научная глава 13
  Решения NCERT для 9 класса Научная глава 14
  Решения NCERT для класса 9 Science Глава 15
  Решения NCERT для класса 10
  Решения NCERT для класса 10 Общественные науки
  Решения NCERT для математики класса 10
  Решения NCERT для математики класса 10 Глава 1
  Решения NCERT для математики класса 10 Глава 2
  решения NCERT для математики класса 10 глава 3
  решения NCERT для математики класса 10 глава 4
  решения NCERT для математики класса 10 глава 5
  решения NCERT для математики класса 10 глава 6
  решения NCERT для математики класса 10 Глава 7
  решения NCERT для математики класса 10 глава 8
  решения NCERT для математики класса 10 глава 9
  решения NCERT для математики класса 10 глава 10
  решения NCERT для математики класса 10 глава 11
  решения NCERT для математики класса 10, глава 12
  Решения NCERT для математики класса 10, глава 13
  соль NCERT Решения для математики класса 10 Глава 14
  Решения NCERT для математики класса 10 Глава 15
  Решения NCERT для науки 10 класса
  Решения NCERT для науки 10 класса Глава 1
  Решения NCERT для науки 10 класса Глава 2
  Решения NCERT для науки 10 класса, глава 3
  Решения NCERT для науки 10 класса, глава 4
  Решения NCERT для науки 10 класса, глава 5
  Решения NCERT для науки 10 класса, глава 6
  Решения NCERT для науки 10 класса, глава 7
  Решения NCERT для науки 10 класса, глава 8
  Решения NCERT для науки 10 класса, глава 9
  Решения NCERT для науки 10 класса, глава 10
  Решения NCERT для науки 10 класса, глава 11
  Решения NCERT для науки 10 класса, глава 12
  Решения NCERT для 10 класса Science Глава 9
  Решения NCERT для 10 класса Science Глава 14
  Решения NCERT для науки 10 класса Глава 15
  Решения NCERT для науки 10 класса Глава 16
  Программа NCERT
  NCERT
- Коммерция
  Класс 11 Коммерческая программа Syllabus
  Учебный курс по бизнес-классу 11000
  Учебная программа по экономическому классу
- Учебная программа по коммерческому классу
  Учебная программа по 12 классу
  Учебная программа по 12 классу
  Учебная программа по экономическому классу
  000000000000000000
  Образцы коммерческих документов класса 11
  Образцы коммерческих документов класса 12
  Решения TS Grewal
  Решения TS Grewal Класс 12 Бухгалтерский учет
  Решения TS Grewal Класс 11 Бухгалтерский учет
  Отчет о движении денежных средств
  eurship
  Защита потребителей
  Что такое фиксированный актив
  Что такое баланс
  Формат баланса
  Что такое акции
  Разница между продажами и маркетингом
- P000S Документы ICSE
- ML Решения Aggarwal
  ML Решения Aggarwal Class 10 Maths
  ML Решения Aggarwal Class 9 Математика
  ML Решения Aggarwal Class 8 Maths
  ML Решения Aggarwal Class 7 Математические решения
  ML 6 0004
  ML 6
- Selina Solutions
  Selina Solution для класса 8
  Selina Solutions для класса 10
  Selina Solution для класса 9
- ICSE класс
  ICSE класс 6
  ICSE класс 7
  ICSE
  ICSE
  ICSE Class 9
  ICSE Class 10
  ISC C lass 11
  ISC Class 12
IAS
IAS экзамен
экзамен по гражданской службе
UPSC Syllabus
бесплатный IAS Prep
текущие дела
экзамен по IAS
IAS 2019 Mock Test 1
IAS 2019 Mock Test 2
Комиссия по государственной службе
KPSC KAS экзамен
UPPSC PCS экзамен
MPSC экзамен
RPSC
группа 1PPS RASP
группа 1SPS
группа 1SPS
группа 1SPS
группа 1SPS
группа 1PPS
группа 1PPS группа
1
Экзамен BPSC
Экзамен WBPSC
Экзамен MPPSC
Экзамен JPSC
Экзамен GPSC
Вопросный документ UPSC 2019
Ключ ответа UPSC 2019
000 8000
000
000
000
000
000000000 Коучинг IAS Дели
Коучинг IAS Ченнаи
Коучинг IAS Хайдарабад
Коуч IAS ing Mumbai
JEE
JEE Программа
JEE Main
JEE Advanced
JEE Образец бумаги
JEE Вопрос о
NEET
Программа NEET Byju
NEET 2020
Критерии соответствия NEET 2020
Образцы документов NEET
Подготовка NEET
Поддержка NEET Syllabus
Поддержка
Служба поддержки клиентов
поддержки клиентов
9000 требует обязательной поддержки для обращения с
государственных советов
GSEB
GSEB Syllabus
Вопросник GSEB
Образец бумаги GSEB
GSEB Книги
MSBSHSE
SBSS000000 MSBSSE Документы estion
AP Board
APSCERT Книги
AP SSC Syllabus
AP 1-й курс Syllabus
AP 2-й год Syllabus
MP Board
MP000 Sample
MP000 Sample Sill Учебники MP Board
Assam Board
Assam Board Syllabus
Assam Board Учебники
Assam Board Образцы документов
BSEB
Bihar Board
000 Документы для моделей Bihar
9000 9000-е годы
PSE для PSE
S000 PBSS
PS000
P0003000 Доска Syllabus
9000 3 RBSE Учебники
RBSE Документы с вопросами
HPBOSE
HPBOSE Syllabus
HPBOSE Учебники
HPBOSE Вопросы для бумаг
JOSBOSE
JOSBOSE
JOSE S000S
TN Board
TN Board Syllabus
TN Board Вопросы к бумагам
TN Board Образцы документов
Samacheer Kalvi Books
JAC
JAC Syllabus
JAC
JASK
учебные пособия
JAS Telangana Board
Telangana Board Syllabus
Telangana Board Учебники для
Telangana Board Вопросные бумаги
KSEEB
KSEEB Syllabus
KSEEB Модель
KB
9000
9000
9000 books
KBPE Вопросы для бумаг
UPMSP
UP Board Syllabus
UP Board Книги для документов
UP Board Вопросы для бумаг
Западная Бенгалия Board
Западно-Бенгальская доска Syllabus
Text
BookBook
Book Book Book Book Book BookBook4 Документы для заседаний Совета Западной Бенгалии
UBSE
TBSE
Goa Board
NBSE
CGBSE
MBSE
Meghalaya Board
Manipur Board
Испанский
Испанский
SBI Exams
PIL, Exams
RBI Exams
PIL, РРБ экзамен
SSC Exams
SSC JE
SSC GD
SSC CPO
SSC CHSL
SSC CGL
РРК Экзамены
RRB JE
RRB NTPC
RRB AL P
Страховые экзамены
LIC экзамены
LIC HFL
LIC ADO
UPSC CAPF
Список государственных экзаменов Статьи
Класс
Дети
Класс 3
Академические вопросы
Физические вопросы
Вопросы химии
Биологические вопросы
Вопросы математики
Научные вопросы
Вопросы ГК

CAT
BYJU’S CAT Программа
CAT Силабус
CAT экзамен
Free CAT Prep
CAT 2020 экзамен шаблон
Byju в App Обзор на CAT
КУПИТЬ КУРС
+919243500460
Формулы
Математические формулы
Формулы алгебры
Формулы алгебры для класса 8
Формулы алгебры для класса 9
Формулы алгебры для класса 10
Формулы алгебры для класса 11
Формулы алгебры для класса 12
Формула алгебры для класса 12
Формулы площади и периметра
Формула площади круга
Формула площади квадрата
Формула ромба
Периметр формулы ромба
Формула
Космоса Обратная формула
Син Тета формула
Tan2x формула
,Алгоритм
— Какова сложность арифметической прогрессии? Переполнение стека
Товары
Клиенты
Случаи использования
Переполнение стека Публичные вопросы и ответы
Команды Частные вопросы и ответы для вашей команды
предприятие Частные вопросы и ответы для вашего предприятия
работы Программирование и связанные с ним технические возможности карьерного роста
Талант Нанимать технический талант
реклама Связаться с разработчиками по всему миру
,
No related posts.

Сумма n первых членов арифметической прогрессии

Примеры

Смотрите также

Онлайн-калькулятор арифметической прогрессии

Определение и примеры арифметической прогрессии

Виды арифметической (алгебраической) прогрессии

Формулы арифметической прогрессии

Примеры задач с решением

Пример 1

Пример 2

Пример 3

Замечания

Понятие арифметической прогрессии

Примеры задач

Пример 1

Пример 2

Добавить комментарий Отменить ответ