Числовые ряды. Знакоположительные ряды | Математика, которая мне нравится
Определение. Пусть — последовательность вещественных чисел. Числовым рядом называется
Сумма называется частной суммой ряда.
Определение. Если последовательность чисел сходится к конечному пределу , то говорят, что ряд сходится и его сумма равна
Если же последовательность расходится, то говорят, что ряд расходится.
Числа называются членами ряда. Всякая конечная сумма называется отрезком ряда.
Если все числа положительны (неположительны, неотрицательны, отрицательны), ряд называется знакоположительным (знаконеположительным, знаконеотрицательным, знакоотрицательным).
Пример. Рассмотрим ряд
где — некоторое фиксированное число. Частные суммы этого ряда
Если , то .
При ряд расходится, так как неограниченно возрастает.
При . Следовательно, ряд расходится.
При Следовательно, не имеет предела, и ряд расходится.
Значит, ряд сходится при , а при расходится.
Теорема (критерий Коши для ряда). Ряд
сходится тогда и только тогда, когда
В частности, если ряд сходится, то для любого . Таким образом, у сходящегося ряда — необходимое условие сходимости. Однако оно не является достаточным.
Для знаконеотрицательных рядов из ограниченности последовательности частичных сумм следует сходимость ряда.
Теорема (признак сравнения). Если знаконеотрицательный ряд сходится и существуют и : , то тогда и ряд сходится.
Доказательство. Пусть , . Тогда при
Последовательность возрастает и ограничена сверху, следовательно, она имеет предел.
Пример. Если для неотрицательного ряда
где и , то ряд сходится.
Теорема (признак Даламбера).
Если для знакоположительного ряда
выполняется неравенство
то ряд сходится.
Если
то ряд расходится.
Доказательство. Если , то существует : начиная с некоторого номера , выполняется неравенство
Отсюда
и по признаку сравнения ряд сходится.
С именем Даламбера связан один забавный случай. Рассказывают, что, обучая математике очень тупого и очень знатного ученика и не добившись понимания доказательства, Даламбер в отчаянии воскликнул: “Ну, честное слово, сударь, эта теорема верна!” На что ученик отвечал: “Сударь, почему вы сразу так мне не сказали? Вы — дворянин, и я — дворянин; Вашего слова для меня вполне достаточно”.
Пример. Ряд
сходится, поскольку
Теорема (признак Коши). Если для знакоположительного ряда
выполняется неравенство
то ряд сходится.
Если же
то ряд расходится.
Доказательство. Если , то существует : . Следовательно, , и по признаку сравнения ряд сходится.
Если же , то существует : . Значит, члены ряда не стремятся к нулю, и ряд расходится.
Пример. Ряд
сходится, так как
Пример. Гармонический ряд (каждый член этого ряда, начиная со второго, — среднее гармоническое двух соседних его членов: ) расходится.
Доказательство.
Частная сумма гармонического ряда может быть сделана больше чего угодно.
hijos.ru
24.Знакоположительные числовые ряды. Ряд геометрической прогрессии.
Числовые ряды – рассмотрим числовую последовательность: un – числа.Составим суммы: ;
;
…………………..
;
Выражение: – называется числовым рядом (1)
Числа — называются членами ряда. Если они положительны, то ряд называется знакоположительным.
— называется n-ый член ряда или общий член ряда.
— частичные суммы.
Числовой ряд (1) называется сходящимся, если последовательность частичных сумм сходится к некоторому числу S, которое называется суммой ряда, т.е. ряд сходится если существует предел: . Если предел не существует или равен бесконечности, то ряд называется
Ряд геометрической прогрессии – Исследуем на сходимость ряд: Этот ряд называетсярядом (2)
геометрической прогрессии. Сумму первых n-членов ряда геометрической прогрессии находим по формуле: ,
Найдем
Рассмотрим следующие случаи:
1), тогда , поэтому – ряд сходится;
2), тогда , и — ряд расходится;
3), тогда ряд (2) имеет вид: , его сумма,- ряд расходится;
Вывод: ряд геометрической прогрессии (2) сходится, при иего и расходится, при.
25.Свойства числовых рядов. Необходимые условия сходимости ряда.
Простейшие свойства числовых рядов:1.Суммой двух рядов иназывается ряд;
2.Произведением ряда на действительное число α называется ряд: ;
3.Сходимость ряда не нарушается, если произвольно изменить (переставить, добавить или отбросить) конечное число членов. Сумма может измениться;
4.Сходящийся ряд можно почленно умножать на любой множитель α, и если сумма ряда равна , то сумма;
5.Сходящиеся ряды можно почленно складывать и вычитать: ; ,то ;
Необходимое условие сходимости ряда:
Теорема: Если ряд сходится, то его общий член, т.е. (1)
Доказательство: Если ряд
,
.Запишем: и
найдем его предел
Если условие (1) не выполняется, то ряд расходится. Условие (1) не является достаточным условием сходимости ряда, т.е. из выполнения равенства не обязательно вытекает сходимость ряда.
26.Достаточные признаки сходимости: признак Даламбера, радикальный признак Коши.
Необходимый признак сходимости не дает, вообще говоря, о том сходится ряд или нет. Сходимость и расходимость ряда можно установить с помощью достаточных признаков.
Признак Даламбера – пусть дан ряд знакоположительный и существует предел отношения последнего члена ряда к предыдущему, т.е.:, тогда, если.
Радикальный признак Коши – дан знакоположительный ряд , если существует предел, тогда если.
27.Достаточный признак сходимости: интегральный признак Коши. Сходимость обобщённого гармонического ряда.
Необходимый признак сходимости не дает, вообще говоря, о том сходится ряд или нет. Сходимость и расходимость ряда можно установить с помощью достаточных признаков.
Интегральный признак Коши – дан знакоположительный ряд , пусть его члены могут быть представлены как числовые значения некоторой функцииf(x), которая убывает на промежутке [1;+∞), т.е.: ;
;
…………..
;
тогда: 1.Если несобственный интеграл: сходится, то и ряд сходится;
2.Если несобственный интеграл: расходится, то и ряд расходится;
Замечание (о сходимости несобственного интеграла):
Обобщенный гармонический ряд:
, где p>0 – действительное число (1)
Ряд (1) называется рядом Дирихле. Исследуем ряд на сходимость по интегральному признаку. Рассмотрим функцию , это функция убывает на интервале (1; ).
Вывод: ряд Дирихле
при
Этот ряд удобно использовать в признаках сравнения.
studfiles.net
Определения
Ряды в настоящее время представляют собой особо широко используемый математический аппарат для точного и приближенного решения различных уравнений.Определение 1. Рядом называется сумма некоторой последовательности, другими словами ряд – есть сумма бесконечного числа членов, каждый из которых является элементом заданной последовательности.
Ряды бывают двух видов:
1) числовые ряды, если каждый член ряда – число, в этом случае
,
причем в правой части записан числовой ряд, в левой части – его сокращенное обозначение, здесь означает суммирование членов ряда от первого до сколь угодно большого,общий (й) член ряда.
2) функциональные ряды, когда каждый член ряда есть функция:
Определение 3. Сумму первых членов ряда называютчастичной суммой ряда.
Очевидно, сумма ряда определяется формулой. Однако применение этой формулы сопряжено с большими, порой непреодолимыми, трудностями. Далеко не всегда удается в компактной форме записатью частичную сумму ряда, а, следовательно, вычислить ее предел. Почленное суммирование ряда — еще менее перспективная процедура, бесконечное число членов не просуммируешь.
Вследствие этого точное значение суммы ряда можно установить в очень небольшом числе случаев.
Приведем пример геометрической прогрессии
,
знаменатель которой .
Известна сумма первых членов этого ряда. Вычислим ее предел. Если, то, следовательно,. При, и. Ряд расходится. Приряд также расходится. Итак, подтверждается утверждение, что геометрическая прогрессия сходится прии расходится при.
В большинстве случаев приходится вычислять суммы рядов приближенно, но для этого необходимо знать, существует ли конечное значение этой суммы, то есть сходящийся ли ряд.
Теория рядов, следовательно, создана для установления сходимости или расходимости рядов. При необходимости сумму сходящегося ряда вычисляют приближенно, расходящиеся ряды практической ценности не представляют.
Числовые ряды Необходимое условие сходимости ряда
Если ряд сходится, то .
Доказательство. Если ряд сходящийся, существует его конечная сумма , причем. Вычислим
.
Основное свойство рядов
Если ряд сходящийся, то его остаток , образованный отбрасыванием первыхчленов ряда, тоже сходится. Если ряд расходящийся, то его остаток также является расходящимся рядом.
В самом деле,
.
Если ряд сходится, то существует его конечная сумма , а- всегда конечна как сумма конечного числа членов. Тогда изследует, чтоконечное число, и остаток ряда – сходится. Когда ряд расходящийся,. Поскольку сумма ряда в правой части равенства не существует (ряд расходящийся), аимеет конечное значение, сумма ряда в левой части также не существует.
Переходим к рассмотрению частных случаев рядов. Вначале исследуем сходимость числовых рядов.
Знакоположительные числовые ряды
Начнем с теорем сравнения знакоположительных рядов.
Первая теорема сравнения. Даны два знакоположительных числовых ряда и, причем. Из сходимости большего ряда следует сходимость меньшего ряда. Из расходимости меньшего ряда следует расходимость большего ряда.
Доказательство.
1) Пусть ряд сходится, и его суммаконечна. Рассмотрим частичные суммы обоих рядови. Так как члены обоих рядов положительны, при любомимеем, из условияимеем. Рассмотрим последовательность частичных сумм ряда. Она монотонно возрастает с ростом(суммируется все большее число положительных членов). В то же время она ограничена сверху числом. Но имеется теорема, утверждающая, что монотонно возрастающая и ограниченная сверху последовательность имеет конечный предел. Итак,, следовательно,является суммой ряда.
2) Пусть ряд расходится. Поскольку все его члены положительны, его сумма равна бесконечности. По условию теоремы, следовательно,, то есть при неограниченном возрастании суммынеограниченно растет и сумма. Больший ряд также расходится.
Вторая теорема сравнения (упрощенная постановка). Даны два знакоположительных ряда и, причем, в этом случае оба ряда ведут себя одинаково: либо оба сходятся, либо оба расходятся.
Доказательство. Из следует, что
.
Из записанной формулы следует, что начиная с и для всех остальных выполняется неравенство, из которого имеем, или.
1)Рассмотрим правую часть неравенства. Пусть ряд сходится, тогда сходится и его остаток, следовательно, сходится и ряд. Поскольку, из первой части первой теоремы сравнения следует сходимость ряда, а, следовательно, и самого ряда.
2) Пусть ряд расходится, тогда расходится и его остаток. Подберемтак, чтобы, тогда рядтоже расходится. Но из левой части полученного выше неравенства следует, что, значит, члены рядабольше членов расходящегося ряда, из первой теоремы сравнения следует, что рядрасходящийся, расходится и ряд.
Доказано, что из сходимости (расходимости) ряда следует сходимость (расходимость) ряда.
Рассмотрим теперь . Очевидно,, то есть условия только что доказанной теоремы выполнены. Но в этом случае можно утверждать, что из сходимости (расходимости) рядаследует сходимость (расходимость) ряда. Итак, ряды при выполнении условий теоремы ведут себя одинаково.
Доказаны две важнейшие теоремы. Однако для сравнения рядов необходимо иметь информацию о сходимости или расходимости хотя бы нескольких рядов, с которыми можно было бы сравнивать другие ряды.
Для этой цели рассмотрим несколько достаточных условий, позволяющих исследовать сходимость конкретных рядов.
Признак Даламбера
сходимости знакоположетельных рядов
Теорема. Ряд при условиисходится, когдарасходится, еслипризнак Даламбера неприменим.
Доказательство. Если , то
,
откуда следует
1) Для доказательства первой части теоремы воспользуемся правой частью неравенства, записав его в виде , где,. По условию теоремы. Зададимнастолько малым, чтобы. Тогда
,
,
,
……………………
Рассмотрим теперь два ряда
и
.
Нижний ряд представляет собой сходящуюся геометрическую прогрессию, так как . Члены верхнего ряда меньше соответствующих членов нижнего ряда, на основании первой теоремы сравнения рядсходится. Но этот ряд является остатком рассматриваемого ряда, следовательно, он тоже сходится.
2) Для доказательства второй части теоремы при воспользуемся полученным ранее неравенством, подобравтак, чтобы. Тогда, то есть положительные члены ряда растут с ростом. Очевидно,, но ряд может сходиться только в случае. Ряд расходится.
3) При условииневозможно доказать сходимость, или расходимость ряда. Следовательно, в этом случае признак Даламбера неприменим.
Рекомендация. Признак Даламбера дает положительный ответ практически всегда, если общий член ряда содержит показательную функцию или факториалы.
Пример 1. . Очевидно,. Тогда
. Ряд сходится.
Пример 2. ..
Чтобы решить этот пример, вспомним некоторые формулы для «факториала» ,.
.
Ряд расходится.
Радикальный признак Коши
сходимости знакоположительных рядов
Теорема. Дан ряд . Если, а, то ряд сходится, приряд расходится, припризнак не работает.
Доказательство. Из следует, что
,
другими словами, начиная с некоторого и для всех последующих, оттуда следует, или, где,.
1. Докажем справедливость первого утверждения теоремы. В этом случае , зададимтак, чтобы выполнялось. Из правой части полученного двойного неравенства следует, что. Если сравнить рядыи, то члены первого ряда меньше соответствующих членов второго ряда, являющегося сходящимся как геометрическая прогрессия со знаменателем меньшим единицы. Из первой теоремы сравнения рядов следует, что ряд, то есть остаток рядасходится, следовательно, сходится и сам ряд.
2. При доказательстве второго утверждения теоремы учтем, что и зададимтак, чтобы. Воспользуемся левой частью двойного неравенства. Сравним рядс расходящейся геометрической прогрессией. И поскольку члены рядабольше соответствующих членов расходящейся геометрической прогрессии, он расходится. Так как этот ряд является остатком ряда, то и сам ряд расходится.
3. При ряд может как сходиться, так и расходиться, следовательно, признак неприменим.
Замечание. Радикальный признак удобно применять, когда хорошо извлекается корень й степени из общего члена ряда.
Пример 1. ., ряд сходится.
Пример 2. .,
ряд расходится.
Интегральный признак Маклорена – Коши
сходимости знакоположительных рядов
Теорема. Знакоположительный ряд сходится (расходится), если сходится (расходится) интеграл, причем подынтегральная функцияполучается из общего члена ряда заменой дискретно меняющейся переменнойна действительную переменную.
Доказательство.
1) Пусть интеграл — сходится, то есть принимает конечное значение. Рассмотрим интеграл, его значение дает площадь криволинейной трапеции, ограниченной прямыми,,и кривой. Разобьем отрезокнаравных частей, длина каждого элементарного отрезка равна 1. Из точек разбиения восстановим перпендикуляры до пересечения с кривой, длины этих перпендикуляров, где- члены исследуемого ряда, что следует из условия теоремы. Построим вписанные в криволинейную трапецию прямоугольники, одна из сторон каждого из них равна 1, другие имеют длинысоответственно. Подсчитаем сумму площадей вписанных прямоугольников
,
сумма площадей численно равна й частичной сумме ряда без первого члена. Рассмотрим последовательность частичных сумм ряда. Она растет с ростом величины верхнего предела интеграла, так как растет количество вписанных прямоугольников. В то же время любая частичная сумма ряда, как уже говорилось выше, совпадающая численно с площадью вписанных прямоугольников, не может превышать площади криволинейной трапеции, которая сама меньше значения интеграла. Итак, последовательность частичных сумм ряда монотонно возрастает и ограничена сверху, следовательно, она имеет конечный предел, но это сумма рядапо определению. Значит, ряд сходится.
2) Пусть интеграл расходящийся. Так как, то. Построим описанные прямоугольники, одна из сторон каждого из них равна 1, другие соответственно. Сумма площадей этих прямоугольников равнаи совпадает счастичной суммой ряда. Поскольку сумма площадей описанных прямоугольников больше площади криволинейной трапеции, которая равна, то и частичные суммы ряда неограниченно возрастают. Очевидно,. Ряд расходится.
Итак, получен универсальный признак сходимости, который, в отличие от предыдущих двух признаков, работает всегда. Но его применение приводит к необходимости исследования сходимости несобственного интеграла, что далеко не просто, да и не всегда возможно.
Исследуем ряд с помощью интегрального признака. Для этого необходимо исследовать сходимость интеграла, что было проделано ранее. Он сходится прии расходится при. Тогда и рядсходится прии расходится при.
Пример 1. . Вычислим интеграл
,
интеграл сходится и ряд тоже.
Пример 2. . Вычислим интеграл
,
интеграл, а вместе с ним ряд сходятся.
Исследование сходимости знакоположительных рядов с помощью МАКСИМЫ
Рассмотрим ряд
Поскольку не выполняется необходимое условие сходимости ряда (предел n — го члена равен бесконечности), он расходящийся.
Рассмотрим ряд
Поскольку предел n — го члена равен нулю, ряд может как сходиться, так и расходиться. Применение признака Даламбера дает , что меньше 1, ряд сходится.
Исследуем ряд

Проверка необходимого условия показывает, что ряд может и сходиться, и расходиться. Признак Даламбера дает 1, то есть не работает. Интегральный признак приводит к сходящемуся интегралу, следовательно, ряд сходится.
Примеры для самостоятельного решения
Исследовать сходимость рядов, используя теоремы сравнения и признаки сходимости
15.1. , 15.2., 15.3., 15.4.,
15.5. , 15.6., 15.7., 15.8,
15.9. , 15.10., 15.11., 15.12..
Ответы. 15.1. Сходится. 15.2. Сходится. 15.3.Сходится. 15.4. Сходится.
15.5. Сходится. 15.6. Расходится. 15.7. Сходится. 15.8. Расходится.
15.9. Сходится. 15.10. Сходится. 15.11. Сходится. 15.12. Расходится.
studfiles.net
Понятие числового ряда. Необходимый признак сходимости. Знакоположительные ряды. Признаки сравнения.
Понятие числового ряда. Числовым рядом называется символ
а1 + а2 + а3 + … + аn,
где а1, а2, а3,…, an – элементы некоторой числовой последовательности. Иначе говоря, ряд есть сумма бесконечного числа слагаемых. Число an называется n-м членом ряда.
Сумма Sn = a1 + a2 +…+an называется n-й частной суммой ряда. Рассмотрим последовательность Sn, сост
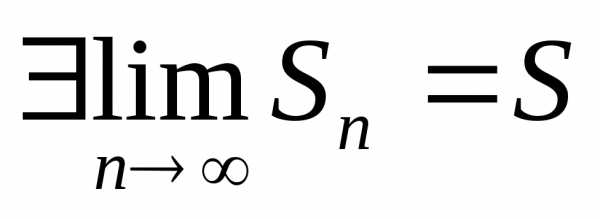 ,
,
авленную из частных сумм некоторого ряда: S1, S2, … Sn… Если
то данный ряд
называется сходящимся,
а число S
= 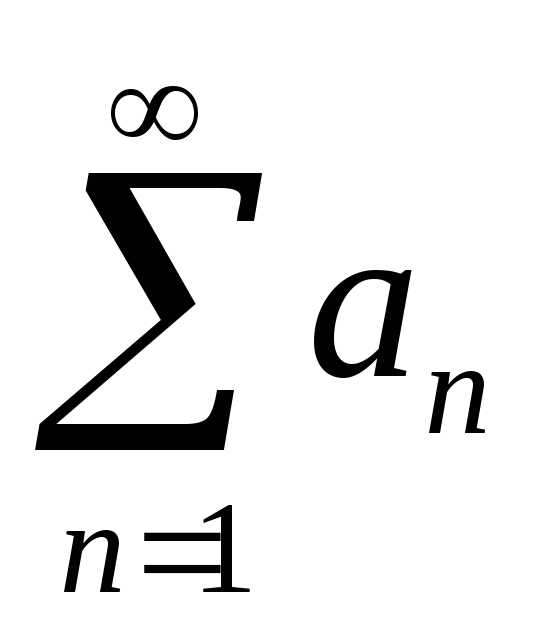 — суммой ряда.
Если последовательность, составленная
из частных сумм ряда не имеет предела,
то ряд называется расходящимся
— суммой ряда.
Если последовательность, составленная
из частных сумм ряда не имеет предела,
то ряд называется расходящимся 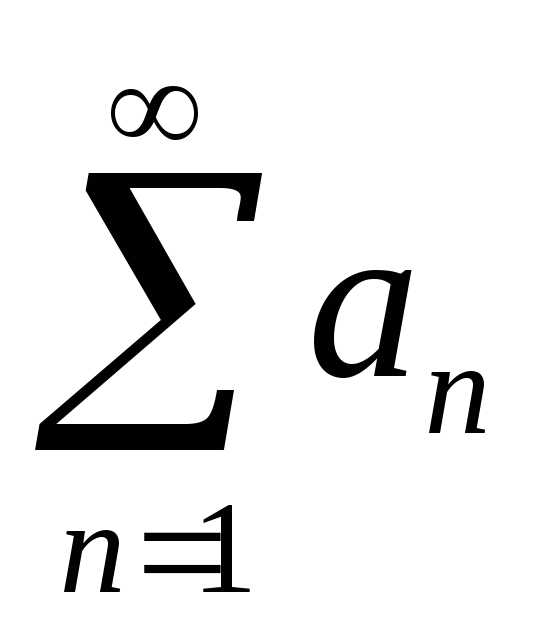 .
Таким образом, сумма бесконечного числа
слагаемых не всегда имеет смысл.
.
Таким образом, сумма бесконечного числа
слагаемых не всегда имеет смысл.
Примеры:
Сумма бесконечного числа членов геометрической прогрессии с
 :
1 +q2 +…+ qn + … Существует сумма ряда
:
1 +q2 +…+ qn + … Существует сумма ряда  .
Поэтому такой ряд является сходящимся.
.
Поэтому такой ряд является сходящимся.Ряд
 сходится.
сходится.Ряд
 (гармонический) расходится.
(гармонический) расходится.
Необходимый
признак сходимости. Необходимый
признак сходимости ряда:
если ряд 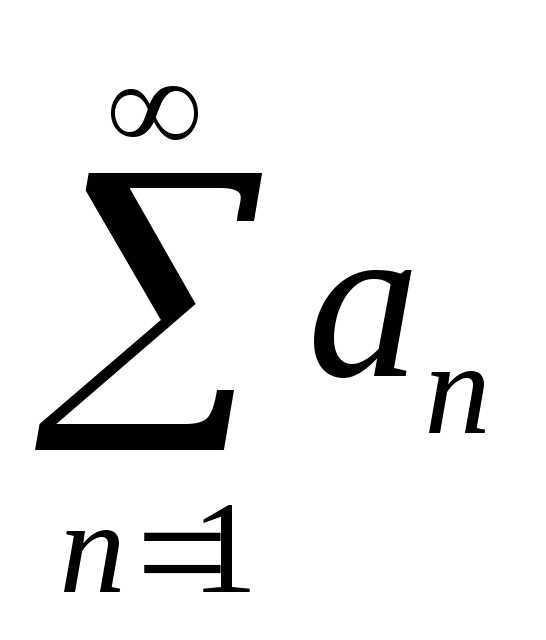 сходится, то
сходится, то 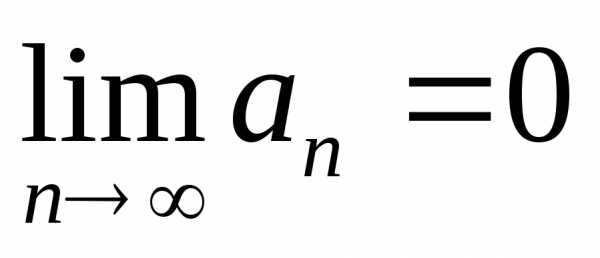 .
Доказательство: мы имеем
.
Доказательство: мы имеем
Sn = a1 + a2 + … + an-1 + an;
Sn-1 = a1 + a2 + … + an-1.
Отсюда an = Sn – Sn-1. Так как данный ряд сходится, то . Следовательно
ч. т. д.
Некоторые ряды (например, гармонический) удовлетворяют этому признаку, однако являются расходящимися.
Замечания:
Если ряд
 сходится и имеет сумму A,
то ряд
сходится и имеет сумму A,
то ряд  (k
= const
0) также сходится и имеет сумму kA.
Если ряд
(k
= const
0) также сходится и имеет сумму kA.
Если ряд  расходится, то
расходится, то  также расходится.
также расходится.
Доказательство:
рассмотрим n-ю
частную сумму ряда 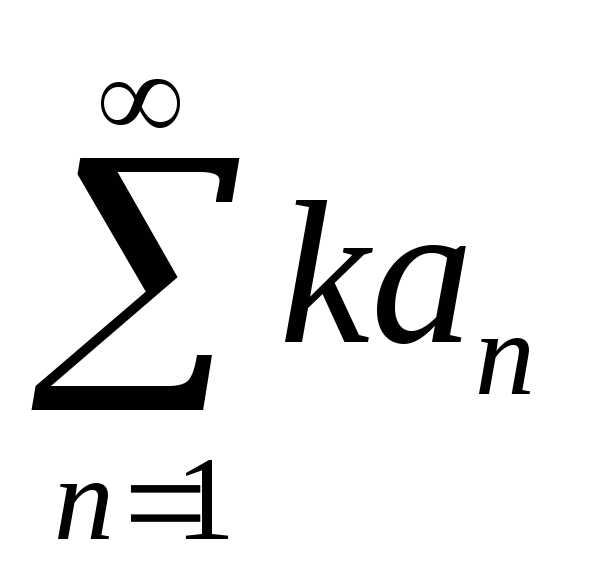 :
:
ka1 + ka2 +…+ kan = k (a1 + an) = kAn.
Константу можно
выносить за знак предела, поэтому ряд 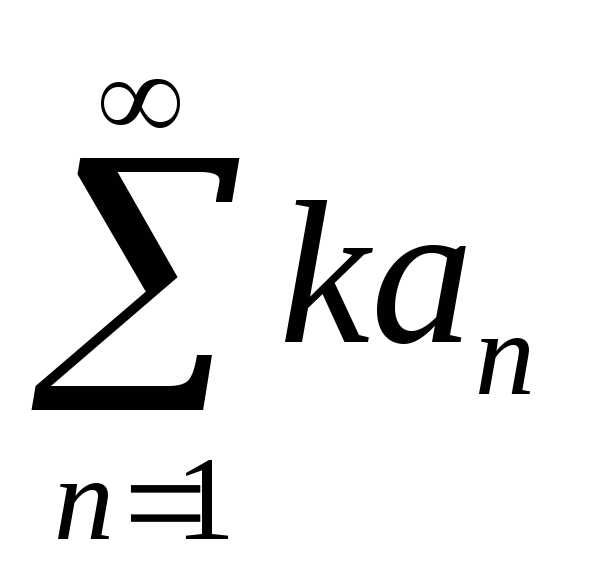 сходится или расходится в зависимости
от того, сходится или расходится ряд
сходится или расходится в зависимости
от того, сходится или расходится ряд 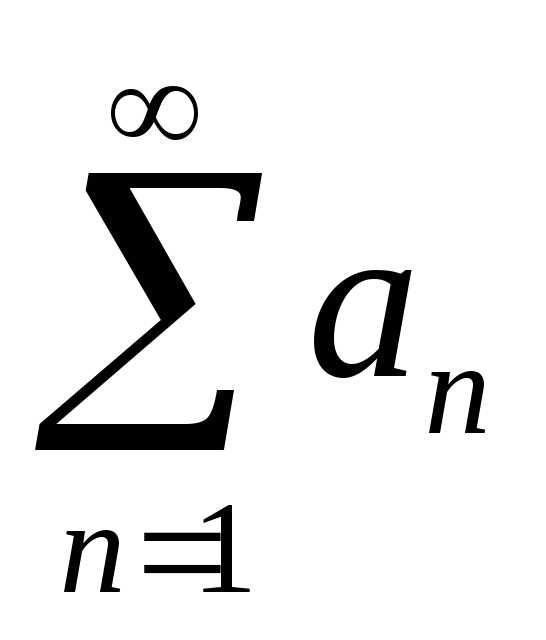 .
.
Если отбросить конечное число первых членов ряда, то характер сходимости не изменится. Доказательство: отбросим первые k членов ряда:
ak+1 + ak + 2 = n = ak+1 +…+ ak+n.
Весь ряд Sk+n:
Sk+n = a1 + a2 +…+ ak + n = n + const.
Поэтому ряд с отброшенными k членами сходится тогда же, когда сходится исходный ряд (по свойствам пределов).
Пусть даны два ряда:
 и
и .
Тогда:
.
Тогда:
а) Если оба ряда
сходятся и имеют суммы А и В соответственно,
то ряд 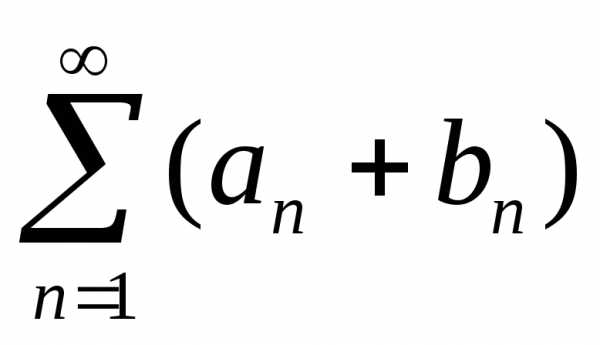 также сходится и имеет сумму А + В.
также сходится и имеет сумму А + В.
б) Если один ряд
сходится, а другой расходится, то ряд 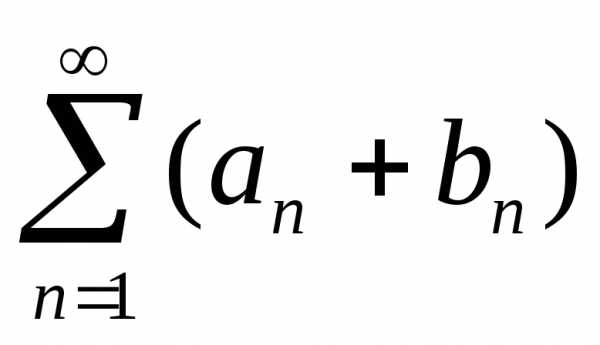 расходится.
расходится.
Доказательство:
а) Ряд 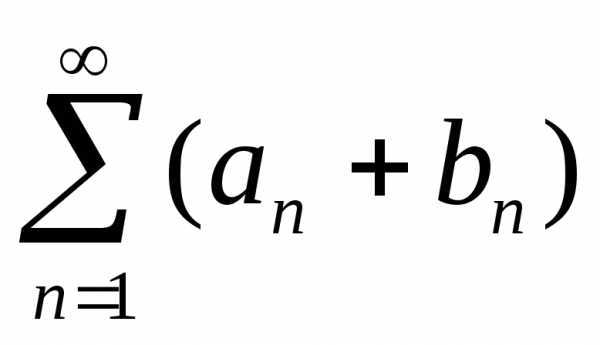 получается почленным сложением двух
исходных, поэтому таким же образом
получаются и частные суммы. Поскольку
предел суммы существует и равен сумме
пределов, то ряд
получается почленным сложением двух
исходных, поэтому таким же образом
получаются и частные суммы. Поскольку
предел суммы существует и равен сумме
пределов, то ряд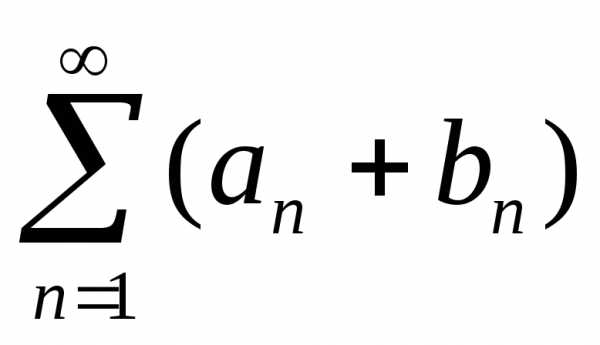 сходится, а его сумма равна А + В; б)
Предположим, что рядSn =
сходится, а его сумма равна А + В; б)
Предположим, что рядSn = 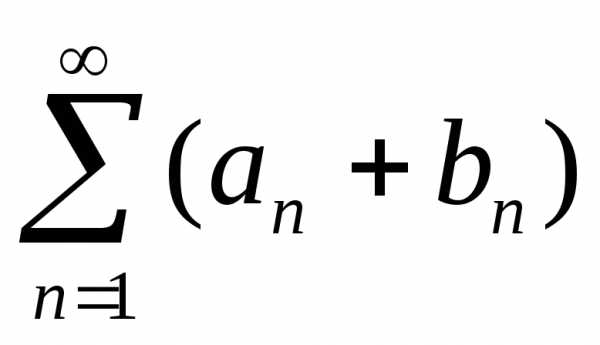 cходится.
Ряд
cходится.
Ряд 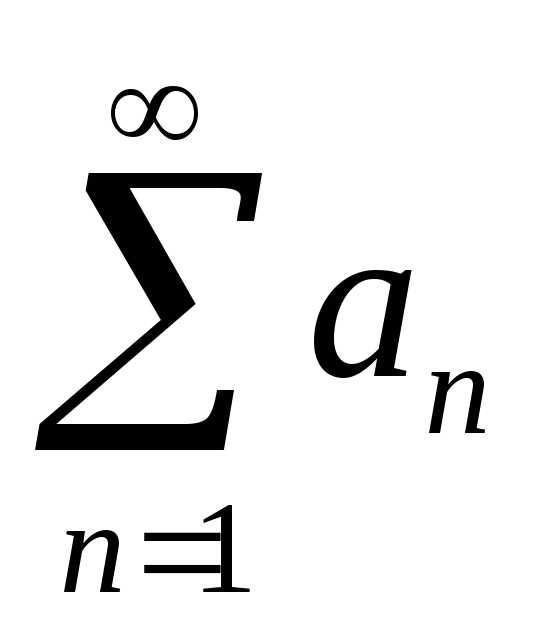 сходится, т.е. существует
сходится, т.е. существует ;
ряд
;
ряд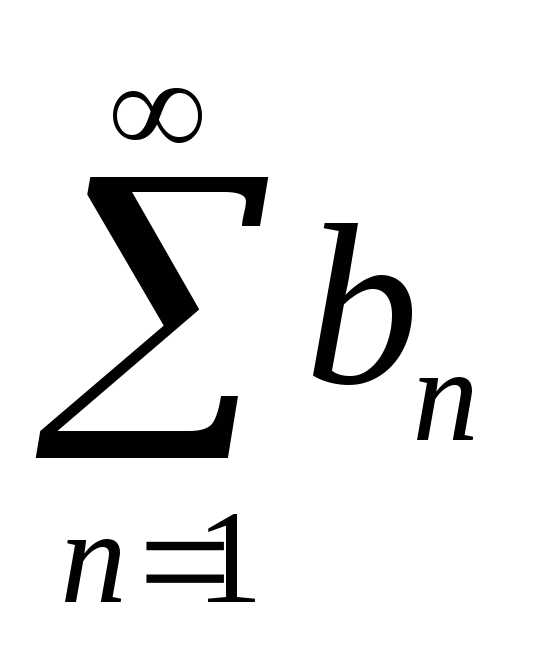 расходится, т.е. не существует предела
последовательности его частных суммBn.
Так как ряд
расходится, т.е. не существует предела
последовательности его частных суммBn.
Так как ряд 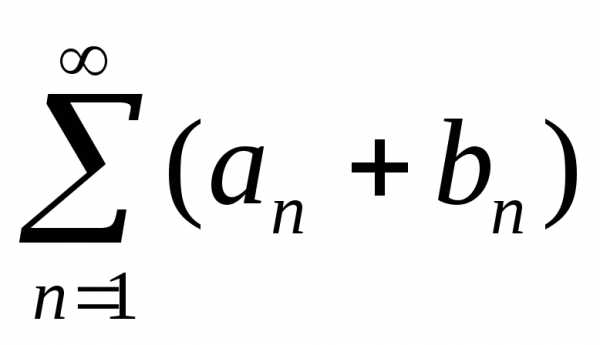 получен почленным сложением двух
исходных, тоBn = Sn – An.
Предел правой части существует,
следовательно должен существовать и
предел левой. Но это не так. Мы пришли к
противоречию. Следовательно, ряд
получен почленным сложением двух
исходных, тоBn = Sn – An.
Предел правой части существует,
следовательно должен существовать и
предел левой. Но это не так. Мы пришли к
противоречию. Следовательно, ряд 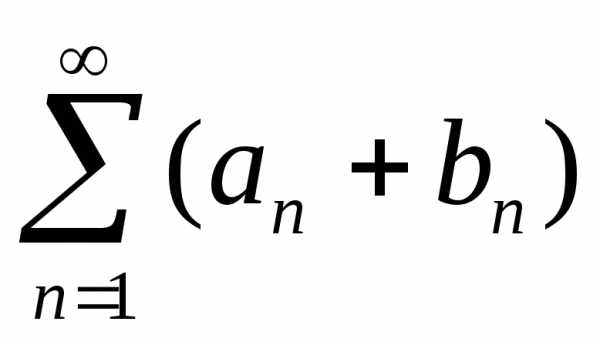 расходится.
расходится.
Если оба ряда расходятся, то о сходимости ряда, полученного их почленным сложением ничего сказать нельзя. Например, ряды 1 + 1 + 1 + 1… и – 1 – 1 – 1 – 1 расходятся, их сумма равна 0 + 0 + 0 + 0, она сходится; ряды 1/n и 2/n расходятся, их сумма 3/n также расходится.
Знакоположительные ряды. Признаки сравнения. Ряд называется знакоположительным, если для всех n аn 0.
1-й
признак сравнения:
пусть даны два знакоположительных ряда 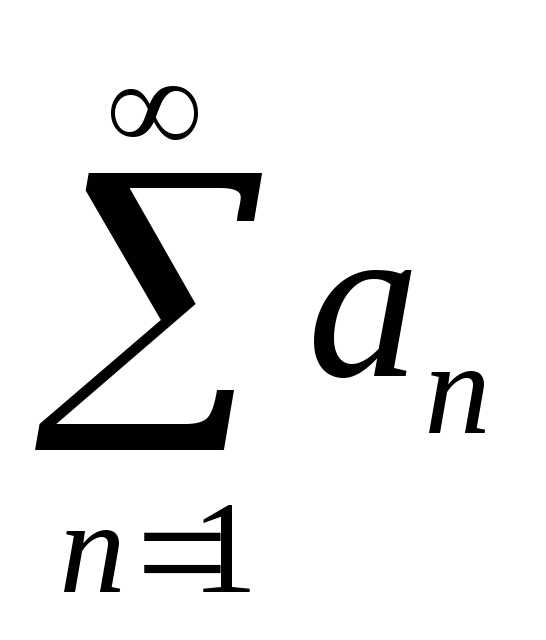 и
и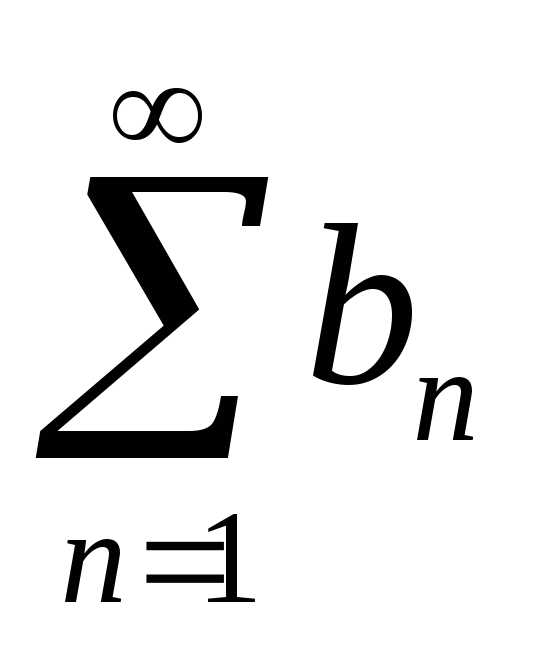 ,
причем все члены первого ряда меньше
соответствующих членов второго ряда:
,
причем все члены первого ряда меньше
соответствующих членов второго ряда: .
Тогда а) если ряд
.
Тогда а) если ряд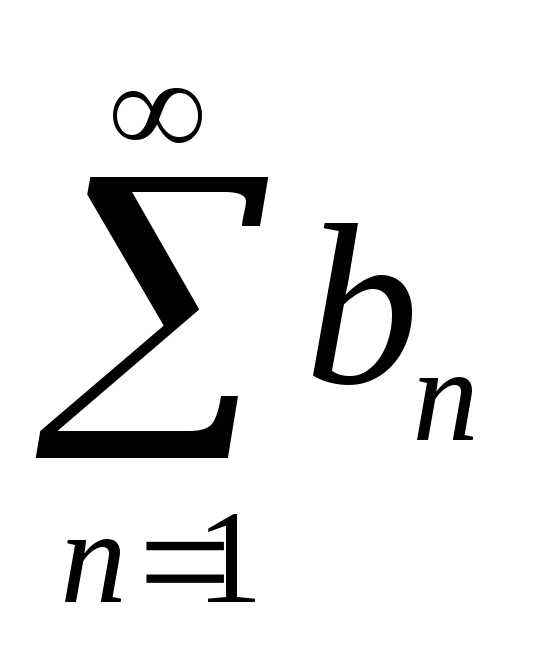 сходится, то и ряд
сходится, то и ряд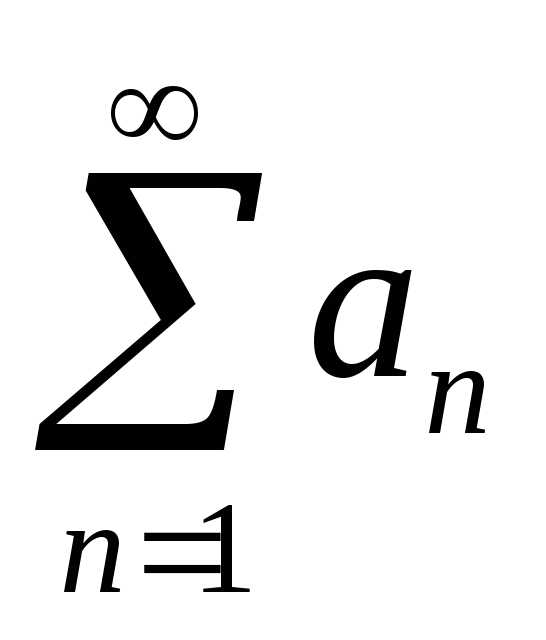 сходится; б) если ряд
сходится; б) если ряд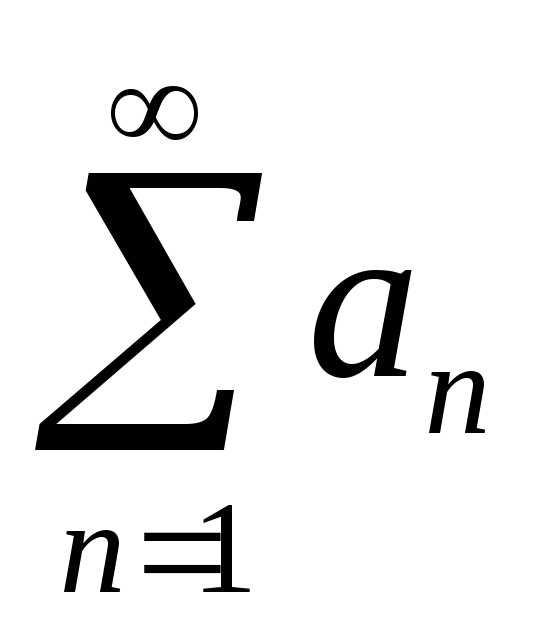 расходится, то и ряд
расходится, то и ряд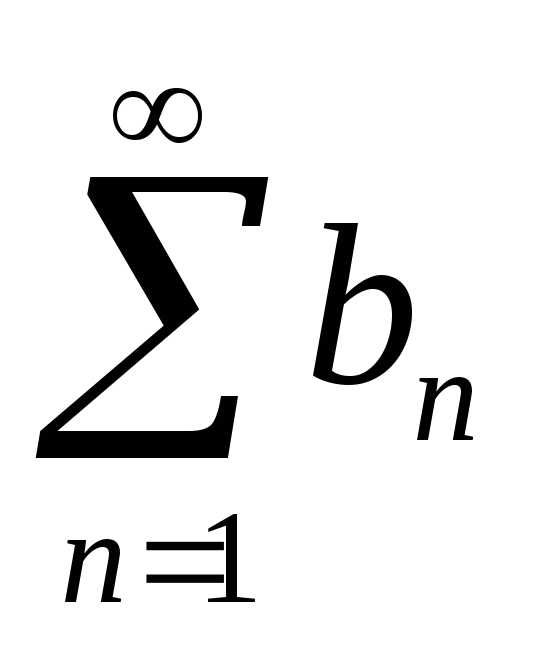 расходится.
расходится.
Доказательство:
а) известно, что знакоположительный ряд 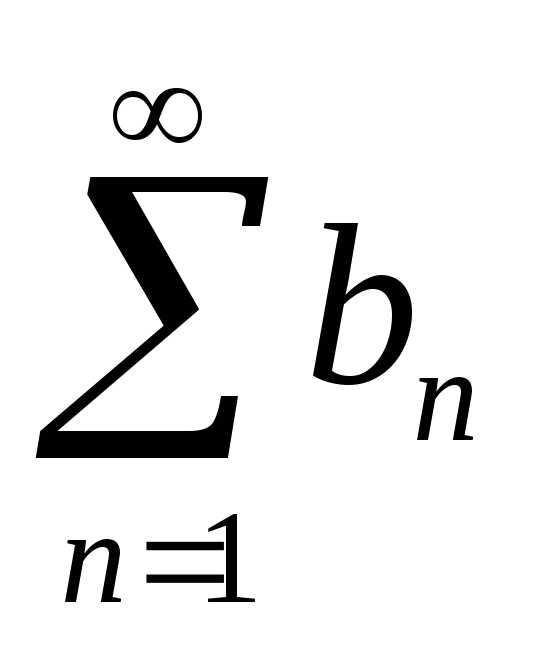 сходится:
сходится: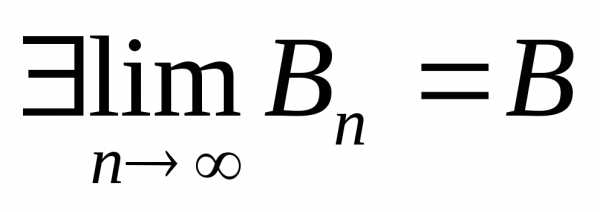 .
Заметим, чтоBn монотонно возрастающая последовательность,
имеющая предел, следовательно, она
ограничена сверху. Поэтому Вn
.
Заметим, чтоBn монотонно возрастающая последовательность,
имеющая предел, следовательно, она
ограничена сверху. Поэтому Вn B
(В – точная верхняя граница). Но
.
Следовательно, последовательность
монотонно возрастающая последовательность
An также ограничена сверху и имеет предел,
следовательно ряд
B
(В – точная верхняя граница). Но
.
Следовательно, последовательность
монотонно возрастающая последовательность
An также ограничена сверху и имеет предел,
следовательно ряд 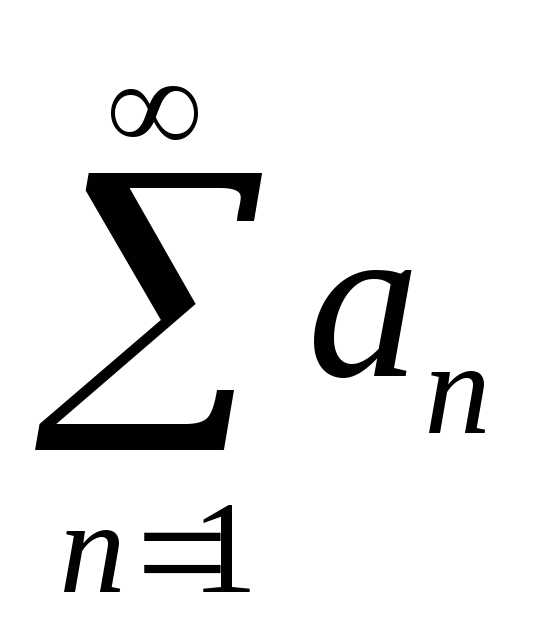 сходится, ч. т. д.; б) имеем расходящийся
ряд
сходится, ч. т. д.; б) имеем расходящийся
ряд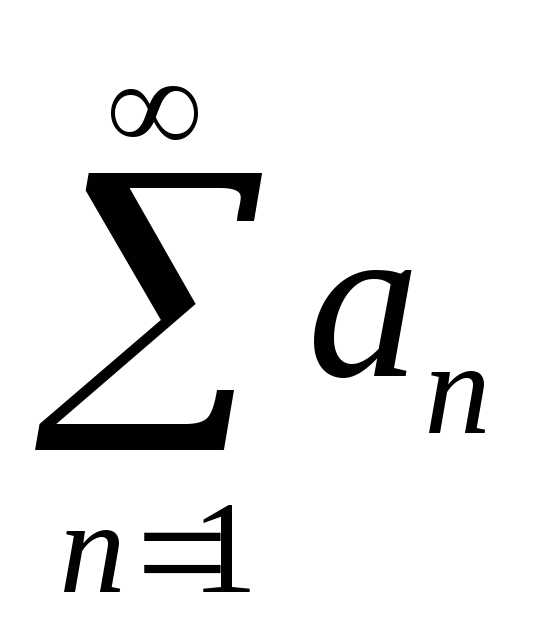 .
Допустим, что ряд
.
Допустим, что ряд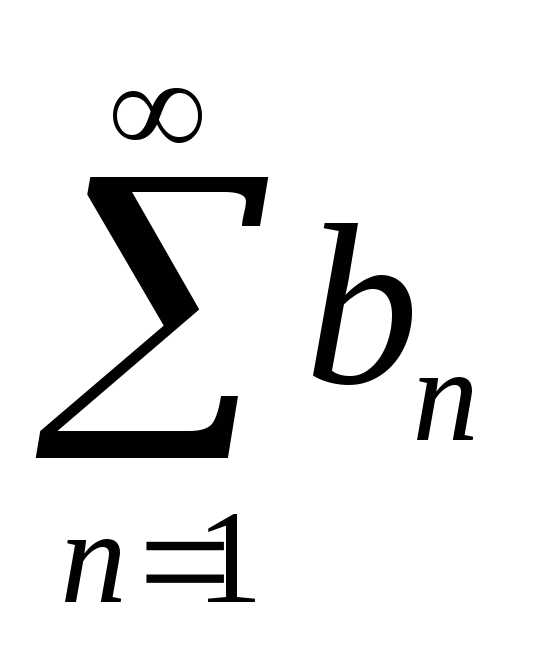 сходится. Тогда меньший ряд
сходится. Тогда меньший ряд также сходится (см. пункт а) данной
теоремы), а это не так. Мы пришли к
противоречию. Следовательно, ряд
также сходится (см. пункт а) данной
теоремы), а это не так. Мы пришли к
противоречию. Следовательно, ряд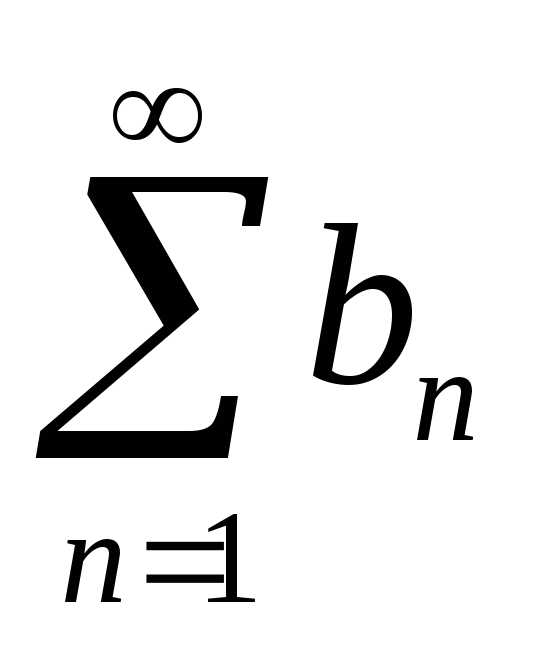 .
.
Замечание: 1-й
признак сравнения остается в силе, если
неравенство an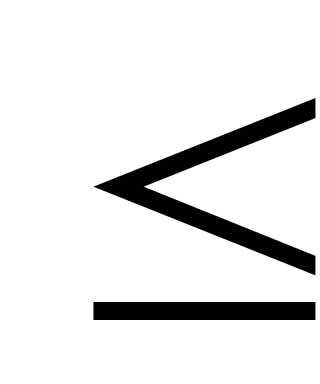 bn верно не для всех n,
а для n
n0.
Это вытекает из свойств сходимости.
bn верно не для всех n,
а для n
n0.
Это вытекает из свойств сходимости.
2-й
признак сходимости:
пусть даны два знакоположительных ряда 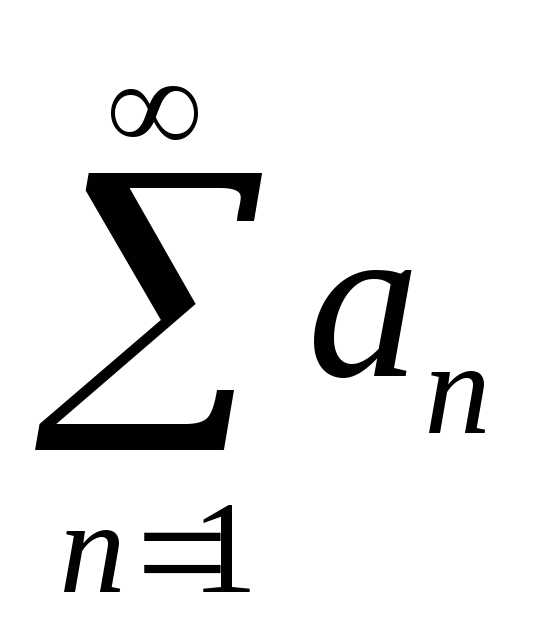 и
и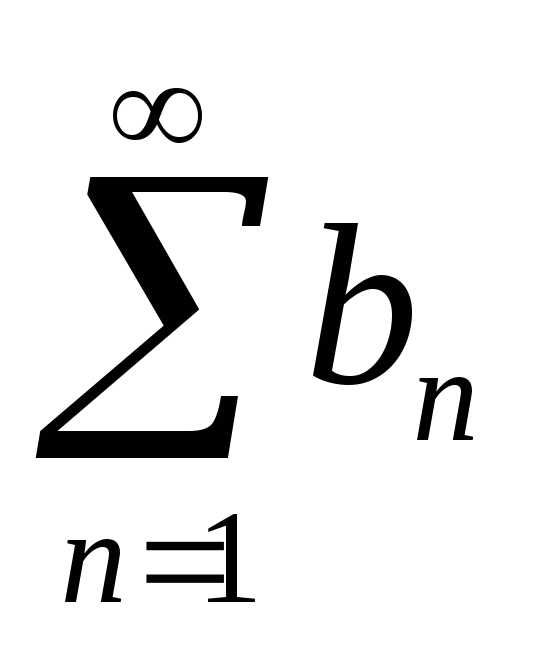 и пусть существует
и пусть существует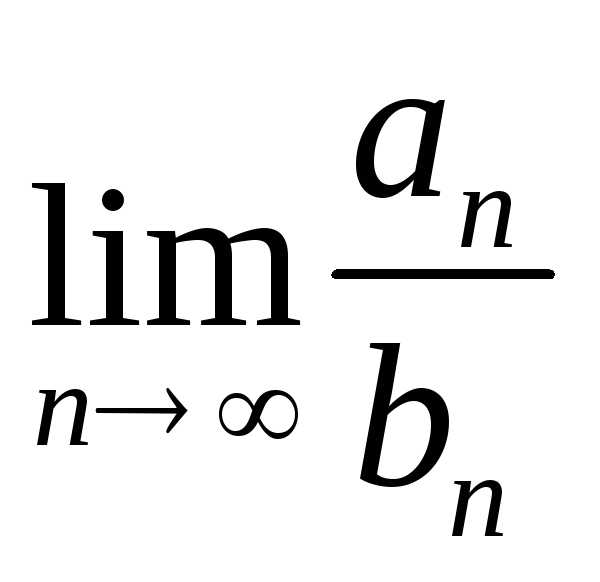 = С
0 (С > 0, т.к. предел отношения двух
положительных последовательностей
также положителен). Тогда оба ряда
сходятся или расходятся одновременно.
= С
0 (С > 0, т.к. предел отношения двух
положительных последовательностей
также положителен). Тогда оба ряда
сходятся или расходятся одновременно.
Доказательство:
по условию 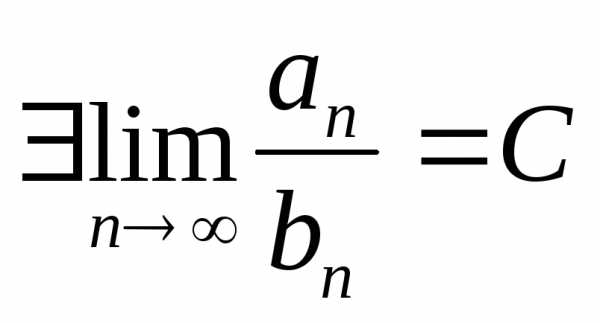 ,
это означает, чтоили -
<
,
это означает, чтоили -
< 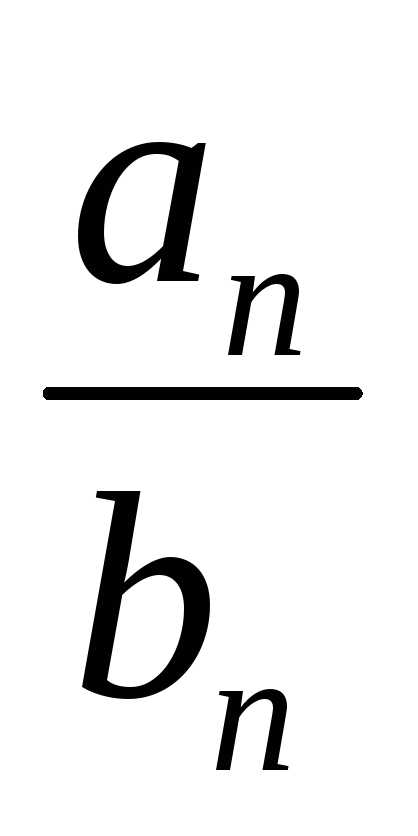 — C
< ;
С —
<
— C
< ;
С —
< 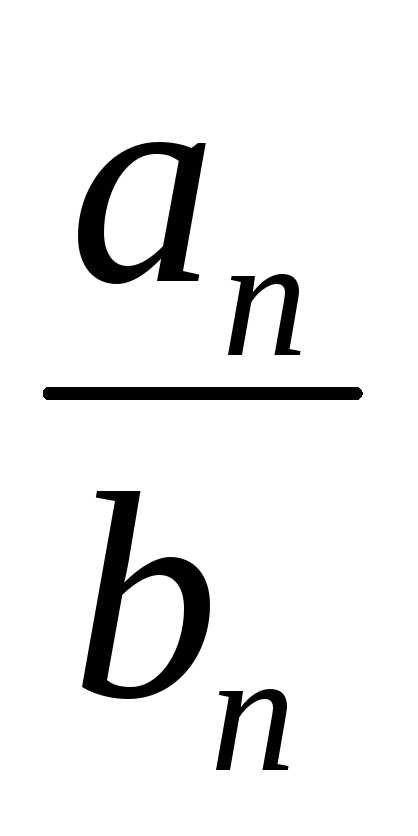 < C
+ ;
< C
+ ;
(C — ) bn < an < (C + ) bn. *)
Поскольку
— любое число, мы можем взять 0 <
< C,
тогда С —
> 0. Допустим, что ряд 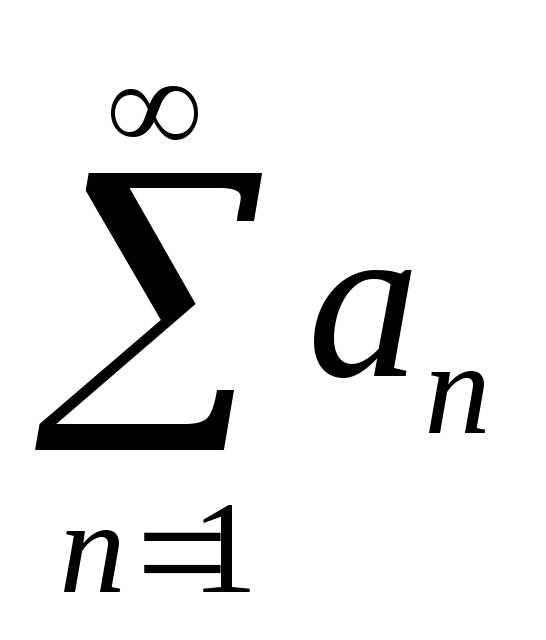 сходится. Тогда, по 1-му признаку сравнения,
ряд
сходится. Тогда, по 1-му признаку сравнения,
ряд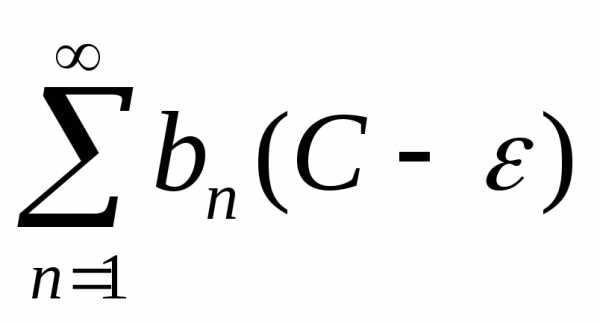 также сходится, следовательно (по тому
же признаку) сходится и ряд
также сходится, следовательно (по тому
же признаку) сходится и ряд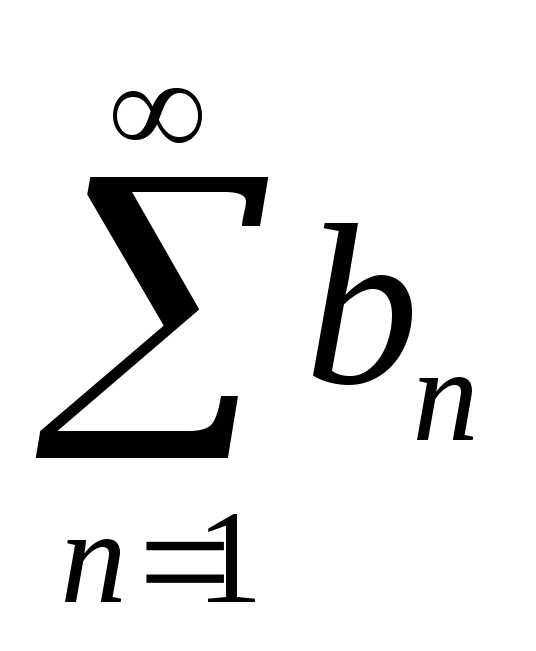 (неравенство выполняется, начиная с
некоторого номера). Аналогично (через
правую часть двойного неравенства *)
доказывается эта теорема для двух
расходящихся рядов.
(неравенство выполняется, начиная с
некоторого номера). Аналогично (через
правую часть двойного неравенства *)
доказывается эта теорема для двух
расходящихся рядов.
studfiles.net
Знакоположительные ряды. Теоремы сравнения.
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Лекция 5
Тема: Числовой ряд. Ряд из членов геометрической прогрессии. Необходимый признак сходимости ряда. Действие над рядами. Законоположительные ряды. Признаки сравнения.
Определение ряда. Определение сходимости ряда. Примеры.
Определение 1. Выражение вида + = называется рядом, , …- члены ряда, — общий член ряда.
Вначале будем изучать ряды, членами которых являются действительные числа.
Приведем примеры рядов:
– гармонический ряд,
= + q+ +… а — первый член прогрессии, q — знаменатель прогрессии.
Определение 2. Ряд называется сходящимся, если существует предел его частных сумм, т.е. , где — сумма первых n членов ряда. Если не существует, то ряд называется расходящимся.
Пример 1. Исследовать на сходимость гармонический ряд
Решение: Рассмотрим группу слагаемых
, где каждая их скобок больше .
Отсюда следует, что , т.е. предел не существует, т.к. при n число скобок в тоже стремиться к . Гармонический ряд расходится.
Пример 2. Исследовать на сходимость ряд из членов геометрической прогрессии , a , q
Решение: Рассмотрим частичную сумму данного ряда.
q
(1-q)
Если q то = .
Рассмотрим предел частичных сумм:
=
Остается рассмотреть случай, когда q=1. В этом случае имеем ряд а+а+а….,
, т.к. а .
Итак, ряд из членов геометрической прогрессии при сходится и его сумма s= , а при расходится.
Пример 3. Найти сумму ряда .
Решение. Данный ряд является рядом из членов геометрической прогрессии, где а=2, q= Так как , то данный ряд сходится и s=
Пример 4. Исследовать на сходимость ряд . Является рядом из членов геометрической прогрессии, где a=-2, q= -1. Так как , то данный ряд расходится.
Необходимый признак сходимости.
Теорема 1. Если ряд сходится, то предел его общего члена равен 0,
т.е. .
Доказательство. По условию данный ряд сходится. Это означает, что
, … = lim( — )= .
Следствие. Если общий член ряда к нулю не стремится, то ряд расходится.
Действие над рядами.
1) Сложение рядов.
Пусть даны два ряда Суммой двух рядов называется ряд
Теорема 2.Если ряды сходятся соответственно к то ряд сходится к .
Доказательство. По условию ряды сходятся, то и
2) Умножение ряда на число.
Произведение ряда на число или числа на ряд называется ряд (3)
Теорема 3. Если ряд сходится и его сумма равна s, то ряд тоже сходится и его сумма равна .
Если то оба ряда и либо одновременно сходятся или одновременно расходятся.
Доказательство. Справедливость теоремы вытекает из равенства:
Теорема 4. Сходимость ряда не измениться если отбросить или прибавить конечное число первых членов ряда.
Доказательство. Рассмотрим два ряда:
+ +….+ + …+ +… (4)
+ +…+ +… (5)
Справедливость теоремы вытекает из равенства:
= + +….+ + …+ = + ,где является константой, не зависящей от n.
Знакоположительные ряды. Теоремы сравнения.
Ряд называется знакоположительным, если .
Теоремы, которые справедливы для знакоположительных рядов, справедливы для знакоотрицательных рядов, так, как умножение ряда на (-1), сходимость ряда не изменяет.
Теорема 5:
Для того, чтобы знакоположительный ряд сходился необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху.
Доказательство. Дан знакоположительный ряд
, , , = + + …+ .
….. ….
Последовательность частичных сумм , неубывающая. Для того, чтобы неубывающая последовательность имела предел, необходимо и достаточно, чтобы она была ограничена сверху.
Теорема 6:
Пусть даны два знакоположительных ряда (1) , для которых выполняются неравенства
Тогда если ряд (2) сходится, то ряд (1) тоже сходится. Если же ряд (1) расходится, то ряд (2) тоже расходится.
Доказательство. Справедливость теоремы вытекает из неравенства = + …+ + +… = и теоремы 4. В самом деле, если ряд (2) сходится, то последовательность { } ограничена сверху, тогда { } ограничена сверху и ряд (1) сходится. Если ряд (1) расходится, то { не ограничена сверху и тем более не ограничена сверху. Следовательно, ряд (2) расходится.
Замечание 1. Учитывая теорему 3, можно утверждать, что теорема 5 справедлива при выполнении неравенств , .
Чтобы применять теорему 5 при исследовании сходимости рядов, нужно иметь набор сходящихся и расходящихся рядов. Примером сходящихся рядов могут служить знакоположительные ряды из членов геометрической прогрессии при q , а примерами расходящихся рядов могут быть знакоположительные ряды из членов геометрической прогрессии, при 1 .
Примером расходящегося ряда может служить гармонический ряд .
Ряды Дирихле:
Ряды Дирихле мы исследуем позже с помощью интегрального признака Коши.
А сейчас отметим, что ряды Дирихле при 1<S сходятся, а при S расходятся.
Ряд Дирихле при S=1 является гармоническим рядом.
Пример 5:Исследовать на сходимость ряд .
Решение: 0 , . Так как ряд Дирихле сходится, то по теореме сравнения данный ряд тоже сходится.
Пример 6:Исследовать на сходимость ряд
Решение: < Так как гармонический ряд расходится, то данный ряд тоже расходится.
Теорема 7:
Пусть даны два знакоположительных ряда (1) ; для которых существует предел = c , то ряды (1) и (2) либо одновременно сходятся, либо одновременно расходятся.
Пример 7:Исследовать на сходимость ряд
Решение: так как Sinx при x то данный ряд надо сравнить с рядом Дирихле , который сходится.
Рассмотрим предел = 1 0 в силу первого замечательного предела.
Следовательно, данный ряд сходится.
megapredmet.ru
Достаточные признаки сходимости знакоположительных рядов
Пусть
. Тогда ряд 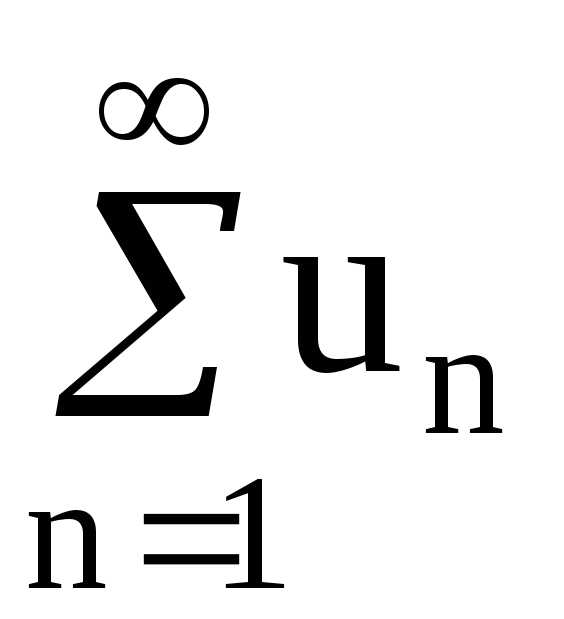 будем называть знакоположительным.
Сформулируем некоторые достаточные
условия сходимости таких рядов.
будем называть знакоположительным.
Сформулируем некоторые достаточные
условия сходимости таких рядов.
Признак сравнения
Пусть 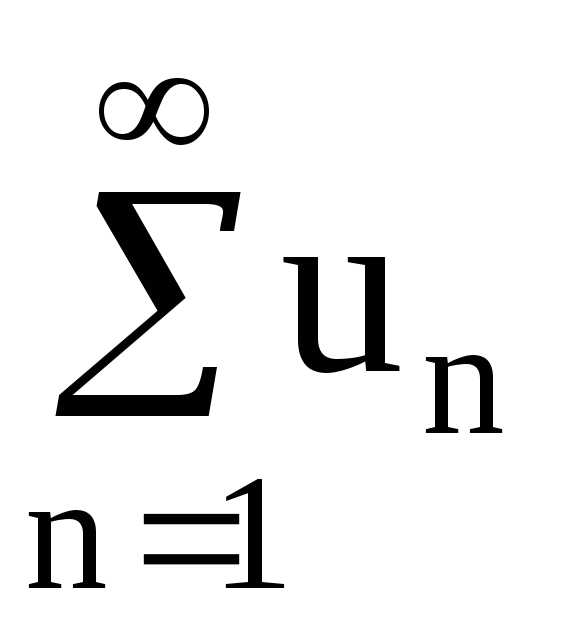 и
и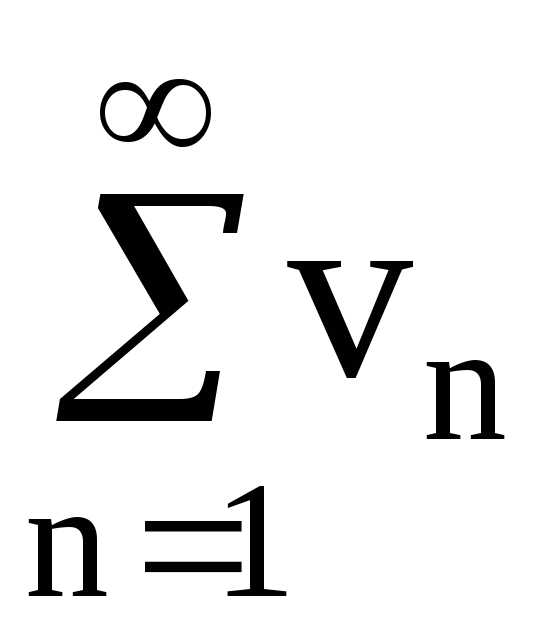 – знакоположительные ряды. Если для
всех
– знакоположительные ряды. Если для
всех выполняется неравенство
выполняется неравенство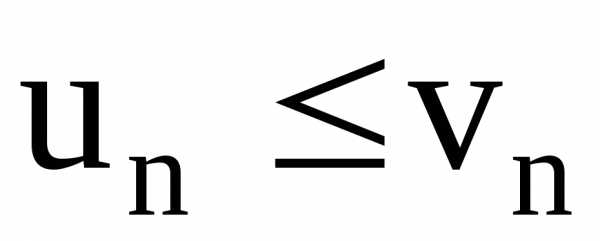 ,
то из сходимости ряда
,
то из сходимости ряда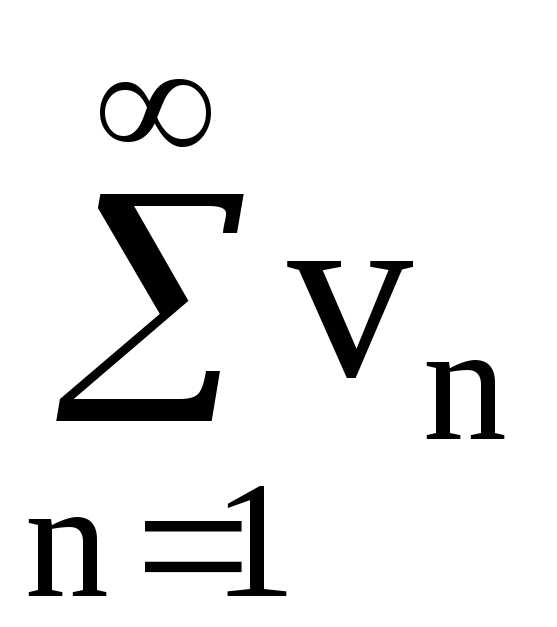 следует сходимость ряда
следует сходимость ряда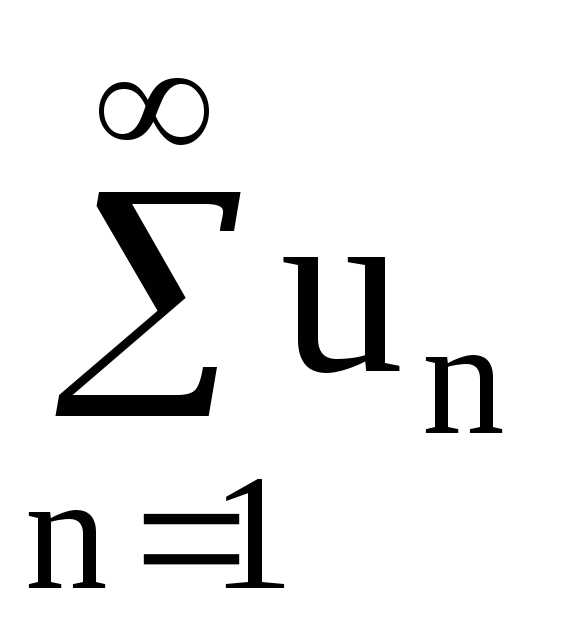 ,
а из расходимости ряда
,
а из расходимости ряда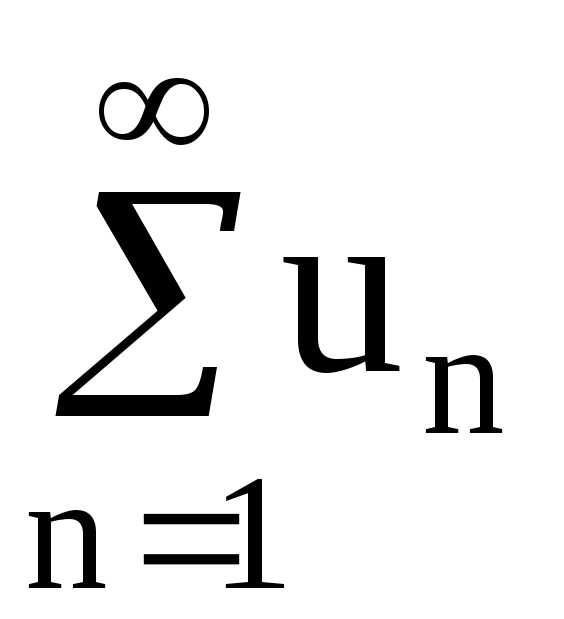 следует расходимость ряда
следует расходимость ряда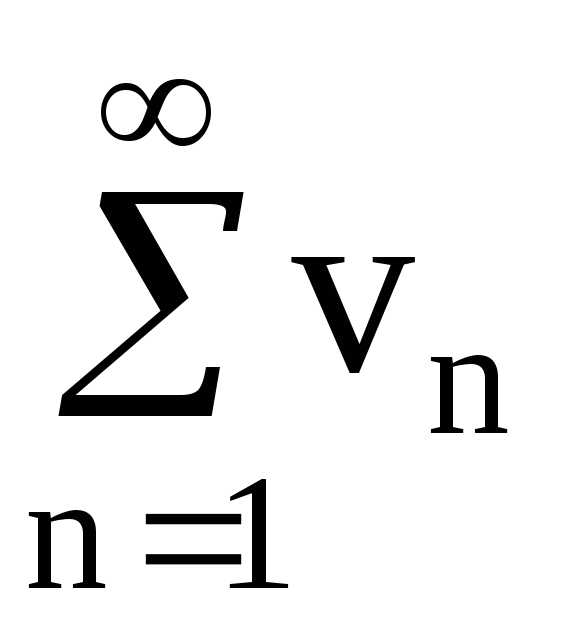 .
.
Этот
признак остается в силе, если неравенство 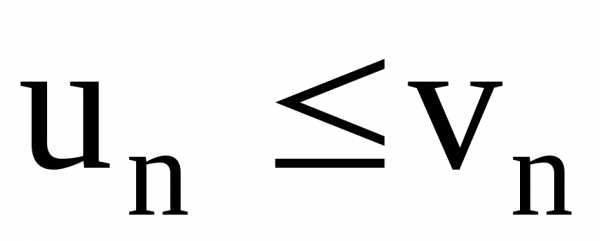 выполняется не при всех
выполняется не при всех ,
а лишь начиная с некоторого номера
,
а лишь начиная с некоторого номера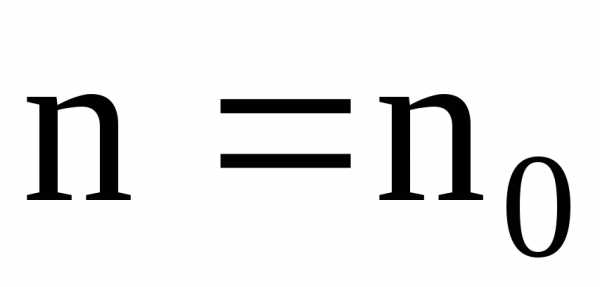 .
Его можно проинтерпретировать следующим
образом: если больший ряд сходится, то
меньший тем более сходится; если
расходится меньший ряд, то больший также
расходится.
.
Его можно проинтерпретировать следующим
образом: если больший ряд сходится, то
меньший тем более сходится; если
расходится меньший ряд, то больший также
расходится.
Пример
4. Исследовать
сходимость ряда 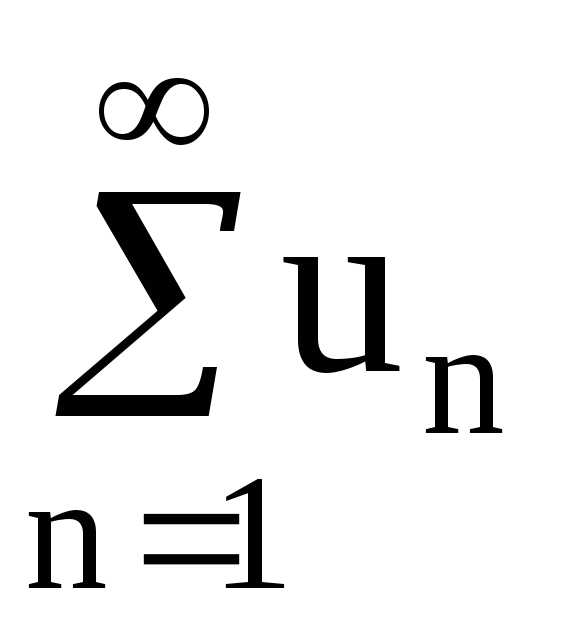 ,
если
,
если
а)
 ;
;б)
 ;
;
Решение.
а)
Заметим, что 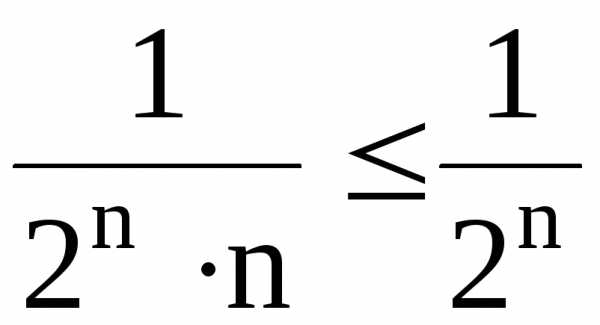 для всех
.
Ряд с общим членом
для всех
.
Ряд с общим членом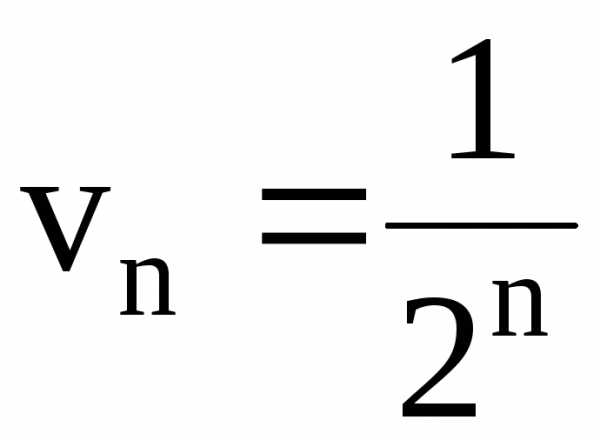 сходится, т.к. является рядом геометрической
прогрессии со знаменателем
сходится, т.к. является рядом геометрической
прогрессии со знаменателем 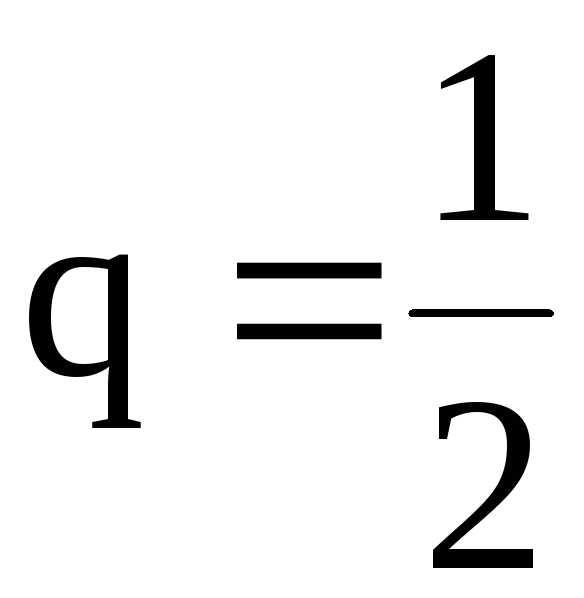 (см. пример 1), поэтому данный ряд
(см. пример 1), поэтому данный ряд 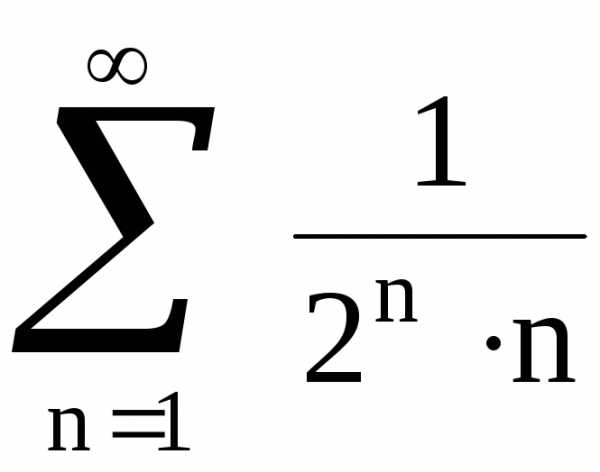 сходится по признаку сравнения.
сходится по признаку сравнения.
б)
Сравним ряд 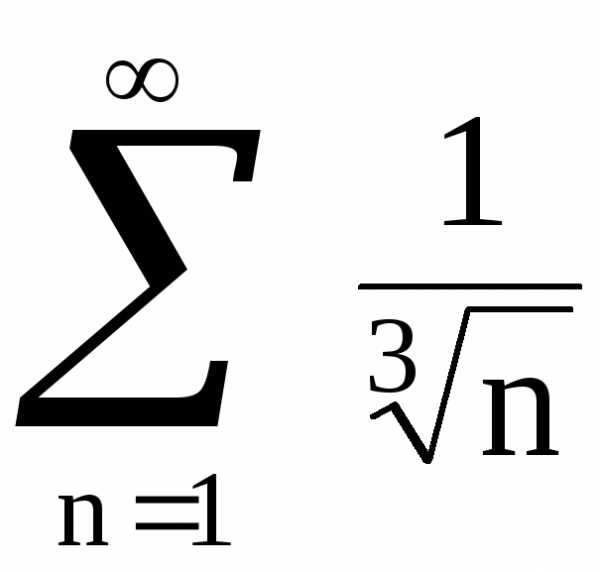 с рядом
с рядом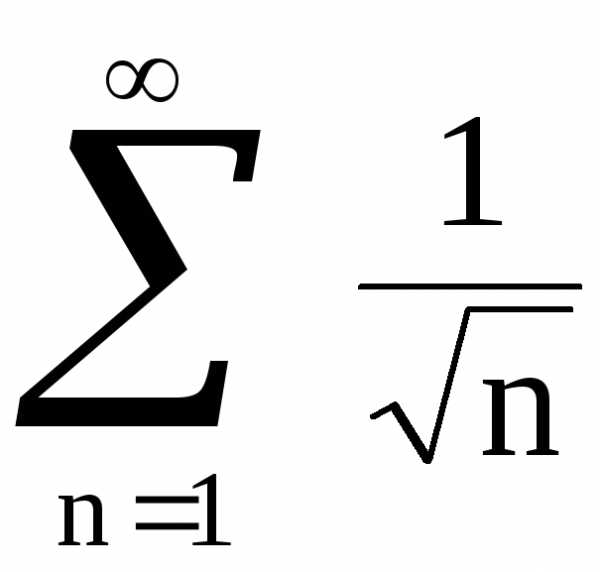 .
Очевидно, что для всех
.
Очевидно, что для всех ,
поэтому
,
поэтому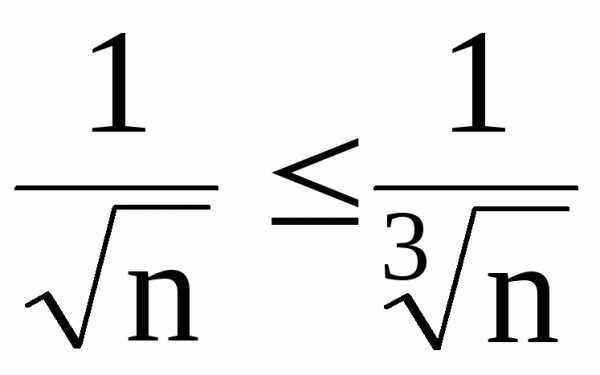 .
В примере 3 было доказано, что ряд с общим
членом
.
В примере 3 было доказано, что ряд с общим
членом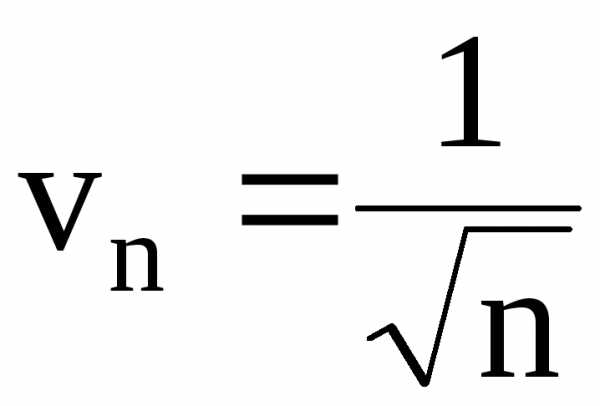 расходится, значит,
данный ряд также расходится.
расходится, значит,
данный ряд также расходится.
Несмотря на простоту формулировки признака сравнения, на практике более удобна следующая теорема, являющаяся его следствием.
Предельный признак сравнения
Пусть 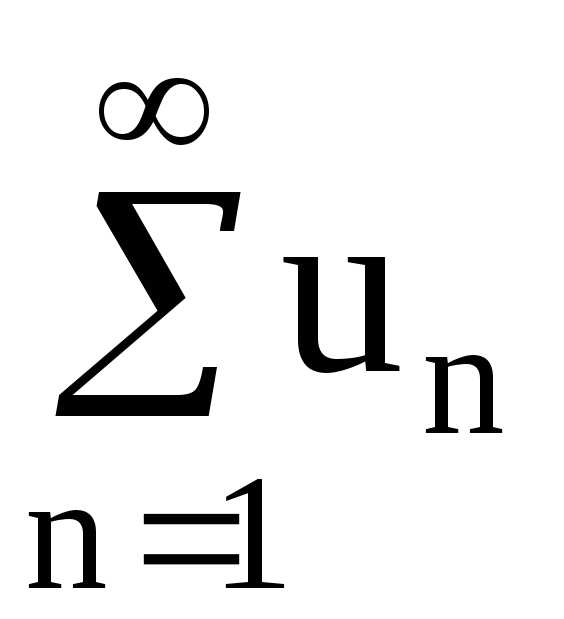 и
и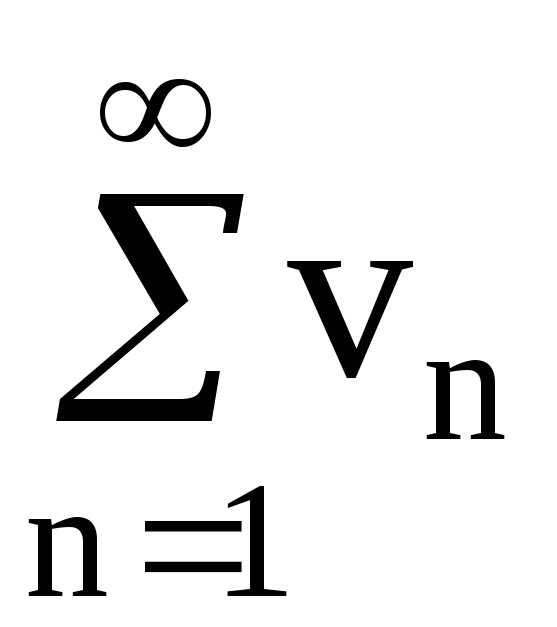 – знакоположительные ряды. Если
существуетконечный и не
равный нулю предел
– знакоположительные ряды. Если
существуетконечный и не
равный нулю предел 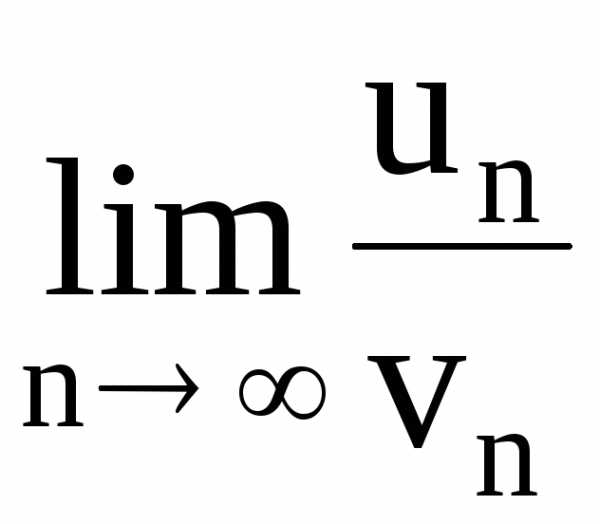 ,
то оба ряда
,
то оба ряда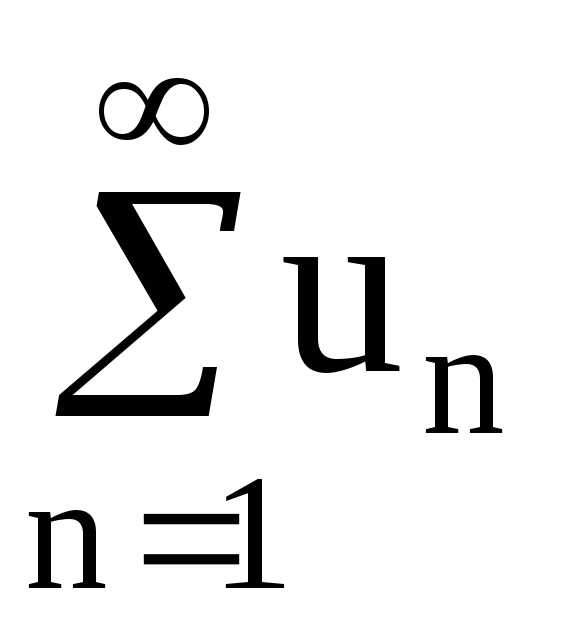 и
и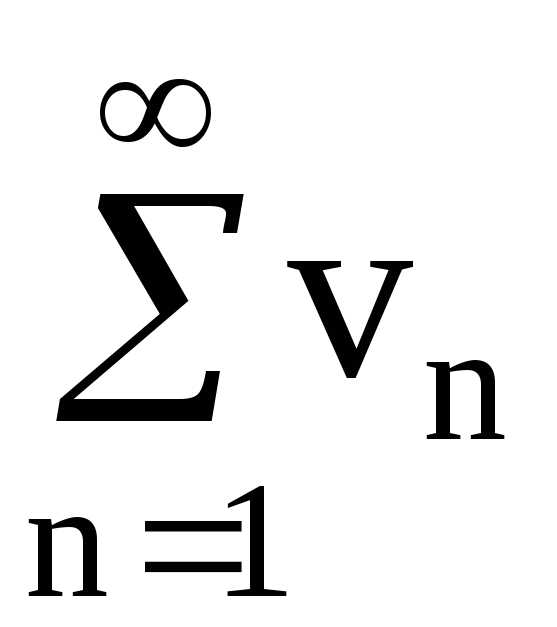
одновременно сходятся или одновременно расходятся.
В
качестве ряда, используемого для
сравнения с данным, часто выбирают ряд
вида 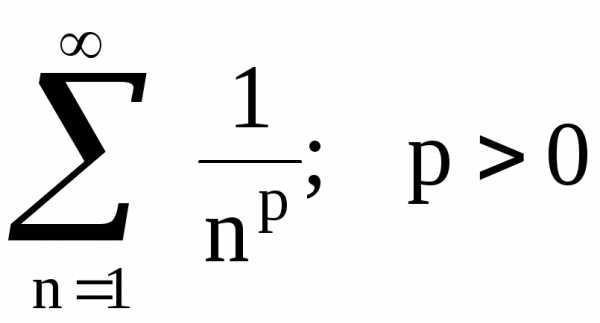 .
Такой ряд называетсярядом
Дирихле. В
примерах 3 и 4 было показано, что ряд
Дирихле с
.
Такой ряд называетсярядом
Дирихле. В
примерах 3 и 4 было показано, что ряд
Дирихле с 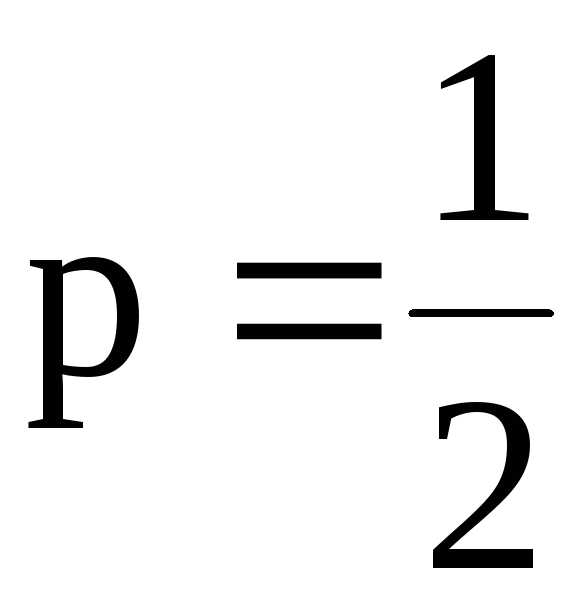 и
и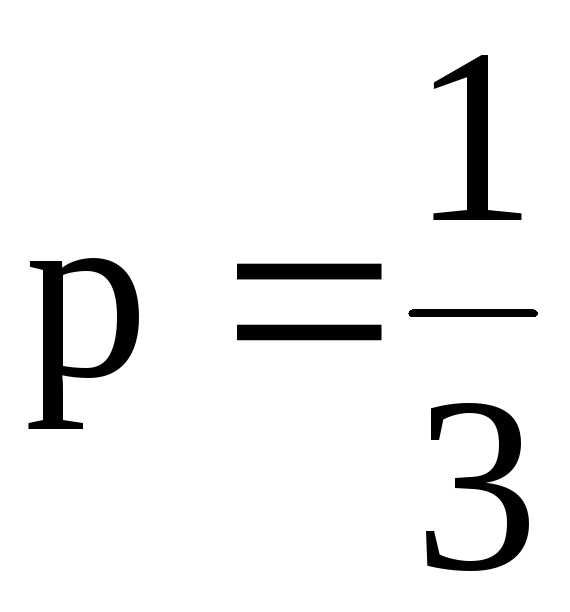 расходится. Можно пока-
расходится. Можно пока-
зать,
что ряд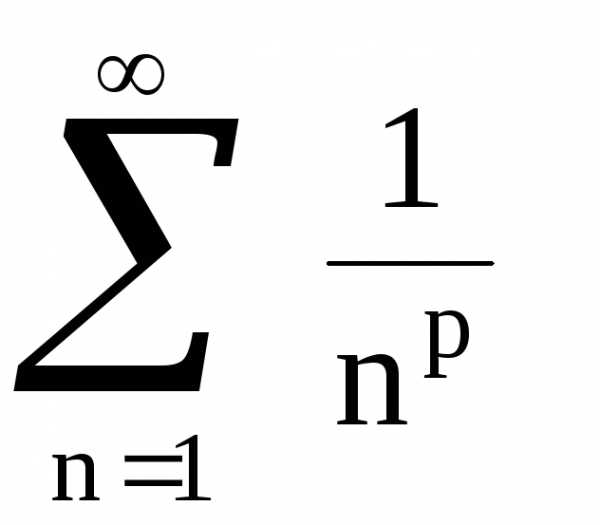 .
.
Если 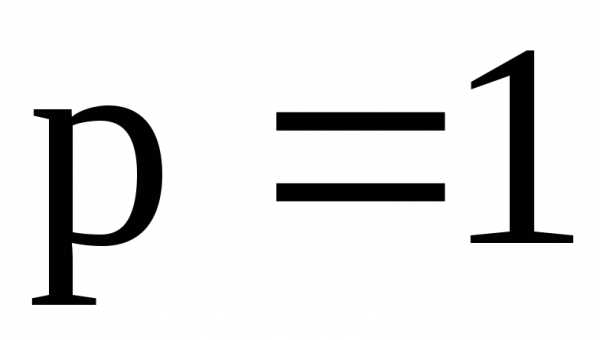 ,
то рядназывается гармоническим.
Гармонический ряд расходится.
,
то рядназывается гармоническим.
Гармонический ряд расходится.
Пример
5. Исследовать
на сходимость ряд 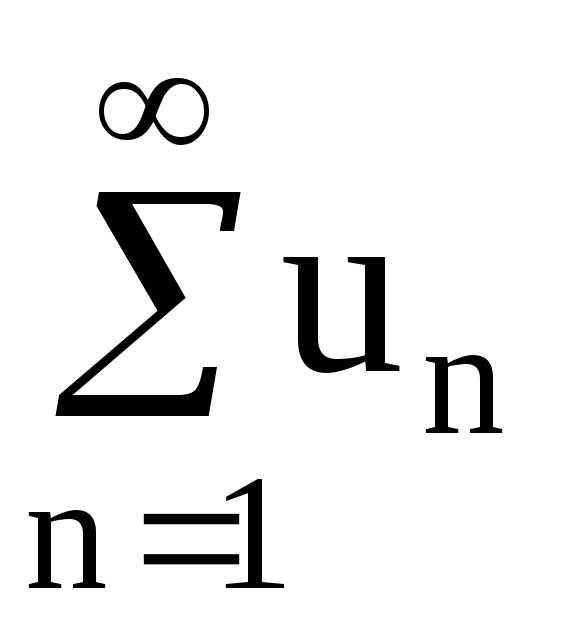 с помощью предельного признака сравнения,
если
с помощью предельного признака сравнения,
если
Решение. а) Так как при достаточно больших 
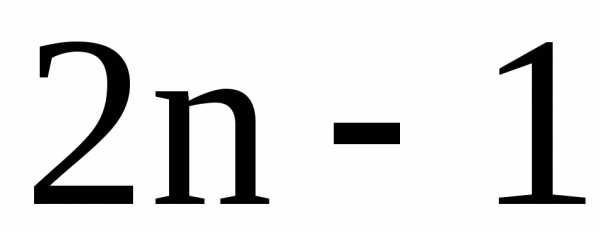 ~
~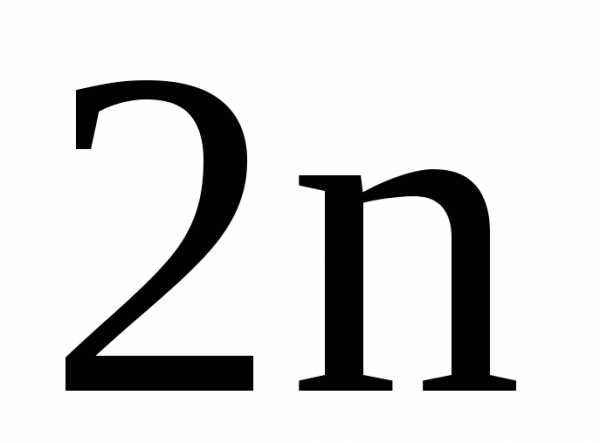 ,
а
,
а
~ 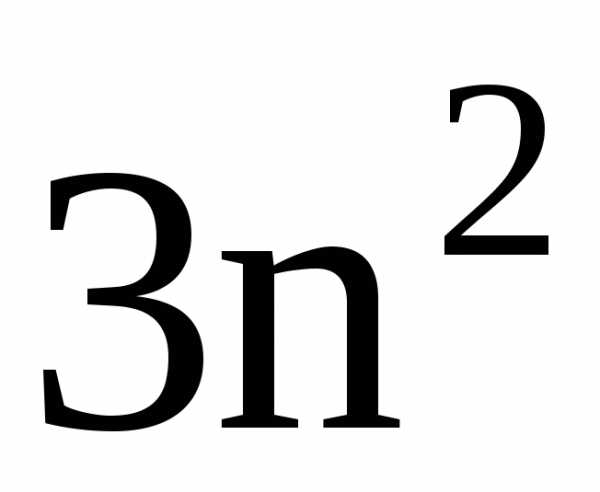 ,
то
,
то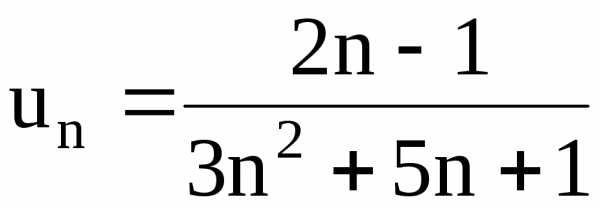 ~
~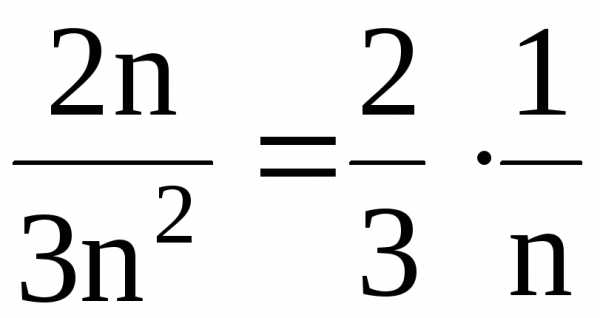 .
Выберем для
.
Выберем для
сравнения
с данным гармонический ряд 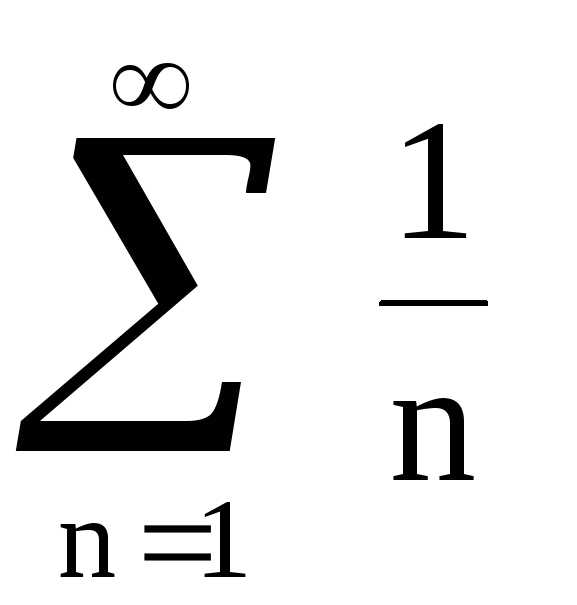 ,
т.е.
,
т.е. 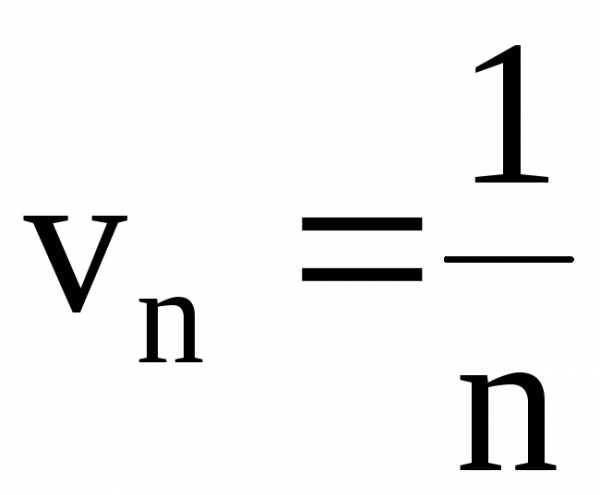 .
.
( см. [5] ).
Поскольку предел конечен и отличен от нуля и гармонический ряд расходится, то расходится и данный ряд.
б)
При достаточно больших  ~
~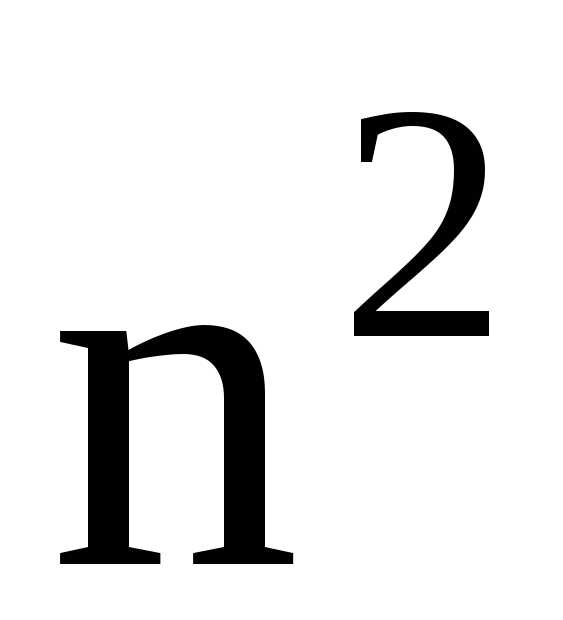 ,~
,~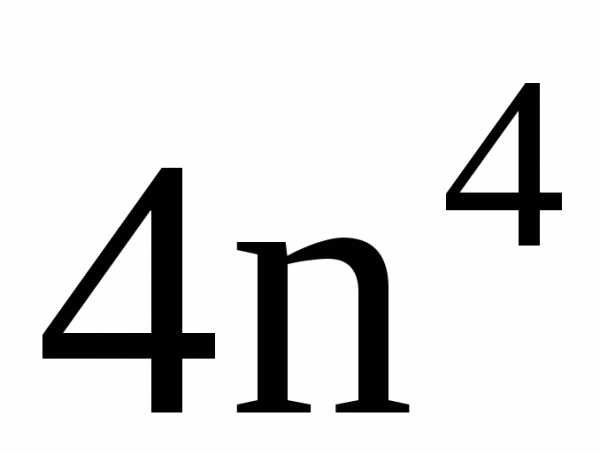 ,
поэтому
,
поэтому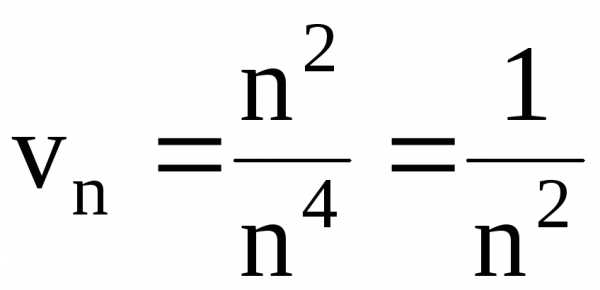 – общий член ряда, с которым будем
сравнивать данный:
– общий член ряда, с которым будем
сравнивать данный:
( см. [5] ).
Ряд 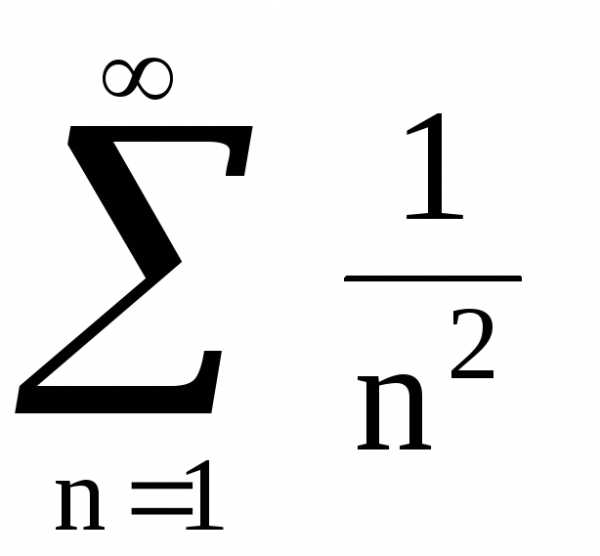 сходится (ряд
Дирихле с
сходится (ряд
Дирихле с 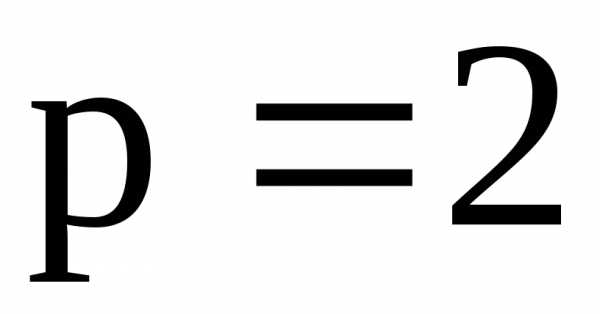 ),
поэтому данный ряд также сходится.
),
поэтому данный ряд также сходится.
в)  ,
поэтому бесконечно малую
,
поэтому бесконечно малую можно
можно
заменить
на эквивалентную ей при
величину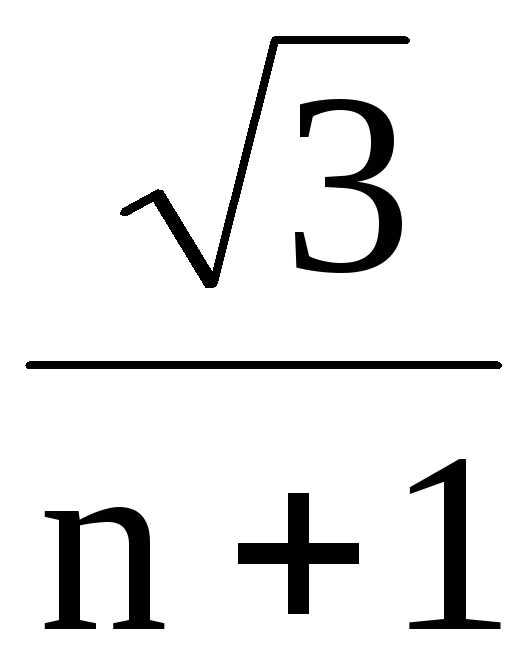 (
(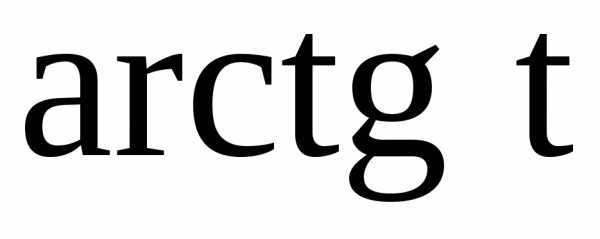 ~
~ при
при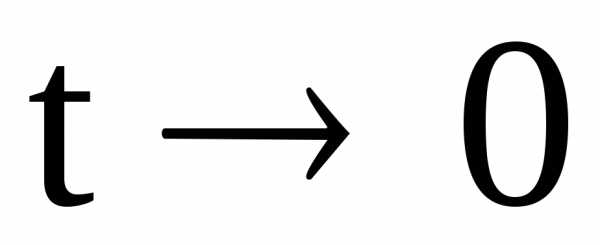 – см. [5]).
– см. [5]).
Тогда 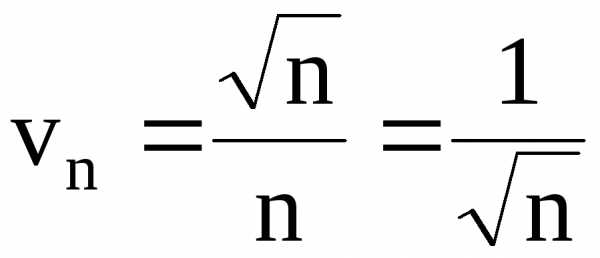 – общий член ряда для сравнения.
– общий член ряда для сравнения.
.
Так
как предел конечен и не равен нулю, а
ряд 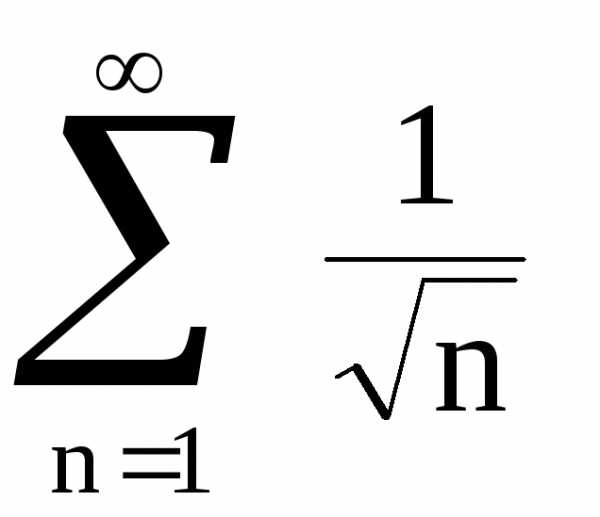 расходится (ряд
Дирихле с
расходится (ряд
Дирихле с 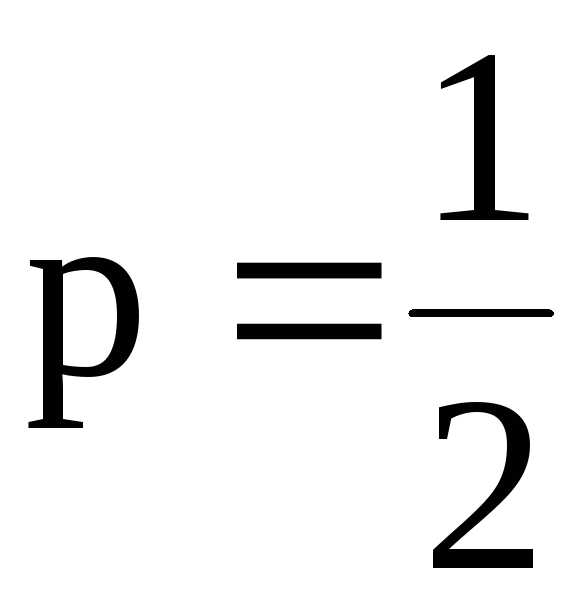 ),
то данный ряд расходится.
),
то данный ряд расходится.
Существуют признаки сходимости рядов, позволяющие непосредственно судить о сходимости или расходимости данного ряда, не сравнивая его с рядом, поведение которого известно.
Признак Даламбера
Пусть 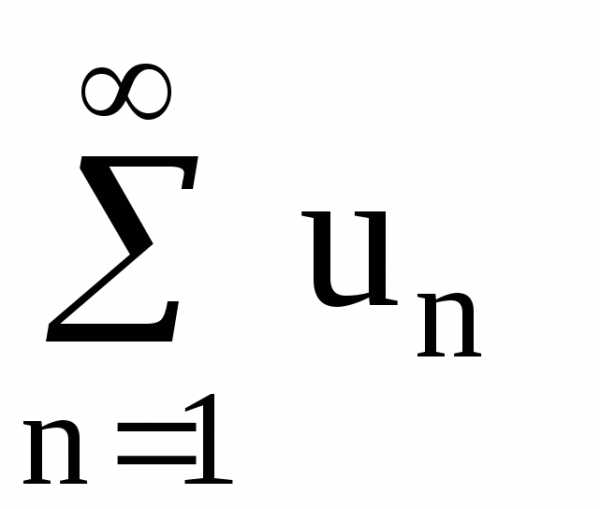 – знакоположительный
ряд. Если существует
– знакоположительный
ряд. Если существует 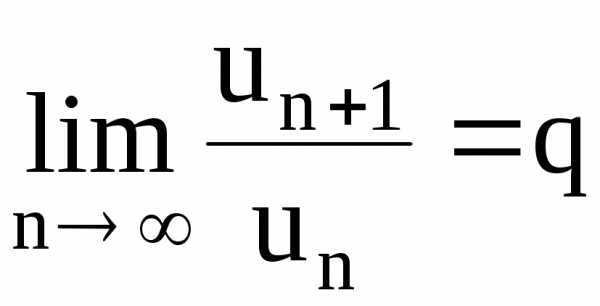 ,
то при
,
то при 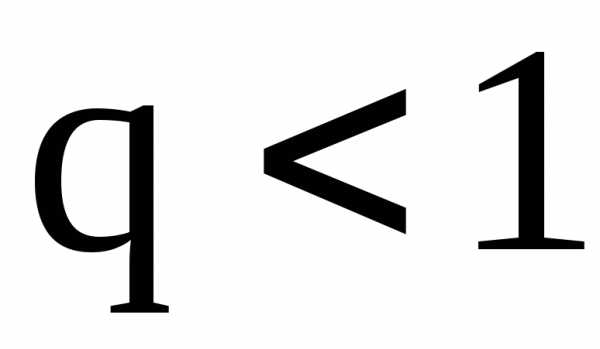 ряд сходится,
а при
ряд сходится,
а при 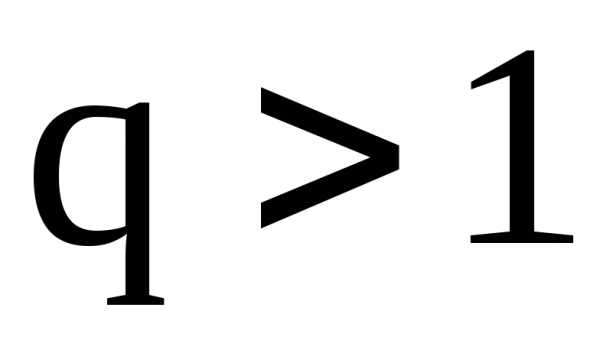 ряд расходится.
ряд расходится.
Если 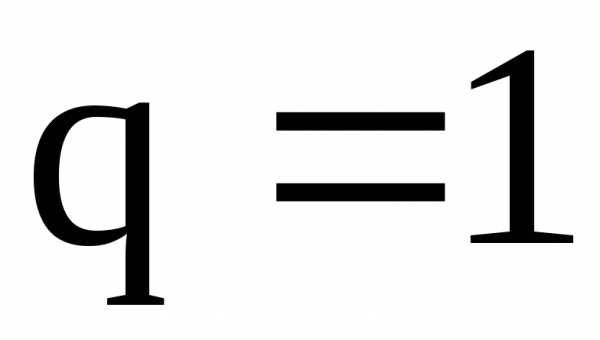 ,
то признак Даламбера не дает возможности
судить о поведении ряда. В этом случае
необходимо дополнительное исследование,
например, с помощью признаков сравнения.
,
то признак Даламбера не дает возможности
судить о поведении ряда. В этом случае
необходимо дополнительное исследование,
например, с помощью признаков сравнения.
В
примерах 5 а), б) с помощью предельного
признака сравнения было установлено,
что ряд  расходится, а ряд
расходится, а ряд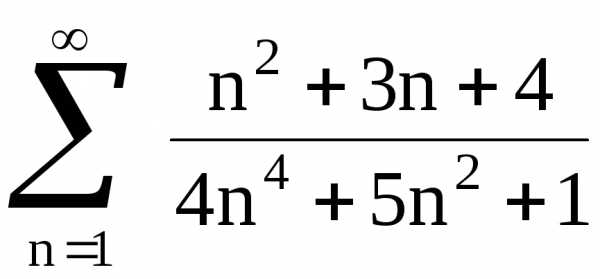 сходится. Посмотрим, как работает
применительно к этим рядам признак
Даламбера:
сходится. Посмотрим, как работает
применительно к этим рядам признак
Даламбера:
| ; |
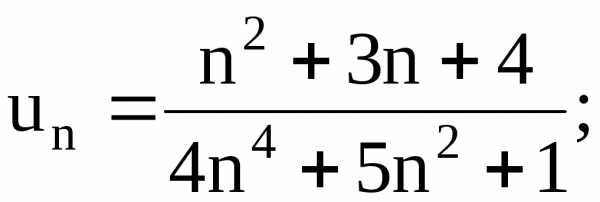
(см. [5]).
Таким
образом, в каждом из этих случаев признак
Даламбера не приводит к определенному
ответу: при 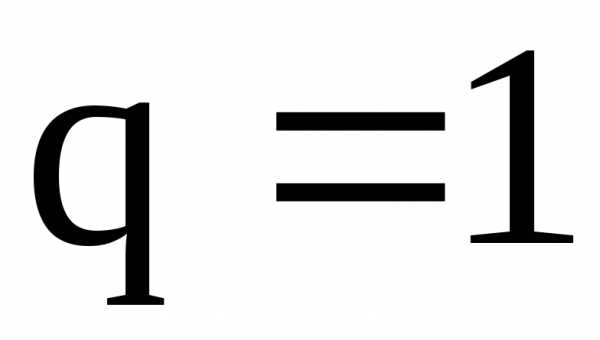 ряд может быть и сходящимся, и расходящимся.
ряд может быть и сходящимся, и расходящимся.
Пример
6. Исследовать
на сходимость ряд 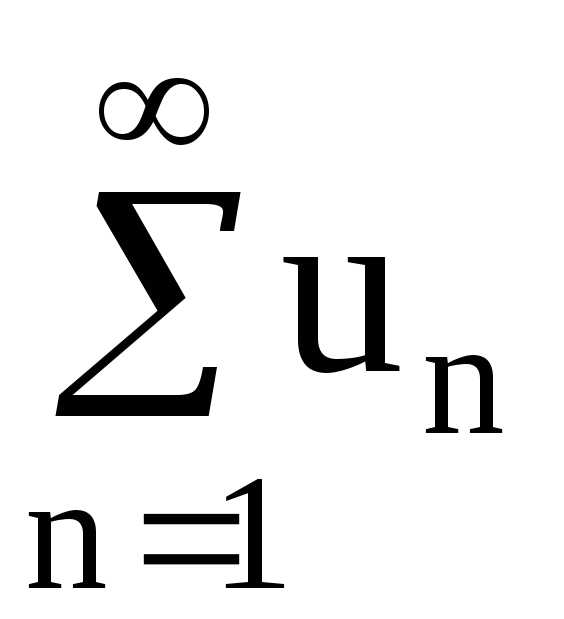 с помощью признака
с помощью признака
Даламбера, если
а) |
| б) |
| в) |
| |||
г) | ; | д) |
| |||||
Решение. а) Так как 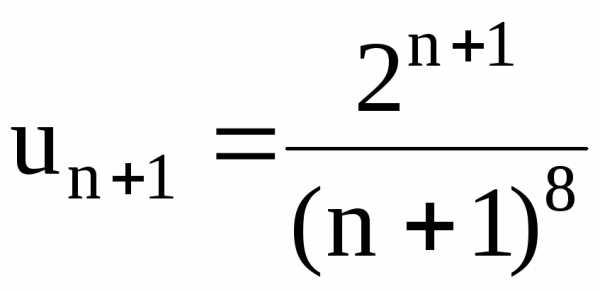 ,
то
,
то
Это
означает, что ряд 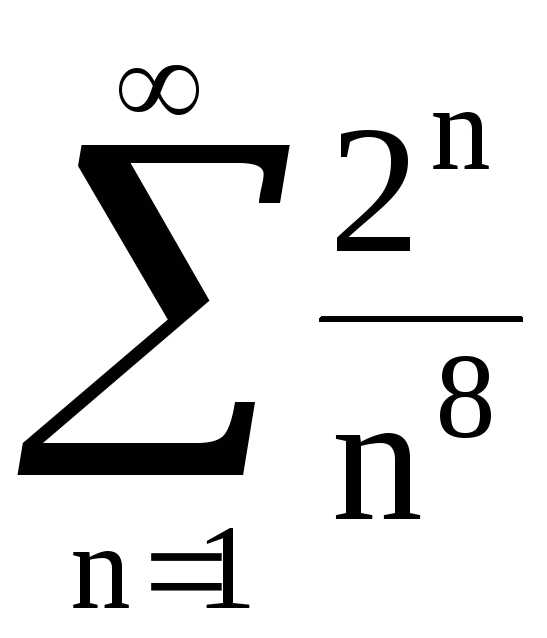 расходится.
расходится.
б)
Символ 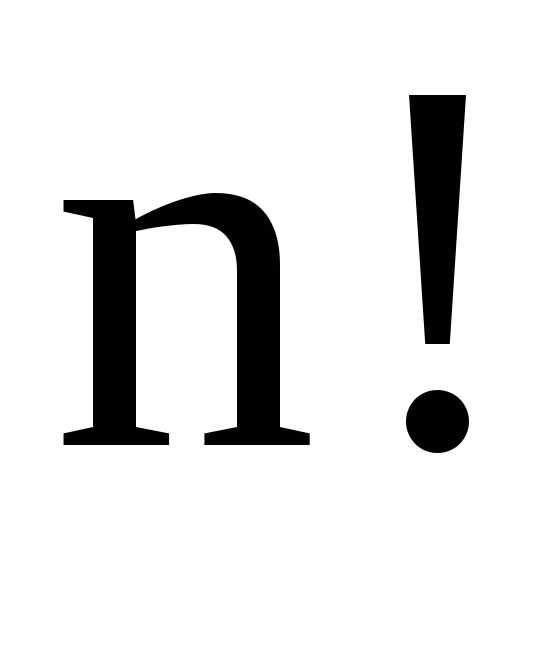 (читается “эн факториал”) – сокращенное
обозначение произведения всех натуральных
чисел от единицы до данного натурального
числаn:
(читается “эн факториал”) – сокращенное
обозначение произведения всех натуральных
чисел от единицы до данного натурального
числаn:
. Например, ,,
,
,
,
.
Так как , то для любого

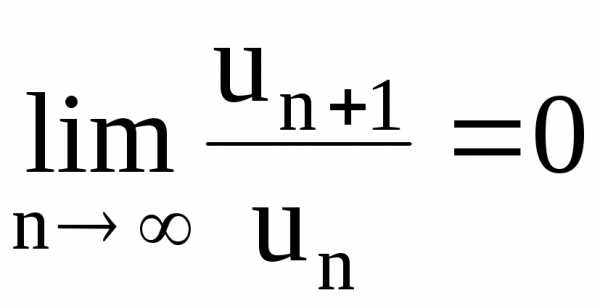 и
поэтому ряд сходится. Отсюда можно
сделать весьма важный вывод: так как
при любом
и
поэтому ряд сходится. Отсюда можно
сделать весьма важный вывод: так как
при любом  ряд
ряд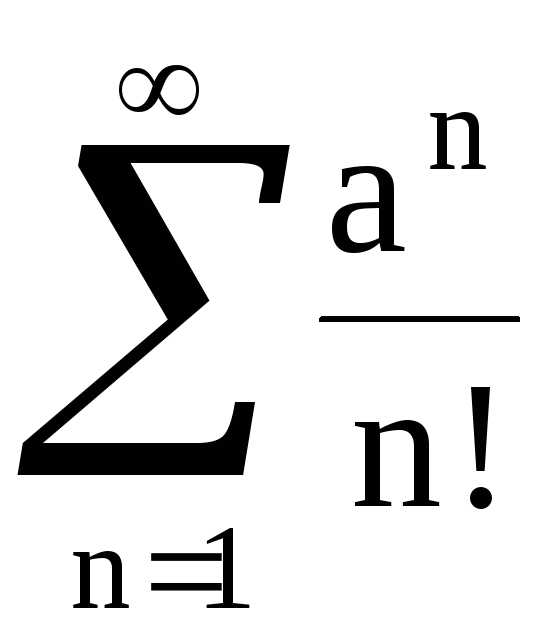 сходится, то по необходимому признаку
сходимости
сходится, то по необходимому признаку
сходимости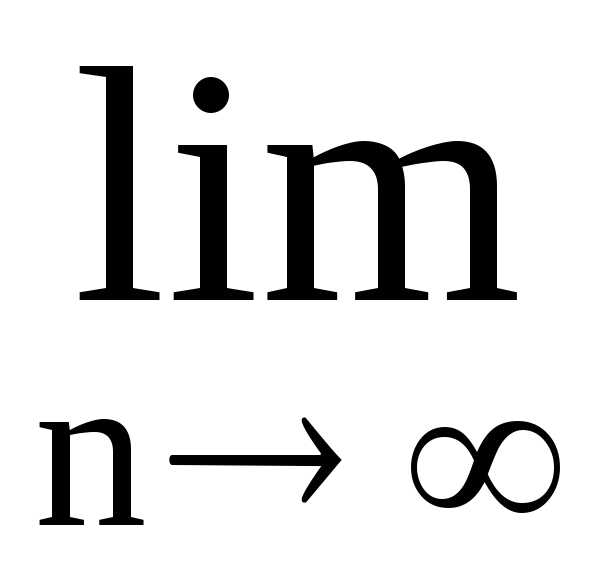
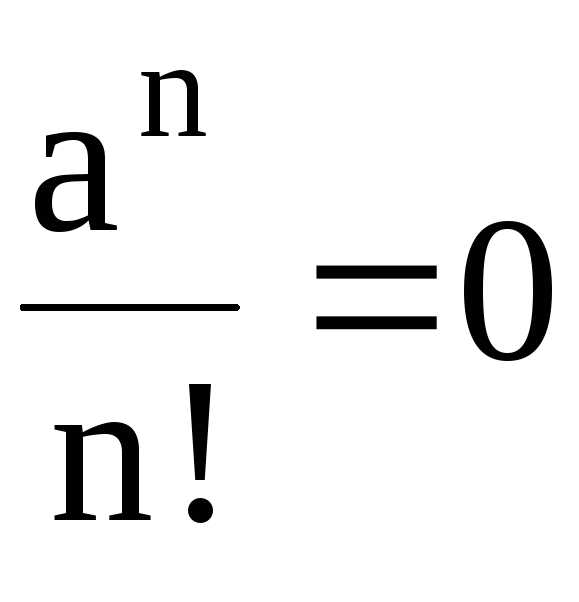 .
.
в) Так как , то
(см. [5]), т. е. ряд сходится.
г)
Для того, чтобы записать  ,
заменим в
,
заменим в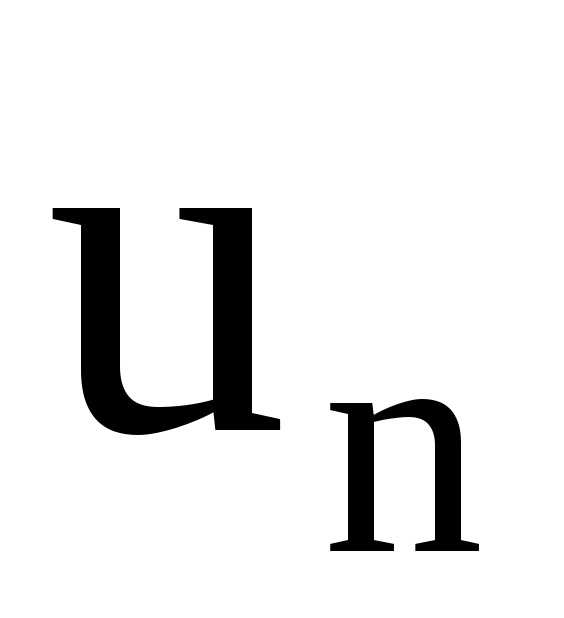
 на
на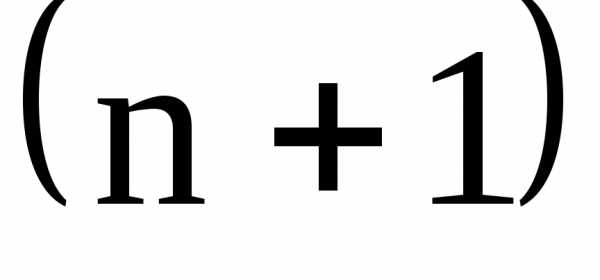 .
Тогда к
.
Тогда к
произведению добавится еще один сомножитель, равный
,
а к произведению 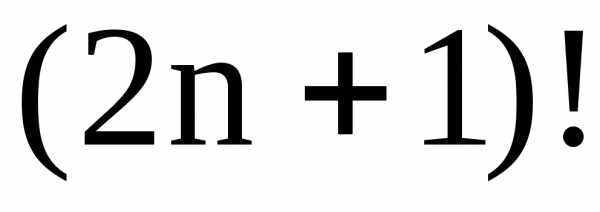 – еще два сомножителя:
– еще два сомножителя:
, поэтому
.
Значит, данный ряд сходится.
д)
Заметим, что при
,
поэтому при вычислении предела можно
воспользоваться принципом замены
эквивалентных бесконечно малых (см.
[5]), заменив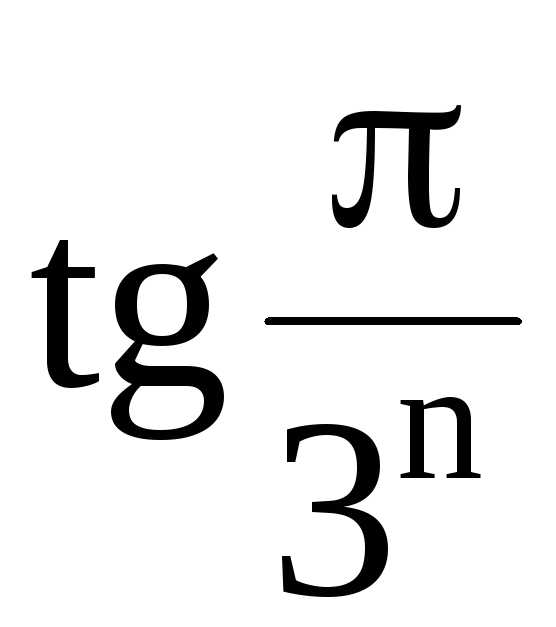 на эквивалентную
бесконечно малую величину
на эквивалентную
бесконечно малую величину 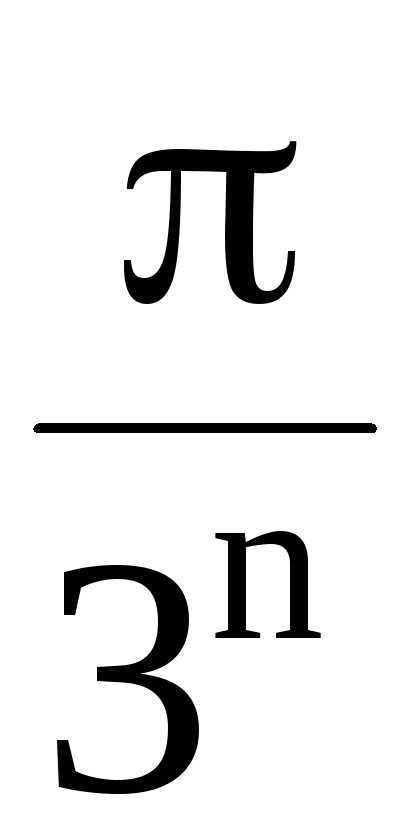 :
:
.
Следовательно, ряд сходится.
Анализ
рассмотренных примеров позволяет
сделать следующий вывод: признак
Даламбера непременно дает ответ на вопрос о
сходимости рядов, общий
член которых содержит факториал или показательную
функцию 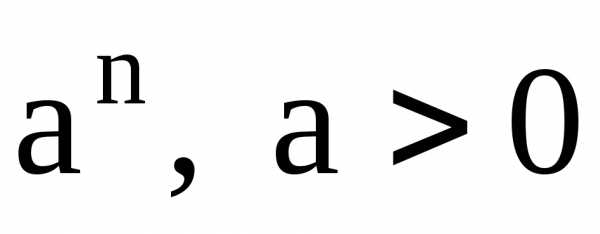 .
.
Радикальный признак Коши
Пусть 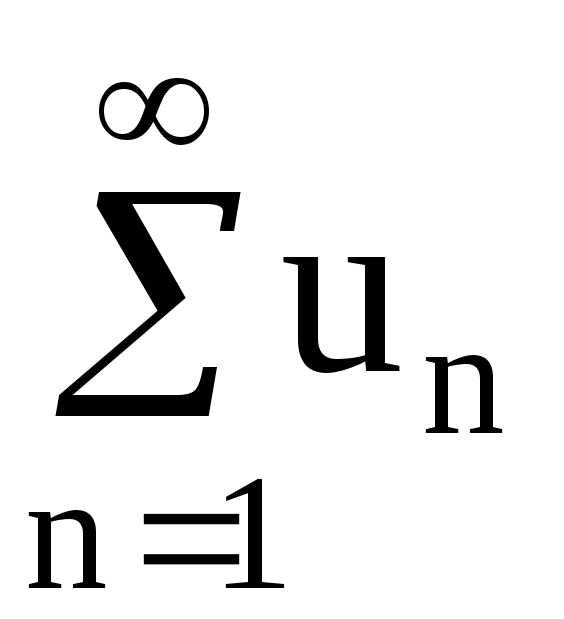 – знакоположительный ряд. Если существует
– знакоположительный ряд. Если существует 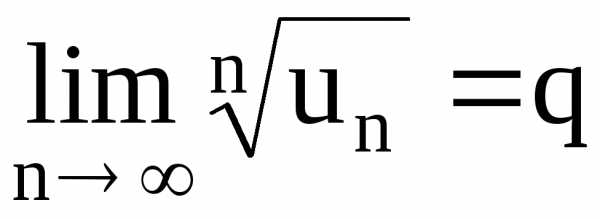 ,
,
то
при 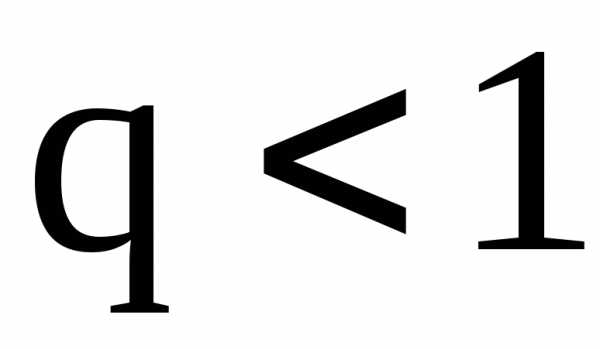 ряд сходится,
а при
ряд сходится,
а при 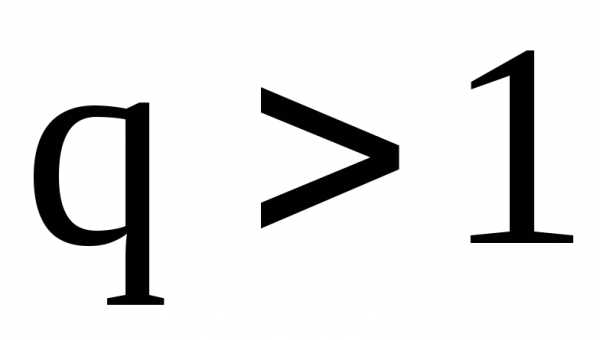 ряд расходится.
ряд расходится.
Если 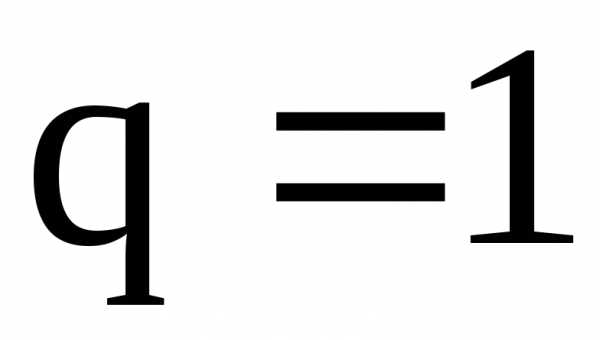 ряд может как сходиться, так и расходиться.
Выяснить это можно с помощью дополнительного
исследования, например, используя
признаки сравнения.
ряд может как сходиться, так и расходиться.
Выяснить это можно с помощью дополнительного
исследования, например, используя
признаки сравнения.
При применении радикального признака Коши бывает полезно знать, что
 .
(3)
.
(3)
Пример
7. Исследовать
на сходимость ряд 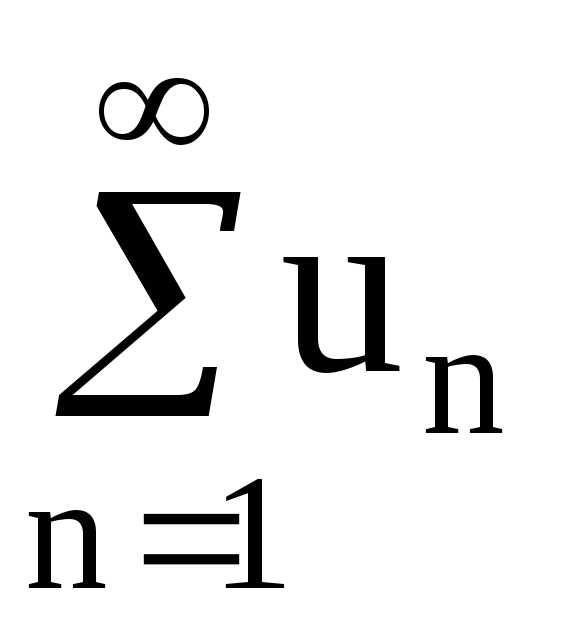 с помощью радикального признака Коши
с помощью радикального признака Коши
г) | ; | д) |
|
Решение. а) Так как и ,
(см.
равенство (3) ), то 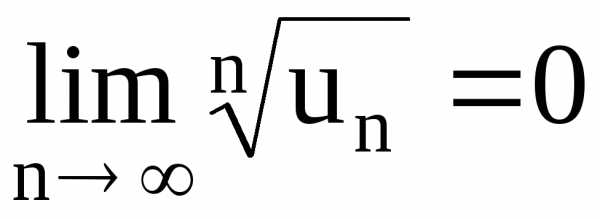 и поэтому ряд
и поэтому ряд 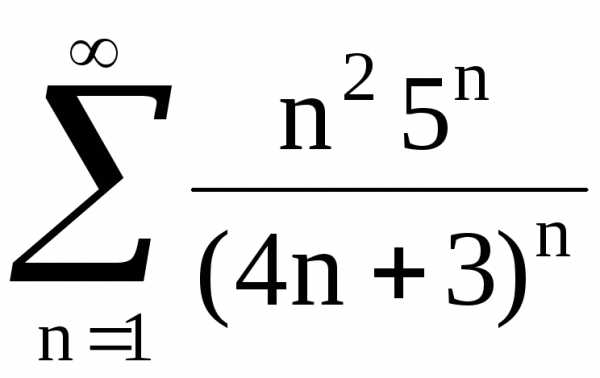 сходится.
сходится.
б) В этом случае . Так как
 (см.
[5]), а
(см.
[5]), а 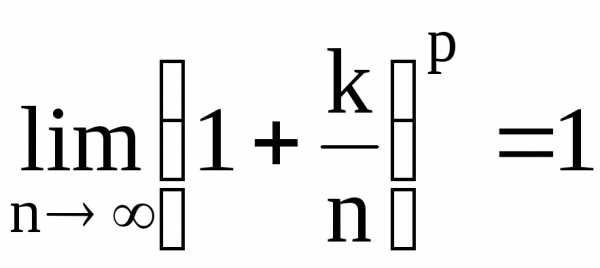 ,
то
,
то
Это означает, что данный ряд сходится.
в)
В этом случае удобно применить признак
Коши, т. к. 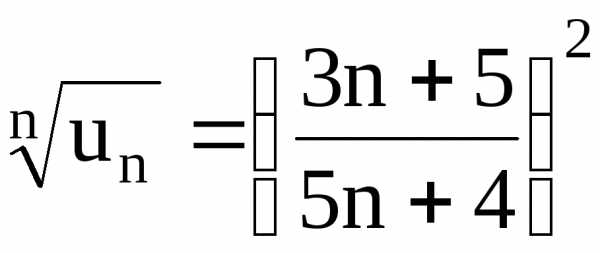 ,
а предел этого выражения находится
просто:
,
а предел этого выражения находится
просто:
.
Значит,
ряд 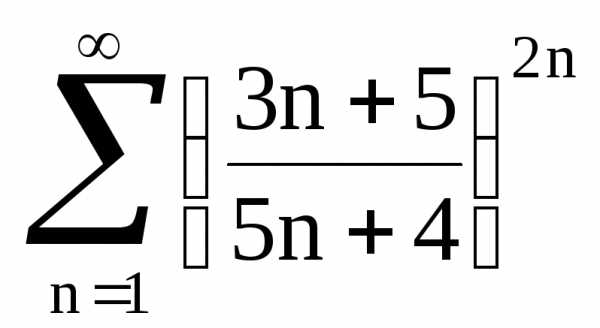 сходится.
сходится.
г)
Заметим, что при
,
а .
.
Кроме
того, т. к. 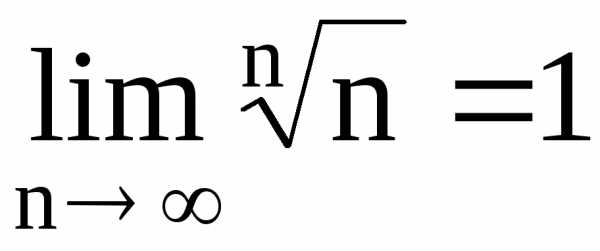 ,
то ,
поэтому
,
то ,
поэтому
и поэтому ряд расходится.
д) Так как и
 (см.
[5] ), то
(см.
[5] ), то  .
.
Следовательно,
ряд  расходится.
расходится.
Признак
Даламбера и радикальный признак Коши
основаны, по существу, только на свойствах
геометрической прогрессии. Поэтому при
исследовании медленно сходящихся или
медленно расходящихся рядов (прогрессии
в их число не входят) эти признаки
оказываются нечувствительными 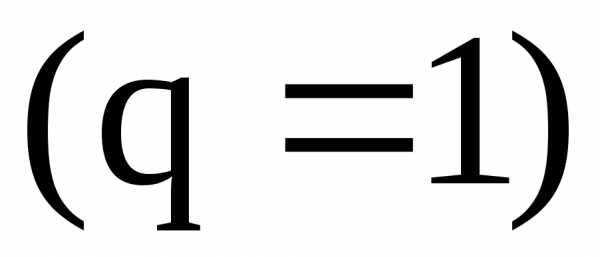 .
В таких случаях, кроме признаков
сравнения, можно использоватьинтегральный
признак Коши.
Этот признак четко проводит различия
между сходящимися и расходящимися
рядами, даже если члены одного из них
лишь незначительно отличаются от членов
другого.
.
В таких случаях, кроме признаков
сравнения, можно использоватьинтегральный
признак Коши.
Этот признак четко проводит различия
между сходящимися и расходящимися
рядами, даже если члены одного из них
лишь незначительно отличаются от членов
другого.
Интегральный признак Коши
Пусть
члены знакоположительного ряда 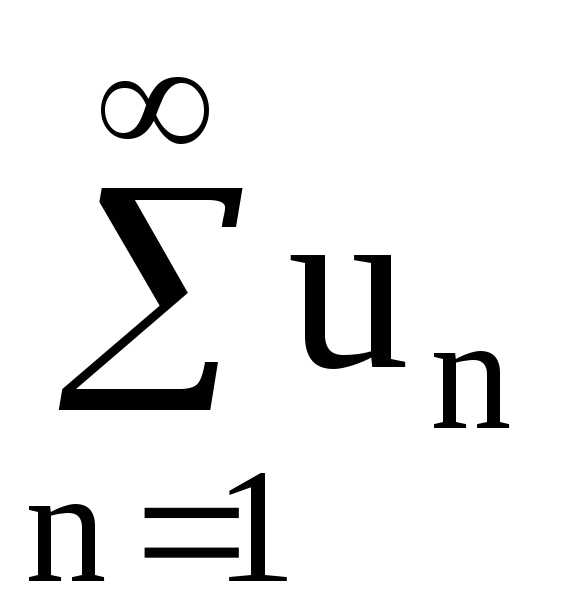 не возрастают:
не возрастают:
.
Пусть, кроме того, 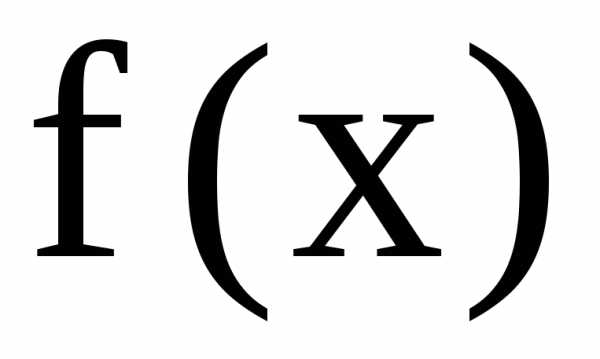 – непрерывная,
– непрерывная,
невозрастающая
функция, определенная для всех 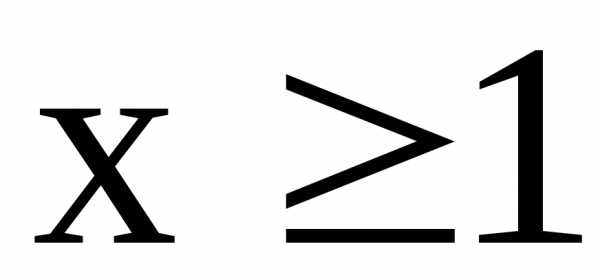 ,
такая, что
,
такая, что
.
Тогда ряд 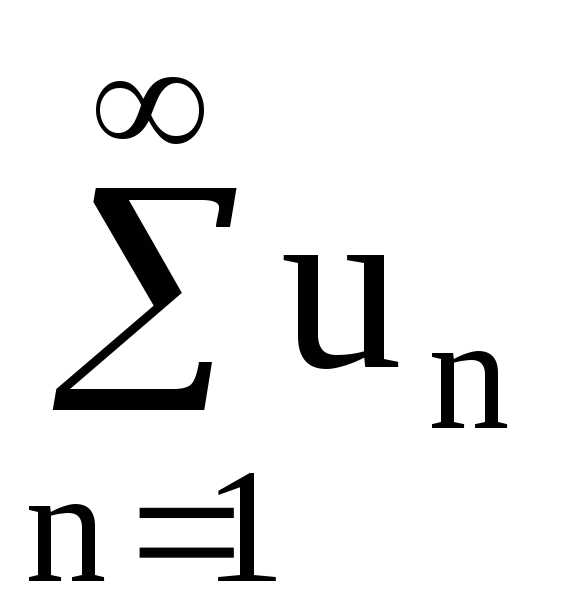 и несобст-
и несобст-
венный
интеграл 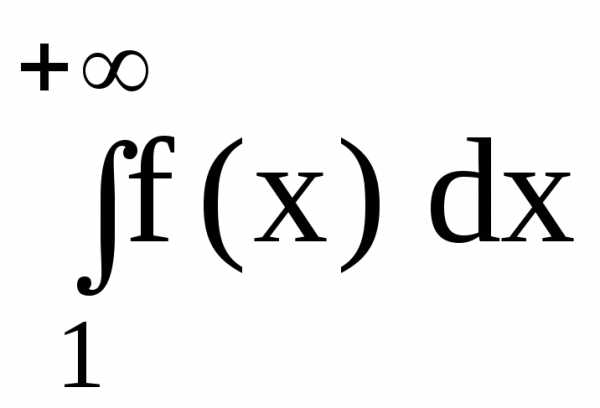 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример
8. Исследовать
на сходимость ряд 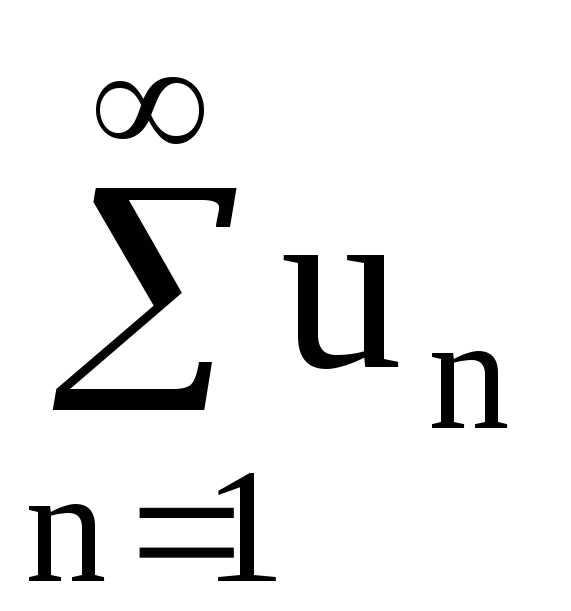 с помощью интегрального признака Коши,
если
с помощью интегрального признака Коши,
если
Решение. а) 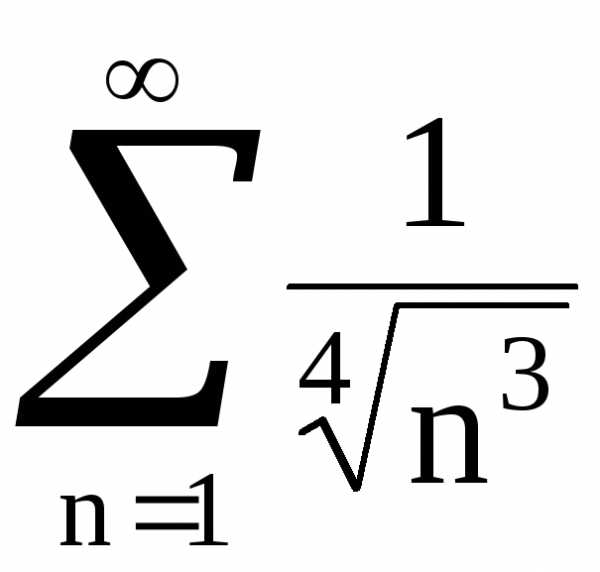 – ряд Дирихле с
– ряд Дирихле с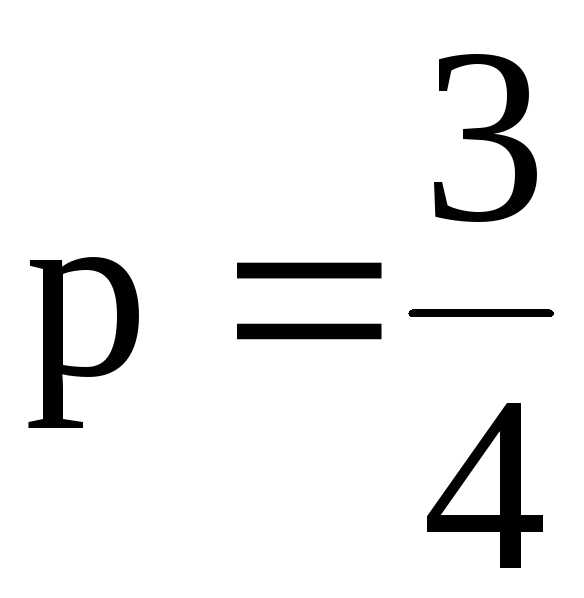 .
Ранее было отмечено, что этот ряд
расходится. Докажем это. Рассмотрим
функцию
.
Ранее было отмечено, что этот ряд
расходится. Докажем это. Рассмотрим
функцию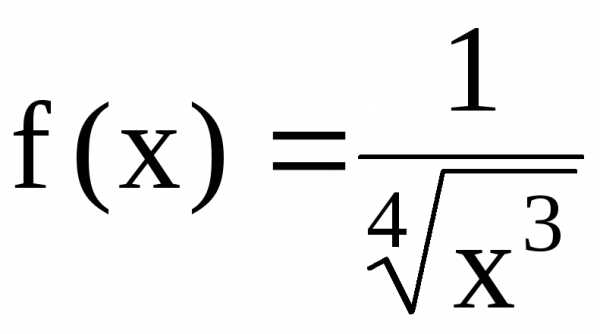 .
Она не-
.
Она не-
прерывна
и убывает при всех 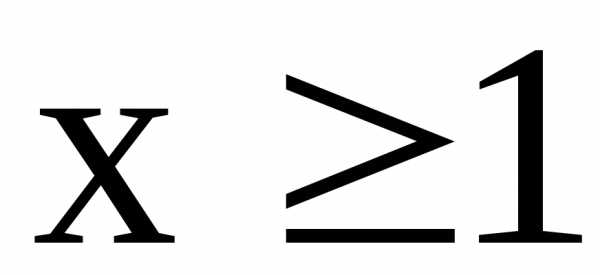 .
Кроме того,
.
Кроме того,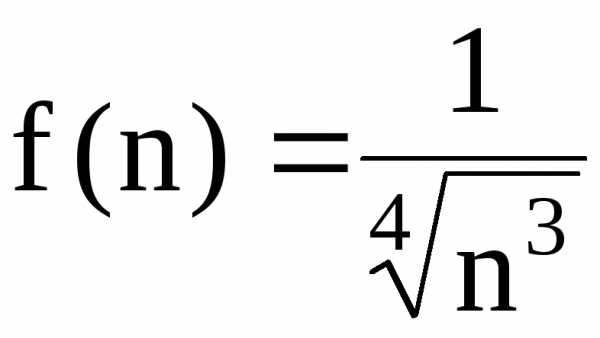 ,
поэтому
,
поэтому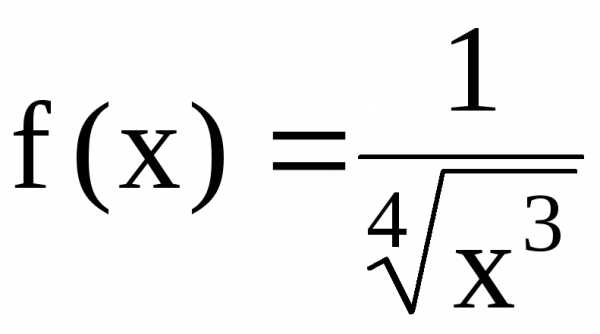 удовлетворяет условиям теоремы.
удовлетворяет условиям теоремы.
Вычислим 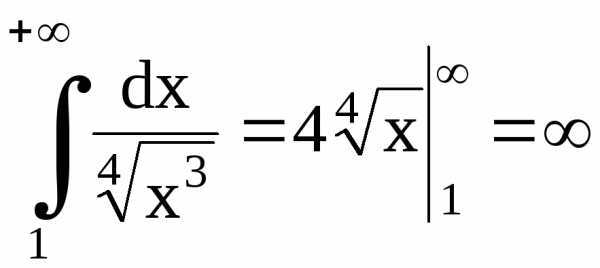 .
.
Несобственный интеграл расходится, значит, расходится и данный ряд.
б) 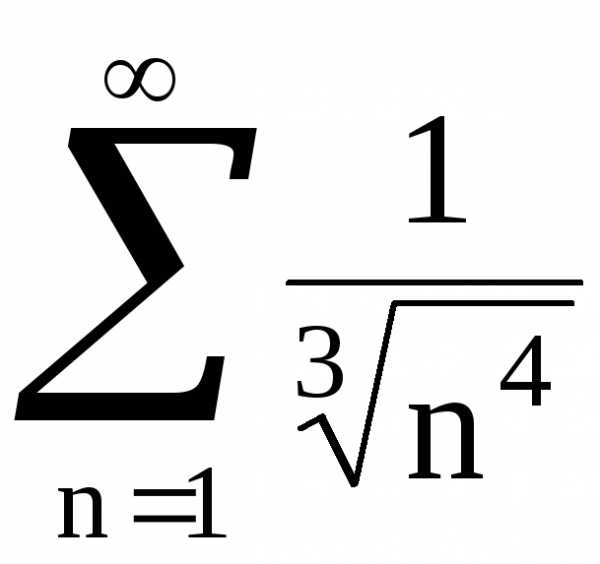 – ряд Дирихле с
– ряд Дирихле с .
Как было отмечено, этот ряд сходится.
.
Как было отмечено, этот ряд сходится.
Чтобы
убедиться в этом, применим интегральный
признак Коши: 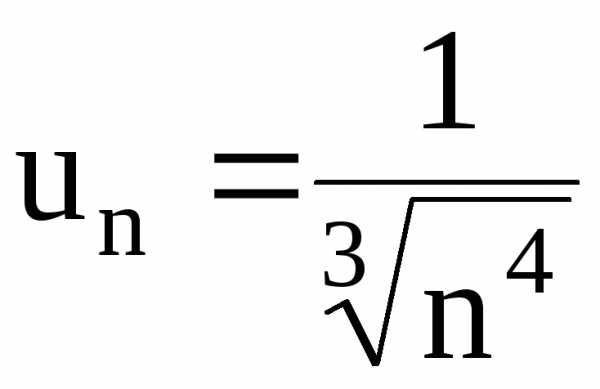 ,
,
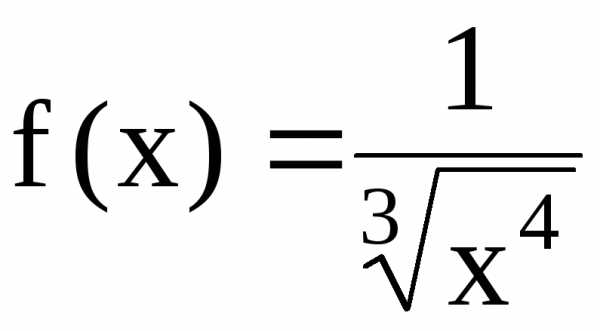 ;
; 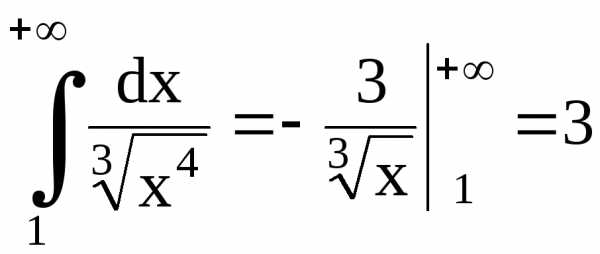 .
.
Несобственный интеграл сходится, поэтому сходится и данный ряд.
в)
Рассмотрим при 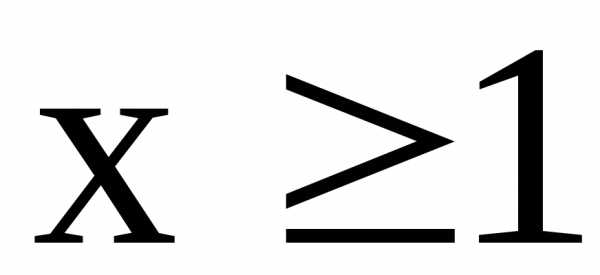 функцию.
Ее производная
функцию.
Ее производная
при
всех 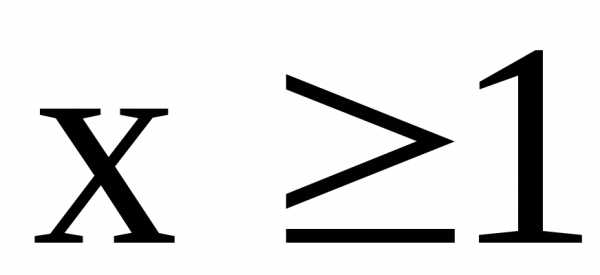 .
Следовательно,
.
Следовательно,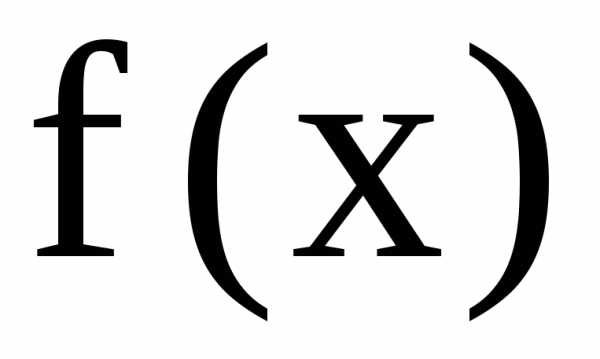 убывает
убывает
и .
.
Несобственный интеграл сходится, а потому сходится и данный ряд.
г)
Функция 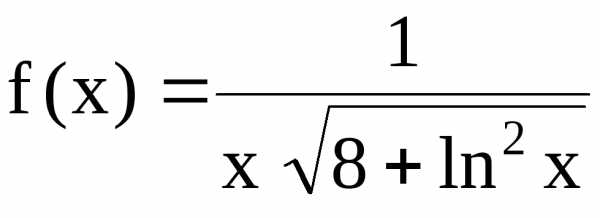 непрерывна и убывает при всех
непрерывна и убывает при всех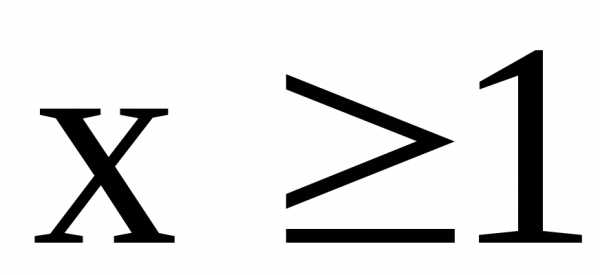 .
Несобственный интеграл
.
Несобственный интеграл
,
т.
е. расходится, значит, ряд 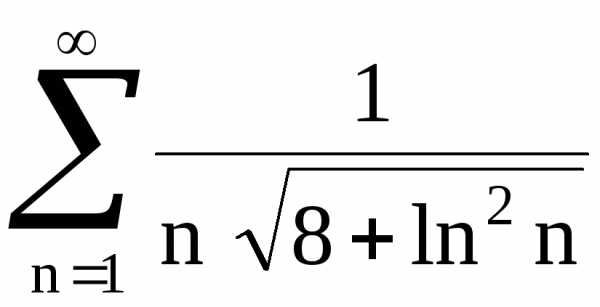 тоже расходится.
тоже расходится.
studfiles.net
Свойства числовых рядов.
1. Если сходится а1+а2+а3+…+аn+…=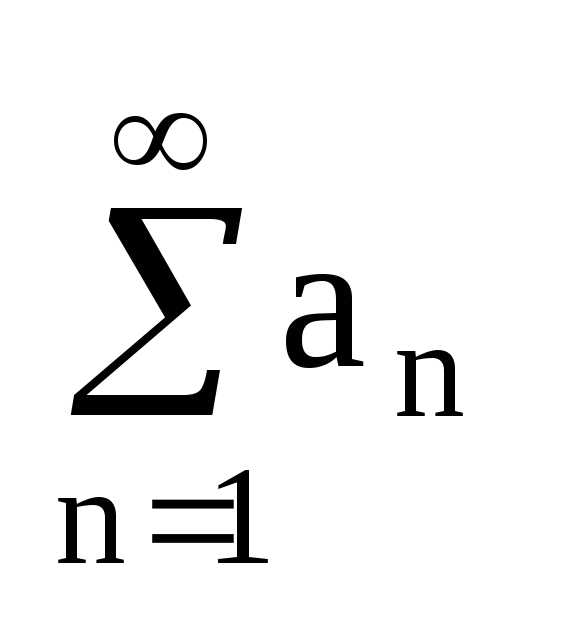 ,
то сходится и ряд аm+1+аm+2+аm+3+…,
полученный из данного ряда отбрасыванием
первых m
членов.
Этот полученный ряд называется m-ым
остатком ряда. И,
наоборот: из сходимости m-го остатка
ряда вытекает сходимость данного ряда.
Т.е. сходимость и расходимость ряда не
нарушается, если прибавить или отбросить
конечное число его членов.
,
то сходится и ряд аm+1+аm+2+аm+3+…,
полученный из данного ряда отбрасыванием
первых m
членов.
Этот полученный ряд называется m-ым
остатком ряда. И,
наоборот: из сходимости m-го остатка
ряда вытекает сходимость данного ряда.
Т.е. сходимость и расходимость ряда не
нарушается, если прибавить или отбросить
конечное число его членов.
2. Если ряд а1+а2+а3+… сходится и его сумма равна S, то ряд Са1+Са2+…, где С= так же сходится и его сумма равна СS.
3. Если ряды а1+а2+… и b1+b2+… сходятся и их суммы равны соответственно S1 и S2, то ряды (а1+b1)+(а2+b2)+(а3+b3)+… и (а1-b1)+(а2-b2)+(а3-b3)+… также сходятся. Их суммы соответственно равны S1+S2 и S1-S2.
4. а). Если ряд сходится, то его n-ый член стремится к 0 при неограниченном возрастании n (обратное утверждение неверно).
— необходимый признак (условие) сходимости ряда.
б).
Если 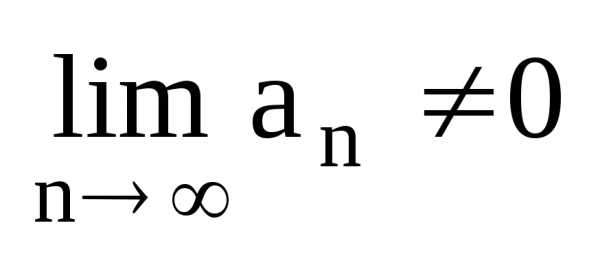 то ряд расходящийся –достаточное условие расходимости ряда.
то ряд расходящийся –достаточное условие расходимости ряда.
 -ряды
такого вида исследуются только по 4
свойству. Это расходящиеся ряды.
-ряды
такого вида исследуются только по 4
свойству. Это расходящиеся ряды.
Знакоположительные ряды.
Признаки сходимости и расходимости знакоположительных рядов.
Знакоположительные ряды это ряды, все члены которых положительные. Эти признаки сходимости и расходимости мы будем рассматривать для знакоположительных рядов.
1. Первый признак сравнения.
Пусть
даны два знакоположительных ряда
а1+а2+а3+…+аn+…=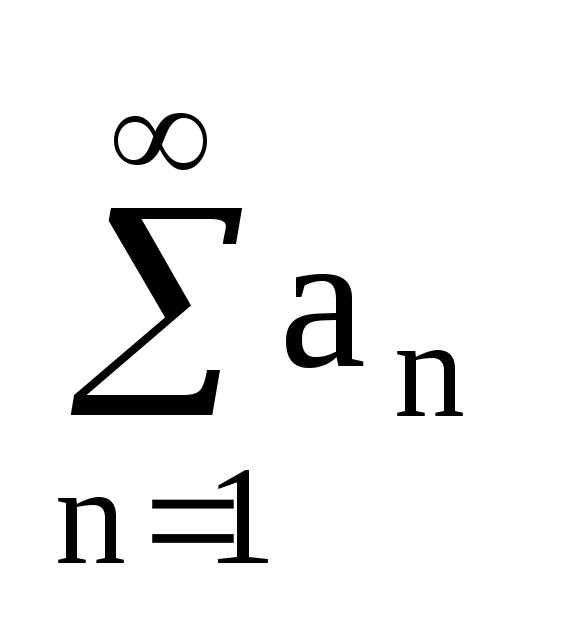 (1)
иb1+b2+b3+…+bn+…=
(1)
иb1+b2+b3+…+bn+…=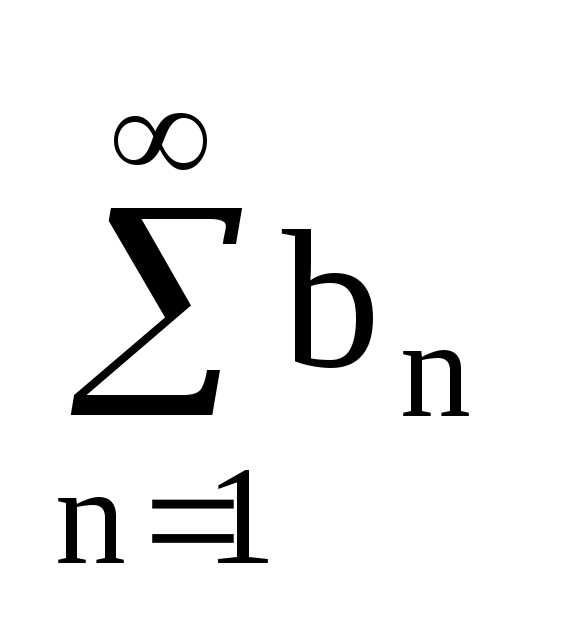 (2).
(2).
Если
члены ряда (1) не
больше соответствующих членов ряда (2), т.е.
аn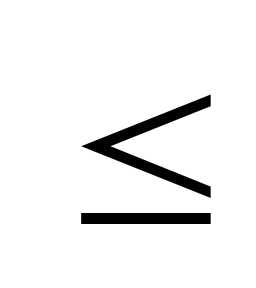 bn и ряд
(2) сходится,
то и ряд (1) также сходится.
bn и ряд
(2) сходится,
то и ряд (1) также сходится.
Если
члены ряда (1) не
меньше соответствующих членов ряда (2), т.е.
аn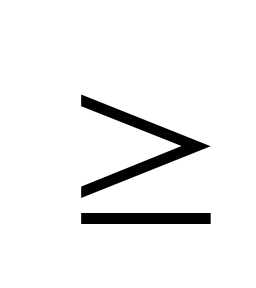 bn и ряд
(2) расходится,
то и ряд (1) также расходится.
bn и ряд
(2) расходится,
то и ряд (1) также расходится.
Этот признак сравнения справедлив, если неравенство выполняется не для всех n, а лишь начиная с некоторого.
2. Второй признак сравнения.
Если
существует конечный и отличный от нуля
предел 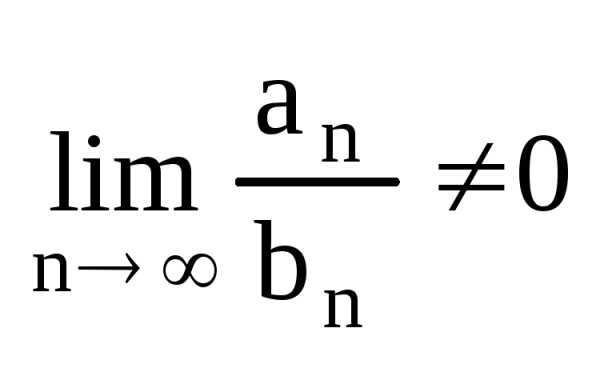 ,
то оба ряда сходятся или расходятся
одновременно.
,
то оба ряда сходятся или расходятся
одновременно.
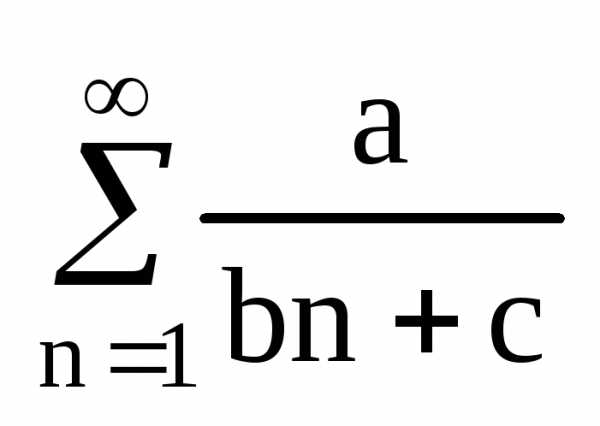 -ряды
такого вида расходятся по второму признаку сравнения. Их надо
сравнивать с гармоническим рядом.
-ряды
такого вида расходятся по второму признаку сравнения. Их надо
сравнивать с гармоническим рядом.
3. Признак Даламбера.
Если
для знакоположительного ряда
(а1+а2+а3+…+аn+…= )
существует
)
существует 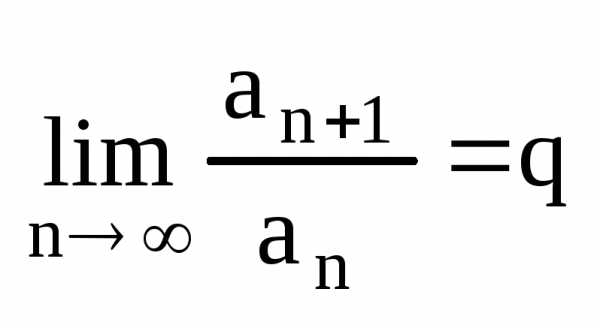 (1),
то ряд сходится, если q<1,
расходится, если
q>1.
Если
q=1
то вопрос остается открытым.
(1),
то ряд сходится, если q<1,
расходится, если
q>1.
Если
q=1
то вопрос остается открытым.
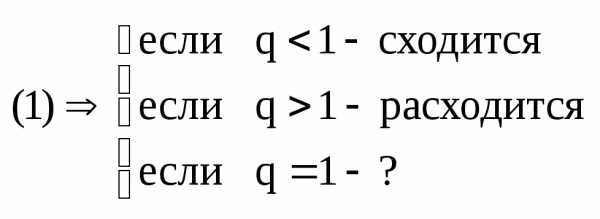
4. Признак Коши радикальный.
Если
для знакоположительного ряда существует
предел 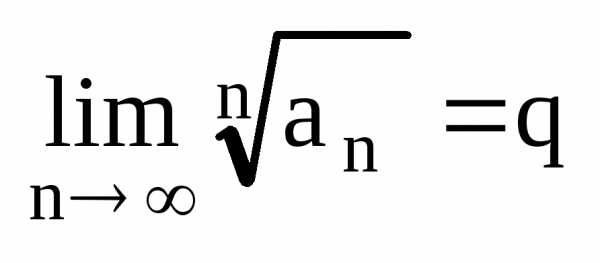 (2),
то ряд сходится, еслиq<1,
расходится, если
q>1.
Если
q=1
то вопрос остается открытым.
(2),
то ряд сходится, еслиq<1,
расходится, если
q>1.
Если
q=1
то вопрос остается открытым.
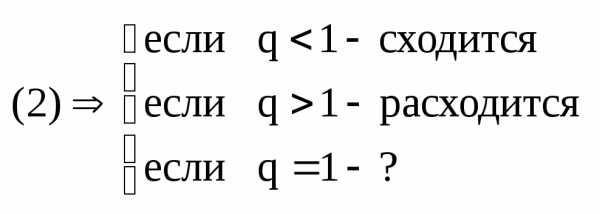
5. Признак Коши интегральный.
Вспомним несобственные интегралы.
Если
существует предел 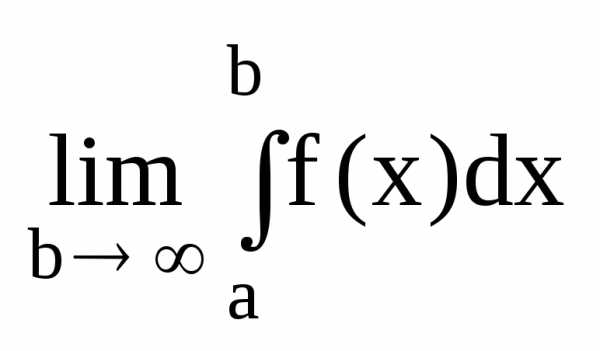 .
Это есть несобственный интеграл и
обозначается
.
Это есть несобственный интеграл и
обозначается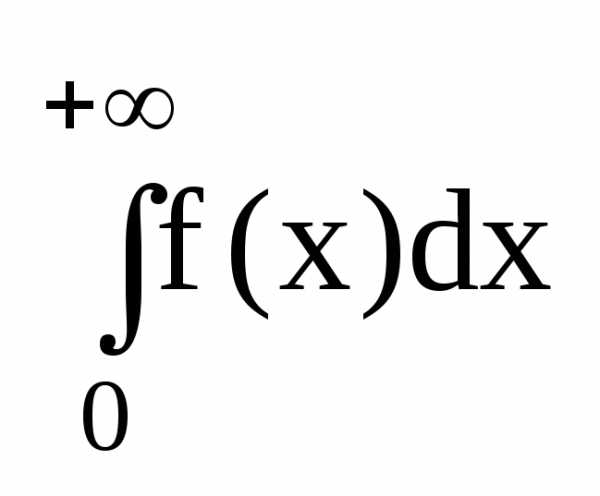 .
.
Если этот предел конечен, то говорят, что несобственный интеграл сходится. Ряд, соответственно, сходится или расходится.
Пусть
ряд а1+а2+а3+…+аn+…=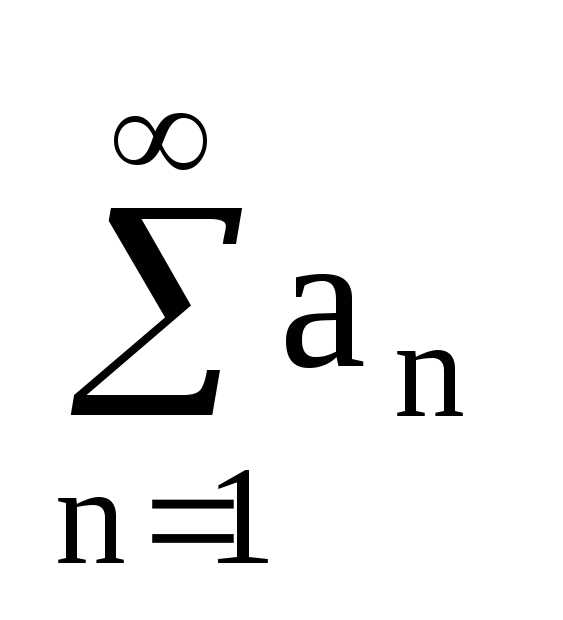 —
знакоположительный ряд.
—
знакоположительный ряд.
Обозначим an=f(x) и рассмотрим функцию f(x). Если f(x)- функция положительная, монотонно убывающая и непрерывная, то, если несобственный интеграл сходится, то и данный ряд сходится. И наоборот: если несобственный интеграл расходится, то и ряд расходится.
Если ряд конечен, то он сходится.
Очень
часто встречаются ряды 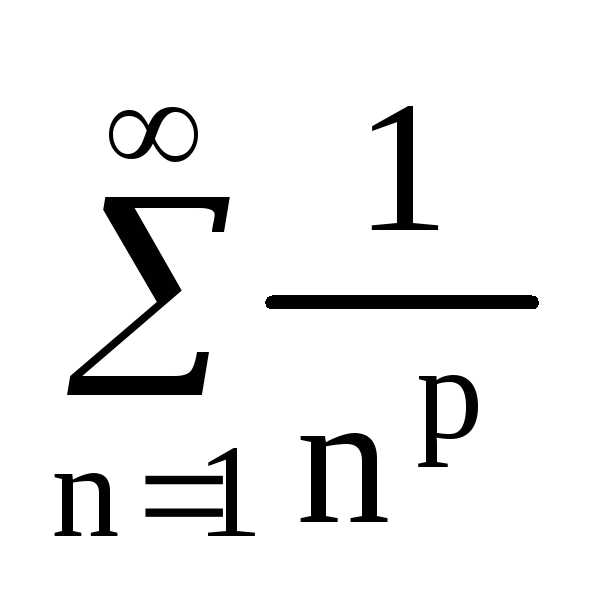 —ряд
Дерихле.
Он сходится, если p>1,
расходится p<1.
Гармонический ряд является рядом Дерихле
при р=1.
Сходимость
и расходимость данного ряда легко
доказать с помощью интегрального
признака Коши.
—ряд
Дерихле.
Он сходится, если p>1,
расходится p<1.
Гармонический ряд является рядом Дерихле
при р=1.
Сходимость
и расходимость данного ряда легко
доказать с помощью интегрального
признака Коши.
studfiles.net

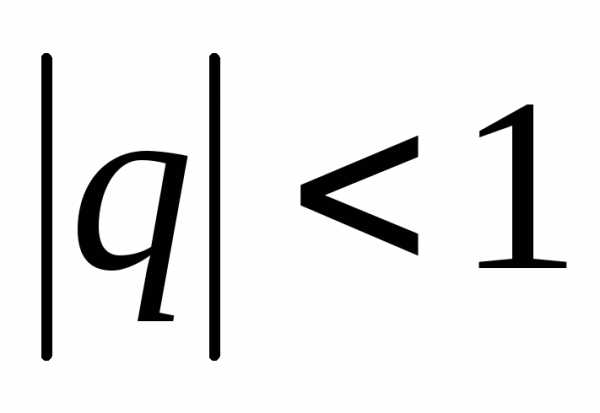 :
1 +q2 +…+ qn + … Существует сумма ряда
:
1 +q2 +…+ qn + … Существует сумма ряда 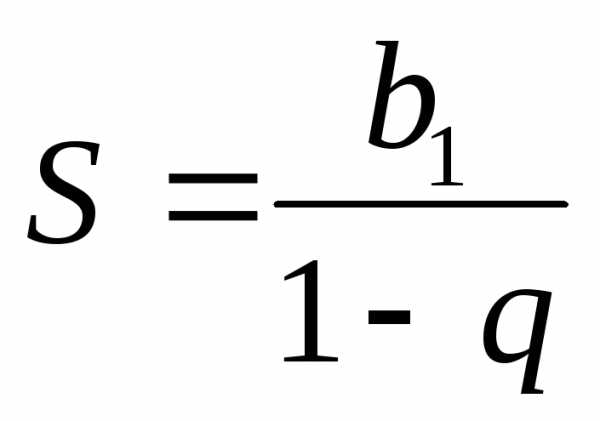 .
Поэтому такой ряд является сходящимся.
.
Поэтому такой ряд является сходящимся.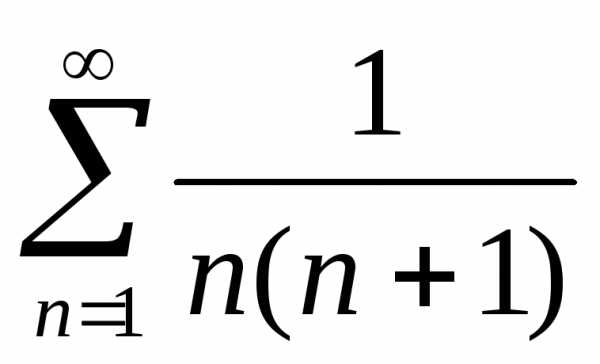 сходится.
сходится.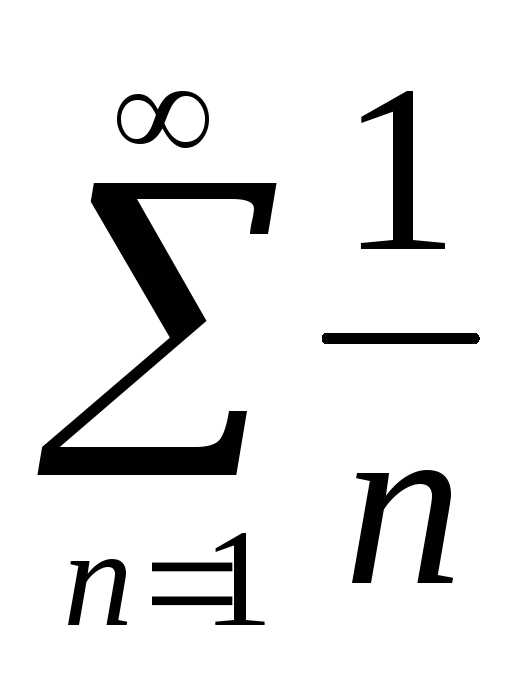 (гармонический) расходится.
(гармонический) расходится.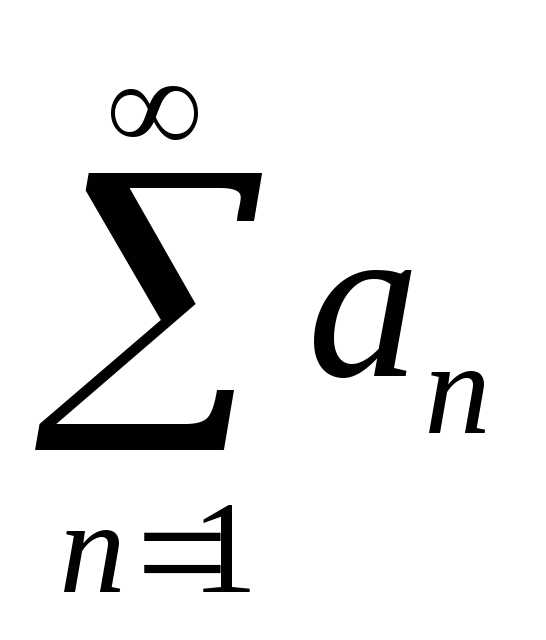 сходится и имеет сумму A,
то ряд
сходится и имеет сумму A,
то ряд 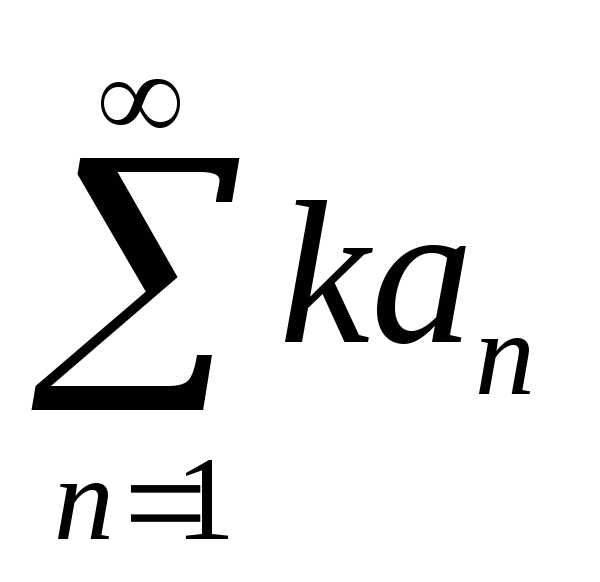 (k
= const
0) также сходится и имеет сумму kA.
Если ряд
(k
= const
0) также сходится и имеет сумму kA.
Если ряд 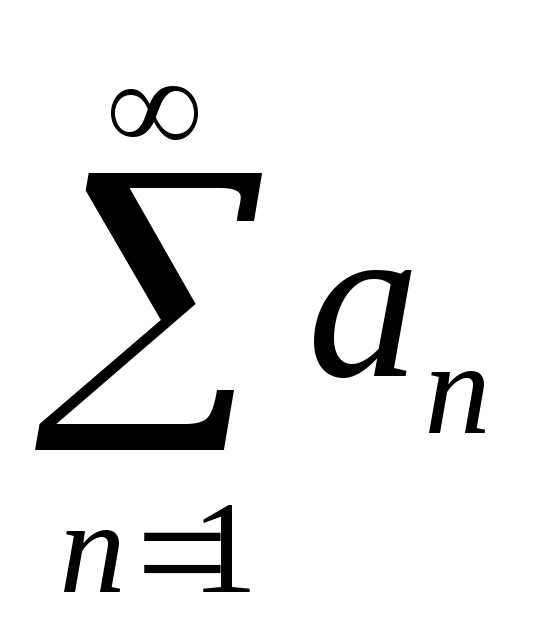 расходится, то
расходится, то 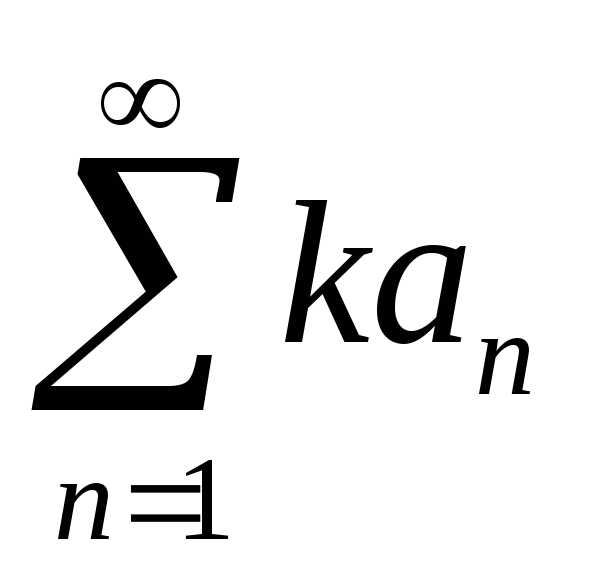 также расходится.
также расходится.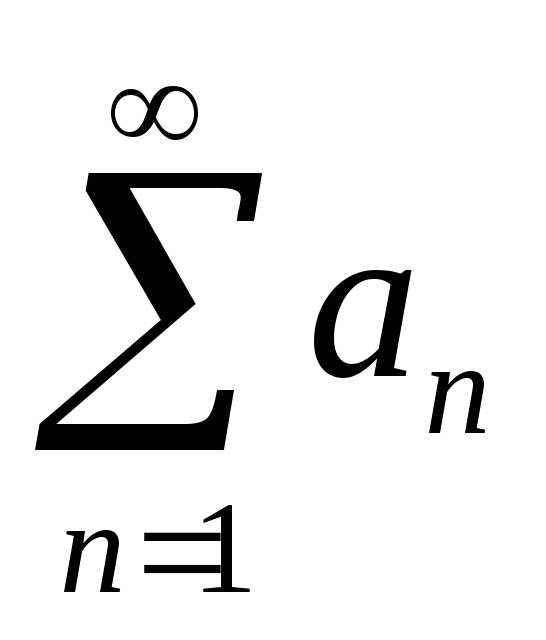 и
и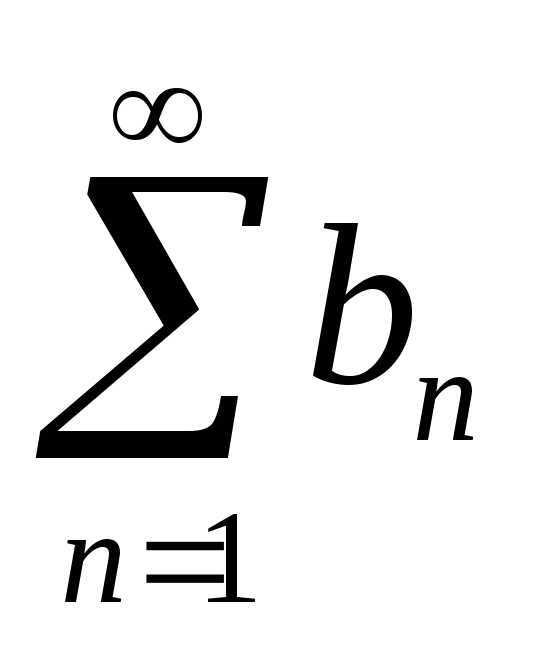 .
Тогда:
.
Тогда: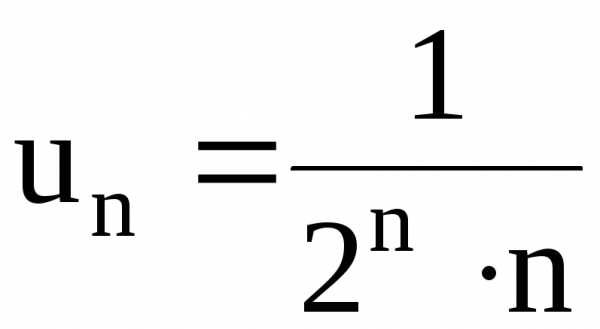 ;
;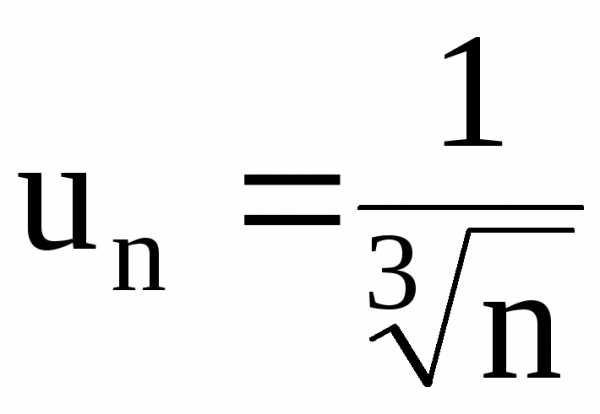 ;
;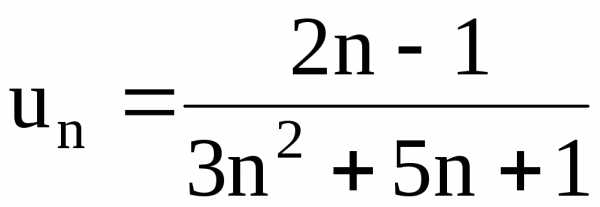 ,
,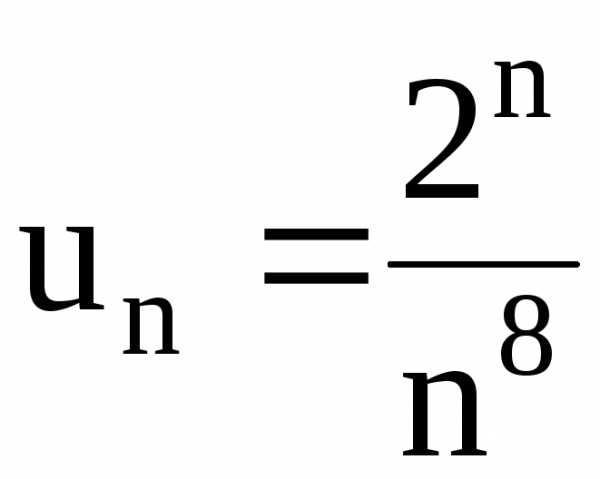 ;
;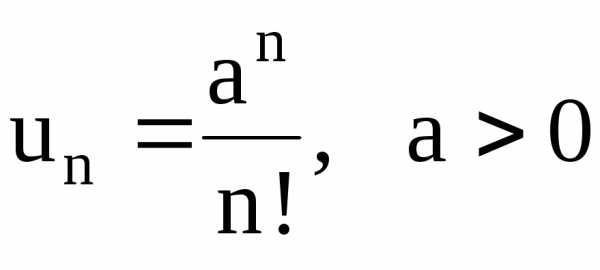 ;
;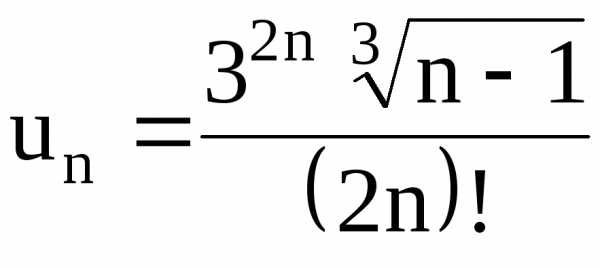 ;
;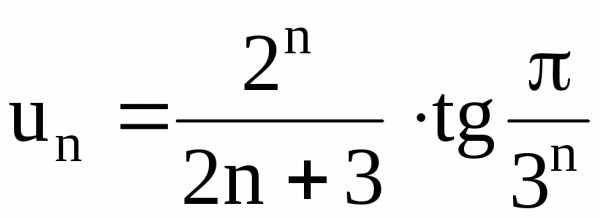 .
. .
.