Производная корень третьей степени из х. Решение квадратных уравнений через производные
Кулинария
На этом занятии мы будем учиться применять формулы и правила дифференцирования.
Примеры. Найти производные функций.
1. y=x 7 +x 5 -x 4 +x 3 -x 2 +x-9. Применяем правило I , формулы 4, 2 и 1 . Получаем:
y’=7x 6 +5x 4 -4x 3 +3x 2 -2x+1.
2. y=3x 6 -2x+5. Решаем аналогично, используя те же формулы и формулу 3.
y’=3∙6x 5 -2=18x 5 -2.
Применяем правило I , формулы 3, 5 и 6 и 1.
Применяем правило IV , формулы 5 и 1 .
В пятом примере по правилу I производная суммы равна сумме производных, а производную 1-го слагаемого мы только что находили (пример 4 ), поэтому, будем находить производные 2-го и 3-го слагаемых, а для 1-го слагаемого можем сразу писать результат.
Дифференцируем 2-ое и 3-е слагаемые по формуле 4 . Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по
Для этого преобразуем корни третьей и четвертой степеней в знаменателях к степеням с отрицательными показателями, а затем, по
Посмотрите на данный пример и полученный результат. Уловили закономерность? Хорошо. Это означает, что мы получили новую формулу и можем добавить ее в нашу таблицу производных.
Решим шестой пример и выведем еще одну формулу.
Используем правило IV и формулу 4 . Получившиеся дроби сократим.
Смотрим на данную функцию и на ее производную. Вы, конечно, поняли закономерность и готовы назвать формулу:
Учим новые формулы!
Примеры.
1. Найти приращение аргумента и приращение функции y=x 2 , если начальное значение аргумента было равно 4 , а новое —4,01 .
Решение.
Новое значение аргумента х=х 0 +Δx . Подставим данные: 4,01=4+Δх, отсюда приращение аргумента Δх =4,01-4=0,01. Приращение функции, по определению, равно разности между новым и прежним значениями функции, т.
2 · 4 · 0,01+(0,01) 2 =0,08+0,0001=0,0801.
Ответ: приращение аргумента Δх =0,01; приращение функции Δу =0,0801.
Можно было приращение функции найти по-другому: Δy =y (х 0 +Δx) -y (х 0)=у(4,01) -у(4)=4,01 2 -4 2 =16,0801-16=0,0801.
2. Найти угол наклона касательной к графику функции y=f (x) в точке х 0 , если f «(х 0) = 1 .
Решение.
Значение производной в точке касания х 0 и есть значение тангенса угла наклона касательной (геометрический смысл производной). Имеем:
Ответ: касательная к графику данной функции образует с положительным направлением оси Ох угол, равный 45° .
3. Вывести формулу производной функции y=x n .
Дифференцирование — это действие нахождения производной функции.
При нахождении производных применяют формулы, которые были выведены на основании определения производной, так же, как мы вывели формулу производной степени: (x n)» = nx n-1 .
Вот эти формулы.
Таблицу производных легче будет заучить, проговаривая словесные формулировки:
1. Производная постоянной величины равна нулю.
2. Икс штрих равен единице.
3. Постоянный множитель можно вынести за знак производной.
4. Производная степени равна произведению показателя этой степени на степень с тем же основанием, но показателем на единицу меньше.
5. Производная корня равна единице, деленной на два таких же корня.
6. Производная единицы, деленной на икс равна минус единице, деленной на икс в квадрате.
7. Производная синуса равна косинусу.
8. Производная косинуса равна минус синусу.
9. Производная тангенса равна единице, деленной на квадрат косинуса.
10. Производная котангенса равна минус единице, деленной на квадрат синуса.
Учим правила дифференцирования .
1. Производная алгебраической суммы равна алгебраической сумме производных слагаемых.
2. Производная произведения равна произведению производной первого множителя на второй плюс произведение первого множителя на производную второго.
3. Производная «у», деленного на «вэ» равна дроби, в числителе которой «у штрих умноженный на «вэ» минус «у, умноженный на вэ штрих», а в знаменателе — «вэ в квадрате».
4. Частный случай формулы 3.
Учим вместе!
Страница 1 из 1 1
Определение. Пусть функция \(y = f(x) \) определена в некотором интервале, содержащем внутри себя точку \(x_0 \).
Дадим аргументу приращение \(\Delta x \) такое, чтобы не выйти из этого интервала. Найдем соответствующее приращение функции
\(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение
\(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то
указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
Найдем соответствующее приращение функции
\(\Delta y \) (при переходе от точки \(x_0 \) к точке \(x_0 + \Delta x \)) и составим отношение
\(\frac{\Delta y}{\Delta x} \). Если существует предел этого отношения при \(\Delta x \rightarrow 0 \), то
указанный предел называют производной функции \(y=f(x) \) в точке \(x_0 \) и обозначают \(f»(x_0) \).
$$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = f»(x_0) $$
Для обозначения производной часто используют символ y». Отметим, что y» = f(x) — это новая функция, но, естественно, связанная с функцией y = f(x), определенная во всех точках x, в которых существует указанный выше предел. Эту функцию называют так: производная функции у = f(x) .
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(x) в точке с абсциссой х=a можно
провести касательную, непараллельную оси y, то f(a) выражает угловой коэффициент касательной:
\(k = f»(a) \)
Поскольку \(k = tg(a) \), то верно равенство \(f»(a) = tg(a) \) . 2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
2 \) справедливо приближенное равенство \(\Delta y \approx 2x \cdot \Delta x \).
Если внимательно проанализировать определение производной, то мы обнаружим, что в нем заложен алгоритм ее нахождения.
Сформулируем его.
Как найти производную функции у = f(x) ?
1. Зафиксировать значение \(x \), найти \(f(x) \)
3. Найти приращение функции: \(\Delta y = f(x + \Delta x) — f(x) \)
4. Составить отношение \(\frac{\Delta y}{\Delta x} \)
5. Вычислить $$ \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} $$
Этот предел и есть производная функции в точке x.
Если функция у = f(x) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру нахождения производной функции у = f(x) называют дифференцированием функции у = f(x).
Обсудим такой вопрос: как связаны между собой непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(x) дифференцируема в точке х. Тогда к графику функции в точке М(х; f(x)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f»(x). Такой график не может «разрываться» в точке М, т. е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем более строгое рассуждение. Если функция у = f(x) дифференцируема в точке х, то выполняется приближенное равенство \(\Delta y \approx f»(x) \cdot \Delta x \). Если в этом равенстве \(\Delta x \) устремить к нулю, то и \(\Delta y \) будет стремиться к нулю, а это и есть условие непрерывности функции в точке.
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке .
Обратное утверждение неверно. Например: функция у = |х| непрерывна везде, в частности в точке х = 0, но касательная к графику
функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой
точке не существует производная.
Еще один пример. Функция \(y=\sqrt{x} \) непрерывна на всей числовой прямой, в том числе в точке х = 0. И касательная к графику функции существует в любой точке, в том числе в точке х = 0. Но в этой точке касательная совпадает с осью у, т. е. перпендикулярна оси абсцисс, ее уравнение имеет вид х = 0. Углового коэффициента у такой прямой нет, значит, не существует и \(f»(0) \)
Итак, мы познакомились с новым свойством функции — дифференцируемостью. А как по графику функции можно сделать вывод о ее дифференцируемости?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция не дифференцируема.
Правила дифференцирования
Операция нахождения производной называется дифференцированием .
При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций»,
то есть сложными функциями.
Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Геометрический и физический смысл производной
Пусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Правило первое: выносим константу
Константу можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте .
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Решение:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
Итак, начнем забивать гвозди микроскопом.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант . Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение ) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД).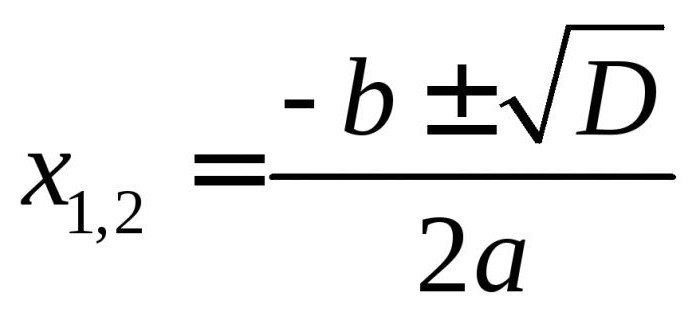 Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Разве формула перемещения для РУД не является следствием решения квадратного уравнения?
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
Операция отыскания производной называется дифференцированием.
В результате решения задач об отыскании производных у самых простых (и не очень простых) функций по определению производной как предела отношения приращения к приращению аргумента появились таблица производных и точно определённые правила дифференцирования. Первыми на ниве нахождения производных потрудились Исаак Ньютон (1643-1727) и Готфрид Вильгельм Лейбниц (1646-1716).
Поэтому в наше время, чтобы найти производную любой функции, не надо вычислять упомянутый выше предел отношения приращения функции к приращению аргумента, а нужно лишь воспользоваться таблицей производных и правилами дифференцирования. Для нахождения производной подходит следующий алгоритм.
Чтобы найти производную , надо выражение под знаком штриха разобрать на составляющие
простые функции и определить, какими действиями (произведение, сумма, частное) связаны эти функции. Далее производные элементарных функций находим в таблице
производных, а формулы производных произведения, суммы и частного — в правилах
дифференцирования. Таблица производных и
правила дифференцирования даны после первых двух примеров.
Таблица производных и
правила дифференцирования даны после первых двух примеров.
Пример 1. Найти производную функции
Решение. Из правил дифференцирования выясняем, что производная суммы функций есть сумма производных функций, т. е.
Из таблицы производных выясняем, что производная «икса» равна единице, а производная синуса — косинусу. Подставляем эти значения в сумму производных и находим требуемую условием задачи производную:
Пример 2. Найти производную функции
Решение. Дифференцируем как производную суммы, в которой второе слагаемое с постоянным множителем, его можно вынести за знак производной:
Если пока возникают вопросы, откуда что берётся, они, как правило, проясняются после ознакомления с таблицей производных и простейшими правилами дифференцирования. К ним мы и переходим прямо сейчас.
Таблица производных простых функций
1. Производная константы (числа). Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто Любого числа (1, 2, 5, 200…), которое есть в выражении функции. Всегда равна нулю. Это очень важно помнить, так как требуется очень часто | |
| 2. Производная независимой переменной. Чаще всего «икса». Всегда равна единице. Это тоже важно запомнить надолго | |
| 3. Производная степени. В степень при решении задач нужно преобразовывать неквадратные корни. | |
| 4. Производная переменной в степени -1 | |
| 5. Производная квадратного корня | |
| 6. Производная синуса | |
| 7. Производная косинуса | |
| 8. Производная тангенса | |
| 9. Производная котангенса | |
| 10. Производная арксинуса | |
| 11. Производная арккосинуса | |
| 12. Производная арктангенса | |
| 13. Производная арккотангенса | |
14. Производная натурального логарифма Производная натурального логарифма | |
| 15. Производная логарифмической функции | |
| 16. Производная экспоненты | |
| 17. Производная показательной функции |
Правила дифференцирования
| 1. Производная суммы или разности | |
| 2. Производная произведения | |
| 2a. Производная выражения, умноженного на постоянный множитель | |
| 3. Производная частного | |
| 4. Производная сложной функции |
Правило 1. Если функции
дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции
причём
т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.
Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны , т. е.
е.
Правило 2. Если функции
дифференцируемы в некоторой точке , то в то же точке дифференцируемо и их произведение
причём
т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.
Следствие 1. Постоянный множитель можно выносить за знак производной :
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.
Например, для трёх множителей:
Правило 3. Если функции
дифференцируемы в некоторой точке и , то в этой точке дифференцируемо и их частное u/v , причём
т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.
Где что искать на других страницах
При нахождении производной произведения и частного в реальных задачах всегда требуется применять сразу несколько правил дифференцирования, поэтому больше примеров на эти производные — в статье «Производная произведения и частного функций » .
Замечание. Следует не путать константу (то есть, число) как слагаемое в сумме и как постоянный множитель! В случае слагаемого её производная равна нулю, а в случае постоянного множителя она выносится за знак производных. Это типичная ошибка, которая встречается на начальном этапе изучения производных, но по мере решения уже нескольких одно- двухсоставных примеров средний студент этой ошибки уже не делает.
А если при дифференцировании произведения или частного у вас появилось слагаемое u «v , в котором u — число,
например, 2 или 5, то есть константа, то производная этого числа будет равна нулю и, следовательно, всё
слагаемое будет равно нулю (такой случай разобран в примере 10).
Другая частая ошибка — механическое решение производной сложной функции как производной простой функции. Поэтому производной сложной функции посвящена отдельная статья. Но сначала будем учиться находить производные простых функций.
По ходу не обойтись без преобразований выражений. Для этого может потребоваться открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями .
Если Вы ищете решения производных дробей со степенями и корнями, то есть, когда функция имеет вид вроде , то следуйте на занятие «Производная суммы дробей со степенями и корнями «.
Если же перед Вами задача вроде , то Вам на занятие «Производные простых тригонометрических функций».
Пошаговые примеры — как найти производную
Пример 3. Найти производную функции
Решение. Определяем части выражения функции: всё выражение представляет произведение,
а его сомножители — суммы, во второй из которых одно из слагаемых содержит постоянный множитель. Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Применяем правило дифференцирования произведения: производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой:
Далее применяем правило дифференцирования суммы: производная алгебраической суммы функций равна алгебраической сумме производных этих функций. В нашем случае в каждой сумме второе слагаемое со знаком минус. В каждой сумме видим и независимую переменную, производная которой равна единице, и константу (число), производная которой равна нулю. Итак, «икс» у нас превращается в единицу, а минус 5 — в ноль. Во втором выражении «икс» умножен на 2, так что двойку умножаем на ту же единицу как производную «икса». Получаем следующие значения производных:
Подставляем найденные производные в сумму произведений и получаем требуемую условием задачи производную всей функции:
Пример 4. Найти производную функции
Решение. От нас требуется найти производную частного. Применяем формулу дифференцирования частного:
производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и
числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя. Получаем:
Получаем:
Производную сомножителей в числителе мы уже нашли в примере 2. Не забудем также, что произведение, являющееся вторым сомножителем в числителе в текущем примере берётся со знаком минус:
Если Вы ищете решения таких задач, в которых надо найти производную функции, где сплошное нагромождение корней и степеней, как, например, , то добро пожаловать на занятие «Производная суммы дробей со степенями и корнями» .
Если же Вам нужно узнать больше о производных синусов, косинусов, тангенсов и других тригонометрических функций, то есть, когда функция имеет вид вроде , то Вам на урок «Производные простых тригонометрических функций» .
Пример 5. Найти производную функции
Решение. В данной функции видим произведение, один из сомножителей которых — квадратный корень из независимой переменной, с производной которого мы ознакомились в таблице производных. По правилу дифференцирования произведения и табличному значению производной квадратного корня получаем:
Пример 6. Найти производную функции
Найти производную функции
Решение. В данной функции видим частное, делимое которого — квадратный корень из независимой переменной. По правилу дифференцирования частного, которое мы повторили и применили в примере 4, и табличному значению производной квадратного корня получаем:
Чтобы избавиться от дроби в числителе, умножаем числитель и знаменатель на .
prime – phrases
Sign in | English | Terms of Use
English ⇄ ArabicBulgarianChineseCzechDanishDutchEnglishEsperantoEstonianFinnishFrenchGermanGreekHungarianIrishItalianJapaneseLatvianLithuanianMalteseNorwegian BokmålPolishPortugueseRomanianRussianSlovakSlovenianSpanishSwedishUkrainianUzbekTerms for subject Mathematics containing prime | all forms | exact matches only
| English | Russian |
| absolutely prime | абсолютно простой |
| absolutely prime ideal | абсолютно простой идеал |
| algebra with prime characteristic | алгебра с простой характеристикой |
| almost prime | почти простой |
| 2-almost prime | полупростое число (moevot) |
| almost prime number | почти простое число |
| Archimedean prime | архимедов простой дивизор |
| associated prime ideal | соответствующий простой идеал (данному примарному) |
| asymmetric prime end | асимметрический простой конец |
| asymptotic prime | асимптотическое простое число |
| bad prime | плохое простое число |
| be of prime importance | иметь важное значение |
| be of prime importance | иметь особо важное значение |
| become a prime target for | стать первой мишенью для |
| beta-prime distribution | бета-простое распределение |
| Caratheodory’s prime end theory | теория простых концов Каратеодори (alexeyaxim) |
| complete set of multiple-output prime implicants | полное множество простых многовыходовых импликант (ssn) |
| completely prime | вполне простой |
| completely prime filter | вполне простой фильтр |
| conic prime | коническое простое число |
| countably prime model | счётно простая модель |
| decomposed prime | разложенное простое число |
| domain of prime ideals | область главных идеалов |
| double prime | два штриха |
| double prime | двойной штрих |
| double prime | знак секунды |
| elementarily prime | элементарно простой (о модели) |
| essential prime implicant | существенно простая импликанта |
| exceptional prime | исключительное простое число |
| f prime of x | эф-штрих от икс ([f ‘(x)] andriy f) |
| Fermat prime | простое число Ферма |
| finite prime | конечное простое число |
| finite prime divisor | конечный простой дивизор |
| Gaussian prime | гауссово простое число |
| generation of multiple-output prime implicants | получение простых многовыходовых импликант (ssn) |
| generic prime | общая гиперплоскость |
| group of prime residue classes | группа классов вычетов |
| group of prime residue classes | взаимно простых с модулем |
| Harrison prime | простое число Харрисона |
| ideal prime | идеальное простое число |
| imaginary prime | мнимое простое число |
| in one’s prime | в расцвете сил |
| inert prime | инертное простое число |
| infinite prime | бесконечное простое число |
| infinite prime divisor | бесконечный простой дивизор |
| irregular prime | иррегулярное простое число |
| left prime | левое простое число |
| Mersenne prime | простое число Мерсенна |
| Mersenne prime number | простое число Мерсенна (MichaelBurov) |
| Mersenne’s prime | простое число Мерсенна (MichaelBurov) |
| Mersenne’s prime number | простое число Мерсенна (MichaelBurov) |
| minimal covering set of multiple-output prime implicants | минимальное покрывающее множество простых многовыходовых импликант (ssn) |
| multiple-output prime implicant | простая многовыходовая импликанта (ssn) |
| mutually prime ideals | взаимно простые идеалы |
| mutually prime integers | взаимно-простые числа (slitely_mad) |
| not prime | непростой |
| odd prime | нечётное простое число |
| of prime importance is | особенно важен (This is of particular importance for mechanics. ; …) ; …) |
| our prime interest is in | интересовать нас главным образом |
| pairwise relatively prime ideals | попарно взаимно простые идеалы |
| point-prime polarity | полярная корреляция, относящая точкам гиперплоскости |
| polar prime | полярная гиперплоскость |
| prime | простой дивизор |
| prime | простой элемент |
| prime | прим |
| prime | гиперплоскость |
| prime | снабжать штрихом |
| prime | штрих |
| prime assertion | исходное утверждение |
| prime at infinity | бесконечно удалённая гиперплоскость |
| prime base | простой базис |
| prime cause | первичная причина |
| prime characteristic | простая характеристика (поля) |
| prime coideal | простой коидеал |
| prime computability | элементарная вычислимость |
| prime-counting function | функция распределения простых чисел (Tion) |
| prime cycle | простой цикл |
| prime discriminant | простой дискриминант |
| prime distance | простое расстояние |
| prime distance graph | граф простых расстояний |
| prime divisor | простой дивизор |
| prime divisor | простой делитель |
| prime-divisor function | функция простого делителя |
| prime eigenvalue | простое собственное значение |
| prime element | простой элемент |
| prime end | простой конец |
| prime-end metric | метрика простых концов |
| prime extension | простое расширение |
| prime factor | простой делитель (Lifestruck) |
| prime factor decomposition | разложение на простые множители |
| prime factorization | разложение на простые множители |
| prime field | простое поле (поле, число элементов которого является простым числом) |
| prime filter | простой фильтр |
| prime form | элементарная форма |
| prime formula | элементарная формула |
| prime gap | интервал между простыми числами (Tion) |
| prime ideal | примарный идеал |
| prime ideal | простой идеал |
| prime ideal space | пространство простых идеалов |
| prime ideal topology | топология простых идеалов |
| prime implicant chart | таблица простых импликантов |
| prime in pairs | попарно простой |
| prime integer | простое число |
| prime interval | простой интервал |
| prime kernel | простое ядро |
| prime knot | простой узел |
| prime magic square | магический квадрат для простых чисел |
| prime manifold | простое многообразие |
| prime mark | штрих |
| prime mark | прим |
| prime meridian | главный меридиан |
| prime model | простая модель |
| prime modulus | простой модуль |
| prime name form | элементарная называющая форма |
| prime necessity | что-либо совершенно необходимое |
| prime number | простое число |
| prime number theorem | теорема о числе простых чисел |
| prime order | равный простому числу |
| prime order | порядок |
| prime pair | близнецы |
| prime pair | пара простых чисел |
| prime-point polarity | полярная корреляция, относящая гиперплоскостям точки |
| prime-point transformation | преобразование гиперплоскостей в точки |
| prime polynomial | неприводимый полином |
| prime polynomial | неприводимый многочлен |
| prime power group | группа порядка, равного степени простого числа |
| prime predicate | простой предикат |
| prime presentation | простое представление |
| prime pseudomodel | простая псевдомодель |
| prime quaternion | простой кватернион |
| prime radical | первичный радикал |
| prime relation | простое отношение |
| prime ring | простое кольцо |
| prime ring | первичное кольцо |
| prime sequence | простая последовательность |
| prime statement | исходное утверждение |
| prime subfield | простое подполе |
| prime symbol | штрих (графический символ и типографский знак, который представляет собой короткую и слегка наклонную вправо линию, ставящуюся обычно за правым верхним краем числового или буквенного обозначения (′).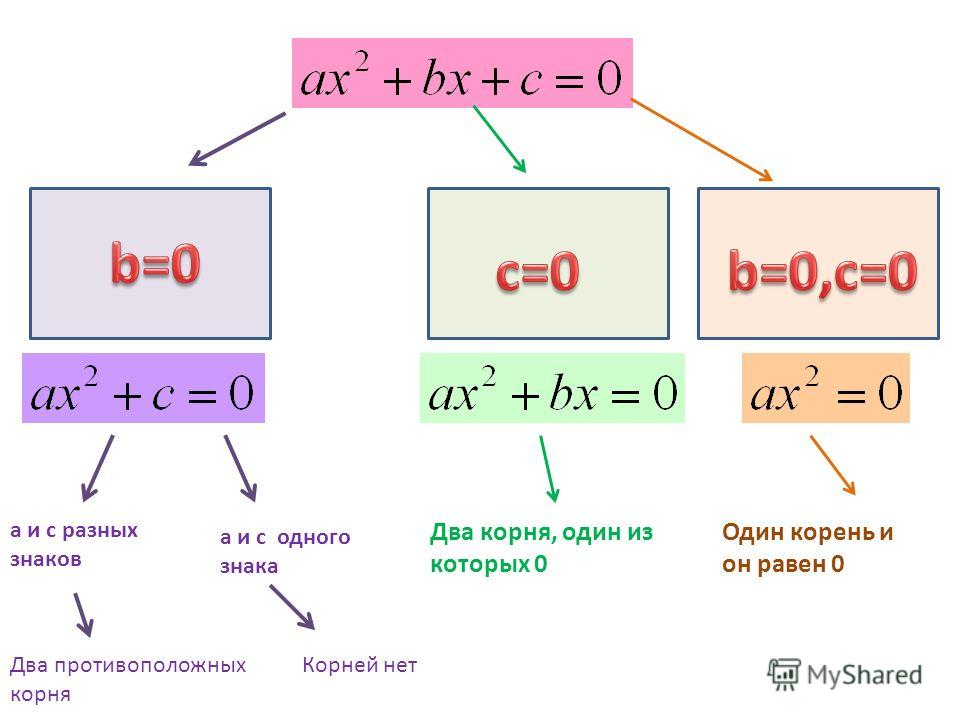 Встречается в научных и технических текстах различного содержания: угловые минуты: 10 ∘ 30 ′ ProtoMolecule) Встречается в научных и технических текстах различного содержания: угловые минуты: 10 ∘ 30 ′ ProtoMolecule) |
| prime system | первичная система |
| prime theory | простая теория |
| prime twins | простые близнецы |
| prime twins | числа-близнецы |
| quasiabsolutely prime | квазиабсолютно простой |
| quasiabsolutely prime ideal | квазиабсолютно простой идеал |
| quasiregular prime | квазирегулярное простое число |
| ramified prime | разветвлённое простое число |
| ramified prime divisor | разветвлённый простой дивизор |
| rational prime | рациональное простое число |
| regular prime | регулярное простое число |
| relatively prime | взаимно простой |
| relatively prime elements | взаимно простые элементы |
| relatively prime germs | взаимно простые ростки |
| relatively prime ideals | взаимно простые идеалы |
| relatively prime integer | взаимно простые числа |
| relatively prime numbers | взаимно простые числа |
| relatively prime pair | пара относительно простых чисел |
| relatively prime polynomials | взаимно простые многочлены |
| relatively prime quantities | кроме единицы |
| relatively prime quantities | величины, не имеющие общих множителей |
| relevant prime ideal | кольцо отношений относительно которого одномерно и регулярно |
| relevant prime ideal | простой идеал |
| selection of a minimal covering set of multiple-output prime implicants | выбор минимального покрывающего множества простых многовыходовых импликант (ssn) |
| semi-prime | полупростой |
| semi-prime ideal | полупростой идеал |
| semi-prime ring | полупервичное кольцо |
| sequence of prime numbers | последовательность простых чисел |
| set of multiple-output prime implicants | множество простых многовыходовых импликант (ssn) |
| strongly prime theory | сильно простая теория |
| symmetric prime end | симметрический простой конец |
| symplectic prime ideal | симплектический простой идеал |
| tangent prime | касательная гиперплоскость |
| the prime denotes differentiation with respect to z | штрих обозначает операцию дифференцирования по переменной z |
| the prime object | основная цель (Нашей основной целью является определение (. ..)) ..)) |
| the prime on the sign of function means that | штрих у знака функции означает, что … |
| the prime on the summation sign indicates that | штрих у знаков суммы |
| the process of factoring a real number involves expressing the number as a product of prime factors | простой множитель |
| torsion prime | простое число кручения |
| triple prime | тройной штрих (LOlga) |
| two-prime factorization | разложение на два простых множителя |
| united prime | неподвижная гиперплоскость |
| unramified prime divisor | неразветвлённый простой дивизор |
Get short URL
С этим файлом связано 5 файл(ов).  Среди них: TGP_MATERIAL.docx, Тактические возможности подразделений по тушению пожаров и ликви, LFK_1.docx, 5-6 лаба Самарбаева.DOCX, Voporosy_viktoriny_Epokha_Petra_1.docx. Среди них: TGP_MATERIAL.docx, Тактические возможности подразделений по тушению пожаров и ликви, LFK_1.docx, 5-6 лаба Самарбаева.DOCX, Voporosy_viktoriny_Epokha_Petra_1.docx.Показать все связанные файлы Подборка по базе: 10 сынып геометрия ҚМЖ.docx, ТИТУЛКА ГЕОМЕТРИЯ.docx, Сборник суммативного оценивания по алгебре и началам анализа и г, ПРОГРАММА 11 кл ГЕОМЕТРИЯ.doc, Анықталған интегралдың геометриялық.docx, Третья аналитическая группа катионов.docx, РТ геометрия _2022.docx, Аннотация к рабочей программе предмета Математика курс Геометрия, клн геометрия 9.docx, Что такое наука геометрия.pdf Аналитическая геометрия Понятие вектора. Линейные операции над векторами. Определение: отрезок АВ называется направленным, если указано, какая из точек А или В является его началом, а какая — концом. Длиной вектора АВ называется длина отрезка АВ. Направленные отрезки АВ и А1В1 называются сонаправленными, если лучи АВ и А1В1 сонаправлены. Напр. отрезки АВ и А1В1 называются равными, если они сонаправлены и имеют одинаковую длину. Если отношение обладает свойствами рефлексивности, симметричности и транзитивности, то оно является отношением эквивалентности, то есть множество всех направленных отрезков распадается на непересекающиеся классы эквивалентных друг другу направленных отрезков. Определение: вектором называется класс эквивалентных между собой направленных отрезков. Каждый направленный отрезок задаёт вектор, при этом эквивалентные отрезки задают один и тот же вектор. Направление всех отрезков данного класса называется направлением вектора, а длина — длиной вектора. Опр: Данный вектор можно отложить от любой точки, и притом единственным образом. Опр: нулевой вектор — длина равна 0, единичный — длина равна единице. Опр: Два вектора, лежащих на ОДНОЙ ИЛИ ПАРАЛЛЕЛЬНОЙ ПРЯМЫХ, называются КОЛЛИНЕАРНЫМИ. Нулевой вектор коллинеарен любому вектору (у него нет направления) Опр. Линейные операции над векторами: Сложение по правилу треугольника: Суммой векторов а и в называют такой вектор с, начало которого совпадает с началом вектора а, а конец — с концом вектора в, при условии, что вектор в отложен из конца вектора а. Свойства операции сложения: коммутативность (перестановка слагаемых) — доказывается по правилу параллелограмма ассоциативность (скобки) при добавлении 0 ничего не меняется при сложении противоположных =0 Разностью двух векторов называется такой вектор а, что в+d=a (a-в=d). Произведением вектора а на число λ называется такой вектор в, что а и в сонаправлены, если λ>0; противоположно направлены, если λ в=λа (векторы с модулем) Свойства операции умножения вектора на число: дистрибутивность (раскрытие скобок сложения) ассоциативность (при умножении числа на вектор в скобках) дистрибутивность относительно чисел (в скобках — числа) Векторы коллинеарны, ели один из них можно разложить на произведение числа и второго вектора. Координаты вектора и точки на плоскости, в пространстве. Векторы а и в неколлинеарны, точка О. Пара векторов а и в — базис, а тройка О, а, в — афинный репер. Базис на плоскости — 2 любых некомпланарных вектора. С — произвольный вектор. Построим паралеллограмм со сторонами l1 l2 и вершинами в точках О и С. Вектор ОА1=а, ОВ1=в. ОА1+ОВ1=ОС. Вектор ОА (направляющий) и ОА1 сонаправлены. ОА1=Х1*ОА или а1=Х1*а. Аналогично вектор ОВ1. а1+в1=с (по пр параллелогр) равно Х1*а+Х2*в=с — разложение вектора с по базису ав. Числа X1 X2 – координаты вектора с в данном базисе (по-другому координаты точки С относительно репера О, а,в). Точка О — начало координат. Координатные оси состоят из прямых l1 l2 вместе с направляющими отрезками OA OB. Координатные оси вместе с началом координат называются афинной СК на плоскости. В пространстве — аналогично предыдущему. Зададим 3 некомпланарных вектора а, в, с — базис. Вместе с произвольной т О — это афинный репер в пространстве. OA1=a1 и далее. По правилу параллелограмма OD1=OA1+OB1; d1=a1+b1 В треугольнике OD1D OD=OD1+D1D или OD=OD1+OC1 d=d1+c1=a1+b1+c1. Итак, по 1 признаку коллинеарности a1=x1*a b1=x2*b c1=x3*c И вектор d=a1+b1+c1=x1*a+ x2*b+x3*c. Вектор d – радиус-вектор точки D в данном репере. l1=OA, l2=OB, l3=OC – координатные оси. Вместе с точкой о — афинная система координат в пространстве. Ортонормированный базис — векторы a b c единичные и взаимноперпендикулярные. Если тройка a b c правая, то СК декартова. Второй признак коллинеарности: для того, чтобы векторы были коллинеарны, необх и достаточно, чтобы их координаты были пропорциональными. Понятие вектора. Линейная зависимость векторов. Понятие см в пункте 2. Линейная зависимость????? Скалярное произведение векторов и его свойства. (Скалярным) произведение векторов a и b называется ЧИСЛО, равное произведению модулей векторов на косинус угла между ними. Скалярный квадрат равен квадрату модуля. Скалярное произведение равно нулю тогда и только тогда, когда векроты перпендикулярны (cos 90=0) Свойства скалярного произведения: Векторное произведение векторов и его свойства. Геометрический смысл. [Векторным] произведением двух векторов a и b называется такой ВЕКТОР с, что Векторное произведение двух векторов Геометрический смысл. Модуль векторного произведения численно равен площади параллелограмма, построенного на направленных отрезках, представляющих эти векторы и отложенных от одной точки. Свойства векторного произведения Векторное произведение ненулевых векторов равно нулевому вектору тогда и только тогда, когда векторы КОЛЛИНЕАРНЫ. Смешанное произведение векторов и его свойства. Геометрический смысл. Смешанным произведением векторов a, b, c называется скалярное произведение векторного произведения первых двух векторов на третий. ЧИСЛО. Смешанное произведение равно 0 когда векторы компланарны, и наоборот. Положительно, если тройка правая, отрицательно, если тройка левая. Свойства: Не зависит от группировки сомножителей Не меняется при циклической перестановке сомножителей Геометрический смысл: модуль смешанного произведения трёх векторов численно равен объёму параллелепипеда, построенного на направленных отрезках, представляющих данные векторы и отложенных от одной точки. Разделив на 6, получаем объём тетраэдра. Формула вычисления смешанного произведения Преобразование декартовых координат на плоскости.  Случай 1: На плоскости заданы 2 декартовы системы координат Oxy и O`x`y`, у которых направления коорд осей совпадают, но начальные точки O и О` разные. Говорят, что вторая система координат получена из первой ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ (переносом начала координат). Пусть нам известна координата O`(a; b) в первой СК. М — произвольная точка плоскости. В первой СК её координаты M (x;y), а во второй — M (x`; y`). КООРДИНАТЫ ТОЧКИ СОВПАДАЮТ С КООРД РАДИУС-ВЕКТОРА. По правилу треугольника: Если СК в пространстве, то к последним формулам добавляется z. Случай 2: На плоскости заданы 2 декартовы СК с общим началом Oxy и Ox`y`. α – ориентированный угол между положительным направлением осей Ox и Ox`. Тогда говорят, что вторая СК получена из первой ПОВОРОТОМ НА УГОЛ α. Пусть М — произвольная точка плоскости. Коорд в первой СК M(x;y), во 2 — M(x`; y`). Связь между ними: пусть 𝜑 — ориентированный угол между положительным напр Ox и вектором OM; ψ — ориентированный угол между положит напр Ox` и вектором OM. Угол 𝜑=α+ψ подставим: поворот на угол α Поскольку вторая СК может быть получена поворотом на — α, то последние формулы преобразовываются cos(- α)=cos α Если в пространстве совершается поворот СЕ вокруг оси Oz, то координата z точки М не изменится, а координаты x, y будут меняться по тем же формулам. Тогда вторую СК можно получить из первой в результате двух преобразований: перенос начала коорд в точку O` и получение промежуточной СК O`x«y«, а затем поворот коорд осей. Тогда формулы x«=x-a становятся y«=y-b Для того, чтобы выразить x y через x` y` воспользуемся формулами Прямая на плоскости: уравнение прямой в общем виде, особенности расположения прямой относительно СК. Пусть дана точка М0(x0; y0) и вектор n (A; B). М(x; y) – произвольная точка прямой без фиксированного положения.  Вектор n (A; B) – нормальный вектор прямой Вектор n (A; B) – нормальный вектор прямойВектор M0M(x-x0; y-y0) n⟂ M0M → n·M0M=0 (скалярное) A(x-x0)+B(y-y0)=0 Ax—Ax0+By—Byo=0
Прямая на плоскости: 1)уравнение прямой с угловым коэффициентом, 2)проходящей через две точки. 1) Угловой коэф — число k, прямая проходит через М0(x0;y0) y=kx+b – уравнение прямой с угловым коэффициентом (1) Для М0 y0=kx0+b (2) Вычтем из (1) (2) — уравнение прямой с угл коэффициентом M1(x1; y1), M2(x2; y2) и произвольная точка прямой M(x; y) коллинеарны (лежат на одной прямой), тогда по 2 признаку коллинеарности их координаты пропорциональны Угол между прямыми. Взаимное расположение прямых на плоскости. Угол 𝜑 между прямыми l1: y=k1x+b1 и l1: y=k2x+b2 k – угол наклона к оси X ( k=tg⍺ k1=tg⍺1 k2=tg⍺2) Угол 𝜑 между прямыми равен Тогда tg𝜑=
Прямая на плоскости: 1)уравнение в отрезках, 2)нормальное уравнение прямой. 1) «в отрезках». Общее уравнение Ax+By+C=0 A≠0 B≠0 C≠0 Ax+By= — C (разделим на -C) Такая прямая пересекает Ox в т (a;0) Oy в т (0;b), отсекает по осям отрезки a и b Каноническое и параметрические уравнения прямой на плоскости.  Расстояние от точки до прямой. Пучок прямых. Расстояние от точки до прямой. Пучок прямых.ПАРАМЕТРИЧЕСКИЕ. Возьмём точку M0(x0;y0) (данная точка с конкретными коорд) и произвольную точку прямой M(x; y). Строим векторы OM OM0 Обозначим OM=r; OM0=r0 Сложим по правилу треугольников Раскроем скобки, получим КАНОНИЧЕСКОЕ. Рассмотрим систему, исключим параметр t Полярная система координат и её связь с декартовой. Полярная СК — это двумерная система координат, в которой каждая точка на плоскости однозначно определяется ПОЛЯРНЫМ УГЛОМ 𝜑 и ПОЛЯРНЫМ РАДИУСОМ. Формулы перехода (выражение декартовых X; Y через ⍴ и 𝜑): Общее уравнение плоскости. Особенности расположения плоскости. Положение плоскости в пространстве может быть задано при помощи различных величин, и от этого зависит вид уравнения плоскости. Составим уравнение плоскости через т M0(x0; y0; z0) (конкретные коорд) перпендикулярно указанному вектору n(A; B; C). (n; r)-p=0 – нормальное уравнение плоскости в векторном виде Получим в координатном виде n*(cos 𝛼; cos 𝛽; cos 𝛾)=0 r(x; y; z) – радиус-вектор (n, r)=p x*cos 𝛼+y*cos 𝛽+z*cos 𝛾=0 – нормальное ур плоскости в координатном виде. Чтобы общее уравнение плоскости привести к НОРМАЛЬНОМУ виду, надо общее уравнение умножить на нормирующий множитель. 2 Уравнение плоскости, проходящей через 3 точки. Через 3 точки проходит единственная плоскость. Пусть даны M1 (x1; y1; z1) M2 (x2; y2; z2) M3 (x3; y3; z3) Составим уравнение плоскости, проходящей через эти точки. Пусть M(x; y; z) – произвольная точка плоскости. Докажем, что 4 точки лежат в одной плоскости. ОТЛОЖИМ ВЕКТОРЫ ОТ ТОЧКИ М1 M1M (x-x1; y-y1; z-z1) M1M2 (x2-x3; y2-y1; z2-z1) M1M3 (x3-x1; y3-y1; z3-z1) Они некомпланарны M1M*M1M2*M1M3=0 1 Уравнение плоскости в отрезках.  2 Угол между двумя плоскостями. 3 Условие параллельности и перпендикулярности двух плоскостей. 2 Угол между двумя плоскостями. 3 Условие параллельности и перпендикулярности двух плоскостей.1 В отрезках. Пусть дано общее уравнение плоскости и A, B, C, D не равны 0. Ax+By+Cz= — D разделим на — D Эта плоскость пересекает оси координат в точках (a; 0; 0), (0; b; 0), (0; 0; c) 2 угол между двумя плоскостями Даны 2 плоскости: A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 Пусть они пересекаются, и тогда они будут образовывать ДВА смежных двугранных угла, каждый из которых измеряется соответствующим линейным углом. Обозначим тот линейный угол через 𝜑, он является острым. Угол 𝜑 равен углу, лежащему между нормальными векторами этих плоскостей. Нормальные вектора n1 (A1; B1; C1) и n2 (A2; B2; C2) 1 Условие параллельности и перпендикулярности двух плоскостей.  Пучок плоскостей. Пучок плоскостей.1 Условия параллельности и перпендникулярности Рассмотрим 2 плоскости: A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0 ПАРАЛЛЕЛЬНЫ, если Чтобы плоскости были ПЕРПЕНДИКУЛЯРНЫ, нормальные векторы должны быть перпендикулярны Пусть даны 2 плоскости в общем виде: A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. Пусть они пересекаются. Тогда уравнение плоскости, проходящей через линию пересечения данных плоскостей: Это уравнение выражает ПУЧОК ПЛОСКОСТЕЙ, то есть множество плоскостей, проходящих через линию их пересечения. Ось пучка — прямая, через которую проходит пучок плоскостей. При решении задач лямбду находят через подстановку данных уравнений плоскостей и координат точки в уравнение. Затем лямбду подставляем в уравнение пучка (где уже подставлены первые уравнения плоскостей) и раскрываем скобку. Параметрические и канонические уравнения прямой в пространстве. Пусть дана точка M0(x0; y0) и вектор s(m; n; p). Составим уравнение прямой, проходящей через точку M0, параллельно вектору s (направляющий). Отложим на прямой вектор M0S=s. Пусть M(x; y; z) – произвольная точка прямой. Обозначим радиус-вектор r0=OM0 и OM=r. Тогда по правилу треугольника: OM0+M0M=OM; т к M0S∥ M0M (на одно прямой), то по 1 признаку коллинеарности M0M=t*M0S=t*s. r0+t*s=r – параметрическое плоскости в векторном виде В координатном виде: r0=x0i+y0j+z0k r=xi+yi+zi s=mi+nj+pk x0i+y0j+z0k+t*(mi+nj+pk)=xi+yi+zi Приводя подобные и приравнивая координаты при одинаковых ортах, получим x=x0+mt y=y0+nt z=z0+pt —ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ Исключим из параметрических уравнений параметр t (выразим из каждого t и приравняем Нормальное уравнение прямой в пространстве.  Общие уравнения прямой, приведение общих уравнений к каноническому виду. Общие уравнения прямой, приведение общих уравнений к каноническому виду.НОРМАЛЬНОЕ. Рассмотрим каноническое уравнение, где s (m; n; p) – напрявляющий. -углы между осями Ox, Oy, Oz Проекции вектора s на оси: Проекции в координатах: Получаем cos 𝛼, cos 𝛽, cos 𝛾– направляющие косинусы прямой Для перехода от КАНОНИЧЕСКОГО к НОРМАЛЬНОМУ воспользуемся следующими формулами: ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ Общие приводят к каноническому виду для удобства. Из общих исключают сначала одну координату, потом другую; затем в полученных уравнениях выражают координаты через общую координату. Прямая в пространстве. Уравнение прямой, проходящей через две точки. Угол между прямыми. Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей. УРАВНЕНИЕ ЧЕРЕЗ 2 ТОЧКИ Пусть даны 2 различные точки M1(x1; y1; z1) M2 (x2; y2; z2). M (x; y; z) – произвольная точка прямой. Возьмём в качестве точки, принадлежащей прямой, М1, а в качестве направляющего вектора —вектор M1M2=(x2-x1; y2-21; z2-z1). Подставляем в каноническое уравнение прямой УГОЛ МЕЖДУ ПРЯМЫМИ Пусть даны прямые Угол 𝜑 между двумя прямыми равен углу между их направляющими векторами. Прямые параллельны: Прямые перпендикулярны: Взаимное расположение прямой и плоскости. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Прямая и плоскость могу быть параллельны, пересекаться, и прямая может лежать в плоскости. Чтобы выяснить взаимное расположение используют общее уравнение плоскости и параметрические уравнения прямой. Решают систему.
_______________________________________________________________ КРИВЫЕ II ПОРЯДКА Эллипс: определение, вывод канонического уравнения, геометрические свойства.  Опр.: эллипсом называется множество точек пространства (ГМТ), для каждой из которых СУММА РАССТОЯНИЙ ДО ФОКУСОВ (это 2 данные точки той же плоскости) ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ. Пусть F1, F2 – фокусы, 2a – постоянная величина из определения. Фокусное расстояние F1F2=2c. Пусть M (x; y) – произвольная точка эллипса. Тогда по определению F1M+F2M=2a. Составим уравнение эллипса относительно декартовой СК. Ось Ох возьмём сонаправленно вектору F1F2 и проходящей через эти точки. Начало координат пусть будет в середине отрезка F1F2. Тогда ость Оу определится однозначно. Геометрические свойства эллипса 1) из канонического уравнения следует, что 2) координатные оси пересекают эллипс в точках — ВЕРШИНЫ ЭЛЛИПСА
A1A2 и B1B2 – большой и малый диаметры, вместе — главные диаметры, a и b – большая и малая полуоси соответственно 3)КООРДИНАТНЫЕ оси являются осями СИММЕТРИИ эллипса (осевая симметрия), а начало координат — центром симметрии (центральная симметр) 4) Эллипс может быть получен из окружности в результате её равномерного сжатия вдоль Oy с коэффициентом сжатия k= 5) Эллипс может быть получен из окружности в результате проекции окружности на плоскость, непараллельную плоскости окружности. Гипербола: определение, вывод канонического уравнения, геометрические свойства. Опр.: Гиперболой называется множество всех точек плоскости (ГМТ), для каждой из которых МОДУЛЬ РАЗНОСТИ РАССТОЯНИЙ ДО ФОКУСОВ (двух данных точек) есть величина постоянная. Пусть F1, F2 – фокусы, 2a – постоянная величина из определения. Фокусное расстояние F1F2=2c и M (x; y) – произвольная точка гиперболы. Тогда по определению F1M – F2M=2a. Составим уравнение гиперболы относительно декартовой СК. Вводим координаты аналогично эллипсовым: Ox сонаправлена F1F2 и проходит через эти точки, О — середина отрезка F1F2. Oy проходит через точку О и перпендикулярно Ох. По определению получаем Геометрические свойства гиперболы 1) Из канонического уравнения следует то есть гипербола целиком находится внутри области, определённой неравенствами 2) Пересечения с осями при x=+-a
Числа a, b – полуоси действительной и мнимой гиперболы. 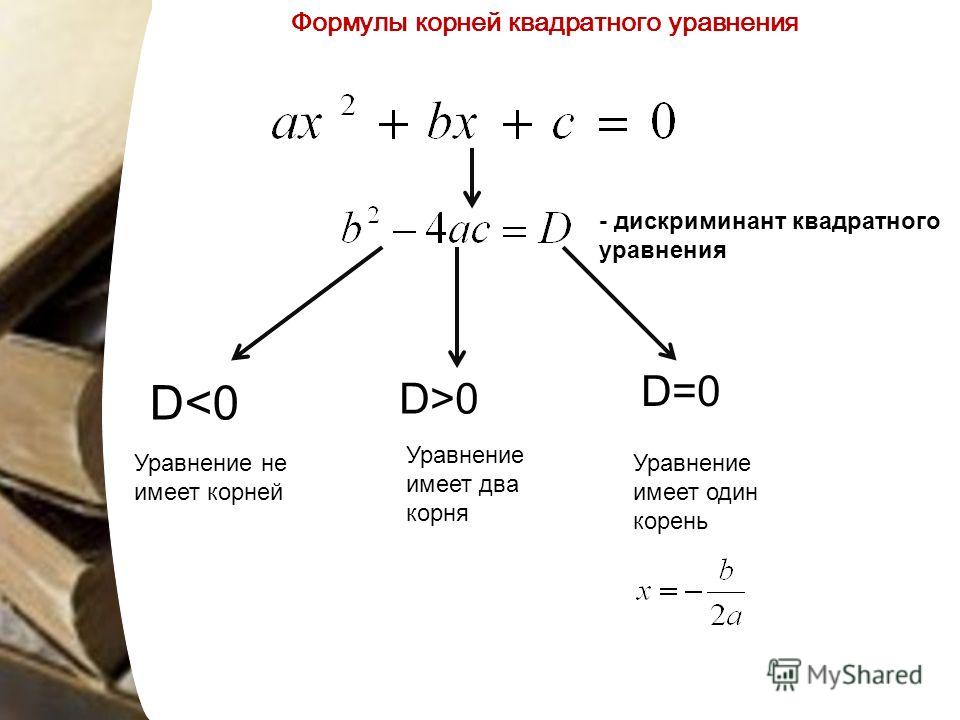 3) по аналогии с эллипсом оси координат являются осями симметрии гиперболы, начало координат — центром симметрии. 4) АСИМПТОТЫ ГИПЕРБОЛЫ Гипербола неограниченно приближается к ним, но не пересекает их. Асимптоты проходят через диагонали ФУНДАМЕНТАЛЬНОГО прямоугольника гиперболы, который определяется неравенствами: Для построения гиперболы рекомендуется сначала построить фундаментальный прямоугольник. 5) При a=b гипербола РАВНОБОКАЯ Тогда её асимптоты У сопряжённой гиперболы тот же фундаментальный прямоугольник, те же асимптоты, только расположена она В ДРУГОЙ ПАРЕ ВЕРТИКАЛЬНЫХ УГЛОВ (пересекает ось ординат y) Парабола: определение, вывод канонического уравнения, геометрические свойства. Опр.: ПАРАБОЛОЙ называется КОНИЧЕСКОЕ СЕЧЕНИЕ, эксцентриситет которого равен 1. ПАРАБОЛОЙ называется ГМТ плоскости, для каждой из которых РАССТОЯНИЯ ДО ФИКСИРОВАННОЙ ТОЧКИ (фокуса) и ОТ ТОЧКИ ДО ФИКСИРОВАННОЙ ПРЯМОЙ РАВНЫ. Составим уравнение параболы в декартовой СК. Выберем начало коорд в середине между фокусом и директрисой. Пусть δ — директриса; F – фокус. FF` — расст между фокусом и директрисой. Тогда начало координат О в середине F`F; ось Ox сонаправлена вектору OF Пусть FF`=p. Ox сонаправлена OF. M (x; y)- точка плоскости. По определению MF=MM` или FM=MM` Свойства параболы 1) Все точки параболы лежат в полуплоскости (ПРАВЕЕ Oy) 2) Ox – ось симметрии Виды параболы Конические сечения. Фокус, директриса, эксцентриситет. Касательные к коническим сечениям. Опр.: КОНИЧЕСКИМ СЕЧЕНИЕМ называется кривая, по которой коническую поверхность пересекает плоскость, не проходящая через вершину этой поверхности. Коническими сечениями могут быть эллипс, гипербола, парабола.  Парабола получается, когда плоскость сечения параллельна одной из образующих конуса. ТЕОРЕМА 1: Для всякого конического сечения кроме окружности существует точка F, называемая ФОКУСОМ, и прямая, называемая ДИРЕКТРИСОЙ δ, такие что ОТНОШЕНИЯ РАССТОЯНИЙ от произвольной точки кривой M до фокуса и расстояния от M до директрисы δ ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ — ЭКСЦЕНТРИСИТЕТ Чем меньше 𝜀, тем ближе кривая расположена к фокусу. При Чем ближе 𝜀 к 1, тем более вытянут эллипс. При 𝜀=1 эллипс как бы «разрывается» и «превращается» в ПАРАБОЛУ. Чем больше 𝜀, тем ближе кривая расположена к директрисе. При ТЕОРЕМА 2: Эксцентриситет 𝜀 эллипса и гиперболы, заданных своими каноническими уравнениями, равен КАСАТЕЛЬНЫЕ К КАНОНИЧЕСКИМ СЕЧЕНИЯМ? Общее уравнение кривой второго порядка. Центр кривой второго порядка. Опр.: КРИВОЙ 2 ПОРЯДКА называется ГМТ, координаты которых удовлетворяют уравнению где Опр. Кривая, которая имеет центр, называется центральной (эллипс, гипербола). Предположим, что СК выбрана так, что её начало коорд находится в центре кривой. Тогда одновременно с точкой (x; y) кривой принадлежит точка (-x; -y). Подставим её в уравнение Вычтем их полученного старое уравнение. — должно выполняться для любой точки (x; y) на кривой. Поэтому , если нач коорд находится в центре. Следовательно, если изначально нач коорд не находится в центре O`, то надо совершить ПЕРЕНОС СК в т O` Т: Координаты (x0; y0) центра кривой, заданной первым уравнением находится из системы линейных уравнений Предположим, что центр кривой находится в начале координат. Попробуем упростить уравнение 3 Пусть СК Ox«y« получена поворотом из Ox`y`на угол альфа. Тогда формулы замены координат имеют вид: Поставим в 3: Раскрывая скобки и приводя подобные при одинаковых коорд, получим (кв уравнение относительно тангенса) Его дискриминант (формула как у всех кв уравнений, нужно будет записать) больше или равен нулю, то есть существует такой угол альфа, что в новой СК мы получим уравнение кривой без слагаемого, содержащего x«y«. В ПЕРВОМ уравнении ЛИНЕЙНАЯ ЧАСТЬ отвечает за ПЕРЕНОС, XY – за поворот (если они есть, то будет перенос и поворот). Получится новая декартова СК с тем же началом O`x`y`. ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ БУДУТ НА ШТРИХ МЕНЬШЕ, тк это первая замена. В этой СК уравнение кривой не будет иметь слагаемого с x`y`. Приведение к каноническому виду общего уравнения кривой второго порядка путём ПЕРЕНОСА НАЧАЛА КООРДИНАТ. Если кривая центральная (узнаём через D), то Находим центр O` Находим C` по формуле Уравнение после переноса: КВАДРАТИЧНАЯ ЧАСТЬ + С` Преобразовываем, x«y« должны уйти. Получается уравнение кривой 2 порядка в НОВОЙ СК По уравнению определяем тип кривой и строим.  Если кривая нецентральная, то центр найти нельзя, и перенос нач коорд не производится. Приведение к каноническому виду общего уравнения кривой второго порядка путём ПОВОРОТА ОСЕЙ КООРДИНАТ. (можно как с центральной, так и с Нецентральной) В обоих случаях: Сразу находим тангенс угла поворота по формуле Cos a, sin a по формулам Формулы преобразования (МЕНЬШЕ НА ШТРИХ) Подставляем в исходное, x`y` уничтожаются. Получается уравнение кривой в повёрнутой СК. По уравнению определяем тип кривой и строим. Цилиндрические поверхности. Опр.: ЦИЛИНДРИЧЕСКОЙ называется поверхность, которую образует МНОЖЕСТВО ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ (образующих прямых), проходящих через каждую точку некоторой кривой (направляющей). Пусть Ф — цилиндрическая поверхность. Выберем декартову СК так, чтобы ось Oz была ПАРАЛЛЕЛЬНА образующим.  Если при этом направляющая 𝛾` (гамма штрих) не лежит в плск Oxy, то спроецируем её в эту плоскость. Получим некоторую кривую 𝛾. Если взять 𝛾 как направляющую, то получим ту же поверхность 𝛟. Поэтому с самого начала будем считать, что направляющая — кривая 𝛾, лежащая в плоскости Oxy. Пусть 𝛟(x, y)=0 – её уравнение в плоскости Oxy. В пространстве она задаётся системой Пусть точка M( x; y; z) — произвольная точка поверхности 𝛟. Тогда её проекция на Oxy будет представлять собой точку M0 (x; y; o). И эта точка должна принадлежать направляющей 𝛾. Поэтому её координаты должны удовлетворять уравнению 𝛟(x, y)=0 Следовательно, этому уравнению будут удовлетворять координаты точки M, т к x, y в т M и M0 одинаковы, а Z В УРАВНЕНИЕ НЕ ВХОДИТ. Т о, 𝛟(x, y) и есть уравнение поверхности 𝛟, то есть, уравнение ЦИЛИНДРИЧЕСКОЙ поверхности СОВПАДАЕТ С уравнением ЕЁ НАПРАВЛЯЮЩЕЙ КРИВОЙ 𝛾 плоскости Oxy, если образующие параллельны оси Ох. Аналогично, если образующие параллельны оси Оy, то уравнение цил поверхности совпадает с с уравнением направляющей кривой в плск-сти Oxz, и обратно, если в уравнении поверхности отсутствует, например, кооордината Х, то сразу можно сделать вывод, что эта поверхность цилиндрическая, а её образующие параллельны Ох.
Конические поверхности. Опр.: КОНИЧЕСКОЙ называется поверхность, которую образует МНОЖЕСТВО ВСЕХ ПРЯМЫХ (образующих), ПРОХОДЯЩИХ ЧЕРЕЗ КАЖДУЮ ТОЧКУ НЕКОТОРОЙ КРИВОЙ (направляющей) и ЧЕРЕЗ НЕКОТОРУЮ ТОЧКУ О (вершину).  Выберем декартову СК так, чтобы нач коорд совпало с вершиной конической поверхности. Пусть F (x, y, z)=0 – уравнение ПОВЕРХНОСТИ Ф в данной СК. Поскольку рассматривается поверхность II порядка, то F – многочлен II степени от трёх переменных. Тогда функция двух переменных 𝜑(x, y)=F(x, y, c) — многочлен II степени для любого действительного числа с (с принадлежит R). Система Получаемую в сечении кривую 𝛾 выберем в качестве НАПРАВЛЯЮЩЕЙ. Т к 𝜑(x, y) – многочлен II степени, то 𝛾 — кривая II порядка. Если 𝛾 — ЦЕНТРАЛЬНАЯ, то можно считать, что Oz ПРОХОДИТ ЧЕРЕЗ ЕЁ ЦЕНТР. Предположим сначала, что направляющая — эллипс Пусть M1 (x1, y1, z1) – произвольная точка поверхности 𝛟. Тогда вся прямая OM1 должна лежать на поверхности (вектор OM – направляющий, т к он принадлежит направляющей прямой). Параметрические уравнения этой поверхности будут выглядеть так: Пусть она пересекает направляющую 𝛾 в точке M0 (x0, y0, c). Если координаты точки M1 (x1, y1, z1) удовлетворяет уравнению КОНИЧЕСКОЙ поверхности (выше), то этому уравнению удовлетворяют координаты любой точки прямой OM1, значит это уравнение 2 — уравнение конической поверхности. — Каноническое уравнение конуса Если НАПРАВЛЯЮЩАЯ — ГИПЕРБОЛА, то получим тот же «эллиптический» конус с осью не Oz, а Oz`. Если НАПРАВЛЯЮЩАЯ —ПАРАБОЛА, то получим конус, осью которого является биссектриса угла угла yOz. Если НАПРАВЛЯЮЩАЯ —ПАРА ПРЯМЫХ, то коническая поверхность — это пара плоскостей, либо пересекающихся, либо совпадающих.
Поверхность вращения.  Опр.: Пусть некоторая кривая 𝛾 расположена в плоскости Oyz. Будем вращать её вокруг оси Oz. Получим некоторую поверхность Ф, которая называется ПОВЕРХНОСТЬ ВРАЩЕНИЯ. Каждая точка кривой 𝛾 описывает окружность, которая называется ПАРАЛЛЕЛЬ l, её центр лежит на оси Oz. Пусть 𝜑(y, z)=0 — уравнение кривой 𝛾 в плоскости Oyz. Тога в пространстве она задаётся системой Пусть M (x, y, z) – произвольная точка поверхности Ф. Тогда она лежит на на одной из таких параллелей lи может быть получена поворотом точки M0 (0, y0, z0)=𝛾 пересекает l. Очевидно, что z0=z и центр O` параллели lимеет координаты l(0; 0; z) Координаты точки M0 (0; y0; z0) должны удовлетворять уравнению 𝜑(y, z)=0, т к точка лежит на кривой 𝜑(y0, z0)=0 Подставляя сюда z=z0 и y0 (*), получаем (4) Обратно, пусть коорд точки M (x; y; z) удовлетворяют уравнению (4). Пример. Эллипсоид. Опр.:ЭЛЛИПСОИДОМ называется поверхность Ф, имеющая каноническое уравнение вида (уравнение 5) Исследуем форму поверхности методом параллельных сечений. (Делаем сечения плоскостями x, y, z – числа).
Прочие геометрические свойства эллипсоида Из ур 5 получаем, что каждая дробь положительная (т к в квадрате), сумма положительных дробей равна 1, значит, они правильные и эллипсоид целиком находится в параллелепипеде, который определяется этими неравенствами: Координатные оси пересекают эллипсоид в точках которые называются вершинами эллипсоида Коорд оси являются осями симметрии эллипсоида; коорд плоскости — плоскостями симметрии; начало координат — центром симметрии.  При a=b эллипсоид будет поверхностью вращения вокруг Oz. Аналогично, при a=c – вокруг Oy b=c – вокруг Ox a=b=c – сфера Однополостной и двуполостной гиперболоиды. Опр.: ОДНОПОЛОСТНЫМ и ДВУПОЛОСТНЫМ ГИПЕРБОЛОИДАМИ называются поверхности, имеющие канонические уравнения соответственно вида Исследуем их форму МЕТОДОМ ПАРАЛЛЕЛЬНЫХ СЕЧЕНИЙ.
В сечениях плоскостями y=hполучим
Аналогично, в сечениях плоскостями x=h получим:
Прочие геометрические свойства гиперболоидов Из ур (7) получаем , то есть в пространственном слое нет точек Ф2.  Координатные оси Ox и Oy пересекают Ф1 и Ф2 в т Ось Oz не пересекает Ф1. Она пересекает Ф2 в точках Точно так же, как и для эллипсоида, доказывается, что коорд оси являются осями симметрии гиперболоида, коорд плоскости — плоскостями симметрии, а т O – центром симметрии. Ось Oz – ось симметрии параболоидов, а коорд плоскости Oxz и Oyz – плоскостями симметрии. ДРУГИХ СИММЕТРИЙ У ПАРАБОЛОИДОВ НЕТ. При a=bФ3 будет поверхностью вращения гиперболы в сечении Ф4 плоскостями z=h будут равнобокими. Эллиптический и гиперболический параболоиды. Опр.: ЭЛЛИПТИЧЕСКИМИ И ГИПЕРБОЛИЧЕСКИМИ ПАРАБОЛОИДАМИ называются поверхности, имеющие канонические уравнения соответственно видов Исследуем их форму методом параллельных сечений. В сечениях плоскостями z=h получим
В сечениях плоскостями y=hполучаем
Эти параболы равны друг другу и получаются параллельным переносом, а при перемещении описывают кривую (вершины) Oyz (параболу), т е оба параболоида получаются движением одной параболы, когда её вершина скользит по другой параболе. Аналогично, полученные в сечениях плоскостями x=h равны друг другу Исследование формы поверхности второго порядка методом параллельных сечений. При таком исследовании производим сечение плоскостями x=h, y=h, z=h (h-число). После подстановки исследуют уравнения, положительные ли дроби выходят. От этого зависят полученные фигуры.0> |
Оценка инсульта Siriraj и проверочное исследование для отличия супратенториального внутримозгового кровоизлияния от инфаркта
. 1991 29 июня; 302 (6792): 1565-7.
doi: 10.1136/bmj.302.6792.1565.
Н Пунгварин 1 , A Viriyavejakul, C Komontri
принадлежность
- 1 Медицинский факультет, Медицинский факультет, Больница Сирирадж, Университет Махидол, Бангкок, Таиланд.

- PMID: 1855041
- PMCID: PMC1670347
- DOI: 10.1136/бмж.302.6792.1565
Бесплатная статья ЧВК
Н. Пунгварин и соавт. БМЖ. .
Бесплатная статья ЧВК
. 1991 29 июня; 302 (6792): 1565-7.
doi: 10.1136/bmj.302.6792.1565.
Авторы
Н Пунгварин 1 , А Вирияведжакул, С Комонтри
принадлежность
- 1 Медицинский факультет, Медицинский факультет, Больница Сирирадж, Университет Махидол, Бангкок, Таиланд.

- PMID: 1855041
- PMCID: PMC1670347
- DOI: 10.1136/bmj.302.6792.1565
Абстрактный
Цели: Разработать простой, надежный и безопасный инструмент диагностики синдромов острого инсульта в условиях, когда компьютерное сканирование мозга было недоступно, и проверить его точность в отношении патологических типов инсульта.
Дизайн: 13 клинических переменных, которые потенциально могли бы отличить супратенториальное кровоизлияние в мозг от инфаркта, были зарегистрированы и протестированы с помощью многофакторного анализа в проспективном исследовании 174 пациентов с острым инсультом. При разработке шкалы оценки инсульта Siriraj за пошаговым дискриминантным анализом переменных последовало линейное дискриминантное уравнение для дифференциации супратенториального кровоизлияния и инфаркта. Полученная оценка была подтверждена по сравнению с оценками 206 других пациентов с инсультом, компьютерное сканирование мозга использовалось для окончательного диагноза.
При разработке шкалы оценки инсульта Siriraj за пошаговым дискриминантным анализом переменных последовало линейное дискриминантное уравнение для дифференциации супратенториального кровоизлияния и инфаркта. Полученная оценка была подтверждена по сравнению с оценками 206 других пациентов с инсультом, компьютерное сканирование мозга использовалось для окончательного диагноза.
Параметр: Медицинская школа госпиталя Сирирадж, Университет Махидол, Бангкок.
Предметы: Проспективное исследование: 174 последовательных пациента с синдромом острого супратенториального инсульта (не с субарахноидальным кровоизлиянием), поступивших в больницу Сирирадж в 1984–1985 гг.; проверочное исследование: 206 пациентов, госпитализированных в больницу Siriraj или другую больницу по поводу супратенториального внутримозгового кровоизлияния или инфаркта.
Полученные результаты: Оценка инсульта Siriraj была разработана и рассчитана как (2,5 х уровень сознания) + (2 х рвота) + (2 х головная боль) + (0,1 х диастолическое артериальное давление) — (3 х маркеры атеромы) — 12. Оценка выше 1 указывает на супратенториальное внутримозговое кровоизлияние, а оценка ниже -1 указывает на инфаркт. Оценка от 1 до -1 представляет собой сомнительный результат, требующий компьютерного сканирования мозга или кривой вероятности для подтверждения диагноза. В валидационном исследовании шкалы Siriraj для оценки инсульта диагностическая чувствительность шкалы кровоизлияния в мозг и инфаркта мозга составила 89.0,3% и 93,2% соответственно, с общей прогностической точностью 90,3%.
Оценка выше 1 указывает на супратенториальное внутримозговое кровоизлияние, а оценка ниже -1 указывает на инфаркт. Оценка от 1 до -1 представляет собой сомнительный результат, требующий компьютерного сканирования мозга или кривой вероятности для подтверждения диагноза. В валидационном исследовании шкалы Siriraj для оценки инсульта диагностическая чувствительность шкалы кровоизлияния в мозг и инфаркта мозга составила 89.0,3% и 93,2% соответственно, с общей прогностической точностью 90,3%.
Вывод: Шкала инсульта Siriraj широко используется и применяется в больницах по всему Таиланду как простой и надежный метод диагностики острого инсульта у постели больного.
Похожие статьи
Клиническое различие между острым геморрагическим и острым ишемическим инсультом по шкале Siriraj.

Хунг Л.И., Ван П.Ю., Ван Ю., Чиа Л.Г. Хунг Л.И. и соавт. Чжунхуа И Сюэ За Чжи (Тайбэй). 1995 март; 55 (3): 248-52. Чжунхуа И Сюэ За Чжи (Тайбэй). 1995. PMID: 7780882
Сравнение баллов Siriraj и Guy’s Hospital для дифференциации супратенториальных ишемических и геморрагических инсультов у населения Индии.
Дага М.К., Сарин К., Неги В.С. Дага М.К. и др. J Assoc врачей Индии. 1994 апр; 42(4):302-3. J Assoc врачей Индии. 1994. PMID: 7860548
Достоверность системы подсчета очков Siriraj Stroke.
Шах Ф.У., Салих М., Саид М.А., Тарик М. Шах Ф.У. и др. J Coll Physicians Surg Pak. 2003 г., июль; 13 (7): 391-3. J Coll Physicians Surg Pak. 2003. PMID: 12887840
Инсульт у молодых людей.
 Постоянная диагностическая проблема.
Постоянная диагностическая проблема.Тоффол Г.Дж., Свионтонёвски М. Тоффол Г.Дж. и соавт. последипломная мед. 1992 март; 91 (4): 123-8. дои: 10.1080/00325481.1992.11701248. последипломная мед. 1992. PMID: 1546006 Обзор.
Надежная оценка доли малых инсультов вследствие внутримозгового кровоизлияния.
Лавлок К.Э., Редгрейв Дж.Н., Брайли Д., Ротвелл П.М. Лавлок С.Э. и др. Инт J Инсульт. 2009 февраль;4(1):6-10. дои: 10.1111/j.1747-4949.2009.00238.х. Инт J Инсульт. 2009. PMID: 19236489 Обзор.
Посмотреть все похожие статьи
Цитируется
Протоколизированное наблюдение в отделении неотложной помощи повышает качество помощи при ишемическом инсульте на Гаити.

Рухани С.А., Марш Р.Х., Римпель Л., Андерсон К., Аутхей М., Эдмонд М.С., Чекетт К.А., Берковиц А.Л., Кван Г.Ф., Боуг К.В., Шур Д.Д. Рухани С.А. и др. Afr J Emerg Med. 2020 сен;10(3):145-151. doi: 10.1016/j.afjem.2020.05.007. Epub 2020 15 июля. Afr J Emerg Med. 2020. PMID: 32923326 Бесплатная статья ЧВК.
Неврология катастроф: новые возможности для практики и вызов для невролога.
Этьен М., Алесси АГ. Этьен М. и соавт. Нейрол Клин Практ. 2013 Декабрь; 3 (6): 493-500. doi: 10.1212/01.CPJ.0000436212.11132.c7. Нейрол Клин Практ. 2013. PMID: 30107026 Бесплатная статья ЧВК.
Транскраниальная допплерография в сочетании с количественным ЭЭГ-мониторингом функций головного мозга и прогнозированием исходов у пациентов с тяжелым острым внутримозговым кровоизлиянием.

Чен Ю, Сюй В, Ван Л, Инь Х, Цао Дж, Дэн Ф, Син Ю, Фэн Дж. Чен Ю и др. Критический уход. 2018 февр. 20;22(1):36. doi: 10.1186/s13054-018-1951-y. Критический уход. 2018. PMID: 29463290 Бесплатная статья ЧВК.
Инсульт в больнице с ограниченными ресурсами на Мадагаскаре.
Stenumgård PS, Rakotondranaivo MJ, Sletvold O, Follestad T, Ellekjær H. Стенумгард П.С. и др. Примечания BMC Res. 2017 24 июля; 10 (1): 307. doi: 10.1186/s13104-017-2627-4. Примечания BMC Res. 2017. PMID: 28738901 Бесплатная статья ЧВК.
Использование диагностической оценки для определения приоритетности компьютерной томографии (КТ) у пациентов с подозрением на ишемический инсульт, которым может помочь тромболитическая терапия.

Хвонг В.И., Ботс М.Л., Селвараджа С., Каппелле Л.Дж., Абдул Азиз З., Сидек Н.Н., Ваартьес И. Хвонг В.Ю. и др. ПЛОС Один. 2016 21 октября; 11 (10): e0165330. doi: 10.1371/journal.pone.0165330. Электронная коллекция 2016. ПЛОС Один. 2016. PMID: 27768752 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
использованная литература
- Клин Нейрофармакол. 1990;13 Приложение 3:S26-33 — пабмед
- Br Med J (Clin Res Ed). 1985 14 декабря; 291 (6510): 1675-7 — пабмед
- Инсульт.
 1981 май-июнь;12(3):288-93
—
пабмед
1981 май-июнь;12(3):288-93
—
пабмед
- Инсульт.
- Postgrad Med J. 1980 Sep; 56 (659): 629-32 — пабмед
- J Neurol Sci. 1968 июль-август;7(1):83-95 — пабмед
термины MeSH
- 1
Прогнозирование афазии при инсультах.
 Инсульты могут возникнуть, когда чья-то кровь… | Джозеф Цзя | Прогнозирование афазии при инсультах
Инсульты могут возникнуть, когда чья-то кровь… | Джозеф Цзя | Прогнозирование афазии при инсультахРезюме:
Инсульты могут возникать, когда у кого-то закупориваются кровеносные сосуды и транспортируемые питательные вещества и кислород не достигают головного мозга. При инсульте клетки мозга не получают необходимых им питательных веществ и начинают умирать [3]. Это может вызвать различные побочные эффекты после инсульта. В этом исследовании мы пытаемся предсказать возможность одного типа побочного эффекта после инсульта, афазии, используя методы машинного обучения (ML). Используя данные исследования повреждения головного мозга после инсульта и того, какие последствия были у пациентов после инсульта, мы обучили модель предсказывать, может ли человек иметь афазию, исходя из того, где было его поражение, насколько оно было большим, как давно. их инсульт был и некоторые другие факторы. Мы оценили несколько методов классификации и обнаружили, что использование линейного дискриминантного анализа было наиболее точным прогнозом, когда мы использовали возраст, пол, местоположение поражения, объем поражения и многое другое. С помощью линейного дискриминантного анализа мы смогли получить 91% общая прогностическая частота пациентов с афазией или без нее после перенесенного инсульта.
С помощью линейного дискриминантного анализа мы смогли получить 91% общая прогностическая частота пациентов с афазией или без нее после перенесенного инсульта.
Введение:
Несмотря на то, что инсульты чаще всего случаются у пожилых людей, все еще существует большая группа молодых пациентов, перенесших инсульт. Молодые люди также подвержены риску, и в нашем наборе данных было почти 15% пациентов в возрасте 50 лет и моложе. В 2017 году CDC опубликовал данные, показывающие, что примерно 795 000 человек в США ежегодно переносят инсульт [2]. По данным из США, каждые 40 секунд у человека случается инсульт, а каждые 4 минуты в США от инсульта умирает человек. Инсульт является одной из основных причин смерти в США [2,3]. Важно понимать, что это может причинить вашему телу, особенно вашему мозгу. Инсульт может привести к множеству побочных эффектов.
В этом исследовании мы сосредоточились на побочном эффекте инсульта, афазии. Люди могут испытывать афазию, когда участки их мозга, ответственные за речь, повреждены, возможно, в результате инсульта или травмы головы.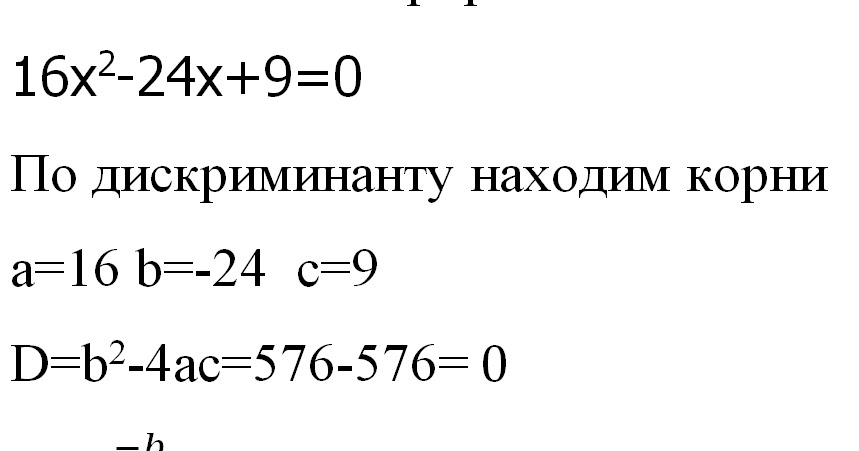 Когда это произойдет, человек будет бороться с пониманием и выражением языков, что повлияет на его способности к чтению и письму [4]. Мы построили модель машинного обучения, чтобы предсказать, будет ли у человека, перенесшего инсульт, афазия или нет. Чтобы достичь этого, модель ML изучила различия между наличием афазии и отсутствием афазии. Для обучения требуется достаточно данных, чтобы сформулировать закономерность, чтобы можно было делать правильные прогнозы о том, какие дефекты, особенно афазия, могут возникнуть у человека в результате инсульта. Также важно подчеркнуть, что афазия — не единственное последствие инсульта, и что мы выбрали ее, потому что она меняет нашу жизнь и заставляет людей вокруг нас адаптироваться.
Когда это произойдет, человек будет бороться с пониманием и выражением языков, что повлияет на его способности к чтению и письму [4]. Мы построили модель машинного обучения, чтобы предсказать, будет ли у человека, перенесшего инсульт, афазия или нет. Чтобы достичь этого, модель ML изучила различия между наличием афазии и отсутствием афазии. Для обучения требуется достаточно данных, чтобы сформулировать закономерность, чтобы можно было делать правильные прогнозы о том, какие дефекты, особенно афазия, могут возникнуть у человека в результате инсульта. Также важно подчеркнуть, что афазия — не единственное последствие инсульта, и что мы выбрали ее, потому что она меняет нашу жизнь и заставляет людей вокруг нас адаптироваться.
Метод:
Мы построили модель машинного обучения, используя данные отдельных пациентов с сайта doi.org[1], в котором проводился эксперимент на людях, ранее перенесших инсульт. В ходе исследования выяснилось, какие типы дефектов были у людей, и одним из дефектов, на который они проверялись, была афазия [1]. Мы разделили данные на две группы: 75% — обучающие данные и 25% — тестовые данные. Чтобы модель хорошо обучалась, нам нужно было определить важные признаки, которые позволили бы нам максимально точно прогнозировать афазию у пациентов. На основании таблицы данных, приведенной в этом источнике, мы использовали 10 признаков: возраст, пол, фаза, тип поражения, локализация поражения, площадь поражения, время после инсульта, FM A, FM B+C и FM Sensation.
Мы разделили данные на две группы: 75% — обучающие данные и 25% — тестовые данные. Чтобы модель хорошо обучалась, нам нужно было определить важные признаки, которые позволили бы нам максимально точно прогнозировать афазию у пациентов. На основании таблицы данных, приведенной в этом источнике, мы использовали 10 признаков: возраст, пол, фаза, тип поражения, локализация поражения, площадь поражения, время после инсульта, FM A, FM B+C и FM Sensation.
Для признаков с ограниченным числом значений нам нужно было иметь достаточно данных для каждого отдельного значения, чтобы модель могла эффективно обучаться. Для некоторых функций мы удалили значения, которые содержат очень мало данных. Примером удаленных данных была базилярная артерия левого полушария для места поражения L-BA, поскольку это место поражения было только у одного человека. Если такие данные использовались для обучения модели, они могут быть отброшены, поскольку это уникальный случай, что может сделать его более неточным. Это позволило модели сосредоточиться на случаях с достаточно богатыми данными.
Это позволило модели сосредоточиться на случаях с достаточно богатыми данными.
Мы протестировали несколько различных методов классификации, чтобы определить наилучший метод для успешной прогностической модели. Методы классификации, которые мы тестировали, включали классификатор логистической регрессии, классификатор дерева решений, классификаторы k-ближайших соседей, линейный дискриминантный анализ, гауссовский наивный байесовский классификатор и классификаторы опорных векторов [5]. Мы заметили, что некоторые классификаторы были более эффективными, чем другие, благодаря используемым функциям. Для модели мы хотим, чтобы она имела высокую точность как для положительных, так и для отрицательных случаев. Однако мы вряд ли можем добиться того, чтобы оба были высокими из-за ложных прогнозов. Интересно, что мы заметили, что гауссовский классификатор имеет 100% точность для отрицательных случаев, но очень низкую точность для положительных случаев. Это означает, что он выберет, что у пациента афазия, только если он будет очень уверен, но в противном случае он всегда будет говорить, что у пациента нет афазии. Это могло бы гарантировать 100% отзыв для людей с афазией, при этом стоимость отзыва всего 65% для людей без афазии. Это показало, что гауссиан не лучше всего подходил для метода классификации, потому что модели было нечему учиться в разных случаях, если она всегда выбирала один результат, если не была полностью уверена в другом. Когда дело дошло до выбора классификатора, который мы собирались использовать, мы рассмотрели, какой тип точности мы хотим, чтобы модель имела. Мы рассмотрели три из них: более высокая точность положительного отзыва и отрицательная точность, равные показатели точности и отзыва, а также высокая точность отрицательного отзыва и точность положительной точности. У каждого из этих типов были свои преимущества, но мы решили иметь равные, высокие показатели точности, а отзыв был лучшим вариантом, поскольку он позволял повысить общую точность. Единственным недостатком этого варианта является то, что прогноз может быть неверным независимо от того, какой вариант они выбирают чаще по сравнению с другими, более консервативными подходами.
Это могло бы гарантировать 100% отзыв для людей с афазией, при этом стоимость отзыва всего 65% для людей без афазии. Это показало, что гауссиан не лучше всего подходил для метода классификации, потому что модели было нечему учиться в разных случаях, если она всегда выбирала один результат, если не была полностью уверена в другом. Когда дело дошло до выбора классификатора, который мы собирались использовать, мы рассмотрели, какой тип точности мы хотим, чтобы модель имела. Мы рассмотрели три из них: более высокая точность положительного отзыва и отрицательная точность, равные показатели точности и отзыва, а также высокая точность отрицательного отзыва и точность положительной точности. У каждого из этих типов были свои преимущества, но мы решили иметь равные, высокие показатели точности, а отзыв был лучшим вариантом, поскольку он позволял повысить общую точность. Единственным недостатком этого варианта является то, что прогноз может быть неверным независимо от того, какой вариант они выбирают чаще по сравнению с другими, более консервативными подходами. Мы также заметили, что модель может переобучиться на основе обучающих данных, но она плохо предсказывает использование тестовых данных. Модель дерева решений достигла 100% точности на обучающих данных, но только 82% на тестовых данных. При значительном сокращении набора тестовых данных мы считаем, что модель подходит. Основываясь на нашей оценке производительности как на обучающих данных, так и на тестовых данных, лучшим методом классификации является линейный дискриминантный анализ.
Мы также заметили, что модель может переобучиться на основе обучающих данных, но она плохо предсказывает использование тестовых данных. Модель дерева решений достигла 100% точности на обучающих данных, но только 82% на тестовых данных. При значительном сокращении набора тестовых данных мы считаем, что модель подходит. Основываясь на нашей оценке производительности как на обучающих данных, так и на тестовых данных, лучшим методом классификации является линейный дискриминантный анализ.
Для модели мы хотим использовать самые эффективные функции. Мы проверили, какую функцию мы могли бы удалить без существенного изменения общей точности. Тестирование метода классификации также позволит нам проверить функции, поскольку мы сможем увидеть изменения неточности различных методов, когда мы изменим, какие функции были включены. После того, как мы решили использовать линейный дискриминантный анализ, поскольку он был наиболее точным, мы протестировали модель, удалив некоторые признаки. Мы обнаружили, что скорость прогнозирования значительно изменилась, когда мы убрали какую-либо функцию. Пол и возраст являются хорошими признаками для включения, потому что они могут помочь классифицировать пациентов, поскольку они являются ограниченными ответами на пол, а возраст полезен для понимания того, в какой возрастной группе могут быть самые тяжелые поражения. Площадь поражения и размер поражения важны, потому что они могут изменить результаты того, какие эффекты будут испытывать люди. Время после инсульта также важно, потому что чем дольше время после инсульта, тем больше вероятность того, что у пациента будет время либо ухудшить афазию, либо, возможно, успеть оправиться от нее. Остальные функции — это тесты, которые проводят пациенты, которые могут помочь определить, какие у них побочные эффекты. Они могли бы давать тесты для проверки языка, чтобы увидеть, есть ли у пациентов афазия или нет.
Пол и возраст являются хорошими признаками для включения, потому что они могут помочь классифицировать пациентов, поскольку они являются ограниченными ответами на пол, а возраст полезен для понимания того, в какой возрастной группе могут быть самые тяжелые поражения. Площадь поражения и размер поражения важны, потому что они могут изменить результаты того, какие эффекты будут испытывать люди. Время после инсульта также важно, потому что чем дольше время после инсульта, тем больше вероятность того, что у пациента будет время либо ухудшить афазию, либо, возможно, успеть оправиться от нее. Остальные функции — это тесты, которые проводят пациенты, которые могут помочь определить, какие у них побочные эффекты. Они могли бы давать тесты для проверки языка, чтобы увидеть, есть ли у пациентов афазия или нет.
Линейный дискриминантный анализ — это метод классификации, использующий данные для создания формулы. Мы бы использовали эту формулу и проверили ее на конкретных данных в нашем наборе данных, чтобы убедиться, что программа так же надежна.
Результат:
Мы не выбрали линейный дискриминантный анализ случайно, а вместо этого протестировали каждый из типов классификации, используя обучающий набор данных. Прогностические показатели точности для 75% данных для обучения показаны ниже:
В этой таблице показаны точность, полнота и общая точность путем случайного разделения набора данных на обучающую и тестовую выборки. Точность определяется ответами модели и тем, насколько они точны по сравнению с фактическими результатами, в то время как отзыв определяется фактическими результатами и тем, насколько точны эти ответы на основе ответов, предсказанных моделью. Поскольку наша цель состояла в том, чтобы предсказать, есть ли у кого-то афазия после перенесенного инсульта, было бы лучше, если бы и полнота, и точность были высокими как для положительных, так и для отрицательных случаев. Исходя из этих условий, результаты тестирования показывают, что линейный дискриминантный анализ является лучшим. Это потому, что точность и отзыв равны 90 %, 82 %, 91 % и 95 %, что соответствует высоким или относительно высоким показателям точности. Этот метод классификации также имеет самую высокую общую точность 91%, а разница между линейным дискриминантным анализом и вторыми по точности методами, такими как K-ближайшие соседи и гауссовский наивный байесовский анализ, составляет 6%.
Это потому, что точность и отзыв равны 90 %, 82 %, 91 % и 95 %, что соответствует высоким или относительно высоким показателям точности. Этот метод классификации также имеет самую высокую общую точность 91%, а разница между линейным дискриминантным анализом и вторыми по точности методами, такими как K-ближайшие соседи и гауссовский наивный байесовский анализ, составляет 6%.
После использования 75% данных для обучения машины созданию формулы, которая будет использоваться при вводе данных пользователем. Как только это было завершено, мы использовали оставшиеся данные для тестирования программы, что составило 25% данных. Ниже приведены результаты тестовых данных:
Вот несколько примеров из тестовых данных в таблице ниже с помощью линейного дискриминантного анализа:
Как видите, большинство результатов точны. Однако в формуле прогнозирования все еще есть некоторые ошибки, связанные, скорее всего, с меньшим объемом данных. При меньшем размере данных в формуле будет меньше данных для создания формулы, поэтому уравнение будет не таким точным, как формула, созданная с тысячами наборов данных.
Будущая работа:
В этой работе использовался ограниченный набор данных из 130 образцов. Мы также рассмотрели подмножество случаев, поскольку в некоторых случаях имеется менее 5 образцов. Поиск большего количества данных и, возможно, более разнообразного и сбалансированного набора данных поможет улучшить результат модели машинного обучения и охватить все возможные случаи. Мы считаем, что причина, по которой мы не можем удалить какие-либо функции, также может быть связана с ограниченными данными, которые у нас есть в этом исследовании. Получив больший сбалансированный набор данных, мы могли протестировать больше комбинаций функций, чтобы увидеть, можем ли мы уменьшить количество функций без существенного изменения точности прогноза модели. Наконец, мы считаем, что этот метод может быть расширен для других эффектов инсульта, как только будет получен хороший набор данных для обучения модели.
Резюме:
В этом исследовании мы использовали набор данных эксперимента по проверке афазии у пациентов, ранее перенесших инсульт. Мы использовали данные пациентов, такие как площадь поражения или размер поражения, чтобы позволить программе определить, у каких пациентов была афазия, а у каких нет. Мы использовали линейный дискриминантный анализ, потому что он был наиболее точным в нашем тестировании среди 6 различных методов классификатора. Используя самый точный метод в целом, мы смогли предсказать, есть ли у некоторых пациентов афазия с 9точность 1%. Однако одна из проблем этой модели заключается в том, что она требует большого количества входных данных, которые могут быть не у всех, поэтому эта модель может быть полезна только для ограниченной группы людей. Еще одной проблемой был ограниченный объем данных. В целом, мы смогли создать модель машинного обучения с хорошей степенью точности и протестировали ее с конкретными индивидуальными данными об отдельных пациентах, чтобы действительно увидеть, насколько хорошо работает наш предиктор.
Мы использовали данные пациентов, такие как площадь поражения или размер поражения, чтобы позволить программе определить, у каких пациентов была афазия, а у каких нет. Мы использовали линейный дискриминантный анализ, потому что он был наиболее точным в нашем тестировании среди 6 различных методов классификатора. Используя самый точный метод в целом, мы смогли предсказать, есть ли у некоторых пациентов афазия с 9точность 1%. Однако одна из проблем этой модели заключается в том, что она требует большого количества входных данных, которые могут быть не у всех, поэтому эта модель может быть полезна только для ограниченной группы людей. Еще одной проблемой был ограниченный объем данных. В целом, мы смогли создать модель машинного обучения с хорошей степенью точности и протестировали ее с конкретными индивидуальными данными об отдельных пациентах, чтобы действительно увидеть, насколько хорошо работает наш предиктор.
Ссылки:
[1]Frenkel-Toledo S, Fridberg G, Ofir S, Bartur G, Lowenthal-Raz J, et al. (2019) Влияние локализации поражения на функциональное восстановление гемипаретизированной верхней конечности. PLOS ONE 14(7): e0219738. https://doi.org/10.1371/journal.pone.0219738
(2019) Влияние локализации поражения на функциональное восстановление гемипаретизированной верхней конечности. PLOS ONE 14(7): e0219738. https://doi.org/10.1371/journal.pone.0219738
[2] Бенджамин, Эмилия Дж. и Майкл Дж. Блаха и др. «Тираж». CDC Stacks , 25 января
2017, stacks.cdc.gov/view/cdc/45425. По состоянию на 26 декабря 2020 г.
[3] «Об инсульте». Stroke.org , Американская кардиологическая ассоциация, https://www.stroke.org/en/about-stroke
[4] «Афазия». Национальный институт глухоты и других коммуникативных расстройств ,
Министерство здравоохранения и социальных служб США, декабрь 2015 г., www.nidcd.nih.gov/
health/aphasia. По состоянию на 26 декабря 2020 г.
[5] Ли, Сьюзен. «Решение простой задачи классификации с помощью Python — Fruits
Lovers’ Edition». Towards Data Science , Medium, 4 декабря 2017 г.,
по направлению к datascience.com/
решение-простой-проблемы-классификации-с-любителями-плодов-питонов-издание-d20ab6b
071d2. По состоянию на 26 декабря 2020 г.
По состоянию на 26 декабря 2020 г.
[6] http://jmlr.csail.mit.edu/papers/v12/pedregosa11a.html, Pedregosa и др. , JMLR 12, стр. 2825–2830, 2011.
Приложения Gale — Технические трудности
Приложение, к которому вы пытаетесь получить доступ, в настоящее время недоступно. Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд.
Если проблемы с доступом сохраняются, обратитесь за помощью в наш отдел технической поддержки по телефону 1-800-877-4253. Еще раз спасибо, что выбрали Gale, обучающую компанию Cengage.
org.springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является com.zeroc.Ice.UnknownException
unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0
в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64)
в java. base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.
base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher. getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.
getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44)
на com.gale.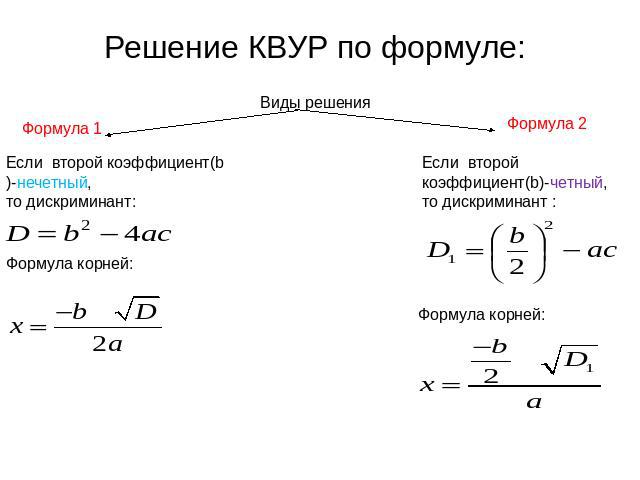 blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal.
blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
в com.gale.blis.auth.AuthorizationService._iceD_authorize(AuthorizationService.java:97)
в com.gale.blis.auth.AuthorizationService._iceDispatch(AuthorizationService.java:406)
в com.zeroc.IceInternal.Incoming.invoke(Incoming.java:221)
в com.zeroc.Ice.ConnectionI.invokeAll(ConnectionI.java:2706)
на com.zeroc.Ice.ConnectionI.dispatch(ConnectionI.java:1292)
в com.zeroc.Ice.ConnectionI.message(ConnectionI.java:1203)
в com.zeroc.IceInternal. ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation.
ThreadPool.run(ThreadPool.java:412)
в com.zeroc.IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в com.zeroc.IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:781)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:348)
org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:310)
org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71)
org.springframework.aop.framework.ReflectiveMethodInvocation. proceed(ReflectiveMethodInvocation.java:186)
org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController.
proceed(ReflectiveMethodInvocation.java:186)
org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:215)
com.sun.proxy.$Proxy151.authorize(Неизвестный источник)
com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61)
com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65)
com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57)
com.gale.apps.controllers.DocumentController. redirectToDocument(DocumentController.java:22)
jdk.internal.reflect.GeneratedMethodAccessor245.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.
redirectToDocument(DocumentController.java:22)
jdk.internal.reflect.GeneratedMethodAccessor245.invoke (неизвестный источник)
java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43)
java.base/java.lang.reflect.Method.invoke(Method.java:566)
org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:205)
org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:150)
org.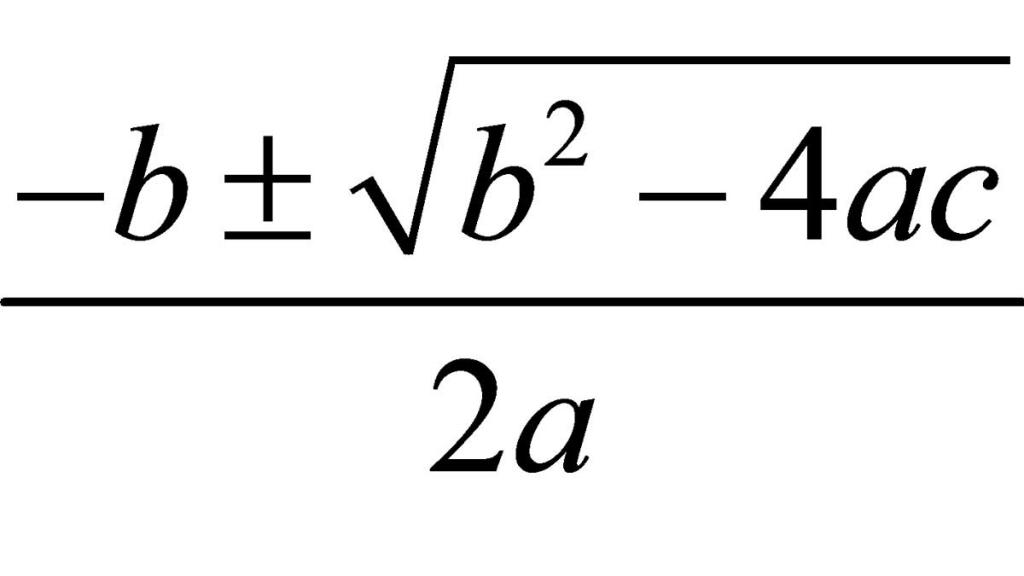 springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org.
springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:117)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895)
org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:808)
org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter.java:87)
org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1067)
org. springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain.
springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:963)
org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:1006)
org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:898)
javax.servlet.http.HttpServlet.service(HttpServlet.java:626)
org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:883)
javax.servlet.http.HttpServlet.service(HttpServlet.java:733)
org.apache.catalina.core.ApplicationFilterChain. internalDoFilter(ApplicationFilterChain.java:227)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org.
internalDoFilter(ApplicationFilterChain.java:227)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126)
org. apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:67)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java:100)
org. springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com.
springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
com. gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.
gale.common.http.filter.SecurityHeaderFilter.doFilterInternal(SecurityHeaderFilter.java:29)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:102)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org. apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org.
apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.owasp.validation.GaleParameterValidationFilter.doFilterInternal(GaleParameterValidationFilter.java:97)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:126)
org. springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:64)
org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:101)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:119)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.
springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:93)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal (WebMvcMetricsFilter.java:96)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org. apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.
apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:201)
org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:117)
org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189)
org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162)
org. apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org.
apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202)
org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97)
org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542)
org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143)
org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92)
org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687)
org. apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.
apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78)
org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357)
org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374)
org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65)
org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893)
org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707)
org.apache.



 : три или более векторов, лежащих В ОДНОЙ ИЛИ ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯХ, называются КОМПЛАНАРНЫМИ.
: три или более векторов, лежащих В ОДНОЙ ИЛИ ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЯХ, называются КОМПЛАНАРНЫМИ.
 d – произвольный вектор. Отложим все векторы от точки О: а=ОА и т д до Проведём l1=OA, l2=OB, l3=OC. Построим параллелепипед с такими тремя рёбрами, а D – вершина. Пусть A1 B1 C1 – вершины, лежащие на l1 l2 l3. Проводим OD1 – диагональ.
d – произвольный вектор. Отложим все векторы от точки О: а=ОА и т д до Проведём l1=OA, l2=OB, l3=OC. Построим параллелепипед с такими тремя рёбрами, а D – вершина. Пусть A1 B1 C1 – вершины, лежащие на l1 l2 l3. Проводим OD1 – диагональ.

 Вектор OM=r
Вектор OM=r
 2(n*n)=0 делим на p
2(n*n)=0 делим на p


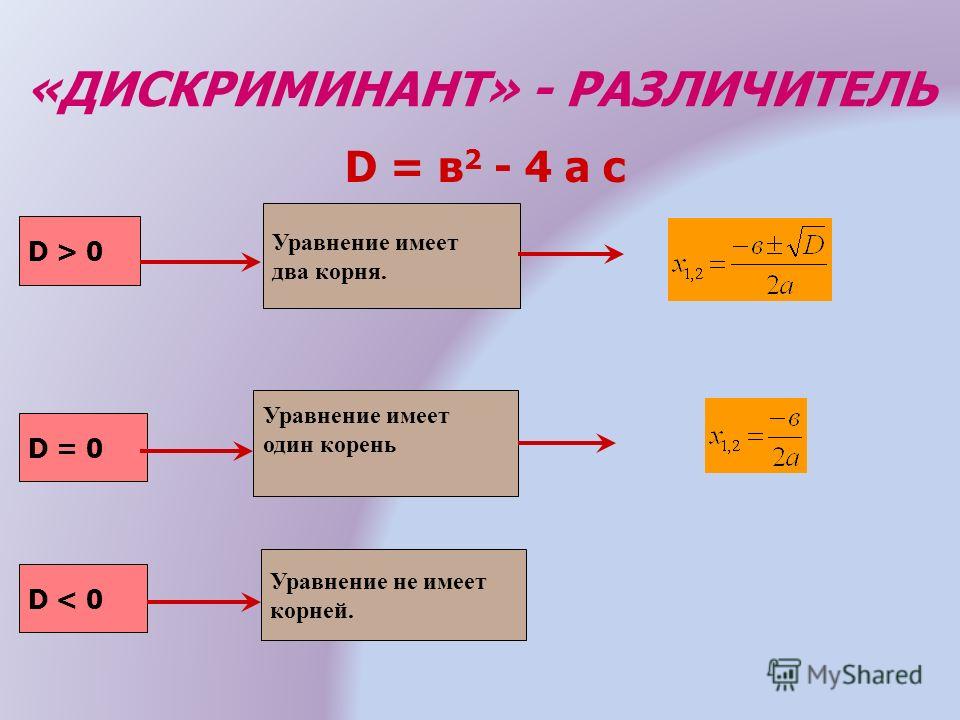
 : Точка O` называется ЦЕНТРОМ КРИВОЙ 2 ПОРЯДКА, если она является её центром симметрии.
: Точка O` называется ЦЕНТРОМ КРИВОЙ 2 ПОРЯДКА, если она является её центром симметрии.

 Тогда её координаты должны удовлетворять уравнению прямой OM:
Тогда её координаты должны удовлетворять уравнению прямой OM: 2), и при этом нигде более координаты x и y в уравнение не входят, то можно сделать вывод, что это поверхность вращения вокруг Oz.
2), и при этом нигде более координаты x и y в уравнение не входят, то можно сделать вывод, что это поверхность вращения вокруг Oz.



 Постоянная диагностическая проблема.
Постоянная диагностическая проблема.


 1981 май-июнь;12(3):288-93
—
пабмед
1981 май-июнь;12(3):288-93
—
пабмед