Основания одинаковые а степени разные: Свойства степеней, действия со степенями

Содержание

Сила степеней числа 10 « Папа Карп

Чтобы спокойно и качественно изучать физику и химию, надо владеть действиями со степенями числа 10 – уверенно и во всех вариациях.

При решении задачек по физике (даже самых начальных и самых простых) любое число удобно представлять в стандартном виде. То есть в виде “число от 1 до 10 умножить на 10 в какой-то степени”. Причем степень числа 10 может быть и положительной, и отрицательной.

Необходимо уметь действовать с числами, записанными таким образом.

Поэтому к началу изучения физики в 7 классе очень желательно, чтобы ученик полностью освоил все навыки, касающиеся степеней числа 10.

Однако базовая школьная программа по математике не полностью это обеспечивает, к сожалению.

Мой опыт преподавания физики показывает, что весьма целесообразно некоторые недостающие моменты (например, отрицательные степени числа 10 и действия с ними) изучить пораньше. Да и все прочие нюансы данной темы хорошо бы повторить и доработать, если они слегка подзабылись.

Важно видеть цель: мы должны дать ученику в руки надежный математический инструмент для расчетов по сложным физическим и химическим формулам. Это именно математический аппарат. Но нужен он в основном как раз в физике и в химии.

В данной статье я кратко перечислю то, что хорошо бы знать про степени числа 10 к самому началу изучения физики.

Разумеется, моя цель – лишь показать общую схему. Если вам понадобится более подробная информация, то ее легко найти в любых школьных учебниках.

Попадая в стихию физики (а затем и химии), школьники вынуждены оперировать с числами в огромном диапазоне величин: от крошечных размеров атомов до межзвездных расстояний, от массы электрона до массы Юпитера или Солнца… Это очень отличается от привычных масштабов, на которых обычно в основном строится изучение математики.

И вот тут-то и пригождаются положительные и отрицательные степени числа 10. В науке о природе без них просто никак.

Запись чисел в стандартном виде – великолепное изобретение человечества! Но оно, разумеется, используется преимущественно в науке и в технике, а не в обычной нашей жизни. Поэтому надо специально приучить школьника к такому стилю математических вычислений. К нему необходимо привыкнуть.

Для начала как следует разберитесь с положительными степенями числа 10. Это проще и понятнее. Это уже знакомо с начальных классов. Какова положительная степень числа 10 – столько ноликов и приписываем к единичке. Умножение и деление таких чисел не вызывает труда.

Существуют простые правила действий со степенями. Я их нарисовал здесь на картинке конкретно для случая, когда основание степени – число 10. Разумеется, для любого другого основания степени правила будут точно те же самые. Но в физике нас интересует обычно именно 10.

Когда мы сталкиваемся с физическими расчетами, где числа записаны с использованием степеней числа 10, то можно использовать все правила действий со степенями и правило сокращения дробей.

Фактически, обычно удобнее отдельно разбираться со степенями числа 10, а отдельно – со всеми другими числами в выражении. И лишь в конце соединить это в один ответ.

Вот я захотел вычислить плотность объекта. Исходно мне известны его масса и объем. Посмотрите, как просто получилось посчитать по формуле!

Теперь добавим и отрицательные степени числа 10.

Надо хорошо понять определение: что такое отрицательная степень.

Посмотрите на картинку ниже.

Я проиллюстрировал там общий принцип: число в отрицательной степени – это единица делить на то же самое число в такой же степени, но только показатель степени уже без знака “минус”.

Так просто договорились – что такое отрицательная степень. И это потрясающе удобно!

Конечно, само понятие отрицательной степени поначалу может вызвать некоторое недоумение… Возможно, потребуется поразмышлять и посмотреть, как такая штука работает – на самых простых примерах…

Возвращаемся к формулам по физике.

Теперь будем использовать и отрицательные степени числа 10.

Все правила действий со степенями остались те же самые. Мы так же складываем или вычитаем показатели степени при умножении или делении. И все остальные правила сохраняются.

Требуется некоторая практика, конечно. Но если понимать принцип, то сложностей особых нет.

Складывая положительные и отрицательные показатели степени, мы действуем точно так же, как и при сложении положительных и отрицательных чисел.

Поглядите, как легко вычисляется масса объекта, если известны его плотность и объем.

Особенная практическая фишка: “перебрасывать” 10 в какой-то степени через дробную черту – снизу вверх или сверху вниз.

Посмотрите на картинке, как 10 в отрицательной степени “перебирается” из-под дробной черты вверх. И после этого считать делается уже совсем просто.

Важно уловить принцип: при таком “перебросе” через дробную черту знак показателя степени у числа 10 меняется на противоположный. Для практических расчетов по формулам очень удобный прием!

Кстати об удобстве расчетов… Не всегда имеет смысл переводить числа именно в стандартный вид. Иногда проще использовать более свободное сочетание степеней числа 10 и обычных чисел.

Важно приучиться действовать именно так, как наиболее индивидуально удобно, как меньше шансов запутаться и ошибиться.

В физике и в химии вообще главное – получить правильный ответ. А как конкретно мы вычисляли – это наше дело.

Здесь еще надо уверенно владеть навыком переноса десятичной запятой.

Казалось бы, такая простая штука…

Скажем, расстояние в 6300 метров мы хотим записать в километрах почему-то. Ясно, что это будет 6,3 км. А наоборот? Снова получим 6300 м.

Или, к примеру, напряжение 0,00065 В – это сколько будет в милливольтах? Надо перенести запятую на три знака вправо. Получится 0,65 мВ.

Такие переходы используются в физике на каждом шагу. И у школьника не должно быть ну абсолютно никаких проблем с тем, чтобы перемещать запятую вправо или влево на нужное количество знаков.

Само собой, когда мы встречаем числа типа 0,0001 или 10000000, то их сразу же удобнее представить в виде степеней числа 10. И далее во всех расчетах действовать по стандартной процедуре со степенями.

Все эти мучительные размышления, куда и на сколько знаков надо перенести запятую при умножении или делении на 0,0000001… Они нам теперь не нужны! Мы умеем представлять все степени числа 10 именно в виде степеней, а не десятичных дробей. Почти всегда это значительно удобнее!

Отдельный вопрос состоит в том, когда надо вообще начинать говорить с детьми о степенях числа 10…

Мне кажется, что уже в начальной школе сие вполне уместно.

Ведь, по сути, это просто еще один способ записи чисел. Особенно легко его понять для положительных степеней числа 10. Скажем, умножить миллиметр на миллион! Сколько это будет?

С другой стороны, можно попробовать разделить километр на миллион равных частей… Почему бы не представить такую процедуру? Так что и отрицательные степени числа 10 тоже легко вводить на самом элементарном уровне.

Мой личный опыт преподавания показывает, что маленькие дети с удовольствием разбираются с большими числами. Это даже интереснее, чем возиться со сложением и вычитанием в пределах 100. Представляете: целый миллиард разделить пополам! И узнать, сколько это будет!

Но самое главное – к началу изучения физики в 7 классе разобраться со всеми нюансами данной темы!

Тогда изучение физики и химии будет значительно более удобным.

Хотя бы вот даже взять перевод единиц измерения физических величин друг в друга… Насколько проще это делать, используя степени числа 10!

Немного практики – и ученик получает ключ ко всему диапазону масштабов: от ангстремов и нанометров до световых лет и парсеков, от постоянной Планка до числа Авогадро…

Посмотрите, например, как изящно происходит для льда переход от одних единиц плотности к другим.

Итак, овладение почти магической математической силой степеней числа 10 – это надежное подспорье для изучения физики и химии. Данный навык пригодится с 7 класса и до 11 класса включительно.

Удобно, что вся эта тема – проста по сути. Ее легко понимать и осваивать. Важно лишь довести знания до устойчивого системного уровня. Чтобы применять при необходимости, не задумываясь особо и не путаясь по мелочам. Как таблицу умножения и действия столбиком.

И просто по жизни весьма полезно ориентироваться в данном вопросе. Сила степеней числа 10 – один из краеугольных камней нашей интеллектуальной культуры.

что это? Все формулы. Простейшие уравнения и неравенства

Что такое логарифм

Свойства логарифма

Логарифмические уравнения

Логарифмические неравенства

Сейчас речь пойдет о трех страшных буквах: l o g.
Существовать в нашем бытии они просто так не могут. Обязательно должен быть какой-нибудь индекс — число снизу (основание логарифма) и число после букв (аргумент логарифма).

Прежде, чем мы перейдем к тому, что такое логарифм, решим парочку подводящих примеров.

Чтобы справиться с этим примером, мы проговариваем в голове: какое число нужно дважды (т.к. корень квадратный) умножить само на себя, чтобы получить 81.

А этот пример можно решить по алгоритму (решения показательных уравнений), а можно так же провести разговор с самим собой (главное не вслух, я считаю это нормально, но кого-то вы можете напугать разговором с самим собой): сколько раз нужно число 3 умножить само на себя, чтобы получить 27. Постепенным перемножением мы дойдем до ответа.

Тогда, если дело касается логарифма:

можно сказать так: в какую степень нужно возвести 3 (число снизу — основание логарифма), чтобы получить 27 (число слева — аргумент логарифма). Не напоминает выше стоящий пример?

На самом деле в этом и заключается основная формула (определение логарифма):

Логарифм говорит нам (кому-то кричит): логарифм числа «b» по основанию «a» равняется числу «c». Тогда без логарифма это можно сформулировать так: чтобы получить число «b», требуется число «a» возвести в степень «c». Логарифм — это действие, обратное возведению в степень.

У отца log есть два родных сына: ln и lg. Так же, как сыновья отличаются возрастом (мы говорим о максимальной точности), так и эти логарифмы отличаются основанием (числовым индексом снизу).

Данные логарифмы придумали для упрощения записи. На самом деле в прикладной математики именно логарифмы по такому основанию встречаются чаще всех остальных. А мы все в глубине души народ ленивый, так что почему бы себе жизнь не упростить?

Что нужно запомнить: ln — это обычный логарифм только по основанию e ( e — это число Эйлера, e = 2,7182…, мой номер телефона, кстати, — это последние 11 цифр числа Эйлера, так что буду ждать звонка).

А lg — это обычный логарифм по основанию 10 (10ая система — это система счисления, в которой мы живем, столько пальцев на руках у среднего человека. В общем 10 — это как 9, только на 1 больше).

Как мы не можем существовать без еды, воды, интернета… Так и логарифм не представляет свое существование без ОДЗ.

Всегда, когда существует логарифм, должно быть:

«Почему это так?» — это первый вопрос, который я предоставляю тебе. Советую начать с того, что логарифм — это обратное действие от возведения в степень.

А теперь разберем теорию на практике:

В какую степень нужно возвести два (число в основании), чтобы получить шестнадцать (аргумент логарифма).

Два нужно четыре раза умножить само на себя, чтобы получить 16.

Ответ: 4.

lg — это логарифм по основанию 10. 10 нужно 3 раза умножить само на себя, чтобы получить 1000.

А теперь посложнее, перейдем по определнию к показательному уравнению :

Следующий пример поможет нам узнать первую формулу логарифмов:

Преобразуем выражение по определению логарифма и получим показательное уравнение. Единица — это же любое значение в нулевой степени?

Тогда можно сделать вывод, что при любом основании и аргументе логарифма, равном 1, все эти логарифмы будут равны нулю.

Нетрудно тогда понять, что есть еще одно следствие:

В какую степень нужно возвести 2, чтобы получить 2? Напряжем все свои извилины и получим — один!

Дальше будут формулы, которые я позволю себе не выводить, чтобы не испугать неискушенных в математике читателей.

Хотя мой вам совет: отследить, откуда эта формула появилась. У логарифмов самое главное помнить, что логарифм — это действие, обратное возведению в степень.

Основное логарифмическое тождество:

В какую степень нужно возвести 3, чтобы получить 9? Значит, логарифм в показателе степени равен двум.

Это единственная формула, где логарифм в показатели степени. Видишь логарифм в степени? Тебе поможет только эта формула.

Еще примерчик, двойка перед логарифмом никак не влияет, формула все так же работает:

А вот квадрат в логарифме тоже быть может, только лучше сначала разложить:

Дальше с этим ничего сделать не сможем.

Дальнейшие формулы тоже уникальны, это тебе не косинус двойного угла.

Видим сложение логарифмов, выпускаем эту формулы:

А вот примерчик, чтобы порадовать тебя этой формулой, только наоборот:

Видим разность логарифмов, выпускаем эту формулы:

А теперь сразу сумма и разность. По отдельности логарифмы не найти, но вместе они и мы сила:

Теперь посмотрим на степени у аргмента логарифма:

Пример:

А в основании тоже можно? Нужно!

Минус два — это степень у основания:

А все вместе можно? Конечно, логарифмы — это такая свобода:

А здесь нужно будет соединить две формулы: 1) вынесение степени из основания и 2) разность логарифмов

С основными формулами разобрались, теперь для решения более сложных уравнений/выражений.

Формула перехода к новому основанию:

Обрати внимание, чем она отличается от разности логарифмов (4). Тут мы делим один логарифм на другой, а там деление происходит под логарифмом.

Тут все просто, разве что стоит вспомнить, что квадратный корень — это степень одна вторая.

Тут первым действием воспользуемся изучаемой формулой, а дальше каждый логарифм в виде числа, потихонечку−полегонечку.

Последняя формула, меняем местами аргумент и основание логарифма:

Используется тоже нечасто, но если ее не знаешь, то никак не выкрутишься через другие формулы.

Простенький примерчик:

Закрепим обе формулы. Используем формулу (9), после (8), а так же не забудь порадовать десятичные дроби — переведи их в обыкновенные, а они порадуют тебя. Теперь посмотрим еще на пару примеров:

Логарифм в логарифме, что может быть прекраснее? Только решенный логарифм в логарифме.

Начинаем с внутреннего:

И постепенно раскрываем каждый последующий:

После того, как с формулами разобрались, (а их всего 9! Согласись, несложно выучить?), перейдем к уравнениям.

Все логарифмические уравнения решаем по одному из двух алгоритмов.

Первый появляется из определения логарифма:

Только не забываем про ОДЗ:

Второй вариант, когда логарифм с одним основанием равен логарифму с точно таким же основнанием:

Не забываем про ОДЗ, тогда получится:

Подставив в ОДЗ x = 15, видим, что все выполняется!

Обязательно только логарифм (без всяких множителей и т.п.) с одним основанием должен быть равен другому логарифму с таким же основанием:

Здесь перед логарифмами стоят разные множители, поэтому прежде всего нужно их внести в логарифм (6 формула), а после убрать логарифмы:

Если стоят одинаковые множители, их можно сократить сразу или сократить на общий множитель:

Бывает, что с одной стороны уравнения есть сумма логарифмов (4) или обычное число, сокращать их сразу нельзя! Только после того, как приведем и левую, и правую часть к одному логарифму:

Что же касается неравенств, убирать логарифмы можно так же, как и в уравнениях, только здесь нужно внимательно смотреть на значение оснований. Если основание логарифма лежит в диапазоне 0 < a < 1 (также как в показательных неравенствах), то после зачеркивания логарифмов знак меняется на противоположный:

Если же основание а > 1, то убираем логарифмы без смены знака и дорешиваем обычное неравенство:

Вывод:

Л О Г — это не три страшные буквы, а обратное действие возведению в степень.
Хоть формул и целых девять, но они никак не пересекаются. Решая пример и ориентируясь в формулах, ты будешь однозначно выбирать необходимую формулу.
Видишь логарифм — ищи ОДЗ и решай его в первую очередь!
Решение уравнений происходит по одному из двух вариантов и больше никак.
В неравенствах главное — помнить об основании логарифма, когда зачеркиваем логарифмы.

Будь в курсе новых статеек, видео и легкого математического юмора.

Обобщающий урок по теме «Показательные уравнения и методы их решения с применением компьютерных технологий», 11-й класс

Ключевые слова: применение компьютерных технологий, углубленное изучение математики

Цели:

обобщение и систематизация знаний,
раскрытие связей и отношений в изучаемом материале,
учить применять знания при решении базовых и нестандартных задач,
подготовить учащихся к ЕГЭ.

Оборудование:

компьютер,
мультимедийный проектор,
экран,
Приложение 1 (слайдовая презентация в PowerPoint) “Методы решения показательных уравнений”

Приложение 2 (Решение уравнения типа “Три разных основания степеней” в Word)
Приложение 3 (раздаточный материал в Word для практической работы).
Приложение 4 (раздаточный материал в Word для домашнего задания).

Ход урока

1. Организационный этап

сообщение темы урока (записана на доске),
необходимость проведения обобщающего урока в 10-11 классах:

в 10 классе – после прохождения темы с целью систематизации знаний;

в 11 классе – итоговое повторение с целью подготовки к ЕГЭ.

Этап подготовки учащихся к активному усвоению знаний

Повторение

Определение.

Показательным уравнением называется уравнение, содержащее переменную в показателе степени (отвечает учащийся).

Замечание учителя. Показательные уравнения относятся к классу трансцендентных уравнений. Это труднопроизносимое название говорит о том, что такие уравнения, вообще говоря, не решаются в виде формул.

Их можно решать только приближенно численными методами на компьютерах. А как же быть с экзаменационными задачами? Вся хитрость состоит в том, что экзаменатор так составляет задачу, что она как раз допускает аналитическое решение. Иными словами, Вы можете (и должны!) проделать такие тождественные преобразования, которые сводят данное показательное уравнение к самому простому показательному уравнению. Это самое простое уравнение так и называется: простейшее показательное уравнение.

Оно решается логарифмированием.

Ситуация с решением показательного уравнения напоминает путешествие по лабиринту, который специально придуман составителем задачи. Из этих весьма общих рассуждений следуют вполне конкретные рекомендации.

Для успешного решения показательных уравнений необходимо:

1. Не только активно знать все показательные тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать лишних корней, а тем более, – не терять решений уравнения.

2. Активно знать все показательные тождества.

3. Четко, подробно и без ошибок проделывать математические преобразования уравнений (переносить слагаемые из одной части уравнения в другую, не забыв про смену знака, приводить к общему знаменателю дроби и тому подобное). Это называется математической культурой.

При этом сами выкладки должны делаться автоматически руками, а голова должна думать об общей путеводной нити решения. Делать преобразования надо как можно тщательней и подробней. Только это даст гарантию верного безошибочного решения. И помнить: небольшая арифметическая ошибка может просто создать трансцендентное уравнение, которое в принципе не решается аналитически. Выходит, Вы сбились с пути и уперлись в стенку лабиринта.

4. Знать методы решения задач (то есть знать все пути прохода по лабиринту решения). Для правильного ориентирования на каждом этапе Вам придется (сознательно или интуитивно!):

определить тип уравнения;
вспомнить соответствующий этому типу метод решения задачи.

Этап обобщения и систематизации изученного материала.

Учителем совместно с учащимися с привлечением компьютера проводится обзорное повторение всех видов показательных уравнений и методов их решения, составляется общая схема. (Используется обучающая компьютерная программа Л.Я. Боревского «Курс математики – 2000», автор презентации в PowerPoint – Т.Н. Купцова .)

Приложение 1

Рис. 1. На рисунке представлена общая схема всех типов показательных уравнений.

Как видно из этой схемы стратегия решения показательных уравнений состоит в том, чтобы привести данное показательное уравнение к уравнению, прежде всего, с одинаковыми основаниями степеней, а затем – и

с одинаковыми показателями степеней.

Получив уравнение с одинаковыми основаниями и показателями степеней, Вы заменяете эту степень на новую переменную и получаете простое алгебраическое уравнение (обычно, дробно-рациональное или квадратное) относительно этой новой переменной.

Решив это уравнение и сделав обратную замену, Вы в результате приходите к совокупности простейших показательных уравнений, которые решаются в общем виде с помощью логарифмирования.

Особняком стоят уравнения, в которых встречаются лишь произведения (частные) степеней. Воспользовавшись показательными тождествами, удается эти уравнения привести сразу к одному основанию, в частности, – к простейшему показательному уравнению.

Рассмотрим, как решается показательное уравнение с тремя разными основаниями степеней.

(Если у учителя есть обучающая компьютерная программа Л.Я. Боревского «Курс математики – 2000» , то естественно работаем с диском, если нет – можно на каждую парту сделать распечатку такого типа уравнения из нее, представленную ниже.)

Приложение 2

Рис. 2. План решения уравнения.

Рис. 3. Начало решения уравнения

Рис. 4. Окончание решения уравнения.

Выполнение практической работы

Приложение 3 (раздаточный материал в Word для практической работы).

Задание: из списка уравнений выбрать уравнения указанного типа (№ ответа занести в таблицу) и решить их (ответ занести в таблицу):

Три разных основания степеней

Два разных основания – разные показатели степени
Основания степеней – степени одного числа
Одинаковые основания – разные показатели степеней
Одинаковые основания степеней – одинаковые показатели степеней
Произведение степеней
Два разных основания степеней – одинаковые показатели
Простейшие показательные уравнения

1.
2.
3.
4.
5.
6. (
7.
8.

Фамилия
№ шага	A	B	C	D	E	F	G	H
№ соотв.типа уравнения
ответ

Выполняется попарная взаимопроверка с выставлением оценок.

Нормы оценок:

«5» – 100%
«4» – 1 ош. – 88%
2 ош. – 75%
«3» – 3 ош. – 63%
«2» – 4 ош. – 50%.

Решение нестандартного показательного уравнения

А теперь решим с вами одно из нестандартных показательных уравнений, которые необходимо научиться решать при подготовке к ЕГЭ (задание уровня С).

№218* (См. А.В. Столин. Комплексные упражнения по математике с решениями, 7-11 классы. Харьков, ИМП “Рубикон”, 1995)

Решить уравнение:

Решение:

Ответ:

Этап информации о домашнем задании

Домашнее задание.

Приложение 4

Определить тип уравнения и решить его.

1.
2.
3. 0,125
4.
5.
6.

Подведение итогов урока

Выставление оценок за урок.

Окончание урока

Для учителя
Схема ответов практической работы.
Задание: из списка уравнений выбрать уравнения указанного типа (№ ответа занести в таблицу):
Три разных основания степеней

Два разных основания – разные показатели степени

Основания степеней – степени одного числа

Одинаковые основания – разные показатели степеней

Одинаковые основания степеней – одинаковые показатели степеней

Произведение степеней

Два разных основания степеней – одинаковые показатели

Простейшие показательные уравнения

1. (произведение степеней)
2. (одинаковые основания – разные показатели степеней)
3. (три разных основания степеней)
4. (два разных основания степеней – одинаковые показатели)
5. (одинаковые основания – одинаковые показатели степеней)
6. ( (простейшее показательное уравнение)
7. (два разных основания – разные показатели степени)
8. (основания степеней – степени одного числа)

№ шага A B C D E F G H
№ соотв. типа уравнения 3 7 8 2 5 1 4 6
ответ -2; 4 -1 -0,5; 0,5 ; 0 -1 0; 2
Домашнее задание
1) (три разных основания степеней)

Ответ:

2) (два разных основания – разные показатели степени)

Ответ: х = 1,5

3) 0,125 (произведение степеней)

Ответ: х = 6

4) (одинаковые основания – разные показатели степеней)

Ответ: х = 1

5) (основания степеней – степени одного числа)

Ответ:

В зависимости от уровня подготовленности класса и, соответственно, темпа урока в оставшееся время можно познакомить учащихся с обучающей компьютерной с программой Л. Я. Боревского «Курс математики – 2000» и с её помощью рассмотреть решение показательного уравнения № 8.41. (Учитель проводит беседу с привлечением компьютера и разбор уравнения типа «Три разных основания степеней».)
Водородные связи — Вики Школы биомедицинских наук
Взято из Вики Школы биомедицинских наук
Перейти к: навигация, search
Водородная связь – это притяжение между атомом водорода и электроотрицательным атомом только с азотом (N), кислородом (O) или фтором (F) ^[1] . Водородные связи часто возникают в биологических молекулах и существуют в полярных соединениях. Типичным примером этого является вода, где существует притягивающее взаимодействие между атомами кислорода и водорода. Водородная связь — это тип межмолекулярной силы, когда водородная связь возникает между разными молекулами, или внутримолекулярная, когда связь существует между разными частями одной и той же молекулы ^[2] .
Водородная связь представляет собой нековалентную связь; они обладают гораздо более сильным притяжением, чем силы Ван-дер-Ваальса и постоянные дипольные взаимодействия, но слабее, чем ионная связь или ковалентная связь. Доказательства наличия водородных связей можно найти при сравнении температур кипения молекул водорода в группах 5, 6 и 7 периодической таблицы. Соединения, в которых присутствует водородная связь, имеют гораздо более высокую температуру кипения, поскольку для разрыва водородных связей требуется больше энергии, чем силы Ван-дер-Ваальса 9.0007 [3] .
Расстояние между двумя частями одной и той же молекулы или разными молекулами может варьироваться, и это влияет на прочность водородной связи. Вот почему водородные связи называются «эластичными», чем больше расстояние между атомом водорода и электроотрицательным атомом, тем длиннее будет водородная связь, и это приводит к более слабой водородной связи.
Водородная связь может быть определена как полярное взаимодействие между электроотрицательным атомом (азота, кислорода или фтора) и атомом водорода, который ковалентно связан с другим электроотрицательным атомом, находящимся в той же или другой молекуле. Связь является наиболее прочной, когда все три этих атома расположены таким образом, что их валентные углы составляют 180 градусов.
Водородные связи чрезвычайно распространены в природе и могут быть обнаружены в воде, взаимодействиях пар оснований ДНК, укладке белков, структуре белков и связывании белок-лиганд.
Образование водородной связи происходит из-за притяжения различных элементов, которые имеют различные электроны. Ряд электроотрицательности O > N > C = H.
Вода
Молекула воды состоит из одного атома кислорода, присоединенного к двум атомам водорода. Водородная связь может образоваться между двумя молекулами воды из-за «неравного распределения электронов внутри молекулы воды» 9.0007 [4] . Кислород имеет сильное притяжение к электронам и имеет отрицательный заряд, тогда как водород имеет слабое притяжение и поэтому имеет небольшой положительный заряд. Когда эти две противоположно заряженные области сближаются, образуется водородная связь ^[5] .
Хотя вода имеет низкую молекулярную массу, она имеет необычно высокую температуру кипения. Это свойство можно объяснить большим количеством водородных связей, существующих в воде. Поскольку эти связи трудно разорвать, температуры плавления и кипения воды относительно высоки по сравнению с другими жидкостями, которые похожи, но не имеют водородной связи.
Еще одно необычное свойство воды — ее плотность выше, чем у ее твердого аналога — льда. Это связано с уникальным образованием водородных связей, образующих решетчатую структуру, благодаря чему прочность и относительная жесткость связей обеспечивают большее разделение между молекулами, чем в жидкой форме, где молекулы взаимодействуют с большей скоростью.
ДНК
В спирали ДНК основания: аденин, цитозин, тимин и гуанин связаны со своим комплементарным основанием водородной связью. Аденин в паре с тимином имеет 2 водородные связи. Гуанин в паре с цитозином с 3 водородными связями ^[6] .Это создает разницу в силе между двумя наборами оснований Уотсона и Крика. Пары оснований, связанные гуанином и цитозином, сильнее, чем пары оснований, связанные тимином и аденином в ДНК. Эта разница в силе связана с разницей в количестве водородных связей.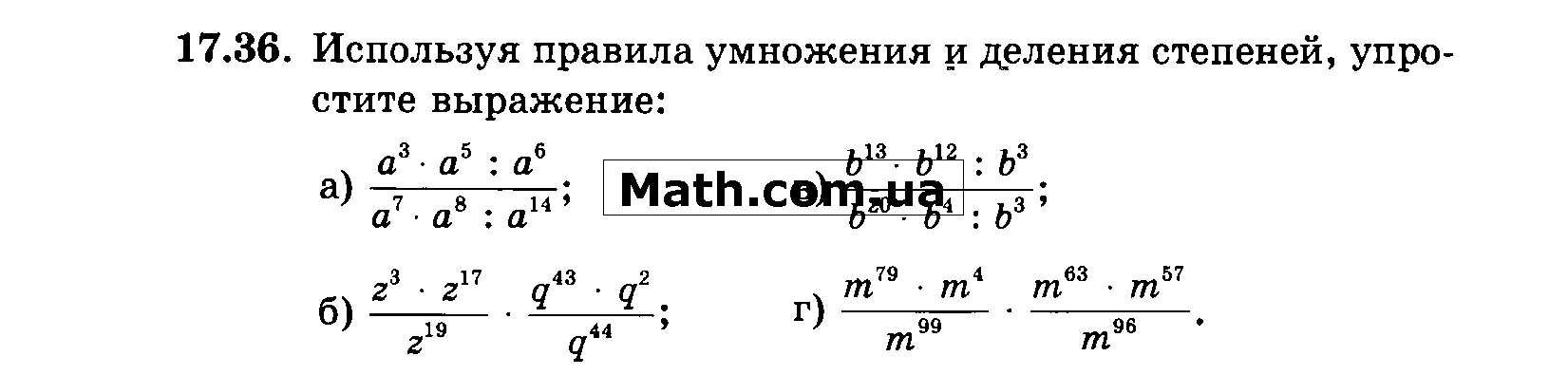 Это позволяет исследователям определить базовое содержание ДНК, наблюдая, при какой температуре она денатурирует. Чем выше температура денатурации ДНК, тем больше пар оснований гуанина и цитозина присутствует. это изменение количества водородных связей, которое нуклеиновое основание может образовать в паре оснований Уотсона-Крика, также имеет значение для разработки праймеров для ПЦР. Чтобы оба праймера отжигались пропорционально их сайтам связывания, они должны быть сконструированы таким образом, чтобы они образовывали водородные связи с одинаковым сродством. Более высокая прочность водородных связей между гуанином и цитозином также используется при разработке праймеров для ПЦР, чтобы гарантировать, что праймеры полностью связаны с ДНК-мишенью на ее 3′-конце, чтобы полимераза могла начать считывание в направлении от 3′ к 5′. Включение гуанина или цитозина на 3′-конце праймера известно как GC-зажим.
Белок
Альфа-спираль содержит водородные связи, которые образуются между карбонильным кислородом остатка N и амидным азотом остатка N + 4. В структуре альфа-спирали на виток приходится 3,6 остатка. каждая из боковых цепей направлена наружу на расстоянии 100 градусов друг от друга. Могут существовать поодиночке, группами, а также в виде длинных витков. Примером альфа-спирали, которая существует в виде длинных завитков, являются кератины, которые можно найти в волосах и коже.
Также отдельные антипараллельные нити бета-складчатого листа имеют водородные связи, которые соединяют пептидные связи разных нитей ^[7] . Все боковые цепи направлены попеременно вверх и вниз на 180 градусов на остаток. пептид полностью растянут, где на остаток приходится 3,5 А. Примером бета-складчатого листа является шелк, который известен своей жесткостью.
Ссылки:
↑ https://www.chemguide.co.uk/atoms/bonding/hbond.html
↑ http://www.chemguide.co.uk/atoms/bonding/hbond.html
↑ http://users.rcn.com/jkimball.ma.ultranet/BiologyPages/H/HydrogenBonds.html
↑ Alberts, B et al. (2008). Молекулярная биология клетки. 5-е изд. США: Гарланд Наука. 1268. стр. 55
↑ Alberts, B et al. (2008). Молекулярная биология клетки. 5-е изд. США: Гарланд Наука. 1268. стр. 55
↑ Дж. М. Берг, Дж. Л. Тимочко, Л. Страйер, (2007) Биохимия, 6-е издание, Нью-Йорк: WHFreeman and Company p112
↑ Alberts, B et al. (2008). Молекулярная биология клетки. 5-е изд. США: Гарланд Наука. 1268. p137
3 степени ценовой дискриминации
Ценовая дискриминация — это стратегия конкурентного ценообразования, используемая предприятиями и продавцами. Ценовая дискриминация предполагает использование разных цен, взимаемых с разных покупателей за один и тот же товар или услугу. Он обычно используется более крупными устоявшимися предприятиями для получения прибыли от различий в спросе и предложении со стороны потребителей.
Компания может увеличить свою прибыль, взимая с каждого клиента максимальную сумму, которую он готов заплатить, тем самым устраняя потребительский излишек. Тем не менее, часто бывает непросто определить точную цену для каждого покупателя. Чтобы ценовая дискриминация была успешной, компании должны понимать свою клиентскую базу и ее потребности. И они должны быть знакомы с различными видами ценовой дискриминации. В этой статье мы рассмотрим три наиболее распространенных типа ценовой дискриминации: дискриминацию первой, второй и третьей степени.
Ключевые выводы
Ценовая дискриминация — это стратегия продажи одного и того же товара или услуги разным покупателям по разным ценам.
Ценовая дискриминация первой степени предполагает продажу товара по точной цене, которую готов заплатить каждый покупатель.
Ценовая дискриминация второй степени нацелена на группы потребителей с более низкими ценами, которые стали возможными благодаря оптовым закупкам.
Ценовая дискриминация третьей степени устанавливает разные цены в зависимости от демографических характеристик подмножеств клиентской базы.
Чтобы ценовая дискриминация работала, предприятия должны предотвращать перепродажи, должны уметь работать на несовершенном рынке и демонстрировать эластичность спроса.
Ценовая дискриминация первой степени
В идеальном деловом мире компании могли бы устранить все потребительские излишки посредством ценовой дискриминации первой степени. Эта стратегия, также называемая персонализированным ценообразованием или совершенной ценовой дискриминацией, возникает, когда компании могут точно определить, сколько каждый клиент будет платить за конкретный продукт или услугу, а затем продать их по этой цене.
Ожидание согласования окончательной цены покупки является частью процесса покупки в некоторых отраслях, таких как производство подержанных автомобилей. Компания, продающая подержанный автомобиль, может собирать информацию посредством интеллектуального анализа данных, касающуюся прошлых покупательских привычек каждого покупателя, его дохода, бюджета и максимального доступного объема производства, чтобы определить, сколько брать за каждый проданный автомобиль.
Эта стратегия ценообразования хорошо подходит для предприятий и отраслей с высокими фиксированными затратами, поскольку позволяет продавцу получать максимально возможную прибыль с каждой продажи. Это может работать только в том случае, если компания способна сегментировать или разделить рынок. Он также должен быть в состоянии помешать клиенту продать продукт или услугу кому-либо еще по более высокой цене.
Одним из недостатков ценовой дискриминации первой степени является то, что она требует много времени и ее трудно усовершенствовать для большинства предприятий. Это не тот процесс, который могут выполнить многие предприятия, особенно крупные компании, у которых много клиентов.
Дифференциация продукта – еще одна конкурентная практика, которую используют предприятия. В этом случае бизнес стремится отличить свой продукт от конкурирующего продукта, чтобы сделать его более привлекательным для определенного целевого рынка.
Ценовая дискриминация второй степени
При ценовой дискриминации второй степени возможность сбора информации о каждом потенциальном покупателе отсутствует. Вместо этого компании оценивают продукты или услуги по-разному в зависимости от предпочтений различных групп потребителей. Проще говоря, цены компаний зависят от того, сколько они могут продать.
Ценовая дискриминация второй степени, которую также называют ценообразованием по версии продукта или ценообразованием в меню, обычно применяется посредством:
Количественные скидки, такие как специальные предложения для клиентов, покупающих оптом, по сравнению с теми, кто покупает один продукт
Предложение «купи два — получи один»
Купоны
Карты лояльности и вознаграждения для постоянных клиентов
Эту стратегию используют складские ритейлеры, такие как Costco или Sam’s Club. Это также можно увидеть в тарифных планах телефона, которые взимают дополнительную плату за дополнительные минуты сверх установленного лимита.
Ценовая дискриминация второй степени не устраняет полностью потребительский излишек, но позволяет компании увеличить норму прибыли на подмножестве своей потребительской базы. Это также очень простая стратегия, поскольку для привлечения и сегментации потребительской базы не требуется много усилий.
Ценовая дискриминация третьей степени
Ценовая дискриминация третьей степени имеет место, когда компании оценивают продукты и услуги по-разному в зависимости от уникальных демографических подмножеств их потребительской базы, таких как студенты, военнослужащие или пожилые люди. Таким образом, это обычно называется групповым ценообразованием.
Вы часто будете видеть этот тип стратегии ценообразования при продаже билетов в кинотеатры, входных билетах в парки развлечений и предложениях ресторанов. Индустрия путешествий и туризма также использует ценовую дискриминацию третьей степени для тех, кто бронирует в последнюю минуту. Группы потребителей, которые в противном случае не могли бы или не захотели покупать продукт из-за их более низкого дохода, могут быть охвачены этой стратегией ценообразования, что увеличивает прибыль компании.
Компаниям легче понять общие характеристики потребителей, чем покупательские предпочтения отдельных покупателей. Ценовая дискриминация третьей степени позволяет сократить потребительский излишек за счет ценовой эластичности спроса конкретных подмножеств потребителей. Чтобы быть эффективными, компании должны быть в состоянии гарантировать, что клиенты не продают эти более дешевые продукты и услуги другим.
Ценовая дискриминация третьей степени является распространенной стратегией ценообразования в индустрии развлечений.
Условия, необходимые для ценовой дискриминации
Любая ценовая дискриминация может быть успешной и прибыльной стратегией, если она осуществляется правильно. Это означает, что компания, использующая его, должна соблюдать определенные условия.
Громкая тема, которая отражается в ценовой дискриминации первой, второй и третьей степени, заключается в том, что компании должны гарантировать отсутствие возможности перепродажи своих продуктов или услуг. Проще говоря, клиенты не должны иметь возможности продавать товары или услуги по более низкой цене кому-либо еще по более высокой цене, иначе возможность получения прибыли будет устранена.
Компания, предлагающая более низкую цену, должна иметь возможность действовать на рынке как своего рода монополия. Это означает, что должна существовать некоторая степень несовершенной конкуренции, когда ей разрешено устанавливать свою собственную структуру ценообразования, ставить определенные барьеры для входа на рынок и конкурировать за долю рынка. Ценовая дискриминация была бы невозможна в условиях совершенной конкуренции, потому что не было бы слишком много
Последним соображением является способность адаптироваться к потребительскому спросу на основе цен. Это известно как ценовая эластичность спроса. Потребители, как правило, увеличивают потребление продуктов и услуг (тем самым увеличивая спрос), когда цены низкие. Эта стратегия не работает, когда люди одинаково реагируют на цены.
Какие условия необходимы для ценовой дискриминации?
Чтобы ценовая дискриминация работала, предприятия должны соответствовать определенным критериям. Они должны гарантировать, что их продукты и услуги по более низкой цене не могут быть перепроданы другим лицам по более высокой цене. Во-вторых, должна быть несовершенная конкуренция, когда компания может устанавливать свою собственную структуру ценообразования и ставить определенные барьеры для входа. Наконец, предприятия должны иметь возможность адаптировать свои стратегии ценообразования к потребительскому спросу.
Как часто конкурирующие фирмы прибегают к ценовой дискриминации?
Ценовая дискриминация очень распространена. Вы можете увидеть, как он используется в различных типах бизнеса, таких как складские клубы и компании сотовой связи, которые предлагают скидки на оптовые закупки. Другие виды ценовой дискриминации проявляются в ценообразовании в ресторанах и кинотеатрах посредством скидок для определенных лиц, таких как действующие военнослужащие и ветераны, а также купонов и поощрений за лояльность для постоянных покупателей.
Законна ли ценовая дискриминация третьей степени?
Ценовая дискриминация третьей степени является законной и является одной из наиболее распространенных форм этой стратегии. Он включает в себя ценообразование товаров и услуг на основе подмножества потребительской базы компании. Например, кинотеатр может предлагать более низкие цены для студентов и пожилых людей, которые более чувствительны к более высоким ценам.
Практический результат
Ценовая дискриминация является очень распространенной стратегией. И хотя это может иметь негативный оттенок, на самом деле это очень законно. Он предполагает установление цены на товары и услуги таким образом, чтобы стимулировать спрос и потребление. Существуют различные степени этой стратегии, в частности ценовая дискриминация первой, второй и третьей степени. Как владелец бизнеса, вы, безусловно, можете увеличить свою прибыль, применяя эти стратегии, но только при соблюдении определенных условий. Убедитесь, что ваши товары или услуги не могут быть перепроданы кому-либо по более высокой цене, что вы работаете на несовершенном рынке и что вы можете реагировать и устанавливать цены в соответствии со спросом.
Неравные по своей природе: взгляд генетика на человеческие различия
В феврале 2001 года Крейг Вентер, президент Celera Genomics, комментируя близкий к завершению проект по изучению генома человека, сказал, что «мы все, по сути, однояйцевые близнецы. ” Заголовок новостей в то время содержал аналогичную мысль: Мы все одна раса? Современная наука говорит так. В следующей статье автор цитирует генетика Кеннета Кидда: «Раса не поддается биологическому определению, мы слишком похожи».
Вентер и Кидд — выдающиеся ученые, поэтому эти заявления должны быть разумными. Основываясь на исследовании нашей ДНК, любые два человека идентичны на 99,9%. Генетические различия между разными группами людей столь же ничтожны.
Тем не менее, стоит только оглянуться вокруг, чтобы увидеть поразительное разнообразие индивидуальных различий в размерах, формах и чертах лица. Столь же очевидны индивидуальные различия в восприимчивости к болезням, а также в спортивных, математических и музыкальных способностях. Индивидуальные различия распространяются на различия между средними группами. Большинство этих средних различий незаметны, но некоторые, например цвет кожи, выделяются.
Откуда это странное несоответствие между свидетельством ДНК и тем, что мы ясно видим? Если не ДНК, то каковы причины различий, которые мы видим между отдельными людьми и между группами людей?
ДНК представляет собой очень длинную молекулу, состоящую из двух нитей, закрученных друг вокруг друга, образующих знаменитую двойную спираль. В клетке человека сорок шесть таких молекул ДНК, каждая из которых (вместе с некоторыми белками) образует хромосому. ДНК в хромосоме человека, если ее растянуть, будет иметь длину в дюйм или больше. Как это сжимается в микроскопическую каплю длиной около 1/1000 дюйма, не запутываясь безнадежно, является инженерным чудом, которое до сих пор остается загадкой.
«Бизнес» часть ДНК, та часть, которая несет генетическую информацию, представляет собой последовательность нуклеотидов или оснований в молекуле. Их четыре, обычно обозначаемые как A, G, T и C. (Я мог бы сказать вам, что означают эти буквы, но вы бы не поняли это эссе лучше, если бы я это сделал, поэтому я не буду.)
В двойной спирали имеется четыре типа пар оснований: AT, GC, TA и CG. Конкретные правила сопряжения — А с Т и Г с С — диктуются трехмерной структурой основ.
В хромосоме пары оснований находятся в точной последовательности, и упорядоченный процесс клеточного деления обеспечивает воспроизведение этой последовательности с очень малым количеством ошибок. Хромосомы встречаются парами, по одному члену каждой пары от каждого родителя, и участки ДНК в двух соответствующих хромосомах совпадают. У нас есть двадцать три пары хромосом, или всего сорок шесть, как упоминалось ранее, в каждой клетке. Эти сорок шесть хромосом содержат около шести миллиардов пар оснований. Если мы случайным образом выберем пару оснований из соответствующих сайтов в двух лицах, 9В 9,9 процентах случаев они будут одинаковыми. Этот процент лишь незначительно зависит от того, являются ли эти два человека с одного и того же или с разных континентов, из одной и той же или из разных групп населения.
Чтобы понять, почему ДНК людей может быть настолько похожей, несмотря на все важные видимые и физиологические различия между людьми и группами, полезно вспомнить нашу эволюционную историю.
Все млекопитающие, в том числе и мы, произошли от предков, живших около ста миллионов лет назад. У наших предков млекопитающих среднее основание менялось, скажем, с А на Т с почти невероятно медленной скоростью, примерно одно изменение за миллиард лет. Это означает, что за это время изменилась лишь небольшая часть оснований, сто миллионов, разделенных на один миллиард, или 1/10. В результате мы разделяем примерно 90 процентов нашей ДНК с мышами, собаками, крупным рогатым скотом и слонами.
Приближаясь к дому, ДНК человека и шимпанзе идентична на 98-99 процентов. Различия между нами, которые мы (и, вероятно, шимпанзе) считаем значительными, зависят только от 1 или 2 процентов нашей ДНК.
Большая часть ДНК человека очень похожа на ДНК еще более далеких предков: рептилий, беспозвоночных и даже растений. Все живые существа имеют много общих функций (например, дыхание), восходящих к очень далекому прошлому. Большая часть нашей ДНК определяет, что мы люди, а не то, чем мы отличаемся от любого другого человека. Так что неудивительно, что ДНК любых двух человеческих существ имеет 99,9 процента идентичны.
Что порождает изменчивость между отдельными организмами и делает возможными эволюционные изменения, так это ошибки в процессе копирования ДНК. Иногда из-за этого одна база меняется на другую — она мутирует. Среди шести миллиардов пар оснований, которые каждый из нас наследует от своих родителей, значительная часть — сотня и более — приходится на новые мутации.
Как мы можем согласовать это большое число с чрезвычайно низкой скоростью эволюционных изменений? Объяснение состоит в том, что лишь небольшая часть мутаций сохраняется с течением времени. Некоторые мутации выживают либо благодаря удаче, либо, если мутация дает биологическое преимущество, благодаря естественному отбору. Даже если индивидуальная мутация выгодна, у нее мало шансов выжить в долгом эволюционном путешествии. Медленная скорость эволюционных изменений объясняет, почему мы, млекопитающие, так похожи в своих ДНК.
Молекулярные исследования ДНК оказались чрезвычайно плодотворными в разработке эволюционной истории жизни. Многое из того, что мы знаем о происхождении человека, получено из исследований ДНК, дополненных довольно разрозненными окаменелостями. Свидетельства ДНК убедительно подтверждают идею о том, что человеческий вид возник в Африке и что европейские и азиатские популяции — на самом деле все неафриканцы — произошли от небольшого числа мигрантов из Африки. Самым убедительным доказательством этого является то, что африканцы более изменчивы в своей ДНК, чем другие популяции.
Анализ ДНК позволяет нам с некоторой точностью измерить генетическое расстояние между различными популяциями людей. По этому критерию европеоиды и азиаты относительно схожи, тогда как азиаты и африканцы отличаются несколько больше. Различия между группами небольшие, но они реальны.
Анализ ДНК дал интересные новые ответы на старые вопросы. Но его выводы также могут ввести в заблуждение. Возьмем случай мужчин и женщин и половых хромосом. У женщин есть две X-хромосомы, а у мужчин — X и Y. Y-хромосома составляет примерно 1 процент ДНК. Но существует очень мало соответствия между Y и другими хромосомами, включая X. Другими словами, ДНК мужчины-человека отличается от ДНК женщины так же сильно, как и ДНК шимпанзе того же пола. Что это значит? Просто анализ ДНК, который дал нам революционно новое понимание генетики и эволюции, не дает разумных ответов на некоторые современные вопросы, интересующие общество.0003
Большинство различий, которые мы замечаем, вызваны очень маленькой частью нашей ДНК. Учитывая шесть миллиардов пар оснований на клетку, крошечная доля — 1/1000 от шести миллиардов пар оснований — по-прежнему составляет шесть миллионов различных пар оснований на клетку. Таким образом, между нами есть много места для генетических различий. Хотя мы отличаемся друг от друга очень малой частью нашей ДНК, мы отличаемся большим количеством оснований ДНК.
Некоторые заслуживающие внимания эволюционные изменения в организме человека произошли относительно быстро, несмотря на низкую общую скорость изменений на уровне ДНК. Разница между цветом кожи африканцев и европейцев, вероятно, возникла менее чем за пятьдесят тысяч лет в результате адаптации к различиям климата. Еще более быстрыми были изменения в генах, обеспечивающих устойчивость к малярии в регионах Африки и Средиземноморья; для развития новых генов потребовалось всего от четырех до восьми тысяч лет. Генетический анализ показывает, что некоторые из генетических изменений, которые кажутся нам столь значительными, зависели от очень крошечной части нашей ДНК.
Но, как я уже сказал, эта крохотная доля по-прежнему представляет собой очень большое количество оснований. Нет двух одинаковых человеческих существ в чертах, которыми они обладают. Одни высокие, другие низкие; одни коренастые, другие худые; одни одарены музыкально, другие глухи; одни спортивные, другие неуклюжие; некоторые общительны, другие интровертны; одни умны, другие глупы; некоторые могут писать великие стихи или музыку, но большинство не может. И так далее.
Чтобы понять наши различия, нам нужно рассмотреть не только ДНК, но и ее клеточные продукты. Эта область исследований является новой, но она быстро развивается. Акцент смещается с последовательностей ДНК на гены. Ген представляет собой участок ДНК, обычно длиной в несколько тысяч пар оснований. Функция большинства генов заключается в производстве белков. Проект секвенирования генома показал, что у людей есть от тридцати до сорока тысяч генов. Но поскольку ген часто производит более одного типа белка, иногда производя разные виды для разных частей тела, количество видов белка приближается к ста тысячам.
У нас есть ряд общих генов с шимпанзе, гены, которые делают нас приматами, а не слонами или червями. Ученые-эволюционисты считают, что многие различия, которые мы наблюдаем между собой и шимпанзе, связаны с изменениями в количестве, а не в характере генных продуктов. Люди и шимпанзе имеют общие белки, которые производят волосы на теле и мозг, но у шимпанзе эти белки производят больше волос и меньше мозга. Почему это должно быть так, еще далеко до полного понимания. Но это область исследований, которая развивается очень быстро, и есть хорошие генетические данные, которые необходимо изучить.
Конечно, не каждое человеческое отличие имеет генетическую причину. Многие из них связаны с окружающей средой или являются результатом взаимодействия между генами и окружающей средой. Даже генетически идентичные близнецы развиваются в разных людей.
Способность к изучению языка в значительной степени является врожденной, встроенной в нервную систему всех нормальных людей, что так прекрасно продемонстрировано в том, как без усилий маленькие дети учатся говорить. Но конкретный язык, который изучает каждый человек, очевидно, зависит от социальной среды. Моцарт был великим композитором отчасти благодаря своим генам и отчасти благодаря своему обучению. У Рамануджана был большой талант к математике, но без учебника — кстати, не очень хорошего — он бы никогда не сделал своих поразительных открытий. У Майкла Джордана есть талант к баскетболу, но он никогда бы не развился, если бы он вырос среди инуитов.
Точно так же, как существуют большие различия между людьми, существуют средние различия, обычно намного меньшие, между группами. Итальянцы и шведы отличаются цветом волос. Иногда различия более заметны, например, контрастный цвет кожи и форма волос у африканцев и европейцев. Но, по большей части, групповые различия невелики и в значительной степени затмеваются индивидуальными различиями.
Биологи думают о расах животных как о группах, которые начинались как одна, но позже разделились и разделились, обычно из-за географического барьера. Поскольку две группы развиваются независимо, они постепенно расходятся генетически. Дивергенции будут происходить быстрее, если отдельные среды различаются, но они произойдут в любом случае, поскольку в двух популяциях неизбежно произойдут разные мутации, и некоторые из них сохранятся. Это наиболее заметно в островных популяциях, где каждый остров является отдельным и между ними нет миграции. Каждый из них имеет свои характерные типы. Однако в большей части животного мира, а также среди людей полная изоляция встречается очень редко. Генетическое единообразие географических групп постоянно разрушается миграцией между ними. В частности, основные географические группы — африканская, европейская и азиатская — смешаны, и это особенно верно в отношении Соединенных Штатов, которые представляют собой нечто вроде плавильного котла.
Из-за такого смешения многие антропологи вполне резонно утверждают, что нет научного обоснования применения слова «раса» к популяциям людей. Но само понятие недвусмысленно, и я полагаю, что это слово имеет ясное значение для большинства людей. Трудность заключается не в концепции, а в осознании того, что основные человеческие расы не являются чистыми расами. В отличие от тех антропологов, которые отрицают полезность этого термина, я считаю, что слово «раса» может быть осмысленно применено к частично смешанным группам.
Различные заболевания явно характерны для разных расовых и этнических групп. Например, серповидноклеточная анемия гораздо более распространена среди лиц африканского происхождения, чем среди европейцев. Ожирение особенно распространено среди индейцев пима в результате внезапного приобретения высококалорийной диеты, к которой у европейцев было достаточно времени, чтобы приспособиться. Болезнь Тея-Сакса гораздо чаще встречается у еврейского населения. Есть и другие примеры, и постоянно открываются новые.
Данные, свидетельствующие о том, что некоторые болезни непропорционально сильно поражают определенные этнические и расовые группы, обычно не вызывают споров. Гораздо более спорным является свидетельство того, что некоторые навыки и поведенческие свойства по-разному распределяются среди разных расовых групп. Имеются веские доказательства того, что такие расовые различия частично являются генетическими, но доказательства более косвенные и убедительны не для всех.
Любому спортивному наблюдателю очевидно, что среди олимпийских прыгунов и спринтеров афроамериканцев гораздо больше, чем можно было бы предсказать по их количеству в популяции.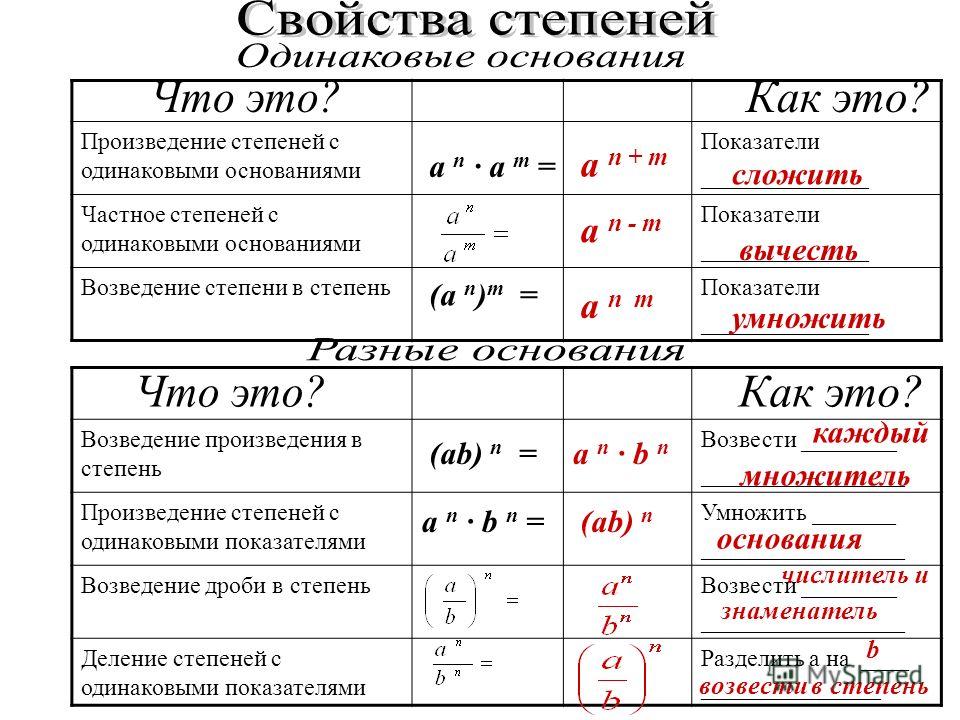 Диспропорция огромная. Тем не менее, мы также знаем, что есть много белых людей, которые лучше бегают и прыгают, чем средний черный человек. Как объяснить это кажущееся несоответствие?
На самом деле существует простое объяснение, хорошо известное генетикам и статистикам, но не очень понятное широкой публике или, если уж на то пошло, политическим лидерам. Рассмотрим количественный признак, который распределяется по нормальной колоколообразной кривой. Примером может служить IQ. Примерно один человек из 750 имеет IQ 148 или выше. В популяции со средним числом около 108, а не 100, едва заметная разница, примерно в 5 раз больше будет в этом высоком диапазоне. В популяции в среднем на 8 пунктов ниже их будет примерно в 6 раз меньше. Небольшая разница в 8 баллов в среднем приводит к многократным различиям в крайних значениях.
Американцы азиатского происхождения составляют около 12 процентов населения Калифорнии, однако они составляют 45 процентов студентов Калифорнийского университета в Беркли. У азиатов средние баллы SAT лишь немного выше, чем у представителей европеоидной расы, но политика университета по приему студентов с самыми высокими баллами SAT привела к тому, что доля студентов с более высоким средним баллом намного выше.
Две популяции могут иметь большое перекрытие и лишь незначительно отличаться по своим средним значениям. Тем не менее, самые выдающиеся люди, как правило, происходят из населения с более высоким средним значением. Вывод, я думаю, ясен: всякий раз, когда институт или общество выделяет людей, которые в чем-то исключительны или выдающиеся, расовые различия становятся более очевидными. Этот факт может быть неудобным, но от него никуда не деться.
Факт существования расовых различий, конечно, не объясняет их происхождения. Причина наблюдаемых различий может быть генетической. Но это также может быть связано с окружающей средой, результатом диеты, структуры семьи, школьного образования или множества других возможных биологических и социальных факторов.
Повторяю, мой вывод состоит в том, что всякий раз, когда общество выделяет выдающихся или необычных в каком-либо отношении лиц, на первый план выходит статистический контраст между средним и крайним. Я думаю, что признание этого может в конечном итоге только помочь политикам и лицам, определяющим социальную политику.
Сейчас время очень быстрых изменений в нашем понимании биологических процессов. Геномный проект — лишь один из примеров. В то же время мы приближаемся к глубокому пониманию нервной системы и поведения человека. Медицинские знания улучшаются, как и сбор данных и компьютерный анализ. Все это говорит нам больше об индивидуальных и групповых различиях. Каково будет влияние этого нового знания на социальные проблемы? Каковы политические последствия современной биологии?
Мы видели, что сходство последовательностей ДНК, обнаруженное в рамках проекта генома, ценное для ответа на многие интересные и важные вопросы, вводит в заблуждение относительно важных человеческих различий. Но эта ситуация быстро меняется. В настоящее время основное внимание уделяется не только простым последовательностям ДНК, но и идентификации отдельных генов, их продуктов и их сложных взаимодействий. В то же время не только виды генных продуктов (обычно белков), но и их относительное количество исследуются с помощью гораздо более точных новых инструментов. Гены сильно различаются по своей продуктивности, включая различия в активности в разных частях тела.
В ближайшем будущем биологи смогут рассказать нам гораздо больше, чем мы знаем сейчас, о генетических и экологических причинах человеческих различий. Самые очевидные и немедленные выгоды для человека будут в медицине. Мы можем предвидеть время, когда многие — мы надеемся, что больше всего — наши индивидуальные предрасположенности к болезням будут поняты, так что болезнь можно будет предсказать заранее, что позволит врачам предвидеть и адаптировать лечение для конкретного человека. Небольшие шаги в этом направлении уже сделаны. Новые методы лечения находятся в стадии разработки. В результате нашего генетического понимания мы также теперь лучше понимаем, как манипулировать окружающей средой, чтобы помочь предотвратить болезнь.
В то же время изучение генных продуктов и их регуляции распространяется на нормальные признаки. Мы можем ожидать, что молекулярная биология будущего, возможно, совсем близкого будущего, будет давать именно ту информацию, которая в прошлом зависела от наблюдения и статистического анализа часто нечетко определенных признаков. Мы сможем, как личности, многое узнать о нашей собственной генетической структуре.
Великолепные достижения в области молекулярной биологии откроют новые глубины понимания человеческих различий, нормальных и патологических, а также того, в какой степени они обусловлены генетическими или экологическими факторами или, как это обычно бывает, и тем, и другим. Примет ли общество охотно это знание и разумно ли воспользуется им, я не знаю. Я надеюсь, что постепенный прогресс, начиная с небольших начинаний, может привести к рациональному индивидуальному поведению и продуманной, гуманной социальной политике.
Для общества важно лучше, чем сейчас, принимать различия как факт жизни. Новые формы научного знания будут указывать на все больше и больше способов нашего разнообразия. Я надеюсь, что различия будут приветствоваться, а не приниматься с неохотой. Кому нужен мир одинаковых людей, даже если они Моцарты или Джорданы?
Хорошее общество должно обеспечивать наилучшие условия для каждого человека и каждой группы населения. Мы уже делаем это частично. Мы даем уроки музыкально одаренным детям. Мы поощряем спортсменов и даем им специальные тренировки (а иногда и сомнительные препараты). Студенты выбирают курсы в соответствии со своими способностями и интересами. У нас есть специальные классы для людей с ограниченными возможностями, и такие классы становятся более конкретными по мере понимания причин инвалидности.
Мы, конечно, не можем создать особую среду для каждого человека, но мы можем продолжать двигаться в этом направлении. Обнаружение генетической основы признака не означает, что окружающая среда не имеет значения. Действительно, постоянно обнаруживается все большее влияние окружающей среды на человеческий организм, часто с помощью генетических исследований.
Проверкой наших демократических институтов будет степень, в которой люди смогут принять все наши различия и найти способы приспособить их к слаженно работающему гуманитарному обществу. И я утверждаю, что мы должны стремиться не только к максимальному личному удовлетворению, но и к максимальному вкладу; каждый из нас обязан обществу плодами своих особых даров. Я твердо убежден, что исследования генетических и экологических причин человеческих различий должны продолжаться и поддерживаться. Новые процедуры, появившиеся благодаря молекулярному прогрессу и компьютерам, значительно ускорят открытия.
Я считаю, что знание, даже неприятное знание, гораздо предпочтительнее невежества. Я надеюсь, что американское общество сможет меньше бояться узнавать правду о биологическом неравенстве и быть более смелым в использовании открытий гуманными способами, способствующими благосостоянию людей.
Вопрос о равных возможностях и равных результатах становится особенно неприятным в тех профессиях и профессиях, на которые может претендовать лишь небольшая часть населения. Я уже упоминал о чрезмерном преобладании афроамериканцев среди олимпийских бегунов. Это ближе к истинной меритократии, чем что-либо еще, что я могу придумать: секундомер не различает цвета. В этом случае кажется, что нет социальной цели в требовании равного расового представительства.
В некоторых важных профессиях, таких как физика и инженерия, американцы азиатского происхождения представлены больше, чем афроамериканцы. По-видимому, из-за этого мы проводим более качественные исследования. Это может или не может перевешивать неравенство неравного группового представительства. Это социальное решение.
А врачи? Вполне могут быть социальные соображения, возможно, временные в нашем обществе, которые сделают расу более важной, чем результаты тестов при отборе студентов в медицинские вузы.
Для достижения политического и социального равенства нет необходимости поддерживать фикцию о том, что важных человеческих различий не существует. Об этом хорошо сказал великий эволюционист Феодосий Добржанский: «Люди не обязательно должны быть однояйцевыми близнецами, чтобы быть равными перед Богом, перед законом и в своих правах на равенство возможностей».
Я подчеркивал, что люди разные, и очень разные. Они отличаются не только формами и размерами, но и способностями и талантами. Они также отличаются вкусами и предпочтениями. Как сказал Шоу: «Не поступай с другими так, как ты хотел бы, чтобы они поступали с тобой. Их вкусы могут не совпадать». Я думаю, что дело общества не в том, чтобы преуменьшать индивидуальные различия. Мы не должны пытаться подгонять людей под одну гребенку.
Хотя я ожидаю, что наука будет продолжать предоставлять нам новые доказательства человеческой изменчивости, и хотя я приветствую такую изменчивость как источник социального обогащения, есть некоторые виды человеческой изменчивости, без которых мы вполне могли бы обойтись. Я имею в виду серьезные, болезненные, изнурительные заболевания.
No related posts.