Отличие арифметической прогрессии геометрической прогрессии: Разница между арифметической и геометрической последовательностью

Содержание

Разница между арифметической и геометрической последовательностью

2019

Последовательность описывается как систематический набор чисел или событий, называемых терминами, которые расположены в определенном порядке. Арифметические и геометрические последовательности — это два типа последовательностей, которые следуют шаблону, описывая, как вещи следуют друг за другом. Когда существует постоянная разница между последовательными членами, последовательность называется арифметической последовательностью,

С другой стороны, если последовательные члены находятся в постоянном соотношении, последовательность является геометрической . В арифметической последовательности термины могут быть получены путем добавления или вычитания константы к предыдущему члену, причем в случае геометрической прогрессии каждый член получается путем умножения или деления константы на предыдущий член.

Здесь, в этой статье, мы собираемся обсудить существенные различия между арифметической и геометрической последовательностью.

Сравнительная таблица

Основа для сравнения	Арифметическая последовательность	Геометрическая последовательность
Имея в виду	Арифметическая последовательность описывается как список чисел, в котором каждый новый термин отличается от предыдущего термина постоянной величиной.	Геометрическая последовательность — это набор чисел, в котором каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент.
Удостоверение личности	Общая разница между последовательными терминами.	Общее соотношение между последовательными сроками.
Продвинутый	Сложение или вычитание	Умножение или деление
Вариация условий	линейный	экспоненциальный
Бесконечные последовательности	расходящийся	Расходящиеся или сходящиеся

Определение арифметической последовательности

Арифметическая последовательность относится к списку чисел, в которых разница между последовательными членами постоянна. Проще говоря, в арифметической прогрессии мы добавляем или вычитаем фиксированное ненулевое число, каждый раз бесконечно. Если a является первым членом последовательности, то это может быть записано как:

a, a + d, a + 2d, a + 3d, a + 4d ..

где а = первый член
d = общая разница между терминами

Пример : 1, 3, 5, 7, 9…
5, 8, 11, 14, 17…

Определение геометрической последовательности

В математике геометрическая последовательность представляет собой набор чисел, в которых каждый член последовательности является постоянным кратным предыдущего члена. В более тонких терминах, последовательность, в которой мы умножаем или делим фиксированное ненулевое число, каждый раз бесконечно, тогда прогрессия называется геометрической. Кроме того, если a является первым элементом последовательности, то это можно выразить как:

a, ar, ar2, ar3, ar 4…

где а = первый член
d = общая разница между терминами

Пример : 3, 9, 27, 81…
4, 16, 64, 256 . .

Следующие пункты заслуживают внимания, поскольку речь идет о разнице между арифметической и геометрической последовательностями:

В качестве списка чисел, в котором каждый новый термин отличается от предыдущего термина на постоянную величину, является арифметическая последовательность. Набор чисел, в котором каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент, называется геометрической последовательностью.
Последовательность может быть арифметической, когда есть общая разница между последовательными членами, обозначенными как «d». Напротив, когда существует общее соотношение между последовательными членами, представленными как «r», последовательность называется геометрической.
В арифметической последовательности новый член получается путем добавления или вычитания фиксированного значения к / из предыдущего члена. В отличие от геометрической последовательности, в которой новый термин определяется путем умножения или деления фиксированного значения от предыдущего.
В арифметической последовательности изменение членов последовательности является линейным. В отличие от этого, изменение в элементах последовательности является экспоненциальным.
Бесконечные арифметические последовательности расходятся, в то время как бесконечные геометрические последовательности сходятся или расходятся, в зависимости от обстоятельств.

Заключение

Следовательно, с учетом приведенного выше обсуждения было бы ясно, что существует огромная разница между двумя типами последовательностей. Кроме того, можно использовать арифметическую последовательность для определения сбережений, затрат, конечного прироста и т. Д. С другой стороны, практическое применение геометрической последовательности заключается в определении прироста населения, интереса и т. Д.

Все о геометрической прогрессии

Что такое геометрическая прогрессия?
Формулы и свойства геометрической прогрессии
Калькуляторы геометрической прогрессии
Примеры решения заданий с геометрической прогрессией

Ученикам может показаться, что изучение геометрической прогрессии – это нечто абстрактное и оторванное от жизни. На самом деле множество экономических процессов построены именно на основе геометрической прогрессии.

Например, если вы положите деньги на банковский депозит и захотите посчитать сколько процентов заработаете за три года, самым удобным способом провести вычисления будет именно через формулу геометрической прогрессии. Этот инструмент также применяется в проектировании, архитектуре и строительстве.

В этом тексте вы сможете узнать базовую информацию о формулах и свойства геометрической прогрессии, а также понять принцип, по которому она действует.

Что такое геометрическая прогрессия?

3, 12, 48, 192, 768, 3072 – это пример геометрической прогрессии. Все эти объединенные единым общим множителем. В теории геометрической прогрессии он называется знаменателем и обозначается как q. В этом случае q = 4. Чтобы создать геометрическую прогрессию, нам нужно сначала три умножить на четыре, затем 12 – снова на 4, потом 48 на 4 и так далее.

Читайте также: Плюсы и минусы образования за рубежом

Определение геометрической прогрессии

Устойчивое число множитель, которое собственно и образует последовательность под названием геометрическая прогрессия, называется знаменателем прогрессии и обозначается, как мы уже отметили выше, буквой q.

Члены прогрессии обозначаются как , где под индикатором n имеется в виду порядковый номер члена в прогрессии. Соответственно, первый член прогрессии (в нашем первом примере равен 3 – это b1, а второй (12) – это b2.

Предполагается, что ни первый член, ни знаменатель прогрессии не равен нулю.

Свойства геометрической прогрессии

Геометрическая прогрессия становится удобным инструментом вычислений, когда вы понимаете, что с помощью ее свойств и связанных с ней формул можно легко вычислить, чему равно

И действительно – если попробуем вручную умножать каждое число ряда на 4, в конце концов восьмым числом этой геометрической прогрессии станет 49152.

После усвоения главного принципа, лежащего в основе геометрической прогрессии, можем закрепить знания, проверив на практике первый пример с банковским депозитом.

Допустим, вы кладете на свой счет $ 100 под 6% годовых, и хотите узнать, какую сумму получите за 3 года. В таком случае вы будете использовать в своих расчетах геометрическую прогрессию, ведь ежегодно вы будете умножать все большую сумму на один и тот же множитель (в данном примере он равен 6%, то есть – 1,06)

Чтобы вычислить сумму вклада в момент завершения действия депозита, используем уже знакомую формулу для нахождения значения любого члена прогрессии:

В чем разница между геометрической и арифметической прогрессией?

В геометрической прогрессии члены прогрессии умножаются на постоянное число, тогда как арифметическая прогрессия воплощает последовательность чисел, в которой к каждому предыдущему члена добавляется одно и то же постоянное число.

Представим это на примерах.

Предположим, что знаменатель (q) в случае геометрической прогрессии составит 3 и так же в арифметической прогрессии устойчивое слагаемое будет равно 3. И стартовый член прогрессии в обоих случаях также составит одно и то же число – 4.

Арифметическая прогрессия тогда будет выглядеть как последовательность 4, 7 (= 4 + 3), 10 (= 7 + 3) .., 13 .., 16 .., 19 …

А геометрическая прогрессия – как последовательность 4, 12 (= 4 * 3), 36 (= 12 * 3), 108 .., 324 …

Читайте также: Учимся играя. Что такое геймификация

Формулы и свойства геометрической прогрессии

Свойства членов геометрической прогрессии – это формулы, упрощающие расчеты. Вот некоторые из них:

Чтобы найти знаменатель геометрической прогрессии, следует использовать следующую формулу:

Произведение членов, равноудаленных от краев геометрической прогрессии, то есть, соседних, всегда является постоянной величиной, то есть:

С формулой расчета любого члена геометрической прогрессии мы уже знакомы.

А формула нахождения суммы п первых членов геометрической прогрессии выглядит так:

Любой член геометрической прогрессии, начиная со второго, будет равняться среднему арифметическому соседних с ним членов, то есть при ,

Калькуляторы геометрической прогрессии

В сети есть множество калькуляторов как арифметической, так и геометрической прогрессии. Некоторые из них могут не только посчитать сумму прогрессии или найти знаменатель, но и отразить пошаговое решение того или иного примера. Пользуясь ими вы не только найдете ответ, но и сможете понять принцип действий и запомнить некоторые из формул.

Однако если вы переживаете сложности с пониманием геометрической прогрессии, эффективным решением может быть работа с репетитором по алгебре. На сайте БУКИ вы можете найти репетитора по любому предмету.

Что касается онлайн-калькуляторов прогрессии, то в Keisan Online Calculator вы можете вычислить или сумму геометрической прогрессии, а также значение любого ее члена с пошаговым решением вашего примера. А в Geometric Sequence Calculator вы сможете вычислить любой составляющая прогрессии: и знаменатель геометрической прогрессии (q), и сумму бесконечный прогрессии (Sn), и сумму первых членов (Sn).

Примеры решения заданий с геометрической прогрессией

Вычислим знаменатель геометрической прогрессии, если b1=5,5; b2=11.

Решение:

Вычислим знаменатель прогрессии, поделив друг на друга соседние члены:

q = b2/b1 = 11/5,5 = 2.

Ответ:

Знаменатель прогрессии (q) равен 2.

Вычислим знаменатель геометрической прогрессии, если b1=0,3; b2= -30.

Решение:

Вычислим знаментель прогрессии, поделив друг на друга соседние члены:

q = b2/b1= -30/0,3= -100.

Ответ:

Знаменатель прогрессии (q) равен -100.

Читайте также: Самые популярные специальности в мире: выбор студентов 2021

Готовимся к ОГЭ: арифметическая прогрессия

Добавлено: 30 мая 2021 в 10:31

Содержание

ОГЭ по математике — комплекс заданий по всему курсу математики до 9 класса. Для получения высокой оценки важно освоить все темы, в том числе и раздел «Числовые последовательности». Для этого необходимо разобраться, что такое арифметическая прогрессия. Тема непростая, но мы попробуем сделать ее доступной для понимания, в том числе и на конкретных примерах из ОГЭ.

Говоря об арифметической прогрессии, следует остановиться на понятии «числовая последовательность». В математическом смысле это набор чисел, которые расположены в определенном порядке. Каждый элемент в этом наборе имеет свой порядковый номер, благодаря которому четко идентифицируется его «положение» в последовательности. Примером может служить конечная (состоящая из определенного числа элементов) последовательность — код для разблокирования смартфона.

Для осуществления этой операции необходимо ввести цифры в определенном – и только в этом порядке. Если нарушить порядок и вместо «1894» набрать «1849», смартфон не разблокируется. Существуют и бесконечные последовательности, которые не ограничены определенным количеством элементов.

Не забудем, что математика помогает упорядочить различные явления, в том числе и последовательности. Наиболее «важными» с точки зрения обывателя и ученика, сдающего ОГЭ, являются последовательности следующего вида:

арифметическая прогрессия — последовательность, в которой каждый последующий член (элемент) отличается от предыдущего на одно и то же число;
геометрическая прогрессия — последовательность, в которой каждый последующий член (элемент) отличается от предыдущего в одно и то же количество раз.

О геометрической прогрессии мы поговорим в следующий раз, хотя и она очень интересна. К примеру, с этим видом последовательности связана одна из известнейших математических задач о мудреце Сиссе ибн Дахире и изобретенных им шахматах. Помните, как король согласился заплатить удвоенное количество зерен за каждую шахматную клетку? Видимо, он не знал свойств геометрической прогрессии, да и арифметической тоже, но правителям это простительно, а вот участникам ОГЭ такие вещи пригодятся.

«Расчет» арифметической прогрессии

Запишем простейшую арифметическую прогрессию:

1, 2, 3, 4, 5, 6, 7, 8…

Очевидно, что в ней каждый следующий член отличается от предыдущего на одну единицу. Это отличие называется разностью арифметической прогрессии и обозначается буквой d. Зная это значение и один из членов, например n-й («энный») член a_n, можно найти последующий a_n₊₁ или предыдущий a_n_-1 элемент:

a_n₊₁= a_n + d

a_n_-1= a_n — d

Более того, каждый «средний» член такой прогрессии является средним арифметическим своих соседей. Именно поэтому такая последовательность носит название «арифметическая прогрессия»:

a_n = (a_n_-1 + a_n₊₁)/2

Зная свойства арифметической прогрессии, можно рассчитать:

сумму нескольких ее членов;
любой из членов, если известен первый член;
первый член, если известен n-й член.

Для этого можно не запоминать формулы из учебника, ведь они приведены в справочной части контрольных измерительных материалов к ОГЭ. Впрочем, лучше понять логику последовательностей и тогда вы всегда сможете самостоятельно вывести формулы для расчета.

Часто арифметическая прогрессия используется не для простого расчета чисел, а как теоретическая основа для решения практических задач (в том числе и на ОГЭ по математике ), о чем мы поговорим в следующем разделе.

Арифметическая прогрессия на ОГЭ

Как правило, в формулировке заданий ОГЭ прямо не указано, что для поиска ответа нужно использовать навыки работы с арифметическими прогрессиями. Ученик должен сам догадаться об этом, прочитав условие. Для примера возьмем задачу из банка заданий ФИПИ.

Внимательно вчитаемся в условие. У нас есть количество мест в первом ряду — это первый член последовательности a₁ = 20. Также в задаче дано увеличение количества мест в каждом последующем ряду — это разность арифметической прогрессии d = 3. Для расчета воспользуемся формулой расчета значения n-ого (в нашем случае десятого, то есть n = 10) члена арифметической прогрессии:

a_n = a₁ + d (n-1) = 20 + 3 (10-1) = 47 мест.

Другой тип задач ориентирован на расчет суммы нескольких членов арифметической прогрессии. В задаче с амфитеатром нам дано 11 рядов — это количество членов арифметической прогрессии n = 11. Также у нас есть количество мест в первом ряду — это первый член последовательности a₁ = 16. В задаче дано и увеличение количества мест в каждом последующем ряду — это разность арифметической прогрессии d = 3. Для расчета общего числа мест в амфитеатре воспользуемся формулой расчета суммы первых n членов арифметической прогрессии:

S_n = ((a₁ + a_n) n)/2

В этом выражении неизвестно значение a_n, которое рассчитывается по уже известной нам из предыдущего примера формуле:

a_n = a₁ + d (n-1) = 16 + 3 (11-1) = 46 мест.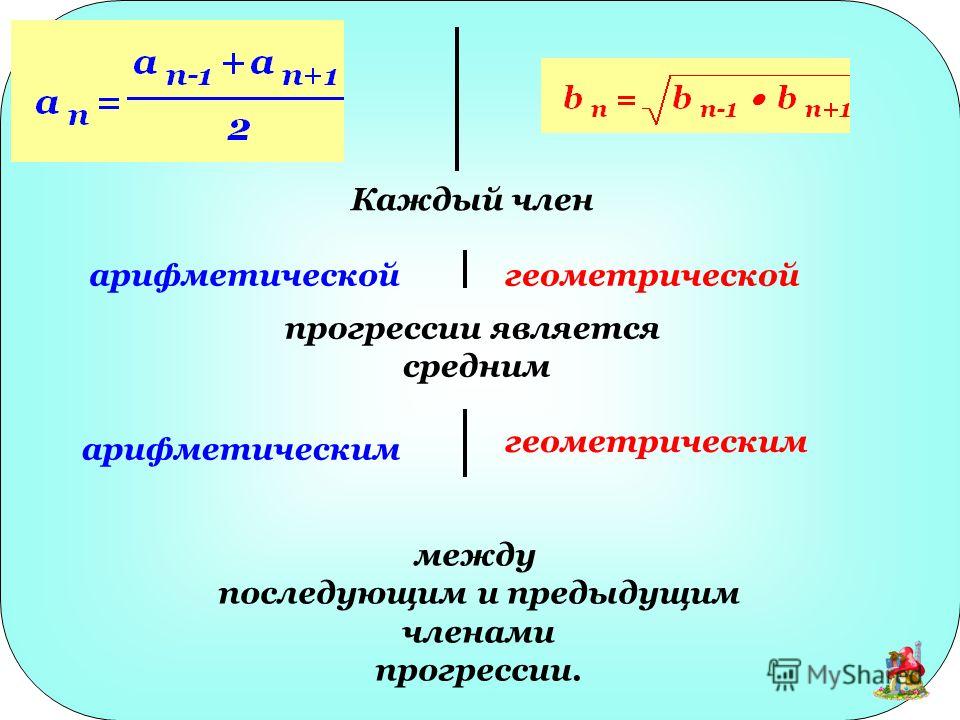

Зная количество мест в последнем ряду, подставим его в выражение для расчета суммы первых n членов арифметической прогрессии:

S_n= ((a₁ + a_n) n)/2 = ((16 + 46) 11)/2 = 341 место.

Эту же задачу можно решить «в одну формулу», но мы воспользовались теми выражениями, которые даны в справочной части контрольных измерительных материалов к ОГЭ.

Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Владислав Барышников

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР

Задать вопрос

Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.

Разница между арифметической последовательностью и геометрической последовательностью

Арифметика — это математическая операция, связанная с числовыми системами и связанными с ними операциями. Он используется для получения единственного определенного значения. Слово «арифметика» происходит от греческого слова «арифмос», что означает «числа». Это область математики, которая фокусируется на изучении чисел и свойств обычных операций, таких как сложение, вычитание, умножение и деление.

Последовательность — это набор элементов в определенном порядке (обычно числа). Арифметические и геометрические последовательности являются двумя наиболее популярными типами математических последовательностей. Каждая следующая пара членов арифметической последовательности имеет постоянную разность. С другой стороны, геометрическая последовательность имеет фиксированное соотношение между каждой парой последовательных членов.

Арифметическая последовательность

Если разница между любыми двумя последовательными элементами всегда одинакова, последовательность целых чисел называется арифметической последовательностью. Проще говоря, это означает, что следующее число в ряду вычисляется путем умножения предыдущего числа на заданное целое число. Кроме того, арифметическая последовательность может быть записана как

a, a + d, a + 2d, a + 3d, a + 4d

, где a = первый член

d = общая разница между терминами.

Например, в следующей последовательности: 5, 11, 17, 23, 29, 35, … постоянная разность равна 6.

Геометрическая последовательность

Если отношение любых двух последовательных членов всегда последовательность чисел называется геометрической последовательностью. Проще говоря, это означает, что следующее число в ряду вычисляется путем умножения заданного числа на предыдущее число. Кроме того, геометрическая последовательность может быть выражена как:

a, ar, ar ² , ar ³ , ar ⁴ …

где a = первый член

d = общая разница между терминами.

Например, 2, 6, 18, 54, 162,… В этом случае постоянный множитель равен 3.

Как отличить арифметическую последовательность от геометрической последовательности?

Чтобы отличить арифметическую и геометрическую последовательность, важны следующие моменты:

Арифметическая последовательность — это набор чисел, в котором каждая новая фраза отличается от предыдущей на фиксированную величину. Геометрическая последовательность — это последовательность целых чисел, в которой каждый элемент после первого получается путем умножения предыдущего числа на постоянный коэффициент.
При наличии общего различия между последующими терминами, обозначенными буквой «d», ряд может быть арифметическим. Последовательность называется геометрической, если существует общее отношение между последующими членами, обозначенное буквой «r».
Новый член арифметической последовательности получается путем прибавления или вычитания фиксированного значения из предыдущего члена. В отличие от геометрической последовательности, новый член находится путем умножения или деления фиксированного значения предыдущего члена.
Изменение между членами арифметической последовательности является линейным. Напротив, изменение элементов последовательности является экспоненциальным.
Бесконечные арифметические последовательности расходятся, а бесконечные геометрические последовательности сходятся или расходятся, в зависимости от ситуации.

Отличие арифметической последовательности от геометрической последовательности

Серийный номер	Арифметическая последовательность	Геометрическая последовательность
1	Арифметическая последовательность — это набор чисел, в котором каждое новое словосочетание отличается от предыдущего на фиксированную величину.	Геометрическая последовательность представляет собой набор целых чисел, в котором каждый последующий элемент создается путем умножения предыдущего числа на постоянный коэффициент.
2	Между последовательными словами есть общее различие.	Между последовательными словами они имеют одинаковое общее соотношение.
3	Вычитание или сложение используются для получения терминов.	Деление или умножение используются для получения терминов.
4	Пример: 5, 11, 17, 23, 29, 35,…	Пример: 2, 6, 18, 54, 162,…

Примеры задач Геометрическая последовательность, и почему она так называется?

Ответ:

Поскольку числа переходят от одного к другому путем погружения или умножения на одинаковое значение, это называется геометрической последовательностью.

Вопрос 2: Может ли арифметическая последовательность быть геометрической?

Ответ:

В математике арифметическая последовательность определяется как последовательность, в которой общая разность или дисперсия между последующими числами остается постоянной. Геометрическая последовательность, напротив, характеризуется устойчивым общим соотношением между последующими величинами. В результате последовательность не может быть одновременно и геометрической, и арифметической.

Вопрос 3. Что такое а в арифметической прогрессии?

Ответ:

Арифметическая последовательность — это набор членов, в котором разность между двумя последовательными членами ряда является постоянным членом, «а» — это первый член а в арифметической последовательности.

Вопрос 4: Какова процедура определения n ^th члена арифметической прогрессии?

Ответ:

a _n = 2n + 1 — это формула для нахождения n ^th членов арифметической прогрессии или n ^-й термин может быть записан как + (n – 1) d.
Где «а» — первый член, а «d» — обычная разность арифметической последовательности.

Вопрос 5: Какова процедура определения n ^th члена геометрической прогрессии?

Ответ:

a _n = ar ^{n − 1} — формула нахождения n ^th членов геометрической прогрессии, где «a» — первый член, а «d» обыкновенное отношение геометрической прогрессии.

5 Важная разница между арифметической и геометрической последовательностями

В чем разница между арифметической и геометрической последовательностями?

Последовательность — это набор чисел, расположенных в определенном порядке. Эти наборы чисел известны как термины. Основными видами последовательностей являются арифметическая и геометрическая последовательности.

Основное различие между арифметической и геометрической последовательностями заключается в том, что арифметическая последовательность — это последовательность, в которой разница между двумя последовательными членами постоянна, а геометрическая последовательность — это последовательность, в которой отношение между двумя последовательными членами является постоянным.

Подробнее: Разница между площадью и периметром Арифметическая последовательность Геометрическая последовательность Значение Это последовательность, в которой разница между двумя последовательными терминами является константой Это последовательность, в которой отношение между двумя последовательными элементами является константой Как определить последовательность Общая разница между последовательными терминами Обыкновенное отношение между последовательными членами Режим работы Сложение или вычитание

Умножение или деление Изменение условий Линейный Экспоненциальный Бесконечная последовательность Дивергент Либо расходящиеся, либо сходящиеся
Что такое арифметическая последовательность?
Также известна как арифметическая прогрессия. Это последовательность, в которой разница в последовательных членах постоянна.
Арифметическая прогрессия либо складывается, либо вычитается. Кроме того, оно всегда происходит в линейной форме.
Пример арифметической последовательности: a, a+d, a+2d, a+3d, a+4d. Где a — первое слагаемое, а d — общая разность.
Следовательно, формула арифметической прогрессии равна a + (n-1) d
Пример вопроса
Определите первый член и вычислите общую разность последовательности. 3, 8, 13, 18, 23. . .
a=3 d= второй член – следовательно, первый член 8-3 = 5
Что такое геометрическая последовательность?
Он также известен как геометрическая прогрессия. Это последовательность, в которой отношение между последовательными членами является постоянным.
Геометрическая прогрессия умножается или делится. Кроме того, геометрическая последовательность встречается в экспоненциальной форме.
Обыкновенный коэффициент является фиксированным и отличным от нуля числом. Например, 3, 6, 12, 24… Обычное отношение здесь 2 .
Геометрическая последовательность выражается как a, ar, ar², ar³, ar ⁴ и так далее. Где a — первый член, а r — обыкновенное отношение.
Следовательно, формула геометрической последовательности: a _n =ar ^n-1
Пример геометрической последовательности 3, 9, 27, 81…
a=3 r=9/3 n= пятый член
Следовательно, a _n = 3 X 3 ^5-1
Окончательный результат равен 3 x 81= 243
Подробнее: Разница между выражением и уравнением Mainif 3 9020 между арифметической и геометрической последовательностями
Арифметическая последовательность — это список чисел, в которых последовательные члены имеют постоянную разность, тогда как геометрическая последовательность — это список чисел, в которых последовательные члены имеют постоянное отношение
Арифметическая последовательность имеет общее различие, тогда как геометрическая последовательность имеет общее отношение
Новый член арифметической прогрессии либо прибавляется, либо вычитается, тогда как член геометрической прогрессии либо умножается, либо делится
Изменение элементов арифметической последовательности является линейным, а геометрической последовательности — экспоненциальным
Бесконечная арифметическая последовательность расходится, тогда как геометрическая последовательность либо расходится, либо сходится
Сходства между арифметической и геометрической последовательностями
Оба следуют строгому шаблону
Оба имеют постоянное количество
Оба варианта сбивают с толку учеников
Подробнее: Разница между длиной и высотой
Часто задаваемые вопросы об арифметических и геометрических последовательностях
Чем похожи арифметические и геометрические последовательности?
Обе последовательности имеют постоянное количество. Это, как правило, сбивает с толку многих студентов во время сдачи экзаменов.
Линейны ли геометрические последовательности?
Нет. Геометрические последовательности — это экспоненциальные функции, в которых значение n увеличивается на постоянное значение, равное единице, а значение f (n) увеличивается на кратное r.
Почему это называется геометрической последовательностью?
Это называется геометрической последовательностью, потому что числа переходят от одного числа к другому путем погружения или умножения на аналогичное значение.
Сравнительное видео

Заключение
Приведенной выше исчерпывающей информации об арифметических и геометрических последовательностях вполне достаточно для более легкого понимания.
Однако эти две последовательности могут показаться похожими в настройках исследования и вызвать много путаницы. Больше практики поможет решить проблему.
Вычислять вопросы, связанные с арифметической последовательностью, очень просто, но вопросы геометрической последовательности, как правило, создают много проблем.
Дополнительные источники и ссылки
Последовательности и серии. Репетитор потока ветра
Арифметика и геометрическая прогрессия. Репетитор по математике
©2022 Coredifferences.com является участником партнерской программы Amazon Services LLC, партнерской рекламной программы, предназначенной для предоставления сайтам средств для получения платы за рекламу за счет рекламы и ссылок на amazon.com.
Разница между арифметической и геометрической последовательностями [обновлено в 2022 г.]
Последнее обновление: 21 сентября 2022 г. / Автор Piyush Yadav / Факт проверен / 7 минут
Все вы, должно быть, были в кинотеатрах, чтобы смотреть фильмы с друзьями или членами семьи. При бронировании билетов вы когда-нибудь замечали, как обычно рассаживаются в кинотеатре?
Количество мест в предыдущем ряду всегда будет меньше, чем в следующем ряду, на определенное число.
Такое расположение сидений обычно представляет собой арифметическую последовательность. Таким образом, можно сказать, что последовательность, которая уменьшается или увеличивается на постоянное число, известна как арифметическая последовательность.
С другой стороны, геометрическая последовательность — это нечто совершенно другое. Большинство из вас в детстве играли с мячами.
Играете ли вы в футбольный или баскетбольный мяч, вы заметите, что высота, на которую он отскакивает, имеет тенденцию уменьшаться каждый раз, когда он падает на землю. Это уменьшение высоты подпрыгивания находится в геометрической последовательности.
Таким образом, можно сказать, что геометрическая последовательность — это в основном последовательность, в которой каждый член умножается или делится на одно и то же значение от одного конкретного члена к следующему. Значение, на которое член делится или умножается, называется обыкновенным отношением.
Арифметическая и геометрическая последовательность
Основное различие между арифметической и геометрической последовательностями заключается в том, что в арифметической последовательности разница между двумя ее последовательными членами остается постоянной, а в геометрической последовательности отношение между двумя ее последовательными членами остается постоянным.
Разница между двумя последовательными элементами арифметической последовательности называется общей разностью. С другой стороны, отношение двух последовательных членов геометрической последовательности называется обыкновенным отношением.
Таблица сравнения между арифметической и геометрической последовательности 99
Параметр сравнения Арифметическая последовательность Геометрическая последовательность
333. определение
33333.0074 Это список чисел, в котором каждый новый член отличается от предыдущего на определенную величину. Это последовательность чисел, в которой каждый новый член вычисляется путем умножения на ненулевое и фиксированное число.
Вычислено по Сложение или вычитание Умножение или деление
Определено по Постоянная разница между двумя последовательными членами. Обычное соотношение между двумя последовательными терминами.
Форма Линейная форма Экспоненциальная форма
Что такое арифметическая последовательность?
Когда вы говорите об арифметической последовательности или арифметической прогрессии, это в основном относится к последовательности различных чисел, в которой разница между двумя последовательными числами всегда постоянна.
В этом типе последовательности разность означает вычитание первого члена из второго члена. Если вы рассматриваете такую последовательность, как 1, 4, 7, 10, 13… это арифметическая последовательность, в которой постоянная разница, если 3.
Как и все остальное в математике, арифметическая последовательность также имеет формулу. Формула, используемая для нахождения арифметической последовательности: a, a+d, a+2d, a+3d и так далее. В этой формуле «а» — это первый член, а «d» — общая разница между двумя последовательными терминами.
Вам важно знать, что поведение арифметической последовательности во многом зависит от общего различия. Если общая разность или «d» в формуле положительна, то члены будут расти в положительную сторону.
Однако, если общая разность отрицательна, члены будут расти в отрицательном направлении.
Что такое геометрическая последовательность?
Геометрическая последовательность или геометрическая прогрессия в математике представляет собой последовательность различных чисел, в которой каждый новый член после предыдущего вычисляется простым умножением предыдущего члена на обыкновенное отношение. Это обыкновенное отношение является фиксированным и ненулевым числом.
Например, последовательность 3, 6, 12, 24 и т. д. представляет собой геометрическую последовательность с знаменателем, равным 2,9.0003
Геометрическая последовательность также имеет собственную формулу. Нормальная форма геометрической последовательности имеет вид a, ar, ar², ar³, ar ⁴ и так далее.
Когда вам нужно найти n-й член в любой геометрической прогрессии, используйте следующую формулу: быть данным. Есть определенные факторы, которые вы должны помнить, когда речь заходит о геометрической последовательности.
Если обыкновенное отношение положительное, члены также будут положительными.
Однако, если обыкновенное отношение отрицательное, члены будут чередоваться между отрицательными и положительными. Если обыкновенное отношение больше 1, рост будет иметь экспоненциальную форму в сторону положительной или даже отрицательной бесконечности.
Если обыкновенное отношение равно 1, то прогрессия будет постоянной последовательностью.
Основные различия между арифметической и геометрической последовательностями
Арифметическая последовательность — это последовательность чисел, которая вычисляется путем вычитания или прибавления фиксированного члена к предыдущему члену. Однако геометрическая последовательность — это последовательность чисел, в которой каждое новое число вычисляется путем умножения предыдущего числа на фиксированное и ненулевое число.
Разность между двумя последовательными членами арифметической последовательности известна как общая разность, которая обозначается буквой «d», а число, на которое члены геометрической последовательности кратны или делятся, называется обыкновенным отношением, обозначаемым буквой «r». .
Когда дело доходит до арифметической последовательности, изменение имеет линейную форму. С другой стороны, когда дело доходит до геометрической последовательности, изменение имеет экспоненциальную форму.
В арифметической последовательности числа могут прогрессировать как положительно, так и отрицательно, в зависимости от общей разницы. Принимая во внимание, что в геометрической последовательности такого правила нет, поскольку числа могут чередоваться в положительном и отрицательном порядке в одной и той же последовательности.
Часто задаваемые вопросы об арифметических и геометрических последовательностях
Почему это называется геометрической последовательностью?
Это называется геометрической последовательностью, потому что числа переходят от одного числа к другому путем погружения или умножения на аналогичное значение.
Число, которое делят или умножают на каждом этапе ряда, называемого обыкновенным отношением. Геометрический ряд — это набор фигур, которые следуют уникальному правилу узора.
Может ли арифметическая последовательность быть геометрической?
В математике арифметический ряд определяется как последовательность, в которой дисперсия между последовательными числами, называемая общей разностью, постоянна.
С другой стороны, в геометрическом ряду отношение между последовательными числами, известное как обыкновенное отношение, является постоянным. Итак, это означает, что последовательность не может быть одновременно геометрической и арифметической.
Что такое формула бесконечного геометрического ряда?
Бесконечная геометрическая последовательность определяется как совокупность бесконечной геометрической последовательности. Последовательность не имеет последней цифры. Этот тип бесконечной последовательности включает a1+a1r+a1r2 +a1r3+…. В этом случае a1 относится к первой цифре, а r относится к обыкновенному отношению.
Вы вычислите общую сумму конечной геометрической последовательности. В случае бесконечной геометрической последовательности, как только знаменатель будет больше единицы, члены ряда будут увеличиваться, а при сложении больших чисел получить окончательный ответ будет невозможно. Единственным ответом будет бесконечность.
Предположим, что r (обыкновенное отношение) находится между -1 и 1/. Вы можете получить сумму бесконечной геометрической прогрессии. То есть сумма существует при r < 1.
Сумма бесконечного геометрического ряда, имеющего -1 S=a1/1-r
Что такое А в арифметической прогрессии?
Арифметическая последовательность относится к ряду терминов, так что разница между двумя последовательными участниками ряда является постоянным термином, при этом a в арифметической последовательности является первым термином.
Как найти n-й член арифметической прогрессии?
Члены арифметического ряда, как известно, увеличиваются на общую разность (d). Например, 2, 4, 6, 8, 10 — это арифметическая прогрессия, а d = 2.
Формула для получения n-го члена этой арифметической прогрессии: 2n+1. Как правило, n-й член арифметической последовательности с 1-м членом и общей разностью равен a+ (n-1) d.
Заключение
С помощью этого подробного обсуждения различий между арифметической последовательностью и геометрической последовательностью вы уже должны понять это. Если вы думаете, что эти 2 последовательности не имеют никакого практического применения, вам следует подумать еще раз.
Оба имеют свое индивидуальное использование и значение в разных повседневных жизнях.
Арифметические последовательности используются в различных финансовых секторах и могут оказаться весьма полезными, когда речь идет о подсчете ваших сбережений и личных финансовых приращений. Тем не менее, геометрическая последовательность также имеет свою долю использования.
Используется для расчета процентных ставок, предоставляемых различными финансовыми учреждениями, а также для расчета прироста населения страны.
Часто можно заметить, что учащиеся путаются, когда дело доходит до решения, является ли данная последовательность арифметической или геометрической последовательностью. Хотя вычисление арифметической последовательности довольно просто, основная проблема заключается в вычислении геометрической прогрессии.
Ключевые различия между арифметической и геометрической последовательностями
(в формате PDF)
Загрузите основные различия в формате .
No related posts.