| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |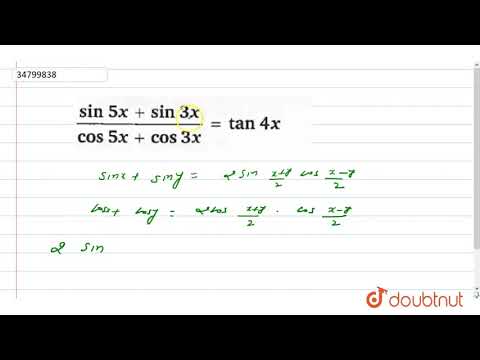
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |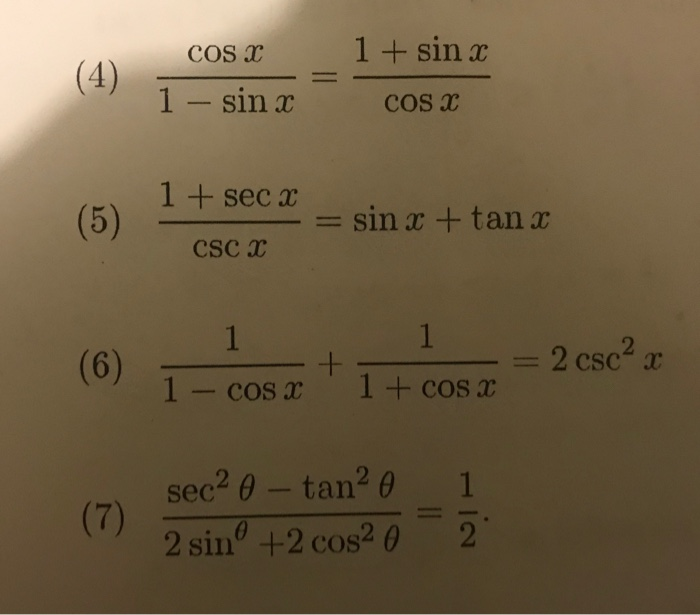
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | arcsin(-1/2) | ||
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |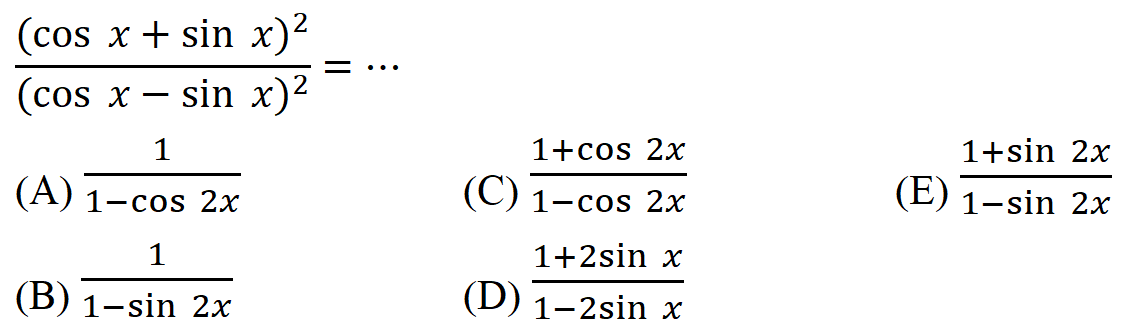
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | ||
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |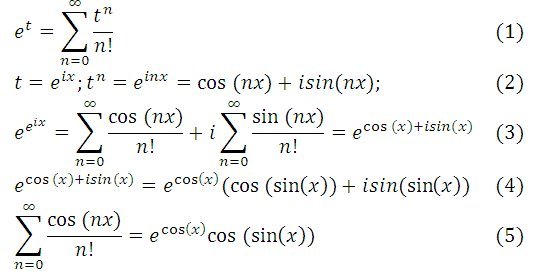
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Как разложить cos на sin
Обновлено: 05.10.2022
после чего формула (13) дает
В остаточном члене множитель как мы видели выше, стремится к нулю при , а абсолютное значение синуса не превышает единицы, и, следовательно, остаточный член стремится к нулю при всех конечных значениях т.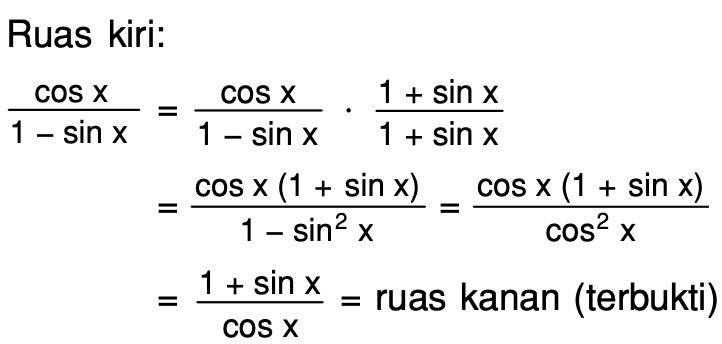
е. разложение
имеет место при всех значениях
Аналогичным образом мы можем доказать, что разложение
имеет место при всех значениях
Ряды (19) и (20) весьма удобны для вычисления значений функций при малых значениях угла При всех значениях как положительных, так и отрицательных, они знакопеременные, так что если мы взяли такое число членов, что дальнейшие идут убывая, то ошибка по абсолютному значению не превосходит первого из отброшенных членов [123].
При больших значениях ряды (19) и (20) также сходятся, но медленно, и для вычисления неудобны. На рис. 156 показано взаимное расположение точной кривой и первых трех приближений:
Чем больше членов взято в приближенной формуле, тем в большем промежутке приближенная кривая близка к точной. Заметим, что во всех написанных формулах угол выражается в дуговой мере, т. е. в радианах 133].
Пример. Вычислить sin 10° с точностью до . Прежде всего переводим градусную меру в дуговую
Остановившись на приближенной формуле
мы делаем ошибку, не превосходящую
В правой части предыдущей формулы надлежит вычислять каждое слагаемое с шестью знаками, так как тогда полная ошибка будет не больше
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
- Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
- В результате деления получаем формулу tg 2 α + 1 =
1 + ctg 2 α = .- Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 = применимо для любого угла α, не равного + π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg 2 α = применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Тангенс и котангенс через синус и косинус
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества
задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества
верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Разложение на множители тригонометрических уравнений (страница 2)
\(\blacktriangleright\) Напомним стандартные тригонометрические уравнения:
\[\begin \hline \text & \text & \text\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin \begin &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end \end \right. \ \ , \ n\in \mathbb\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\, x=a & a\in \mathbb & x=\mathrm\, a+\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\,x=a & a\in \mathbb & x=\mathrm\, a+\pi n, \ n\in \mathbb\\&&\\ \hline \end\] Иногда для более короткой записи ответ для \(\sin x=a\) записывают как
\(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb\) .
\(\blacktriangleright\) Разложить на множители выражение — это значит представить его в виде произведения нескольких множителей.
Основная формула \[a\cdot b+a\cdot c=a\cdot (b+c)\]
\(\blacktriangleright\) Произведение нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а остальные при этом не теряют смысла!: \[f(x)\cdot g(x)=0 \ \Longleftrightarrow \ \begin \left[ \begin \begin &f(x)=0\\ &g(x)=0\\ \end \end \right.\\\text \end\]
\(\blacktriangleright\) Частное двух выражений равно нулю тогда и только тогда, когда числитель равен нулю, а знаменатель не равен нулю. \[\dfrac=0 \ \Longleftrightarrow \ \begin f(x)=0\\ g(x)\ne 0 \end\]
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число.
В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Взаимно обратные числа — это два числа, произведение которых равно 1.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
-
Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Задачка 2.
Найдите значение cos α,
если:
-
Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Разложение на множители тригонометрических уравнений
\(\blacktriangleright\) Напомним стандартные тригонометрические уравнения:
\[\begin \hline \text & \text & \text\\ \hline &&\\ \sin x=a & -1\leq a\leq 1 & \left[ \begin \begin &x=\arcsin a+2\pi n\\ &x=\pi -\arcsin a+2\pi n \end \end \right. \ \ , \ n\in \mathbb\\&&\\ \hline &&\\ \cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\, x=a & a\in \mathbb & x=\mathrm\, a+\pi n, \ n\in \mathbb\\&&\\ \hline &&\\ \mathrm\,x=a & a\in \mathbb & x=\mathrm\, a+\pi n, \ n\in \mathbb\\&&\\ \hline \end\] Иногда для более короткой записи ответ для \(\sin x=a\) записывают как
\(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb\) .
\(\blacktriangleright\) Разложить на множители выражение — это значит представить его в виде произведения нескольких множителей.
Основная формула \[a\cdot b+a\cdot c=a\cdot (b+c)\]
\(\blacktriangleright\) Произведение нескольких множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю, а остальные при этом не теряют смысла!: \[f(x)\cdot g(x)=0 \ \Longleftrightarrow \ \begin \left[ \begin \begin &f(x)=0\\ &g(x)=0\\ \end \end \right.\\\text \end\]
\(\blacktriangleright\) Частное двух выражений равно нулю тогда и только тогда, когда числитель равен нулю, а знаменатель не равен нулю. \[\dfrac=0 \ \Longleftrightarrow \ \begin f(x)=0\\ g(x)\ne 0 \end\]
Основное тригонометрическое тождество
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Читайте также:
- Osu градусы кто ты
- Что такое maybelline new york
- Как сделать палку в майнкрафте
- Как получать знания в black desert
- Как создать квами в реальной жизни
5.
3. Разложение в ряд Маклорена функций sin X, cos XСначала разложим функцию sin x в ряд Маклорена. Для этого в основу кладется формула Маклорена, которую удобно записать в более подробной форме
(7.82)
Положим здесь f(x) = sin x. Последовательное дифференцирование дает
Отсюда находим
Подставляя эти значения в (7.82), получим
. (7.83)
Остаточный
член при n стремится к пределу 0. Действительно,
последовательность является подпоследовательностью
последовательности ,
которая при n (см. предельное равенство (7.76)) стремится
к пределу 0, следовательно, имеем, а так как величина ограниченная, то .
Тот факт, что для функции sin x в формуле Тейлора (7.83) , согласно теореме 1, §5, п.5.1 означает, что функция sin x в точке х = 0 аналитическая и для нее справедливо разложение
. (7.84)
Аналогичными рассуждениями доказываем, что
. (7.85)
Почленное дифференцирование разложений (7.84) и (7.85) дает
, .
Следовательно, этим подтверждается, что при дифференцировании разложений (7.84) и (7.85) равенство сохраняется.
5.4. Разложение в ряд Маклорена функции ln(1+x)
Исходим из того, что в интервале (–1,1) справедливо разложение
. (7.86)
Степенной
ряд в правой части есть сходящаяся
геометрическая прогрессия, знаменатель
которой равен –x,
а интервалом сходимости его служит
(–1,1). Далее считаем и рассмотрим сегмент [0,x]
(или [x,0],
если x < 0).
Этот сегмент целиком лежит в интервале
сходимости степенного ряда, а тогда,
равенство (7.86) можно интегрировать
почленно. В результате получаем
.
Выполняя несложные интегрирования, получим после упрощений
. (7.87)
Справедливость этого разложения установлена для , а поскольку, при почленном интегрировании сходящегося ряда, его радиус сходимости не изменяется (§4, п.4.3), поэтому ряд в правой части равенства (7.87) имеет тот же радиус сходимости, что и исходный степенной ряд в правой части равенства (7.86), т.е. R = 1. Это означает, что степенной ряд в правой части равенства (7.87) вне сегмента [–1,1] расходится, а потому остается исследовать разложение (7.87) в точках x = ±1. Ряд, полученный в правой части равенства (7.87) после подстановки в него x = –1 является расходящимся гармоническим рядом все члены, которого умножены на –1
.
Поэтому
в точке x=
–1
равенство (7.
87) не выполнено.
В точке x = +1 в правой части разложения (7.87) получается полугармонический ряд который, по признаку Лейбница, сходится. Докажем, что его суммой является ln2, и, следовательно, равенство (7.87) соблюдается в точке x = +1.
Из двух тождеств
и
выводим новое тождество .
Деля обе части на 1+x, получаем
. (7.88)
Интегрирование этой конечной суммы в сегменте [0,1] дает
. (7.89)
Оценим остаточный член
Сначала имеем
. (7.90)
Уменьшим знаменатель подинтегральной функции (7.90), заменяя 1+ x через x. Это приведет к увеличению правой части (7.90) и тогда получим неравенство
.
Итак, и отсюда заключаем, что
. (7.91)
Это
означает, что функция в точке х =
+1 аналитическая и равенство (7.89) может
быть заменено на равенство (7.
87) если в
нем положить х =
+1
. (7.92)
Теперь окончательно приходим к выводу, что разложение (7.87)
справедливо в полусегменте .
Дальше рассмотрим практическое использование разложения (7.87) для вычисления логарифмов натуральных чисел.
Для функции ln(1 – x) разложение в ряд Маклорена получается из (7.87) заменой x через –x
(7.93)
справедливо при .
Вычитая из (7.87) равенство (7.93), получим
(7.94)
причем ряд в правой части сходится в интервале (–1,+1).
Пусть m – натуральное число m = 1, 2,… и положим
. (7.95)
При указанных значениях для m справедливо неравенство
и потому, при таком значении x разложение (7.94) остается справедливым.
Подставляя (7.95) в (7.94), получим после упрощений
(7.96)
Равенство
(7.
96) ввиду быстрой сходимости ряда в
правой части этого равенства является
наиболее удобным для приближенного
вычиления логарифмов натуральных чисел.
Рассмотрим некоторые примеры такого
вычисления.
Полагая в (7.96) m = 1, получим
. (7.97)
Для приближенного вычисления ln2 ограничемся первыми пятью членами данного разложения = 0,69314.
Ошибка ρ такого приближенного вычисления равна
.
Ряд в скобках есть сходящаяся геометрическая прогрессия со знаменателем и его сумма равна и потому . Отсюда можно заключить об эффективности использования разложения (7.97) для вычисления ln2, которое уже для пяти членов разложения дает ошибку меньше 10−5.
Если в (7.96) положить m = 4, то получаем .
Отсюда найдем ln5 = 1,60944….
Зная
ln2
и ln5
можем найти ln10 = ln2+ln5 = 2,30258.
..,
а также модуль перехода от натуральных логарифмов
к десятичным
Полагая в (7.96) m = 80 = 24·5, тогда
.
Отсюда находим ln3=1,0986 и .
2-1}\sin(2nx), \quad \forall \ n\in\mathbb{N}\tag{4}$$Осталось 2 вопроса:
- Я использовал wolfram alpha для вычисления интеграла в $( 3)$. Какие методы я использую для этого? Повторное интегрирование по частям и решение интеграла?
- Как рассчитать нужную сумму?
- анализ Фурье
- ряд Фурье
$\endgroup$
2
$\begingroup$
Как сообщил OP, осталось два шага: 92}{64} $$
$\endgroup$
7
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найдите точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек (30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар(45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | грех((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценка | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-(квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт. )/4 | |
| 79 | Найти точное значение | грех((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | грех((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан( квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | грех((2pi)/3) | |
| 88 | Найти точное значение | желтовато-коричневый ((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найдите точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | грех((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Получить разложение в ряд Тейлора для log left cos x class 11 maths CBSE
Ответ
Проверено
158,4 тыс.
+ просмотров
Подсказка: \right)$ относительно точки $x=a$. Затем найдем производную данной функции. Поскольку в разложении Тейлора есть члены с производными более высокого порядка, мы вычислим их для данной функции. Затем мы подставим значение $x=\dfrac{\pi }{3}$ в полученные производные. Полученные результаты запишем в разложение в ряд Тейлора. 9{3}}+\cdots $
Данной функцией является $f\left( x \right)=\log \left( \cos x \right)$. Нам нужно найти разложение данной функции в ряд Тейлора до члена четвертой степени. Итак, мы вычислим до четвертой производной заданной функции.
Значение функции в точке $x=\dfrac{\pi }{3}$ равно $f\left( \dfrac{\pi }{3} \right)=\log \left( \cos \dfrac{\ pi }{3} \right)=\log \left( \dfrac{1}{2} \right)$.
Первая производная от $f\left( x \right)$ равна ${f}’\left( x \right)=\dfrac{1}{\cos x}\times -\sin x$. Значение первой производной в точке $x=\dfrac{\pi }{3}$ равно ${f}’\left( \dfrac{\pi }{3} \right)=\dfrac{1}{\cos \dfrac{\pi} {3}}\times -\sin \dfrac{\pi}}{3}=\dfrac{1}{\left(\dfrac{1}{2} \right)}\times -\ dfrac{\sqrt{3}}{2}=-\sqrt{3}$.
9{4}}$
Приведенное выше уравнение представляет собой разложение в ряд Тейлора до члена четвертой степени функции $f\left( x \right)=\log \left( \cos x \right)$.
Примечание: В этом типе вопросов необходимо, чтобы мы были знакомы с производными стандартных функций. Также важно, чтобы мы знали значения тригонометрических функций для стандартных углов. Это немного облегчит расчеты. Полезно вычислять каждую производную отдельно, чтобы избежать ошибок в вычислениях.
Недавно обновленные страницы
Рассчитайте изменение энтропии, связанное с преобразованием класса 11 химии JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики класса 11 химии JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении класса A 11 химия JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химия JEE_Main
Для реакции rm2Clg в rmCrmlrm2rmg признаки 11 класса химии JEE_Main
Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main
Рассчитайте изменение энтропии при переходе в химический класс 11 JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики.